Frozen Coherence in an Emergent Universe with Anisotropy
Abstract
1. Introduction
2. Quantum Fields in an Anisotropic Universe
3. The Scale Factor
4. Particle Creation Entropy
5. Alice and Bob in an Expanding Spacetime
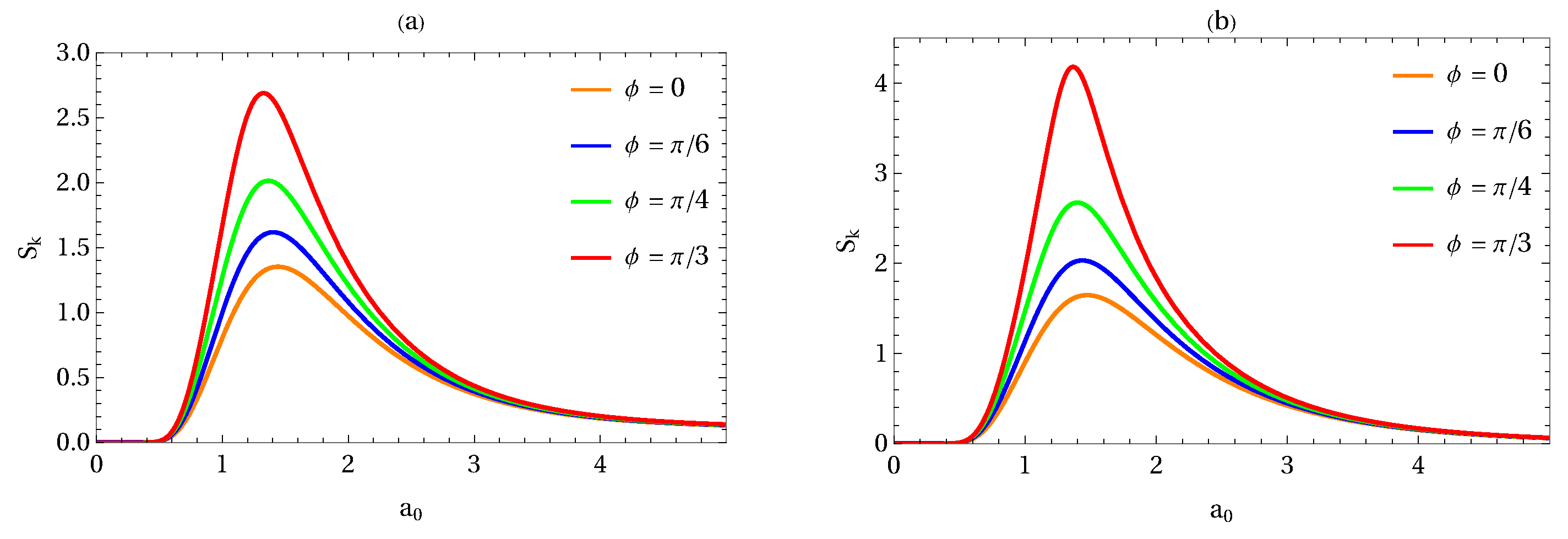
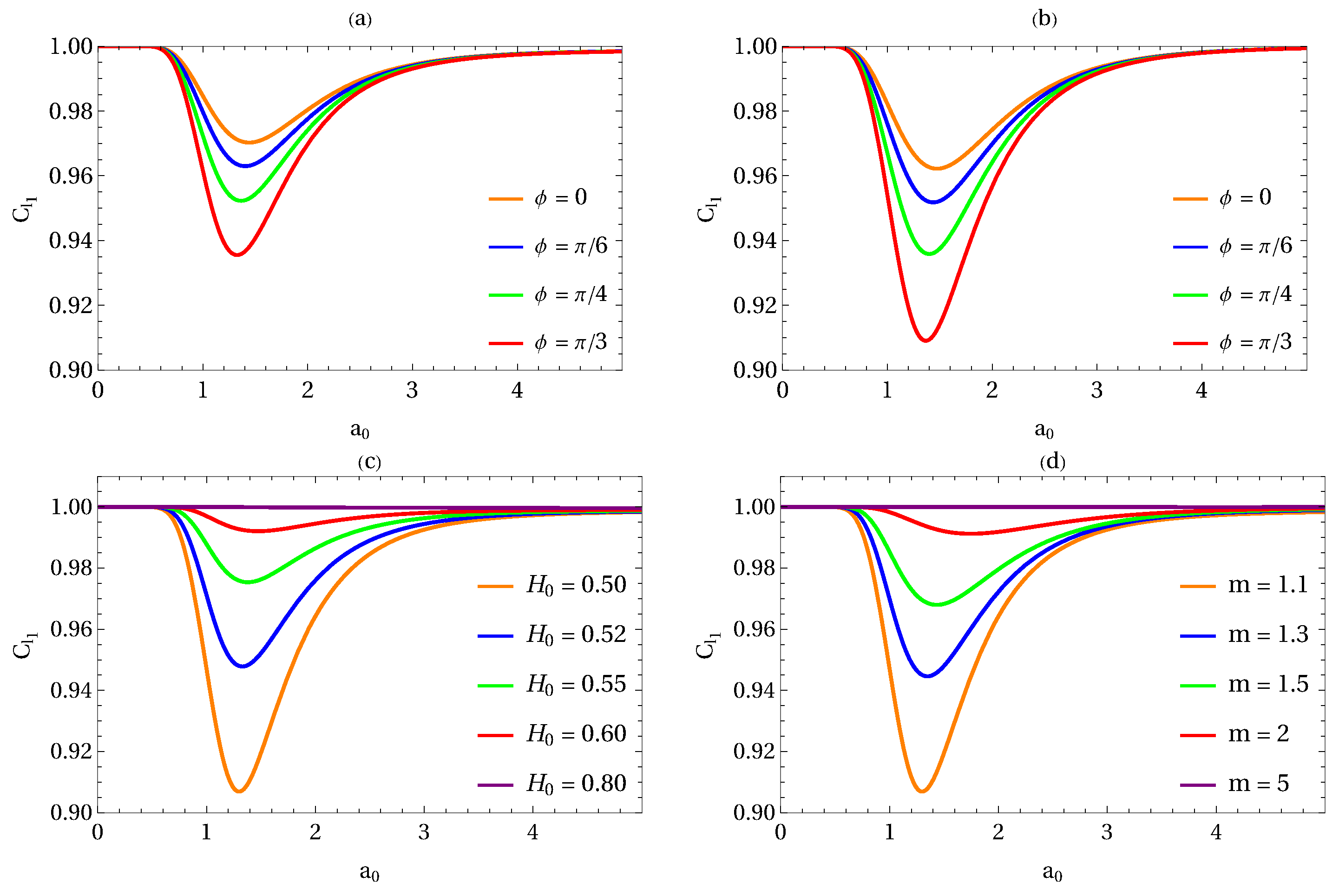
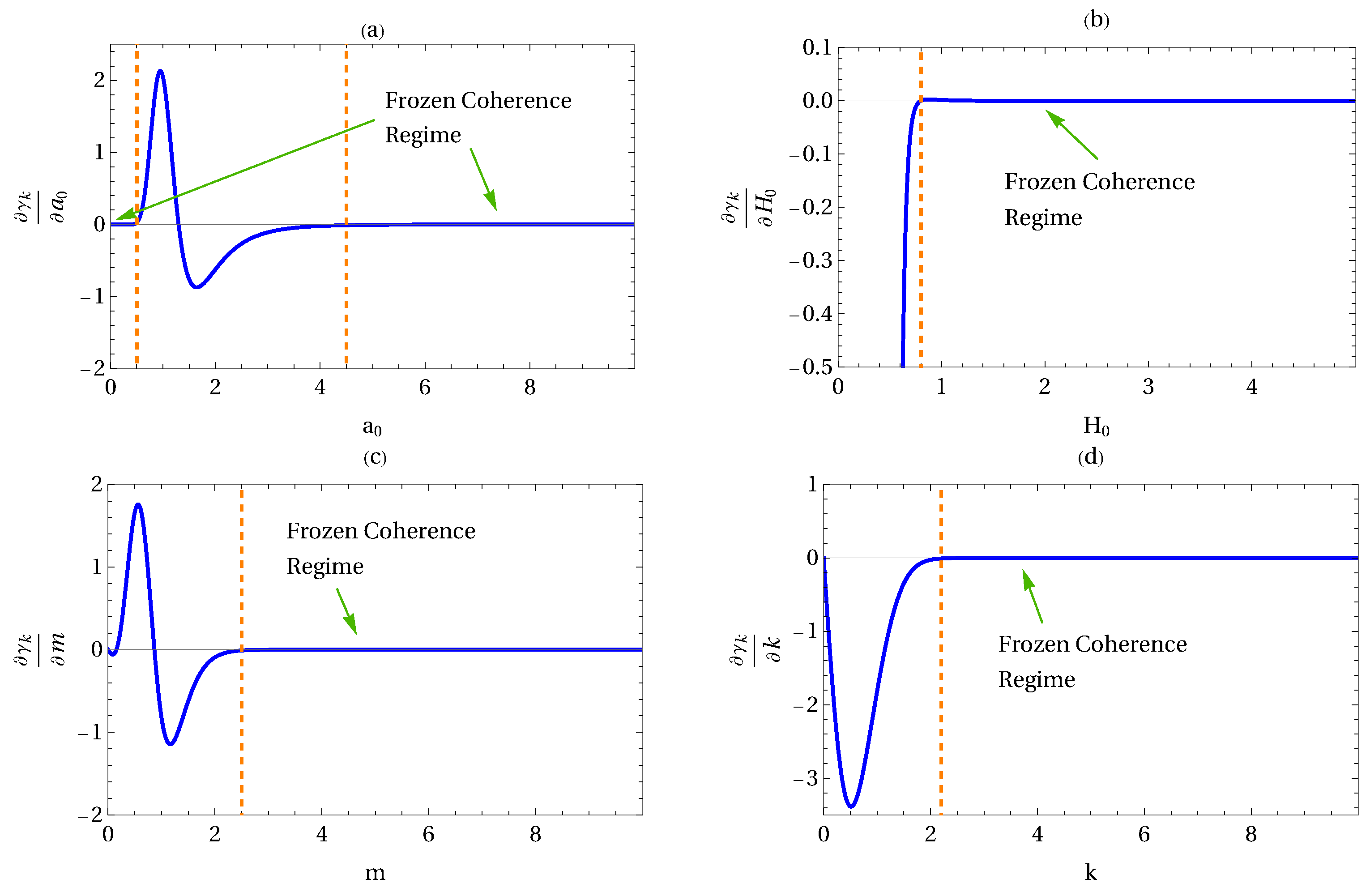
6. Numerical Results
7. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information, 10th ed.; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Streltsov, A.; Adesso, G.; Plenio, M.B. Quantum coherence as a resource. Rev. Mod. Phys. 2017, 89, 041003. [Google Scholar] [CrossRef]
- Hillery, M. Coherence as a resource in decision problems: The Deutsch-Jozsa algorithm and a variation. Phys. Rev. A 2016, 93, 012111. [Google Scholar] [CrossRef]
- Pan, M.; Qiu, D. Operator coherence dynamics in Grover’s quantum search algorithm. Phys. Rev. A 2019, 100, 012349. [Google Scholar] [CrossRef]
- Ahnefeld, F.; Theurer, T.; Egloff, D.; Matera, J.M.; Plenio, M.B. Coherence as a Resource for Shor’s Algorithm. Phys. Rev. Lett. 2022, 129, 120501. [Google Scholar] [CrossRef]
- Karimi, M.; Javadi-Abhari, A.; Simon, C.; Ghobadi, R. The power of one clean qubit in supervised machine learning. Sci. Rep. 2023, 13, 19975. [Google Scholar] [CrossRef]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Quantum-Enhanced Measurements: Beating the Standard Quantum Limit. Science 2004, 306, 1330–1336. [Google Scholar] [CrossRef]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Advances in quantum metrology. Nat. Photonics 2011, 5, 222–229. [Google Scholar] [CrossRef]
- Demkowicz-Dobrzański, R.; Maccone, L. Using Entanglement Against Noise in Quantum Metrology. Phys. Rev. Lett. 2014, 113, 250801. [Google Scholar] [CrossRef]
- Aberg, J. Catalytic Coherence. Phys. Rev. Lett. 2014, 113, 150402. [Google Scholar] [CrossRef]
- Narasimhachar, V.; Gour, G. Low-temperature thermodynamics with quantum coherence. Nat. Commun. 2015, 6, 7689. [Google Scholar] [CrossRef]
- Ćwikliński, P.; Studziński, M.; Horodecki, M.; Oppenheim, J. Limitations on the Evolution of Quantum Coherences: Towards Fully Quantum Second Laws of Thermodynamics. Phys. Rev. Lett. 2015, 115, 210403. [Google Scholar] [CrossRef]
- Lostaglio, M.; Jennings, D.; Rudolph, T. Description of quantum coherence in thermodynamic processes requires constraints beyond free energy. Nat. Commun. 2015, 6, 6383. [Google Scholar] [CrossRef]
- Plenio, M.B.; Huelga, S.F. Dephasing-assisted transport: Quantum networks and biomolecules. New J. Phys. 2008, 10, 113019. [Google Scholar] [CrossRef]
- Huelga, S.F.; Plenio, M.B. Vibrations, quanta and biology. Contemp. Phys. 2013, 54, 181–207. [Google Scholar] [CrossRef]
- Li, C.-M.; Lambert, N.; Chen, Y.-N.; Chen, G.-Y.; Nori, F. Witnessing Quantum Coherence: From solid-state to biological systems. Sci. Rep. 2012, 2, 885. [Google Scholar] [CrossRef]
- Levi, F.; Mintert, F. A quantitative theory of coherent delocalization. New J. Phys. 2014, 16, 033007. [Google Scholar] [CrossRef]
- Karpat, G.; Cakmak, B.; Fanchini, F.F. Quantum coherence and uncertainty in the anisotropic XY chain. Phys. Rev. B 2014, 90, 104431. [Google Scholar] [CrossRef]
- Girolami, D. Observable Measure of Quantum Coherence in Finite Dimensional Systems. Phys. Rev. Lett. 2014, 113, 170401. [Google Scholar] [CrossRef]
- Cakmak, B.; Karpat, G.; Fanchini, F. Factorization and Criticality in the Anisotropic XY Chain via Correlations. Entropy 2015, 17, 790–817. [Google Scholar] [CrossRef]
- Malvezzi, A.L.; Karpat, G.; Cakmak, B.; Fanchini, F.F.; Debarba, T.; Vianna, R.O. Quantum correlations and coherence in spin-1 Heisenberg chains. Phys. Rev. B 2016, 93, 184428. [Google Scholar] [CrossRef]
- Chen, J.J.; Cui, J.; Zhang, Y.R.; Fan, H. Coherence susceptibility as a probe of quantum phase transitions. Phys. Rev. A 2016, 94, 022112. [Google Scholar] [CrossRef]
- Li, Y.; Lin, H. Quantum coherence and quantum phase transitions. Sci. Rep. 2016, 6, 26365. [Google Scholar] [CrossRef]
- Baumgratz, T.; Cramer, M.; Plenio, M. Quantifying coherence. Phys. Rev. Lett. 2014, 113, 140401. [Google Scholar] [CrossRef]
- Shao, L.-H.; Xi, Z.; Fan, H.; Li, Y. Fidelity and trace-norm distances for quantifying coherence. Phys. Rev. A 2015, 91, 042120. [Google Scholar] [CrossRef]
- Rastegin, A.E. Quantum-coherence quantifiers based on the Tsallis relative α entropies. Phys. Rev. A 2016, 93, 032136. [Google Scholar] [CrossRef]
- Chitambar, E.; Gour, G. Comparison of incoherent operations and measures of coherence. Phys. Rev. A 2016, 94, 052336. [Google Scholar] [CrossRef]
- Wang, S.-C.; Yu, Z.-W.; Zhou, W.-J.; Wang, X.-B. Protecting quantum states from decoherence of finite temperature using weak measurement. Phys. Rev. A 2014, 89, 022318. [Google Scholar] [CrossRef]
- Wang, Y.-K.; Fei, S.-M.; Wang, Z.-X. Dynamics of quantum coherence in Bell-diagonal states under Markovian channels. Commun. Theor. Phys. 2019, 71, 555. [Google Scholar] [CrossRef]
- Bromley, T.R.; Cianciaruso, M.; Adesso, G. Frozen Quantum Coherence. Phys. Rev. Lett. 2015, 114, 210401. [Google Scholar] [CrossRef]
- Yu, X.-D.; Zhang, D.-J.; Liu, C.L.; Tong, D.M. Measure-independent freezing of quantum coherence. Phys. Rev. A 2016, 93, 060303. [Google Scholar] [CrossRef]
- Silva, I.A.; Souza, A.M.; Bromley, T.R.; Cianciaruso, M.; Marx, R.; Sarthour, R.S.; Oliveira, I.S.; Franco, R.L.; Glaser, S.J.; deAzevedo, E.R.; et al. Observation of Time-Invariant Coherence in a Nuclear Magnetic Resonance Quantum Simulator. Phys. Rev. Lett. 2016, 117, 160402. [Google Scholar] [CrossRef]
- Yu, S.; Wang, Y.-T.; Ke, Z.-J.; Liu, W.; Zhang, W.-H.; Chen, G.; Tang, J.-S.; Li, C.-F.; Guo, G.-C. Experimental realization of self-guided quantum coherence freezing. Phys. Rev. A 2017, 96, 062324. [Google Scholar] [CrossRef]
- Shi, J.; Chen, J.; He, J.; Wu, T.; Ye, L. Inevitable degradation and inconsistency of quantum coherence in a curved space-time. Quantum Inf. Process. 2019, 18, 300. [Google Scholar] [CrossRef]
- Huang, Z.; Situ, H. Quantum coherence behaviors of fermionic system in non-inertial frame. Quantum Inf. Process. 2018, 17, 95. [Google Scholar] [CrossRef]
- Huang, Z. Dynamics of quantum correlation and coherence in de Sitter universe. Quantum Inf. Process. 2017, 16, 207. [Google Scholar] [CrossRef]
- Wu, S.-M.; Wang, C.-X.; Wang, R.-D.; Li, J.-X.; Huang, X.-L.; Zeng, H.-S. Curvature-enhanced multipartite coherence in the multiverse. Chin. Phys. C 2024, 48, 075107. [Google Scholar] [CrossRef]
- Du, M.-M.; Li, H.-W.; Tao, Z.; Shen, S.-T.; Yan, X.-J.; Li, X.-Y.; Zhong, W.; Sheng, Y.-B. Basis-independent quantum coherence and its distribution under relativistic motion. Eur. Phys. J. C 2024, 84, 838. [Google Scholar] [CrossRef]
- Wu, S.-M.; Wang, C.-X.; Liu, D.-D.; Huang, X.-L. Would quantum coherence be increased by curvature effect in de Sitter space? J. High Energy Phys. 2023, 2023, 115. [Google Scholar] [CrossRef]
- Wu, S.-M.; Zeng, H.-S.; Liu, T. Quantum correlation between a qubit and a relativistic boson in an expanding spacetime. Class. Quantum Gravity 2022, 39, 135016. [Google Scholar] [CrossRef]
- Parker, L. Quantized fields and particle creation in expanding universes. Part 1. Phys. Rev. 1969, 183, 1057. [Google Scholar] [CrossRef]
- Parker, L. Quantized fields and particle creation in expanding universes. Part 2. Phys. Rev. D 1971, 3, 346. [Google Scholar] [CrossRef]
- Birrell, N.D.; Davies, P.C.W. Quantum Fields in Curved Space; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Ford, L.H. Cosmological particle production: A review. Rep. Prog. Phys. 2021, 84, 116901. [Google Scholar] [CrossRef]
- Zeldovich, Y.A. Particle Creation and Vacuum Polarization in Anisotropic Gravitational Field. Zh. Exp. Theor. Fiz. 1971, 61, 2161–2175. [Google Scholar]
- Birrell, N.D. Momentum space techniques for curved space–time quantum field theory. Proc. R. Soc. Lond. A 1979, 367, 123–141. [Google Scholar]
- Ellis, G.F.R.; Murugan, J.; Tsagas, C.G. The emergent universe: An explicit construction. Class. Quantum Gravity 2003, 21, 233. [Google Scholar] [CrossRef]
- Ellis, G.F.R.; Maartens, R. The emergent universe: Inflationary cosmology with no singularity. Class. Quantum Gravity 2003, 21, 223. [Google Scholar] [CrossRef]
- Bai, Z.; Du, S. Frozen condition of quantum coherence. Phys. Scr. 2024, 99, 105102. [Google Scholar] [CrossRef]

| Parameter | |
|---|---|
| Spacetime | |
| Spacetime | |
| Field | |
| Field |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costa, H.A.S.; Carvalho, P.R.S. Frozen Coherence in an Emergent Universe with Anisotropy. Universe 2025, 11, 185. https://doi.org/10.3390/universe11060185
Costa HAS, Carvalho PRS. Frozen Coherence in an Emergent Universe with Anisotropy. Universe. 2025; 11(6):185. https://doi.org/10.3390/universe11060185
Chicago/Turabian StyleCosta, Helder A. S., and Paulo R. S. Carvalho. 2025. "Frozen Coherence in an Emergent Universe with Anisotropy" Universe 11, no. 6: 185. https://doi.org/10.3390/universe11060185
APA StyleCosta, H. A. S., & Carvalho, P. R. S. (2025). Frozen Coherence in an Emergent Universe with Anisotropy. Universe, 11(6), 185. https://doi.org/10.3390/universe11060185







