Solar Astrometry in Rome at the End of the Maunder Minimum

Abstract

With the great Clementine Gnomon in St. Maria degli Angeli, a 45 m pinhole meridian line, built in 1700–1702 upon the will of Pope Clemens XI, Francesco Bianchini inaugurated the Roman tradition of solar astrometry. We analyze two thousand dedicated observations at the Clementine Gnomon between 2018 and 2025, with solar altitudes from 20° to 71° and in various meteorological conditions, in order to assess the observational uncertainties on the solar diameter and their causes. We compare the meridian diameters measured by Bianchini near the winter solstices of 1701–1702 with the ones measured by Sigismondi in 2018–2025, reporting the observational errorbars per single measure and the systematic diminutions of the observed diameters with respect to the ephemerides, due to the turbulence and image contrast loss. Simulated datasets based on our measured uncertainties show that pinhole meridian lines cannot resolve solar diameter variations smaller than 1″ over 80 years. These limitations prevent tighter constraints on solar evolution across centuries using such instruments.

1. Structure of the Article

The Clementine Gnomon and the historical background of the pinhole meridian lines in the churches used as observatories in 17th and 18th centuries are presented in Section 2. In Section 3, we introduce the study on the solar parameters during the Maunder minimum. In Section 4, we present the observations at the Clementine Gnomon in Rome, used for the modern observations of the Sun (2018–2025). The local turbulent seeing affects the measures of the meridian lengths of the solar image. Geometrical and environmental factors, the meteorology, and the reflecting conditions of the marbles on and out of the meridian line are examined to understand the uncertainties of the observations. The measures of Bianchini in the winter solstices of 1701–1702 are presented in Section 5, and they are compared with the measure of Sigismondi (2018–2025) in Section 6. In Section 7, we approach the problem of the secular variation in the solar diameter and its detectability, through simulations with realistic errorbars obtained from the observations.

Finally, in Section 8, we discuss how our data contribute to unveiling the observational uncertainties in the 17th and 18th century.

2. The Clementine Gnomon and Its Historical Background

The Clementine Gnomon, also called the Meridian Line of St. Maria degli Angeli in Rome, is the instrument that we used to compare XVIII century observations to the present ones. It was built between 1700 and 1702 under the direction of the astronomer Mons. Francesco Bianchini (1662–1729). The Gnomon was financed by the Cardinal Gian-Francesco Albani before becoming Pope on 23 November 1700, with the name of Clemens XI (1700–1721).

This instrument is a gigantic pinhole camera designed to obtain an unprecedented accuracy in the daily meridian positions of the Sun, in order to measure the length of the tropical year, and the secular variations in the obliquity of the ecliptic. A horizontal pinhole of 25 mm diameter illuminates the meridian line nowadays.

Bianchini studied in Bologna and in Padova. He came into contact with the most prominent scholars of his time [1,2]. With the Clementine Gnomon, Bianchini designed the most advanced instrument of his time to assess the bases of the Gregorian Reformation of the Calendar in 1582. Newton invited Bianchini to join the Royal Society of London as a foreign fellow. The Clementine Gnomon remained, after Bianchini, a reference instrument also studied by Celsius in 1734 and Boscovich in 1750 [1].

Bianchini (1703) improved the instrumental performances of the Gnomon, with respect to the Heliometer of Bologna, using better-reflecting marbles, enabling observations of brighter stars from the meridian line, to obtain the sidereal time through their meridian transits, and making a very stable pinhole carved in the Diocletian’s walls, 1400 years old [1]. For each observation, Bianchini [3,4] darkened the Basilica with fabric applied to the windows from outside, and the observations started some hours before the meridian transit, a time necessary for total obscuration of the Basilica.

In 1750, the cotto tiles of the floor of the Basilica were renovated by Luigi Vanvitelli with marbles. The whole meridian line and the starred paths of the stars Sirius and Arcturus and the paths of the Sun on the equinoxes and on 20 August 1702 (visit of Clemens XI) spread on the floor of the Basilica were preserved.

The function of civil time keeping of the Clementine Gnomon ceased in 1846, when the Collegio Romano Observatory took this service: a big ball left falling along a tube, on top of St. Ignatius’ Church, was the visual signal for shooting the cannon on Castel St. Angelo [5,6].

Historical Context: Churches as Observatories

The previous instruments dedicated to measure the Earth’s orbit and obliquity are in the Cathedral of Florence designed by Toscanelli in 1475 (the gnomon of the Cathedral of Santa Maria del Fiore) and in Bologna in the Basilica of St. Petronio. Egnazio Danti made the first version in 1577 [7]; Cassini completely re-traced it in 1655 and restaured it in 1695 [8].

Giovan Domenico Cassini (1625–1712) and his collaborators monitored the solar diameter from 1655. Eustachio Manfredi [9] reported their and his observations, already corrected for the “penumbra” (the pinhole size) and for refraction effects. Tovar et al. [10] analyzed these data, concluding that the data of 1655–1715 in the grand sunspots’ minimum, and the ones of 1716–1736 immediately after, are compatible with the same solar diameter, within 0.6″.

With the meridian line created by De Cesaris in 1782 in the Duomo of Milan, the accuracy of the meridian’s azimuth reached 6″, but the astrometric purposes were no more in the scopes of its construction [11]. The meridian in the Cathedral of Palermo created by Piazzi in 1803 was devoted to the local noon’s determination for the Angelus’ prayer and for public timing, without any more astrometric scopes. The local noon gradually ceased to be relevant for public life, beyond religion, as World time zones and their mean time become in official use after the conference of Washington of 1884.

3. Secular Variations in the Solar Parameters in the Maunder Minimum

Since the antiquity, the Sun was considered as a celestial spherical body of fixed radius and given orbital motion. The variation in the distance with the Earth would change its angular diameter, according to the form and the center of its orbit. Cassini realized the meridian line of Bologna in 1655 to measure the solar angular diameter along the year and the irregularity of the Earth’s orbit.

The number of sunspots was the first solar parameter to be identified as variable, since the first observations of Galileo [12], and H. Schwabe [13] found a 10-year regularity, decades after him this was recognized as a 11-year cycle. E. W. Maunder and his wife [14,15] discovered, in archive data, a long period almost completely without spots, which nowadays is called the Maunder minimum. Finally, other great solar minima [16] were discovered and J. Eddy proposed to dedicate these periods to Oort (period around 1040) and to Spörer (in 15th century) [17].

Carrasco and Vaquero [18] studied the Sun’s rotation during the Maunder minimum from the correspondence of John Flamsteed. The aspect of the sunspots at the beginning of the minimum as observed by Hevelius was analyzed by Carrasco, Vaquero, Gallego et al., [19] as well as the umbra/penumbra ratio during the Maunder minimum (Carrasco, Garcia-Romero, Vaquero et al. [20]) and observations with the naked eye in the same period (Carrasco, Gallego, Arlt et al. [21]).

Several authors (e.g., [22,23]); Penza et al. [24] studied the variations in the solar irradiance correlated with the little ice age, which occurred in 17th and 18th centuries.

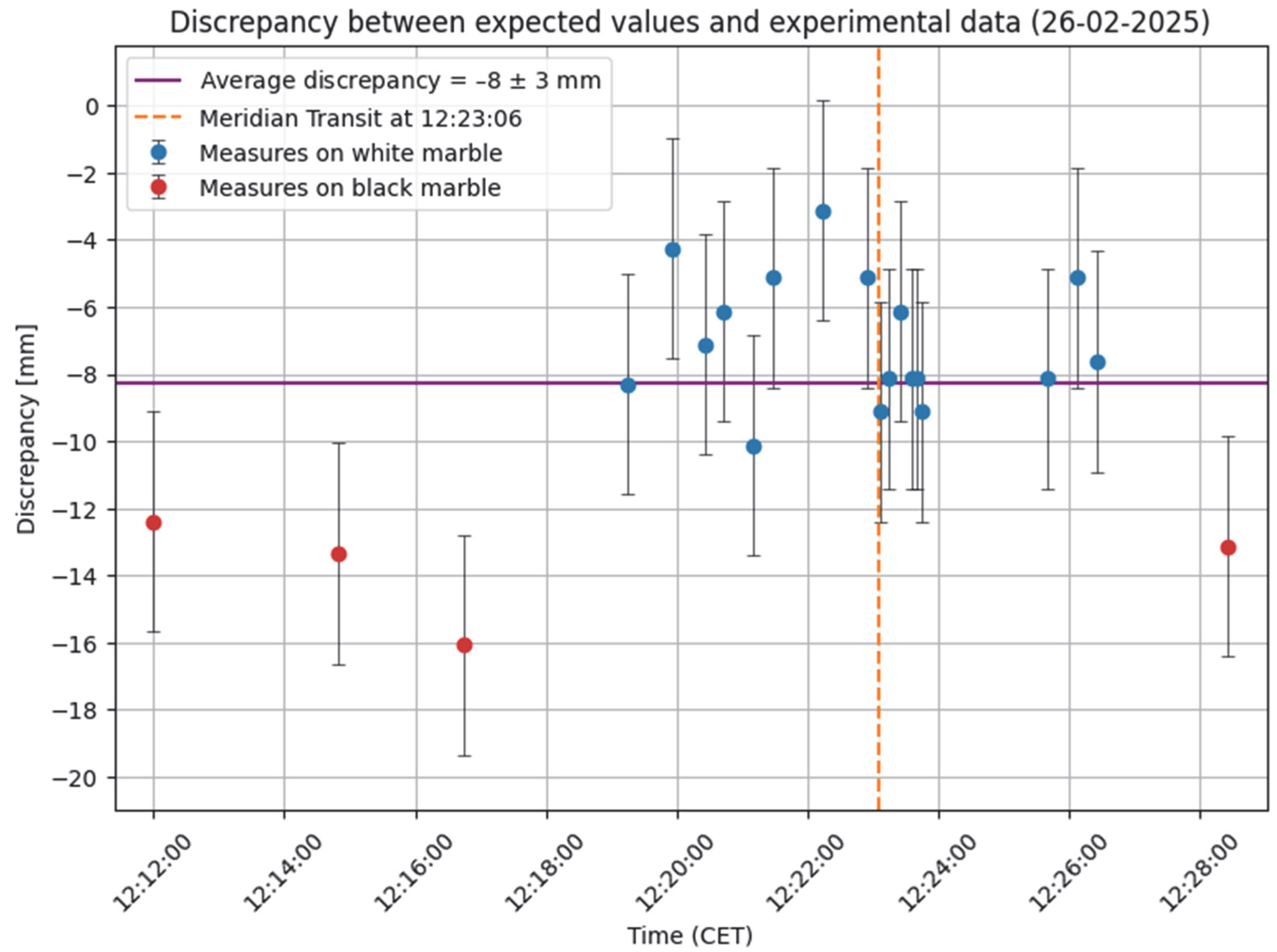
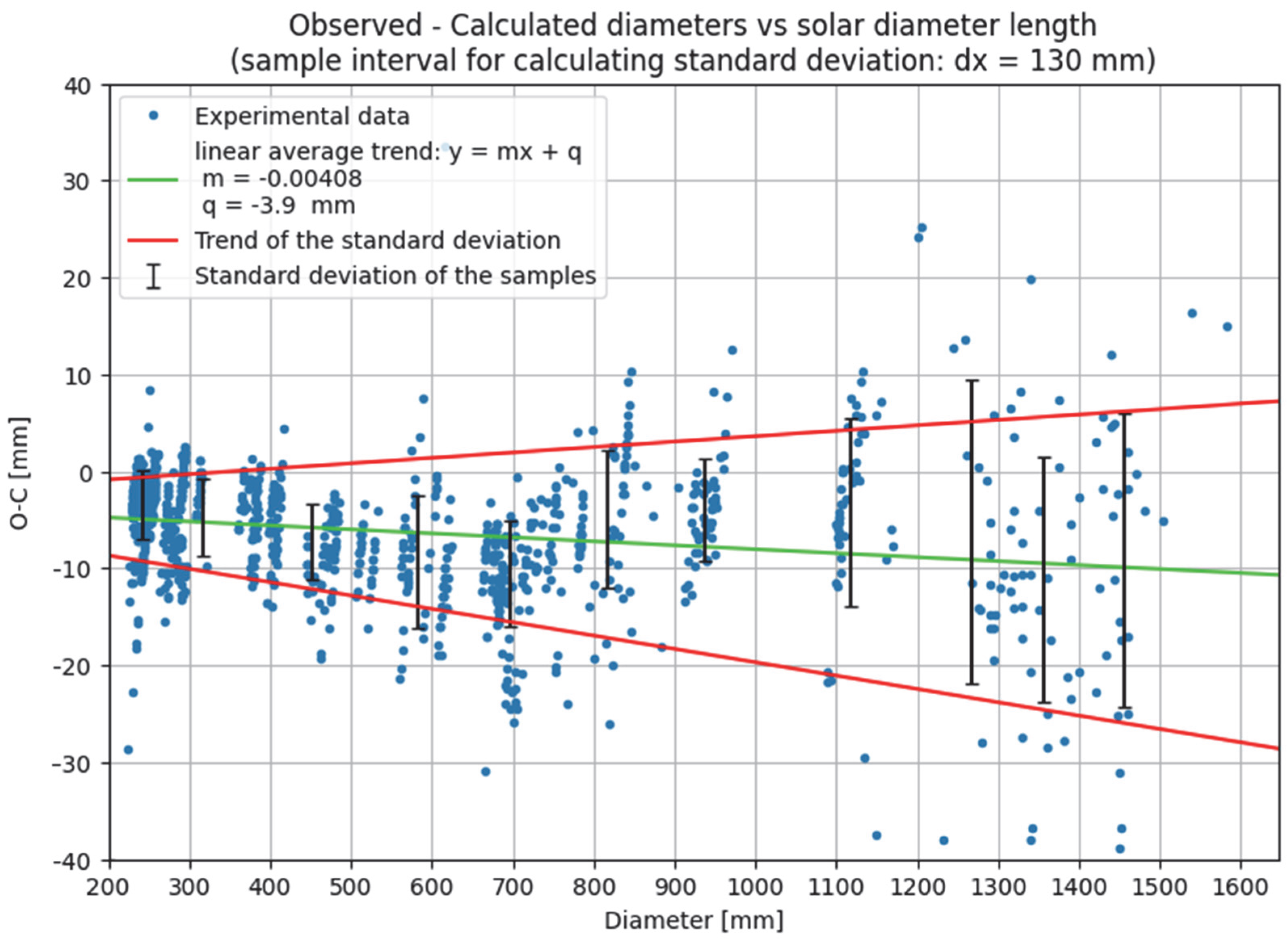
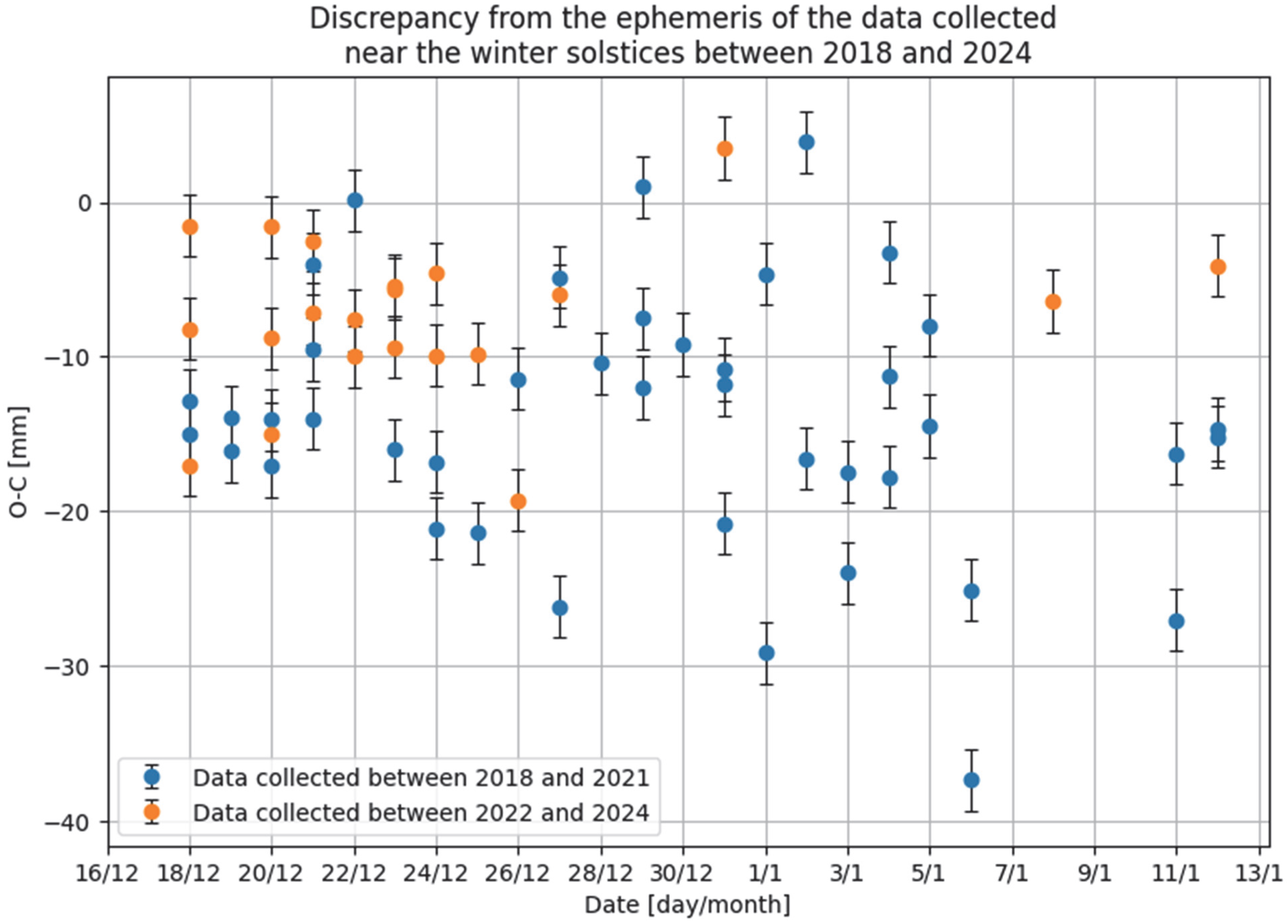
4. Modern Solar Observations at the Clementine Gnomon

Since 1999 C., Sigismondi has measured the positions of the Sun with respect to some fixed points (solstices, equinoxes, and some centesimal parts on the line. The nutation and the obliquity variations are measurable all days of the year (Sullivan, [25]), with a particularly high accuracy around the winter solstice, with a 1.77″/mm scaling at the meridian transit. The pinhole was found not to be calibrated with the rest of the meridian line, because of un-documented changes in its shape and position. In 2018, the pinhole was re-shaped and calibrated. On 27 October 2018, Costantino Sigismondi started an extensive astrometric observational campaign called IGEA (Informatized Geometric Ephemerides for Astrometry) with ZIA (Zenithal Imaging Analysis) in order to obtain accurate local references along the meridian line [26].

• The meridian measures of the solar diameter have been accompanied by meteorological data (pressure, temperature, and humidity) and sky aspects (cloudy, with veils or clear) to understand their contributions to the observed diameter’s length.
• All the meridian transits have been recorded and they are available on YouTube. (https://www.youtube.com/channel/UCe18v3EZ8w2qmd8jW6mYV5w/videos accessed on 4 June 2025 search “Transito meridiano a S. Maria degli Angeli” + the date in Italian, e.g., “3 maggio 2025”).
• The daily meridian positions of the solar limbs on the brass line are compared with the ephemerides to disentangle systematics from the astronomical seeing, meteorological, and personal equations.

Several sunspots during the present XXV solar cycle were visible on the meridian marbles, especially in the winter’s season, when the solar image was as large as hundred times the effective pinhole’s size: the highest resolution for such lensless telescope [27] is reached.

With a routine written in Excel, we compare the observed data with the predicted ones by the ephemerides. In the text we will consider the differences between our measures and the ephemerides (Stellarium 0.20 for present times or NASA for 18th century [28]) as O-C “observed minus calculated” data.

The solar diameter measured by Cassini, Bianchini, and by us is the length between the two meridian limbs of North and South; it is shorter than the ephemerides because of the following:

a.

The signal to noise ratio reduced by meteorological conditions and ambient light;

b.

Solar limb darkening;

c.

The penumbra (diameter of the horizontal pinhole, fixed);

d.

The cylinder effect (pinhole vertical thickness, which changes the effective pinhole area);

e.

The light reflected inside the marble, which enlarges the image southwards in summer time;

f.

The airmass extinction combined with the effective pinhole area.

The meridian diameter is then systematically 9 mm less than the ephemerides near the winter solstices (2018–2024), and it becomes 4 mm less at the half-meridian line and about 2 mm less in summer time. The intensity of the summer image is 5 times larger than in winter. Moreover a meteorological fluctuation of ±1.5 mm may appear as the meteo departs from STP (15 °C, 1013 hPa): at approximately 1 mm/10 °C and 1 mm/10 hPa near the winter solstice, the effect is less evident at lower focal lengths (distance pinhole image), i.e., toward summer time.

Nevertheless, near the meridian line, the motion of the image is perpendicular to the meridian line and this allows one to very precisely detect the limbs, if a fit over five positions per limb (pencil’s signs) is performed, and the center of the image can be located with a nominal precision often better than 1 mm.

4.1. The Pinhole of the Clementine Gnomon

The present pinhole is a cylinder 6.2 mm thick and 25 mm wide; this reduces the effective pinhole to about 11 mm meridian per 23 mm transverse in winter time, moving its center up to 7 mm in the meridian direction, periodically, during the year.

Originally, in 1702, the pinhole was a horizontal circle 20 mm wide, 1:1000 of its height [29]; it was designed by Giuseppe Campani (1635–1715), the best lens maker of his times, on a 2 mm-thick bronze plate [30].

The solar limb darkening convolutes with the pinhole aperture (called penumbra, because from there a part of the sky around the Sun is visible through the pinhole) and the diffraction produces a red rim of the solar image, up to 5 mm or 10″ width at the winter solstice. A dimmer ring of penumbra is always visible, especially in video.

4.2. The Meridian Line and Its Marbles

The central brass meridian line is 30 mm wide. It is inserted in two white marble slabs (910 mm width in total) and in two external yellow marble strips of 224 mm each (see Figure 1). The whole design is symmetrical, to enable the possibility to measure the meridian positions of the Sun ± 7.5 min from the meridian transit.

The reflection inside the marble is non-symmetrical because it is sensitive to the direction of the light, and on the Northern limb, closer to the pinhole (upper part of Figure 1), the light spreads into the solar image, while in the Southern limb, it spreads out, enlarging the measured diameter.

Moreover, the reflection on different marbles changes the perceived diameter (Figure 2 and Figure 3).

4.3. Extra-Meridian Measurements on Vanvitelli’s Marbles

The pinhole casts the solar image on the marbles of the floor of the Basilica about 2 h before the meridian transits and its length can be measured, similarly to the meridian cases, marking the limbs of the major axis with a pencil on the polished marbles of Vanvitelli on the floor.

These marks are not simultaneous for both limbs, and the motion of the image off-meridian immediately covers the limb closer to the pinhole (the Sun is rising).

We could evaluate the lengths of the images and their statistical dispersions in different seasons, airmasses, and with different weathers.

We assume them to be similar to the one experienced by Bianchini in Rome and by Cassini and collaborators in Bologna.

The extra-meridian measurements taken in 2024–2025 aim to verify the observing conditions with solar altitudes ranging from 20° to 67°, the same range of the meridian transits in Bologna. With tens of measures in a single observing session, instead of a single meridian transit per day, we strengthen the statistics of our measurements. Over one thousand such observations (Figure 4) have been collected, along with meteorological data of pressure, temperature, and humidity and the opacity/clearness of the solar image.

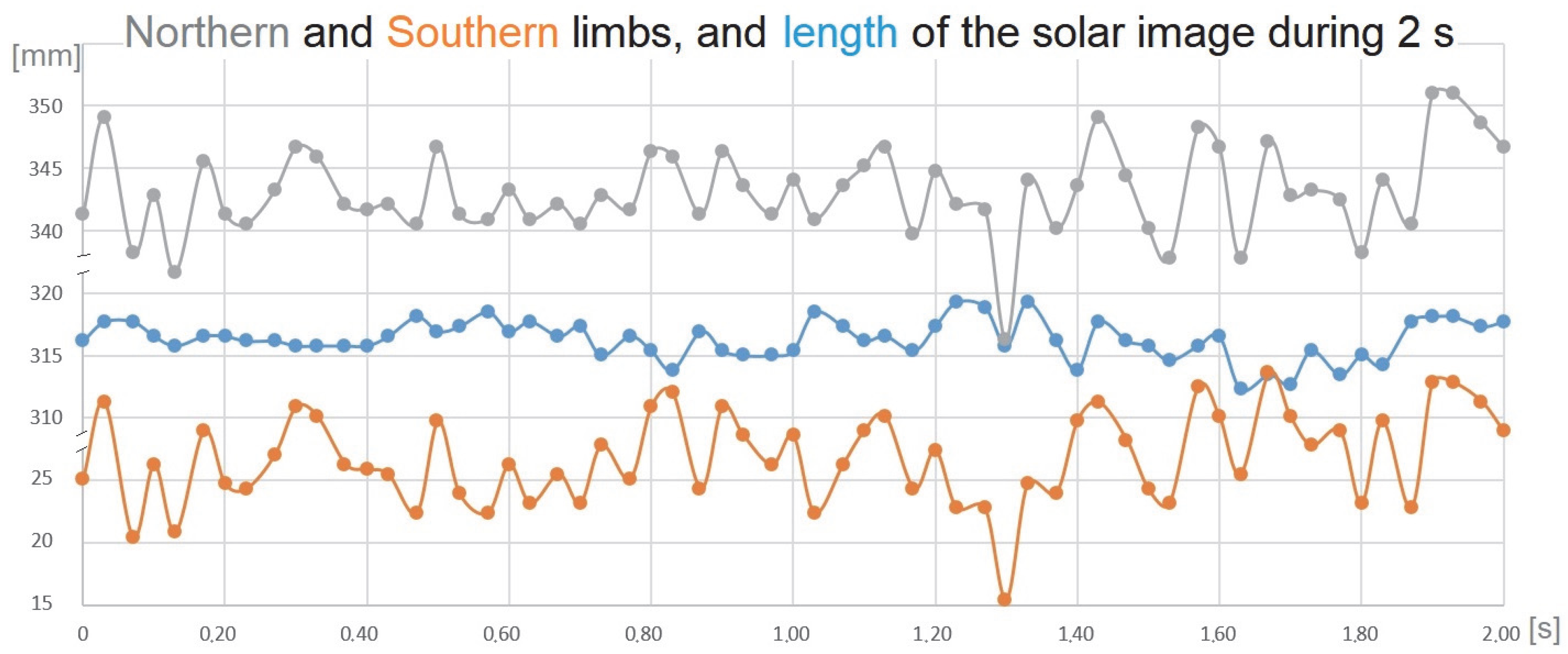
4.4. The Turbulence at the Clementine Gnomon

The air turbulence is responsible for the view of the solar image in the Basilica of St. Maria degli Angeli. The turbulence occurs mainly in the first meters just outside the pinhole, since the image rapidly shakes all at once, and this is to be expected when hot bubbles move close to the pinhole, on the line of sight of the Sun. (Images recorded from the vertical on 29 March 2022: https://youtu.be/cSTsJVOTy1g. Moreover, it is possible to see the superposition of various images in the preceding and proceeding limbs, e.g., https://youtu.be/HgCgjM_6uwQ (accessed on 11 April 2025), especially looking at the projection on paper).

In Figure 5 and Figure 6, we present the case of 29 March 2022.

The lengths of the images of Figure 5 have a spread ±1.5 mm (corresponding to a 9″ viewing), which is much lower than the limbs spreading in phase of ±3.6 mm (22″ of viewing). The average length of the image is 316.3 mm from one to another inflection point, and it corresponds to 1922″ of angular dimension (ephemerides). The positions are defined by the inflection points of the light curves for each frame, along the meridian direction. The camera is a Samsung SM-J500FN (Samsung Digital City [KO], Samsungno 129, Maetan-dong, Yeongtong District, Suwon, Republic of Korea) in VGA 640 × 480 pixels in automatic mode.

4.5. Images with Tiny Clouds

The measured length of the solar diameter along the meridian line has been found to be different in scenarios of thin clouds with cover to a fully clear sky.

Different cloud coverages (Figure 7) modify the luminosity of the image.

When the luminosity diminishes, the dispersion of the diameter measures increases, and the perceived diameter tends to diminish.

5. Solar Diameters in 1701 and 1702

Francesco Bianchini, around the 1701–1702 winter solstices, performed 11 measurements at the Clementine Gnomon under good weather conditions [3,4]. Ten of them are represented in Figure 8, and one was rejected. (One of the observations near the solstices, on 29 December 1701, resulted in an outlier, with a measured image 42 mm shorter than the ephemerides, while all other measures were in very good agreement with them, with a systematic reduction of 9 mm. Nevertheless, the clear sky conditions of Rome are generally better than the “Sole languido” or “Sole languidissimo” (−/+ clouds’ veil) mentioned in the Manfredi’s report [9]). The mean value of the difference between the observed and calculated diameter (ephemerides with 1920″ solar angular diameter at 1AU) is O-C = −9 mm.

The measured solar meridian diameters of Bianchini near the end of the solar Maunder minimum (winters 1701–702) are −9 ± 6 mm shorter than the ephemerides (Figure 8), calculated with a solar standard diameter of θ_⊙ = 1919.26″, here assumed as θ_⊙ = 1920″ (Lamy et al. [31], Quaglia et al. [32]).

6. Comparison Between Bianchini (1702) and Present Data (2018–2025)

The gigantic dimension of the Clementine Gnomon, up to 50 m of focal length, maximizes the signal (1100 mm at the winter solstice) to noise (down to ±1 mm of the image’s turbulent vibration) ratio for the solar image’s measurement.

The dates around the winter solstices from 2018 to 2024 (Figure 9) yielded a meridian solar diameter of −12 ± 8 mm, measured by C. Sigismondi during the IGEA-ZIA campaign. The statistical dispersion is larger than the estimated uncertainties of the single measures. The slightly larger statistical uncertainty is due to having included days with some clouds or veils, and solar image’s motion occurred in the moments of the transits, that are a random effect, while Bianchini [3,4] only observed it under very good conditions.

The datapoints under comparison here total 10 from Bianchini (2 winter solstices) and 61 from Sigismondi (7 winter solstices). We chose the data near the winter solstice for their larger relative and absolute accuracy, given the dimensions of the solar images. (The “inaugural” meridian diameter of 6 October 1702 [3] was 415.6 mm long, with the Southern limb coincident with the ephemerides, while the Northern one was −10 mm, so the diameter was −10.6 mm with respect to the ephemerides. Rescaling to the winter solstice this would be −28.6 mm. The choice of using the winter solstices data is for obtaining better relative errors and a largest ratio of image to penumbra (pinhole size). Assuming similar personal equations (the capability to detect the image’s limbs under similar environmental luminosity, in these cases) for Bianchini and Sigismondi, the meridian images have diameters systematically different by 3 mm, since Bianchini underestimated the solar diameter by 9 mm and Sigismondi by 12 mm (Figure 9). The Sun has shrunk by 3 mm or 6″ since then, but the errorbars are ±20″.

Normalizing to the standard angular solar diameter and adjusting for the systematic errors, the averaged winter solstice data of Bianchini are θ_⊙ = 1926″ ± 12″, while the modern ones are θ_⊙ = 1920″ ± 16″.

The solar diameter’s variation, Δθ_⊙ = −6″ ± 20″, is evidently compatible with zero but also with the variations claimed with historical total eclipses. The eclipses of Clavius occurred in Rome in 1567, before the Maunder minimum [33], the one of Halley occurred in England in 1715, which was later [34] analyzed by Eddy and Boornazian [35], and the one over Manhattan (New York) and Providence occurred in 1925 and was analyzed by Dunham et al. [36], along with the eclipse of 1979.

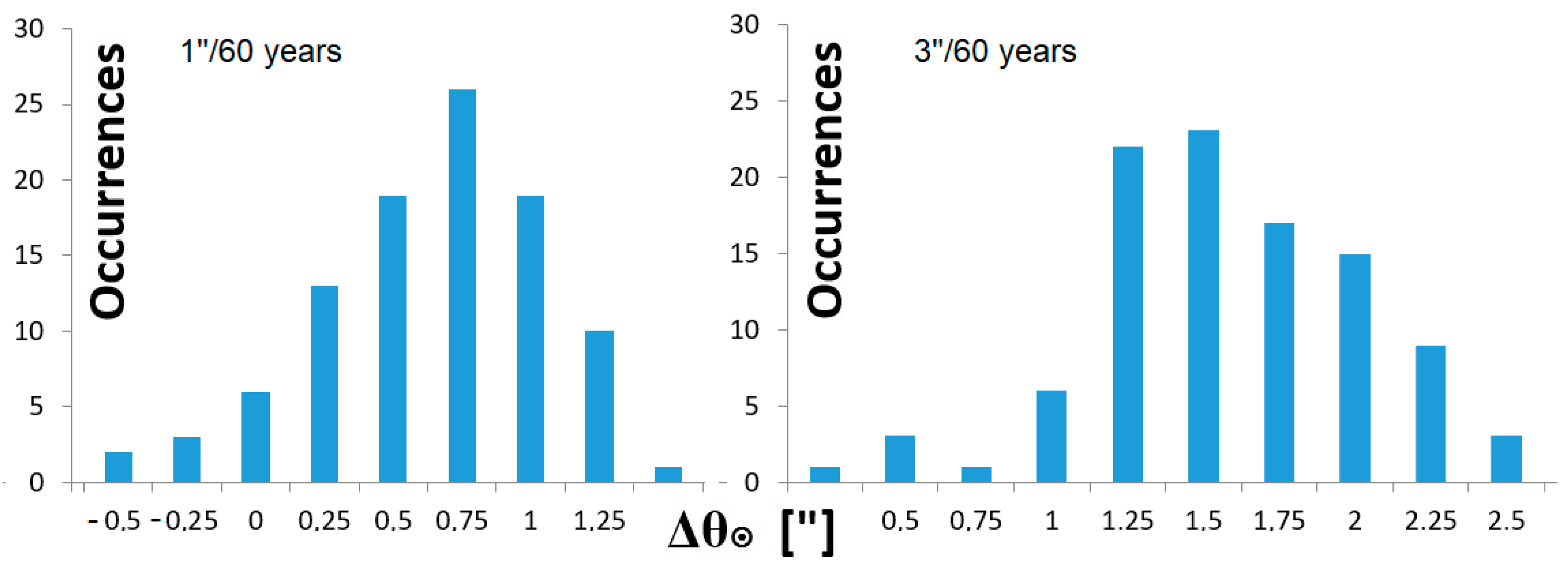
7. Simulating Solar Diameter Variations and the Observations Made in 1655–1736

To study the results obtained by Tovar et al. (2021) on the data published by Manfredi [9], we designed simulations with a gradual change of 1″and 3″ in solar diameter over the years (1655–1715) when the Maunder minimum occurred and a constant value after 1715–1736.

The attribution of a slow positive diameter variation of +1″/80 or +3″/80 years during the Maunder minimum is inspired by the Secchi–Rosa law [37], which anticorrelated the maximum of the solar activity cycle with the minimum diameter measured. The verification of this law continued to inspire the experiments on the solar diameter variations realized in recent years as in the SDS experiment by Egidi et al. [38] and in Picard satellite + ground counterpart (Corbard et al. [39]).

In the simulations, we distinguished two cases: winter and summer:

• Winter. We added realistic Gaussian noise to each data of an average of −18″ and ±18″ of standard deviation (angular values averaged from St. Maria degli Angeli extra-meridian, Figure 4, and on-meridian, winter: Figure 9).
• Summer. The Gaussian noise is −18″ ± 48″ (from extra-meridian data, since the summer solstice in St. Maria degli Angeli occurs on the figure of Cancer).

Both the systematic shifts (−18″, rather constant along the year, according to our analyses) with respect to the expected values from ephemerides, and the errorbars (±18″ in winter and ±48″ in summer) of the single measures, are the same as those observed in St. Maria degli Angeli.

We simulated 4000 datapoints, as in Manfredi [9], in the two cases winter and summer, obtaining a difference of Δθ_⊙ = (0.53 ± 0.43)″ between the last 1000 datapoints (the ones simulating 1715–1736 are with constant solar diameter) and the first 3000 datapoints (1655–1715, are with rising diameter during the Maunder minimum).

The dispersion of the averaged difference Δθ_⊙ was obtained through 100 repetitions of 4000 simulated datapoints each (see Figure 10).

The expected value of this difference Δθ_⊙, without the added Gaussian noise, is Δθ_⊙ = 0.5″ ± 0.3″.

Changing the ratio of solar diameter variations to +3″ over the first 60 years yr in the timespan of 1655–1715, and constant in the last 20 years, we obtain differences of Δθ_⊙ = (1.47 ± 0.46)″, always on 100 repetitions. The expected value in this second case was Δθ_⊙ = 1.5″ ± 0.9″.

The distributions of the results are asymmetrical.

The differences of the averages are plotted in the Figure 10 with simulated increments of the solar diameter of 1″ per 60 years or 3″ per 60 years and the following 20 years constant. These simulations have been repeated 100 times times, and we found that there are occurrences very far from the expected values.

For example there are 25% of the occurrences of Δθ_⊙ in the range of [0.75–1]″ with the expected value 0.5″ or 15% of the occurrences of Δθ_⊙ in the range of [1.75–2]″ with the expected value 1.5″. We deduce from this analysis that a definition of the solar diameter with a sub-arcsecond accuracy, and based on a single random set of 4000 data, cannot be reliable for the structure of the simulated distribution.

The changes in the solar angular diameter, if they occur, are expected to be of the order of ≤1″/century. All instrumental (e.g., the temperature variating the focal length as in the SDS experiment, Egidi et al. [38]) and experimental effects (e.g., refraction, as in Picard experiment, Corbard et al. [39]), or the black drop effect in planetary transits (Schneider et al. [40]), have to be excluded.

Recent experimental data on the solar angular radius have been obtained with ground-based and satellite experiments, such as the Picard satellite with a twin telescope on the ground (θr_⊙ = 959.78″ ± 0.19″ Meftah et al. [41]). Recent Baily’s beads analyses in solar eclipses have yielded values of the solar radius (θr_⊙ = 959.99″ ± 0.06″ Lamy et al. [31], θr_⊙ = 959.95″ ± 0.05″ Quaglia et al. [32]). These values of θr_⊙ are up to 0.4″ larger than the standard value of the solar radius at 1AU: θr_⊙ = 959.63″ ± 0.02″ (Auwers, [42]). (The solar radius found in the recent aforementioned experiments is 0.8″ larger than the nominal value obtained by the IAU General Assembly 2015 resolution B3 [43] of R_⊙ = 695.7 Mm, based on the Rosseland radius at optical depth τ = 2/3 (rounded without errorbars from Haberreiter et al. [44]). This nominal radius yields an angular solar radius of θr_⊙ = 959.23″ at 1AU. It should be noted that this nominal value aims to find an agreement between the helioseismological radius and the photometric radii, based on the definition of the solar limb with the inflection point of the radial photometric profiles. R_⊙ = 695.7 Mm is a value to be used, with fair precision, in stellar astronomy, based on nominal solar parameters. But the final scope of this study and others regarding solar diameter variations is to better comprehend the physics of the Sun, which may be more complex than expected, being the Sun the only star that we can observe under very high resolution. That’s why we refer to the photospheric solar radius and to its variations.

8. Conclusions and Perspectives

The data of Bianchini 1701–1702 [3,4] and of Sigismondi 2018–2024 were obtained at the winter solstices when the relative uncertainty was lower. After considering the personal equations, the reduced solar diameter was θ_⊙ = 1926″ ± 12″ for Bianchini and θ_⊙ = 1920″ ± 18″ for Sigismondi, with Δθ_⊙ = −6″ ± 20″ occurred after 3 ¼ centuries. There is no possibility to meaningfully constrain our current understanding on the Sun’s evolution better than ±20″ with such instrument.

More than one thousand measures obtained in 2024–2025 with extra-meridian observations (Figure 4) allowed us to better constrain the seasonal errorbars and diameter shifts in S. Maria degli Angeli and to infer the corresponding values for the meridian line of Cassini in S. Petronio, Bologna.

According to these results, we realized opportune realistic simulations to reproduce datasets similar to the one of Manfredi [9] and analyzed by Tovar et al. [10].

With observational errorbars ranging from ±18″ to ±48″ over the year, simulations of 4000 datapoints, reproducing the ones of Manfredi [9], repeated 100 times, yielded averaged diameter variations of Δθ_⊙ = (0.4 ± 1.2)″ with respect to a solar diameter increased by +1″ over 80 years.

These differences become Δθ_⊙ = (1.6 ± 1.3)″ if the solar diameter varies +3″ during the same examined period.

We conclude that due to a large number of systematic effects and variable biases, no issues regarding the solar diameter variations between the Maunder minimum and the 20 years immediately following can be found with a sub-arcsecond of accuracy, even working with cluster averages.