Thermodynamics of Fluid Elements in the Context of Turbulent Isothermal Self-Gravitating Molecular Clouds
Abstract
1. Introduction
2. The General Frame
3. Set Up of the Model
4. Results
4.1. First Principle and Entropy of Macro-Gas
4.2. Free Energy
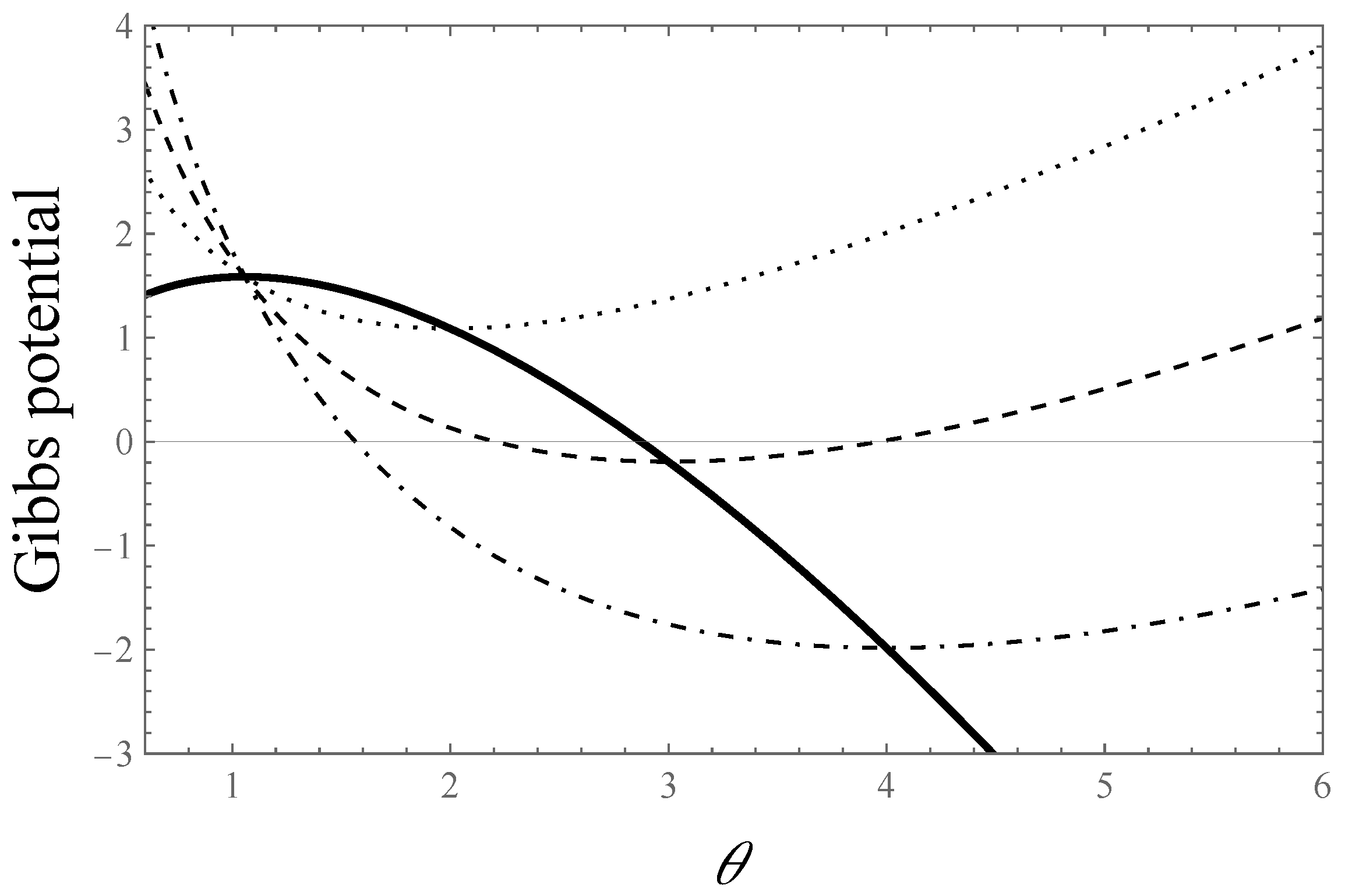
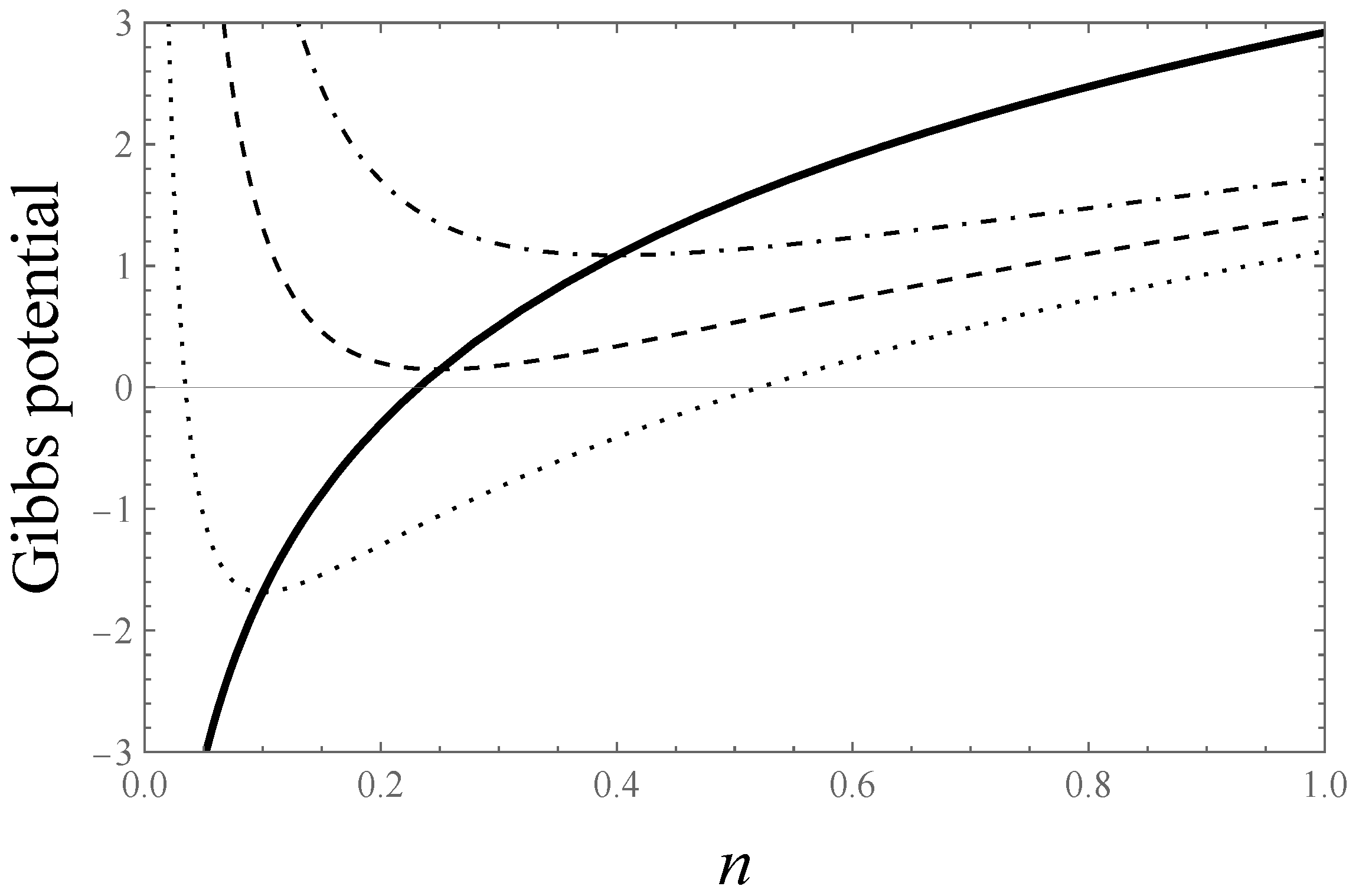
4.3. Gibbs Potential
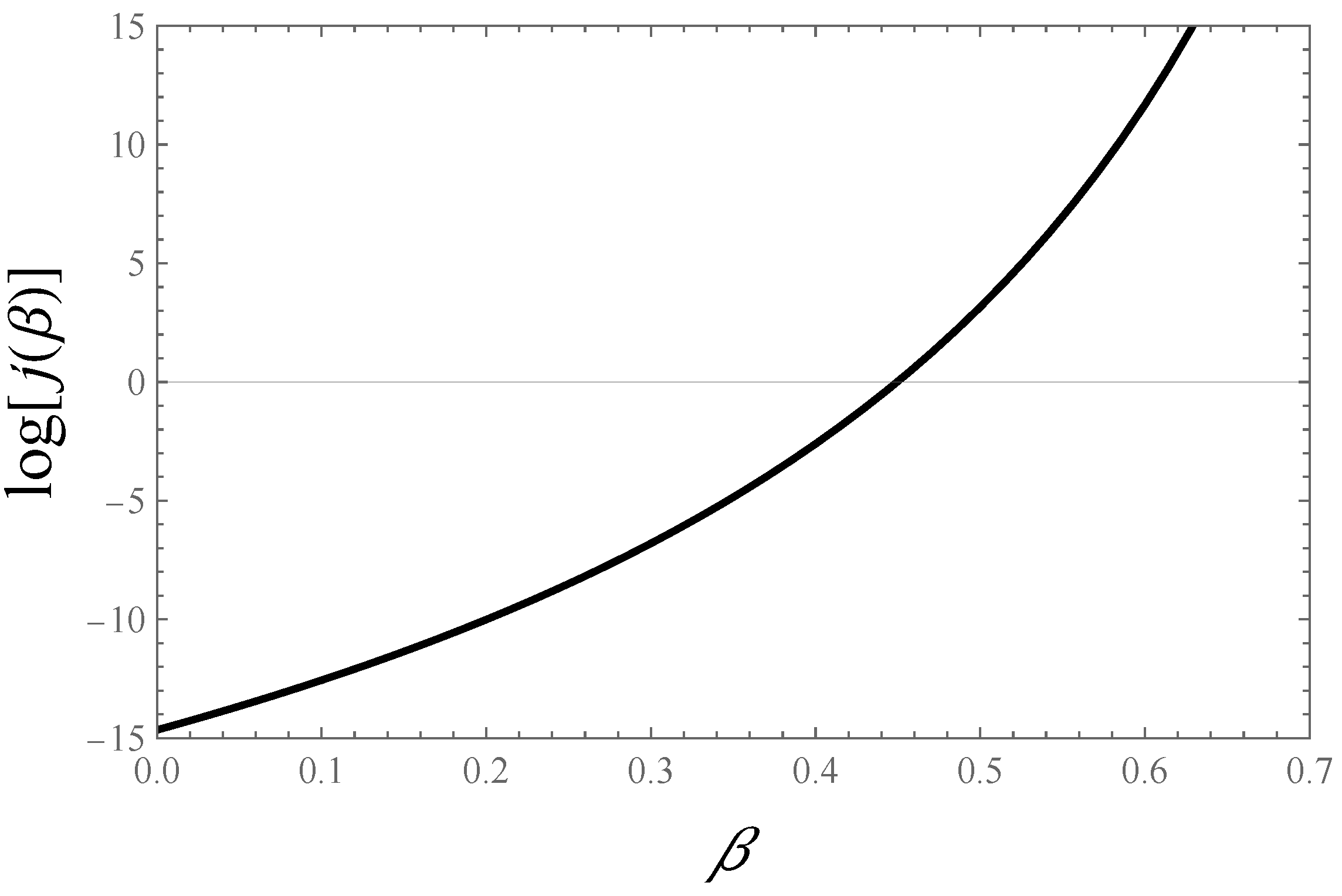
4.4. Stability Analysis
4.4.1. Canonical Ensemble
4.4.2. Grand Canonical Ensemble
5. Discussion
5.1. Basic Assumptions and Main Results
5.2. Number of Microstates
5.3. Caveats
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MC(s) | Molecular Cloud(s) |
| ISM | Interstellar Medium |
| 6D phase-space | six-dimensional phase-space |
| AGN | Active Galactic Nuclei |
Appendix A. Legendre Transformations for the Free Energy and Gibbs Potential
Appendix B. The Off-Equilibrium Form of the Gibbs Potential
| 1 | As was mentioned in Introduction, this range roughly spans between and |
| 2 | To avoid the so called “Jeans swindle”: the assumption for infinite homogeneous medium is actually not really consistent, because the Poisson equation cannot be solved unless the medium density is zero. |
| 3 | Hereafter, we will omit this term, because we suppose and regard fluid elements as a simple particles. |
| 4 | The thermodynamic limit hypothesis presumes that if the volume of the system V and the number of particles N in it tend to infinity simultaneously, then the number density maintains a constant value. |
| 5 | For obtaining the differential forms of free energy and Gibbs potential, see the calculations in Appendix A. |
| 6 | A detailed derivation of the off-equilibrium form for the Gibbs potential is provided in Appendix B. The derivation for the free energy is not determined, because the calculations in the case of canonical ensemble are (a subcase and) simpler than that for the grand canonical ensemble. |
| 7 | See the Appendix B. |
| 8 | Here, we present an assessment of –the macro-temperature of the macro-gas at dissipation scale. According to Equation (3) and to considerations in Section 4.1, the formula for is . If then K and this temperature will be the same for the whole cloud. If , then K and the temperature will increase with the scale (for example, if ∼1000 then K). These enormous values are not surprising if one accounts for the kinetic energy per fluid element: ∼ J, in contrast the energy per hydrogen molecule with the same velocity is ∼ J. (The latter energy corresponds to the equilibrium molecule motion at temperature T∼1200 K). |
| 9 | Note that the number density of molecular gas is proportional to the number density of macro-gas through a constant . |
References
- Ferriere, K.M. The interstellar environment of our galaxy. Rev. Mod. Phys. 2001, 73, 1031–1066. [Google Scholar] [CrossRef]
- Elmegreen, B.; Scalo, J. Interstellar Turbulence I: Observations and Processes. Annu. Rev. Astron. Astrophys. 2004, 42, 211–273. [Google Scholar] [CrossRef]
- Hennebelle, P.; Falgarone, E. Turbulent molecular clouds. Astron. Astrophys. Rev. 2012, 20, 55. [Google Scholar] [CrossRef]
- Klessen, R.S.; Glover, S.C.O. Physical Processes in the Interstellar Medium. In Star Formation in Galaxy Evolution: Connecting Numerical Models to Reality, Saas-Fee Advanced Course; Springer: Berlin/Heidelberg, Germany, 2016; pp. 85–249. ISBN 978-3-662-47889-9. [Google Scholar]
- Frisch, U.; Donnelly, R.J. Turbulence: The Legacy of A. N. Kolmogorov. Phys. Today 1995, 49, 82. [Google Scholar] [CrossRef]
- Kolmogorov, A. The Local Structure of Turbulence in Incompressible Viscous Fluid for Very Large Reynolds’ Numbers. Dokl. Akad. Nauk SSSR 1941, 30, 301–305. [Google Scholar]
- Galtier, S.; Banerjee, S. Exact Relation for Correlation Functions in Compressible Isothermal Turbulence. Phys. Rev. Lett. 2011, 107, 134501. [Google Scholar] [CrossRef]
- Kritsuk, A.; Norman, M.; Padoan, P.; Wagner, R. The Statistics of Supersonic Isothermal Turbulence. Astrophys. J. 2007, 665, 416–431. [Google Scholar] [CrossRef]
- Aluie, H. Compressible Turbulence: The Cascade and its Locality. Phys. Rev. Lett. 2011, 106, 174502. [Google Scholar] [CrossRef]
- Keto, E. Scales of Stability and Turbulence in the Molecular ISM. Astron. Nachrichten 2024, 345, e20240044. [Google Scholar] [CrossRef]
- Antonov, V.A. Most probable phase distribution in spherical star systems and conditions for its existence. Vest. Leningr. Gos. Univ. 1962, 7, 135. [Google Scholar] [CrossRef]
- Katz, J. On the number of unstable modes of an equilibrium. Mon. Not. R. Astron. Soc. 1978, 183, 765–770. [Google Scholar] [CrossRef]
- Lynden-Bell, D.; Wood, R. The gravo-thermal catastrophe in isothermal spheres and the onset of red-giant structure for stellar systems. Mon. Not. R. Astron. Soc. 1968, 138, 495–525. [Google Scholar] [CrossRef]
- Padmanabhan, T. Antonov Instability and Gravothermal Catastrophe–Revisited. Astrophys. J. Suppl. 1989, 71, 651. [Google Scholar] [CrossRef]
- Padmanabhan, T. Statistical mechanics of gravitating systems. Phys. Rep. 1990, 188, 285–362. [Google Scholar] [CrossRef]
- Chavanis, P.-H. Gravitational instability of finite isothermal spheres. Astron. Astrophys. 2002, 381, 340–356. [Google Scholar] [CrossRef]
- Chavanis, P.-H. Gravitational instability of isothermal and polytropic spheres. Astron. Astrophys. 2003, 401, 15–42. [Google Scholar] [CrossRef]
- Chavanis, P.-H. Dynamical stability of collisionless stellar systems and barotropic stars: The nonlinear Antonov first law. Astron. Astrophys. 2006, 451, 109–123. [Google Scholar] [CrossRef]
- de Vega, H.J.; Sanchez, N.; Combes, F. Self-gravity as an explanation of the fractal structure of the interstellar medium. Nature 1996, 383, 56–58. [Google Scholar] [CrossRef]
- de Vega, H.J.; Sanchez, N.; Combes, F. Fractal dimensions and scaling laws in the interstellar medium: A new field theory approach. Phys. Rev. D 1996, 54, 6008–6020. [Google Scholar] [CrossRef]
- de Vega, H.J.; Sanchez, N. The statistical mechanics of the self-gravitating gas: Equation of state and fractal dimension. Phys. Lett. B 2000, 490, 180–186. [Google Scholar] [CrossRef]
- Sormani, M.C.; Bertin, G. Gravothermal catastrophe: The dynamical stability of a fluid model. Astron. Astrophys. 2013, 552, A37. [Google Scholar] [CrossRef]
- Vázquez-Semadeni, E.; Palau, A.; Ballesteros-Paredes, J.; Gómez, G.; Zamora-Aviles, M. Global hierarchical collapse in molecular clouds. Towards a comprehensive scenario. Mon. Not. R. Astron. Soc. 2019, 490, 3061–3097. [Google Scholar] [CrossRef]
- Keto, E.; Field, G.B.; Blackman, E.G. A turbulent-entropic instability and the fragmentation of star-forming clouds. Mon. Not. R. Astron. Soc. 2020, 492, 5870–5877. [Google Scholar] [CrossRef]
- Binney, J.; Tremaine, S. Galactic dynamics. In Galactic Dynamics (Princeton Series in Astrophysics); Princeton University Press: Princeton, NJ, USA, 1987; pp. 567–573. [Google Scholar]
- Bonnor, W.B. Boyle’s Law and gravitational instability. Mon. Not. R. Astron. Soc. 1956, 116, 351–359. [Google Scholar] [CrossRef]
- Ebert, R. Zur Instabilität kugelsymmetrischer Gasverteilungen. Mit 2 Textabbildungen. Z. Astrophys. 1957, 42, 263. [Google Scholar]
- Yabushita, S. Jeans’s type gravitational instability of finite isothermal gas spheres. Mon. Not. R. Astron. Soc. 1968, 140, 109–120. [Google Scholar] [CrossRef][Green Version]
- Lombardi, M.; Bertin, G. Boyle’s law and gravitational instability. Astron. Astrophys. 2001, 375, 1091–1099. [Google Scholar] [CrossRef]
- Federrath, C.; Roman-Duval, J.; Klessen, R.; Schmidt, W.; Mac Low, M.-M. Comparing the statistics of interstellar turbulence in simulations and observations. Solenoidal versus compressive turbulence forcing. Astron. Astrophys. 2010, 512, A81. [Google Scholar] [CrossRef]
- Larson, R. Turbulence and star formation in molecular clouds. Mon. Not. R. Astron. Soc. 1981, 194, 809–826. [Google Scholar] [CrossRef]
- Padoan, P.; Juvela, M.; Kritsuk, A.; Norman, M. The Power Spectrum of Supersonic Turbulence in Perseus. Astrophys. J. 2006, 653, L125–L128. [Google Scholar] [CrossRef][Green Version]
- Shapiro, S.L.; Teukolsky, S.A. Black Holes, White Dwarfs, and Neutron Stars: The Physics of Compact Objects; A Wiley-Interscience Publication; Wiley: New York, NY, USA, 1983; pp. 32–63. [Google Scholar]
- Reif, F. Fundamentals of Statistical and Thermal Physics; Published by Waveland Press Inc.: Nong Grove, IL USA, 1965; pp. 288–319. ISBN 978-1-57766-612-7. [Google Scholar]
- Donkov, S.; Stefanov, I.Z.; Veltchev, T.V. Thermodynamics of fluid elements in the context of saturated isothermal turbulence in molecular clouds. Bulg. Astron. J. 2023, 38, 91–97. [Google Scholar]
- Ballesteros-Paredes, J.; Hartmann, L.W.; Vázquez-Semadeni, E.; Heitsch, F.; Zamora-Avilés, M.A. Gravity or turbulence? Velocity dispersion-size relation. Mon. Not. R. Astron. Soc. 2011, 411, 65–70. [Google Scholar] [CrossRef]
- Ballesteros-Paredes, J.; Vázquez-Semadeni, E.; Gazol, A.; Hartmann, L.W.; Heitsch, F.; Colin, P. Gravity or turbulence? -II. Evolving column density probability distribution functions in molecular clouds. Mon. Not. R. Astron. Soc. 2011, 416, 1436–1442. [Google Scholar] [CrossRef]
- Burkert, A. A bathtub model for the star-forming interstellar medium. Mem. Della Soc. Astron. Ital. 2017, 88, 533–537. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Donkov, S.; Stefanov, I.Z.; Kopchev, V. Thermodynamics of Fluid Elements in the Context of Turbulent Isothermal Self-Gravitating Molecular Clouds. Universe 2025, 11, 184. https://doi.org/10.3390/universe11060184
Donkov S, Stefanov IZ, Kopchev V. Thermodynamics of Fluid Elements in the Context of Turbulent Isothermal Self-Gravitating Molecular Clouds. Universe. 2025; 11(6):184. https://doi.org/10.3390/universe11060184
Chicago/Turabian StyleDonkov, Sava, Ivan Zh. Stefanov, and Valentin Kopchev. 2025. "Thermodynamics of Fluid Elements in the Context of Turbulent Isothermal Self-Gravitating Molecular Clouds" Universe 11, no. 6: 184. https://doi.org/10.3390/universe11060184
APA StyleDonkov, S., Stefanov, I. Z., & Kopchev, V. (2025). Thermodynamics of Fluid Elements in the Context of Turbulent Isothermal Self-Gravitating Molecular Clouds. Universe, 11(6), 184. https://doi.org/10.3390/universe11060184





