Flare Set-Prediction Transformer: A Transformer-Based Set-Prediction Model for Detailed Solar Flare Forecasting
Abstract
1. Introduction
2. Dataset
2.1. Label Generation for Set Prediction
2.2. Dataset-Splitting Strategy
2.3. Data Processing and Augmentation
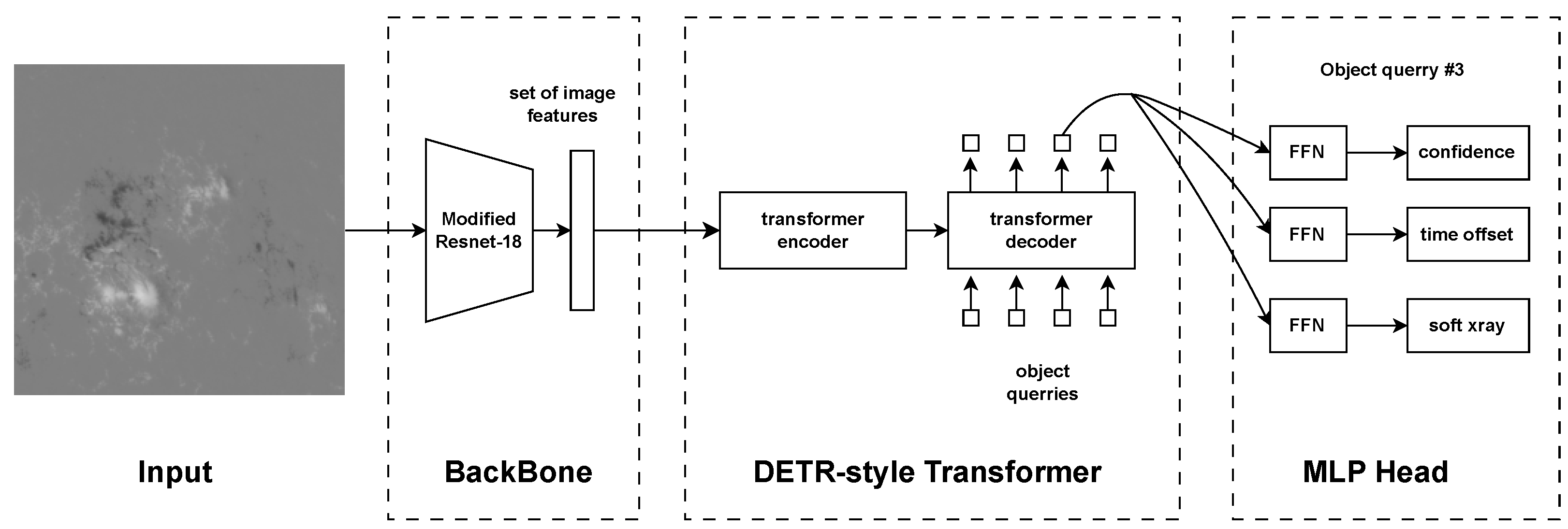
3. Model
3.1. Model Architecture
3.2. Matching Strategy
3.3. Loss Function
3.4. Training Pipeline
4. Evaluation and Discussion
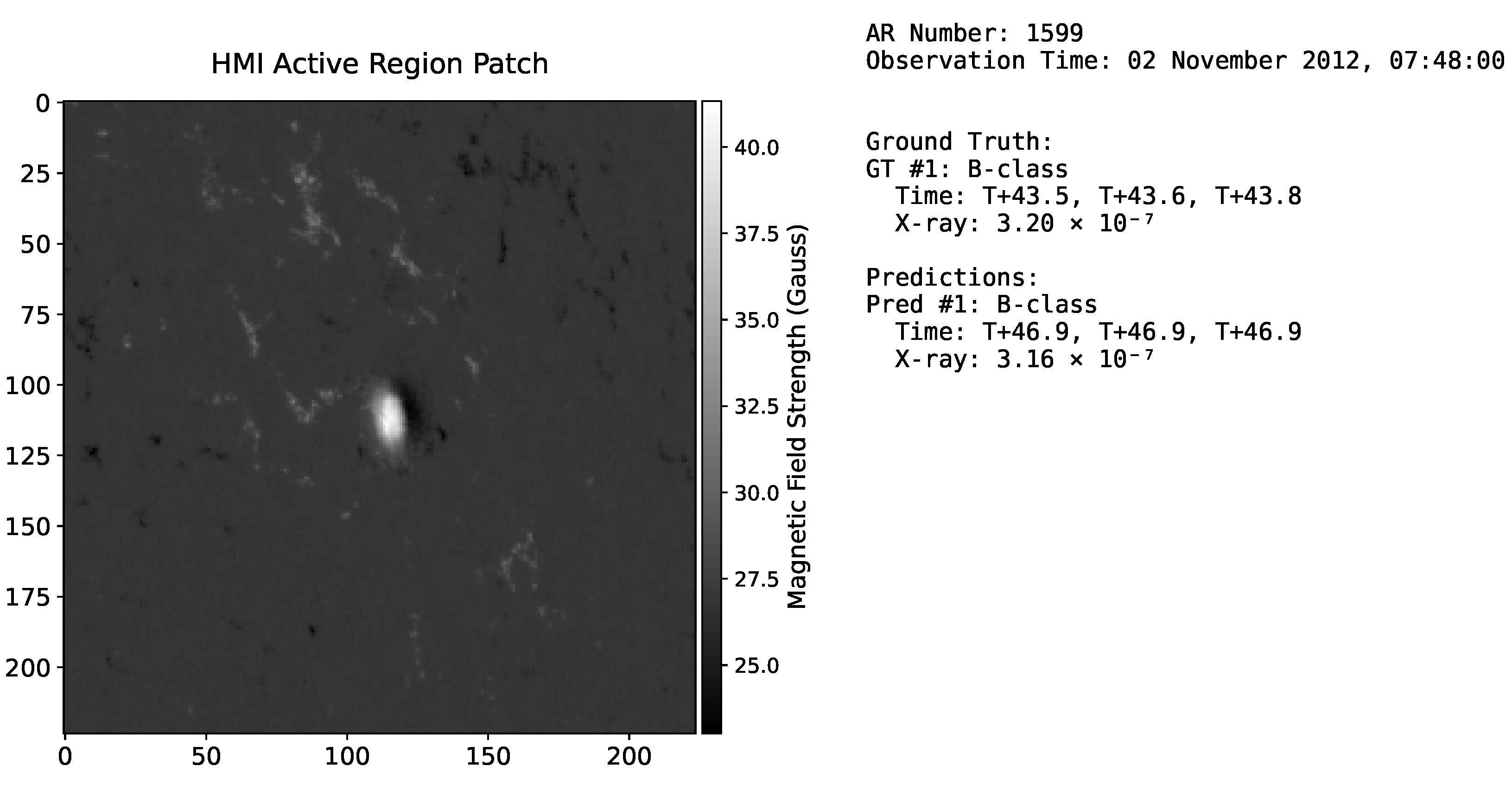
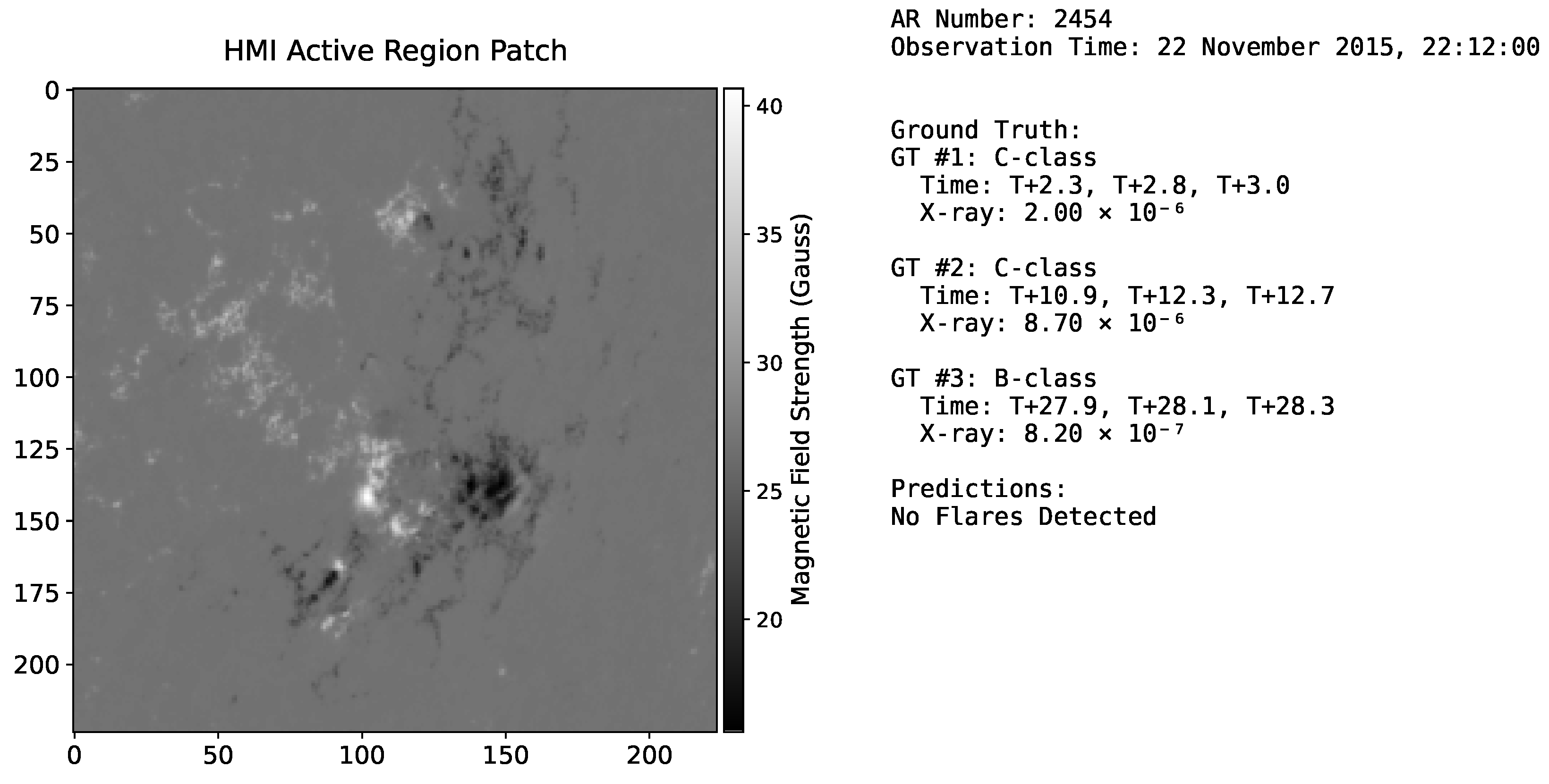
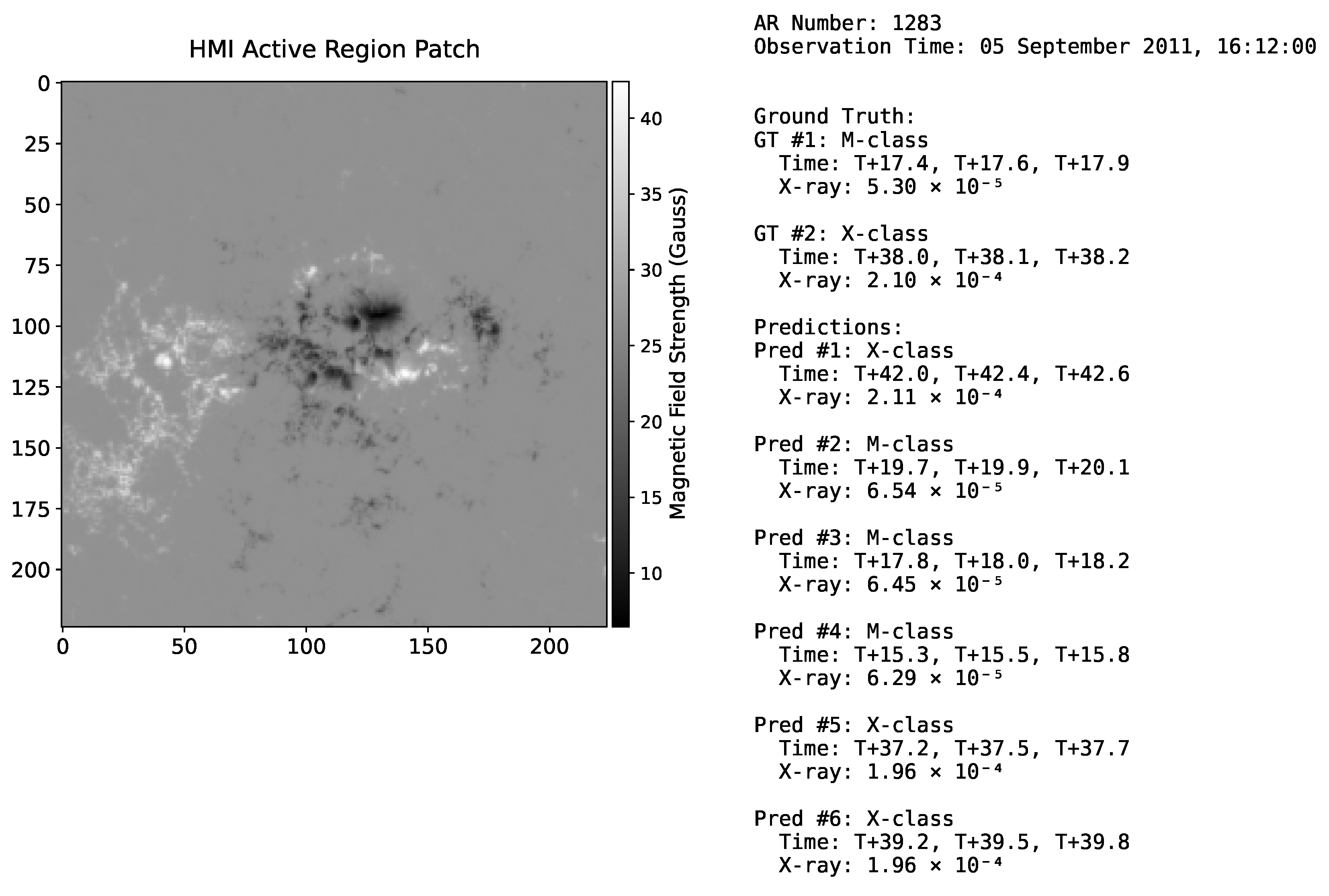
4.1. Inference Pipeline and Evaluation Matching
4.2. Evaluation Metrics
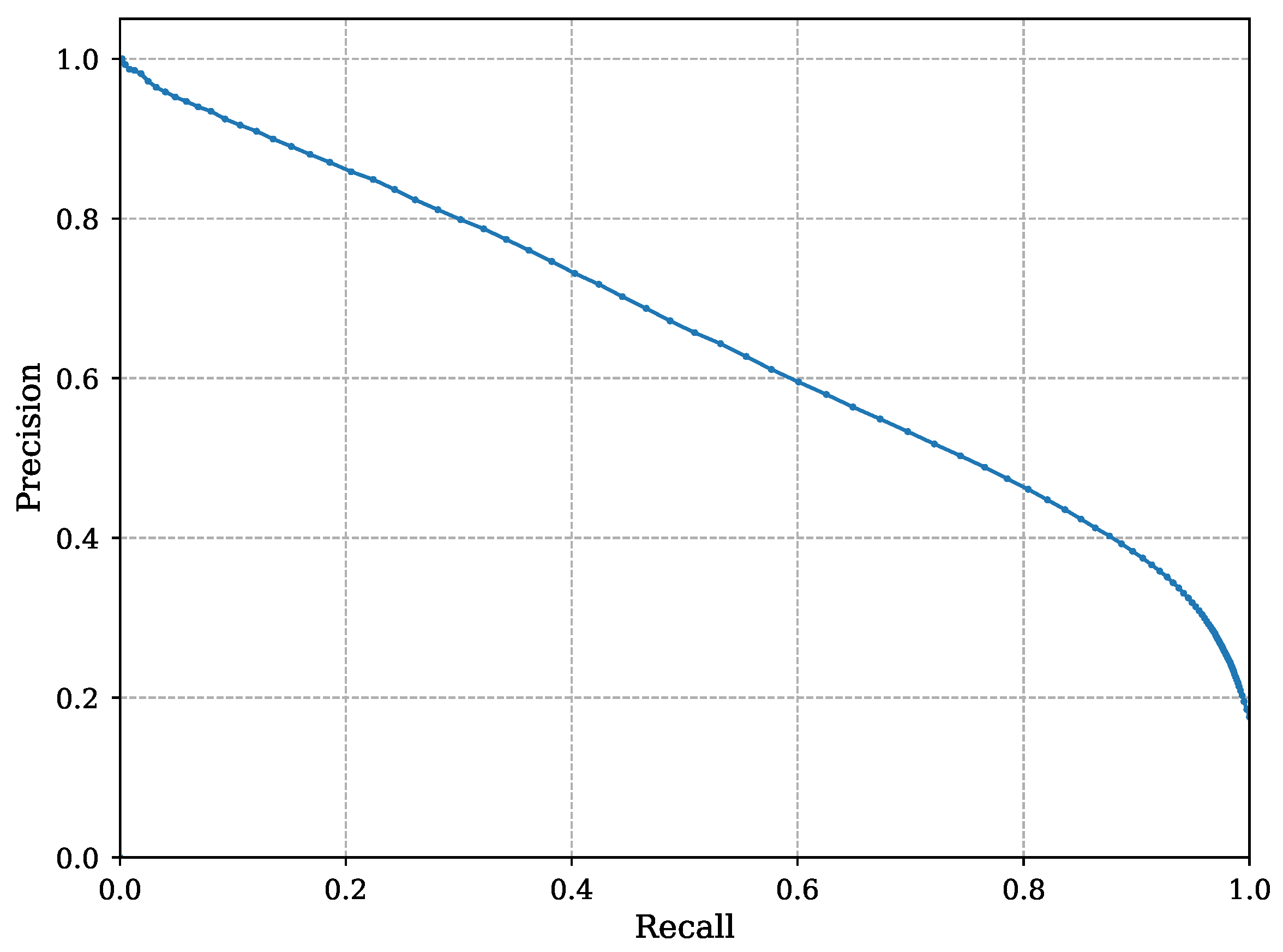
4.3. Evaluation Results
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FSPT | Flare Set-Prediction Transformer |
| DETR | DEtection TRansformer |
| MLP | Multi-Layer Perceptron |
| CNN | Convolutional Neural Network |
| LSTM | Long Short-Term Memory |
| GOES | Geostationary Operational Environmental Satellite |
| HMI | Helioseismic and Magnetic Imager |
| SDO | Solar Dynamics Observatory |
| SHARP | Space-weather HMI Active-Region Patch |
| NOAA | National Oceanic and Atmospheric Administration |
| NASA | National Aeronautics and Space Administration |
References
- Priest, E.R.; Forbes, T.G. Magnetic Reconnection. Astron. Astrophys. Rev. 2002, 10, 313–377. [Google Scholar] [CrossRef]
- Bornmann, P.L.; Shaw, D. Flare Rates and the McIntosh Active-Region Classifications. Sol. Phys. 1994, 150, 127–146. [Google Scholar] [CrossRef]
- Wheatland, M.S. A Bayesian Approach to Solar Flare Prediction. Astrophys. J. 2004, 609, 1134–1139. [Google Scholar] [CrossRef]
- Bloomfield, D.S.; Higgins, P.A.; McAteer, R.T.J.; Gallagher, P.T. Toward Reliable Benchmarking of Solar Flare Forecasting Methods. Astrophys. J. Lett. 2012, 747, L41. [Google Scholar] [CrossRef]
- Bobra, M.G.; Couvidat, S. Solar Flare Prediction Using SDO/HMI Vector Magnetic Field Data with a Machine-learning Algorithm. Astrophys. J. 2015, 798, 135. [Google Scholar] [CrossRef]
- Liu, C.; Deng, N.; Wang, J.T.L.; Wang, H. Predicting Solar Flares Using SDO/HMI Vector Magnetic Data Products and a Random Forest Algorithm. Astrophys. J. 2017, 843, 104. [Google Scholar] [CrossRef]
- Florios, K.; Kontogiannis, I.; Park, S.H.; Guerra, J.A.; Benvenuto, F.; Bloomfield, D.S.; Georgoulis, M.K. Forecasting Solar Flares Using Magnetogram-based Predictors and Machine Learning. Sol. Phys. 2018, 293, 28. [Google Scholar] [CrossRef]
- Nishizuka, N.; Sugiura, K.; Kubo, Y.; Den, M.; Watari, S.; Ishii, M. Solar Flare Prediction Model with Three Machine-learning Algorithms using Ultraviolet Brightening and Vector Magnetograms. Astrophys. J. 2017, 835, 156. [Google Scholar] [CrossRef]
- Nishizuka, N.; Sugiura, K.; Kubo, Y.; Den, M.; Ishii, M. Deep Flare Net (DeFN) for Stokes Profiles of Solar Flares. Astrophys. J. 2018, 858, 118. [Google Scholar] [CrossRef]
- Zheng, J.; Xu, J.; Wang, W.; Zhang, H. Solar Flare Prediction Using Hybrid Deep Neural Networks. Sol. Phys. 2019, 294, 11. [Google Scholar] [CrossRef]
- Huang, X.; Wang, H.; Xu, L.; Liu, J.; Li, R.; Dai, X. Deep Learning Based Solar Flare Forecasting Model. I. Results for Line-of-sight Magnetograms. Astrophys. J. 2018, 856, 7. [Google Scholar] [CrossRef]
- Park, E.; Moon, Y.J.; Shin, S.; Yi, K.; Lim, D.; Lee, H.; Shin, G. Application of the Deep Convolutional Neural Network to the Forecast of Solar Flare Occurrence Using Full-disk Solar Magnetograms. Astrophys. J. 2018, 869, 91. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Q.; Yang, Y.; Jing, J.; Wang, J.T.L.; Wang, H.; Shang, Z. Solar flare index prediction using SDO/HMI vector magnetic data products with statistical and machine-learning methods. Astrophys. J. Suppl. Ser. 2022, 263, 28. [Google Scholar] [CrossRef]
- Li, X.; Zheng, Y.; Wang, X.; Wang, L. Predicting Solar Flares Using a Novel Deep Convolutional Neural Network. Astrophys. J. 2020, 891, 10. [Google Scholar] [CrossRef]
- Chen, Y.; Manchester, W.B.; Hero, A.O.; Toth, G.; DuFumier, B.; Zhou, T.; Wang, X.; Zhu, H.; Sun, Z.; Gombosi, T.I. Identifying Solar Flare Precursors Using Time Series of SDO/HMI Images and SHARP Parameters. Space Weather 2019, 17, 1404–1426. [Google Scholar] [CrossRef]
- Wang, X.; Chen, Y.; Toth, G.; Manchester, W.B.; Gombosi, T.I.; Hero, A.O.; Jiao, Z.; Sun, H.; Jin, M.; Liu, Y. Predicting Solar Flares with Machine Learning: Investigating Solar Cycle Dependence. Astrophys. J. 2020, 895, 3. [Google Scholar] [CrossRef]
- Pandey, C.; Adeyeha, T.; Hong, J.; Angryk, R.A.; Aydin, B. Advancing Solar Flare Prediction Using Deep Learning with Active Region Patches. In Proceedings of the Machine Learning and Knowledge Discovery in Databases. Applied Data Science Track (ECML PKDD 2024), Vilnius, Lithuania, 9–13 September 2024; Springer: Berlin/Heidelberg, Germany, 2024; pp. 50–65. [Google Scholar] [CrossRef]
- Qin, G.; Zhang, M.; Rassoul, H.K. Transport of Solar Energetic Particles in Interplanetary Space. J. Geophys. Res. Space Phys. 2009, 114, A09104. [Google Scholar] [CrossRef]
- Carion, N.; Massa, F.; Synnaeve, G.; Usunier, N.; Kirillov, A.; Zagoruyko, S. End-to-end object detection with transformers. In Proceedings of the Computer Vision—ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 213–229. [Google Scholar] [CrossRef]
- Boucheron, L.E.; Vincent, T.; Grajeda, J.A.; Wuest, E. Solar active region magnetogram image dataset for studies of space weather. Sci. Data 2023, 10, 825. [Google Scholar] [CrossRef]
- Schou, J.; Scherrer, P.H.; Bush, R.I.; Wachter, R.; Couvidat, S.; Rabello-Soares, M.C.; Bogart, R.S.; Hoeksema, J.T.; Liu, Y.; Duvall, T.L.; et al. Design and Ground Calibration of the Helioseismic and Magnetic Imager (HMI) Instrument on the Solar Dynamics Observatory (SDO). Sol. Phys. 2012, 275, 229–259. [Google Scholar] [CrossRef]
- Bobra, M.G.; Sun, X.; Hoeksema, J.T.; Turmon, M.; Liu, Y.; Hayashi, K.; Barnes, G.; Leka, K.D. The Helioseismic and Magnetic Imager (HMI) Vector Magnetic Field Pipeline: SHARPs–Space-Weather HMI Active Region Patches. Sol. Phys. 2014, 289, 3549–3578. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Advances in neural information processing systems. arXiv 2017, arXiv:1706.03762. [Google Scholar] [CrossRef]
- Kuhn, H.W. The Hungarian method for the assignment problem. Nav. Res. Logist. Q. 1955, 2, 83–97. [Google Scholar] [CrossRef]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal Loss for Dense Object Detection. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2999–3007. [Google Scholar]
- Loshchilov, I.; Hutter, F. Decoupled weight decay regularization. arXiv 2017, arXiv:1711.05101. [Google Scholar] [CrossRef]
- Smith, L.N.; Topin, N. Super-convergence: Very fast training of neural networks using large learning rates. In Artificial Intelligence and Machine Learning for Multi-Domain Operations Applications; SPIE: Bellingham, WA, USA, 2019; Volume 11006, pp. 369–386. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Li, F.F. ImageNet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–26 June 2009; pp. 248–255. [Google Scholar]
- Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft COCO: Common Objects in Context. In Proceedings of the Computer Vision–ECCV 2014, Zurich, Switzerland, 6–12 September 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 740–755. [Google Scholar]
- Barnes, G.; Leka, K.D.; Schrijver, C.J.; Colak, T.; Qahwaji, R.; Ashamari, O.W.; Yuan, Y.; Zhang, J.; McAteer, R.T.J.; Bloomfield, D.S.; et al. A Comparison of Flare Forecasting Methods. I. Results from the “All-Clear” Workshop. Astrophys. J. 2016, 829, 89. [Google Scholar] [CrossRef]
| Statistic | Training Set | Test Set |
|---|---|---|
| Total Samples | 849,134 | 94,322 |
| Samples with Flares (%) | 32.63% | 31.28% |
| Total Target Flares | 787,416 | 87,262 |
| Flare-Class Distribution: | ||
| A-Class (%) | 0.10% | 0.17% |
| B-Class (%) | 28.73% | 29.45% |
| C-Class (%) | 64.09% | 63.16% |
| M-Class (%) | 6.59% | 6.55% |
| X-Class (%) | 0.49% | 0.67% |
| Hyperparameter Description | Value |
|---|---|
| Transformer hidden dimension | 256 |
| Number of multi-head attention heads | 8 |
| Number of transformer encoder layers | 3 |
| Number of transformer decoder layers | 3 |
| Dimension of transformer feed-forward networks | 2048 |
| Dropout rate within transformer layers | 0.1 |
| Number of object queries input to decoder | 100 |
| Confidence head output dimension | 64 |
| Time/X-ray head MLP hidden dimension | 128 |
| Time/X-ray head MLP layers | 2 |
| Confidence Threshold () | Precision () | Recall () | F1-Score () |
|---|---|---|---|
| 0.1 | 0.2209 | 0.9495 | 0.3584 |
| 0.3 | 0.2817 | 0.9299 | 0.4324 |
| 0.5 | 0.4609 | 0.7719 | 0.5772 |
| 0.7 | 0.8258 | 0.2474 | 0.3808 |
| 0.9 | 0.0000 | 0.0000 | 0.0000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, L.; Qin, G. Flare Set-Prediction Transformer: A Transformer-Based Set-Prediction Model for Detailed Solar Flare Forecasting. Universe 2025, 11, 174. https://doi.org/10.3390/universe11060174
Qiao L, Qin G. Flare Set-Prediction Transformer: A Transformer-Based Set-Prediction Model for Detailed Solar Flare Forecasting. Universe. 2025; 11(6):174. https://doi.org/10.3390/universe11060174
Chicago/Turabian StyleQiao, Liang, and Gang Qin. 2025. "Flare Set-Prediction Transformer: A Transformer-Based Set-Prediction Model for Detailed Solar Flare Forecasting" Universe 11, no. 6: 174. https://doi.org/10.3390/universe11060174
APA StyleQiao, L., & Qin, G. (2025). Flare Set-Prediction Transformer: A Transformer-Based Set-Prediction Model for Detailed Solar Flare Forecasting. Universe, 11(6), 174. https://doi.org/10.3390/universe11060174









