Abstract
The mid-infrared band is the last major observational window for the ground-based large solar telescopes in the 21st century. Achieving ultra-narrowband filter imaging is a fundamental challenge that all solar telescopes encounter as they progress towards the mid-infrared spectrum. The guided-mode resonance filtering (GMRF) technology provides a promising solution to this critical issue. This paper describes in detail the fundamental principles and calculation procedure of guided-mode resonance filtering. Building upon this foundation, a preliminary design and simulation of a mid-infrared guided-mode resonance filter are carried out. The results show that when the thickness of the sub-wavelength grating is an even multiple of the half-wavelength, it is feasible to attain ultra-narrowband filtering with a bandwidth below 0.03 nm by increasing the grating thickness and decreasing the grating fill factor. Nevertheless, the high sensitivity of the resonant wavelength to the angle of incidence still stands as a formidable obstacle that demands further investigation and resolution.
1. Introduction
The Sun is the only star that can be meticulously observed in great detail. Its imaging observations, characterized by high time resolution, high spatial resolution, high spectral resolution, and high polarization precision, serve as the cornerstone for in-depth research and understanding in astrophysics. The Sun’s high-temperature plasma environment provides a huge magnetohydrodynamic laboratory that cannot be simulated on Earth. Delving into and comprehending this unique environment can significantly propel our understanding of related fundamental physical phenomena. In addition, the Sun is the main driver and source of space weather. Solar activities like solar flares and coronal mass ejections can potentially bring about catastrophic consequences for modern civilization, affecting aerospace operations, navigation systems, communication networks, and even global economic stability. Hence, the observation and study of the Sun hold significant scientific and practical significance.
So far, solar observation has mainly focused on X-rays (0.01–10 nm) [1], ultraviolet (10 nm–400 nm) [2], visible light (400 nm–700 nm) [3], near-infrared (700 nm–2.5 μm) [4], and radio bands [5]. By contrast, owing to constraints in observational technology, the mid-infrared band (2.5 μm–25 μm) has mainly been observed on the McMath telescope at the NSO/Kitt Peak in the United States [6,7,8,9,10], the new 30 THz solar Telescope in Brazil [11,12,13,14], and a solar mid-infrared telescope in Mexico [15] in recent years. It is crucial to note, however, that the mid-infrared band is the last observation window yet to be fully exploited for ground-based solar telescopes. Observations in the mid-infrared band offer several unique advantages. These include minimal atmospheric scattered light, low instrumental scattered light, weak instrumental polarization, and high sensitivity to the solar magnetic field [16]. As a result, mid-infrared solar observations present abundant scientific opportunities and are expected to be a major competitive frontier in ground-based astronomical observations in the 21st century.
In recent years, a new generation of solar telescopes has gradually begun to work in the mid-infrared band. For instance, the Goode Solar Telescope (GST) at the Big Bear Solar Observatory in the United States is equipped with a mid-infrared cryogenic grating spectrograph (CrYogenic solar spectrogRAph, CYRA). CYRA has the ability to measure double-beam polarization in the 1–5 μm band and cryogenic spectral detection in the 3–5 μm band. It focuses on the identification and observation research of molecular spectral lines and magnetic-sensitive spectral lines near 4 μm [17]. The Daniel K. Inouye Solar Telescope (DKIST) in the United States, which is the world’s largest aperture optical solar telescope with a 4 m aperture, extends its observation band to the infrared band, reaching up to 30 μm. Its first-generation focal plane devices, Cryo-NIRSP and DL-NIRSP, will provide polarized spectral imaging observations in the 1–5 μm band [18]. Moreover, the Mid-Infrared System for the Accurate Measurement of Solar Magnetic Field (AIMS) is China’s first mid-infrared solar observation equipment. The AIMS telescope will observe the solar magnetic field at Mg I 12.32 μm, which is the most sensitive spectral line to solar magnetic fields discovered so far [19].
Unlike other types of astronomical observations, ultra-narrowband observation is a basic requirement for solar telescopes. The measurement of solar magnetic fields can be achieved by analyzing the splitting or polarization of spectral lines produced by the Zeeman effect. However, these magnetic signals are usually weak and mixed with the thermal Doppler broadening of the lines, making their detection and interpretation challenging. Ultra-high spectral resolution is critical to distinguish the polarization information from the Doppler-broadened profiles, enabling more precise and reliable extraction of magnetic field information. Figure 1 simulates the Stokes parameters of different observed spectral lines under the same solar magnetic field, where the transverse and the longitudinal magnetic field strengths are both 1000 G. The first column shows the simulation results of the observed spectral line Fe I at 617.3 nm, with a spectral resolution of 0.01 nm. The remaining four columns present the simulation configurations of the observed spectral line Mg I at 12.32 μm. Different columns represent different spectral resolutions, which are 0.02 nm, 0.1 nm, 0.2 nm, and 0.3 nm, respectively. For solar magnetic field measurement in the visible band, the filtering bandwidth of the telescope needs to be about 0.01 nm [20]. For example, for The Helioseismic and Magnetic Imager (HMI) onboard the Solar Dynamics Observatory (SDO), its observed spectral line is the absorption spectral line Fe I 617.3 nm in the photosphere, and the instrument bandwidth is 0.0076 nm (FWHM) [3]. The results in the first column of Figure 1 also indicate that for visible light observations, a spectral resolution of 0.01 nm is appropriate. By contrast, in the mid-infrared band, although the Doppler broadening is greater, the spectra splitting distance is also larger due to the Zeeman effect. Therefore, a spectral line resolution above 0.1 nm cannot meet the precise measurement of the Stokes parameters’ profiles. Thus, in the mid-infrared band, it is generally required that the observation bandwidth be below 0.03 nm, with 0.01 nm being the optimal value.
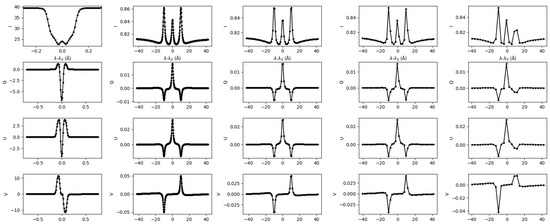
Figure 1.
Profile simulation of Stokes parameters with different observation spectral lines (Fe I at 617.3 nm and Mg I 12.32 μm) under the same solar magnetic field. Column 1: Fe I 617.3 nm with spectral resolution of 0.01 nm. Columns 2–5: Mg I 12.32 μm with spectral resolution of 0.02 nm, 0.1 nm, 0.2 nm and 0.3 nm, respectively.
In the visible and infrared bands, the narrow bandwidth requirement can be fulfilled through various filtering technologies, such as Lyot birefringent filters, Fabry–Perot interferometers, and echelle spectrographs [21,22,23]. However, for longer wavelengths within the mid-infrared range (2.5 μm–25 μm), the available filtering technologies are severely limited. Currently, the primary equipment for narrowband filtering in the mid-infrared is the Fourier Transform Infrared Spectrometer (FTIR). Nevertheless, the spectral resolution of the FTIR is closely intertwined with its time resolution. Taking the AIMS telescope as an example, the spectral resolution of FTIR is 0.06 nm, and the acquisition time of the imaging is 30 s, far from the observation requirements of fast polarization modulation. Therefore, it is a crucial challenge for the new generation of solar telescopes to achieve rapid narrowband filter imaging in the mid-infrared band.
The guided-mode resonance filter (GMRF) is a special resonant subwavelength grating developed in recent years [24,25]. When the guided wave mode of the grating waveguide structure is in phase-matching with the higher-order diffraction wave of the grating, the guided wave mode will exhibit a strong coupling reaction with the external incident wave. Subsequently, resonance occurs, enabling 100% reflection or transmission of light at a specific wavelength. Theoretically, its reflection/transmission bandwidth can reach as narrow as 0.01 nm. Furthermore, the period of the subwavelength grating is smaller than the wavelength of the incident light. Both the transmitted and reflected waves possess only zero-order diffraction waves, which effectively avoids the energy loss caused by higher-order diffraction. Therefore, the guided-mode resonance filter offers a promising solution for achieving ultra-narrowband filtering in the mid-infrared band.
The discovery of guided-mode resonance can be traced back to 1902. In that year, Wood first experimentally observed the “Wood’s anomaly” phenomenon, where the diffraction efficiency of metal reflection gratings changed abruptly. This phenomenon could not be explained by the existing grating theories at that time [14]. For several decades thereafter, the “Wood’s anomaly” remained unexplained by a reasonable physical model. It was not until 1965 that Hessel and Oliner, during their study of the guided-mode resonance phenomenon in reflection gratings, proposed using waveguide theory to interpret the “Wood’s anomaly” [25]. They established a mathematical model from a physical perspective for the first time. However, the model at that time was still an approximation. Subsequently, with the continuous development of vector diffraction theory, S. S. Wang et al. proposed that the rigorous coupled-wave analysis (RCWA) can be used to analyze, design, and control the characteristics of guided-mode resonance gratings [26]. Their research successfully reproduced various output characteristics of guided-mode resonance gratings, laying a theoretical foundation for the optimization design and practical application of GMRF [27].
Despite significant progress in GMRFs over the past three decades, the research has predominantly been centered on the visible and near-infrared bands [28,29,30,31,32,33]. By contrast, the exploration of the mid-infrared band remains severely limited. Based on the publicly accessible literature, only the U.S. Army Research Laboratory, led by N. Gupta, has consistently conducted research on guided-mode resonance filter technology in the 8–12 μm mid-infrared band since 2014 [34,35,36,37,38,39]. In 2016, they designed mid-infrared guided-mode resonance filters based on germanium and zinc selenide materials using rigorous coupled-wave analysis and analyzed the effect of angle tilt on tuning the transmission wavelength. In 2020, they extended the design from one-dimensional to two-dimensional, reducing polarization sensitivity, and designed a set of detection equipment based on FTIR for detecting the filtering performance of guided-mode resonance gratings. However, due to different research objectives and application scenarios, their filter bandwidth is around 20 nm, failing to meet the ultra-narrowband filtering requirements of solar telescopes.
Based on this, this paper describes in detail the fundamental principles and calculation procedure of guided-mode resonance filtering in Section 2. On this basis, a preliminary design and simulation of a mid-infrared guided-mode resonance filter are carried out in Section 3, where more analysis is performed to study how to realize an ultra-narrowband. In Section 4, a discussion about current issues and key research contents is given.
2. Theory
In this section, we provide a brief overview of the theoretical foundation for the calculation of guided-mode resonance filtering developed in [27,40,41,42], including resonance range, the resonance location in wavelength, grating thickness, and materials’ refractive index.
As shown in Figure 2, the basic structure of a GMRF is a waveguide composed of a planar grating [27]. GMRF consists of a cover layer (Region 1), a waveguide layer (Region 2), and a substrate layer (Region 3). The relative permittivity of the cover and substrate layers are and , respectively. The waveguide layer is a rectangular grating with a period of , a groove depth of d (grating thickness), and a fill factor of f. The relative permittivity of the grating ridges and grooves are and , respectively. Taking the z-axis perpendicular to the boundary direction, with the grating vector in the x-direction, the periodic relative permittivity within the grating region (0 < z < d) can be expanded into the following Fourier series form
where is the h-th component of the relative permittivity in the grating region, and is given by
which is complex in the presence of lossy or non-uniform media. The average relative permittivity of the grating region is . Since Region 2 is equivalent to a waveguide, it requires .
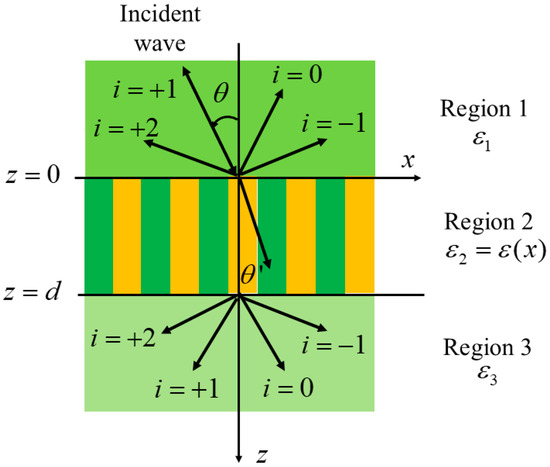
Figure 2.
Sketch of GMRF [27]. It consists of a cover layer (Region 1), a waveguide layer (Region 2), and a substrate layer (Region 3).
When a TE plane wave (the electric field vector perpendicular to the plane of incidence) is incident on a waveguide grating, the wave equation of grating is
The expression represents the total electric field inside the grating and can be expressed as
where is a function of z only, and [40].
Substituting Equations (4), (1), and (2) into Equation (3), it gives for each i-th order diffracted wave
Equation (5) is the coupled-wave equation of waveguide grating. It is seen that the wave corresponding to each value of i is coupled to its adjacent (i + h and i − h) space harmonics. But as , the coupling term becomes negligibly small, and the coupled-wave equation reduces to
This equation has the same form as the wave equation with a homogeneous slab waveguide, given by
where is the propagation constant of the mode supported by the waveguide. By direct comparison of Equations (6) and (7), the grating layer can be approximated with an equivalent homogeneous-slab waveguide with its refractive index equal to the average of the refractive index of the grating layer. The effective mode propagation constant corresponding to the i-th order evanescent diffracted wave is given by
For homogeneous-slab waveguide, a guided wave can be excited if the effective waveguide index of refraction is in the range of . Therefore, in the waveguide grating, for the i-th order diffracted wave corresponding to a leaky guided mode, the effective refractive index of the waveguide has to be in the range of
This condition approximately defines the resonance regime within which the resonance corresponding to the i-th diffraction order occurs.
Like as a homogeneous slab waveguide, the eigenvalue equation of GMRF can be given as
where , , and [41].
Moreover, the GRMF can obtain an ideal or near ideal filtering line shape and low sideband only when its refractive index and thickness are chosen such that it works as an AR coating. The AR conditions require that the grating thickness be a multiple of half-wavelength [42], i.e.,
The Equations (9)–(11) can approximately constrain resonance range, the resonance location in the wavelength, grating thickness, the materials’ refractive index, etc. The exact resonance wavelength with the line width and efficiencies of GMRF have to be determined by the rigorous coupled-wave analysis theory (RCWA).
3. Preliminary Design and Simulation
Figure 3 presents the design process of the GMRF. First, the dielectric materials for the cover layer, substrate layer, and grating layer are chosen, along with the central wavelength, grating fill factor, angle of incidence, and incident wave mode. Next, Equation (9) is utilized to determine the range of the grating period. Subsequently, based on Equation (11), the initial grating thickness is founded. With that completed, Equation (10) is solved to obtain the grating period. At this stage, all of the parameters necessary for the RCWA calculation are set. In this study, we employ the DiffracMod module in the Rsoft software. This module uses RCWA to precisely calculate the transmission and reflection efficiencies. We assess whether the FHWM meets the requirements according to the calculation results. If it does not, we adjust the grating thickness and reuse Equation (10) to obtain a new grating period. Then, DiffracMod recalculates and re-evaluates the FWHM until the requirements are satisfied. Finally, the grating period is finely adjusted so that the reflection peak is at the central wavelength.
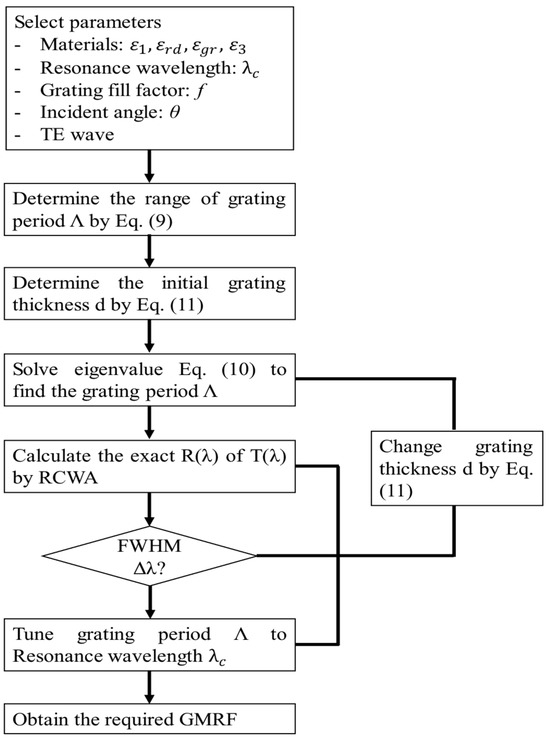
Figure 3.
The design procedure of a GMRF.
Table 1 presents the current commonly used and under-researched mid-infrared optical materials, which mainly include the following: group IV semiconductor materials such as Ge and diamond; II-V group compounds like GaAs, GaP, etc.; III-VI group compounds such as ZnS, ZnSe, CdTe, etc.; alkali halide compound crystals (NaCl, KRS-5); and chalcogenide glass GASIR. The practical infrared optical materials suitable for the 8–13 μm band are mainly Ge, ZnS, ZnSe, GaAs, diamond, and chalcogenide glass. Among them, Ge, ZnS, ZnSe, and chalcogenide glass are currently being used in large quantities. Wavefront detection of devices in the mid-infrared band is extremely challenging. To reduce the difficulty of wavefront detection for the guided-mode resonance filter, it is better to select optical materials that are also transmissive in the visible—near infrared band. Based on this, ZnS, ZnSe, and chalcogenide glass are preferred as the basic materials for the filter in mid-infrared.

Table 1.
Basic properties of mid-infrared optical materials.
In this case, as depicted in Figure 4, ZnS is chosen as both the covering layer and the base layer (n1 = n3 = 2.1585). The sub-wavelength grating consists of ZnS (ngr = 2.1585) and ZnSe (nrd = 2.3858). The GMRF we aim to design is of the reflective type, with a central wavelength of 12.32 μm and an incident angle of 45 degrees (). The range of the period Λ of the sub-wavelength grating is computed using Formulas (8) and (9), and is presented as Figure 5. The pink-colored area indicates the range of grating periods for different values of fill factor f, where , , , , and . Notably, the smaller the fill factor f, the narrower the available range for the selection of the grating period Λ.

Figure 4.
Schematic illustration for the design of mid-infrared GMRF. Purple and red represent ZnS and ZnSe respectively.
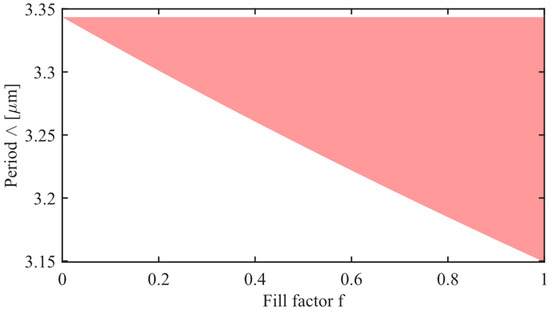
Figure 5.
The correlation between the period of sub-wavelength gratings and the filling factor f. Pink represents the period range under different f.
According to the design procedure of the GMRF depicted in Figure 3, the thickness of the grating is derived from Equation (11),
where m denotes the number of half-waves. By utilizing Equation (10) in conjunction with Rsoft software, the grating period Λ and the reflectivity line shape R(λ) can be precisely computed.
Figure 6 illustrates the grating period Λ, the reflectivity R(λ), and the full width at half maximum (FWHM) of the GMRF under various values of m when the grating filling factor f is set to 0.2 (as shown in Figure 6a and Figure 6b, respectively). It is revealed that the bandwidth of the GMRF exhibits an approximate bilinear relationship with m. Specifically, as m increases, the bandwidth decreases in an approximately linear fashion, and also the linear coefficient varies depending on whether m is odd or even. Additionally, the bandwidth when m = 2k (k being a positive integer) is about 1/62 of that when m = 2k + 1. When m = 2 and f = 0.2, the FWHM reaches 0.098 nm; when m = 6 and f = 0.2, the FWHM attains 0.034 nm.
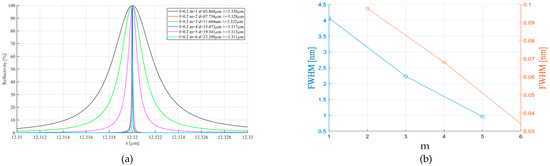
Figure 6.
Reflectivity R(λ) and FWHM of GMRF in different grating thickness d calculated by RCWA. (a) Reflectivity R(λ); (b) FWHM.
In Figure 7a,b, the reflectivity profiles R(λ) under different grating filling factors f are calculated for m = 1 and m = 2, respectively. It is evident that the bandwidth decreases as f decreases. Figure 7c,d present the corresponding relationships between the FWHM and f. It can be observed that the FWHM approximately has a linear relationship with f. When f = 0.1 and m = 2, the FWHM reaches 0.0092 nm.
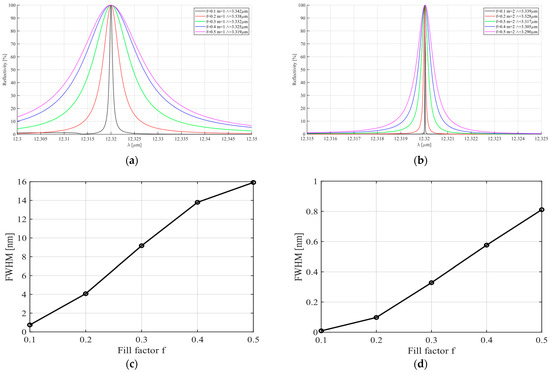
Figure 7.
Reflectivity R(λ) and FWHM of GMRF in different grating fill factors. (a) R(λ) in m = 1; (b) R(λ) in m = 2; (c,d) correspond to the FWHM of the reflectivity profiles R(λ) in (a,b), respectively.
By synthesizing the information from Figure 6 and Figure 7, we conclude that to obtain a narrower bandwidth, the thickness of the grating d should be an even multiple of the half-wavelength. Moreover, achieving an ultra-narrowband filtering can be realized by increasing the thickness of the grating and reducing the grating filling factor. In addition, Figure 8 presents the reflectivity R(λ) and FWHM of GMRF with different grating thickness error Δd in It= 2, f = 0.2, and Λ = 3.328 μm. it is shown that FWHM varies approximately linearly with the thickness error, and an error of 0.05 μm is acceptable.
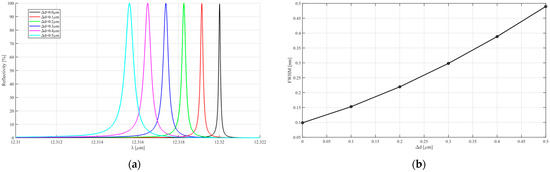
Figure 8.
Reflectivity R(λ) and FWHM of GMRF with different grating thickness error. Δd is calculated by RCWA in m = 2, f = 0.2, and Λ = 3.328 μm. (a) Reflectivity R(λ); (b) FWHM.
Figure 9 shows the calculated reflectivity curves at different incident angles when f = 0.2, m = 2, and Λ = 3.328 μm. Different colors represent different incident angles, and the incident angle varies from 44.5 degrees to 45.5 degrees with an interval of 0.25 degrees. It is clearly evident that the peak wavelength shifts rapidly towards the longer wavelength direction as the incident angle increases. It means that the resonant wavelength is highly sensitive to the incident angle under this design.
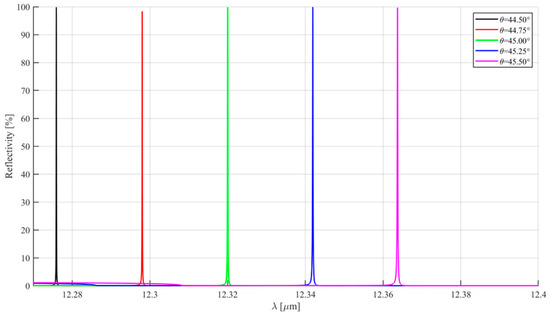
Figure 9.
Reflectivity R(λ) at different incident angle θ.
4. Discussion and Conclusions
The mid-infrared band is the last observational window for the new generation of ground-based large solar telescopes in the 21st century. However, how to achieve ultra-narrowband filter imaging in the mid-infrared band is a fundamental issue faced by all solar telescopes when developing for the mid-infrared band. The guided-mode resonance filtering technology provides a possibility for solving this fundamental problem. Moreover, GMRF represents an inevitable trend in the development of optical technology. Physically, it has evolved from the scalar diffraction theory to the vector diffraction theory, significantly reducing the geometric size and weight of narrowband filtering devices. For example, the length of a traditional visible light birefringent filter is approximately 0.4 m, and it weighs about 25 kg; the length of a mid-infrared Fourier spectrometer is approximately 1.5 m, and it weighs about 600 kg; the thickness of a GMRF is only in the millimeter range, and it weighs about 0.3 kg. In the future, it will greatly enhance the flexibility of terminal devices and be widely applied in fields such as astronomy, the military, remote sensing, and biology, showing very broad application prospects.
In this paper, we carried out the preliminary design and simulation of the mid-infrared ultra-narrowband guided-mode resonance filter (GMRF). The results show that when the thickness of the sub-wavelength grating is an even multiple of the half-wavelength, ultra-narrowband filtering below 0.03 nm can be achieved by increasing the grating thickness and reducing the grating fill factor, which meets the scientific observation requirements of solar telescopes in the mid-infrared band.
Nevertheless, the high sensitivity of the resonant wavelength to the angle of incidence remains a substantial challenge. Researchers such as M. G. Moharam and A. Sen-tenac have carried out extensive fundamental theoretical investigations aimed at reducing this sensitivity to the angle of incidence [43,44,45,46,47]. In the next step, it is necessary and important to enlarge the observable field of view of the ultra-narrowband GMRF. Additionally, the fabrication process of mid-infrared GMRF and the tuning of its center wavelength will also be the key research focuses in the future.
Funding
This research was funded by National Natural Science Foundation of China (grant numbers 12473086 and 1142790), National Key Research and Development Program of China (grant numbers 2021YFA1600500), and Youth Innovation Promotion Association of the Chinese Academy of Sciences (2022057).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data in this paper have been presented in figures or tables.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhang, Z.; Chen, D.Y.; Wu, J.; Chang, J.; Hu, Y.M.; Su, Y.; Zhang, Y.; Wang, J.P.; Liang, Y.M.; Ma, T.; et al. Hard X-ray Imager (HXI) onboard the ASO-S mission. Res. Astron. Astrophys. 2019, 19, 160. [Google Scholar] [CrossRef]
- Lemen, J.R.; Title, A.M.; Akin, D.J.; Boerner, P.F.; Chou, C.; Drake, J.F.; Duncan, D.W.; Edwards, C.G.; Friedlaender, F.M.; Heyman, G.F. The Atmospheric Imaging Assembly (AIA) on the Solar Dynamics Observatory (SDO). Sol. Phys. 2012, 275, 17–40. [Google Scholar] [CrossRef]
- Scherrer, P.H.; Schou, J.; Bush, R.I.; Kosovichev, A.G.; Bogart, R.S.; Hoeksema, J.T.; Liu, Y.; Duvall, T.L., Jr.; Zhao, J.; Title, A.M. The Helioseismic and Magnetic Imager (HMI) Investigation for the Solar Dynamics Observatory (SDO). Sol. Phys. 2012, 275, 207–227. [Google Scholar] [CrossRef]
- Meng, W.J.; Xu, F.Y.; Jin, Z.Y. New Vacuum Solar Telescope Achieves Narrowband Infrared Solar Imaging Observation at HeI 10830Å. Res. Astron. Astrophys. 2024, 24, 055008. [Google Scholar] [CrossRef]
- Zhang, L.; Su, Y.R.; Wu, Z.; Chang, S.W.; Chen, Y.; Yan, F.B. A New 6–15 GHz Solar Radio Observation System. Astrophys. J. Suppl. Ser. 2023, 268, 27. [Google Scholar] [CrossRef]
- Zirin, H.; Popp, B. Observations of the 12 micron Mg I lines in various solar features. Astrophys. J. 1989, 340, 571–678. [Google Scholar] [CrossRef]
- Hewagama, T.; Deming, D.L.; Jennings, D.E.; Osherovich, V.; Wiedemann, G.; Zipoy, D.; Mickey, D.L.; Garcia, H. Solar magnetic field studies using the 12 micron emission lines. II–Stokes profiles and vector field samples in sunspots. Astrophys. J. Suppl. Ser. 1993, 86, 313–332. [Google Scholar] [CrossRef]
- Moran, T.; Deming, D.L.; Jennings, D.E.; McCabe, G. Solar Magnetic Field Studies Using the 12 Micron Emission Lines. III. Simultaneous Measurements at 12 and 1.6 Microns. Astrophys. J. 2000, 533, 1035–1042. [Google Scholar] [CrossRef]
- Jennings, D.E.; Deming, D.L.; McCabe, G.; Sada, P.; Moran, T. Solar Magnetic Field Studies Using the 12 Micron Emission Lines. IV. Observations of a Delta Region Solar Flare. Astrophys. J. 2002, 568, 1043–1048. [Google Scholar] [CrossRef]
- Moran, T.G.; Jennings, D.E.; Deming, L.D.; McCabe, G.; Sada, P.; Boyle, R. Solar Magnetograms at 12 μm Using the Celeste Spectrograph. Sol. Phys. 2007, 241, 213–222. [Google Scholar] [CrossRef]
- Melo, A.M.; Kaufmann, P.; Kudaka, A.S.; Raulin, J.P. A New Setup for Ground-based Measurements of Solar Activity at 10 μm. Publ. Astron. Soc. Pac. 2006, 118, 1558–1563. [Google Scholar] [CrossRef]
- Cassiano, M.M.; Kaufmann, P.; Marcon, R.; Kudaka, A.S.; Marun, A.; Godoy, R.; Pereyra, P.; Melo, A.M.; Levato, H. Fast Mid-IR Flashes Detected During Small Solar X-Ray Bursts. Solar Phys. 2010, 264, 71–79. [Google Scholar] [CrossRef]
- Kudaka, A.S.; Cassiano, M.M.; Marcon, R.; Cabezas, D.P.; Fernandes, L.O.T.; Hidaigo Ramirez, R.F.; Kaufmann, P.; De Souza, R.V. The New 30 THz Solar Telescope in São Paulo, Brazil. Sol. Phys. 2015, 290, 2373–2379. [Google Scholar] [CrossRef]
- Trottet, G.; Raulin, J.P.; Mackinnon, A.; De Castro, G.G.; Simões, D.; Cabezas, P.J.A.; de La Luz, V.; Luoni, M.; Kaufmann, P. Origin of the 30 THz Emission Detected During the Solar Flare on 2012 March 13 at 17:20 UT. Solar Phys. 2015, 290, 2809–2826. [Google Scholar] [CrossRef]
- Mendoza-Torres, J.E.; Palacios-Fonseca, J.S.; Velázquez-de-la-Rosa, M.; Rodríguez-Montero, P.; De-Roa-Campoy, A.; Valadez-Campos, E.; Arias-Estrada, M.O.; Peña-Saint-Martín, J.; Rodríguez-Pedroza, B.; Gómez-Arista, I.; et al. A solar mid-infrared telescope. Rev. Mex.Astron. Astrofísica 2019, 55, 11–16. [Google Scholar] [CrossRef]
- Penn, M.J. Infrared Solar Physics. Living Rev. Sol. Phys. 2014, 11, 2. [Google Scholar] [CrossRef] [PubMed]
- Cao, W.; Gorceix, N.; Coulter, R.; Ahn, K.; Rimmele, T.R.; Goode, P.R. Scientific instrumentation for the 1.6 m New Solar Telescope in Big Bear. Astron. Nachr. 2010, 331, 636–639. [Google Scholar] [CrossRef]
- Rimmele, T.R.; Warner, M.; Keil, S.L.; Goode, P.R.; Knölker, M.; Kuhn, J.R.; Rosner, R.R.; McMullin, J.P.; Casini, R.; Lin, H.S. The Daniel, K. Inouye Solar Telescope—Observatory Overview. Sol Phys. 2020, 295, 172. [Google Scholar] [CrossRef]
- Shen, Y.; Kewei, E.; Fu, X.; Wang, D.; Hou, J.; Liang, M.; Xu, S. Alignment technology based on a central small aperture for the AIMS telescope. Appl. Opt. 2022, 61, 5646–5656. [Google Scholar] [CrossRef]
- Stenflo, J.O. Measurements of magnetic fields and the analysis of stokes profiles. Sol. Phys. 1985, 100, 189–208. [Google Scholar] [CrossRef]
- Evans, J.W. The Birefringent Filter. J. Opt. Soc. Am. 1949, 39, 229–237. [Google Scholar] [CrossRef]
- Solanki, S.K.; Del Toro Iniesta, J.C.; Woch, J.; Gandorfer, A.; Hirzberger, J.; Alvarez-Herrero, A.; Appourchaux, A.; Pillet, V.M.; Pérez-Grande, I.; Sanchis Kilders, E. The Polarimetric and Helioseismic Imager on Solar Orbiter. Astron. Astrophys. 2020, 642, A11. [Google Scholar] [CrossRef]
- Hou, J.F.; Xu, Z.; Yuan, S.; Chen, Y.C.; Peng, J.G.; Wang, D.G.; Xu, J.; Deng, Y.Y.; Jin, Z.Y.; Ji, K.F. Spectro-polarimetric observations at the NVST: I. instrumental polarization calibration and primary measurements. Res. Astron. Astrophys. 2020, 20, 45. [Google Scholar] [CrossRef]
- Wood, R.W. On a remarkable case of uneven distribution of light in a diffraction grating spectrum. Philos. Mag. 1902, 4, 396–402. [Google Scholar] [CrossRef]
- Hessel, A.; Oliner, A.A. A new theory of Wood’s anomalies on optical gratings. Appl. Opt. 1965, 4, 1275–1297. [Google Scholar] [CrossRef]
- Wang, S.S.; Magnusson, R.; Bagby, J.S.; Moharam, M.G. Guided-mode resonances in planar dielectric-layer diffraction gratings. J. Opt. Soc. Am. A 1990, 7, 1470–1474. [Google Scholar] [CrossRef]
- Wang, S.S.; Magnusson, R. Theory and applications of guided-mode resonance filters. Appl. Opt. 1993, 32, 2606–2613. [Google Scholar] [CrossRef]
- Dudovich, N.; Levy-Yurista, G.; Sharon, A.Z.; Friesem, A.A.; Weber, H. Active semiconductor-based grating waveguide structures. IEEE J. Quantum Electron. 2001, 37, 1030–1039. [Google Scholar] [CrossRef]
- Samuel, T.T.; Morris, G.M. Controlling the spectral response in guided-mode resonance filter design. Appl. Opt. 2003, 42, 3225–3233. [Google Scholar] [CrossRef]
- Ding, Y.; Magnusson, R. Doubly resonant single-layer bandpass optical filters. Opt. Lett. 2004, 29, 1135–1137. [Google Scholar] [CrossRef]
- Yang, F.; Yen, G.; Rasigade, G.; Soares, J.A.N.T.; Cunningham, B.T. Optically tuned resonant optical reflectance filter. Appl. Phys. Lett. 2008, 92, 091115. [Google Scholar] [CrossRef]
- Kodali, A.K.; Schulmerich, M.; Ip, J.; Yen, G.; Cunningham, B.T.; Bhargava, R. Narrowband Midinfrared Reflectance Filters Using Guided Mode Resonance. Anal. Chem. 2010, 82, 5697–5706. [Google Scholar] [CrossRef]
- Quaranta, G.; Basset, G.; Martin, O.J.; Gallinet, B. Recent Advances in Resonant Waveguide Gratings. Laser Photonics Rev. 2018, 12, 1800017. [Google Scholar] [CrossRef]
- Hogan, B.; Hegarty, S.P.; Lewis, L.; Romero-Vivas, J.; Ochalski, T.J.; Huyetet, G. Realization of high-contrast gratings operating at 10 μm. Opt. Lett. 2016, 41, 5130–5133. [Google Scholar] [CrossRef] [PubMed]
- Gupta, N.; Mirotznik, M.S. Performance characterization of tunable longwave infrared notch filters using quantum cascade lasers. Opt. Eng. 2018, 57, 127101. [Google Scholar] [CrossRef]
- Gupta, N.; Song, J. High-quality large-scale electron-beam-written resonant filters for the long-wave infrared region. Opt. Lett. 2021, 46, 348–351. [Google Scholar] [CrossRef] [PubMed]
- Gupta, N.; Song, J. Longwave infrared polarization independent Monolithic guided mode resonance filters with double-sided orthogonal linear gratings. Opt. Contin. 2022, 1, 674–683. [Google Scholar] [CrossRef]
- Gupta, N.; Song, J. Polarization independent electron-beam written 2-D longwave infrared guided-mode resonant filters. Opt. Contin. 2023, 2, 197–204. [Google Scholar] [CrossRef]
- Matsuoka, Y.; Mathonnèire, S.; Peters, S.; Masselink, W.T. Broadband multilayer anti-reflection coating for mid-infrared range from 7 μm to 12 μm. Appl. Opt. 2018, 57, 1645–1649. [Google Scholar] [CrossRef]
- Gaylord, T.K.; Moharam, M.G. Analysis and applications of optical diffraction by gratings. Proc. IEEE 1985, 73, 894–937. [Google Scholar] [CrossRef]
- Wang, S.S.; Magnusson, R. Multilayer waveguide-grating filters. Appl. Opt. 1995, 34, 2414–2420. [Google Scholar] [CrossRef]
- Wang, S.S.; Magnusson, R. Design of waveguide-grating filters with symmetrical line shapes and low sidebands. Opt. Lett. 1994, 19, 919–921. [Google Scholar] [CrossRef]
- Lemarchand, F.; Sentenac, A.; Giovannini, H. Increasing the angular tolerance of resonant grating filters with doubly periodic structures. Opt. Lett. 1998, 23, 1149–1151. [Google Scholar] [CrossRef] [PubMed]
- Boonruang, S.; Greenwell, A.; Moharam, M.G. Broadening the angular tolerance in two-dimensional grating resonance structures at oblique incidence. Appl. Opt. 2007, 46, 7982–7992. [Google Scholar] [CrossRef] [PubMed]
- Jacob, D.K.; Dunn, S.C.; Moharam, M.G. Normally incident resonant grating reflection filter for efficient narrow-band spectral filtering of finite beams. J. Opt. Soc. Am. A. 2001, 18, 2109–2120. [Google Scholar] [CrossRef] [PubMed]
- Sentenac, A.; Fehrembach, A.L. Angular tolerant resonant grating filters under oblique incidence. J. Opt. Soc. Am. A 2005, 22, 475–480. [Google Scholar] [CrossRef]
- Lemarchand, F.; Sentenac, A.; Cambril, E.; Giovannini, H. Study of the resonant behavior of waveguide gratings: Increasing the angular tolerance of guided-mode filters. J. Opt. A Pure Appl. Opt. 1999, 1, 545–551. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).