Neutron Star Inner Crust at Finite Temperatures: A Comparison Between Compressible Liquid Drop and Extended Thomas–Fermi Approaches
Abstract
1. Introduction
2. Treatment of the Inner Crust at Finite Temperature
2.1. The Temperature-Dependent ETF
2.2. The Temperature-Dependent CLDM
- (i)
- (ii)
- (iii)
3. Neutron Star Crust at Finite Temperature
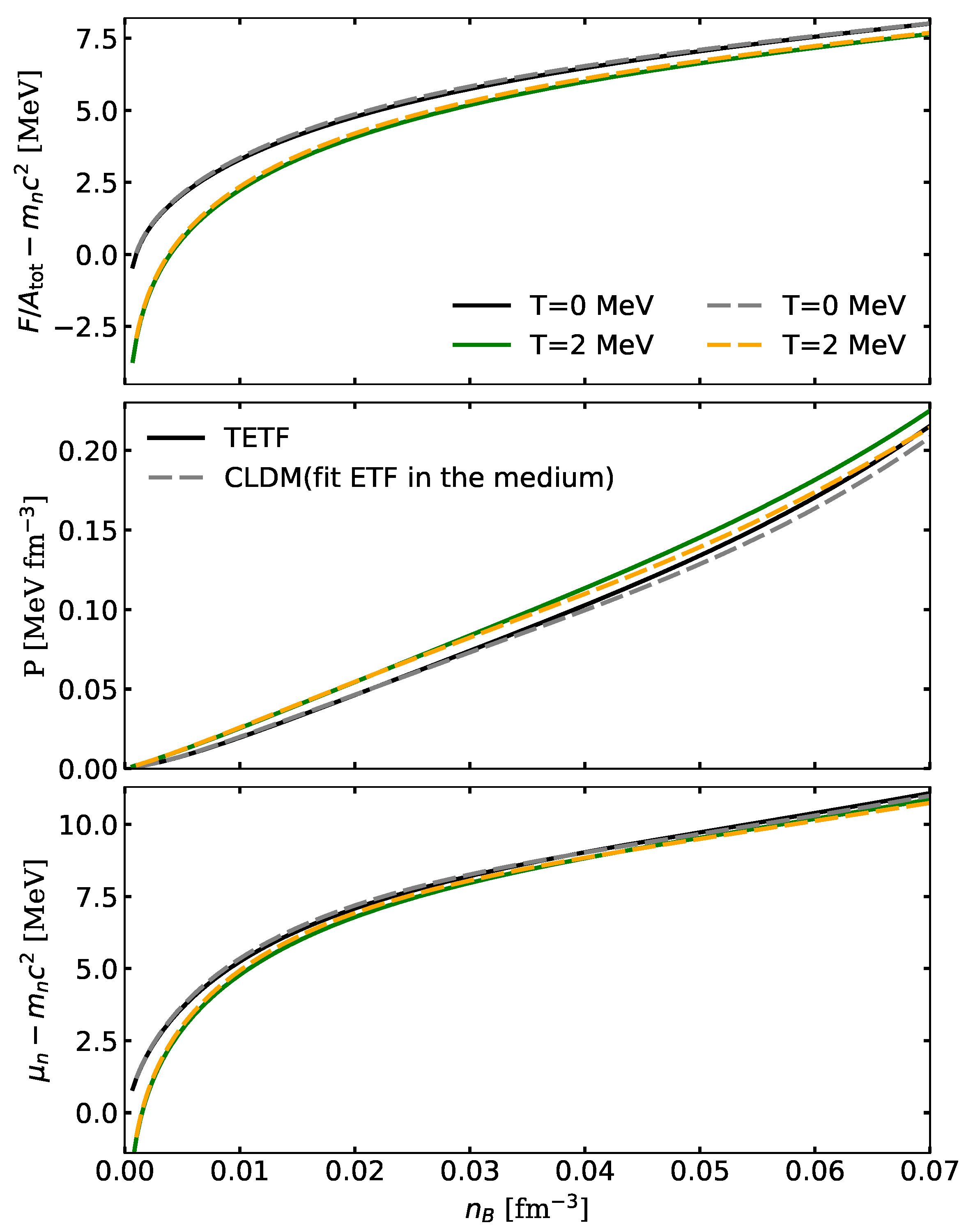
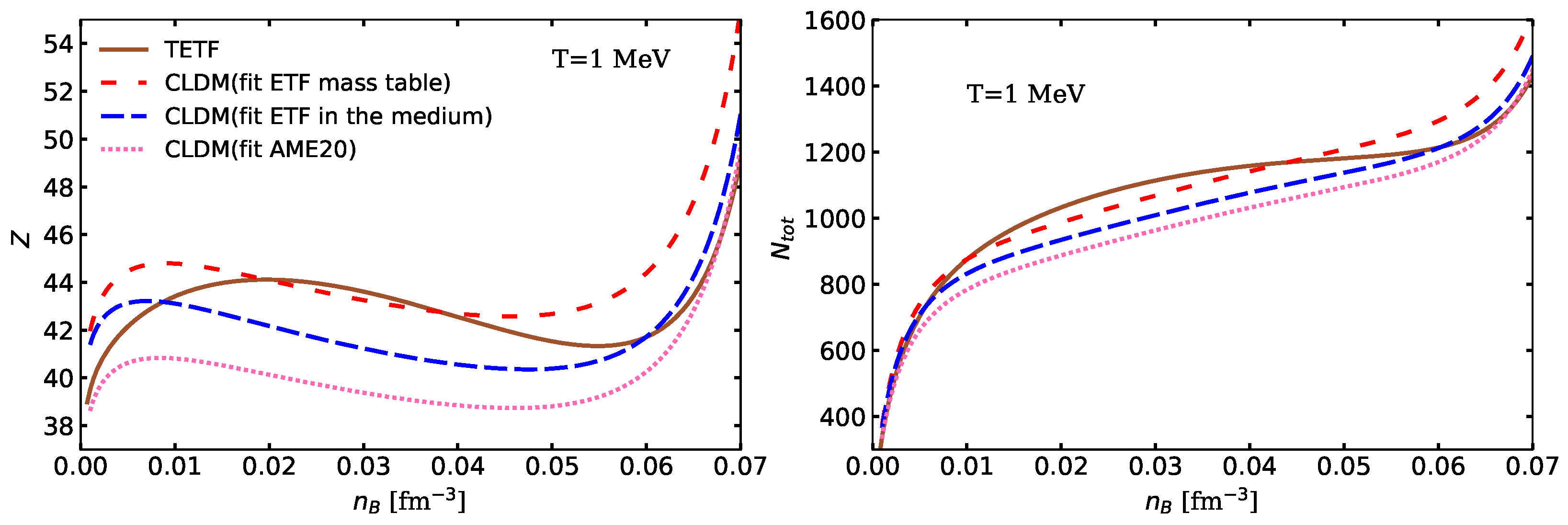
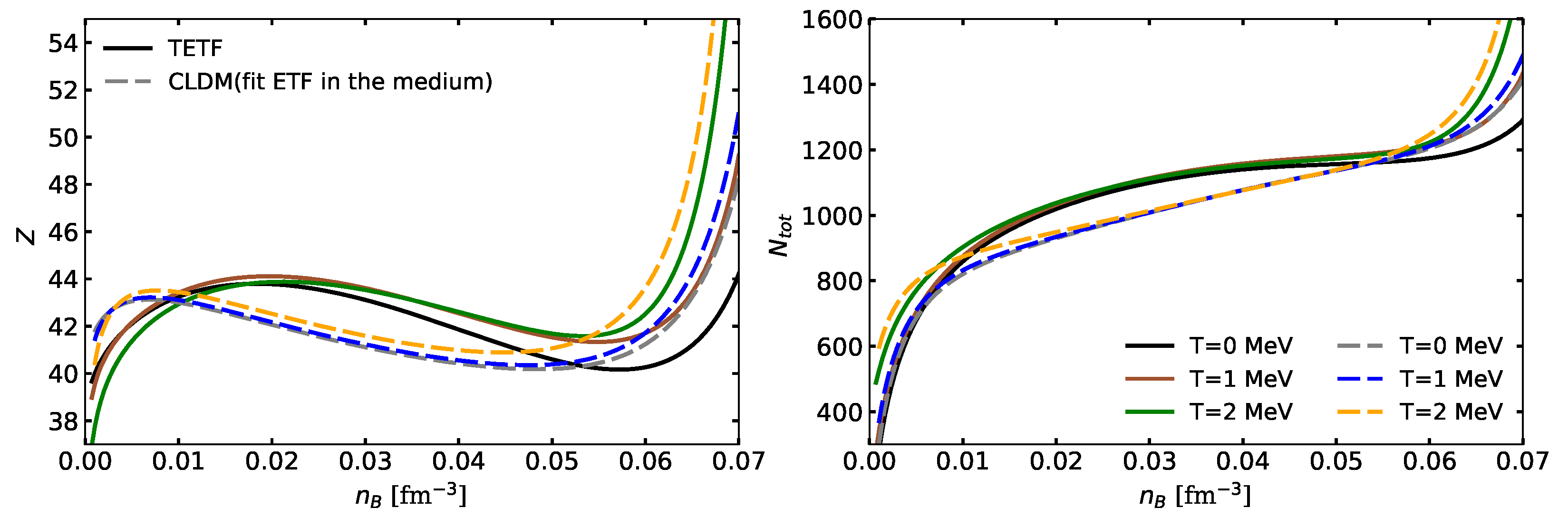
3.1. Thermodynamic Properties and Composition
3.2. Density Profiles at Zero and Finite Temperature
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AME | Atomic Mass Evaluation |
| CLDM | compressible liquid-drop model |
| EoS | equation of state |
| (E)TF | (extended) Thomas–Fermi |
| ETFSI | extended Thomas–Fermi plus Strutinsky integral |
| HFB | Hartree–Fock–Bogoliubov |
| MM | meta-model |
| NS | neutron star |
| OCP | one-component plasma |
| TTF | temperature-dependent Thomas–Fermi |
| TETF | temperature-dependent extended Thomas–Fermi |
| TETFSI | temperature-dependent extended Thomas–Fermi plus Strutinsky integral |
| WS | Wigner–Seitz |
Appendix A. Fit of the CLDM Surface Parameters to ETF Calculations
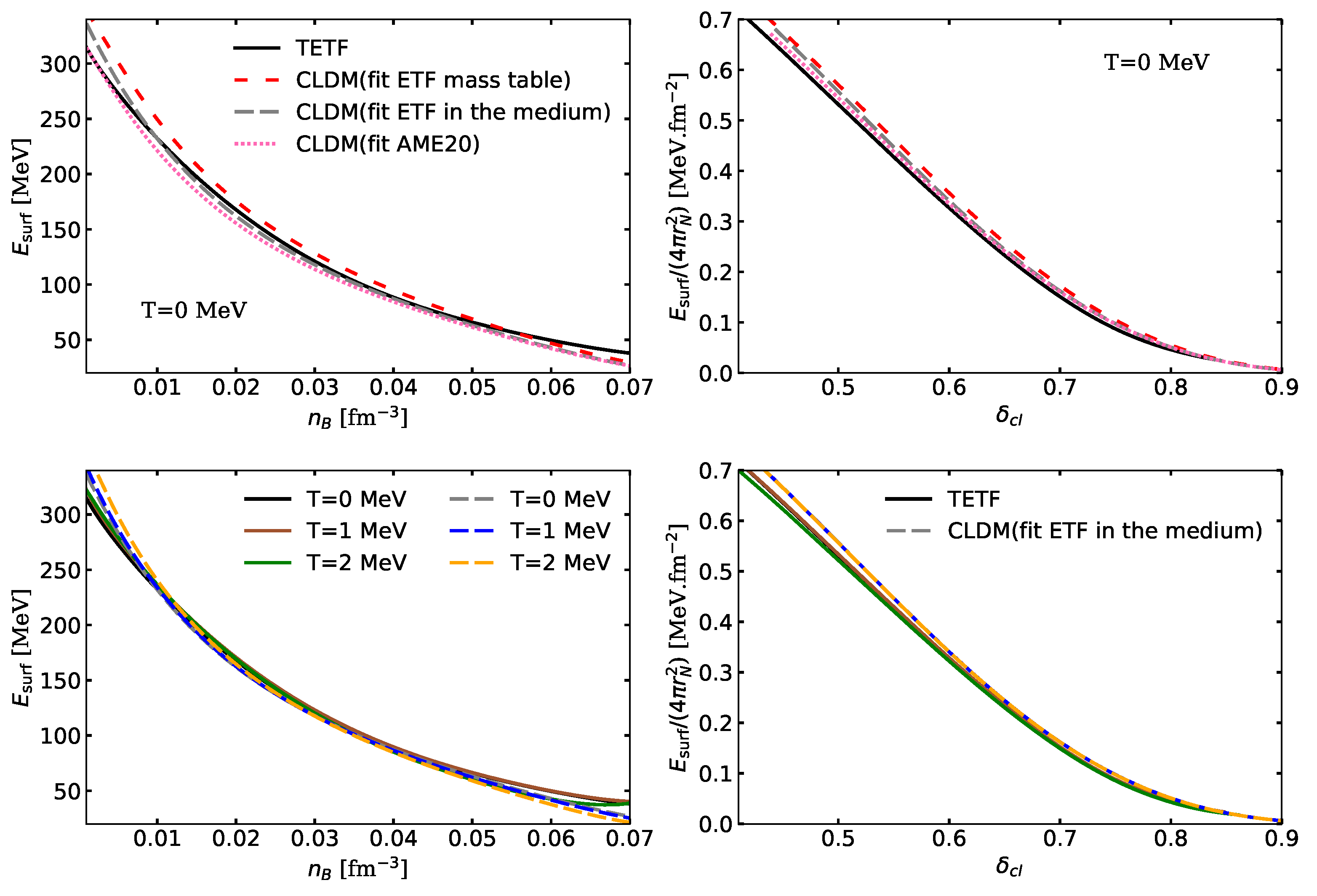
Appendix B. Comparison of the Surface Energy Between the TETF and the CLDM
| 1 | We use the F and to denote the free energy per cell and the free energy per unit volume, respectively. |
| 2 | We compute the Fermi integrals of order 3/2 and 1/2 with the GSL routines available at https://gsl.ampl.com/ref/fermi-dirac.html (accessed on 5 May 2025). For the Fermi integral of order −1/2 and −3/2 we rely on the formulae introduced in Ref. [54]. |
| 3 | We checked that for all the conditions explored in this work, the temperature always remains below the critical temperature. |
| 4 | For this fit, the ETF energy is calculated for different fixed proton fractions and ion proton numbers, associated with different background gas densities; see Appendix A for details. |
| 5 | The ETF mass table calculated with the BSk24 functional is available at https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/635/A84 (accessed on 5 May 2025). |
| 6 | |
| 7 | We actually checked the impact of the above-mentioned points and fitted the surface parameters on ETF calculations in the medium using a standard Fermi profile and the SLy4 functional, and including the proton exchange in the Coulomb term. The best-fit value of the p parameter thus obtained is if we use the parametrization of the curvature tension as in Equation (25), and if we use Equation (49) in Ref. [64], that is, neglecting the term. These latter results are in better agreement with those of Refs. [34,64], confirming that the differences in the fitting procedure mentioned above can account for the discrepancy in the resulting p values. |
| 8 | We have also performed a fit including a neutron skin. However, this yielded a higher , in accordance with the results of Ref. [64]. Therefore, we only kept the prescription without the neutron skin for this work. |
References
- Chamel, N.; Haensel, P. Physics of Neutron Star Crusts. Living Rev. Relativ. 2008, 11, 10. [Google Scholar] [CrossRef] [PubMed]
- Gittins, F.; Andersson, N.; Jones, D.I. Modelling neutron star mountains. Mon. Not. R. Astron. Soc. 2020, 500, 5570–5582. [Google Scholar] [CrossRef]
- Foucart, F. Neutrino transport in general relativistic neutron star merger simulations. Living Rev. Comput. Astrophys. 2023, 9, 1. [Google Scholar] [CrossRef]
- Prakash, M.; Bombaci, I.; Prakash, M.; Ellis, P.J.; Lattimer, J.M.; Knorren, R. Composition and structure of protoneutron stars. Phys. Rep. 1997, 280, 1–77. [Google Scholar] [CrossRef]
- Yakovlev, D.G.; Pethick, C.J. Neutron Star Cooling. Annu. Rev. Astron. Astrophys. 2004, 42, 169–210. [Google Scholar] [CrossRef]
- Pons, J.A.; Reddy, S.; Prakash, M.; Lattimer, J.M.; Miralles, J.A. Evolution of protoneutron stars. Astrophys. J. 1999, 513, 780. [Google Scholar] [CrossRef]
- Dinh Thi, H.; Fantina, A.F.; Gulminelli, F. The proto-neutron star inner crust in the liquid phase. A&A 2023, 672, A160. [Google Scholar] [CrossRef]
- Dehman, C.; Centelles, M.; Viñas, X. Impact of the hot inner crust on compact stars at finite temperature. A&A 2024, 687, A236. [Google Scholar] [CrossRef]
- Scurto, L.; Carvalho, V.; Pais, H.; Providência, C. Assessing the joint effect of temperature and magnetic field on the neutron star equation of state. Phys. Rev. C 2024, 110, 045805. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Douglas Swesty, F. A generalized equation of state for hot, dense matter. Nucl. Phys. A 1991, 535, 331–376. [Google Scholar] [CrossRef]
- Oertel, M.; Hempel, M.; Klähn, T.; Typel, S. Equations of state for supernovae and compact stars. Rev. Mod. Phys. 2017, 89, 015007. [Google Scholar] [CrossRef]
- Schneider, A.S.; Roberts, L.F.; Ott, C.D. Open-source nuclear equation of state framework based on the liquid-drop model with Skyrme interaction. Phys. Rev. C 2017, 96, 065802. [Google Scholar] [CrossRef]
- Tsiopelas, S.; Sedrakian, A.; Oertel, M. Finite-temperature equations of state of compact stars with hyperons: Three-dimensional tables. Eur. Phys. J. A 2024, 60, 127. [Google Scholar] [CrossRef]
- Fiorella Burgio, G.; Fantina, A.F. Nuclear Equation of State for Compact Stars and Supernovae. In The Physics and Astrophysics of Neutron Stars; Rezzolla, L., Pizzochero, P., Jones, D.I., Rea, N., Vidaña, I., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 255–335. [Google Scholar] [CrossRef]
- Burgio, G.F.; Schulze, H.J.; Vidana, I.; Wei, J.B. Neutron stars and the nuclear equation of state. Prog. Part. Nucl. Phys. 2021, 120, 103879. [Google Scholar] [CrossRef]
- Carreau, T.; Gulminelli, F.; Chamel, N.; Fantina, A.F.; Pearson, J.M. Crystallization of the inner crust of a neutron star and the influence of shell effects. A&A 2020, 635, A84. [Google Scholar] [CrossRef]
- Brack, M.; Guet, C.; Håkansson, H.B. Selfconsistent semiclassical description of average nuclear properties a link between microscopic and macroscopic models. Phys. Rep. 1985, 123, 275–364. [Google Scholar] [CrossRef]
- Bartel, J.; Brack, M.; Durand, M. Extended Thomas–Fermi theory at finite temperature. Nucl. Phys. A 1985, 445, 263–303. [Google Scholar] [CrossRef]
- Shen, H.; Toki, H.; Oyamatsu, K.; Sumiyoshi, K. Relativistic Equation of State for core-collapse Supernova Simulations. Astrophys. J. Suppl. Ser. 2011, 197, 20. [Google Scholar] [CrossRef]
- Onsi, M.; Przysiezniak, H.; Pearson, J.M. Equation of state of stellar nuclear matter in the temperature-dependent extended Thomas–Fermi formalism. Phys. Rev. C 1997, 55, 3139–3148. [Google Scholar] [CrossRef]
- Onsi, M.; Dutta, A.K.; Chatri, H.; Goriely, S.; Chamel, N.; Pearson, J.M. Semi-classical equation of state and specific-heat expressions with proton shell corrections for the inner crust of a neutron star. Phys. Rev. C 2008, 77, 065805. [Google Scholar] [CrossRef]
- Hempel, M.; Schaffner-Bielich, J. A statistical model for a complete supernova equation of state. Nucl. Phys. A 2010, 837, 210–254. [Google Scholar] [CrossRef]
- Raduta, A.R.; Gulminelli, F. Nuclear Statistical Equilibrium Equation of State for Core Collapse. Nucl. Phys. A 2019, 983, 252–275. [Google Scholar] [CrossRef]
- Steiner, A.W.; Hempel, M.; Fischer, T. Core-collapse Supernova Equations of State Based on Neutron Star Observations. Astrophys. J. 2013, 774, 17. [Google Scholar] [CrossRef]
- Furusawa, S.; Sumiyoshi, K.; Yamada, S.; Suzuki, H. New Equations of State Based on the Liquid Drop Model of Heavy Nuclei and Quantum Approach to Light Nuclei for Core-collapse Supernova Simulations. Astrophys. J. 2013, 772, 95. [Google Scholar] [CrossRef]
- Togashi, H.; Nakazato, K.; Takehara, Y.; Yamamuro, S.; Suzuki, H.; Takano, M. Nuclear equation of state for core-collapse supernova simulations with realistic nuclear forces. Nucl. Phys. A 2017, 961, 78–105. [Google Scholar] [CrossRef]
- Grams, G.; Margueron, J.; Somasundaram, R.; Chamel, N.; Goriely, S. Neutron star crust properties: Comparison between the compressible liquid-drop model and the extended Thomas–Fermi approach. J. Physi. Conf. Ser. 2022, 2340, 012030. [Google Scholar] [CrossRef]
- Goriely, S.; Chamel, N.; Pearson, J.M. Further explorations of Skyrme-Hartree-Fock-Bogoliubov mass formulas. XIII. The 2012 atomic mass evaluation and the symmetry coefficient. Phys. Rev. C 2013, 88, 024308. [Google Scholar] [CrossRef]
- Pearson, J.M.; Chamel, N.; Potekhin, A.Y.; Fantina, A.F.; Ducoin, C.; Dutta, A.K.; Goriely, S. Unified equations of state for cold non-accreting neutron stars with Brussels-Montreal functionals—I. Role of symmetry energy. Mon. Not. R. Astron. Soc. 2018, 481, 2994–3026. [Google Scholar] [CrossRef]
- Carreau, T.; Fantina, A.F.; Gulminelli, F. Inner crust of a neutron star at the point of crystallization in a multicomponent approach. A&A 2020, 640, A77. [Google Scholar] [CrossRef]
- Dinh Thi, H.; Fantina, A.F.; Gulminelli, F. The proto-neutron star inner crust in a multi-component plasma approach. A&A 2023, 677, A174. [Google Scholar] [CrossRef]
- Haensel, P.; Potekhin, A.Y.; Yakovlev, D.G. Neutron Stars 1: Equation of State and Structure; Springer: New York, NY, USA, 2007. [Google Scholar]
- Burrows, A.; Lattimer, J.M. On the accuracy of the single-nucleus approximation in the equation of state of hot, dense matter. Astrophys. J. 1984, 285, 294–303. [Google Scholar] [CrossRef]
- Balliet, L.E.; Newton, W.G.; Cantu, S.; Budimir, S. Prior Probability Distributions of Neutron Star Crust Models. Astrophys. J. 2021, 918, 79. [Google Scholar] [CrossRef]
- Dinh Thi, H.; Carreau, T.; Fantina, A.F.; Gulminelli, F. Uncertainties in the pasta-phase properties of catalysed neutron stars. A&A 2021, 654, A114. [Google Scholar] [CrossRef]
- Pearson, J.M.; Chamel, N.; Potekhin, A.Y. Unified equations of state for cold nonaccreting neutron stars with Brussels-Montreal functionals. II. Pasta phases in semiclassical approximation. Phys. Rev. C 2020, 101, 015802. [Google Scholar] [CrossRef]
- Parmar, V.; Das, H.C.; Kumar, A.; Sharma, M.K.; Arumugam, P.; Patra, S.K. Pasta properties of the neutron star within effective relativistic mean-field model. Phys. Rev. D 2022, 106, 023031. [Google Scholar] [CrossRef]
- Lim, Y.; Holt, J.W. Structure of neutron star crusts from new Skyrme effective interactions constrained by chiral effective field theory. Phys. Rev. C 2017, 95, 065805. [Google Scholar] [CrossRef]
- Shchechilin, N.N.; Zemlyakov, N.A.; Chugunov, A.I.; Gusakov, M.E. Pasta Phases in Neutron Star Mantle: Extended Thomas–Fermi vs. Compressible Liquid Drop Approaches. Universe 2022, 8, 582. [Google Scholar] [CrossRef]
- Pearson, J.M.; Chamel, N. Unified equations of state for cold nonaccreting neutron stars with Brussels-Montreal functionals. III. Inclusion of microscopic corrections to pasta phases. Phys. Rev. C 2022, 105, 015803. [Google Scholar] [CrossRef]
- Shchechilin, N.N.; Chamel, N.; Pearson, J.M. Unified equations of state for cold nonaccreting neutron stars with Brussels-Montreal functionals. IV. Role of the symmetry energy in pasta phases. Phys. Rev. C 2023, 108, 025805. [Google Scholar] [CrossRef]
- Pascal, A.; Novak, J.; Oertel, M. Proto-neutron star evolution with improved charged-current neutrino–nucleon interactions. Mon. Not. Roy. Astron. Soc. 2022, 511, 356–370. [Google Scholar] [CrossRef]
- Alford, M.G.; Haber, A.; Harris, S.P.; Zhang, Z. Beta Equilibrium Under Neutron Star Merger Conditions. Universe 2021, 7, 399. [Google Scholar] [CrossRef]
- Camelio, G.; Lovato, A.; Gualtieri, L.; Benhar, O.; Pons, J.A.; Ferrari, V. Evolution of a proto-neutron star with a nuclear many-body equation of state: Neutrino luminosity and gravitational wave frequencies. Phys. Rev. D 2017, 96, 043015. [Google Scholar] [CrossRef]
- Wigner, E.; Seitz, F. On the Constitution of Metallic Sodium. Phys. Rev. 1933, 43, 804–810. [Google Scholar] [CrossRef]
- Wigner, E.; Seitz, F. On the Constitution of Metallic Sodium. II. Phys. Rev. 1934, 46, 509–524. [Google Scholar] [CrossRef]
- Baym, G.; Bethe, H.A.; Pethick, C.J. Neutron star matter. Nucl. Phys. A 1971, 175, 225–271. [Google Scholar] [CrossRef]
- Salpeter, E.E. Energy and Pressure of a Zero-Temperature Plasma. Astrophys. J. 1961, 134, 669. [Google Scholar] [CrossRef]
- Negele, J.; Vautherin, D. Neutron star matter at sub-nuclear densities. Nucl. Phys. A 1973, 207, 298–320. [Google Scholar] [CrossRef]
- Bonche, P.; Vautherin, D. A mean-field calculation of the equation of state of supernova matter. Nucl. Phys. A 1981, 372, 496–526. [Google Scholar] [CrossRef]
- Chamel, N.; Naimi, S.; Khan, E.; Margueron, J. Validity of the Wigner-Seitz approximation in neutron star crust. Phys. Rev. C 2007, 75, 055806. [Google Scholar] [CrossRef]
- Newton, W.G.; Stone, J.R. Modeling nuclear “pasta” and the transition to uniform nuclear matter with the 3D Skyrme-Hartree-Fock method at finite temperature: Core-collapse supernovae. Phys. Rev. C 2009, 79, 055801. [Google Scholar] [CrossRef]
- Chamel, N.; Goriely, S.; Pearson, J.M. Further explorations of Skyrme-Hartree-Fock-Bogoliubov mass formulas. XI. Stabilizing neutron stars against a ferromagnetic collapse. Phys Rev C 2009, 80, 065804. [Google Scholar] [CrossRef]
- Onsi, M.; Chaara, A.M.; Pearson, J.M. On the Fermi functions I -(n+1/2). Z. Fur. Phys. Hadron. Nucl. 1994, 348, 255–256. [Google Scholar] [CrossRef]
- Shchechilin, N.N.; Chamel, N.; Pearson, J.M.; Chugunov, A.I.; Potekhin, A.Y. Unified equations of state for cold nonaccreting neutron stars with Brussels-Montreal functionals. V. Improved parametrization of the nucleon density distributions. Phys. Rev. C 2024, 109, 055802. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Pethick, C.J.; Ravenhall, D.G.; Lamb, D.Q. Physical properties of hot, dense matter: The general case. Nucl. Phys. A 1985, 432, 646–742. [Google Scholar] [CrossRef]
- Ducoin, C.; Chomaz, P.; Gulminelli, F. Isospin-dependent clusterization of neutron-star matter. Nucl. Phys. A 2007, 789, 403–425. [Google Scholar] [CrossRef]
- Margueron, J.; Hoffmann Casali, R.; Gulminelli, F. Equation of state for dense nucleonic matter from metamodeling. I. Foundational aspects. Phys. Rev. C 2018, 97, 025805. [Google Scholar] [CrossRef]
- Ravenhall, D.G.; Pethick, C.J.; Wilson, J.R. Structure of matter below nuclear saturation density. Phys. Rev. Lett. 1983, 50, 2066–2069. [Google Scholar] [CrossRef]
- Maruyama, T.; Tatsumi, T.; Voskresensky, D.N.; Tanigawa, T.; Chiba, S. Nuclear “pasta” structures and the charge screening effect. Phys. Rev. C 2005, 72, 015802. [Google Scholar] [CrossRef]
- Newton, W.G.; Gearheart, M.; Li, B.A. A Survey of the Parameter Space of the Compressible Liquid Drop Model as Applied to the Neutron Star Inner Crust. Astrophys. J. Suppl. Ser. 2013, 204, 9. [Google Scholar] [CrossRef]
- Ravenhall, D.G.; Pethick, C.J.; Lattimer, J.M. Nuclear interface energy at finite temperatures. Nucl. Phys. A 1983, 407, 571–591. [Google Scholar] [CrossRef]
- Pearson, J.M. (Département de Physique, Université de Montréal, Montréal, QC, Canada). Private communications, 2024.
- Furtado, U.J.; Gulminelli, F. Parametrization of the surface energy in the ETF approximation. J. Phys. Nucl. Phys. 2021, 48, 015102. [Google Scholar] [CrossRef]
- Wang, M.; Huang, W.J.; Kondev, F.G.; Audi, G.; Naimi, S. The AME 2020 atomic mass evaluation (II). Tables, graphs and references. Chin. Phys. C 2021, 45, 030003. [Google Scholar] [CrossRef]
- Wang, M.; Audi, G.; Kondev, F.G.; Huang, W.J.; Naimi, S.; Xu, X. The AME2016 atomic mass evaluation (II). Tables, graphs and references. Chin. Phys. C 2017, 41, 030003. [Google Scholar] [CrossRef]
- Kaminker, A.D.; Pethick, C.J.; Potekhin, A.Y.; Thorsson, V.; Yakovlev, D.G. Neutrino pair bremsstrahlung by electrons in neutron star crusts. A&A 1999, 343, 1009. [Google Scholar] [CrossRef]
- Gnedin, O.Y.; Yakovlev, D.G.; Potekhin, A.Y. Thermal relaxation in young neutron stars. Mon. Not. Roy. Astron. Soc. 2001, 324, 725. [Google Scholar] [CrossRef]
- Chamel, N.; Pearson, J.M.; Shchechilin, N.N. Role of neutron pairing with density-gradient dependence in the semimicroscopic treatment of the inner crust of neutron stars. Phys. Rev. C 2024, 110, 045808. [Google Scholar] [CrossRef]
- Shelley, M.; Pastore, A. Comparison between the Thomas–Fermi and Hartree–Fock–Bogoliubov Methods in the Inner Crust of a Neutron Star: The Role of Pairing Correlations. Universe 2020, 6, 206. [Google Scholar] [CrossRef]
- Pęcak, D.; Zdanowicz, A.; Chamel, N.; Magierski, P.; Wlazłowski, G. Time-Dependent Nuclear Energy-Density Functional Theory Toolkit for Neutron Star Crust: Dynamics of a Nucleus in a Neutron Superfluid. Phys. Rev. X 2024, 14, 041054. [Google Scholar] [CrossRef]


| p | |||||
|---|---|---|---|---|---|
| ETF calculations in the medium | 1.033329 | 0.172145 | 29.418725 | 0.747555 | 3.0 |
| ETF mass table | 0.98636 | 0.09008 | 36.22714 | 1.16310 | 3.0 |
| AME2020 | 1.04971 | 0.12094 | 30.45764 | 0.66720 | 3.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grams, G.; Shchechilin, N.N.; Diverrès, T.; Fantina, A.F.; Chamel, N.; Gulminelli, F. Neutron Star Inner Crust at Finite Temperatures: A Comparison Between Compressible Liquid Drop and Extended Thomas–Fermi Approaches. Universe 2025, 11, 172. https://doi.org/10.3390/universe11060172
Grams G, Shchechilin NN, Diverrès T, Fantina AF, Chamel N, Gulminelli F. Neutron Star Inner Crust at Finite Temperatures: A Comparison Between Compressible Liquid Drop and Extended Thomas–Fermi Approaches. Universe. 2025; 11(6):172. https://doi.org/10.3390/universe11060172
Chicago/Turabian StyleGrams, Guilherme, Nikolai N. Shchechilin, Théau Diverrès, Anthea F. Fantina, Nicolas Chamel, and Francesca Gulminelli. 2025. "Neutron Star Inner Crust at Finite Temperatures: A Comparison Between Compressible Liquid Drop and Extended Thomas–Fermi Approaches" Universe 11, no. 6: 172. https://doi.org/10.3390/universe11060172
APA StyleGrams, G., Shchechilin, N. N., Diverrès, T., Fantina, A. F., Chamel, N., & Gulminelli, F. (2025). Neutron Star Inner Crust at Finite Temperatures: A Comparison Between Compressible Liquid Drop and Extended Thomas–Fermi Approaches. Universe, 11(6), 172. https://doi.org/10.3390/universe11060172







