Optical Photometric Monitoring of the Blazar OT 355 and Local Standard Stars’ Calibration
Abstract
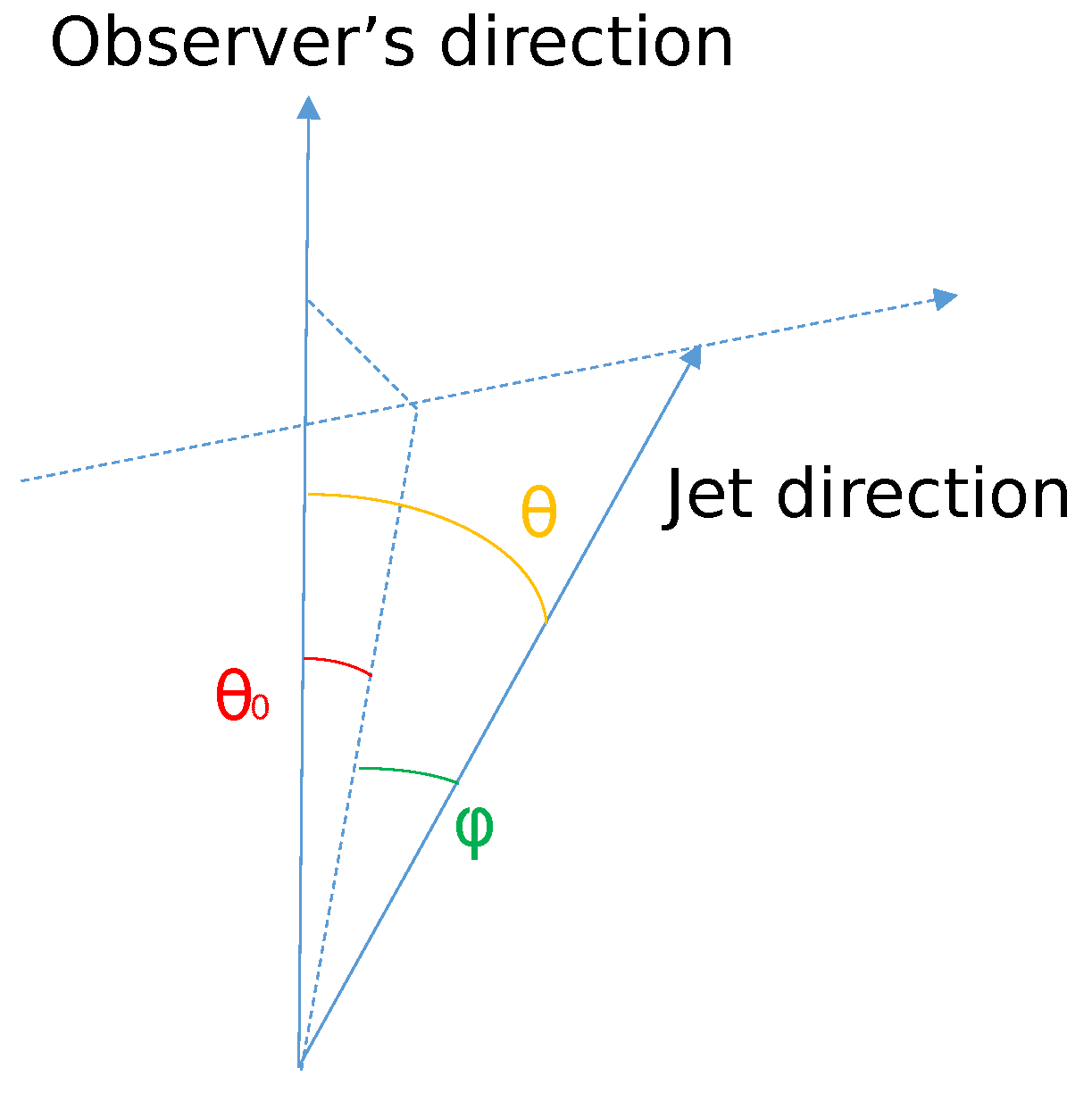
1. Introduction
2. Observations
3. Methods of Analysis and Results
3.1. Secondary Standards
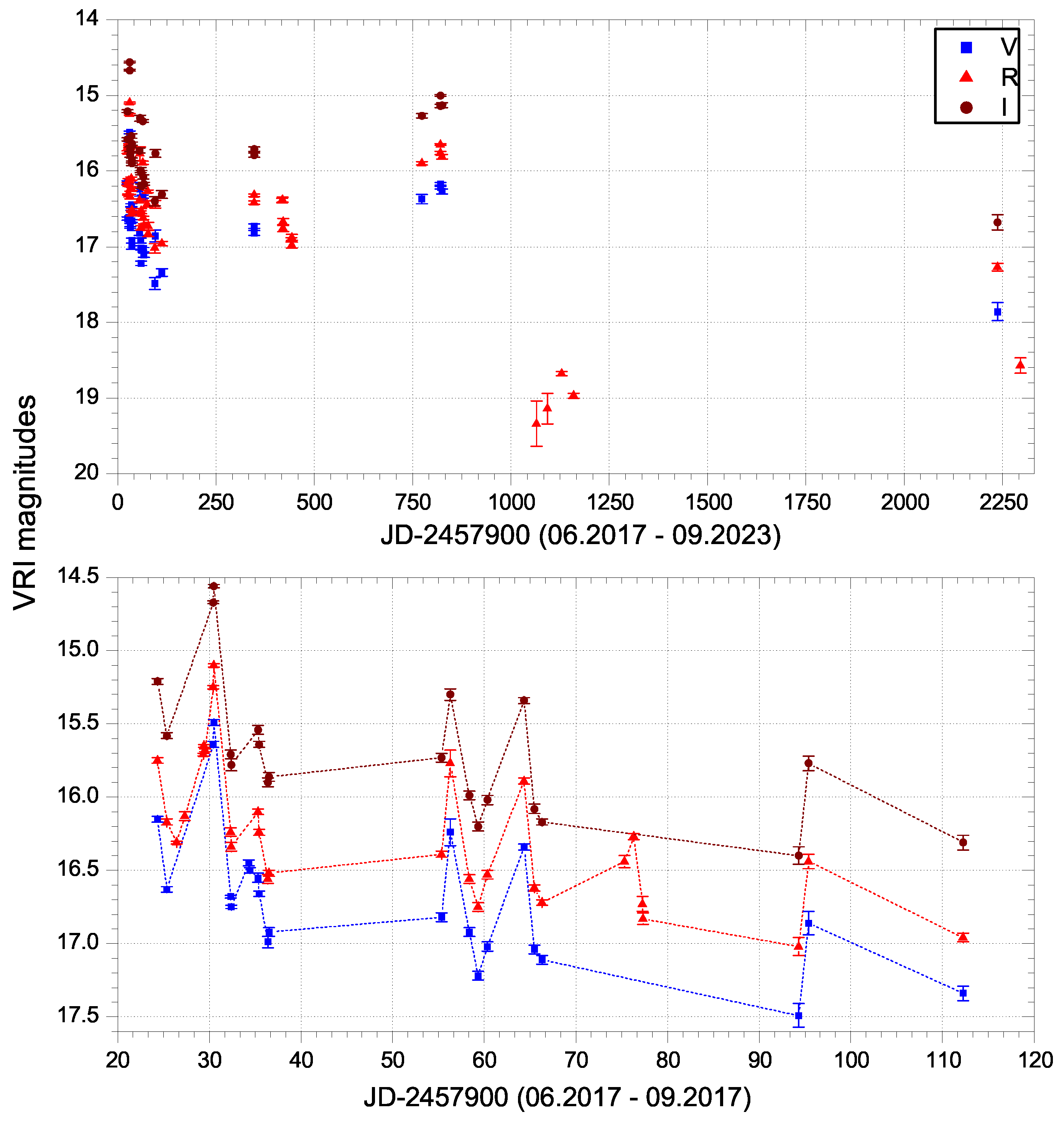
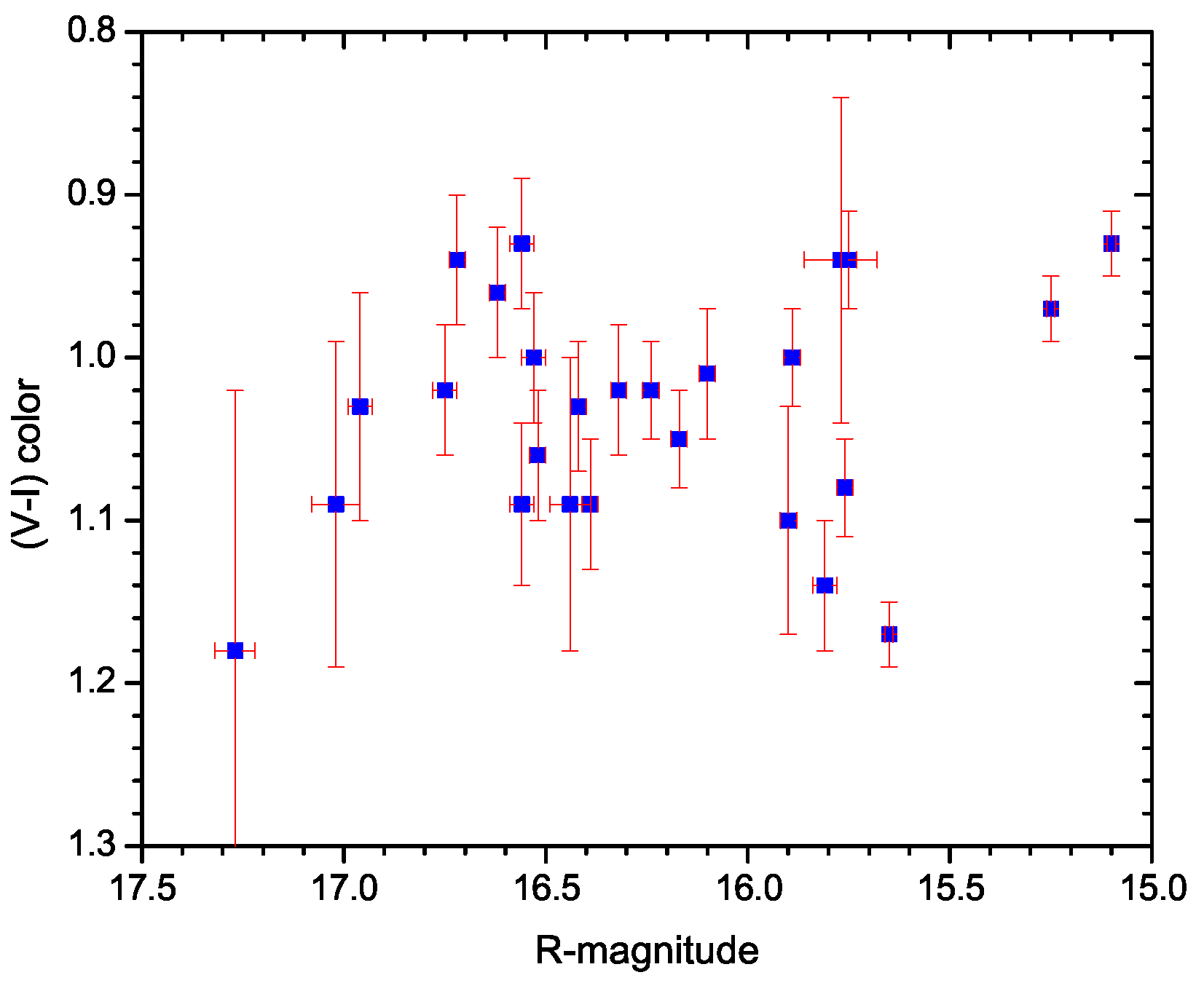
3.2. Long-Term Flux and Color Variability
3.3. Intra-Day Flux Variability
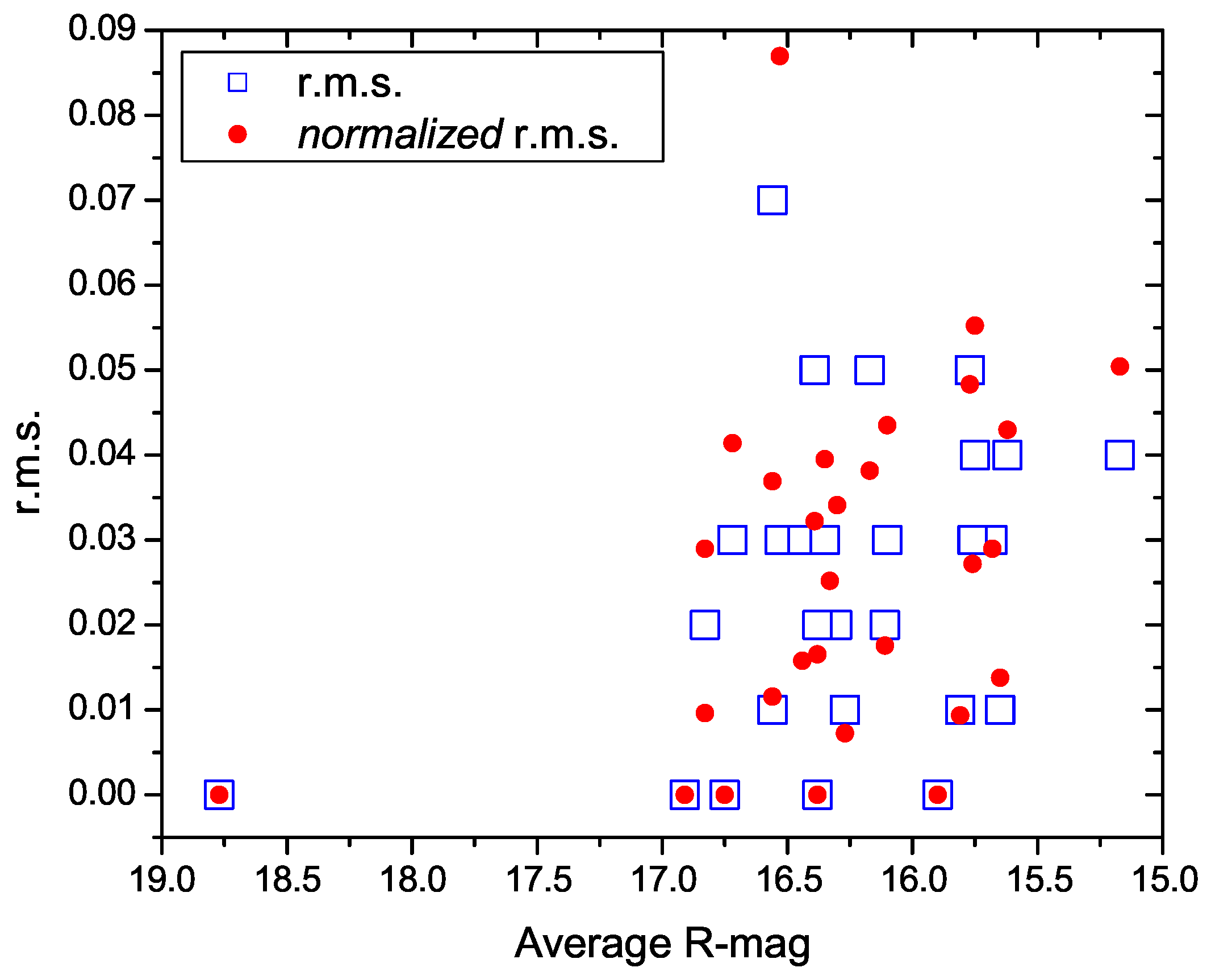
3.4. Intra-Day Variability Amplitude
3.5. Structure Function
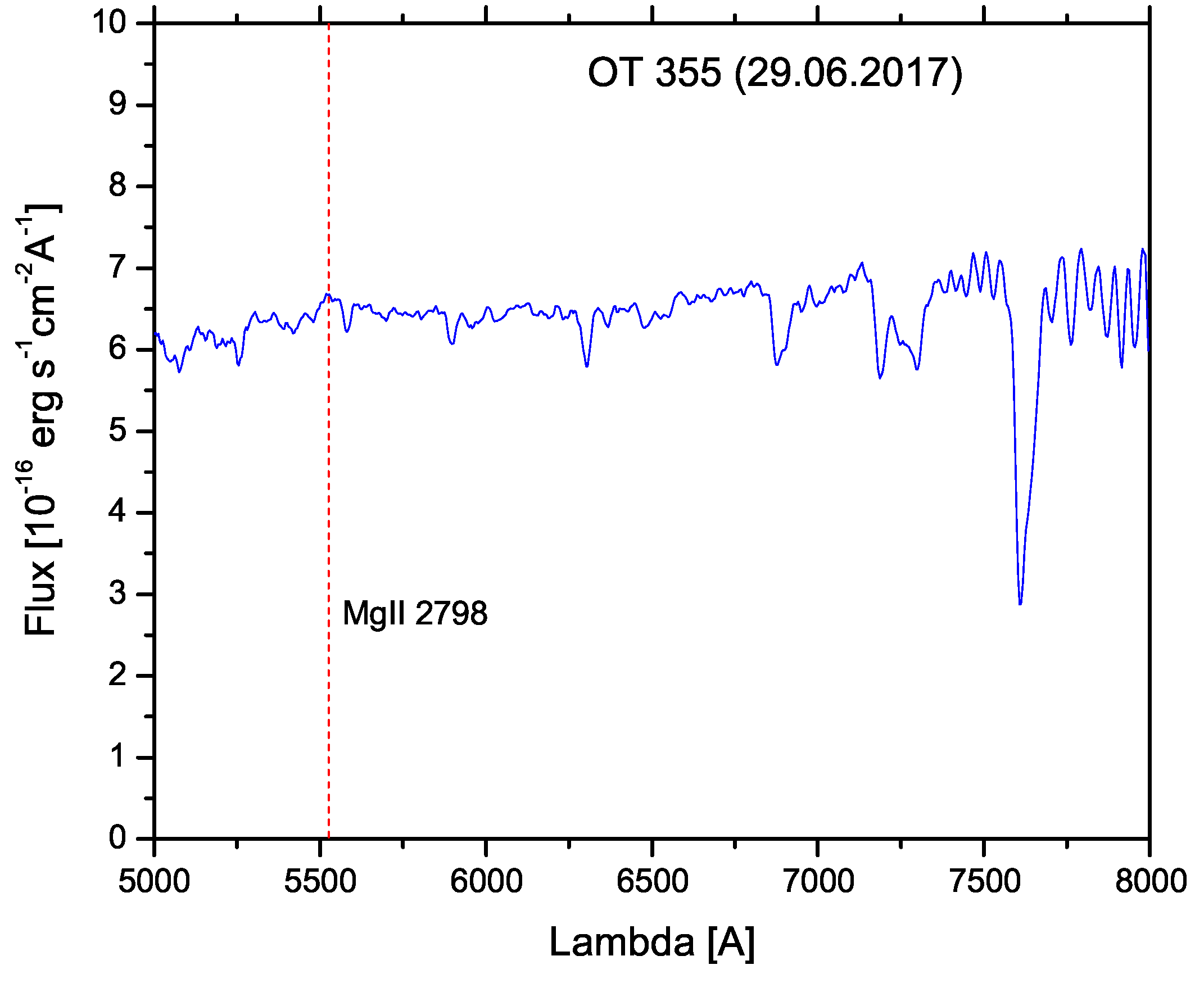
3.6. Optical Spectrum
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
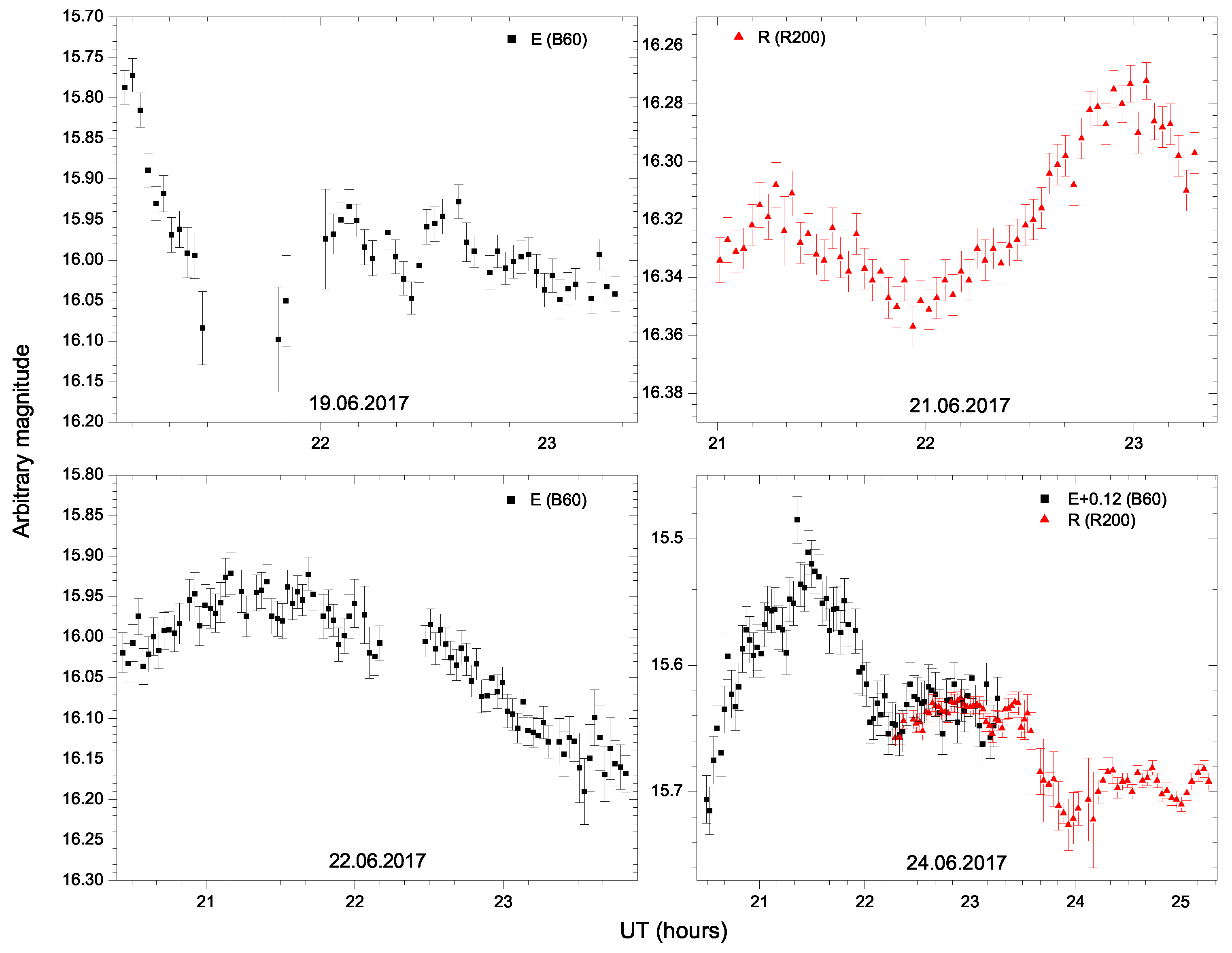
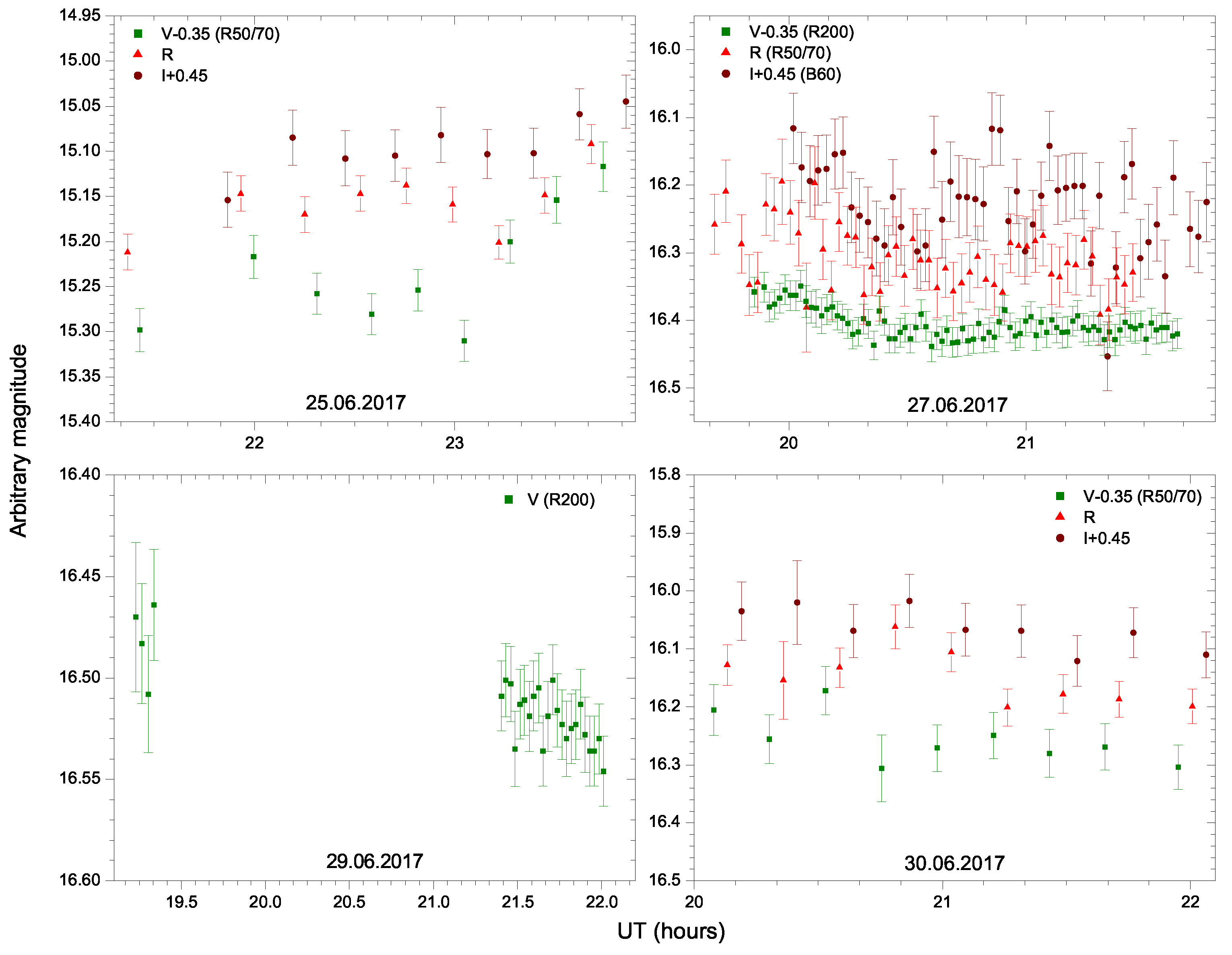
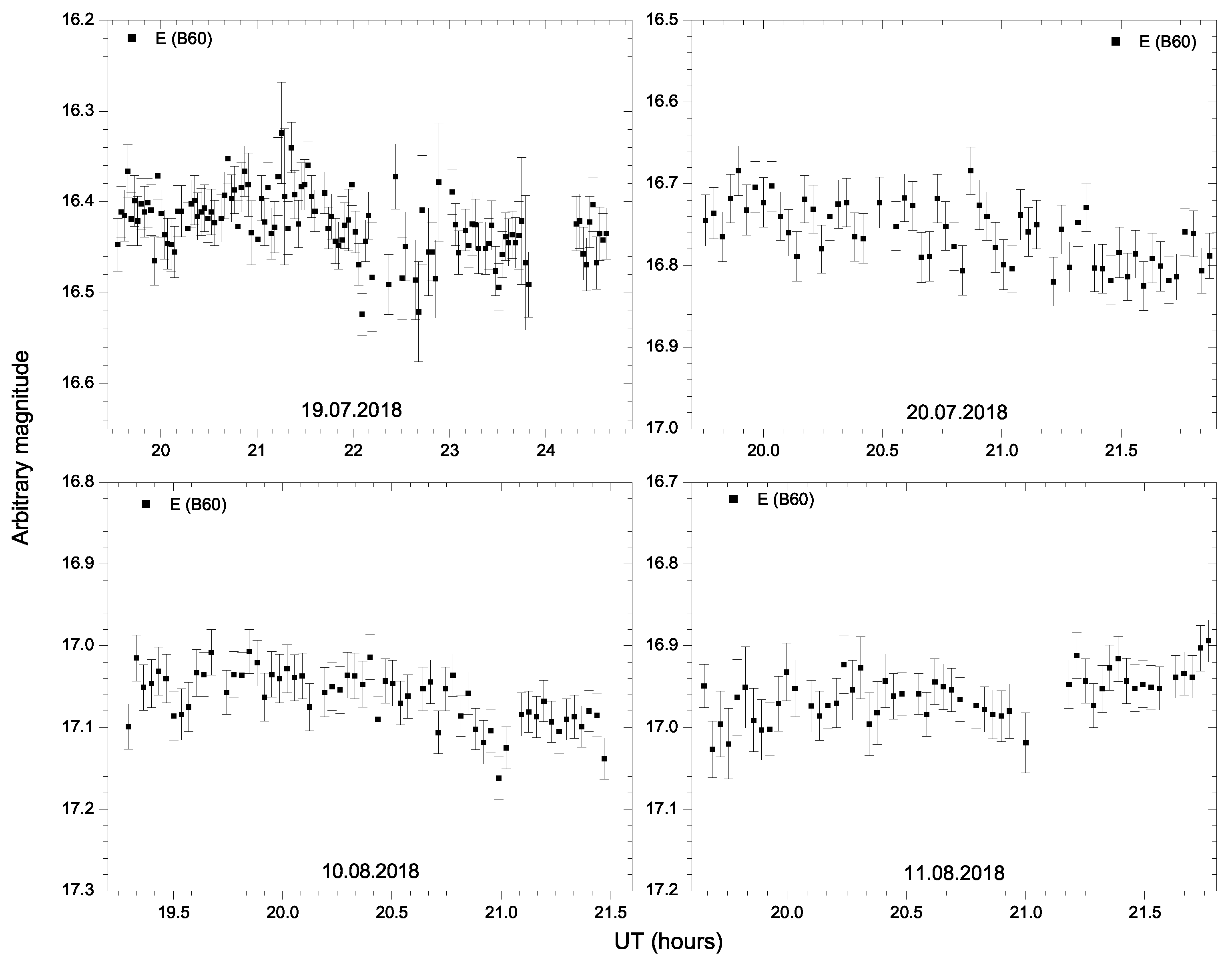
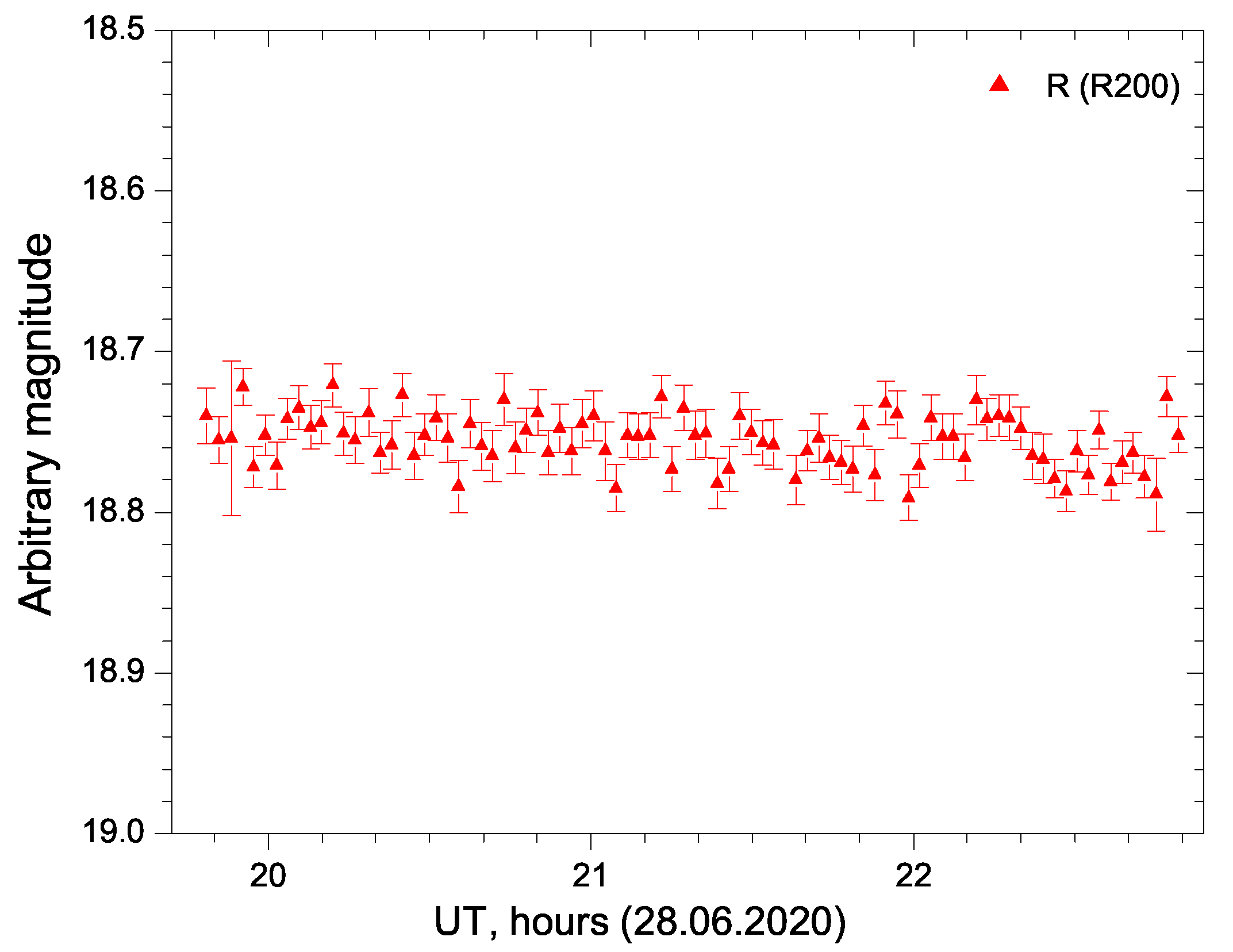
Appendix A. Intra-Night Variability Examples



| 1 | http://crts.caltech.edu/ (accessed on 26 May 2025). |
| 2 | http://nao-rozhen.org/ (accessed on 26 May 2025). |
| 3 | Defined as , |
| 4 | https://www.eso.org/sci/observing/tools/standards/spectra/stanlis.html (accessed on 26 May 2025). |
References
- Fossati, G.; Maraschi, L.; Celotti, A.; Comastri, A.; Ghisellini, G. A unifying view of the spectral energy distributions of blazars. Mon. Not. Roy. Astron. Soc. 1998, 299, 433. [Google Scholar] [CrossRef]
- Prandini, E.; Ghisellini, G. The blazar sequence and its physical understanding. Galaxies 2022, 10, 35. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, M.; Agudo, I.; Ajello, M.; Aller, H.D.; Aller, M.F.; Angelakis, E.; Arkharov, A.A.; Axelsson, M.; Bach, U.; et al. The spectral energy distribution of Fermi bright blazars. Astrophys. J. 2010, 716, 30. [Google Scholar] [CrossRef]
- Anjum, A.; Stalin, C.S.; Rakshit, S.; Gudennavar, S.B.; Durgapal, A. Mid-infrared variability of γ-ray emitting blazars. Mon. Not. Roy. Astron. Soc. 2020, 494, 764. [Google Scholar] [CrossRef]
- Bachev, R. The connection between the giant optical outbursts of the flat spectrum radio quasars and the black hole precession. Bulg. Astron. J. 2018, 28, 22. [Google Scholar]
- Hovatta, T.; Pavlidou, V.; King, O.G. Connection between optical and γ-ray variability in blazars. Mon. Not. Roy. Astron. Soc. 2014, 439, 690–702. [Google Scholar] [CrossRef]
- Zhang, B.-K.; Zhou, X.-S.; Zhao, X.-Y.; Dai, B.-Z. Long-term optical-infrared color variability of blazars. Res. Astron. Astrophys. 2015, 15, 1784. [Google Scholar] [CrossRef]
- Zhang, T.; Doi, M.; Kokubo, M.; Sako, S.; Ohsawa, R.; Tominaga, N.; Tanaka, M.; Fukazawa, Y.; Takahashi, H.; Arima, N.; et al. Optical Variability of Blazars in the Tomo-e Gozen Northern Sky Transient Survey. Astrophys. J. 2024, 968, 71. [Google Scholar] [CrossRef]
- Bottcher, M.; Reimer, A.; Sweeney, K.; Prakash, A. Leptonic and Hadronic Modeling of Fermi-detected Blazars. Astrophys. J. 2013, 768, 54. [Google Scholar] [CrossRef]
- Marscher, A. Turbulent, Extreme Multi-zone Model for Simulating Flux and Polarization Variability in Blazars. Astrophys. J. 2014, 780, 87. [Google Scholar] [CrossRef]
- Marscher, A.P. Extragalactic Jets Every Angle. Proc. Int. Astron. Union 2015, 313, 122. [Google Scholar]
- Zhang, H.; Chen, X.; Bottcher, M. Synchrotron Polarization in Blazars. Astrophys. J. 2014, 789, 66. [Google Scholar] [CrossRef]
- Raiteri, C.M.; Villata, M.; Jorstad, S.G.; Marscher, A.P.; Acosta Pulido, J.A.; Carosati, D.; Chen, W.P.; Joner, M.D.; Kurtanidze, S.O.; Lorey , C.; et al. The optical behaviour of BL Lacertae at its maximum brightness levels: A blend of geometry and energetics. Mon. Not. Roy. Astron. Soc. 2023, 522, 102–116. [Google Scholar] [CrossRef]
- Shaw, M.S.; Romani, R.W.; Cotter, G.; Healey, S.E.; Michelson, P.F.; Readhead, A.C.S.; Richards, J.L.; Max-Moerbeck, W.; King, O.G.; Potter, W.J. Spectroscopy of Broad-line Blazars from 1LAC. Astrophys. J. 2012, 748, 49. [Google Scholar] [CrossRef]
- Bachev, R.; Kurtenkov, A.; Nikolov, Y.; Spassov, B.; Boeva, S.; Latev, G.; Dimitrova, R.V. Munoz ATel. 2017. No 10540. Available online: https://www.astronomerstelegram.org/?read=10540 (accessed on 30 March 2025).
- Strigachev, A.; Bachev, R. A new CCD camera at the 60-cm telescope of the Belogradchik Astronomical Observatory. Bulg. Astron. J. 2011, 16, 144–152. [Google Scholar]
- Raiteri, C.M.; Villata, M.; Tosti, G.; Fiorucci, M.; Ghisellini, G.; Takalo, L.O.; Sillanpaa, A.; Valtaoja, E.; Terasranta, H.; Tornikoski, M.; et al. Optical and radio behaviour of the blazar S4 0954+65. Astron. Astrophys. 1999, 352, 19. [Google Scholar]
- Fiorucci, M.; Tosti, G. VRI photometry of stars in the fields of 12 BL Lacertae objects. Astron. Astrophys. Suppl. Ser. 1996, 116, 403. [Google Scholar] [CrossRef]
- Gaur, H.; Gupta, A.C.; Strigachev, A.; Bachev, R.; Semkov, E.; Wiita, P.J.; Peneva, S.; Boeva, S.; Slavcheva-Mihova, L.; Mihov, B.; et al. Optical flux and spectral variability of blazars. Mon. Not. Roy. Astron. Soc. 2012, 425, 3002. [Google Scholar] [CrossRef]
- Gu, M.F.; Lee, C.-U.; Pak, S.; Yim, H.S.; Fletcher, A.B. Multi-colour optical monitoring of eight red blazars. Astron. Astrophys. 2006, 450, 39. [Google Scholar]
- Tripathi, T.; Gupta, A.C.; Takey, A.; Bachev, R.; Vince, O.; Strigachev, A.; Kushwaha, P.; Elhosseiny, E.G.; Wiita, P.J.; Damljanovic, G.; et al. Optical intraday variability of the blazar S5 0716+714. Mon. Not. Roy. Astron. Soc. 2024, 450, 39–51. [Google Scholar]
- de Diego, J.A.; Polednikova, J.; Bongiovanni, A.; Pérez García, A.M.; De Leo, M.A.; Verdugo, T.; Cepa, J. Testing microvariability in quasar differential light curves using several field stars. Astron. J. 2015, 150, 44. [Google Scholar] [CrossRef]
- Miller, C.J.; Genovese, C.; Nichol, R.C.; Wasserman, L.; Connolly, A.; Reichart, D.; Hopkins, A.; Schneider, J.; Moore, A. Controlling the false-discovery rate in astrophysical data analysis. Astron. J. 2001, 122, 3492. [Google Scholar]
- Heidt, J.; Wagner, S.J. Statistics of optical intraday variability in a complete sample of radio-selected BL Lacertae objects. Astron. Astrophys. 1996, 305, 42. [Google Scholar]
- Bachev, R.; Popov, V.; Strigachev, A.; Semkov, E.; Ibryamov, S.; Spassov, B.; Latev, G.; Munoz Dimitrova, R.V.; Boeva, S. Intra-night variability of the blazar CTA 102 during its 2012 and 2016 giant outbursts. Mon. Not. Roy. Astron. Soc. 2017, 471, 2216. [Google Scholar] [CrossRef]
- Bachev, R.; Tripathi, T.; Gupta, A.C.; Kushwaha, P.; Strigachev, A.; Kurtenkov, A.; Nikolov, Y.; Boeva, S.; Damljanovic, G.; Vince, O.; et al. Intra-night optical flux and polarization variability of BL Lacertae during its 2020-2021 high state. Mon. Not. Roy. Astron. Soc. 2023, 522, 3018. [Google Scholar]
- Simonetti, J.H.; Cordes, J.M.; Heeschen, D.S. Flicker of extragalactic radio sources at two frequencies. Astrophys. J. 1985, 296, 46. [Google Scholar] [CrossRef]
- Emmanoulopoulos, D.; McHardy, I.M.; Uttley, P. On the use of structure functions to study blazar variability: Caveats and problems. Mon. Not. Roy. Astron. Soc. 2010, 404, 931. [Google Scholar] [CrossRef]
- Raiteri, C.M.; Villata, M.; Carosati, D.; Benítez, E.; Kurtanidze, S.O.; Gupta, A.C.; Mirzaqulov, D.O.; D’Amm, F.; Larionov, V.M.; Pursimo, T.; et al. The dual nature of blazar fast variability. Space and ground observations of S5 0716+714. Mon. Not. Roy. Astron. Soc. 2021, 501, 1100. [Google Scholar] [CrossRef]
- Kawaguchi, T.; Mineshige, S.; Umemura, M.; Turner, E.L. Optical Variability in Active Galactic Nuclei: Starbursts or Disk Instabilities? Astrophys. J. 1998, 504, 671. [Google Scholar] [CrossRef]
- Xiao, H.; Fan, J.; Ouyang, Z.; Hu, L.; Chen, G.; Fu, L.; Zhang, S. An Extensive Study of Blazar Broad Emission Line: Changing-look Blazars and the Baldwin Effect. Astrophys. J. 2022, 936, 146. [Google Scholar] [CrossRef]
- Negi, V.; Joshi, R.; Chand, K.; Chand, H.; Wiita, P.; Ho, L.C.; Singh, R.S. Optical flux and colour variability of blazars in the ZTF survey. Mon. Not. Roy. Astron. Soc. 2022, 510, 1791. [Google Scholar] [CrossRef]
- Bachev, R.; Strigachev, A.; Semkov, E.; Dimitrova, R.V.M.; Latev, G.; Spassov, B.; Petrov, B. The Extremes in Intra-Night Blazar Variability: The S4 0954+65 Case. Galaxies 2016, 4, 13. [Google Scholar] [CrossRef]
- Aschwanden, M. A Macroscopic Description of a Generalized Self-organized Criticality System: Astrophysical Applications. Astrophys. J. 2014, 782, 54. [Google Scholar] [CrossRef]
- Fan, J.H.; Su, C.Y.; Lin, R.H. Optical periodicity analysis for radio selected BL Lacertae objects (RBLs). Publ. Astron. Soc. Jpn. 2002, 54, 175–178. [Google Scholar] [CrossRef]
- Kundu, A.; Chatterjee, R.; Mitra, K.; Mondal, S. rms–flux relation and disc–jet connection in blazars in the context of the internal shocks model. Mon. Not. Roy. Astron. Soc. 2022, 510, 3688. [Google Scholar] [CrossRef]
- Fan, J.H.; Kurtanidze, S.O.; Liu, Y.; Kurtanidze, O.M.; Nikolashvili, M.G.; Liu, X.; Zhang, L.X.; Cai, J.T.; Zhu, J.T.; He, S.L.; et al. Optical Photometry of the Quasar 3C 454.3 during the Period 2006–2018 and the Long-term Periodicity Analysis. Astron. Astrophys. Suppl. Ser. 2021, 253, 10. [Google Scholar] [CrossRef]
- Zhang, B.K.; Dai, B.Z.; Wang, L.P.; Zhao, M.; Zhang, L.; Cao, Z. Intraday optical variability of the BL Lacertae object S5 0716+714. Mon. Not. Roy. Astron. Soc. 2012, 421, 3111. [Google Scholar] [CrossRef]
- Zhang, B.K.; Wang, S.; Zhao, X.Y.; Dai, B.Z.; Zha, M. Long-term optical and infrared variability of the BL Lac object PKS 0537–441. Mon. Not. Roy. Astron. Soc. 2013, 428, 3630. [Google Scholar] [CrossRef]



| JD | Evening | Duration [h] | Filter | Telescope | ||
|---|---|---|---|---|---|---|
| 2,457,924.368 | 19.06.2017 | 2.1 | E | 15.75 | 0.04 | B60 |
| 2,457,925.349 | 20.06.2017 | 3.8 | E | 16.17 | 0.05 | B60 |
| 2,457,926.424 | 21.06.2017 | 2.3 | R | 16.33 | 0.02 | R200 |
| 2,457,927.347 | 22.06.2017 | 3.3 | E | 16.11 | 0.02 | B60 |
| 2,457,929.351 | 24.06.2017 | 2.7 | E | 15.62 | 0.04 | B60 |
| 2,457,929.492 | 24.06.2017 | 3.0 | R | 15.68 | 0.03 | R200 |
| 2,457,930.448 | 25.06.2017 | 2.3 | R | 15.17 | 0.04 | R50/70 |
| 2,457,932.365 | 27.06.2017 | 1.8 | V | 0.02 | R200 | |
| 2,457,932.360 | 27.06.2017 | 1.7 | I | 0.04 | B60 | |
| 2,457,932.355 | 27.06.2017 | 1.7 | R | 16.30 | 0.02 | R50/70 |
| 2,457,934.399 | 29.06.2017 | 2.8 | V | 0.01 | R200 | |
| 2,457,935.334 | 30.06.2017 | 2.0 | R | 16.10 | 0.03 | R50/70 |
| 2,457,936.374 | 01.07.2017 | 2.5 | R | 16.56 | 0.01 | R50/70 |
| 2,457,955.319 | 20.07.2017 | 4.5 | E | 16.39 | 0.05 | B60 |
| 2,457,956.308 | 21.07.2017 | 3.0 | E | 15.77 | 0.05 | B60 |
| 2,457,958.357 | 23.07.2017 | 5.5 | E | 16.56 | 0.07 | B60 |
| 2,457,959.337 | 24.07.2017 | 1.0 | E | 16.75 | 0 | B60 |
| 2,457,960.353 | 25.07.2017 | 1.0 | E | 16.53 | 0.03 | B60 |
| 2,457,964.331 | 29.07.2017 | − | − | 15.89 | − | R50/70 |
| 2,457,965.452 | 30.07.2017 | − | − | 16.62 | − | R50/70 |
| 2,457,966.321 | 31.07.2017 | − | − | 16.72 | − | R50/70 |
| 2,457,975.289 | 09.08.2017 | 5.5 | E | 16.44 | 0.03 | B60 |
| 2,457,976.293 | 10.08.2017 | 4.0 | E | 16.27 | 0.01 | B60 |
| 2,457,977.284 | 11.08.2017 | 6.0 | E | 16.83 | 0.02 | B60 |
| 2,457,994.325 | 28.08.2017 | − | − | 17.02 | − | B60 |
| 2,457,995.359 | 29.08.2017 | − | − | 16.44 | − | B60 |
| 2,458,012.254 | 15.09.2017 | − | − | 16.96 | − | B60 |
| 2,458,247.473 | 08.05.2018 | 2.2 | R | 16.35 | 0.03 | B60 |
| 2,458,317.403 | 17.07.2018 | 3.5 | E | 16.38 | 0.02 | B60 |
| 2,458,319.402 | 19.07.2018 | 5.0 | E | 16.38 | 0 | B60 |
| 2,458,320.365 | 20.07.2018 | 2.1 | E | 16.72 | 0.03 | B60 |
| 2,458,341.344 | 10.08.2018 | 2.2 | E | 16.91 | 0 | B60 |
| 2,458,342.362 | 11.08.2018 | 2.0 | E | 16.83 | 0.02 | B60 |
| 2,458,673.389 | 08.07.2019 | 2.0 | R | 15.90 | 0 | B60 |
| 2,458,720.294 | 24.08.2019 | 2.1 | E | 15.65 | 0.01 | B60 |
| 2,458,721.282 | 25.08.2019 | 3.2 | E | 15.76 | 0.03 | B60 |
| 2,458,724.270 | 28.08.2019 | 3.1 | E | 15.81 | 0.01 | B60 |
| 2,458,964.565 | 24.04.2020 | − | − | 19.34 | − | B60 |
| 2,458,992.362 | 22.05.2020 | − | − | 19.14 | − | B60 |
| 2,459,029.330 | 28.06.2020 | − | − | 18.68 | − | R200 |
| 2,459,029.355 | 28.06.2020 | 3.0 | R | 18.77 | 0 | R200 |
| 2,459,059.509 | 28.07.2020 | − | − | 18.97 | − | R200 |
| 2,460,137.322 | 11.07.2023 | − | − | 17.27 | − | B60 |
| 2,460,195.267 | 07.09.2023 | − | − | 18.57 | − | B60 |
| Star | V | Err V | R | Err R | I | Err I |
|---|---|---|---|---|---|---|
| A | 14.39 | 0.04 | 14.04 | 0.04 | 13.73 | 0.05 |
| C | 16.98 | 0.06 | 16.47 | 0.05 | 16.01 | 0.05 |
| D | 13.94 | 0.04 | 13.59 | 0.04 | 13.29 | 0.05 |
| Obs Date | Band | DoF(,) | F | p | Status | Amp (%) | |||
|---|---|---|---|---|---|---|---|---|---|
| 19.06.2017 | E | 10,33 | 8.48 | 4.10 | 1.2 | 2.3 | Yes | Var | 28.29 |
| 20.06.2017 | E | 22,69 | 43.79 | 2.68 | 4.2 | 6.1 | Yes | Var | 22.19 |
| 21.06.2017 | R | 13,42 | 84.96 | 3.50 | 8.1 | 3.4 | Yes | Var | 9.30 |
| 22.06.2017 | E | 20,63 | 13.10 | 2.80 | 1.7 | 4.5 | Yes | Var | 19.79 |
| 24.06.2017 | E | 19,60 | 47.81 | 2.87 | 3.5 | 2.0 | Yes | Var | 21.39 |
| R | 17,54 | 63.80 | 3.03 | 1.4 | 1.0 | Yes | Var | 9.00 | |
| 27.06.2017 | V | 19,60 | 15.75 | 2.87 | 1.1 | 3.6 | Yes | Var | 8.90 |
| R | 11,36 | 2.35 | 3.87 | 2.6 | 3.2 | No | NV | - | |
| I | 11,36 | 3.44 | 3.87 | 2.4 | 3.2 | No | NV | - | |
| 29.06.2017 | V | 6,21 | 11.18 | 5.88 | 1.3 | 2.1 | Yes | Var | 9.80 |
| 20.07.2017 | E | 30,93 | 39.72 | 2.34 | 6.7 | 1.9 | Yes | Var | 22.29 |
| 21.07.2017 | E | 19,60 | 52.16 | 2.87 | 3.2 | 3.1 | Yes | Var | 27.06 |
| 23.07.2017 | E | 31,96 | 3.46 | 2.31 | 1.8 | 3.2 | Yes | Var | 84.76 |
| 24.07.2017 | E | 5,18 | 1.13 | 6.81 | 3.8 | 4.1 | No | NV | - |
| 25.07.2017 | E | 6,21 | 8.22 | 5.88 | 1.2 | 1.7 | Yes | Var | 30.49 |
| 09.08.2017 | E | 35,108 | 7.09 | 2.21 | 1.6 | 4.5 | Yes | Var | 28.58 |
| 10.08.2017 | E | 24,75 | 5.19 | 2.57 | 2.0 | 4.1 | Yes | Var | 19.57 |
| 11.08.2017 | E | 37,114 | 14.01 | 2.17 | 6.1 | 2.9 | Yes | Var | 40.18 |
| 08.05.2018 | R | 3,12 | 23.91 | 10.80 | 2.4 | 3.6 | Yes | Var | 13.56 |
| 17.07.2018 | E | 20,63 | 4.36 | 2.80 | 3.8 | 6.4 | Yes | Var | 13.99 |
| 19.07.2018 | E | 31,96 | 0.80 | 2.31 | 7.6 | 7.9 | No | NV | - |
| 20.07.2018 | E | 14,45 | 3.75 | 3.36 | 3.7 | 5.1 | Yes | Var | 24.70 |
| 10.08.2018 | E | 13,42 | 1.56 | 3.50 | 1.4 | 1.6 | No | NV | - |
| 11.08.2018 | E | 12,39 | 14.38 | 3.67 | 8.6 | 1.9 | Yes | Var | 19.59 |
| 08.07.2019 | R | 4,15 | 0.07 | 8.25 | 9.9 | 9.9 | No | NV | - |
| 24.08.2019 | E | 13,42 | 3.02 | 3.50 | 3.3 | 4.2 | No | NV | - |
| 25.08.2019 | E | 21,66 | 18.31 | 2.73 | 6.5 | 2.3 | Yes | Var | 17.50 |
| 28.08.2019 | E | 21,66 | 8.78 | 2.73 | 4.4 | 1.1 | Yes | Var | 14.55 |
| 28.06.2020 | R | 20,63 | 1.14 | 2.80 | 3.4 | 3.8 | No | NV | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bachev, R.; Tripathi, T.; Gupta, A.C.; Kurtenkov, A.; Nikolov, Y.; Strigachev, A.; Boeva, S.; Latev, G.; Spassov, B.; Minev, M.; et al. Optical Photometric Monitoring of the Blazar OT 355 and Local Standard Stars’ Calibration. Universe 2025, 11, 171. https://doi.org/10.3390/universe11060171
Bachev R, Tripathi T, Gupta AC, Kurtenkov A, Nikolov Y, Strigachev A, Boeva S, Latev G, Spassov B, Minev M, et al. Optical Photometric Monitoring of the Blazar OT 355 and Local Standard Stars’ Calibration. Universe. 2025; 11(6):171. https://doi.org/10.3390/universe11060171
Chicago/Turabian StyleBachev, R., Tushar Tripathi, Alok C. Gupta, A. Kurtenkov, Y. Nikolov, A. Strigachev, S. Boeva, G. Latev, B. Spassov, M. Minev, and et al. 2025. "Optical Photometric Monitoring of the Blazar OT 355 and Local Standard Stars’ Calibration" Universe 11, no. 6: 171. https://doi.org/10.3390/universe11060171
APA StyleBachev, R., Tripathi, T., Gupta, A. C., Kurtenkov, A., Nikolov, Y., Strigachev, A., Boeva, S., Latev, G., Spassov, B., Minev, M., Ovcharov, E., Yang, W.-X., Liu, Y., & Fan, J.-H. (2025). Optical Photometric Monitoring of the Blazar OT 355 and Local Standard Stars’ Calibration. Universe, 11(6), 171. https://doi.org/10.3390/universe11060171









