Structure Formation Through Magnetohydrodynamical Instabilities in Primordial Disks

Abstract

The shear flow instabilities under the presence of magnetic fields in the primordial disk can greatly facilitate the formation of density structures that serve as seeds prior to the onset of the gravitational Jeans instability. We evaluate the effects of the Parker, magnetorotational and kinematic dynamo instabilities by comparing the properties of these instabilities. We calculate the mass spectra of coagulated density structures by the above mechanism in the radial direction for an axisymmetric magnetohydrodynamic (MHD) torus equilibrium and power density profile models. Our local three-dimensional MHD simulation indicates that the coupling of the Parker and magnetorotational instability creates spiral arms and gas blobs in an accretion disk, reinforcing the theory and model. Such a mechanism for the early structure formation may be tested in a laboratory. The recent progress in experiments involving shear flows in rotating tokamak, field reversed configuration (FRC) and laser plasmas may become a key element to advance in nonlinear studies.

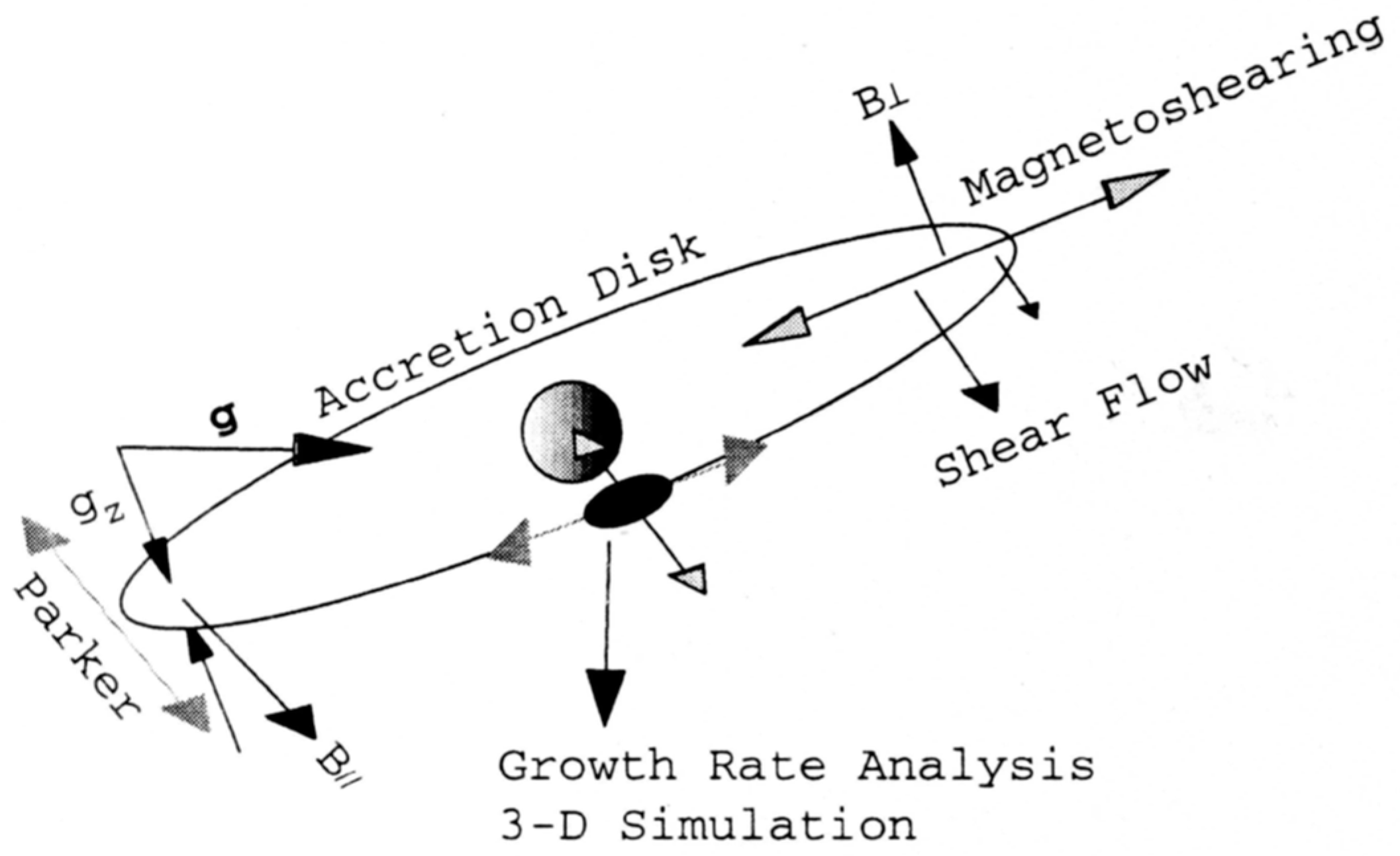
1. Introduction: Magnetohydrodynamic Processes of the Primordial Disk

Magnetohydrodynamic (MHD) instabilities are important in the early stage of primordial evolution for the following reasons. (We show a schematic view of the system in Figure 1). In the inner region of the accretion disk, axial and azimuthal magnetic fields from the central object, which reciprocally convert back and forth to each other, can be enhanced exponentially in several disk rotations due to the kinematic dynamo. In the outer region, the magnetorotational instability renders the disk turbulent, which also converts axial and azimuthal components of magnetic field into each other and enhances their strength exponentially in time. As the magnetic pressure inside of the disk grows, the disk becomes unstable to the Parker instability because of the magnetic buoyancy. The Parker instability accumulates matter as blobs at the foot points of the magnetic loops on the disk, while it reduces magnetic fields away from the disk. Once these blobs develop, the Jeans instability sets in to dominate the disk evolution. All of these processes, except for the Jeans instability, do not need self-gravitation, accelerating the evolution of primordial disks in the early pre-self-gravitation stage.

The evolution of an accretion disk remains a challenging problem. The main problem arises from the treatment of the flow shear in the accretion disk [1,2,3,4,5]. A local analysis of shear flows (i.e., the Fourier analysis) fails due to the radial nonuniformity of the accretion disk, which also prevents one from applying the WKB method to this issue. We adopt the nonlocal eigenvalue problem [5].

The other problem is the creation and annihilation of magnetic fields. The magnetic field in an accretion disk is enhanced due to the magnetorotational instability [6], leading to the buoyancy becoming strong enough to make the disk unstable to the Parker instability. Magnetic fields form loops emanating from the inside to outside of the disk due to the Parker instability. Since the magnetic field is incessantly created from both the magnetorotational instability and the kinematic dynamo, this dynamic process occurs recursively, or in another word, is self-sustained. Moreover, the disk remains turbulent due to the magnetorotational instability that is essential for sustaining the kinematic dynamo. The combination of these instabilities is a complex problem. In this paper, we compare these instabilities to estimate which instability is dominant under what conditions. These processes lead to highly nonlinear and mutually interacting plasma flows and magnetic fields under gravitational influence, which also manifest not only turbulent transport, but also structure formation (such as jets and relaxation oscillations).

Some of the processes associated with this structure formation of plasma with shear flows may be studied in laboratory plasmas such as tokamaks [7,8,9], liquid metal Couette flow [10,11], FRC [12,13,14] and in laser experiments [15,16]. Recent experiments show that toroidal shear flows in tokamak creates the radial momentum transport and the barrier inside of plasma that regulates momentum transfer to the wall. Though the strength of the magnetic field and density of plasma may be different from the accretion disk case, the configuration of the system and the instabilities that may occur in tokamak experiments can be similar to those of the accretion disk system. Shear flows and magnetic fields make plasma unstable to the magnetorotational instability, and the curvature of magnetic field in the toroidal direction makes plasma Rayleigh–Taylor (Parker) unstable. Thus, the unstable conditions may be experimentally examined in tokamak devices. In experiments trying to simulate supernovae, the surface of target suffers the Rayleigh–Taylor instability. If we apply sheared rotation and the magnetic field, essential for the magnetorotational instability, to the target, we may be able to simulate the accretion disk evolution by laser experiments. We estimate parameters for those cases and discuss if such experiments are plausible.

2. The Parker, Magnetorotational and Kinematic Dynamo Instabilities

The MHD shear flow instabilities, either the magnetorotational or the dynamo instabilities, play a role as an agent that keeps (or even enhances) the presence and strength of the disk magnetic field and its level of turbulence. These shear flow instabilities, by and large, determine the amount of mass that may be aggregated. The elevated level of magnetic fields in the disk through these instabilities gives rise to the activation of the Parker instability. The nonlinear evolution of the Parker instability is known [17,18,19] to produce high density plasma blobs at the feet of the unstable buoyant loop. This nonlinear evolution can become a robust mechanism that yields a significant density structure within a matter of several multiples of the rotational period. Note that this mechanism can be operative even much before the self-gravitating Jeans instability becomes effective. The instabilities for plasma evolution require a weak, but finite initial poloidal or dipolar magnetic field.

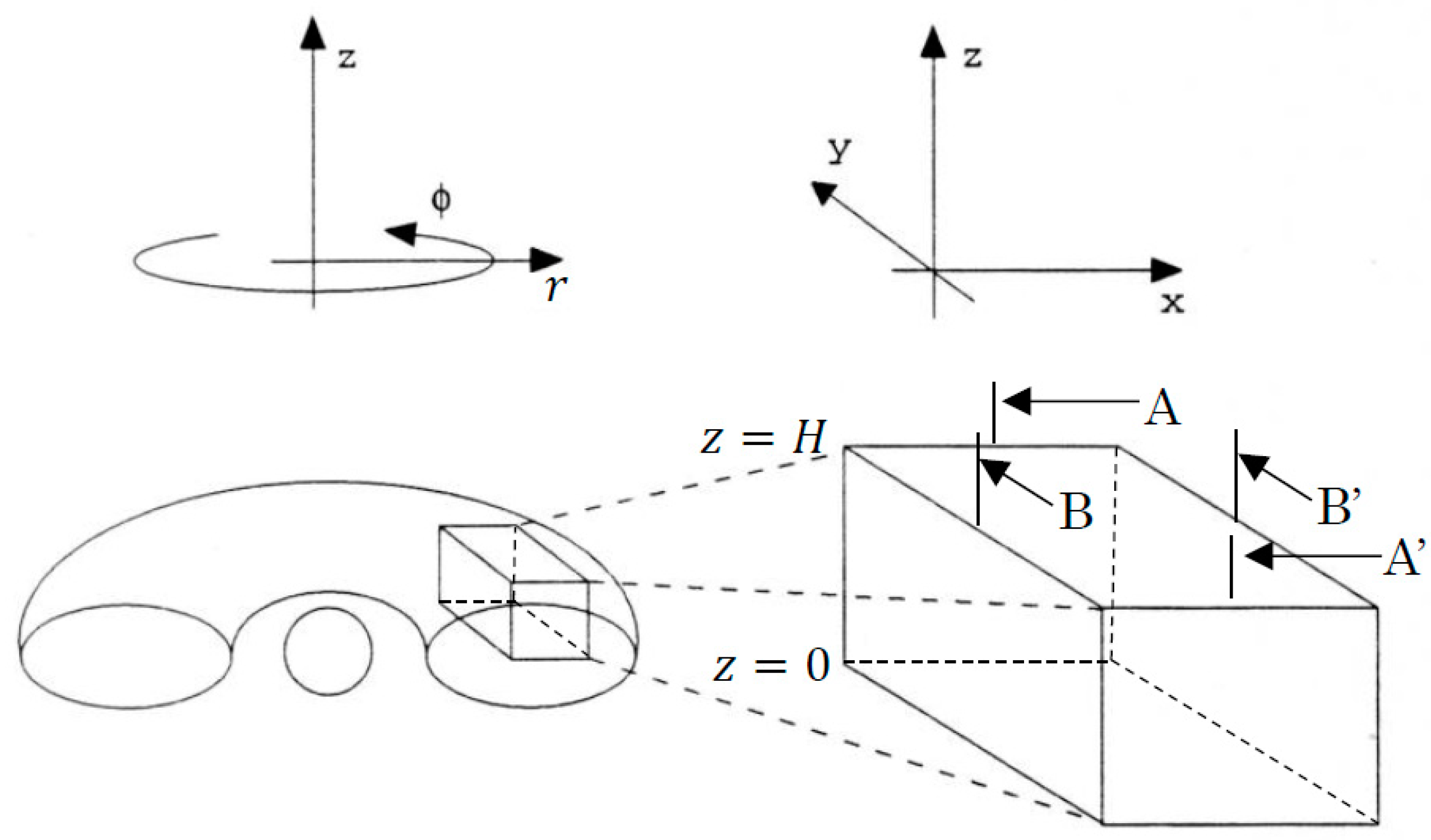
For simplicity, we ignore the curvature effect and use the local Cartesian coordinates $\left(x,y,z\right)$ in the local co-rotating frame at $r_0$ at frequency $\mathsf{\Omega }\left(r_0\right)$ ($x,y,z$ are the radial, azimuthal and vertical direction, respectively) and assume the sheared angular velocity $v_y$ arising from $\mathsf{\Omega }\left(x/r_0\right)=\mathsf{\Omega }\left(r_0\right)-2A\left(x/r_0\right)$ for $x=r-r_0$, where $A=-(rd\mathsf{\Omega }/\mathrm{d}\mathrm{r})/2$ is the Oort’s constant (Figure 2). Under a constant vertical gravity $g_z$, the growth rate of the Parker instability ${\gamma }_P$ is [20]

$${\gamma }_P^2={\displaystyle \frac{C_s^2}{\beta +2}}\left[\sqrt{4{\left(1+{\displaystyle \frac{1}{\beta }}\right)}^2{\left(k_y^2+{\displaystyle \frac{1}{4H^2}}\right)}^2+2\left(1+{\displaystyle \frac{2}{\beta }}\right)\left({\displaystyle \frac{1+\frac{1}{\beta }}{H^2}}-2k_y^2\right)k_y^2}-2\left(1+{\displaystyle \frac{1}{\beta }}\right)\left(k_y^2+{\displaystyle \frac{1}{4H^2}}\right)\right],$$

(1)

where H is the vertical scale height of the disk, $C_S=\sqrt{\gamma P/\rho }$ is the sound speed, $\beta =8\pi P/B^2$ and $k_y$ is the wavenumber in the azimuthal direction. The height $H$ depends on $g_z$ by $g_z=\left(1+1/\beta \right)C_s^2/H.$ We also assume $k_{x}H\ll 1$ for maximum growth rate, where $k_x$ is the radial component of the wavenumber. When $\beta \gg 1,k_y^2=3/16H^2$ makes the growth rate maximum,

$${\gamma }_P^2={\displaystyle \frac{C_S^2}{8{\beta H}^2}}={\displaystyle \frac{g_z}{8\left(1+\beta \right)H}},$$

(2)

while $\beta \ll 1,k_y^2=\left(2\sqrt{1+4/\beta }-3\right)/4H^2$ gives the maximum growth rate

$${\gamma }_P^2=C_S^2{\displaystyle \frac{\beta -\sqrt{{\beta }^2+4\beta }}{2{\beta H}^2}}={\displaystyle \frac{1-\sqrt{{\beta }^2+4\beta }}{2\left(1+\beta \right)H}}{g}_z.$$

(3)

When the magnetic field is purely toroidal, the maximum growth rate of the magnetorotational instability ${\gamma }_{mr}$ can be estimated from the following local dispersion relation [5]:

$${\gamma }_{mr}^2={\displaystyle \frac{A}{\mathsf{\Omega }-A}}{\omega }_A^2\propto {\displaystyle \frac{A}{\mathsf{\Omega }}}{\omega }_A^2\times {10}^{-1},$$

(4)

where ${\omega }_A^2={\left(k\cdot B\right)}^2/4\pi \rho$ is the Alfvén frequency. Since global analysis shows that the growth rate is maximum when ${\omega }_A/\mathsf{\Omega }~1$ [5], the maximum grow rate for magnetorotational instability is ${{\gamma }_{mr}}^2~A\mathsf{\Omega }\times {10}^{-1}.$ The growth time is revealed to be a dozen multiples of the rotation period of the disk.

We introduce the ratio $\mathcal{R}$ of the squared growth rates to assess the relative importance of these two processes as

$$\mathcal{R}={\displaystyle \frac{{{\gamma }_{mr}}^2}{{{\gamma }_P}^2}}\simeq A\mathsf{\Omega }{\displaystyle \frac{8\left(1+\beta \right)H}{g_z}}\times {10}^{-1},$$

(5)

for $\beta \gg 1$ and

$$\mathcal{R}={\displaystyle \frac{{{\gamma }_{mr}}^2}{{{\gamma }_P}^2}}\simeq A\mathsf{\Omega }{\displaystyle \frac{2\left(1+\beta \right)H}{g_z\left(1-\sqrt{{\beta }^2+4\beta }\right)}}\times {10}^{-1},$$

(6)

for $\beta \ll 1$. For the primordial disk, $\beta \gg 1$ since the magnetic field in an accretion disk is weak to begin with. The vertical gravitational force of the central object can be expressed by the radius r from the center and the height z from the equator of the disk:

$$g_z={\displaystyle \frac{GMz}{{\left(r^2+z^2\right)}^{\frac{3}{2}}}},$$

(7)

where $G$ is the gravitational constant and $M$ is the mass of the central object. When $r\gg z,$ $g_z$ can be reduced to $GMz/r^3.$ Since $\mathsf{\Omega }=\sqrt{GM/r^3}$ and $A=3\mathsf{\Omega }/4$ for the Keplerian disk, the ratio $\mathcal{R}$ is written as

$$\mathcal{R}=6\left(1+\beta \right){\displaystyle \frac{H}{\left|z\right|}}\times {10}^{-1}.$$

(8)

In this case, the number of Parker e-foldings in one rotation period is

$${\displaystyle \frac{2\pi {\gamma }_P}{\mathsf{\Omega }}}={\displaystyle \frac{\pi \beta }{1+\beta }}\sqrt{{\displaystyle \frac{1}{2\beta }}}{\displaystyle \frac{\mathsf{\Omega }\left|z\right|}{C_s}},$$

(9)

showing the dominance of the Parker instability away from the equatorial plane of the disk. On the surface of the accretion disk ($\left|z\right|=H$), $\mathcal{R}$ only depends on $\beta$. If a protostellar disk is weakly magnetized ($\beta$ = 10), $\mathcal{R}$ is the order of unity. Since the vertical gravity decreases towards the equatorial plane of the disk, $\mathcal{R}$ increases when $\left|z\right|$ decreases. However, if it is more strongly magnetized ($\beta \le 1$), the ratio $\mathcal{R}$ is calculated from Equation (6),

$$\mathcal{R}={\displaystyle \frac{3\left(1+\beta \right)}{2\left(1-\sqrt{{\beta }^2+4\beta }\right)}}{\displaystyle \frac{H}{\left|z\right|}}\times {10}^{-1}.$$

(10)

Though the magnetization of the disk rarely becomes this high, Equation (10) indicates the dominance of the Parker instability on the surface of the strongly magnetized disks ($\mathcal{R}\le 1$). Therefore, the magnetorotational instability is dominant in the early stage of the disk evolution ($\beta \gg 1$), and the magnetization of the disk increases with time due to the magnetorotational instability. In the later stage ($\beta ~1$), the Parker instability sets in because of the enhanced magnetic fields, and the Parker instability dominates the evolution of the surface of the disk, whereas the magnetorotational instability still enhances magnetic fields near the equatorial plane $(\left|z\right|\ll H$).

Next, we compare the growth rates of the kinematic dynamo and the Parker instability. We evaluate the $\alpha \omega$ dynamo, which includes the effect from helicity ($\alpha$ effect) and the differential rotation effect ($\omega$ effect). The governing equations of kinematic dynamo are [20]

$$\left({\displaystyle \frac{\partial }{\partial t}}-\eta {\nabla }^2\right)B_y={\displaystyle \frac{d{v}_y}{dz}}{\displaystyle \frac{\partial A_y}{\partial x}}-v_y{\displaystyle \frac{\partial B_y}{\partial y}},$$

(11)

$$\left({\displaystyle \frac{\partial }{\partial t}}-\eta {\nabla }^2\right)A_y=\alpha B_y-v_y{\displaystyle \frac{\partial A_y}{\partial y}},$$

(12)

where ${\alpha }_d$ is the mean helicity, $\eta$ is the effective magnetic diffusivity and $A_y$ is the azimuthal component of the vector potential. The growth rate of the $\alpha \omega$ dynamo is given by [17]

$${\gamma }_d=\eta k_d^2\left[\mathrm{Re}\left(\sqrt{-{\displaystyle \frac{k_y^4{v}_y^2}{4\eta k^4}}+2\mathrm{i}{N}_d}\right)-1\right],$$

(13)

where $k^2=k_x^2+k_y^2+k_z^2$ is the square of the dynamo wavenumber, and

$$N_d={\displaystyle \frac{\alpha k_z}{2{\eta }^2{k}^4}}{\displaystyle \frac{d{v}_y}{dx}},$$

(14)

is the dynamo number, respectively. The base level resistivity set by electron-neutral collisions is small, typically estimated as ${\eta }_r={10}^6\mathrm{c}{\mathrm{m}}^2{\mathrm{s}}^{-1}.$ However, the turbulent fluid motions produce a large effective resistivity. We assume that the turbulent motion in the inner region produces a resistivity of $\eta ={10}^{16}\mathrm{c}{\mathrm{m}}^2{\mathrm{s}}^{-1}$ [21] for a typical dynamo number for dipole, $N_d~600.$ Since $\alpha$ can be estimated as $\alpha ={\alpha }_0{(r/r_0)}^{-3/2}=v_y\left(r_0\right){(r/r_0)}^{-3/2}\times {10}^{-2},$ $N_d$ depends on $r$ as $N_d=N_d\left(r_0\right){(r/r_0)}^{-3}$ [21]. We estimate $k_d$ by assuming $k_x\simeq k_z\ge k_y$ in Equation (14), which yields $k_x\simeq k_z=O\left({10}^{-14}\right).$ In this case, we cannot use the dispersion relation (1) since $k_{x}H\ll 1$ and we introduce another expression [22]

$${\gamma }_P^2={\displaystyle \frac{C_s^2}{2}}\left[\sqrt{{\left(1+{\displaystyle \frac{2}{\beta }}\right)}^2{\left(k_y^2+{\displaystyle \frac{1}{4H^2}}\right)}^2+{\displaystyle \frac{{4\mathrm{k}}_{\mathrm{y}}^2}{\beta }}\left({\displaystyle \frac{1+\frac{1}{\beta }}{H^2}}-2k_y^2-{\displaystyle \frac{1}{2H^2}}\right)}-\left(1+{\displaystyle \frac{2}{\beta }}\right)\left(k_y^2+{\displaystyle \frac{1}{4H^2}}\right)\right].$$

(15)

When $\beta \gg 1$, the maximum growth rate arises for $k_y^2=\left(\sqrt{2}-1\right)/4H^2$ and is

$${\gamma }_P^2={\displaystyle \frac{\left(\sqrt{2}-1\right)g_z}{\left(1+\beta \right)H}},$$

(16)

While for $\beta \ll 1$, $k_y^2=\left(\sqrt{2/\beta }-3\right)/4H^2$ makes the growth rate maximum,

$${\gamma }_P^2={\displaystyle \frac{\sqrt{\beta }g}{4\left(1-\sqrt{\beta }\right)\left(1+\beta \right)H}}.$$

(17)

Now, we introduce another growth rate ratio ${\mathcal{R}}_d$ comparing the growth rate of the Parker instability to that of the $\alpha \omega$ dynamo with the same wavenumber $k_P,$

$${\mathcal{R}}_d={\displaystyle \frac{{{\gamma }_d}^2}{{{\gamma }_P}^2}}={\displaystyle \frac{2(1+\beta )}{3-2\surd 2}}{\displaystyle \frac{{\eta }^2{k}_d^{4}H}{{\mathsf{\Omega }}^{2}z}}\left[\mathrm{Re}\left(\sqrt{-{\displaystyle \frac{k_y^2{v}_y^2}{4{\eta }^2{k}^4}}}+2\mathrm{i}{N}_d\right)-1\right],$$

(18)

for $\beta \gg 1,$ and

$${\mathcal{R}}_d={\displaystyle \frac{2(1+\beta )}{(1-\sqrt{\beta /2})}}{\displaystyle \frac{{\eta }^2{k}_d^{4}H}{{\mathsf{\Omega }}^{2}z}}\left[\mathrm{Re}\left(\sqrt{-{\displaystyle \frac{k_y^2{v}_y^2}{4{\eta }^2{k}^4}}}+2\mathrm{i}{N}_d\right)-1\right],$$

(19)

for $\beta \ll 1$. For the small thick disk case ($r~1$ AU, $H/r~0.1)$ with a temperature of 100 K, ${\mathcal{R}}_d=O\left({10}^{-4}\right)$ with $\beta =10$ and ${\mathcal{R}}_d=O\left(1\right)$ with $\beta =0.1$ on the surface of the disk. Thus, the dynamo effect is weak at the beginning of the protostellar evolution ($\beta \ll 1$), and magnetic fields created by the dynamo ($z\ll H$) cannot be maintained because of the Parker instability. However, in the later stage of the evolution ($\beta \ll 1$), the magnetic field is maintained by the dynamo effect and the Parker instability creates large structures in the inner region. Note that the $\alpha \omega$ dynamo grows faster than that of the Parker instability even when $\beta \ll 1$ and makes the inner region turbulent.

3. Radial Mass Spectrum of Accretion Disk

The radial mass spectrum of aggregated matter that may be organized as a result of the nonlinear evolution of the MHD instabilities given in Section 2 for a primordial accretion disk is now estimated from the characteristics of the magnetorotational and kinematic dynamo instabilities. We choose two different types of density profiles and compare the mass spectra of these profiles. First, we assume the radial dependence of density is parameterized by [23]

$$\rho ={\rho }_0{\left({\displaystyle \frac{r_0}{r}}\right)}^{\nu }.$$

(20)

Then, the total mass $M_s\left(r\right)$ between two Alfvén singular points in corotational coordinates, which is the typical scale length of the magnetorotational instability in the radial direction, can be given by

$$M_s=2\pi r\rho \times {\displaystyle \frac{v_A}{A}}={\displaystyle \frac{4}{3}}\sqrt{{\displaystyle \frac{\pi {\rho }_0}{GM}}}B{r}^{{\displaystyle \frac{5-\nu }{2}}},$$

(21)

for pure azimuthal perturbation in a Keplerian disk. Since the typical value of $\nu$ is 2 in an early stage of accretion disk evolution [17,23,24], $M_s$ increases even though the density decreases with $r$. $M_s$ is the maximum seed mass available from the MHD evolution between the two Alfvén layers separated by $\mathsf{\Delta }r=v_A/A$.

Another, more specific mass density model introduced by Okada et al. [25] assumes that the magnetic field exists only in the azimuthal direction and that the density distribution is obtained by integrating the equations of motion into the potential form,

$$\rho ={\left({\displaystyle \frac{\max \left[{\mathsf{\Phi }}_0+\frac{1}{R}-\frac{L^2}{2r^2},0\right]}{K\left[\frac{\gamma }{\gamma -1}\left[1+{\beta }_0^{-1}{r}^{2\left(\gamma -1\right)}\right]\right]}}\right)}^{{\displaystyle \frac{1}{\gamma -1}}},$$

(22)

where

$${\mathsf{\Phi }}_0=-{\displaystyle \frac{1}{R}}+{\displaystyle \frac{L^2}{2r^2}}+{\displaystyle \frac{1}{\gamma -1}}{v}_s^2+{\displaystyle \frac{\gamma }{2\left(\gamma -1\right)}}{v}_A^2,$$

(23)

is the value of potential on the surface of the torus, where the mass density is $\rho =0$, $K$ is a constant, $R={\left(r^2+z^2\right)}^{{\displaystyle \frac{1}{2}}},$ $L$ is the angular momentum, $\gamma$ is the specific heat ratio and ${\beta }_0=2K/H$ is the plasma $\beta$ at $\left(r,z\right)=\left(r_0,0\right).$ In the outer region $(r\gg z)$, $\rho$ reduces to

$$\rho ={\rho }_0{\left({\displaystyle \frac{\max \left[{\mathsf{\Phi }}_0+\frac{1}{r},0\right]}{K\left[\frac{\gamma }{\gamma -1}\right]}}\right)}^{{\displaystyle \frac{1}{\gamma -1}}},$$

(24)

which yields the mass spectrum of the maximum coagulated matter between the Alfvén resonance,

$$M_s={\displaystyle \frac{4}{3}}\sqrt{{\displaystyle \frac{\pi {\rho }_0}{GM}}}{B}_{\varphi }{r}^{{\displaystyle \frac{5}{2}}}{\left({\displaystyle \frac{\max \left[{\mathsf{\Phi }}_0+\frac{1}{r},0\right]}{K\left[\frac{\gamma }{\gamma -1}\right]}}\right)}^{{\displaystyle \frac{1}{2\left(\gamma -1\right)}}}.$$

(25)

Thus, the radial dependence of $M_s$ is determined by the factors ${\mathsf{\Phi }}_0$ and $\gamma$. It vanishes if ${\mathsf{\Phi }}_0<0$.

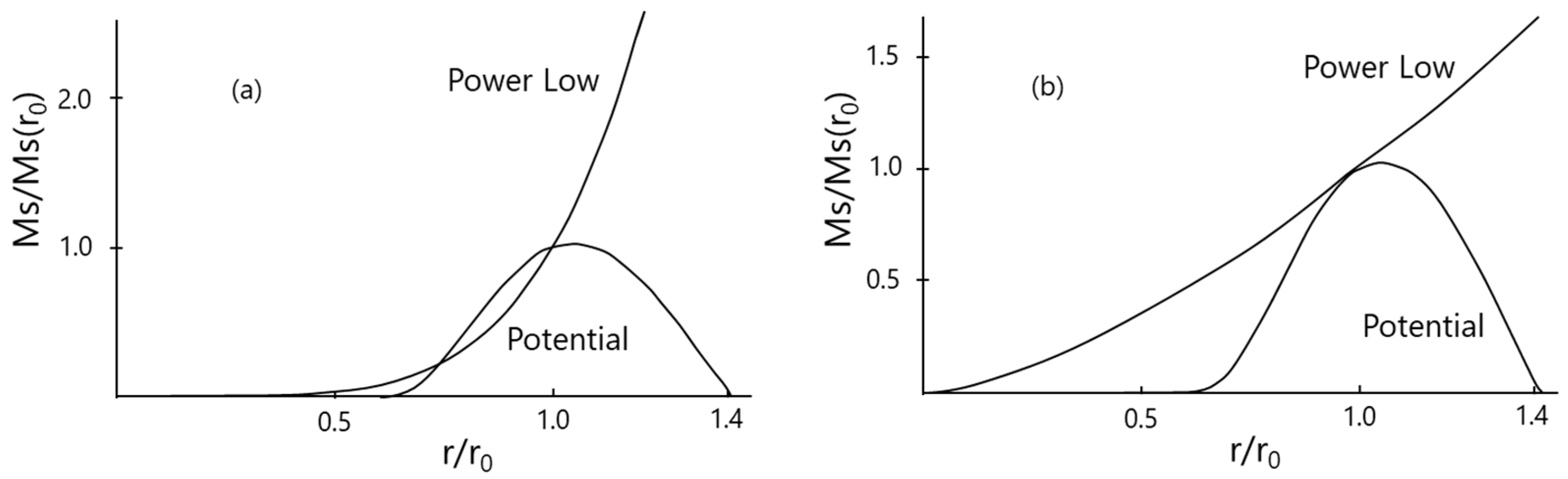
We show the $r$ dependence of those two mass spectra in Figure 3. For the power law model in Equation (21), we choose $\mathsf{\nu }=2$ and the other parameters are chosen to match the initial condition of the simulation performed by Machida et al. [6]. As we described above, the mass spectrum increases with r if the density profile obeys the power law. On the other hand, if the density profile is given by the potential model in Equation (22), it takes a maximum value at some radius.

In the inner region (r < 1 AU), the kinematic dynamo is predominant in determining the turbulence of plasma. In this case, structure formation is inhibited inside of the Roche limit $r_R=2.546{\left({\rho }_{\odot }/\rho \right)}^{1/3}{R}_{\odot }$, where ${\rho }_{\odot }$ and $R_{\odot }$ are the density and the radius of the central object, respectively. If we only consider the tidal force and self-gravitation, the typical wavelength for exponentially growth of density waves in the radial direction is

$${\lambda }_c={\displaystyle \frac{\pi G\rho }{r{\mathsf{\Omega }}^2}},$$

(26)

which yields the mass spectrum

$$M_s=2\pi r\rho {\lambda }_c={\displaystyle \frac{2{\pi }^2{r}^3{\rho }^2}{M}}.$$

(27)

This mass spectrum can either increase or decrease with $r$, depending on what kind of density profile we choose.

Another characteristic wavelength is the width of dynamo eigenmodes. Stepinski et al. [21] showed the eigenmodes extend from the axis of the rotation to $r=5~10H$. Since the height of the disk $H$ is given by

$$H={\displaystyle \frac{C_s^2\left(1+\frac{1}{\beta }\right)}{\gamma g_z}}={\displaystyle \frac{C_s^2\left(1+\frac{1}{\beta }\right){\left(r^2+z^2\right)}^{\frac{3}{2}}}{\gamma GMz}},$$

(28)

the mass spectrum due to the dynamo effect can be estimated in the form

$$M_s=10\times 2\pi \rho {\displaystyle \frac{C_s^2\left(1+\frac{1}{\beta }\right){\left(r^2+z^2\right)}^{\frac{3}{2}}}{\gamma GMz}}.$$

(29)

The mass spectra of those cases are shown in Figure 4. In Figure 4a, we calculate the mass spectrum due to the self-gravitation of gas. When the density profile is constant, the spectrum monotonically increases with $r$. The peak near the rotational axis may be too close to the central object. This dense region creates a disk because of the tidal force. However, when the density profile obeys Equation (22), the spectrum rises from $r~0.65H$, has a peak around $r=1.5H$ and then decreases.

We show the mass spectrum due to the magnetic dynamo in Figure 4b. We assume constant pressure ($T\left(r\right)=T_0(r/r_0{)}^{\nu }$) for a power law profile, and for the potential model Equation (22), $C_s$ is given by

$$C_s^2=K\gamma {\rho }^{\gamma -1}.$$

(30)

The mass spectrum increases monotonically with r in this case, but the power law profile increases less rapidly than in the torus case.

4. Numerical Simulation of Coupled Instabilities

We present the results of three-dimensional MHD simulations in a corotating reference frame. The basic equation we use are ideal MHD equations in the rotating frame where the gas is stationary at $r=r_0$. In this frame, $2\mathsf{\Omega }\left(r_0\right)$ gives the Coriolis acceleration and $\mathsf{\Omega }\left(x\right)=Ax$, where $x=r-r_0$ and $A=rd\mathsf{\Omega }/dr$. We assume that the curvature effect is negligible and use the local cartesian coordinate system $(x,y,z)$. A schematic of the simulation box is shown in Figure 2. The bottom ($z=0$) and top ($z=H$) of the box corresponds to the equatorial plane and surface of the disk, and uniform gravity is applied in the $z$ direction. An initial shear flow is applied in the $y$ direction, which corresponds to the flow in the azimuthal direction in the accretion disk case, and magnetic field in the $y$ direction supports fluid against gravity. We assume the periodic boundary in the $x$(radial) direction and a free boundary at $z=H$. The boundary condition at $z=0$ is antisymmetric for the magnetic field and symmetric for other field variables. We adopt the shear boundary condition in the $x$ direction [2,5],

$$\begin{array}{c}\hfill f\left(x,y,z,t\right)=f\left(x+L_x,y-2A{L}_{x}t,z,t\right),\\ \hfill \begin{array}{c}{v}_y\left(x,y,z,t\right)=v_y\left(x+L_x,y-2A{L}_{x}t,z\right)+2A{L}_x,\end{array}\end{array}$$

(31)

where $L_x,L_y,L_z$ is the sizes of the simulation box in the $x,y,z$ directions, respectively.

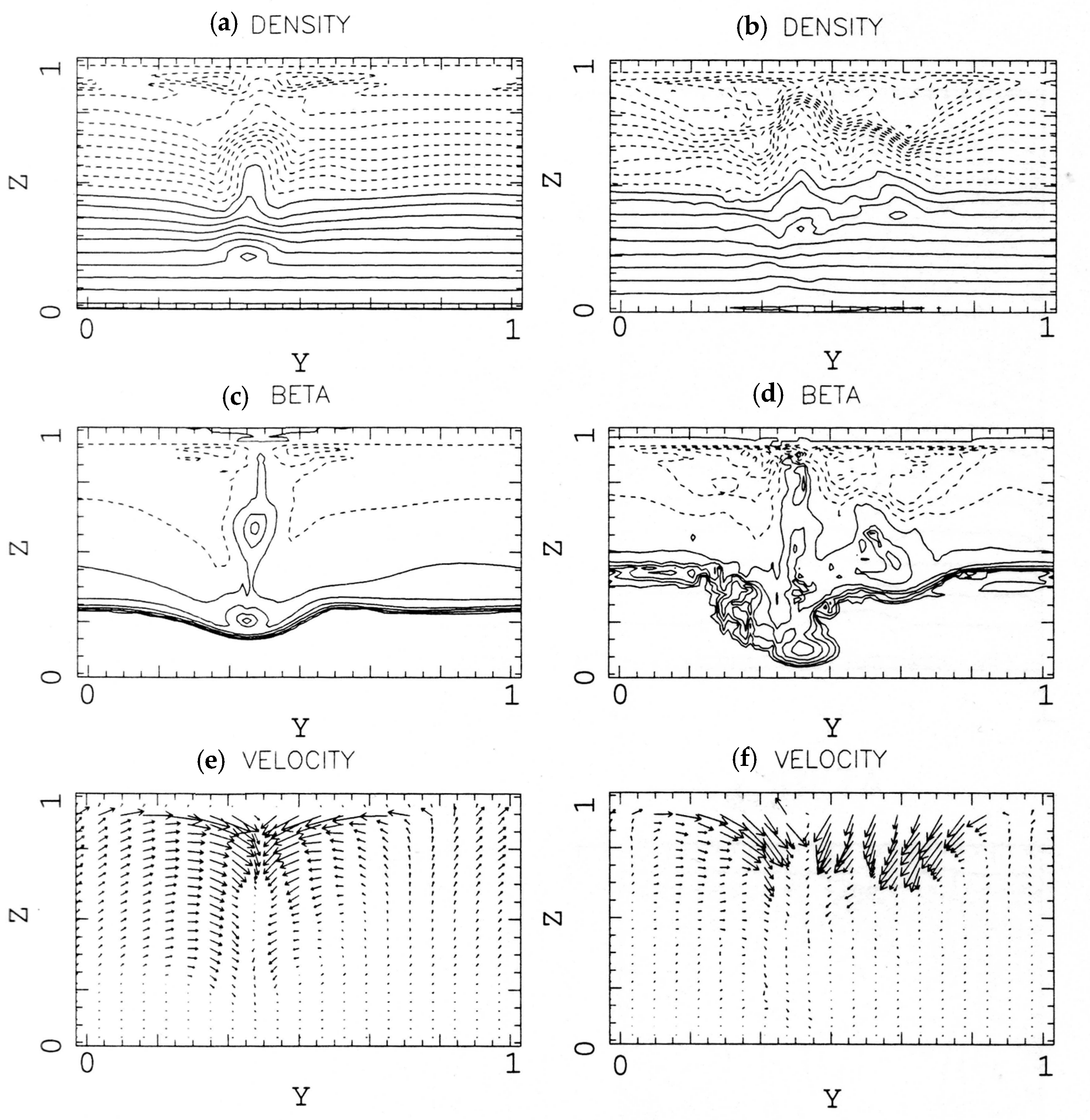
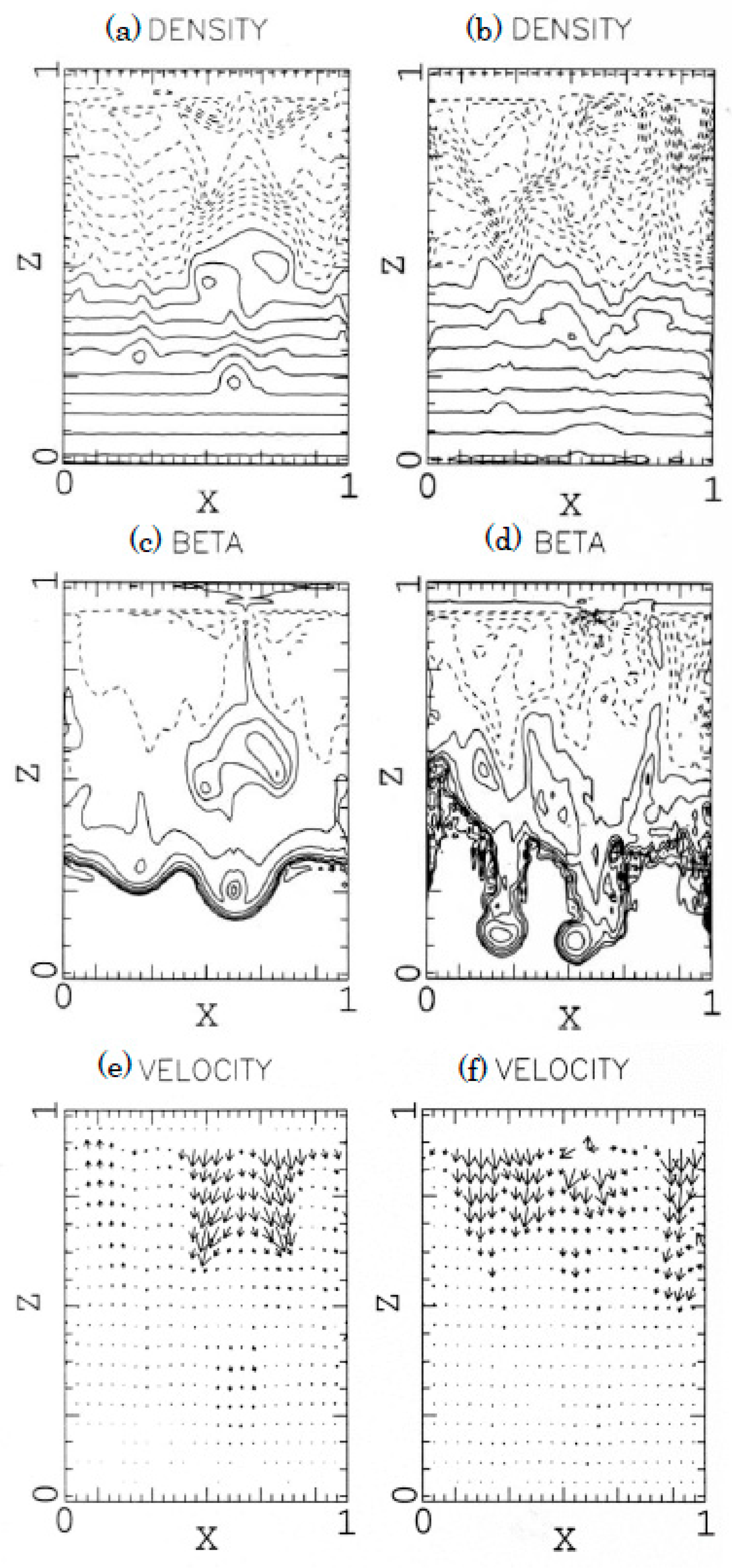
We show the simulation results in Figure 5 and Figure 6, where plasma $\beta$ is unity on the equatorial plane ($z=0$), and $\gamma =1.05$ for nearly isothermal dynamics. We put sinusoidal incompressible perturbation whose wavelength corresponds to $k_R$ in $x$ direction and $k_P$ in y direction to the velocity field. At $t=2.05{\mathsf{\Omega }}^{-1}$, the Parker instability creates magnetic loops in the azimuthal direction and plasma accretes to the foot points of loops. Plasma also accretes in the radial direction due to the magnetorotational instability. The combination of these two instabilities makes high density stripe regions in the equatorial plane.

At a later time ($t=2.93{\mathsf{\Omega }}^{-1}$), the density at the bottom becomes larger and shows fewer dense blobs. We note that even though strong shear flows exist, blobs and spiral dense regions do not disappear due to phase mixing. Magnetic fields continuously escape through the top of the box because of the buoyancy, but the maximum strength of magnetic field increases because magnetic fields are continuously created by the magnetorotational instability.

Global simulations [6] showed that the competition between the magnetorotational and the Parker instability become quasi-periodic after some rotations. We have stopped the simulation before it reaches the quasi-periodic state, but we can see all the major features of the global simulation appear in the local simulation.

5. Shear Flow-Induced Structures in Laboratory Plasmas

Next, we consider the “simulation” of the above processes of structure formation in laboratory plasmas. In recent tokamak plasmas, strong shear flows have been observed either due to the external drive, such as the neutral beam injection (NBI) [7,26], or due to the internal flow drive mechanism [8]. In another magnetic configuration called FRC (field reversible configuration), there are end plugs at the end of the FRC where shear rotated plasmas may be formed [12,13,14]. It may be also possible to generate shear flows in laser-irradiated targets [15,16].

For a plasma in tokamak, the gravitational force is replaced by the centrifugal force, which is created by the thermal velocity and/or flow in toroidal direction and is some substantial fraction $ϵ$ of $C_s$,

$$g={\displaystyle \frac{{\left(ϵC_s\right)}^2}{R_t}},$$

(32)

where $R_t$ is the major radius of the torus. Then, the growth rate ration in Equation (6) can be written in the form

$$\mathcal{R}={\displaystyle \frac{2A\mathsf{\Omega }{R}_t^2{\left(1+\beta \right)}^2}{{ϵ}^4{C}_s^2\beta \left(1-\sqrt{{\beta }^2+4\beta }\right)}}\times {10}^{-1}.$$

(33)

Since the toroidal flow $\mathsf{\Omega }{R}_t$ is equal to $\delta C_s$ and $\beta \ll 1$, we can further reduce R to

$$\mathcal{R}={\displaystyle \frac{A}{\mathsf{\Omega }}}{\displaystyle \frac{2}{\beta {ϵ}^2}}\times {10}^{-1}.$$

(34)

The value of $\beta$ in a typical experiment is about 0.01 at peak and is smaller near the wall. If we assume $\beta ={10}^{-3}~{10}^{-2}$ and $ϵ=0.1$, $\mathcal{R}$ becomes a function of the ratio $A/\mathsf{\Omega }$

$$\mathcal{R}={\displaystyle \frac{A}{\mathsf{\Omega }}}\times {10}^3~{10}^4.$$

(35)

The flow shear rate $A$ in the transport barrier region can be estimated from the toroidal flow profile. The typical value of $A$ is 100 kHz [27]. The toroidal rotation of the plasma is driven by the neutral beam injection. In modern large tokamaks, the toroidal velocity reaches 200~300 km/s, which yields $\mathsf{\Omega }~$100 kHz. The estimated value of $\mathcal{R}$ is about ${10}^3~{10}^4$ for the transport barrier region. Thus, for a typical experiment configuration, the magnetorotational instability grows faster to make plasma turbulent. The details of the turbulent transport from both rotational shear, magnetic shear and the thermal gradient are complex in tokamaks [27].

Another problem is to maximize the growth rate of the magnetorotational instability by equalizing the Alfvén frequency ${\omega }_A$ to the rotational speed $\mathsf{\Omega }$. For typical tokamak devices, the poloidal magnetic field is ~0.1T and density $n$ is ${10}^{13} {\mathrm{cm}}^{-3}$, which yields a Alfvén velocity of the order of ${10}^2$ km/s. Thus, the typical length of the magnetorotational instability in the poloidal direction [5],

$${\lambda }_B={\displaystyle \frac{v_A}{A}}\simeq Rt{\displaystyle \frac{\sqrt{\alpha }}{ϵ}},$$

(36)

is the order of ${10}^4~{10}^5$ cm. The typical wavelength of the Parker instability in the toroidal direction is

$${\lambda }_P={\displaystyle \frac{2\pi }{k_P}}={\displaystyle \frac{4\pi \left(1+\beta \right)}{\sqrt{\beta }{\left(2\sqrt{{\beta }^2+4\beta }-3\beta \right)}^{\frac{1}{2}}}}{\displaystyle \frac{R_t}{{ϵ}^2}},$$

(37)

whose value is ${10}^6~{10}^7$ cm.

The magnetic (Maxwell stress) viscosity coefficient ${\alpha }_B$ caused by the magnetorotational instability is given by [5]

$${\alpha }_B=-{\displaystyle \frac{〈\delta B_x\delta B_y〉}{4\pi \rho C_s^2}}<{\displaystyle \frac{〈\delta B^2〉}{4\pi \rho C_s^2}}.$$

(38)

Substituting all the variables in Equation (38), the magnetic viscosity in tokamak device is estimated to be $a_B\ll 0.01$.

Next, we consider the possibility of laser plasma experiments. A schematic view of an experiment is shown in Figure 7 [15]. Though it may not be easy to apply a strong magnetic field to the target, we may apply an electric current to a target perpendicular to the direction of laser injections to create a magnetic field in the azimuthal direction. The injection directions of lasers are offset from the symmetry axis, so that the target obtains angular momentum from the laser beams. The target is nonuniform to create a sheared rotation in the horizontal plane. Since the target is Rayleigh–Taylor unstable due to the pressure of the laser and magnetorotationally unstable due to the sheared rotation and magnetic field, we should be able to observe how the global structure grows experimentally if we choose the variables properly.

A critical condition for laser–space plasma experiments is to make the equations of motion invariant under the scale transformation [16]:

$$\begin{gathered} {\rho }_d=a_1{\rho }_e, \\ {p}_d=a_2{p}_e, \\ \begin{array}{c}{h}_d=a_3{h}_e,\end{array} \end{gathered}$$

(39)

where $\rho$, $p$ and $h$ are the characteristic values of density, pressure and spatial scale, respectively, and subscripts $d$ and $e$ indicate that those values correspond to the accretion disk or experiment. The ratios $a_1,a_2,a_3$ are determined from those parameters. Under the transformation, the characteristic values of time scale $\tau$, magnetic field $B$ and angular frequency $\mathsf{\Omega }$ are transformed as

$$\begin{gathered} {\tau }_d=\sqrt{{\displaystyle \frac{a_1}{a_2}}}{a}_3{\tau }_e\equiv a_4{\tau }_e, \\ {B}_d=a_2^{{\displaystyle \frac{1}{2}}}{B}_e, \\ \begin{array}{c}{\mathsf{\Omega }}_{i}d=\sqrt{{\displaystyle \frac{a_2}{a_1}}}{\displaystyle \frac{1}{a_3}}{\mathsf{\Omega }}_e={\displaystyle \frac{1}{a_4}}{\mathsf{\Omega }}_e.\end{array} \end{gathered}$$

(40)

First, we determine the ranges of $a_1$ and $a_2$ from the density and magnetic field strength. The typical strengths of magnetic field are $B_d={10}^{-3}~1$ G and $B_e=1\mathrm{G}~1\mathrm{T}$, which yields $a_2={10}^{-14}~{10}^0$. Since the typical number density of a protostellar accretion disk is $n={10}^9~{10}^{12}\mathrm{c}{\mathrm{m}}^{-3}$, whose content is mostly hydrogen (${\rho }_d={10}^{-15}~{10}^{-12}\mathrm{g}/\mathrm{c}{\mathrm{m}}^3$), and that of target is ${\rho }_e=1~10{\mathrm{g}/\mathrm{cm}}^3$, the ratio $a_1$ is the order of ${10}^{-16}~{10}^{-12}$. The pressure of the disk is estimated by assuming its temperature $T~100\mathrm{K}$, which yields $p_d=C_s^2\rho /\gamma ={10}^{-6}~{10}^{-3}$ Pa and an experiment $P_e=p_d/a_2={10}^{-6}~{10}^{11}$ Pa.

Next, we determine the range of $a_2$ again, with a typical scale length and time scale. The typical scale length of a primordial disk can be determined by the distance between the Alfvén singularities in corotational frame [5],

$$h_d~{\displaystyle \frac{v_A}{A}}={\displaystyle \frac{B}{\sqrt{4\pi \rho }A}}={10}^9~{10}^{13}\mathrm{cm},$$

(41)

where we use $A=3\mathsf{\Omega }/4$ and $\mathsf{\Omega }={10}^{-9}~{10}^{-7}{\mathrm{s}}^{-1}$, whose period is $10~{10}^3$ yr. For laser experiments, $h_e={10}^{-4}~{10}^{-2}$, which yields $a_3={10}^{11}~{10}^{17}$. The typical time scale of accretion disk evolution is estimated by the growth rate of the magnetorotational instability,

$${\tau }_d={\displaystyle \frac{1}{{\omega }_A}}~{\displaystyle \frac{1}{\mathsf{\Omega }}}={10}^7~{10}^9\mathrm{s}.$$

(42)

The typical time scale of experiments is $h_e={10}^{-8}~{10}^{-2}\mathrm{s}$, which makes scaling factor $a_4$ as ${10}^{11}~{10}^{17}$. Since $a_2$ is given by

$$a_2=a_1{\left({\displaystyle \frac{a_3}{a_4}}\right)}^2,$$

(43)

to make the equation of motion invariant under the transformation, the range of $a_2$ is ${10}^{-28}~{10}^0$(due to the square in Equation (43)), which overlaps with the range of $a_2$ calculated from the magnetic field strength. Thus, we find that a laser experiment for an accretion disk may be achieved in the range ${10}^{-14}<a_2<{10}^0$.

The rotation frequency for experiments ${\mathsf{\Omega }}_e$ is given by

$${\mathsf{\Omega }}_e=a_3\sqrt{{\displaystyle \frac{a_1}{a_2}}}{\mathsf{\Omega }}_d={10}^{-10}~{10}^2.$$

(44)

For realistic experiments, ${\mathsf{\Omega }}_e~{10}^3{\mathrm{s}}^{-1}$, which corresponds to $B_e~1$ G, $P_e~{10}^4$ Pa, $h_e~{10}^{-2}$ cm, ${\tau }_e~{10}^{-2}$ s.

We also apply this scale transformation to active galactic nuclei (AGNs). The typical ranges of variables for AGNs are $B_{AG}={10}^{-3}~{10}^{-1}$, ${\rho }_{AG}={10}^5~{10}^6\mathrm{g}/\mathrm{c}{\mathrm{m}}^3$, $T_{AG}={10}^3~{10}^{4}K$ and $M_{AG}=M_{\odot }\times {10}^8,r_{AG}=1~100\mathrm{AU}$. Substituting all the variables to Equations (39) and (40), we can estimate realistic experimental values as $B_e={10}^{-1}$ G, ${\rho }_e=10$ g/cm³, $P_e={10}^9~{10}^{11}\mathrm{Pa}$, $h_e~{10}^{-2}$ cm, ${\tau }_e~{10}^{-2}$ s and ${\mathsf{\Omega }}_e=10{\mathrm{s}}^{-1}$. The comparison of the estimated values is shown in

Table 1. Typical quantities of primordial disks and experimental plasmas.

Quantities	Primordial Disks	Tokamak	Laser
L (cm)	1013~1015	103~107	10−4~10−2
t (s)	106~1012	10−5~10−4	10−8~10−2
P (Pa)	109~1011	103~104	109~1011
ρ (g/cm3)	105~106	10−11~10−10	1~10
B (G)	10−3~10−1	103	10−1
T (eV)	10−1~1	104	1
a (cm/s2)	10−11~10−6	1010~1013	1011~1016
${\mathcal{R}}^{1/2}$	106~109	101~102	≪1

. In both cases, the ratios $\mathcal{R}$ and ${\mathcal{R}}_d$ may be small. It is not easy to adjust the rotation frequency and the shear rate of the target to the ideal values. The Parker instability is relatively easy to control since the pressure of the laser directly makes the target Parker unstable. The resulting gas buoyancy may be too strong to couple either the magnetorotational instability or kinematic dynamo.

A similar physical situation of dynamically twisting magnetic field lines and consequent plasma dynamics may be seen in the FRC plasma [12,13,14,28]. The FRC plasma are often injected by rotating beams in the middle (See Figure 8). Such a rotation of one part of the FRC plasma in one part of the axial position may be different at the other part of the axial position, which could cause a shearing magnetic field that originally lacked an azimuthal component. This situation is not different from the situation with the astrophysical disk-induced magnetic shear [28]. It would be of interest to see some evidence of various plasma instabilities, their nonlinear evolutions and a certain class of structure formation of plasmas seen in astrophysical plasmas [16] in laboratories.

6. Discussion

We have shown that the combined effects of the magnetorotational and Parker instabilities give rise to density blobs in a primordial disk. We have calculated the mass spectrum of such aggregations from the typical wavelengths of the magnetorotational instability, self-gravitation and magnetic dynamo. By transforming the equations of motion, we have found that this coupling instability may be observed experimentally in laboratory plasma. (The azimuthal dependence of the coupled instability remains to be an issue of investigation.)

The wavenumber dependence of the magnetorotational instability arises only from the ratio $q=k_{\theta }^2/k_z^2$, where $k_{\theta }$ is the wavenumber in the azimuthal direction, and $k_z$ is in the direction of the rotation axis [5]. By using the radius of the disk $r$ and azimuthal mode number $m$, we estimate $k_{\theta }$ as $k_{\theta }=m/r$. For the thick disk case, $k_z$ can be estimated by the reciprocal of the $\pi$ divided by the half height of the disk $H$ and a vertical mode number $n$ as $k_z=n\pi /H$. The ratio $q$ is then given by

$$q={\left({\displaystyle \frac{mH}{\pi nr}}\right)}^2.$$

(45)

We have discussed the possibility of experiments of analogous phenomena in laboratory plasmas. First, the radiation pressure may be stronger in laser plasmas than primordial accretion disks (perhaps more fitting in disks with AGNs). Since the temperature of the accretion disk gas is typically low ($T~{10}^{2}K$), we neglect the radiation pressure in our calculation and simulation. However, the temperature in the analog laser experiments is typically high (10~100 eV) so that the radiation pressure is not negligible. Second, the control of shear flows is challenging in laboratory plasmas for its role in the transport of angular momentum. In tokamak devices, shear flows are created by an unbalanced NBI and maintained by plasma itself. To create near-Keplerian shear flows in the device, the injection angle of the NBI, external magnetic field and plasma density should be carefully considered. In laser plasmas, shear flows may be created by injected laser from opposite direction. Rigid rotating flows may be possible to create. Inhomogeneites of the laser irradiation to a target also prevent shear flows from achieving uniformity. Despite these issues, analogous experiments may be important to observe and provide a database for nonlinear evolutions of accretion disks with large density and magnetic field ranges. Our estimations can be applied to not only to AGNs, but also to any accretion disks with strongly magnetized plasma, such as accretion disks around dwarf novae and black holes. Analog experiments of these disks are also possible.

As discussed above, the cooperation of magnetic field and plasma in the astrophysical objects (of a certain class) initiates and/or enhances the structure formation, provides efficient conversion of gravitational energies into flows and accelerates the structure formation and evolution of astrophysical objects [17]. By combining the proposed experiments with theoretical considerations, we should be able to gain a deeper understanding of structure formation in the disk, and the star- and galaxy-scale structure formations that are linked to it.