Abstract
In this article, we present current results of the experiment searching for double beta decay of 106Cd with the help of an enriched 106CdWO4 crystal scintillator in coincidence with two CdWO4 scintillation detectors. The experiment is carried out at the Gran Sasso underground laboratory of the National Institute for Nuclear Physics (LNGS INFN, Italy). After 1075 days of data-taking, no double-beta effects were observed. New half-life limits have been set for the different modes and channels of double beta processes in 106Cd at the level of years.
1. Introduction
Despite the great success of the Standard Model of particles and interactions (SM), neutrino remains the least studied particle due to its extremely weak interaction with matter. In addition, experimentally observed left-handed neutrino states are massless particles according to SM. On the other hand, the observation of the neutrino oscillation provides insight into a non-zero mass of at least two of the three neutrino states [1]. Unfortunately, neutrino oscillation experiments do not give the absolute values of the neutrino masses and the neutrino mass hierarchy [2]. It is also an open question whether neutrinos are of Dirac or Majorana nature. The existence of massive Majorana neutrinos causes the violation of the lepton number symmetry [3,4,5,6] that could explain an asymmetry between matter and antimatter in the Universe [7]. One of the most promising approaches to elaborate the properties of neutrino is the study of the neutrinoless mode of double beta decay () of atomic nuclei [8,9,10,11,12,13].
Double beta decay is the rarest nuclear process, with half-lives of = − years [14,15]. The process, comprising a nuclear charge increase by two units and the emission of two electron and antineutrino pairs (2), has been detected in 11 nuclei (48Ca, 76Ge, 82Se, 96Zr, 100Mo, 116Cd, 128Te, 130Te, 136Xe, 150Nd, and 238U). There are also possible “double beta plus” processes characterized by a decrease in nuclear charge by two units: double electron capture (2EC), electron capture with positron emission (EC), and double positron decay (2). The experimental sensitivity to the double beta plus processes is substantially lower. There are three indications of 22EC decay: 78Kr (in experiment with a proportional counter [16]), 130Ba (in two geochemical experiments [17,18]), and 124Xe [19,20,21]. The 2 decay, allowed in the SM, does not depend on the nature of the neutrino and the absolute neutrino mass scale, though it is very useful for testing theoretical approaches to describe processes [9].
The most sensitive experiments searching for 0 decay reach half-life sensitivity at the level of years, which corresponds to the Majorana neutrino mass limits in the range eV [22,23,24,25,26,27]. These and future more sensitive experiments focus on the search for 0 decay. However, the physical mechanisms that violate lepton number symmetry in “double beta plus” processes are essentially the same as for the decay with electrons emission. 0EC and 02 decays study is also motivated by the opportunity to clarify the possible contribution of the right-handed currents to the 0 decay [28]. In addition, resonant enhancement is possible in the process that could cause an increase in the transition probability by up to six orders of magnitude [29,30,31,32].
The 106Cd nuclide is a promising candidate to search for double beta plus decays, thanks to several features. This nuclide has one of the highest transition energies keV [33] and a comparatively high isotopic abundance [34]. A simplified decay scheme of 106Cd is presented in Figure 1. There is also the availability of enrichment methods using gas centrifugation to consider. A crucial point is that there are well developed methods of cadmium purification and the existence of technology to produce high-quality radiopure cadmium tungstate (CdWO4) crystal scintillators [35,36] that can be used in calorimetric experiments with a high detection efficiency. This approach was implemented in the present experiment, searching for the decay of 106Cd.
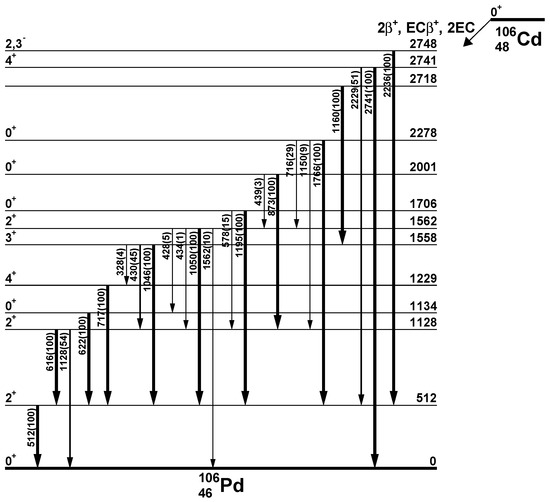
Figure 1.
A simplified decay scheme of 106Cd. Energies of the -rays and excited levels of 106Pd are given in keV. Levels from 2283 keV to 2714 keV and above 2748 keV are omitted. The thickness of the arrow is proportional to the gamma quanta relative emission intensity.
2. Experimental Setup
A schematic diagram of the experimental setup is shown in Figure 2. The main part of the detector system is three CdWO4 crystal scintillators. A central near-cylindrical-shaped scintillator with dimensions ⊘27 mm × 50 mm and mass 215.4 g is enriched with 106Cd to 66% (106CdWO4) [36]. The scintillator is viewed by low radioactive photomultiplier tube (PMT) Hamamatsu R11065-MOD through a high-purity quartz light-guide (⊘66 mm × 100 mm) and polystyrene-based plastic scintillator (⊘40 mm × 83 mm). A Teflon spring is installed between the crystal scintillator and the copper brick to ensure the optical contact between the 106CdWO4 detector components. Two high volume CdWO4 scintillators (⊘70 mm × 38 mm; with the natural cadmium abundance) have cylindrical cutouts to tightly enclose the 106CdWO4 crystal. The CdWO4 scintillators are viewed by radiopure PMTs Hamamatsu R6233MOD through high-purity quartz light-guides (⊘70 mm × 200 mm). Optical contacts between the detector details are treated with optical-grade silicone grease. To improve the light collection, the detector system is wrapped in Teflon tape and aluminized plastic film. The Teflon holds all the components together to ensure the detector system’s geometry. To reduce background interference from PMTs, the detectors are surrounded by high-purity copper bricks (“internal copper”). The detector system is placed in a 11 cm-thick high-purity copper box (“external copper”) surrounded by low-radioactive lead (15 cm), cadmium (2 mm), and polyethylene (10 cm). The inner volume of the copper box is continuously flushed with high-purity N2 gas with a low radon contamination (<58 mBq/m3 [37]) to remove radon present in environmental air. The experiment is carried out at 3.8 km of water equivalent depth at the Gran Sasso underground laboratory of the National Institute for Nuclear Physics (LNGS INFN, Italy).
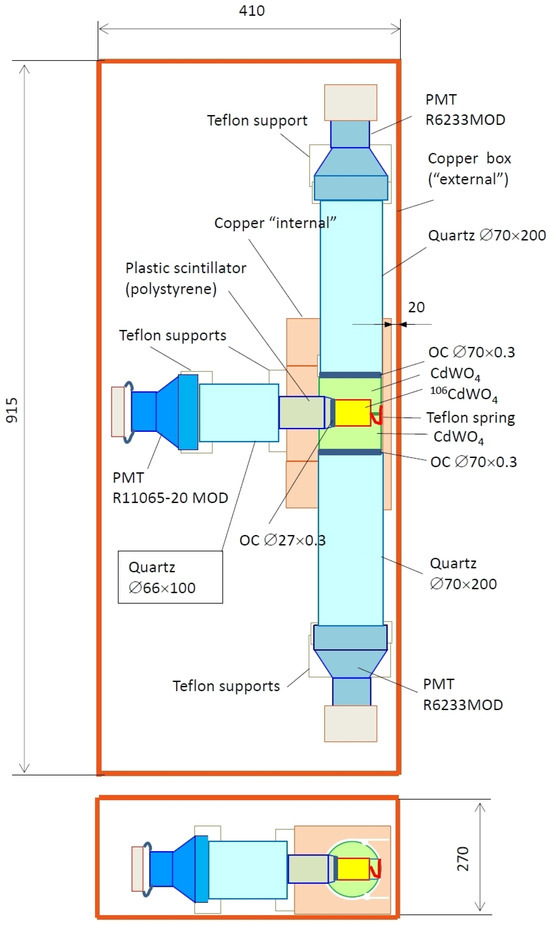
Figure 2.
Schematic of the experimental set-up with the 106CdWO4 scintillation detector. PMT denotes photomultiplier tube. OC refers to optical couplant. Dimensions are given in mm.
The event-by-event data acquisition system is realized using a 1-GSample/s 8-bit transient digitizer DC270 by Agilent Technologies with a bandwidth of 250 MHz. The system records the shape of each signal in 100 s time window with a 50 ns time bin. The CdWO4 scintillator has a relatively long decay time with four components: ∼15 s (89%); ∼4.6 s (9%); ∼0.8 s (2%); and ∼0.15 s (0.5%) [38]. The first 100 time bins (5 s) are used to calculate the mean value of the baseline. The energy of the event in the scintillator (E) is evaluated as the area of the digitized waveform:
where the sum is over time channels k, starting from the origin of the signal up to 25 s, and is the digitized waveform (at the time ) of a given signal after subtraction of the mean value of the baseline.
To reduce the data volume caused by decays of 113Cd ( = 324 keV) and 113mCd ( = 587 keV) nuclides, present in the 106CdWO4 crystal [36,39], the data acquisition system recorded events when one of two conditions was met:
- (1)
- an event in the 106CdWO4 detector with an energy > 0.5 MeV;
- (2)
- an event in the 106CdWO4 detector with an energy > 0.05 MeV in coincidence with a signal in at least one of the CdWO4 counters with energy > 0.05 MeV.
Despite a high counting rate (∼15 Hz) below ∼0.6 MeV, the presence of 113mCd nuclide in the 106CdWO4 scintillator made it possible to monitor the stability of the detector system by analyzing the position of its spectrum edge. More information about the 106CdWO4 and CdWO4 detectors stability can be found in [40]. The main reason for the energy scale time shift of the 106CdWO4 detector was the degradation of the PMTs gain. Therefore, after 649 days of data taking, the PMT of the 106CdWO4 detector was replaced with another unit of the same model. Additionally, a Teflon pipe was installed, which made it possible to periodically calibrate the detector system with sources without switching off the high voltage and opening the setup.
3. Data Analysis
3.1. Energy and Time Resolutions
The detector system was calibrated using 22Na, 60Co, 137Cs, and 228Th -ray sources in the beginning, and several times during the experiment. The energy spectra of the sources measured by the 106CdWO4 and one of the CdWO4 detectors are shown in Figure 3. The energy resolution of the detectors can be described by the function FWHM = A × √Eγ, where Eγ is the energy of -ray quanta in keV, FWHM is the full width at half maximum in keV, and A is a constant. For the entire data set, the averaged value of A is equal to 4.92 for the 106CdWO4, and 3.65 and 3.20 for the CdWO4 detectors.
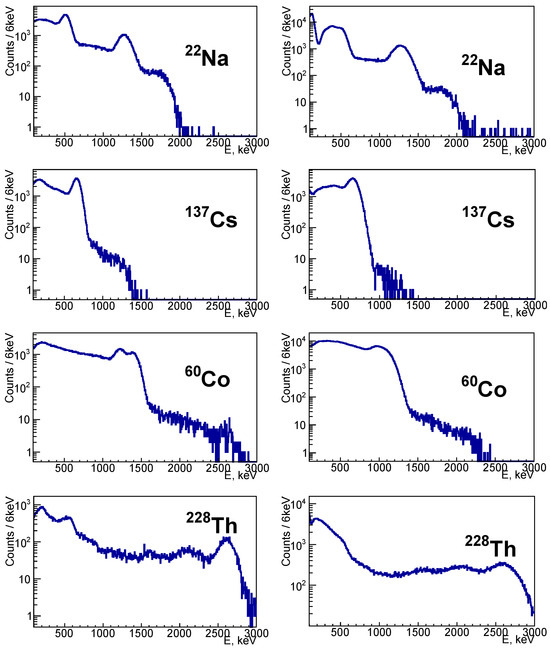
Figure 3.
Energy spectra of 22Na, 137Cs, 60Co, and 228Th -ray sources measured by one of the CdWO4 (left column) and 106CdWO4 (right column) detectors.
To determine the time resolution of the detector system, we used calibration data collected with a 22Na -ray source. 22Na is both a source of 1274.5 keV quanta and of positrons. Figure 4 shows the distribution of differences () between the start of signals in the 106CdWO4 and in the CdWO4 detectors with energy 511 ± 2 keV, which occur after the positrons annihilation ( is the energy resolution of the CdWO4 counters for 511-keV -quanta). The distribution was approximated by an exponentially modified Gaussian function:
where and k are free parameters of the fit. By analyzing the number of events in the 1274.5 keV peak in coincidence with 511 keV -quanta we obtained a selection efficiency of = in the ns ≤ < 100 ns time interval.
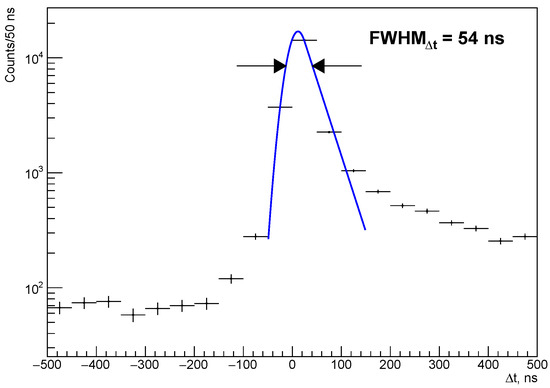
Figure 4.
Distribution of the time intervals () between signals of the 106CdWO4 detector and one of the CdWO4 counters with energy keV, where is the standard deviation of energy resolution of the CdWO4 counters. The distribution is fitted with an exponentially modified Gaussian function (Equation (2)) with FWHM = 54 ns.
3.2. Pulse-Shape Discrimination
The difference between the pulse shape of and scintillation signals was used to reject background due to particles. A numerical characteristic called the Shape Indicator (SI) was calculated for each signal:
The weight function is defined as:
where the reference pulse shapes and were built by analysing the -quanta events from the calibration data and internal events. More about the pulse-shape discrimination of scintillation signals using the optimal filter method can be found in ref. [41]. The dependence of SI on energy for one of the CdWO4 detectors is shown in Figure 5. As shown, particles are clearly distinguished from . The SI distributions for and events are well described by a Gaussian function (Figure 5a inset). The mean value () and standard deviation () of the Gaussian function depend on energy (E) as = and , where are parameters. For CdWO4 detectors, the selection cut for events is , which gives the selection efficiency , while for events it is . For the 106CdWO4 detectors the selection cut is more complex: for events with E < 1500 keV () and for events with E > 1500 keV (). This choice of selection conditions was made due to the worse discrimination between the and signals exhibited by the 106CdWO4 detector [40].
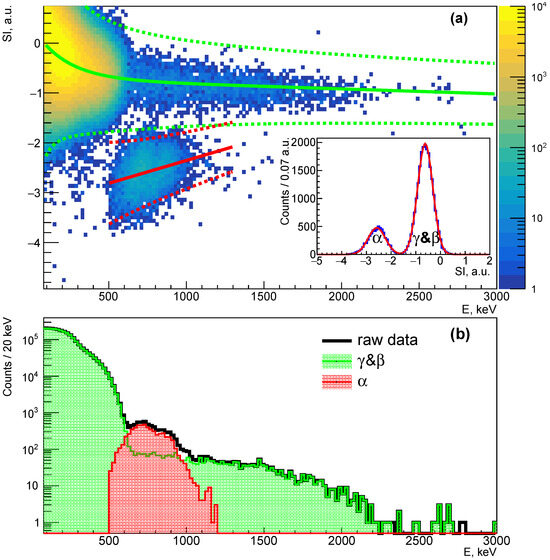
Figure 5.
Two-dimensional distribution of the background events measured by CdWO4 detector in energy (E) versus Shape Indicator (SI) coordinates (a). Distributions of the SI parameters for and particles approximated by two Gaussian functions in the energy interval 500–1200 keV (inset in (a)). The green and red solid lines in the panel (a) represent for and events, respectively. The green and red dashed lines in the panel (a) represent for events and for events. Selected and events between the dashed lines projected on the energy axis are shown in the panel (b).
It is worth noting that the energy of particles () which belong to the U/Th families is 5.7–6.9 MeV. Due to the quenching of particles in the scale, the spectrum is shifted to lower energies [42]. A dependence of the / ratio (i.e., ratio of energy of particle in scale to its real energy) was determined for the 106CdWO4 detector as / = 0.12(2) + 0.011(2)× and for CdWO4 detectors as / = 0.08(1) + 0.015(2)×, where is in MeV [40]. Also, the analysis of spectra made it possible to determine the contamination of crystals by -active daughter nuclides of the U/Th chains [40].
3.3. Experimental Energy Spectra
The experimental energy spectra measured over 1075 days by the 106CdWO4 and CdWO4 detectors under different selection conditions are shown in Figure 6. It was possible to achieve a noticeable reduction of the background measured by the 106CdWO4 detector in the energy range of 0.5–1.5 MeV by separating events from ones by the pulse-shape discrimination. The main part of the spectrum measured by the 106CdWO4 detector with energy < 0.5 MeV in anti-coincidence (AC) with the CdWO4 counters is the 113mCd distribution. For the events in coincidence (CC) with the CdWO4 counters, the data acquisition system records events with the low energy trigger of the 106CdWO4 detector (see Section 2). As a result, the 113mCd spectrum represents the main part of the spectra for all the detectors below 0.5 MeV. Also, an important selection condition is a coincidence with 511 keV -quantum (quanta) in the CdWO4 counter(s), which should occur during the annihilation of a positron from the double beta processes in 106Cd with positron(s) emission (Figure 6, CC = 511 ± 2 keV, where is an energy deposit in at least one of CdWO4 detectors). The only two peaks with energies of 202 keV and 307 keV that can be seen in the spectrum measured by the CdWO4 counters in coincidence with events in the 106CdWO4 detector with energy above 500 keV (Figure 6, CC > 500 keV, where is an energy deposit in 106CdWO4 detector) correspond to the decay of 176Lu.
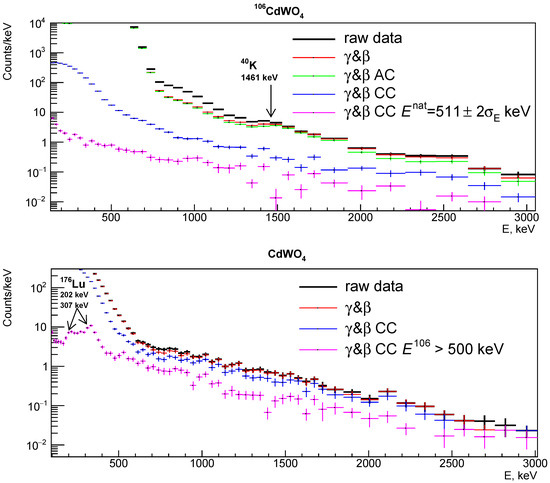
Figure 6.
Energy spectra measured by 106CdWO4 (top) and both CdWO4 detectors (bottom) for 1075 days under the different selection conditions. denotes spectrum of -events. AC (CC) means anti-coincidence (coincidence) mode, respectively. = 511 ± 2 keV denotes energy deposit in at least one of the CdWO4 detectors in the energy interval 511 ± 2 keV, where is the standard deviation of energy resolution. > 500 keV denotes energy deposit in 106CdWO4 detector more than 500 keV. The bin width is proportional to the energy resolution.
3.4. Radioactive Contamination of the Experimental Setup
To describe the experimental data measured by the 106CdWO4 detector above 0.8 MeV in AC and above 0.4 MeV in CC, a background model was constructed from the following components:
- (1)
- 40K and 232Th, 238U with their daughters in all the setup components;
- (2)
- Residual distribution in the 106CdWO4 crystal (7.3% of the alpha distribution);
- (3)
- Beta decay of 176Lu and 113mCd, and 2 decay of 116Cd with a half-life of years in the 106CdWO4 crystal scintillator. The number of 116Cd 2 decays in the experimental spectra is well known due to the known isotopic concentration of 116Cd in the 106CdWO4 crystal [36];
- (4)
- 113Cd in the CdWO4 and 106CdWO4 crystal scintillators;
- (5)
- 56Co and 60Co in the internal copper.
The secular equilibrium of the 232Th and 238U chains is assumed to be broken due to physical and chemical processes utilized for the production of the experimental setup materials. Therefore, the following sub-chains were considered separately: 228Ra ⟶ 228Th and 228Th ⟶ 208Pb (the 232Th chain); 238U ⟶ 234U, 226Ra ⟶ 210Pb and 210Pb ⟶ 206Pb (the 238U chain).
The energy distributions of the background components were simulated using the Monte Carlo package EGSnrc [43] with the initial kinematics provided by the DECAY0 event generator [44]. Each distribution was properly normalized by the parameter representing the number of decays. This parameter is obtained through fitting the experimental data by the Monte Carlo simulated distributions. The spectral shape of the distributions account also for the SI and selection cuts that were applied to the data. Each simulated event was multiplied by and . Figure 7 shows the result of the simultaneous binned maximum likelihood fit of five spectra: three spectra measured by the 106CdWO4 detector under selection conditions AC, CC, and CC = 511 ± 2 keV; and two spectra measured by the CdWO4 detectors under the selection conditions CC and CC > 500 keV. The maximum likelihood was applied since many bins have very low data statistics. The goodness of the fit is calculated with the Baker–Cousins approach [45] , where is a number of degrees of freedom. The fit quality is rather low. However, the problem may be that one cannot be sure all the contaminations of the set-up materials are included in the background model. Moreover, despite efforts to reconstruct the setup geometry in the Monte Carlo simulations as accurately as possible, it does not perfectly reproduce the actual experiment’s geometry. Some worsening of the fit quality could also be due to imperfect knowledge of the detector system’s spectrometric characteristics, their degradation in time, etc. The radioactive contaminations of the main components of the experimental setup are reported in Table 1. The 228Th contaminations in the 106CdWO4 and in CdWO4 detectors were determined by using the time-amplitude analysis [40]. Activities of 238U, 234U, 230Th, 226Ra, 210Pb, and 232Th in the CdWO4 detectors were determined by the spectrum analysis [40].
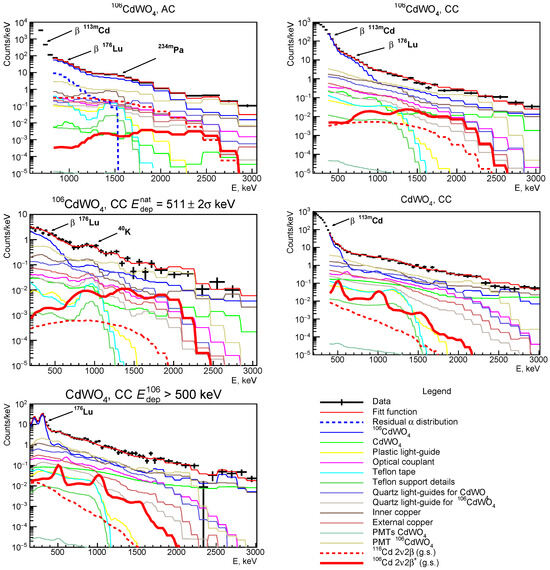
Figure 7.
Results of the combined approximation of the spectra measured by the 106CdWO4 and two CdWO4 detectors under different selection conditions (see Section 3.3). The fit function represents the approximation result. The contributions from the contamination of the setup details are shown separately (see legend). An excluded distribution of the decay of 106Cd to the ground state of 106Pd with a half-life years is shown by solid red line in all the spectra.

Table 1.
Radioactive contamination (mBq/kg) of the setup details. Upper limits are given at 90% confidence level, uncertainties of the last digit are given with 68% confidence level. Activities labeled by (*) were determined by using the time-amplitude analysis, the values marked by (†) were determined by analysis of the distribution [40]. Q. lg. denotes quartz light guide.
4. Half-Life Limits on Decay Processes in 106Cd
There were no peculiarities in the experimental data that could be attributed to the 2 decay of 106Cd. Therefore, half-life limits for different channels and modes of 2 decay were set using the formula:
where is the number of 106Cd nuclei in the 106CdWO4 crystal, and are detection and selection efficiencies, t is the measurement live time, and is a number of events of the effect searched for that can be excluded with a given confidence level (C.L.). Values of depend on selection conditions and can be obtained from the approximation of the experimental energy spectrum with a background model plus an effect searched for. For simultaneous approximation of several spectra, the Equation (5) must be modified. Since the spectral shape of the Monte Carlo distributions account for the parameters and , Equation (5) can be rewritten as:
where is a number of decays of the process searched for. Now, values of can be obtained from simultaneous approximation of the energy spectra with different selection conditions. The parameters of the approximation were bounded, taking into account the data on the radioactive contamination of the experimental setup details (see Table 1).
For example, for the decay of 106Cd to the ground state of 106Pd, the fit gives = 0 ± 18. According to [46], we took events at 90% C.L., which gives years (the distribution is shown in Figure 7). The total detection efficiency for decay to the ground state of 106Pd for the different selection conditions and detectors are: , , , , and . The half-life limits on different modes of decay of 106Cd were obtained in a similar way and are presented in Table 2.
One of the most interesting processes is EC decay of 106Cd to the ground state of 106Pd. In this work, we give a new half-life limit on this process as years, which is in the region of the theoretical prediction years [47,48,49,50,51,52,53]. The most optimistic theoretical calculations years are for EC decay to the ground state of 106Pd. But due to the large background from the decays of 113mCd and 113Cd, it is difficult to obtain a high-sensitivity search for the characteristic X-rays from EC decay that are expected in the low energy region.
Another interesting feature is the possibility of near resonant 2EC decays of 106Cd to excited levels of 106Pd when the initial and final states are degenerate [32]. There are three possible near resonant transitions to the 2718 keV, 2741 keV, and 2748 keV excited levels of 106Pd. In this work we give the half-life limits on the near resonance processes as years (see Table 2).

Table 2.
Half-life limits on different modes and channels of decay of 106Cd given at 90% confidence level. The most sensitive previous results and the theoretical predictions are also presented.
Table 2.
Half-life limits on different modes and channels of decay of 106Cd given at 90% confidence level. The most sensitive previous results and the theoretical predictions are also presented.
| Decay | Level of 106Pd, | Theoretical | lim | |
|---|---|---|---|---|
| keV | Previous Result | Present Work | ||
| g.s. | [47,48,50], [49] | [54] | ||
| 512 | [47,55,56] | [54] | ||
| g.s. | [47,55,56,57,58,59,60,61] | [62] | ||
| 512 | [54] | |||
| EC | g.s. | [47,48,50,51,52,53], [49] | [62] | |
| 512 | [51,52], [49] | [54] | ||
| 1128 | [51] | [54] | ||
| 1134 | [51,52], [49] | [54] | ||
| EC | g.s. | [32,47,55,56] | [62] | |
| 512 | [62] | |||
| 1128 | [62] | |||
| 1134 | [32,55,57,58] | [54] | ||
| EC | g.s. | [47,48,50,51,52,53] | [63] | – |
| 512 | [51,52], [49] | [64] | ||
| 1128 | [51] | [62] | ||
| 1134 | [51,52] | [64] | ||
| 1562 | [52], [49] | [62] | ||
| 1706 | [49] | [64] | ||
| 2001 | [49] | [62] | ||
| 2278 | [49] | [64] | ||
| EC | g.s. | [39] | ||
| 512 | [39] | |||
| 1128 | [64] | |||
| 1134 | [64] | |||
| 1562 | [62] | |||
| 1706 | [62] | |||
| 2001 | [64] | |||
| 2278 | [62] | |||
| Res. EC | 2718 | [57], [65,66], [32] | [62] | |
| 2741 | [66] | [39] | ||
| 2748 | [29] | [64] | ||
5. Conclusions
One of the most sensitive double beta plus experiments to search for decay of 106Cd with an enriched 106CdWO4 scintillator in coincidence with two large volume CdWO4 counters was carried out at the Gran Sasso underground laboratory of the INFN (Italy). After 1075 days of data taking, we were able to provide new improved half-life limits on the different channels and modes of 106Cd decay at the level of – years. A new half-life limit on EC decay to the ground state of 106Pd was set as years, in the region of the theoretical predictions of – years. The half-life limits on near resonant 2EC decay transitions to the 2718 keV, 2741 keV, and 2748 keV excited levels of 106Pd have been set at the level years. Analysis of the complete data set of the experiment is in progress.
Author Contributions
Conceptualization, P.B., R.B. and F.A.D.; Data curation, P.B., V.C., R.C., A.L. and O.G.P.; Formal analysis, F.C., F.A.D., V.R.K. and A.L.; Funding acquisition, P.B., R.B., F.A.D. and V.V.K.; Investigation, P.B., R.B., V.C., R.C., F.A.D., A.I., D.V.K., V.R.K., A.L., O.G.P. and V.I.T.; Methodology, P.B., R.B. and F.A.D.; Project administration, P.B., R.B., F.A.D. and V.V.K.; Resources, P.B., R.B. and F.A.D.; Software, P.B., F.C., V.C., R.C., F.A.D., V.R.K. and V.I.T.; Supervision, P.B., R.B. and F.A.D.; Validation, P.B., R.B., F.C., F.A.D., V.R.K. and V.I.T.; Visualization, F.C., F.A.D. and V.R.K.; Writing—original draft, V.R.K.; Writing—review & editing, P.B., R.B., F.C., V.C., R.C., F.A.D., A.I., D.V.K., V.V.K., A.L., V.M., O.G.P. and V.I.T. All authors have read and agreed to the published version of the manuscript.
Funding
V.R.K., D.V.K., V.V.K. and O.G.P. were supported in part by the National Research Foundation of Ukraine (Grant No. 2023.03/0213). V.R.K. and D.V.K. were supported in part by the project “Study of double beta decay of 106Cd and 116Cd with scintillators from enriched isotopes” of the program of the National Academy of Sciences of Ukraine “Research of young scientists of the National Academy of Sciences of Ukraine in 2023–2024”
Data Availability Statement
The data produced in this study are contained in the publication.
Acknowledgments
F.A. Danevich, O.G. Polischuk, and V.I. Tretyak thank the INFN and the people of the DAMA group for the great support and kind hospitality in the present difficult times; moreover, all the Ukrainian authors express great gratitude to the Armed Forces of Ukraine, which defend the independence of the country and protect the lives of its citizens from the present Russian aggression.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bilenky, S. Introduction to the Physics of Massive and Mixed Neutrinos; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Qian, X.; Vogel, P. Neutrino mass hierarchy. Prog. Part. Nucl. Phys. 2015, 83, 1–30. [Google Scholar]
- Fukugita, M.; Yanagida, T. Baryogenesis without Grand Unification. Phys. Lett. B 1986, 174, 45–47. [Google Scholar] [CrossRef]
- Davidson, S.; Nardi, E.; Nir, Y. Leptogenesis. Phys. Rept. 2008, 466, 105–177. [Google Scholar]
- Branco, G.C.; Gonzalez Felipe, R.; Joaquim, F.R. Leptonic CP violation. Rev. Mod. Phys. 2012, 84, 515–565. [Google Scholar]
- Blanchet, S.; Di Bari, P. The minimal scenario of leptogenesis. New J. Phys. 2012, 14, 125012. [Google Scholar]
- Deppisch, F.F.; Graf, L.; Harz, J.; Huang, W.-C. Neutrinoless double beta decay and the baryon asymmetry of the Universe. Phys. Rev. D 2018, 98, 055029. [Google Scholar]
- Gomez-Cadenas, J.J.; Martin-Albo, J.; Menendez, J.; Mezzetto, M.; Monrabal, F.; Sorel, M. The search for neutrinoless double-beta decay. Riv. Nuovo Cim. 2023, 46, 619–692. [Google Scholar]
- Agostini, M.; Benato, G.; Detwiler, J.A.; Menendez, J.; Vissani, F. Toward the discovery of matter creation with neutrinoless ββ decay. Rev. Mod. Phys. 2023, 95, 025002. [Google Scholar]
- Bossio, E.; Agostini, M. Probing beyond the standard model physics with double-beta decays. J. Phys. G 2024, 51, 023001. [Google Scholar]
- Parno, D.S.; Poon, A.W.P.; Singh, V. Experimental neutrino physics in a nuclear landscape. Phil. Trans. R. Soc. A 2024, 382, 20230122. [Google Scholar]
- Dolinski, M.J.; Poon, A.W.P.; Rodejohann, W. Neutrinoless Double-Beta Decay: Status and Prospects. Annu. Rev. Nucl. Part. Sci. 2019, 25, 19–51. [Google Scholar]
- Schechter, J.; Valle, J.W.F. Neutrinoless double-β decay in SU(2) × U(1) theories. Phys. Rev. D 1982, 25, 2951–2954. [Google Scholar] [CrossRef]
- Saakyan, R. Two-Neutrino Double-Beta Decay. Annu. Rev. Nucl. Part. Sci. 2013, 63, 503–529. [Google Scholar]
- Pritychenko, B.; Tretyak, V.I. Comprehensive review of 2β decay half-lives. At. Data Nucl. Data Tables 2025, 161, 101694. [Google Scholar] [CrossRef]
- Gavrilyuk, Y.M.; Gangapshev, A.M.; Kazalov, V.V.; Kuzminov, V.V.; Panasenko, S.I.; Ratkevich, S.S. Indications of 2ν2K capture in 78Kr. Phys. Rev. C 2013, 87, 035501. [Google Scholar] [CrossRef]
- Meshik, A.P.; Hohenberg, C.M.; Pravdivtseva, O.V.; Kapusta, Y.S. Weak decay of 130Ba and 132Ba: Geochemical measurements. Phys. Rev. C 2001, 64, 035205. [Google Scholar]
- Pujol, M.; Marty, B.; Burnard, P.; Philippot, P. Xenon in Archean barite: Weak decay of 130Ba, mass-dependent isotopic fractionation and implication for barite formation. Geochim. Cosmochim. Acta 2009, 73, 6834–6846. [Google Scholar]
- Aprile, E. et al. [XENON Collaboration] Search for New Physics in Electronic Recoil Data from XENONnT. Phys. Rev. Lett. 2022, 129, 161805. [Google Scholar]
- Aalbers, J. et al. [LZ Collaboration] Two-neutrino double electron capture of 124Xe in the first LUX-ZEPLIN exposure. J. Phys. G 2025, 52, 015103. [Google Scholar]
- Bo, Z. et al. [PandaX Collaboration] Search for Majorana Neutrinos with the Complete KamLAND-Zen Dataset. arXiv 2024, arXiv:2411.14355. [Google Scholar]
- Abe, S. et al. [KamLAND-Zen Collaboration] Search for Majorana Neutrinos with the Complete KamLAND-Zen Dataset. arXiv arXiv:2406.11438.
- Adams, D.Q. et al. [CUORE Collaboration] With or without ν? Hunting for the seed of the matter-antimatter asymmetry. arXiv arXiv:2404.04453.
- Agrawal, A. et al. [AMoRE Collaboration] Improved limit on neutrinoless double beta decay of 100Mo from AMoRE-I. Phys. Rev. Lett. 2025, 134, 082501. [Google Scholar]
- Agostini, M. et al. [GERDA Collaboration] Final Results of GERDA on the Search for Neutrinoless Double-β Decay. Phys. Rev. Lett. 2020, 125, 252502. [Google Scholar]
- Arnquist, I.J. et al. [Majorana Collaboration] Final Result of the MAJORANA DEMONSTRATOR’s Search for Neutrinoless Double-β Decay in 76Ge. Phys. Rev. Lett. 2023, 130, 062501. [Google Scholar]
- Abgrall, N. et al. [LEGEND Collaboration] LEGEND-1000 Preconceptual Design Report. arXiv 2021, arXiv:2107.11462. [Google Scholar]
- Hirsch, M.; Muto, K.; Oda, T.; Klapdor-Kleingrothaus, H.V. Nuclear structure calculation of β+β+, β+/EC and EC/EC decay matrix elements. Z. Phys. A 1994, 347, 151–160. [Google Scholar]
- Blaum, K.; Eliseev, S.; Danevich, F.A.; Tretyak, V.I.; Kovalenko, S.; Krivoruchenko, M.I.; Novikov, Y.N.; Suhonen, J. Neutrinoless double-electron capture. Rev. Mod. Phys. 2020, 92, 045007. [Google Scholar]
- Winter, R. Double K Capture and Single K Capture with Positron Emission. Phys. Rev. 1955, 100, 142–144. [Google Scholar]
- Bernabeu, J.; De Rujula, A.; Jarlskog, C. Neutrinoless double electron capture as a tool to measure the electron neutrino mass. Nucl. Phys. B 1983, 223, 15–28. [Google Scholar]
- Suhonen, J. Neutrinoless double beta decays of 106Cd revisited. Phys. Lett. B 2011, 701, 490–495. [Google Scholar] [CrossRef]
- Wang, M.; Huang, W.J.; Kondev, F.G.; Audi, G.; Naimi, S. The AME 2020 atomic mass evaluation (II). Tables, graphs and references. Chin. Phys. C 2021, 45, 030003. [Google Scholar] [CrossRef]
- Meija, J.; Coplen, T.B.; Berglund, M.; Brand, W.A.; De Bievre, P.; Groning, M.; Holden, N.E.; Irrgeher, J.; Loss, R.D.; Walczyk, T.; et al. Isotopic compositions of the elements 2013 (IUPAC Technical Report). Pure Appl. Chem. 2016, 88, 293–306. [Google Scholar] [CrossRef]
- Barabash, A.S.; Belli, P.; Bernabei, R.; Boiko, R.S.; Cappella, F.; Caracciolo, V.; Chernyak, D.M.; Cerulli, R.; Danevich, F.A.; Di Vacri, M.L.; et al. Low background detector with enriched 116CdWO4 crystal scintillators to search for double beta decay of 116Cd. JINST 2011, 6, P08011. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Boiko, R.S.; Brudanin, V.B.; Bukilic, N.; Cerulli, R.; Chernyak, D.M.; Danevich, F.A.; D’Angelo, S.; Degoda, V.Y.; et al. Development of enriched 106CdWO4 crystal scintillators to search for double beta decay processes in 106Cd. Nucl. Instrum. Meth. A 2010, 615, 301–306. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Cappella, F.; Cerulli, R.; Dai, C.J.; D’Angelo, A.; He, H.L.; Incicchitti, A.; Kuang, H.H.; Ma, J.M.; et al. First results from DAMA/LIBRA and the combined results with DAMA/NaI. Eur. Phys. J. C 2008, 56, 333–355. [Google Scholar] [CrossRef]
- Bardelli, L.; Bini, M.; Bizzeti, P.G.; Carraresi, L.; Danevich, F.A.; Fazzini, T.F.; Grinyov, B.V.; Ivannikova, N.V.; Kobychev, V.V.; Kropivyansky, B.N.; et al. Further study of CdWO4 crystal scintillators as detectors for high sensitivity 2β experiments: Scintillation properties and pulse-shape discrimination. Nucl. Instrum. Meth. A 2006, 569, 743–753. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Boiko, R.S.; Brudanin, V.B.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Chernyak, D.M.; Danevich, F.A.; D’Angelo, S.; et al. Search for double-β decay processes in 106Cd with the help of a 106CdWO4 crystal scintillator. Phys. Rev. C 2012, 85, 044610. [Google Scholar]
- Belli, P.; Bernabei, R.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.A.; Inchicchitti, A.; Kasperovych, D.V.; Klavdiienko, V.R.; Kobychev, V.V.; et al. Low-background experiment to search for double beta decay of 106Cd using 106CdWO4 scintillator. Nucl. Phys. At. Energy 2023, 24, 193–208. [Google Scholar] [CrossRef]
- Danevich, F.A.; Georgadze, A.S.; Kobychev, V.V.; Kropivyansky, B.N.; Nikolaiko, A.S.; Ponkratenko, O.A.; Tretyak, V.I.; Zdesenko, S.Y.; Zdesenko, Y.G.; Bizzeti, P.G.; et al. Search for 2β decay of cadmium and tungsten isotopes: Final results of the Solotvina experiment. Phys. Rev. C 2003, 68, 035501. [Google Scholar] [CrossRef]
- Tretyak, V.I. Semi-empirical calculation of quenching factors for ions in scintillators. Astropart. Phys. 2010, 33, 40–53. [Google Scholar]
- Kawrakow, I.; Mainegra-Hing, E.; Rogers, D.W.O.; Tessier, F.; Walters, B.R.B. The EGSnrc Code System: Monte Carlo Simulation of Electron and Photon Transport; NRC: Ottawa, ON, Canada, 2023; 321p. [Google Scholar]
- Ponkratenko, O.A.; Tretyak, V.I.; Zdesenko, Y.G. Event generator DECAY4 for simulating double-beta processes and decays of radioactive nuclei. Phys. At. Nucl. 2000, 63, 1282–1287. [Google Scholar] [CrossRef]
- Baker, S.; Cousins, R.D. Clarification of the use of chi-square and likelihood functions in fits to histograms. Nucl. Instrum. Meth. 1984, 221, 437–442. [Google Scholar]
- Feldman, G.J.; Cousins, R.D. Unified approach to the classical statistical analysis of small signals. Phys. Rev. D 1998, 57, 3873–3889. [Google Scholar] [CrossRef]
- Stoica, S.; Klapdor-Kleingrothaus, H.V. β-β-, β+β+, β+/EC and EC/EC half-lives for 106Cd within a second QRPA method. Eur. Phys. J. A 2003, 17, 529–536. [Google Scholar] [CrossRef]
- Shukla, A.; Raina, P.K.; Chandra, R.; Rath, P.K.; Hirsch, J.G. Two neutrino positron double beta decay of 106Cd for 0+→0+ transition. Eur. Phys. J. A 2005, 23, 235–242. [Google Scholar]
- Domin, P.; Kovalenko, S.; Simkovic, F.; Semenov, S.V. Neutrino accompanied β±β±, β+/EC and EC/EC processes within single state dominance hypothesis. Nucl. Phys. A 2005, 753, 337–363. [Google Scholar]
- Raina, P.K.; Shukla, A.; Singh, S.; Rath, P.K.; Hirsch, J.G. The 0+→0+ positron double-β decay with emission of two neutrinos in the nuclei 96Ru, 102Pd, 106Cd and 108Cd. Eur. Phys. J. A 2006, 28, 27–36. [Google Scholar]
- Suhonen, J. Double beta decays of 106Cd. AIP Conf. Proc. 2011, 1417, 115–119. [Google Scholar]
- Pirinen, P.; Suhonen, J. Systematic approach to β and 2νββ decays of mass A = 100 – 136 nuclei. Phys. Rev. C 2015, 91, 054309. [Google Scholar]
- Ejiri, H. Fermi surface quasi particle model nuclear matrix elements for two neutrino double beta decays. J. Phys. G 2017, 44, 115201. [Google Scholar] [CrossRef][Green Version]
- Leoncini, A.; Belli, P.; Bernabei, R.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.A.; Inchicchitti, A.; Kasperovych, D.V.; Klavdiienko, V.R.; et al. New results on search for 2β decay processes in 106Cd using 106CdWO4 scintillator. Phys. Scr. 2022, 97, 064006. [Google Scholar] [CrossRef]
- Suhonen, J.; Aunola, M. Systematic study of neutrinoless double beta decay to excited 0+ states. Nucl. Phys. A 2003, 723, 271–288. [Google Scholar] [CrossRef]
- Rath, P.K.; Chandra, R.; Chaturvedi, K.; Raina, P.K.; Hirsch, J.G. Deformation effects and neutrinoless positron ββ decay of 96Ru, 102Pd, 106Cd, 124Xe, 130Ba, and 156Dy isotopes within a mechanism involving Majorana neutrino mass. Phys. Rev. C 2009, 80, 044303. [Google Scholar] [CrossRef]
- Suhonen, J. Physics of Nuclear Processes Triggered by the Interplay of Strong and Weak Interactions. J. Phys. Conf. Ser. 2012, 338, 012030. [Google Scholar] [CrossRef]
- Suhonen, J. Particle-, nuclear- and atomic-physics aspects of rare weak decays of nuclei. Phys. Scripta T 2012, 150, 014039. [Google Scholar] [CrossRef]
- Rath, P.K.; Chandra, R.; Chaturvedi, K.; Lohani, P.; Raina, P.K.; Hirsch, J.G. Uncertainties in nuclear transition matrix elements for β+β+ and ϵβ+ modes of neutrinoless positron double-β decay within the projected Hartree-Fock-Bogoliubov model. Phys. Rev. C 2013, 87, 014301. [Google Scholar] [CrossRef]
- Barea, J.; Kotila, J.; Iachello, F. Neutrinoless double-positron decay and positron-emitting electron capture in the interacting boson model. Phys. Rev. C 2013, 87, 057301. [Google Scholar] [CrossRef]
- Staudt, A.; Muto, K.; Klapdor-Kleingrothaus, H.V. Nuclear matrix elements for double positron emission. Phys. Lett. B 1991, 268, 312–316. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Brudanin, V.B.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.A.; Incicchitti, A.; Kasperovych, D.V.; Klavdiienko, V.R.; et al. Search for Double Beta Decay of 106Cd with an Enriched 106CdWO4 Crystal Scintillator in Coincidence with CdWO4 Scintillation Counters. Universe 2020, 6, 182. [Google Scholar] [CrossRef]
- Rukhadze, N.I.; Gusev, K.N.; Klimenko, A.A.; Rozov, S.V.; Rukhadze, E.; Salamatin, A.V.; Simkovic, F.; Shitov, Y.A.; Stekl, I.; Timkin, V.V.; et al. New results for double beta decay of 106Cd. In Proceedings of the Book of Abstracts of the LXXII International Conference NUCLEUS-2022, Moscow, Russia, 11–16 July 2022; p. 261. [Google Scholar]
- Belli, P.; Bernabei, R.; Brudanin, V.B.; Cappella, F.; Caracciolo, V.; Cerulli, V.; Chernyak, D.M.; Danevich, F.A.; D’Angelo, S.; Di Marco, A.; et al. Search for decay of 106Cd with an enriched 106CdWO4 crystal scintillator in coincidence with four HPGe detectors. Phys. Rev. C 2016, 93, 045502. [Google Scholar]
- Suhonen, J. Interplay of particle, nuclear and atomic physics in rare weak decays. AIP Conf. Proc. 2010, 1304, 85–93. [Google Scholar]
- Belli, P.; Bernabei, R.; Boiko, R.S.; Brudanin, V.B.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Chernyak, D.M.; Danevich, F.A.; D’Angelo, S.; et al. First Results of the Experiment to Search for 2β Decay of 106Cd with the Help of 106CdWO4 Crystal Scintillators. AIP Conf. Proc. 2010, 1304, 354–358. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).