The Impact of Electron Phase Shifts on ββ-Decay Kinematics
Abstract
1. Introduction
2. Formalism for DBD
2.1. 2-Decay
2.2. 0-Decay
2.3. Electron Wave Function and Phase Shift
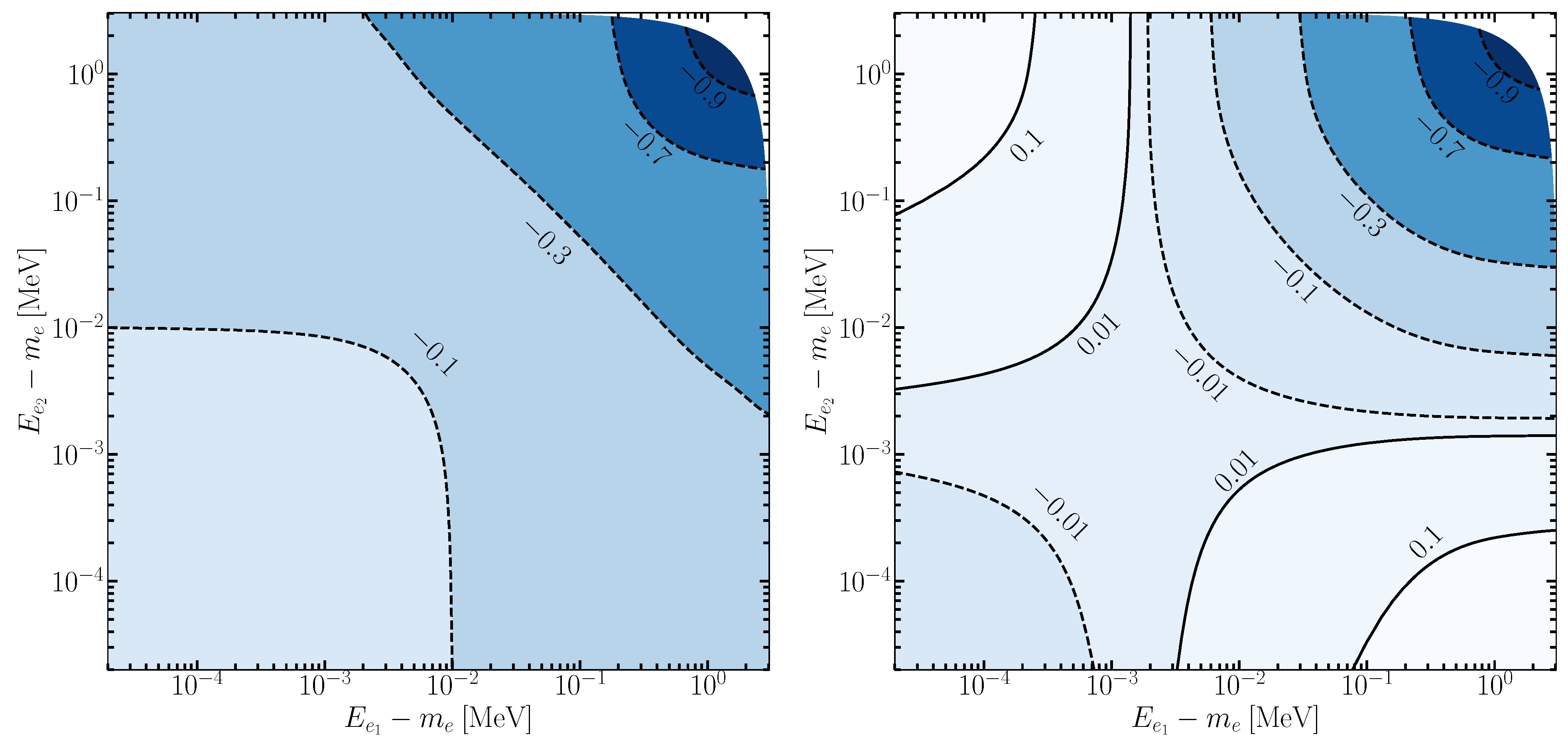
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Barabash, A. Precise Half-Life Values for Two-Neutrino Double-β Decay: 2020 Review. Universe 2020, 6, 159. [Google Scholar] [CrossRef]
- Agostini, M.; Araujo, G.R.; Bakalyarov, A.M.; Balata, M.; Barabanov, I.; Baudis, L.; Bauer, C.; Bellotti, E.; Belogurov, S.; Bettini, A.; et al. Final Results of GERDA on the Search for Neutrinoless Double-β Decay. Phys. Rev. Lett. 2020, 125, 252502. [Google Scholar] [CrossRef] [PubMed]
- Abe, S.; Asami, S.; Eizuka, M.; Futagi, S.; Gando, A.; Gando, Y.; Gima, T.; Goto, A.; Hachiya, T.; Hata, K.; et al. Search for the Majorana Nature of Neutrinos in the Inverted Mass Ordering Region with KamLAND-Zen. Phys. Rev. Lett. 2023, 130, 051801. [Google Scholar] [CrossRef] [PubMed]
- Abe, S.; Araki, T.; Chiba, K.; Eda, T.; Eizuka, M.; Funahashi, Y.; Furuto, A.; Gando, A.; Gando, Y.; Goto, S.; et al. Search for Majorana Neutrinos with the Complete KamLAND-Zen Dataset. arXiv 2024, arXiv:2406.11438. [Google Scholar] [CrossRef]
- Fukugita, M.; Yanagida, T. Barygenesis without grand unification. Phys. Lett. B 1986, 174, 45–47. [Google Scholar] [CrossRef]
- Buchmüller, W.; Peccei, R.; Yanagida, T. LEPTOGENESIS AS THE ORIGIN OF MATTER. Annu. Rev. Nucl. Part. Sci. 2005, 55, 311–355. [Google Scholar] [CrossRef]
- Majorana, E. Teoria simmetrica dell’elettrone e del positrone. Il Nuovo Cimento 1937, 14, 171–184. [Google Scholar] [CrossRef]
- Schechter, J.; Valle, J.W.F. Neutrino decay and spontaneous violation of lepton number. Phys. Rev. D 1982, 25, 774–783. [Google Scholar] [CrossRef]
- Sujkowski, Z.; Wycech, S. Neutrinoless double electron capture: A tool to search for Majorana neutrinos. Phys. Rev. C 2004, 70, 052501. [Google Scholar] [CrossRef]
- Pascoli, S.; Petcov, S.; Schwetz, T. The absolute neutrino mass scale, neutrino mass spectrum, Majorana CP-violation and neutrinoless double-beta decay. Nucl. Phys. B 2006, 734, 24–49. [Google Scholar] [CrossRef]
- Bilenky, S.M.; Giunti, C. Neutrinoless double-beta decay: A probe of physics beyond the Standard Model. Int. J. Mod. Phys. A 2015, 30, 1530001. [Google Scholar] [CrossRef]
- Girardi, I.; Petcov, S.; Titov, A. Predictions for the Majorana CP violation phases in the neutrino mixing matrix and neutrinoless double beta decay. Nucl. Phys. B 2016, 911, 754–804. [Google Scholar] [CrossRef]
- Šimkovic, F. Neutrino masses and interactions and neutrino experiments in the laboratory. Physics-Uspekhi 2021, 64, 1238. [Google Scholar] [CrossRef]
- Agostini, M.; Benato, G.; Detwiler, J.A.; Menéndez, J.; Vissani, F. Toward the discovery of matter creation with neutrinoless ββ decay. Rev. Mod. Phys. 2023, 95, 025002. [Google Scholar] [CrossRef]
- Adams, C.; Alfonso, K.; Andreoiu, C.; Angelico, E.; Arnquist, I.J.; Asaadi, J.A.A.; Avignone, F.T.; Axani, S.N.; Barabash, A.S.; Barbeau, P.S.; et al. Neutrinoless Double Beta Decay. arXiv 2022, arXiv:2212.11099. [Google Scholar] [CrossRef]
- Inghram, M.G.; Reynolds, J.H. Double Beta-Decay of Te130. Phys. Rev. 1950, 78, 822–823. [Google Scholar] [CrossRef]
- Elliott, S.R.; Hahn, A.A.; Moe, M.K. Direct evidence for two-neutrino double-beta decay in 82Se. Phys. Rev. Lett. 1987, 59, 2020–2023. [Google Scholar] [CrossRef]
- Moe, M.K. The First Direct Observation of Double-Beta Decay. Annu. Rev. Nucl. Part. Sci. 2014, 64, 247–267. [Google Scholar] [CrossRef]
- Pritychenko, B.; Tretyak, V. Comprehensive review of 2β decay half-lives. At. Data Nucl. Data Tables 2024, 101694. [Google Scholar] [CrossRef]
- Barabash, A.S.; Saakyan, R.R. Experimental limits on 2β+, Kβ+, and 2K processes for 130Ba and on 2K capture for 132Ba. Phys. At. Nucl. 1996, 59, 179–184. [Google Scholar]
- Meshik, A.P.; Hohenberg, C.M.; Pravdivtseva, O.V.; Kapusta, Y.S. Weak decay of 130Ba and 132Ba: Geochemical measurements. Phys. Rev. C 2001, 64, 035205. [Google Scholar] [CrossRef]
- Pujol, M.; Marty, B.; Burnard, P.; Philippot, P. Xenon in Archean barite: Weak decay of 130Ba, mass-dependent isotopic fractionation and implication for barite formation. Geochim. Cosmochim. Acta 2009, 73, 6834–6846. [Google Scholar] [CrossRef]
- Gavrilyuk, Y.M.; Gangapshev, A.M.; Kazalov, V.V.; Kuzminov, V.V.; Panasenko, S.I.; Ratkevich, S.S. Indications of 2ν2K capture in 78Kr. Phys. Rev. C 2013, 87, 035501. [Google Scholar] [CrossRef]
- Ratkevich, S.S.; Gangapshev, A.M.; Gavrilyuk, Y.M.; Karpeshin, F.F.; Kazalov, V.V.; Kuzminov, V.V.; Panasenko, S.I.; Trzhaskovskaya, M.B.; Yakimenko, S.P. Comparative study of the double-K-shell-vacancy production in single- and double-electron-capture decay. Phys. Rev. C 2017, 96, 065502. [Google Scholar] [CrossRef]
- Aprile, E.; Aalbers, J.; Agostini, F.; Alfonsi, M.; Althueser, L.; Amaro, F.D.; Anthony, M.; Antochi, V.C.; Arneodo, F.; Baudis, L.; et al. Observation of two-neutrino double electron capture in 124Xe with XENON1T. Nature 2019, 568, 532–535. [Google Scholar] [CrossRef]
- Aprile, E.; Abe, K.; Agostini, F.; Ahmed Maouloud, S.; Alfonsi, M.; Althueser, L.; Andrieu, B.; Angelino, E.; Angevaare, J.R.; Antochi, V.C.; et al. Double-weak decays of 124Xe and 136Xe in the XENON1T and XENONnT experiments. Phys. Rev. C 2022, 106, 024328. [Google Scholar] [CrossRef]
- Aalbers, J.; Akerib, D.S.; Musalhi, A.K.A.; Alder, F.; Amarasinghe, C.S.; Ames, A.; Anderson, T.J.; Angelides, N.; Araújo, H.M.; Armstrong, J.E.; et al. Two-neutrino double electron capture of 124Xe in the first LUX-ZEPLIN exposure. arXiv 2024, arXiv:2408.17391. [Google Scholar] [CrossRef]
- Rukhadze, N.I.; Gascon, J.; Gusev, K.N.; Klimenko, A.A.; Fürst, M.; Rozov, S.V.; Rukhadze, E.; Salamatin, A.V.; Šimkovic, F.; Shitov, Y.A.; et al. Investigation of β+β+, β+EC, EC/EC decay of 106Cd with the spectrometer TGV-2. J. Phys. Conf. Ser. 2021, 2156, 012134. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Caracciolo, V. Status and Perspectives of 2ϵ, ϵβ+ and 2β Decays. Particles 2021, 4, 241–274. [Google Scholar] [CrossRef]
- Bossio, E.; Agostini, M. Probing beyond the standard model physics with double-beta decays. J. Phys. G Nucl. Part. Phys. 2023, 51, 023001. [Google Scholar] [CrossRef]
- Deppisch, F.F.; Graf, L.; Šimkovic, F. Searching for New Physics in Two-Neutrino Double Beta Decay. Phys. Rev. Lett. 2020, 125, 171801. [Google Scholar] [CrossRef] [PubMed]
- Deppisch, F.F.; Graf, L.; Rodejohann, W.; Xu, X.J. Neutrino self-interactions and double beta decay. Phys. Rev. D 2020, 102, 051701. [Google Scholar] [CrossRef]
- Barabash, A.; Dolgov, A.; Dvornický, R.; Šimkovic, F.; Smirnov, A. Statistics of neutrinos and the double beta decay. Nucl. Phys. B 2007, 783, 90–111. [Google Scholar] [CrossRef]
- Díaz, J.S. Limits on Lorentz and CPT violation from double beta decay. Phys. Rev. D 2014, 89, 036002. [Google Scholar] [CrossRef]
- Niţescu, O.; Ghinescu, S.; Stoica, S. Lorentz violation effects in 2νββ decay. J. Phys. G Nucl. Part. Phys. 2020, 47, 055112. [Google Scholar] [CrossRef]
- Niţescu, O.V.; Ghinescu, S.A.; Mirea, M.; Stoica, S. Probing Lorentz violation in 2νββ using single electron spectra and angular correlations. Phys. Rev. D 2021, 103, L031701. [Google Scholar] [CrossRef]
- Ghinescu, S.A.; Niţescu, O.; Stoica, S. Investigation of the Lorentz invariance violation in two-neutrino double-beta decay. Phys. Rev. D 2022, 105, 055032. [Google Scholar] [CrossRef]
- Bolton, P.D.; Deppisch, F.F.; Gráf, L.; Šimkovic, F. Two-neutrino double beta decay with sterile neutrinos. Phys. Rev. D 2021, 103, 055019. [Google Scholar] [CrossRef]
- Agostini, M.; Bossio, E.; Ibarra, A.; Marcano, X. Search for light exotic fermions in double-beta decays. Phys. Lett. B 2021, 815, 136127. [Google Scholar] [CrossRef]
- Mohapatra, R.; Takasugi, E. Neutrinoless double beta decay with double majoron emission. Phys. Lett. B 1988, 211, 192–196. [Google Scholar] [CrossRef]
- Berezhiani, Z.; Smirnov, A.; Valle, J. Observable majoron emission in neutrinoless double beta decay. Phys. Lett. B 1992, 291, 99–105. [Google Scholar] [CrossRef]
- Burgess, C.; Cline, J. Majorons without majorana masses and neutrinoless double beta decay. Phys. Lett. B 1993, 298, 141–148. [Google Scholar] [CrossRef]
- Carone, C.D. Double beta decay with vector majorons. Phys. Lett. B 1993, 308, 85–88. [Google Scholar] [CrossRef]
- Burgess, C.P.; Cline, J.M. New class of Majoron-emitting double-β decays. Phys. Rev. D 1994, 49, 5925–5944. [Google Scholar] [CrossRef] [PubMed]
- Bamert, P.; Burgess, C.; Mohapatra, R. Multi-majoron modes for neutrinoless double-beta decay. Nucl. Phys. B 1995, 449, 25–48. [Google Scholar] [CrossRef]
- Hirsch, M.; Klapdor-Kleingrothaus, H.; Kovalenko, S.; Päs, H. On the observability of Majoron emitting double beta decays. Phys. Lett. B 1996, 372, 8–14. [Google Scholar] [CrossRef]
- Mohapatra, R.; Pérez-Lorenzana, A.; de S. Pires, C. Neutrino mass, bulk majoron and neutrinoless double beta decay. Phys. Lett. B 2000, 491, 143–147. [Google Scholar] [CrossRef]
- Kotila, J.; Barea, J.; Iachello, F. Phase-space factors and half-life predictions for Majoron-emitting β–β– decay. Phys. Rev. C 2015, 91, 064310. [Google Scholar] [CrossRef]
- Cepedello, R.; Deppisch, F.F.; González, L.; Hati, C.; Hirsch, M. Neutrinoless Double-β Decay with Nonstandard Majoron Emission. Phys. Rev. Lett. 2019, 122, 181801. [Google Scholar] [CrossRef]
- Kotila, J.; Iachello, F. Nuclear matrix elements for Majoron-emitting double-β decay. Phys. Rev. C 2021, 103, 044302. [Google Scholar] [CrossRef]
- Arnold, R.; Augier, C.; Barabash, A.S.; Basharina-Freshville, A.; Blondel, S.; Blot, S.; Bongr, M.; Boursette, D.; Brudanin, V.; Busto, J.; et al. Search for Neutrinoless Quadruple-β Decay of 150Nd with the NEMO-3 Detector. Phys. Rev. Lett. 2017, 119, 041801. [Google Scholar] [CrossRef] [PubMed]
- Arnold, R.; Augier, C.; Barabash, A.S.; Basharina-Freshville, A.; Blondel, S.; Blot, S.; Bongr, M.; Boursette, D.; Brudanin, V.; Busto, J.; et al. Detailed studies of 100Mo two-neutrino double beta decay in NEMO-3. Eur. Phys. J. C 2019, 79, 440. [Google Scholar] [CrossRef]
- Arnold, R.; Augier, C.; Baker, J.; Barabash, A.S.; Basharina-Freshville, A.; Bongrand, M.; Brudanin, V.; Caffrey, A.J.; Cebrián, S.; Chapon, A.; et al. Probing new physics models of neutrinoless double beta decay with SuperNEMO. Eur. Phys. J. C 2010, 70, 927–943. [Google Scholar] [CrossRef]
- Ferrario, P.; Laing, A.; López-March, N.; Gómez-Cadenas, J.J.; Álvarez, V.; Azevedo, C.D.R.; Borges, F.I.G.; Cárcel, S.; Cebrián, S.; Cervera, A.; et al. First proof of topological signature in the high pressure xenon gas TPC with electroluminescence amplification for the NEXT experiment. J. High Energy Phys. 2016, 2016, 104. [Google Scholar] [CrossRef]
- Neacsu, A.; Horoi, M. Shell Model Studies of Competing Mechanisms to the Neutrinoless Double-Beta Decay in 124Sn, 130Te, and 136Xe. Adv. High Energy Phys. 2016, 2016, 1903767. [Google Scholar] [CrossRef]
- Horoi, M.; Neacsu, A. Analysis of mechanisms that could contribute to neutrinoless double-beta decay. Phys. Rev. D 2016, 93, 113014. [Google Scholar] [CrossRef]
- Štefánik, D.; Dvornický, R.; Šimkovic, F.; Vogel, P. Reexamining the light neutrino exchange mechanism of the 0νββ decay with left- and right-handed leptonic and hadronic currents. Phys. Rev. C 2015, 92, 055502. [Google Scholar] [CrossRef]
- Gráf, L.; Lindner, M.; Scholer, O. Unraveling the 0νββ decay mechanisms. Phys. Rev. D 2022, 106, 035022. [Google Scholar] [CrossRef]
- Scholer, O.; de Vries, J.; Gráf, L. νDoBe—A Python tool for neutrinoless double beta decay. J. High Energy Phys. 2023, 2023, 43. [Google Scholar] [CrossRef]
- Šimkovic, F.; Dvornický, R.; Štefánik, D.; Faessler, A. Improved description of the 2νββ-decay and a possibility to determine the effective axial-vector coupling constant. Phys. Rev. C 2018, 97, 034315. [Google Scholar] [CrossRef]
- Niţescu, O.; Dvornický, R.; Stoica, S.; Šimkovic, F. Angular Distributions of Emitted Electrons in the Two-Neutrino ββ Decay. Universe 2021, 7, 147. [Google Scholar] [CrossRef]
- Rahaman, S.; Elomaa, V.V.; Eronen, T.; Hakala, J.; Jokinen, A.; Julin, J.; Kankainen, A.; Saastamoinen, A.; Suhonen, J.; Weber, C.; et al. Q values of the 76Ge and 100Mo double-beta decays. Phys. Lett. B 2008, 662, 111–116. [Google Scholar] [CrossRef]
- Niţescu, O.; Šimkovic, F. A Semi-Empirical Formula for Two-Neutrino Double-Beta Decay. arXiv 2024, arXiv:2407.10422. [Google Scholar] [CrossRef]
- Gando, A.; Gando, Y.; Hachiya, T.; Ha Minh, M.; Hayashida, S.; Honda, Y.; Hosokawa, K.; Ikeda, H.; Inoue, K.; Ishidoshiro, K.; et al. Precision Analysis of the 136Xe Two-Neutrino ββ Spectrum in KamLAND-Zen and Its Impact on the Quenching of Nuclear Matrix Elements. Phys. Rev. Lett. 2019, 122, 192501. [Google Scholar] [CrossRef] [PubMed]
- Augier, C.; Barabash, A.S.; Bellini, F.; Benato, G.; Beretta, M.; Bergé, L.; Billard, J.; Borovlev, Y.A.; Cardani, L.; Casali, N.; et al. Measurement of the 2νββ Decay Rate and Spectral Shape of 100Mo from the CUPID-Mo Experiment. Phys. Rev. Lett. 2023, 131, 162501. [Google Scholar] [CrossRef] [PubMed]
- Tomoda, T. Double beta decay. Rep. Prog. Phys. 1991, 54, 53. [Google Scholar] [CrossRef]
- Kotila, J.; Iachello, F. Phase-space factors for double-β decay. Phys. Rev. C 2012, 85, 034316. [Google Scholar] [CrossRef]
- Yao, J.; Meng, J.; Niu, Y.; Ring, P. Beyond-mean-field approaches for nuclear neutrinoless double beta decay in the standard mechanism. Prog. Part. Nucl. Phys. 2022, 126, 103965. [Google Scholar] [CrossRef]
- Rose, M.E. Relativistic Electron Theory; John Wiley and Sons: Hoboken, NJ, USA, 1961. [Google Scholar]
- Doi, M.; Kotani, T.; Takasugi, E. Double Beta Decay and Majorana Neutrino. Prog. Theor. Phys. Suppl. 1985, 83, 1–175. [Google Scholar] [CrossRef]
- Rose, M.E. Elementary Theory of Angular Momentum; Dover: Mineola, NY, USA, 1995. [Google Scholar]
- Varshalovich, D.A.; Moskalev, A.N.; Khersonskii, V.K. Quantum Theory of Angular Momentum; World Scientific: Singapore, 1995. [Google Scholar]
- Niţescu, O.; Stoica, S.; Šimkovic, F. Exchange correction for allowed β decay. Phys. Rev. C 2023, 107, 025501. [Google Scholar] [CrossRef]
- Niţescu, O.; Dvornický, R.; Šimkovic, F. Atomic corrections for the unique first-forbidden β transition of 187Re. Phys. Rev. C 2024, 109, 025501. [Google Scholar] [CrossRef]
- Salvat, F.; Fernández-Varea, J.M. RADIAL: A Fortran subroutine package for the solution of the radial Schrödinger and Dirac wave equations. Comput. Phys. Commun. 2019, 240, 165–177. [Google Scholar] [CrossRef]
- Drukarev, E.G.; Amusia, M.Y.; Chernysheva, L.V. Role of the atomic electron shell in the double β decay. Phys. Rev. C 2016, 94, 035504. [Google Scholar] [CrossRef]
- Krivoruchenko, M.I.; Tyrin, K.S. Overlap of electron shells in β and double-β decays. Eur. Phys. J. A 2020, 56, 16. [Google Scholar] [CrossRef]
- Krivoruchenko, M.I.; Tyrin, K.S.; Karpeshin, F.F. Energy Spectrum of β Electrons in Neutrinoless Double-β Decay Including the Excitation of the Electron Shell of Atoms. JETP Lett. 2023, 117, 884–888. [Google Scholar] [CrossRef]
- Detwiler, J.A.; Robertson, R.G.H. Shake-up and shake-off effects in neutrinoless double-β decay. Phys. Rev. C 2023, 107, L042501. [Google Scholar] [CrossRef]
- Stoica, S.; Mirea, M. Phase Space Factors for Double-Beta Decays. Front. Phys. 2019, 7, 12. [Google Scholar] [CrossRef]
- Šimkovic, F.; Domin, P.; Semenov, S.V. The single state dominance hypothesis and the two-neutrino double beta decay of 100Mo. J. Phys. G Nucl. Part. Phys. 2001, 27, 2233. [Google Scholar] [CrossRef][Green Version]
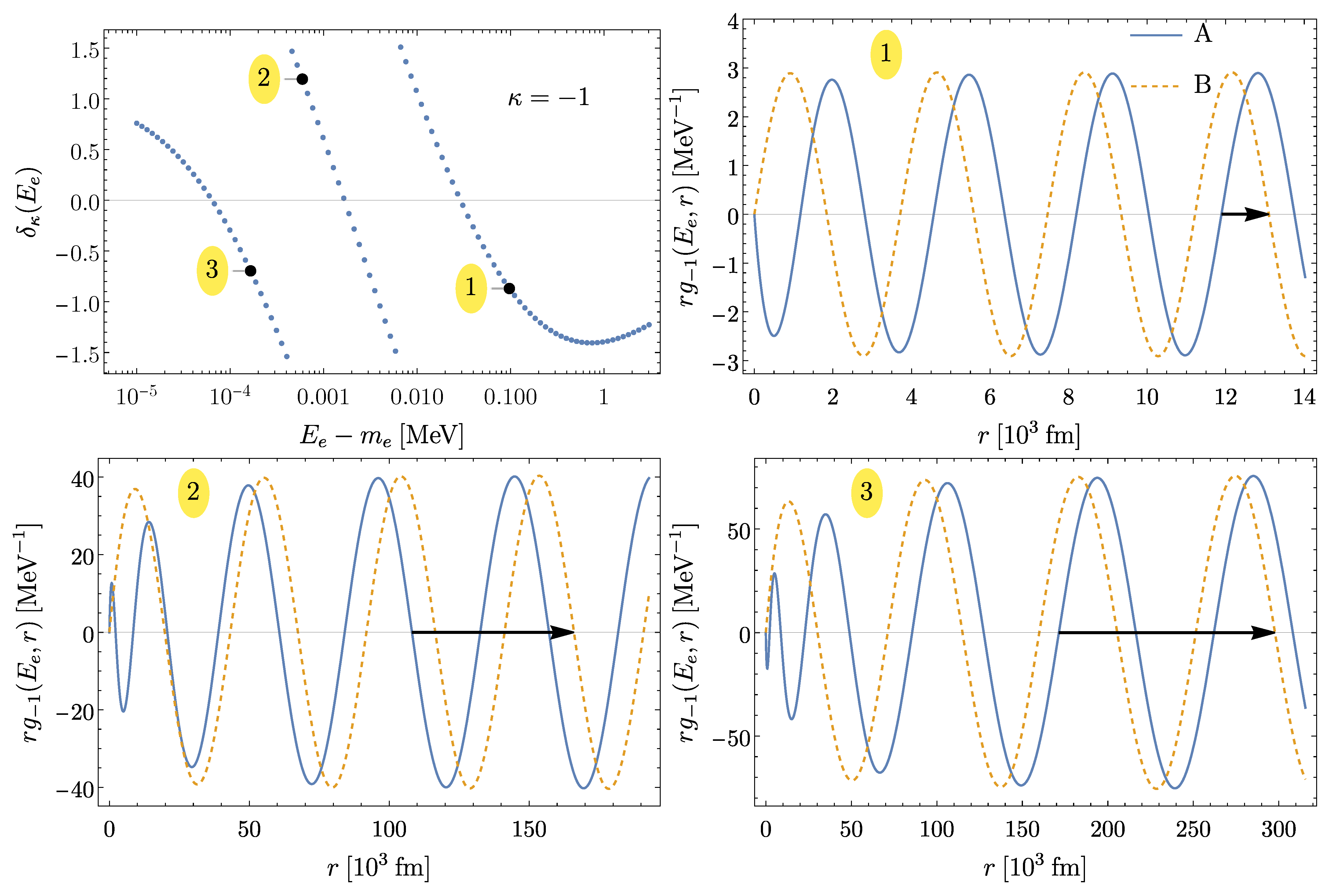
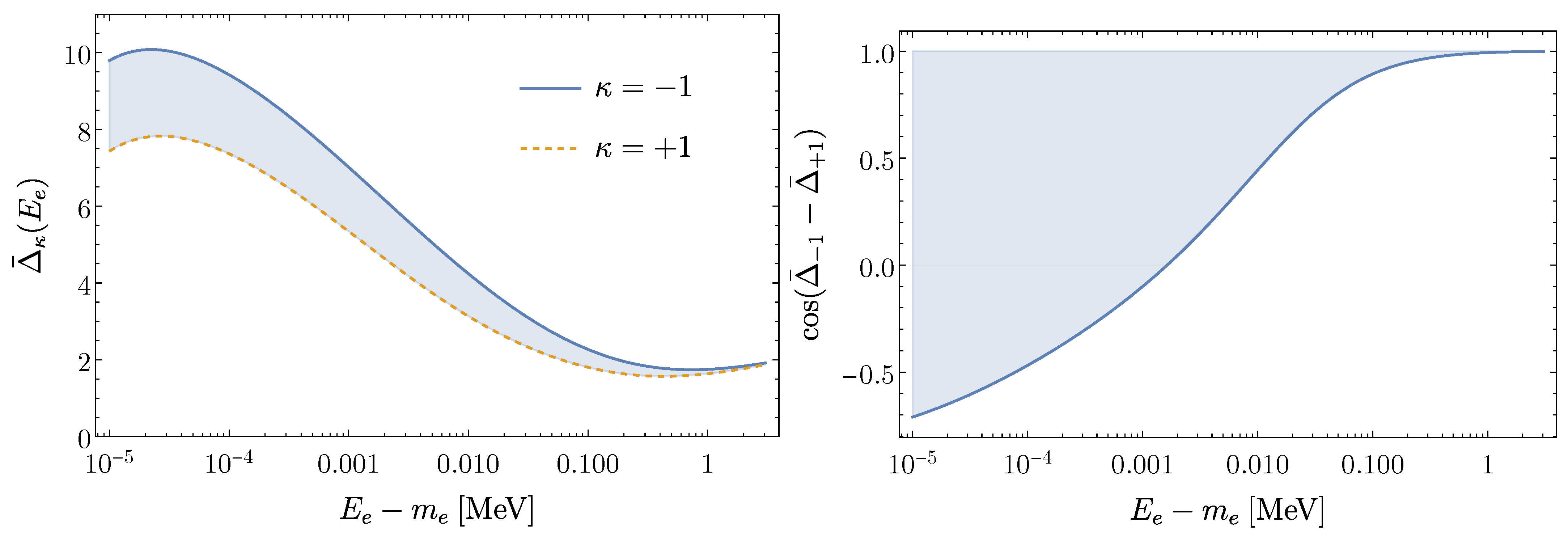
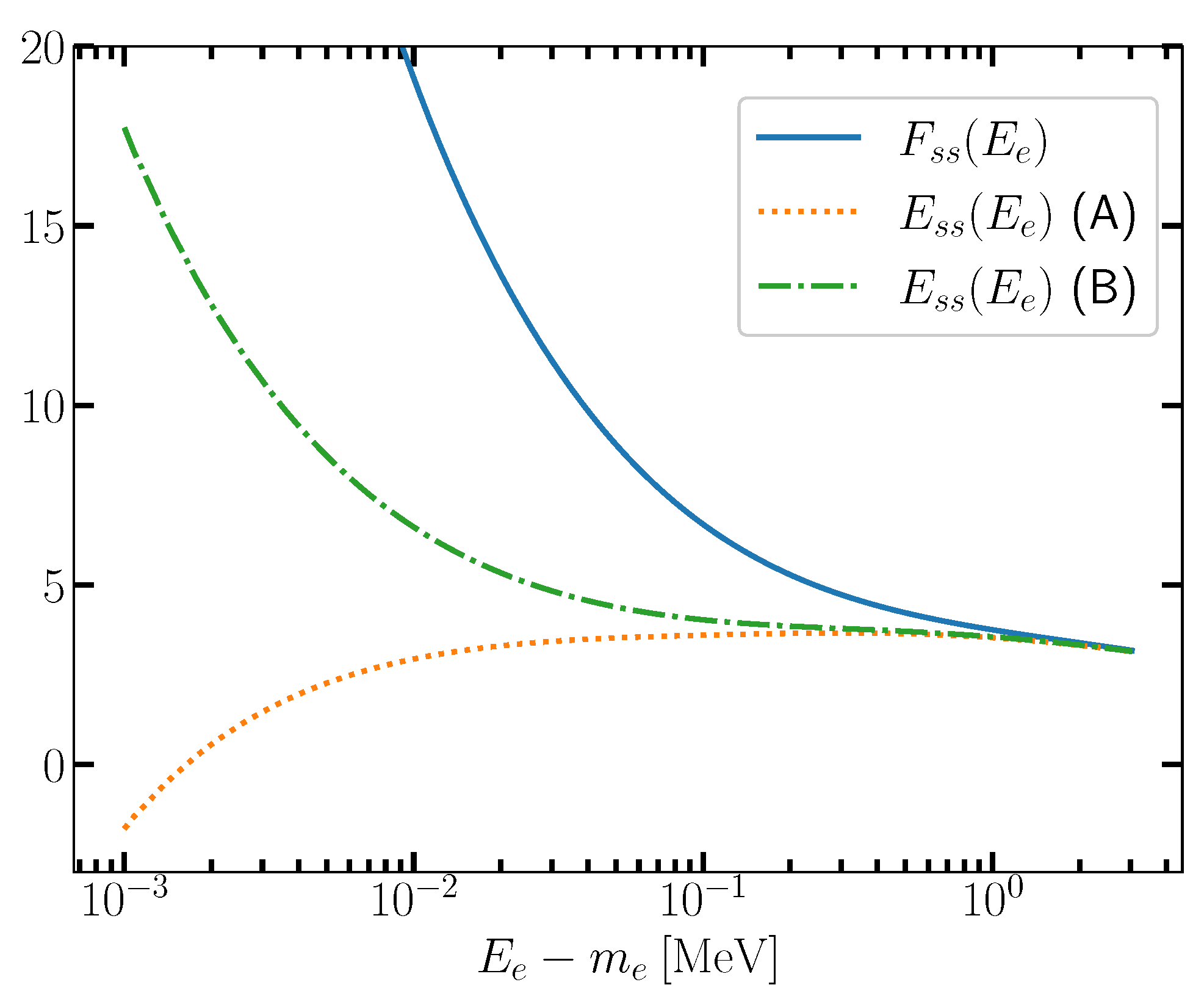
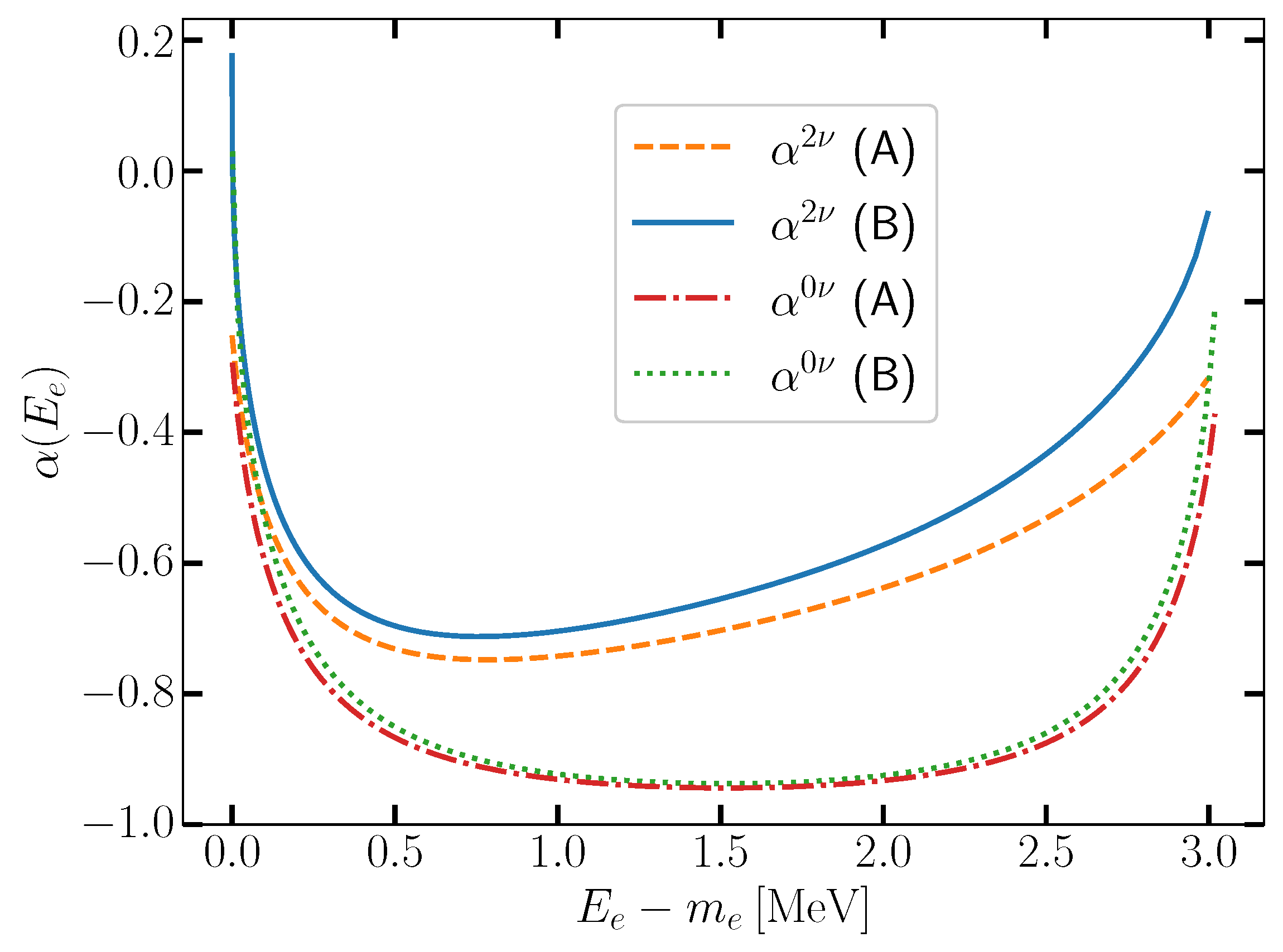
| Without Phase Shifts | With Phase Shifts | ||
|---|---|---|---|
| No Screening | Realistic Screening | Realistic Screening | |
| HSD | −0.650 [32] | −0.684 [61] | −0.640 (TW) |
| (; ) | −0.646 [33] | −0.684 [67] | |
| −0.646 [61] | −0.685 (TW) | ||
| −0.646 [81] | |||
| SSD | −0.627 [33] | −0.668 [36] | −0.627 (TW) |
| (; ) | −0.627 [81] | −0.669 [37] | |
| −0.633 [61] | −0.668 [67] | ||
| −0.674 [61] | |||
| −0.675 (TW) | |||
| EXP | −0.630 [61] | −0.671 [61] | −0.624 (TW) |
| (; [65]) | −0.672 (TW) | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niţescu, O.; Ghinescu, S.; Šimkovic, F. The Impact of Electron Phase Shifts on ββ-Decay Kinematics. Universe 2024, 10, 442. https://doi.org/10.3390/universe10120442
Niţescu O, Ghinescu S, Šimkovic F. The Impact of Electron Phase Shifts on ββ-Decay Kinematics. Universe. 2024; 10(12):442. https://doi.org/10.3390/universe10120442
Chicago/Turabian StyleNiţescu, Ovidiu, Stefan Ghinescu, and Fedor Šimkovic. 2024. "The Impact of Electron Phase Shifts on ββ-Decay Kinematics" Universe 10, no. 12: 442. https://doi.org/10.3390/universe10120442
APA StyleNiţescu, O., Ghinescu, S., & Šimkovic, F. (2024). The Impact of Electron Phase Shifts on ββ-Decay Kinematics. Universe, 10(12), 442. https://doi.org/10.3390/universe10120442







