Machine Learning to Simulate Quantum Computing System Errors from Physical Observations
Abstract
1. Introduction
- (i)
- Imperfect quantum gate operations.
- (ii)
- Environmental decoherence through system–bath interactions.
- (iii)
- Discrepancies between theoretical designs and physical implementations.
- Dephasing errors (X/Y Pauli errors) through computational subspace leakage.
- Phase errors (Z Pauli errors) via parity-violating transitions [17].
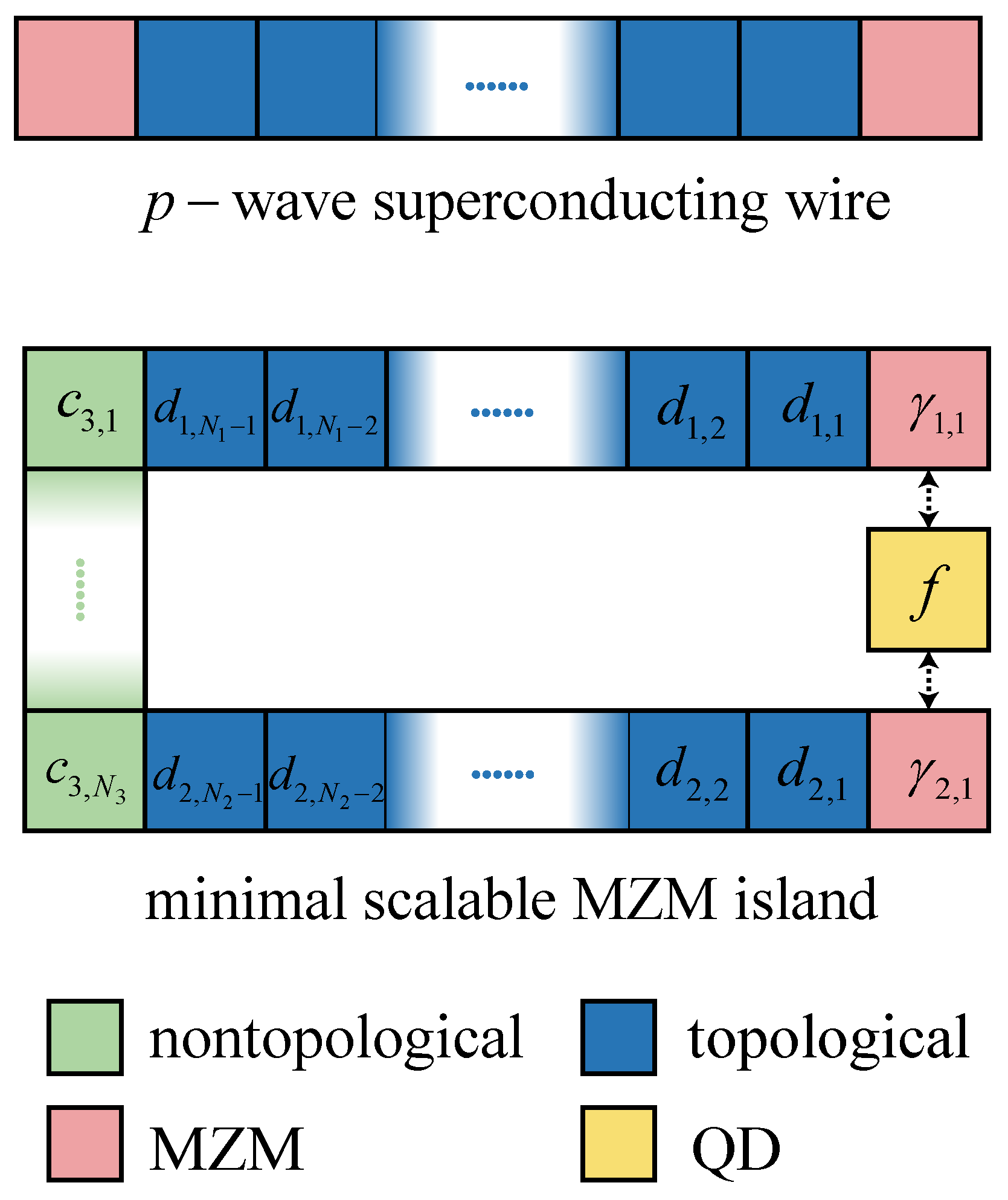
2. Minimal Scalable 2-MZM Island
Monte Carlo Study of 2-MZM Island
- 1.
- Initialize the relevant parameters and initialize the system to the state .
- 2.
- Determine the time , where u is a random number uniformly distributed in the interval .
- 3.
- Update the simulation time to and if , go to step 4, or go directly to step 5.
- 4.
- Implement the jump operators at random in the system according to the transition rate .
- 5.
- Record the states of the two MZMs.
- The length of the bulk segments, ;
- The chemical potential of the backbone, ;
- The induced superconducting gap, ;
- The effective orbital energy of the quantum dot, h;
- The charging energy of the quantum dot, ;
- The induced charge on the island, ;
- The transition amplitude in the Pauli master equation, ;
- The inverse temperature in the thermal bath, .
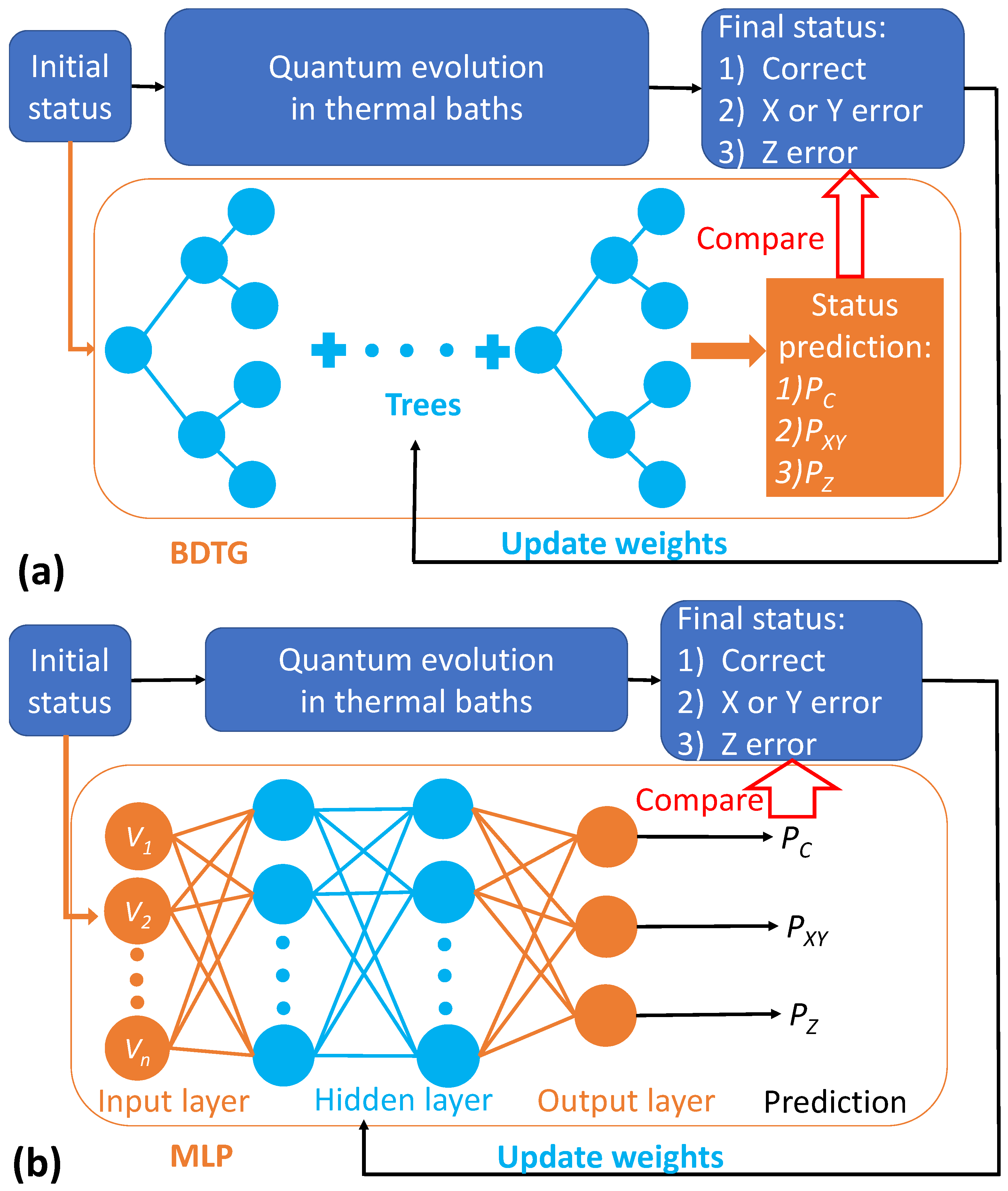
3. Machine Learning Methods
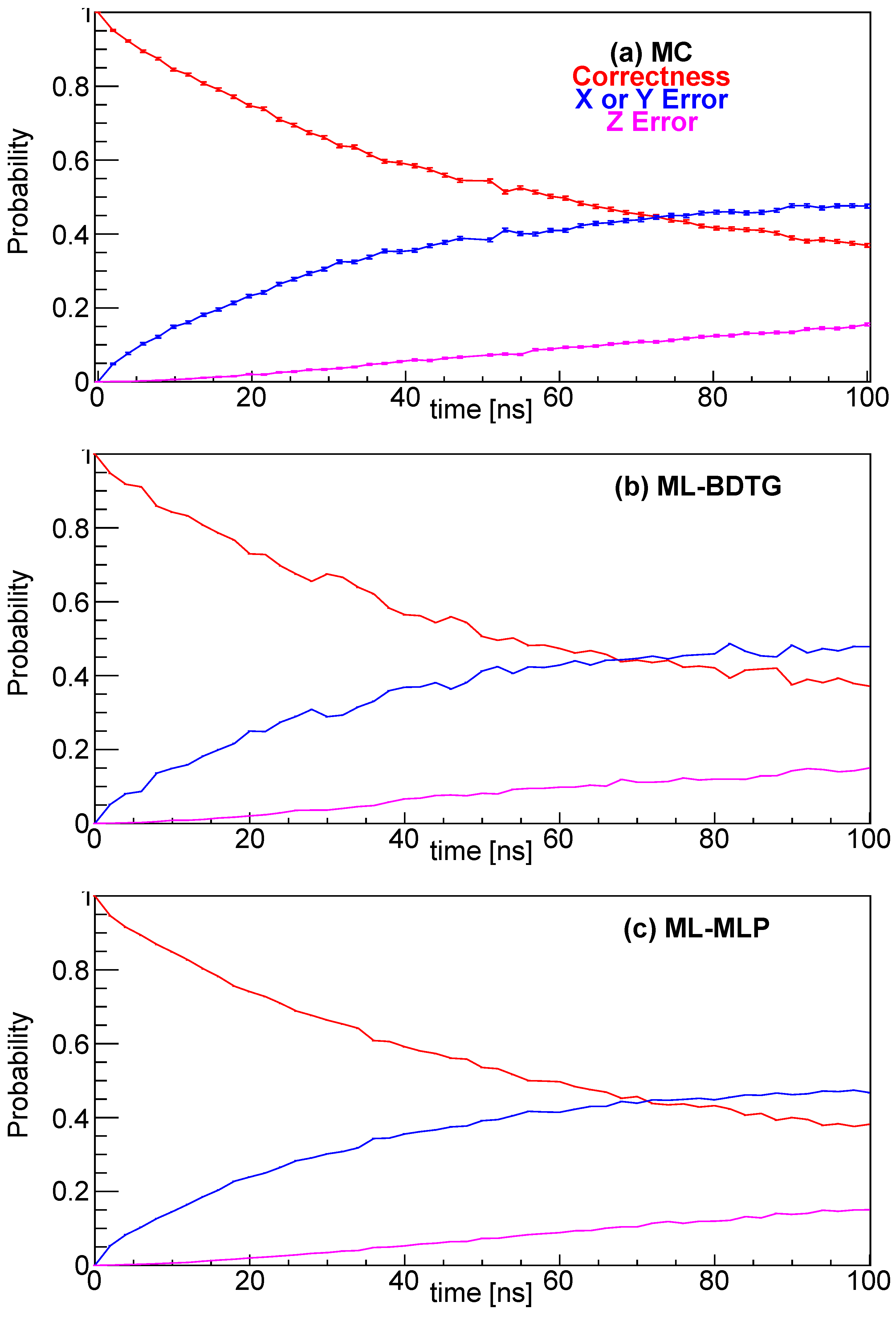
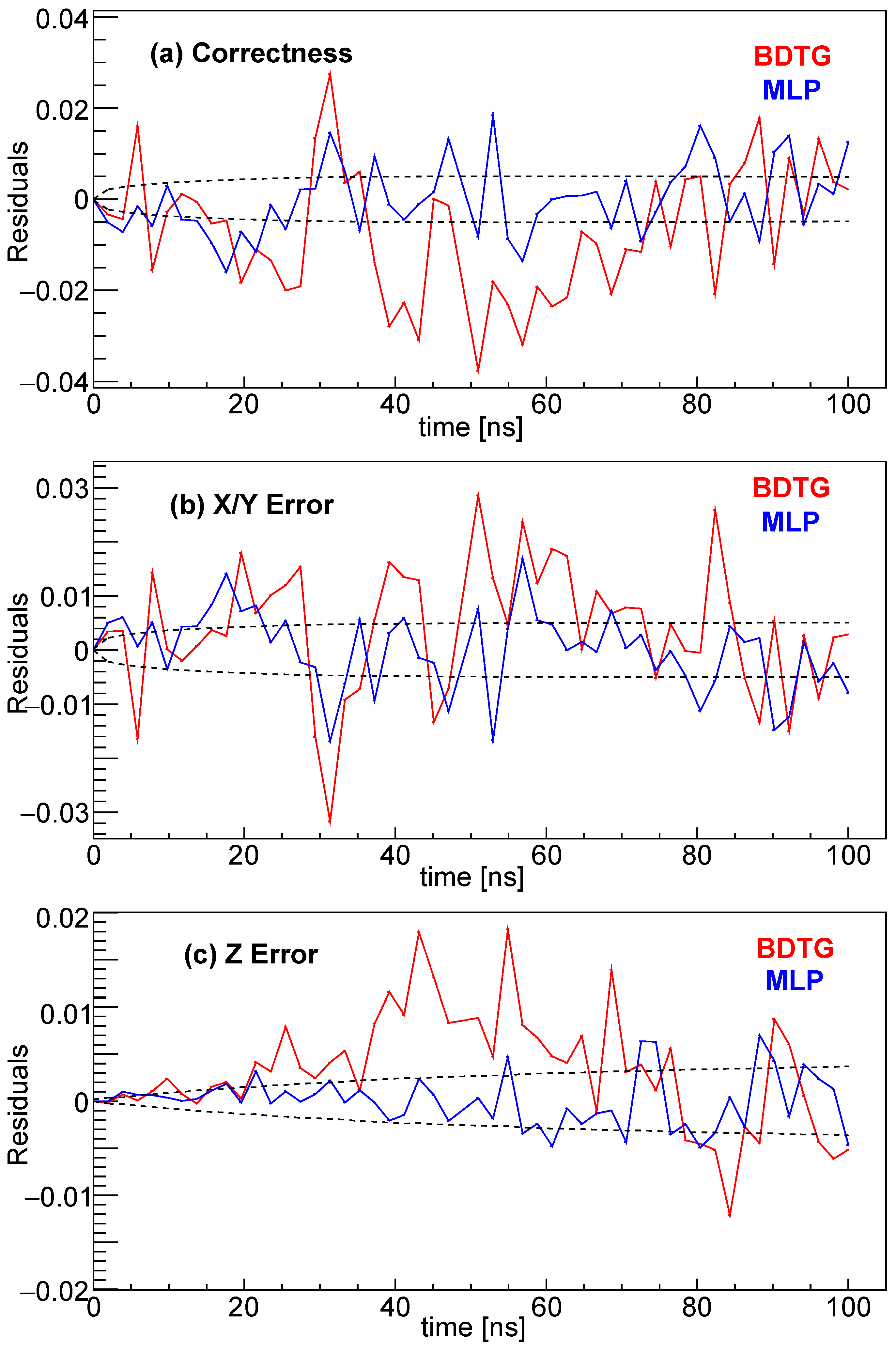
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Jones, J.A.; Mosca, M. Implementation of a quantum algorithm to solve Deutsch’s problem on a nuclear magnetic resonance quantum computer. J. Chem. Phys. 1998, 109, 1648–1653. [Google Scholar] [CrossRef]
- Chuang, I.; Gershenfeld, N.; Kubinec, M. Experimental Implementation of Fast Quantum Searching. Phys. Rev. Lett. 1998, 80, 3408–3411. [Google Scholar]
- Vandersypen, L.M.K.; Steffen, M.; Breyta, G.; Yannoni, C.S.; Sherwood, M.H.; Chuang, I.L. Experimental realization of Shor’s quantum factoring algorithm using nuclear magnetic resonance. Nature 2001, 414, 883–887. [Google Scholar] [CrossRef] [PubMed]
- Stolze, J.; Suter, D. Quantum Computing—A Short Course from Theory to Experiment, 2nd ed.; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Kitaev, A.Y. Fault-Tolerant Quantum Computation by Anyons. Ann. Phys. 2003, 303, 2–30. [Google Scholar] [CrossRef]
- Kitaev, A.Y. Unpaired Majorana fermions in quantum wires. Physics-Uspekhi 2001, 44, 131–136. [Google Scholar] [CrossRef]
- Lutchyn, R.M.; Sau, J.D.; Das Sarma, S. Majorana Fermions and a Topological Phase Transition in Semiconductor-Superconductor Heterostructures. Phys. Rev. Lett. 2010, 105, 077001. [Google Scholar] [CrossRef] [PubMed]
- Oreg, Y.; Refael, G.; von Oppen, F. Helical Liquids and Majorana Bound States in Quantum Wires. Phys. Rev. Lett. 2010, 105, 177002. [Google Scholar] [CrossRef]
- Sarma, S.D.; Freedman, M.; Nayak, C. Majorana zero modes and topological quantum computation. NPJ Quantum Inf. 2015, 1, 15001. [Google Scholar] [CrossRef]
- Nayak, C.; Simon, S.H.; Stern, A.; Freedman, M.; Das Sarma, S. Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys. 2008, 80, 1083–1159. [Google Scholar] [CrossRef]
- Sau, J.D.; Lutchyn, R.M.; Tewari, S.; Das Sarma, S. Generic New Platform for Topological Quantum Computation Using Semiconductor Heterostructures. Phys. Rev. Lett. 2010, 104, 040502. [Google Scholar] [CrossRef]
- Lutchyn, R.M.; Bakkers, E.P.A.M.; Kouwenhoven, L.P.; Krogstrup, P.; Marcus, C.M.; Oreg, Y. Majorana zero modes in superconductor–semiconductor heterostructures. Nat. Rev. Mater. 2018, 3, 52–68. [Google Scholar] [CrossRef]
- Alicea, J.; Oreg, Y.; Refael, G.; von Oppen, F.; Fisher, M.P.A. Non-Abelian statistics and topological quantum information processing in 1D wire networks. Nat. Phys. 2011, 7, 412. [Google Scholar] [CrossRef]
- Ivanov, D.A. Non-Abelian Statistics of Half-Quantum Vortices in p-Wave Superconductors. Phys. Rev. Lett. 2001, 86, 268–271. [Google Scholar] [CrossRef]
- Stone, M.; Chung, S.B. Fusion rules and vortices in px+ipy superconductors. Phys. Rev. B 2006, 73, 014505. [Google Scholar] [CrossRef]
- Karzig, T.; Cole, W.S.; Pikulin, D.I. Quasiparticle Poisoning of Majorana Qubits. Phys. Rev. Lett. 2021, 126, 057702. [Google Scholar] [CrossRef] [PubMed]
- Knapp, C.; Karzig, T.; Lutchyn, R.M.; Nayak, C. Dephasing of Majorana-based qubits. Phys. Rev. B 2018, 97, 125404. [Google Scholar] [CrossRef]
- Pedrocchi, F.L.; Bonesteel, N.E.; DiVincenzo, D.P. Monte Carlo studies of the self-correcting properties of the Majorana quantum error correction code under braiding. Phys. Rev. B 2015, 92, 115441. [Google Scholar] [CrossRef]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Flurin, E.; Martin, L.S.; Hacohen-Gourgy, S.; Siddiqi, I. Using a Recurrent Neural Network to Reconstruct Quantum Dynamics of a Superconducting Qubit from Physical Observations. Phys. Rev. X 2020, 10, 011006. [Google Scholar] [CrossRef]
- Cincio, L.; Rudinger, K.; Sarovar, M.; Coles, P.J. Machine Learning of Noise-Resilient Quantum Circuits. PRX Quantum 2021, 2, 010324. [Google Scholar] [CrossRef]
- Wise, D.F.; Morton, J.J.; Dhomkar, S. Using Deep Learning to Understand and Mitigate the Qubit Noise Environment. PRX Quantum 2021, 2, 010316. [Google Scholar] [CrossRef]
- Fiderer, L.J.; Schuff, J.; Braun, D. Neural-Network Heuristics for Adaptive Bayesian Quantum Estimation. PRX Quantum 2021, 2, 020303. [Google Scholar] [CrossRef]
- Liao, H.; Wang, D.S.; Sitdikov, I.; Salcedo, C.; Seif, A.; Minev, Z.K. Machine learning for practical quantum error mitigation. Nat. Mach. Intell. 2024, 6, 1478–1486. [Google Scholar] [CrossRef]
- Karzig, T.; Knapp, C.; Lutchyn, R.M.; Bonderson, P.; Hastings, M.B.; Nayak, C.; Alicea, J.; Flensberg, K.; Plugge, S.; Oreg, Y.; et al. Scalable designs for quasiparticle-poisoning-protected topological quantum computation with Majorana zero modes. Phys. Rev. B 2017, 95, 235305. [Google Scholar] [CrossRef]
- Feng, G.H.; Chen, J.; Zhang, H.H. Monte Carlo studies of modified scalable designs for quantum computation. arXiv 2019, arXiv:1911.06755. [Google Scholar]
- Tanabashi, M.; Hagiwara, K.; Hikasa, K.; Nakamura, K.; Sumino, Y.; Takahashi, F.; Tanaka, J.; Agashe, K.; Aielli, G.; Particle Data Group; et al. Review of Particle Physics. Phys. Rev. D 2018, 98, 030001. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Fukushima, K. Training multi-layered neural network Neocognitron. Neural Netw. 2013, 40, 18–31. [Google Scholar] [CrossRef]
- Hoecker, A.; Speckmayer, P.; Stelzer, J.; Therhaag, J.; von Toerne, E.; Voss, H.; Backes, M.; Carli, T.; Cohen, O.; Christov, A.; et al. TMVA—Toolkit for Multivariate Data Analysis. arXiv 2009, arXiv:physics/0703039. [Google Scholar]
| t | N (Site) | (Site) | |||||
|---|---|---|---|---|---|---|---|
| 2 | 5 | 2 | 10 | 2 | 3009 | 6 |
| Parameter | Minimum Value | Maximum Value |
|---|---|---|
| (nm) | 40 | 2504 |
| (eV) | −900 | −400 |
| (eV) | 80 | 500 |
| h (eV) | 80 | 1200 |
| (eV) | 1200 | 18,000 |
| 0.02 | 0.3 | |
| 0.1 | 1.5 | |
| 0.002 | 0.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, J.; Zhang, X.; Feng, G.; Zhang, H.-H. Machine Learning to Simulate Quantum Computing System Errors from Physical Observations. Universe 2025, 11, 120. https://doi.org/10.3390/universe11040120
Feng J, Zhang X, Feng G, Zhang H-H. Machine Learning to Simulate Quantum Computing System Errors from Physical Observations. Universe. 2025; 11(4):120. https://doi.org/10.3390/universe11040120
Chicago/Turabian StyleFeng, Jie, Xingchen Zhang, Guanhao Feng, and Hong-Hao Zhang. 2025. "Machine Learning to Simulate Quantum Computing System Errors from Physical Observations" Universe 11, no. 4: 120. https://doi.org/10.3390/universe11040120
APA StyleFeng, J., Zhang, X., Feng, G., & Zhang, H.-H. (2025). Machine Learning to Simulate Quantum Computing System Errors from Physical Observations. Universe, 11(4), 120. https://doi.org/10.3390/universe11040120






