Gauss–Bonnet-Induced Symmetry Breaking/Restoration During Inflation
Abstract
1. Introduction
2. De Sitter Background
2.1. GB-Induced SSB
2.2. GB-Induced Symmetry Restoration
3. Application to Inflation
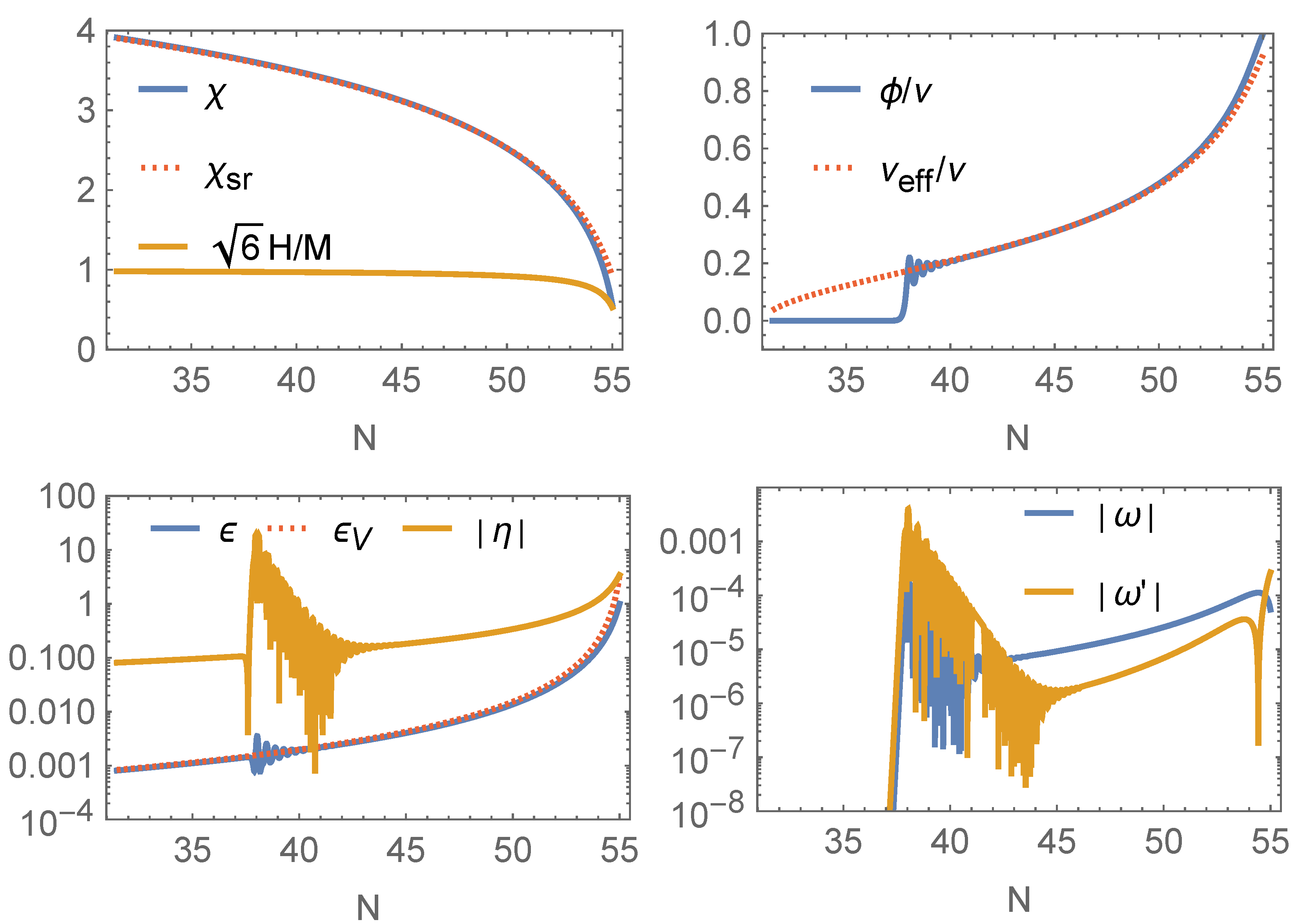
3.1. Symmetry-Restoration Scenario
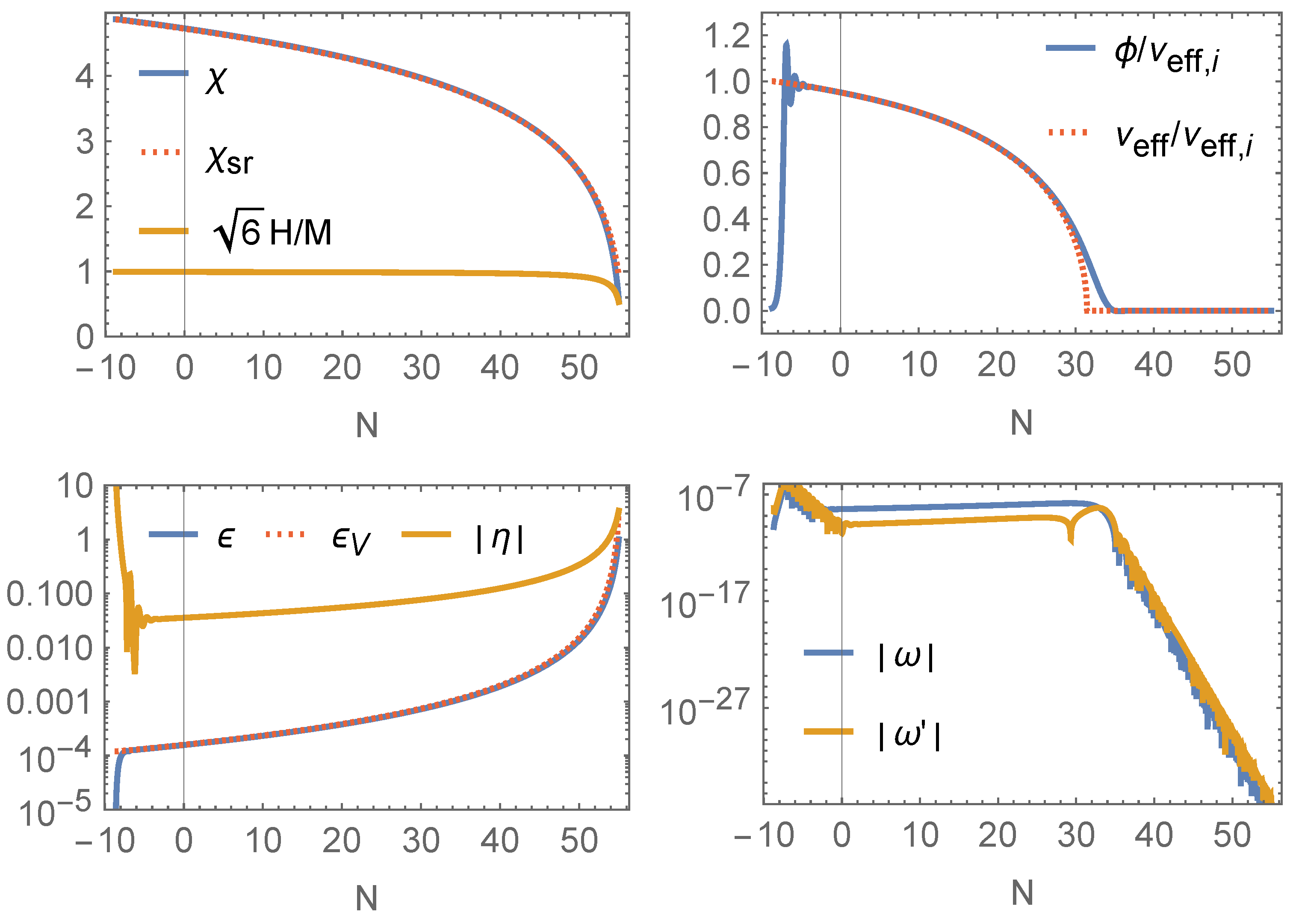
3.2. Symmetry-Breaking Scenario
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
| 1 | It should be mentioned that in such a scenario the suppression of cubic and higher-order curvature terms is not automatic, and it should be explained by the underlying UV physics or by symmetry arguments. |
| 2 | |
| 3 | In the previous section, the dS expansion was driven by a cosmological constant, which we denoted as . In this section, we consider an inflationary quasi-dS background, and, therefore, we replace by an inflationary potential . A small, positive cosmological constant (dark energy) can be included as well, but it is insignificant during inflation, so we ignore it here. |
| 4 | In principle, one can consider different functions for and under suitable conditions for GB-induced symmetry breaking. The condition for the absence of GB backreaction from inflation would be unchanged, and it is given by (35), in terms of the slow-roll parameters. |
| 5 | Alternatively, GW can be generated due to the GB-induced dip in the sound speed, as found in [72]. |
References
- Fernandes, P.G.S.; Carrilho, P.; Clifton, T.; Mulryne, D.J. The 4D Einstein–Gauss–Bonnet theory of gravity: A review. Class. Quant. Grav. 2022, 39, 063001. [Google Scholar] [CrossRef]
- Cartier, C.; Hwang, J.-C.; Copeland, E.J. Evolution of cosmological perturbations in nonsingular string cosmologies. Phys. Rev. D 2001, 64, 103504. [Google Scholar] [CrossRef]
- Guo, Z.-K.; Ohta, N.; Tsujikawa, S. Realizing scale-invariant density perturbations in low-energy effective string theory. Phys. Rev. D 2007, 75, 023520. [Google Scholar] [CrossRef]
- Satoh, M.; Soda, J. Higher Curvature Corrections to Primordial Fluctuations in Slow-roll Inflation. J. Cosmol. Astropart. Phys. 2008, 9, 19. [Google Scholar] [CrossRef]
- Guo, Z.-K.; Schwarz, D.J. Power spectra from an inflaton coupled to the Gauss-Bonnet term. Phys. Rev. D 2009, 80, 063523. [Google Scholar] [CrossRef]
- Guo, Z.-K.; Schwarz, D.J. Slow-roll inflation with a Gauss-Bonnet correction. Phys. Rev. D 2010, 81, 123520. [Google Scholar] [CrossRef]
- Jiang, P.-X.; Hu, J.-W.; Guo, Z.-K. Inflation coupled to a Gauss-Bonnet term. Phys. Rev. D 2013, 88, 123508. [Google Scholar] [CrossRef]
- Koh, S.; Lee, B.-H.; Lee, W.; Tumurtushaa, G. Observational constraints on slow-roll inflation coupled to a Gauss-Bonnet term. Phys. Rev. D 2014, 90, 063527. [Google Scholar] [CrossRef]
- Yi, Z.; Gong, Y.; Sabir, M. Inflation with Gauss-Bonnet coupling. Phys. Rev. D 2018, 98, 083521. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Viable Inflation in Scalar-Gauss-Bonnet Gravity and Reconstruction from Observational Indices. Phys. Rev. D 2018, 98, 044039. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Inflationary Phenomenology of Einstein Gauss-Bonnet Gravity Compatible with GW170817. Phys. Lett. B 2019, 797, 134874. [Google Scholar] [CrossRef]
- Pozdeeva, E.O.; Gangopadhyay, M.R.; Sami, M.; Toporensky, A.V.; Vernov, S.Y. Inflation with a quartic potential in the framework of Einstein-Gauss-Bonnet gravity. Phys. Rev. D 2020, 102, 043525. [Google Scholar] [CrossRef]
- Pozdeeva, E.O.; Skugoreva, M.A.; Toporensky, A.V.; Vernov, S.Y. New slow-roll approximations for inflation in Einstein-Gauss-Bonnet gravity. J. Cosmol. Astropart. Phys. 2024, 9, 50. [Google Scholar] [CrossRef]
- Antoniadis, I.; Rizos, J.; Tamvakis, K. Singularity—Free cosmological solutions of the superstring effective action. Nucl. Phys. B 1994, 415, 497–514. [Google Scholar] [CrossRef]
- Kawai, S.; Sakagami, M.-A.; Soda, J. Instability of one loop superstring cosmology. Phys. Lett. B 1998, 437, 284–290. [Google Scholar] [CrossRef]
- Kawai, S.; Soda, J. Evolution of fluctuations during graceful exit in string cosmology. Phys. Lett. B 1999, 460, 41–46. [Google Scholar] [CrossRef]
- Weinberg, S. Effective Field Theory for Inflation. Phys. Rev. D 2008, 77, 123541. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Sasaki, M. Gauss-Bonnet dark energy. Phys. Rev. D 2005, 71, 123509. [Google Scholar] [CrossRef]
- Calcagni, G.; Tsujikawa, S.; Sami, M. Dark energy and cosmological solutions in second-order string gravity. Class. Quant. Grav. 2005, 22, 3977–4006. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Sami, M. Dark energy cosmology from higher-order, string-inspired gravity and its reconstruction. Phys. Rev. D 2006, 74, 046004. [Google Scholar] [CrossRef]
- Tsujikawa, S.; Sami, M. String-inspired cosmology: Late time transition from scaling matter era to dark energy universe caused by a Gauss-Bonnet coupling. J. Cosmol. Astropart. Phys. 2007, 1, 6. [Google Scholar] [CrossRef]
- Koivisto, T.; Mota, D.F. Gauss-Bonnet Quintessence: Background Evolution, Large Scale Structure and Cosmological Constraints. Phys. Rev. D 2007, 75, 023518. [Google Scholar] [CrossRef]
- Neupane, I.P. On compatibility of string effective action with an accelerating universe. Class. Quant. Grav. 2006, 23, 7493–7520. [Google Scholar] [CrossRef]
- Granda, L.N.; Jimenez, D.F. Dynamical analysis for a scalar–tensor model with Gauss–Bonnet and non-minimal couplings. Eur. Phys. J. C 2017, 77, 679. [Google Scholar] [CrossRef]
- Chatzarakis, N.; Oikonomou, V.K. Autonomous dynamical system of Einstein–Gauss–Bonnet cosmologies. Ann. Phys. 2020, 419, 168216. [Google Scholar] [CrossRef]
- Pozdeeva, E.O.; Sami, M.; Toporensky, A.V.; Vernov, S.Y. Stability analysis of de Sitter solutions in models with the Gauss-Bonnet term. Phys. Rev. D 2019, 100, 083527. [Google Scholar] [CrossRef]
- Vernov, S.; Pozdeeva, E. De Sitter Solutions in Einstein–Gauss–Bonnet Gravity. Universe 2021, 7, 149. [Google Scholar] [CrossRef]
- Kawai, S.; Kim, J. CMB from a Gauss-Bonnet-induced de Sitter fixed point. Phys. Rev. D 2021, 104, 043525. [Google Scholar] [CrossRef]
- Sadjadi, H.M. Scalar-Gauss-Bonnet model, the coincidence problem and the gravitational wave speed. Phys. Lett. B 2024, 850, 138508. [Google Scholar] [CrossRef]
- Pinto, M.A.S.; Rosa, J.A.L. ΛCDM-like evolution in Einstein-scalar-Gauss-Bonnet gravity. arXiv 2024, arXiv:2411.04066. [Google Scholar]
- Linde, A.D. Hybrid inflation. Phys. Rev. D 1994, 49, 748–754. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Bellido, J.; Linde, A.D.; Wands, D. Density perturbations and black hole formation in hybrid inflation. Phys. Rev. D 1996, 54, 6040–6058. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Bellido, J.; Wands, D. The Spectrum of curvature perturbations from hybrid inflation. Phys. Rev. D 1996, 54, 7181–7185. [Google Scholar] [CrossRef] [PubMed]
- Koh, S.; Minamitsuji, M. Non-minimally coupled hybrid inflation. Phys. Rev. D 2011, 83, 046009. [Google Scholar] [CrossRef]
- Bettoni, D.; Rubio, J. Quintessential Affleck-Dine baryogenesis with non-minimal couplings. Phys. Lett. B 2018, 784, 122–129. [Google Scholar] [CrossRef]
- Bettoni, D.; Domènech, G.; Rubio, J. Gravitational waves from global cosmic strings in quintessential inflation. J. Cosmol. Astropart. Phys. 2019, 2, 34. [Google Scholar] [CrossRef]
- Bettoni, D.; Rubio, J. Hubble-induced phase transitions: Walls are not forever. J. Cosmol. Astropart. Phys. 2020, 1, 2. [Google Scholar] [CrossRef]
- Bettoni, D.; Lopez-Eiguren, A.; Rubio, J. Hubble-induced phase transitions on the lattice with applications to Ricci reheating. J. Cosmol. Astropart. Phys. 2022, 1, 2. [Google Scholar] [CrossRef]
- Arapoğlu, A.S.; Yükselci, A.E. The effect of non-minimally coupled scalar field on gravitational waves from first-order vacuum phase transitions. Phys. Dark Univ. 2023, 40, 101176. [Google Scholar] [CrossRef]
- Kierkla, M.; Laverda, G.; Lewicki, M.; Mantziris, A.; Piani, M.; Rubio, J.; Zych, M. From Hubble to Bubble. J. High Energy Phys. 2023, 11, 77. [Google Scholar] [CrossRef]
- Laverda, G.; Rubio, J. Ricci reheating reloaded. J. Cosmol. Astropart. Phys. 2024, 3, 33. [Google Scholar] [CrossRef]
- Sadjadi, H.M. Non-minimally coupled quintessence in the Gauss-Bonnet model, symmetry breaking, and cosmic acceleration. arXiv 2023, arXiv:2310.03697. [Google Scholar]
- Aldabergenov, Y.; Ding, D.; Lin, W.; Wan, Y. Meso-inflationary Peccei–Quinn Symmetry Breaking with Nonminimal Coupling. Astrophys. J. Suppl. 2024, 275, 14. [Google Scholar] [CrossRef]
- Bettoni, D.; Laverda, G.; Eiguren, A.L.; Rubio, J. Hubble-Induced Phase Transitions: Gravitational-Wave Imprint of Ricci Reheating from Lattice Simulations. arXiv 2024, arXiv:2409.15450. [Google Scholar] [CrossRef]
- Berera, A. Warm inflation. Phys. Rev. Lett. 1995, 75, 3218–3221. [Google Scholar] [CrossRef]
- Rosa, J.A.G.; Ventura, L.B. Spontaneous breaking of the Peccei-Quinn symmetry during warm inflation. arXiv 2021, arXiv:2105.05771. [Google Scholar]
- An, H.; Tong, X.; Zhou, S. Superheavy dark matter production from a symmetry-restoring first-order phase transition during inflation. Phys. Rev. D 2023, 107, 023522. [Google Scholar] [CrossRef]
- Goolsby-Cole, C.; Sorbo, L. Nonperturbative production of massless scalars during inflation and generation of gravitational waves. J. Cosmol. Astropart. Phys. 2017, 8, 5. [Google Scholar] [CrossRef]
- An, H.; Lyu, K.-F.; Wang, L.-T.; Zhou, S. Gravitational waves from an inflation triggered first-order phase transition. J. High Energy Phys. 2022, 6, 50. [Google Scholar] [CrossRef]
- Barir, J.; Geller, M.; Sun, C.; Volansky, T. Gravitational waves from incomplete inflationary phase transitions. Phys. Rev. D 2023, 108, 115016. [Google Scholar] [CrossRef]
- An, H.; Su, B.; Tai, H.; Wang, L.-T.; Yang, C. Phase transition during inflation and the gravitational wave signal at pulsar timing arrays. Phys. Rev. D 2024, 109, L121304. [Google Scholar] [CrossRef]
- An, H.; Chen, Q.; Li, Y.; Yin, Y. Large non-Gaussianities corresponding to first-order phase transitions during inflation. arXiv 2024, arXiv:2411.12699. [Google Scholar]
- Garcia-Bellido, J.; Morales, E.R. Particle production from symmetry breaking after inflation. Phys. Lett. B 2002, 536, 193–202. [Google Scholar] [CrossRef]
- Pearce, L.; Yang, L.; Kusenko, A.; Peloso, M. Leptogenesis via neutrino production during Higgs condensate relaxation. Phys. Rev. D 2015, 92, 023509. [Google Scholar] [CrossRef]
- Yang, L.; Pearce, L.; Kusenko, A. Leptogenesis via Higgs Condensate Relaxation. Phys. Rev. D 2015, 92, 043506. [Google Scholar] [CrossRef]
- Graham, P.W.; Kaplan, D.E.; Rajendran, S. Cosmological Relaxation of the Electroweak Scale. Phys. Rev. Lett. 2015, 115, 221801. [Google Scholar] [CrossRef]
- He, M.; Jinno, R.; Kamada, K.; Park, S.C.; Starobinsky, A.A.; Yokoyama, J. On the violent preheating in the mixed Higgs-R2 inflationary model. Phys. Lett. B 2019, 791, 36–42. [Google Scholar] [CrossRef]
- Kumar, S.; Sundrum, R. Heavy-Lifting of Gauge Theories By Cosmic Inflation. J. High Energy Phys. 2018, 5, 11. [Google Scholar] [CrossRef]
- Wu, Y.-P. Higgs as heavy-lifted physics during inflation. J. High Energy Phys. 2019, 4, 125. [Google Scholar] [CrossRef]
- Opferkuch, T.; Schwaller, P.; Stefanek, B.A. Ricci Reheating. J. Cosmol. Astropart. Phys. 2019, 7, 16. [Google Scholar] [CrossRef]
- Wu, Y.-P.; Yang, L.; Kusenko, A. Leptogenesis from spontaneous symmetry breaking during inflation. J. High Energy Phys. 2019, 12, 88. [Google Scholar] [CrossRef]
- Liang, Q.; Sakstein, J.; Trodden, M. Baryogenesis via gravitational spontaneous symmetry breaking. Phys. Rev. D 2019, 100, 063518. [Google Scholar] [CrossRef]
- Sadjadi, H.M. Early dark energy and scalarization in a scalar-tensor model. Phys. Lett. B 2024, 857, 138967. [Google Scholar] [CrossRef]
- Akrami, Y. et al. [Planck Collaboration]. Planck 2018 results. X. Constraints on inflation. Astron. Astrophys. 2020, 641, A10. [Google Scholar] [CrossRef]
- Linde, A.D. Generation of Isothermal Density Perturbations in the Inflationary Universe. Phys. Lett. B 1985, 158, 375–380. [Google Scholar] [CrossRef]
- Starobinsky, A.A.; Yokoyama, J. Equilibrium state of a selfinteracting scalar field in the De Sitter background. Phys. Rev. D 1994, 50, 6357–6368. [Google Scholar] [CrossRef]
- Kawai, S.; Kim, J. Primordial black holes from Gauss-Bonnet-corrected single field inflation. Phys. Rev. D 2021, 104, 083545. [Google Scholar] [CrossRef]
- Kawaguchi, R.; Tsujikawa, S. Primordial black holes from Higgs inflation with a Gauss-Bonnet coupling. Phys. Rev. D 2023, 107, 063508. [Google Scholar] [CrossRef]
- Ashrafzadeh, A.; Karami, K. Primordial Black Holes in Scalar Field Inflation Coupled to the Gauss–Bonnet Term with Fractional Power-law Potentials. Astrophys. J. 2024, 965, 11. [Google Scholar] [CrossRef]
- Solbi, M.; Karami, K. Primordial black holes in non-minimal Gauss–Bonnet inflation in light of the PTA data. Eur. Phys. J. C 2024, 84, 918. [Google Scholar] [CrossRef]
- Addazi, A.; Aldabergenov, Y.; Cai, Y. Sound speed resonance of gravitational waves in Gauss-Bonnet-coupled inflation. Phys. Rev. D 2024, 110, 123530. [Google Scholar] [CrossRef]
- Kawai, S.; Kim, J. Probing the inflationary moduli space with gravitational waves. Phys. Rev. D 2023, 108, 103537. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aldabergenov, Y.; Berkimbayev, D. Gauss–Bonnet-Induced Symmetry Breaking/Restoration During Inflation. Universe 2025, 11, 98. https://doi.org/10.3390/universe11030098
Aldabergenov Y, Berkimbayev D. Gauss–Bonnet-Induced Symmetry Breaking/Restoration During Inflation. Universe. 2025; 11(3):98. https://doi.org/10.3390/universe11030098
Chicago/Turabian StyleAldabergenov, Yermek, and Daulet Berkimbayev. 2025. "Gauss–Bonnet-Induced Symmetry Breaking/Restoration During Inflation" Universe 11, no. 3: 98. https://doi.org/10.3390/universe11030098
APA StyleAldabergenov, Y., & Berkimbayev, D. (2025). Gauss–Bonnet-Induced Symmetry Breaking/Restoration During Inflation. Universe, 11(3), 98. https://doi.org/10.3390/universe11030098