Starobinsky Inflation with T-Model Kähler Geometries
Abstract
1. Introduction
- Wess–Zumino models with a matter-like inflaton [19,20,21,22,23,24]. Polynomial superpotentials, W—of the Wess–Zumino form [11]—are adopted in this class of models and the Kähler potentials K parameterize specific Kähler manifolds of the form , inspired by the no-scale models [25,26] of SUSY breaking. The stabilization of the inflaton-accompanying modulus at a Planck-scale value [20] is achieved by a deformation of the internal geometry.
- Ceccoti-like [27] models with a modulus-like inflaton [20,28,29,30,31,32,33,34,35,36,37]. Similar K’s are used here whereas W is linear [38] with respect to the matter-like inflaton-accompanying field which may be stabilized at the origin via several mechanisms [6,10,35,39,40,41,42,43]. In a subclass of these models [31,32,33,34,36,37], the conjecture of induced gravity [44,45] is incorporated leading to a dynamical generation of the reduced Planck scale, through the vacuum expectation value (v.e.v) of the inflaton at the end of its evolution.
- Models which exhibit a pole [51,52,53,54,55] of order one in the kinetic term of the inflaton [56,57,58]. As in every SI model, the inflationary potential develops one shoulder for large values, where is the canonically normalized inflaton which can be expressed in terms of the original field as [58]The presence of the real positive variable N—aligned to the conventions of ref. [58]—leads to a generalized version of SI called -SI [20] or E-Model inflation. This model can be contrasted with the T-Model inflation [59,60] which arises thanks to a pole of order two in the inflaton kinetic term and features a potential with two symmetric plateaus away from the origin. Namely, the relation assumes the formIndependently of their particularities, both models share [8] common predictions for the inflationary observables and for this reason they are called collectively -attractors [5,61,62,63].
2. SUGRA Framework
2.1. General Setup
2.2. Guidelines
2.2.1. Achieving D-Flatness
- If the inflaton is (the radial part of) a gauge-singlet superfield . In this case, has obviously zero contribution to .
- If the inflaton is the radial part of a conjugate pair of Higgs superfields, and , in the fundamental representation of . In such a case (see Section 4.3 below) we obtain . The same result can be obtained if is more structured than employing just one superfield in the adjoint representation of and using as inflaton its neutral component (see e.g., ref. [85]).
2.2.2. Selecting the Suitable W
- It assists in determining W. To achieve it, we require that S appears linearly in W and so both are equally charged under a global R symmetry.
- It can be stabilized at without invoking higher order terms, if we select [35]The index 2 stems from the fact that parameterizes the compact manifold [35]. Note that for , S is canonically normalized and so we do not care about its kinetic normalization henceforth. For other stabilization methods of S see refs. [6,39,40,41,42,43].
- It assures the boundedness of . Indeed, if we set , then for , and . Obviously, non-vanishing values of the last term may render unbounded from below.
- It generates for and for monomial W the numerator of in Equation (3) via the only term of which remains “alive”. Indeed, we obtainAssuming that no mixing terms between S and the inflaton exist in K, we obtain , and so the numerator of in Equation (3) emerges if W has the formgiven that the assumption yields mostly stable configuration; here, we focus on a gauge-singlet . On the other hand, the denominator of in Equation (3) may be generated via the exponential prefactor in Equation (6) through logarithmic contributions to K, as we explain below.
2.2.3. Selecting the Convenient Kähler Potential
- It has to generate the desired relation in Equation (2). Therefore, we need to introduce a contribution into K including and in the same function. After inspection (see Appendix of ref. [86]) we infer that a pole of order two in the kinetic term of inflaton is achieved if whereHere, and the subscript “T” indicates that this part of the total K is responsible for the T-model Kähler metric (see Equation (4b)). However, from Equation (6), we remark that K affects—in addition to the kinetic mixing— via the prefactor . Therefore, is generically expected to emerge also in the denominator of making difficult the establishment of an inflationary era. This problem can be surpassed [58,66] by two alternative strategies:
- −
- −
- Replacing with so that the desired kinetic terms in Equation (4a) remain unaltered and, simultaneously [56,58,66]In other words, the symmetry of is augmented by some shift symmetry (see Appendix A) without disturbing in Equation (4b). To accomplish this, includes holomorphic and anti-holomorphic terms which yield vanishing contribution to the mixed derivatives of . Taking into account the form of in Equation (8), we may select formallyNote that the same construction is valid even in case of polynomial K’s if we check the structure of the relevant K’s in refs. [70,74,75,76,77,78,79].
3. Gauge-Singlet Inflaton
3.1. Setup
3.2. Canonical Normalization
3.3. Inflationary Potential
4. Gauge Non-Singlet Inflaton
4.1. Setup
4.2. Canonical Normalization
4.3. Inflationary Potential
4.4. Phase Transition
5. Inflation Analysis
5.1. Analytic Results
5.2. Numerical Results
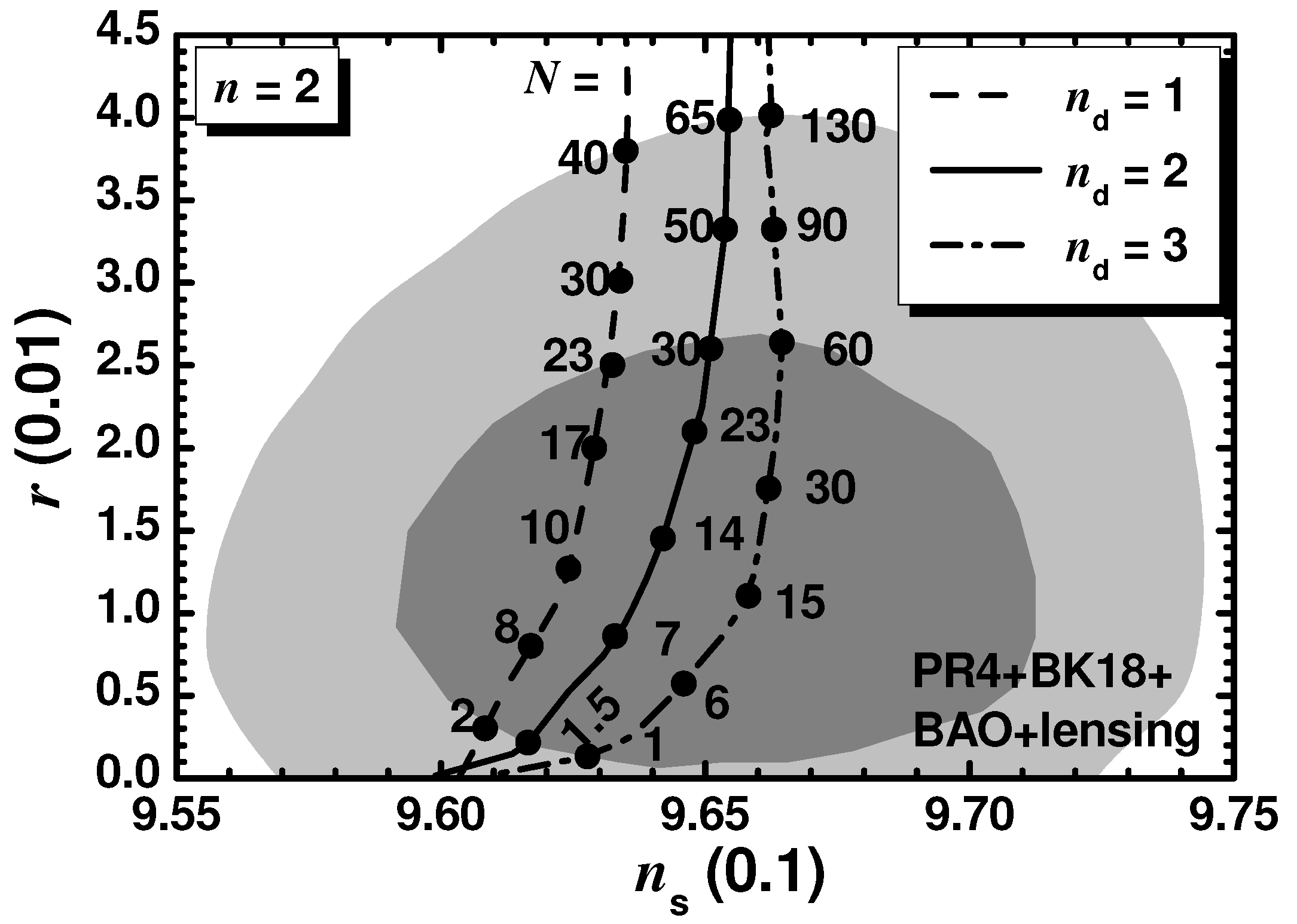
5.2.1. SI with a Gauge-Singlet Inflaton (CSI)
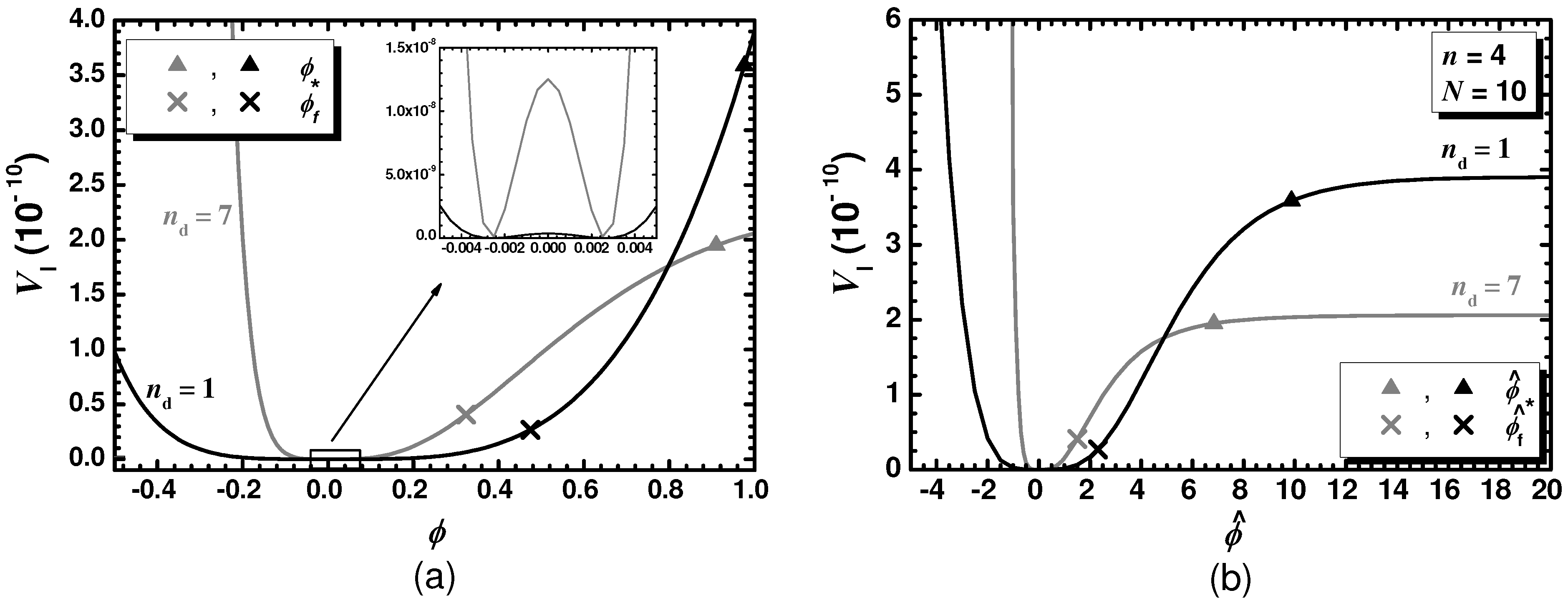
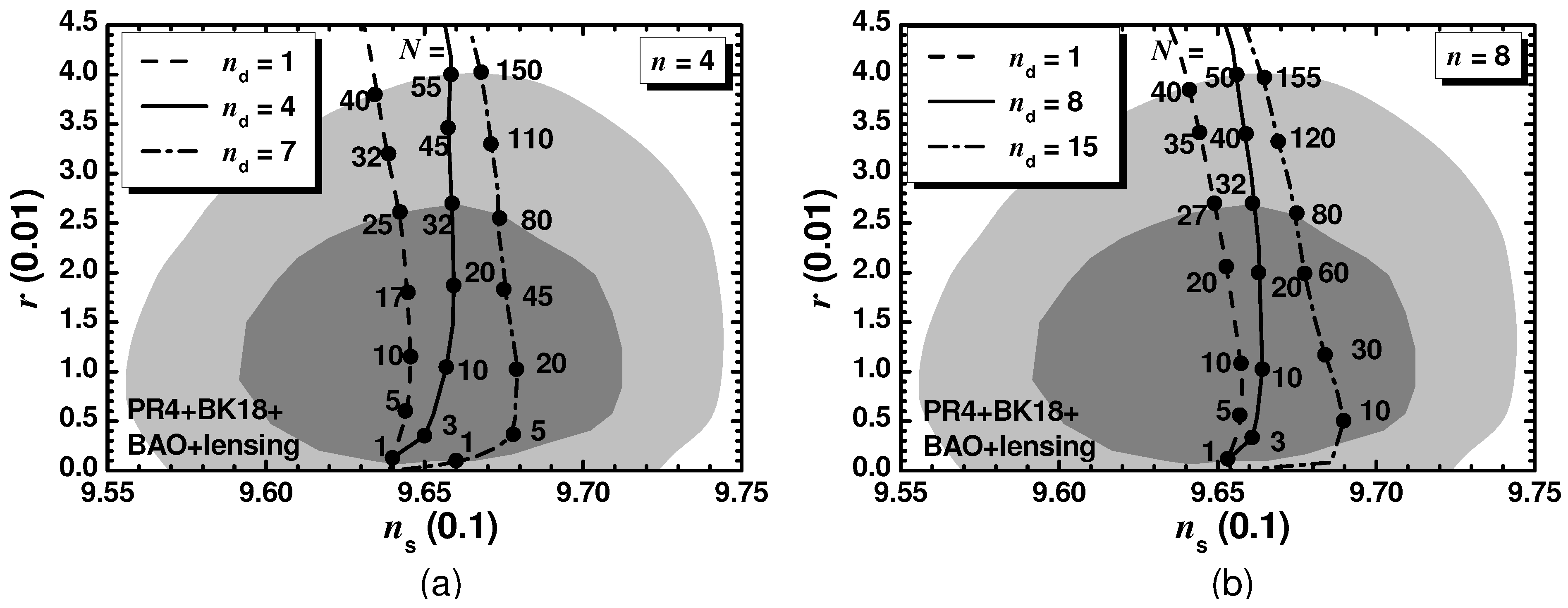
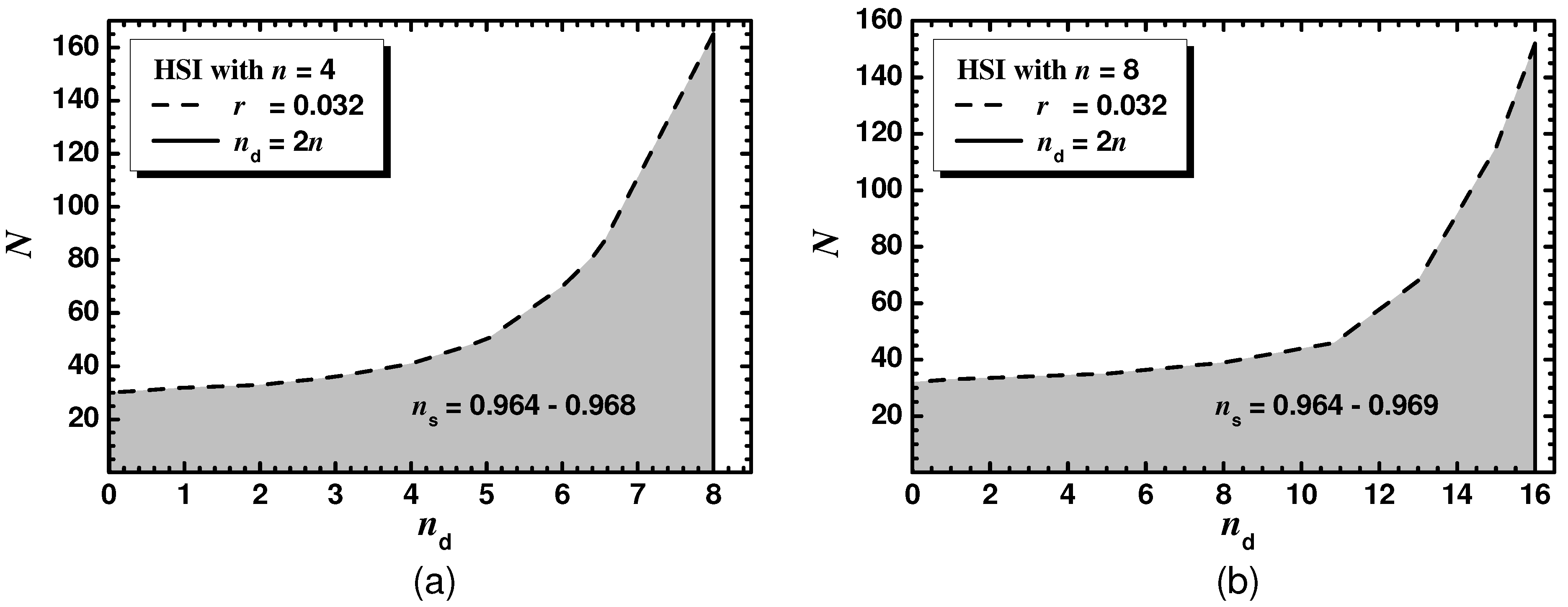
5.2.2. SI with a Higgs Field (HSI)
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Shift Symmetry & Hyperbolic Kähler Geometries
Appendix A.1. Shift Symmetry for CSI
Appendix A.2. Shift Symmetry for HSI
Appendix A.2.1. Kähler Manifold
Appendix A.2.2. Kähler Manifold
References
- Starobinsky, A.A. A New Type of Isotropic Cosmological Models Without Singularity. Phys. Lett. B 1980, 91, 99–102. [Google Scholar] [CrossRef]
- Martin, J.; Ringeval, C.; Vennin, V. Encyclopædia Inflationaris. Phys. Dark Univ. 2014, 5, 75. [Google Scholar] [CrossRef]
- Martin, J.; Ringeval, C.; Trotta, R.; Vennin, V. The Best Inflationary Models After Planck. J. Cosmol. Astropart. Phys. 2014, 03, 39. [Google Scholar] [CrossRef]
- Grøn, Ø. Predictions of Spectral Parameters by Several Inflationary Universe Models in Light of the Planck Results. Universe 2018, 4, 15. [Google Scholar] [CrossRef]
- Akrami, Y. et al. [Planck Collaboration] Planck 2018 results. X. Constraints on inflation. Astron. Astrophys. 2020, 641, A10. [Google Scholar]
- Kounnas, C.; Lüst, D.; Toumbas, N. R2 inflation from scale invariant supergravity and anomaly free superstrings with fluxes. Fortsch. Phys. 2015, 63, 12. [Google Scholar] [CrossRef]
- Galante, M.; Kallosh, R.; Linde, A.; Roest, D. Unity of Cosmological Inflation Attractors. Phys. Rev. Lett. 2015, 114, 141302. [Google Scholar] [CrossRef]
- Ellis, J.; Nanopoulos, D.V.; Olive, K.A.; Verner, S. A general classification of Starobinsky-like inflationary avatars of SU(2, 1)/SU(2) × U(1) no-scale supergravity. J. High Energy Phys. 2019, 3, 099. [Google Scholar] [CrossRef]
- Ellis, J.; Garcia, M.A.G.; Nagata, N.; Nanopoulos, D.V.; Olive, K.A.; Verner, S. Building Models of Inflation in No-Scale Supergravity. Int. J. Mod. Phys. D 2020, 16, 2030011. [Google Scholar] [CrossRef]
- Pallis, C.; Toumbas, N. Starobinsky Inflation: From Non-SUSY To SUGRA Realizations. Adv. High Energy Phys. 2017, 2017, 6759267. [Google Scholar] [CrossRef]
- Binétruy, P. Supersymmetry: Theory, Experiment and Cosmology; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Navas, S. et al. [Particle Data Group] Review of particle physics. Phys. Rev. D 2024, 110, 030001. [Google Scholar] [CrossRef]
- Wang, F.; Wang, W.; Yang, J.; Zhang, Y.; Zhu, B. Low Energy Supersymmetry Confronted with Current Experiments: An Overview. Universe 2022, 8, 178. [Google Scholar] [CrossRef]
- Buchmüller, W.; Domcke, V.; Kamada, K. The Starobinsky Model from Superconformal D-Term Inflation. Phys. Lett. B 2013, 726, 467. [Google Scholar] [CrossRef]
- Basilakos, S.; Mavromatos, N.E.; Sola, J. Starobinsky-like inflation and running vacuum in the context of Supergravity. Universe 2016, 2, 14. [Google Scholar] [CrossRef]
- Ketov, S.V.; Starobinsky, A.A. Embedding (R + R2)-Inflation into Supergravity. Phys. Rev. D 2011, 83, 063512. [Google Scholar] [CrossRef]
- Blumenhagen, R.; Font, A.; Fuchs, M.; Herschmann, D.; Plauschinn, E. Towards axionic Starobinsky-like inflation in string theory. Phys. Lett. B 2015, 746, 217. [Google Scholar] [CrossRef]
- Li, T.; Li, Z.; Nanopoulos, D.V. Helical phase inflation via non-geometric flux compactifications: From natural to Starobinsky-like inflation. J. High Energy Phys. 2015, 10, 138. [Google Scholar] [CrossRef]
- Ellis, J.; Nanopoulos, D.V.; Olive, K.A. No-Scale Supergravity Realization of the Starobinsky Model of Inflation. Phys. Rev. Lett. 2013, 111, 111301, Erratum in Phys. Rev. Lett. 2013, 111, 129902. [Google Scholar] [CrossRef]
- Ellis, J.; Nanopoulos, D.V.; Olive, K. Starobinsky-like Inflationary Models as Avatars of No-Scale Supergravity. J. Cosmol. Astropart. Phys. 2013, 10, 009. [Google Scholar] [CrossRef]
- Ellis, J.; He, H.-J.; Xianyu, Z.-Z. New Higgs inflation in a no-scale supersymmetric SU(5) GUT. Phys. Rev. D 2015, 91, 021302. [Google Scholar] [CrossRef]
- Garg, I.; Mohanty, S. No-scale SUGRA SO(10) derived Starobinsky model of inflation. Phys. Lett. B 2015, 751, 7. [Google Scholar] [CrossRef][Green Version]
- Ellis, J.; Garcia, M.A.G.; Nagata, N.; Nanopoulos, D.V.; Olive, K.A. Starobinsky-like Inflation, Supercosmology and Neutrino Masses in No-Scale Flipped SU(5). J. Cosmol. Astropart. Phys. 2017, 7, 006. [Google Scholar] [CrossRef]
- Ellis, J.; Garcia, M.A.G.; Nagata, N.; Nanopoulos, D.V.; Olive, K.A. Starobinsky-Like Inflation and Neutrino Masses in a No-Scale SO(10) Model. J. Cosmol. Astropart. Phys. 2016, 11, 018. [Google Scholar] [CrossRef]
- Cremmer, E.; Ferrara, S.; Kounnas, C.; Nanopoulos, D.V. Naturally Vanishing Cosmological Constant in N = 1 Supergravity. Phys. Lett. B 1983, 133, 61. [Google Scholar] [CrossRef]
- Lahanas, A.B.; Nanopoulos, D.V. The Road to No-Scale Supergravity. Phys. Rept. 1987, 145, 198. [Google Scholar] [CrossRef]
- Cecotti, S. Higher Derivative Supergravity Is Equivalent To Standard Supergravity Coupled To Matter. Phys. Lett. B 1987, 190, 86. [Google Scholar] [CrossRef]
- Farakos, F.; Kehagias, A.; Riotto, A. On the Starobinsky Model of Inflation from Supergravity. Nucl. Phys. 2013, B876, 187. [Google Scholar] [CrossRef]
- Kallosh, R.; Linde, A. Superconformal generalizations of the Starobinsky model. J. Cosmol. Astropart. Phys. 2013, 6, 28. [Google Scholar] [CrossRef]
- Lahanas, A.B.; Tamvakis, K. Inflation in no-scale supergravity. Phys. Rev. D 2015, 91, 085001. [Google Scholar] [CrossRef]
- Pallis, C. Linking Starobinsky-Type Inflation in no-Scale Supergravity to MSSM. J. Cosmol. Astropart. Phys. 2014, 4, 024, Erratum in J. Cosmol. Astropart. Phys. 2017, 7, 01(E). [Google Scholar] [CrossRef]
- Pallis, C. Induced-Gravity Inflation in no-Scale Supergravity and Beyond. J. Cosmol. Astropart. Phys. 2014, 08, 057. [Google Scholar] [CrossRef]
- Pallis, C. Reconciling induced-gravity inflation in supergravity with the Planck 2013 & BICEP2 results. J. Cosmol. Astropart. Phys. 2014, 10, 58. [Google Scholar]
- Kallosh, R. More on Universal Superconformal Attractors. Phys. Rev. D 2014, 89, 087703. [Google Scholar] [CrossRef]
- Pallis, C.; Toumbas, N. Starobinsky-Type Inflation with Products of Kähler Manifolds. J. Cosmol. Astropart. Phys. 2016, 5, 15. [Google Scholar] [CrossRef]
- Pallis, C.; Shafi, Q. Induced-Gravity GUT-Scale Higgs Inflation in Supergravity. Eur. Phys. J. C 2018, 78, 523. [Google Scholar] [CrossRef]
- Pallis, C. Starobinsky-Type B–L Higgs Inflation Leading Beyond MSSM. arXiv 2023, arXiv:2305.00523. [Google Scholar]
- Kallosh, R.; Linde, A.; Rube, T. General inflaton potentials in supergravity. Phys. Rev. D 2011, 83, 043507. [Google Scholar] [CrossRef]
- Lee, H.M. Chaotic inflation in Jordan frame supergravity. J. Cosmol. Astropart. Phys. 2010, 08, 003. [Google Scholar] [CrossRef]
- Antoniadis, I.; Dudas, E.; Ferrara, S.; Sagnotti, A. The Volkov—Akulov—Starobinsky Supergravity. Phys. Lett. B 2014, 733, 32. [Google Scholar] [CrossRef]
- Aldabergenov, Y. Volkov–Akulov–Starobinsky supergravity revisited. Eur. Phys. J. C 2020, 80, 329. [Google Scholar] [CrossRef]
- Ferrara, S.; Kallosh, R.; Linde, A. Cosmology with Nilpotent Superfields. J. High Energy Phys. 2014, 10, 143. [Google Scholar] [CrossRef]
- Antoniadis, I.; Nanopoulos, D.V.; Olive, K.A. R2–Inflation Derived from 4d Strings, the Role of the Dilaton, and Turning the Swampland into a Mirage. arXiv 2024, arXiv:2410.16541. [Google Scholar]
- Zee, A. A Broken Symmetric Theory of Gravity. Phys. Rev. Lett. 1979, 42, 417. [Google Scholar] [CrossRef]
- Giudice, G.F.; Lee, H.M. Starobinsky-like inflation from induced gravity. Phys. Lett. B 2014, 733, 58. [Google Scholar] [CrossRef]
- Pallis, C.; Shafi, Q. Non-minimal chaotic inflation, Peccei-Quinn phase transition and non-thermal leptogenesis. Phys. Rev. D 2012, 86, 023523. [Google Scholar] [CrossRef]
- Pallis, C.; Shafi, Q. Gravity Waves From Non-Minimal Quadratic Inflation. J. Cosmol. Astropart. Phys. 2015, 3, 23. [Google Scholar] [CrossRef]
- Pallis, C. Unitarity-Safe Models of Non-Minimal Inflation in Supergravity. Eur. Phys. J. C 2018, 78, 1014. [Google Scholar] [CrossRef]
- Pallis, C. Unitarizing non-Minimal Inflation via a Linear Contribution to the Frame Function. Phys. Lett. B 2019, 789, 243. [Google Scholar] [CrossRef]
- Kehagias, A.; Dizgah, A.M.; Riotto, A. Remarks on the Starobinsky model of in ation and its descendants. Phys. Rev. D 2014, 89, 043527. [Google Scholar] [CrossRef]
- Terada, T. Generalized Pole Inflation: Hilltop, Natural, and Chaotic Inflationary Attractors. Phys. Lett. B 2016, 760, 674. [Google Scholar] [CrossRef]
- Broy, B.J.; Galante, M.; Roest, D.; Westphal, A. Pole inflation, Shift symmetry and universal corrections. J. High Energy Phys. 2015, 12, 149. [Google Scholar] [CrossRef]
- Kobayashi, T.; Seto, O.; Tatsuishi, T.H. Toward pole inflation and attractors in supergravity: Chiral matter field inflation. Prog. Theor. Phys. 2017, 2017, 123B04. [Google Scholar] [CrossRef]
- Pallis, C. Pole Inflation in Supergravity. PoS CORFU 2022, 2021, 78. [Google Scholar]
- Karamitsos, S.; Strumia, A. Pole inflation from non-minimal coupling to gravity. J. High Energy Phys. 2022, 2022, 16. [Google Scholar] [CrossRef]
- Carrasco, J.J.M.; Kallosh, R.; Linde, A.; Roest, D. Hyperbolic geometry of cosmological attractors. Phys. Rev. D 2015, 92, 041301. [Google Scholar] [CrossRef]
- Carrasco, J.J.M.; Kallosh, R.; Linde, A. α-Attractors: Planck, LHC and Dark Energy. J. High Energy Phys. 2015, 10, 147. [Google Scholar] [CrossRef]
- Pallis, C. An Alternative Framework for E-Model Inflation in Supergravity. Eur. Phys. J. C 2022, 82, 444. [Google Scholar] [CrossRef]
- Kallosh, R.; Linde, A.; Roest, D. Superconformal Inflationary a-Attractors. J. High Energy Phys. 2013, 11, 198. [Google Scholar] [CrossRef]
- Kallosh, R.; Linde, A. Universality Class in Conformal Inflation. J. Cosmol. Astropart. Phys. 2013, 2013, 002. [Google Scholar] [CrossRef]
- Kallosh, R.; Linde, A. BICEP/Keck and cosmological attractors. J. Cosmol. Astropart. Phys. 2021, 2021, 1–13. [Google Scholar] [CrossRef]
- Ellis, J.; Garcia, M.A.G.; Nanopoulos, D.V.; Olive, K.A.; Verner, S. BICEP/Keck constraints on attractor models of inflation and reheating. Phys. Rev. D 2022, 105, 043504. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Dutta, K.; Gangopadhyay, M.R.; Maharana, A. α-attractor inflation: Models and predictions. Phys. Rev. D 2023, 107, 103530. [Google Scholar] [CrossRef]
- Dimopoulos, K. Introduction to Cosmic Inflation and Dark Energy; CRC Press: Boca Raton, FL, USA, 2020; ISBN 978-0-367-61104-0. [Google Scholar]
- Ellis, J.; Nanopoulos, D.V.; Olive, K.A.; Verner, S. Unified No-Scale Attractors. J. Cosmol. Astropart. Phys. 2019, 9, 40. [Google Scholar] [CrossRef]
- Pallis, C. Pole-induced Higgs inflation with hyperbolic Kähler geometries. J. Cosmol. Astropart. Phys. 2021, 5, 43. [Google Scholar] [CrossRef]
- Pallis, C. SU(2, 1)/(SU(2) × U(1)) B-L Higgs Inflation. J. Phys. Conf. Ser. 2021, 2105, 12. [Google Scholar] [CrossRef]
- Pallis, C. T-Model Higgs Inflation in Supergravity. arXiv 2023, arXiv:2307.14652. [Google Scholar]
- Hooft, G. Naturalness, chiral symmetry, and spontaneous chiral symmetry breaking. NATO Sci. Ser. B 1980, 59, 135. [Google Scholar]
- Kawasaki, M.; Yamaguchi, M.; Yanagida, T. Natural chaotic inflation in supergravity. Phys. Rev. Lett. 2000, 85, 3572. [Google Scholar] [CrossRef]
- Brax, P.; Martin, J. Shift symmetry and inflation in supergravity. Phys. Rev. D 2005, 72, 023518. [Google Scholar] [CrossRef]
- Antusch, S.; Dutta, K.; Kostka, P.M. SUGRA Hybrid Inflation with Shift Symmetry. Phys. Lett. B 2009, 677, 221. [Google Scholar] [CrossRef]
- Li, T.; Li, Z.; Nanopoulos, D.V. Supergravity Inflation with Broken Shift Symmetry and Large Tensor-to-Scalar Ratio. J. Cosmol. Astropart. Phys. 2014, 2, 028. [Google Scholar] [CrossRef]
- Pallis, C. Kinetically modified nonminimal chaotic inflation. Phys. Rev. D 2015, 91, 123508. [Google Scholar] [CrossRef]
- Pallis, C. Kinetically Modified Non-Minimal Inflation with Exponential Frame Function. Eur. Phys. J. C 2017, 77, 633. [Google Scholar] [CrossRef]
- Ben-Dayan, I.; Einhorn, M.B. Supergravity Higgs Inflation and Shift Symmetry in Electroweak Theory. J. Cosmol. Astropart. Phys. 2010, 12, 002. [Google Scholar] [CrossRef]
- Lazarides, G.; Pallis, C. Shift Symmetry and Higgs Inflation in Supergravity with Observable Gravitational Waves. J. High Energy Phys. 2015, 11, 114. [Google Scholar] [CrossRef]
- Pallis, C. Kinetically modified nonminimal Higgs inflation in supergravity. Phys. Rev. D 2015, 92, 121305. [Google Scholar] [CrossRef]
- Pallis, C. Variants of Kinetically Modified Non-Minimal Higgs Inflation in Supergravity. J. Cosmol. Astropart. Phys. 2016, 10, 37. [Google Scholar] [CrossRef]
- Kallosh, R.; Linde, A.; Roest, D.; Wrase, T. Sneutrino inflation with α-attractors. J. Cosmol. Astropart. Phys. 2016, 11, 046. [Google Scholar] [CrossRef][Green Version]
- Gonzalo, T.E.; Heurtier, L.; Moursy, A. Sneutrino driven GUT Inflation in Supergravity. J. High Energy Phys. 2017, 6, 109. [Google Scholar] [CrossRef][Green Version]
- Kaneta, K.; Mambrini, Y.; Olive, K.A.; Verner, S. Inflation and Leptogenesis in High-Scale Supersymmetry. Phys. Rev. D 2020, 101, 015002. [Google Scholar] [CrossRef]
- Ellis, J.; Garcia, M.A.G.; Nanopoulos, D.V.; Olive, K.A. Phenomenological aspects of no-scale inflation models. J. Cosmol. Astropart. Phys. 2015, 10, 3. [Google Scholar] [CrossRef]
- Ema, Y.; Garcia, M.A.G.; Ke, W.; Olive, K.A.; Verner, S. Inflaton Decay in No-Scale Supergravity and Starobinsky-like Models. Universe 2024, 10, 239. [Google Scholar] [CrossRef]
- Pallis, C. T-Model Higgs Inflation and Metastable Cosmic Strings. J. High Energy Phys. 2025, 1, 178. [Google Scholar] [CrossRef]
- Pallis, C. E- and T-model hybrid inflation. Eur. Phys. J. C 2023, 83, 2. [Google Scholar] [CrossRef]
- Aghanim, N. et al. [Planck Collaboration] Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6, Erratum in Astron. Astrophys. 2021, 652, C4. [Google Scholar]
- Martin, J.; Ringeval, C. First CMB Constraints on the Inflationary Reheating Temperature. Phys. Rev. D 2010, 82, 023511. [Google Scholar] [CrossRef]
- Ellis, J.; Garcia, M.A.G.; Nanopoulos, D.V.; Olive, K.A. Calculations of Inflaton Decays and Reheating: With Applications to No-Scale Inflation Models. J. Cosmol. Astropart. Phys. 2015, 7, 50. [Google Scholar] [CrossRef]
- Lin, C.M. On the oscillations of the inflaton field of the simplest α-attractor T-model. Chin. J. Phys. 2023, 86, 323. [Google Scholar] [CrossRef]
- Turner, M.S. Coherent Scalar-Field Oscillations in an Expanding Universe. Phys. Rev. D 1983, 28, 1243. [Google Scholar] [CrossRef]
- Tristram, M.; Banday, M.J.; Górski, K.M.; Keskitalo, R.; Lawrence, C.R.; Andersen, K.J.; Barreiro, R.B.; Borrill, J.; Colombo, L.P.L.; Eriksen, H.K.; et al. Improved limits on the tensor-to-scalar ratio using BICEP and Planck. Phys. Rev. Lett. 2021, 127, 151301. [Google Scholar] [CrossRef]
- Ade, P.A.R. et al. [BICEP and Keck Collaboration] Improved Constraints on Primordial Gravitational Waves using Planck, WMAP, and BICEP/Keck Observations through the 2018 Observing Season. Phys. Rev. Lett. 2021, 127, 151301. [Google Scholar] [CrossRef] [PubMed]
- Abazajian, K.; Addison, G.E.; Adshead, P.; Ahmed, Z.; Allen, S.W.; Alonso, D.; Alvarez, M.; Anderson, A.; Arnold, K.S.; Baccigalupi, C.; et al. CMB-S4 Science Case, Reference Design, and Project Plan. arXiv 2019, arXiv:1907.04473. [Google Scholar]
- Andre, P. et al. [PRISM Collaboration] PRISM (Polarized Radiation Imaging and Spectroscopy Mission): A White Paper on the Ultimate Polarimetric Spectro-Imaging of the Microwave and Far-Infrared Sky. arXiv 2013, arXiv:1306.2259. [Google Scholar]
- Montier, L. et al. [LiteBIRD Collaboration] Overview of the Medium and High Frequency Telescopes of the LiteBIRD satellite mission. Proc. SPIE Int. Soc. Opt. Eng. 2020, 11443, 114432G. [Google Scholar]
- Baumann, D. et al. [CMBPol Study Team Collaboration] CMBPol Mission Concept Study: Probing Inflation with CMB Polarization. AIP Conf. Proc. 2009, 1141, 10. [Google Scholar]
- Kallosh, R.; Linde, A. Polynomial α-attractors. J. Cosmol. Astropart. Phys. 2022, 4, 17. [Google Scholar] [CrossRef]
- Bauer, F.; Demir, D.A. Higgs-Palatini Inflation and Unitarity. Phys. Lett. B 2011, 698, 425. [Google Scholar] [CrossRef]
- Enckell, V.M.; Enqvist, K.; Rasanen, S.; Wahlman, L.P. Inflation with R2 term in the Palatini formalism. J. Cosmol. Astropart. Phys. 2019, 2, 22. [Google Scholar] [CrossRef]
- Antoniadis, I.; Karam, A.; Lykkas, A.; Tamvakis, K. Palatini inflation in models with an R2 term. J. Cosmol. Astropart. Phys. 2018, 11, 28. [Google Scholar] [CrossRef]
- Vafa, C. The String landscape and the swampland. arXiv 2005, arXiv:hep-th/0509212. [Google Scholar]
- Garg, S.K.; Krishnan, C. Bounds on Slow Roll and the de Sitter Swampland. J. High Energy Phys. 2019, 11, 75. [Google Scholar] [CrossRef]
- Ooguri, H.; Palti, E.; Shiu, G.; Vafa, C. Distance and de Sitter Conjectures on the Swampland. Phys. Lett. B 2019, 788, 180. [Google Scholar] [CrossRef]
- Ferrara, S.; Tournoy, M.; Van Proeyen, A. de Sitter Conjectures in N=1 Supergravity. Fortsch. Phys. 2020, 68, 1900107. [Google Scholar] [CrossRef]
- Atli, U.; Guleryuz, O. A Solution to the de Sitter Swampland Conjecture versus Inflation Tension via Supergravity. J. Cosmol. Astropart. Phys. 2021, 4, 27. [Google Scholar] [CrossRef]
- Rasulian, I.M.; Torabian, M.; Velasco-Sevilla, L. Swampland de Sitter conjectures in no-scale supergravity models. Phys. Rev. D 2021, 104, 044028. [Google Scholar] [CrossRef]

| Fields | Eigenstates | Masses Squared | |
|---|---|---|---|
| 1 real scalar | |||
| 2 real scalars | |||
| 2 Weyl spinors | |||
| Fields | Eigenstates | Masses Squared | ||
|---|---|---|---|---|
| 4 | ||||
| real | ||||
| scalars | ||||
| 1 gauge boson | ||||
| 4 Weyl | ||||
| spinors | ||||
| Model: | CSI | HSI | HSI | |||
|---|---|---|---|---|---|---|
| n | 2 | 4 | 8 | |||
| 1 | 3 | 1 | 7 | 1 | 15 | |
| 9 | 7 | |||||
| {1.9} | ||||||
| M | − | |||||
| 22.6 ZeV | 36.4 ZeV | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pallis, C. Starobinsky Inflation with T-Model Kähler Geometries. Universe 2025, 11, 75. https://doi.org/10.3390/universe11030075
Pallis C. Starobinsky Inflation with T-Model Kähler Geometries. Universe. 2025; 11(3):75. https://doi.org/10.3390/universe11030075
Chicago/Turabian StylePallis, Constantinos. 2025. "Starobinsky Inflation with T-Model Kähler Geometries" Universe 11, no. 3: 75. https://doi.org/10.3390/universe11030075
APA StylePallis, C. (2025). Starobinsky Inflation with T-Model Kähler Geometries. Universe, 11(3), 75. https://doi.org/10.3390/universe11030075







