Logamediate Warm Axion Inflation in Light of Planck Data

Abstract

Axion warm inflation is studied within the framework of Logamediate inflation. Using a novel approach, we constrain the parameter space of the model and find a reasonable region of free parameters compatible with the temperature, polarization, and lensing CMB data. We focus on an inflaton evolution characterized by a high dissipative regime, where particle production impacts the inflaton dynamics more than the expansion rate. Specifically, we consider the cubic form of the dissipation coefficient, $\mathrm{{\rm Y}}={\mathrm{{\rm Y}}}_0{T}^3$, as proposed in minimal warm inflation. We show that this parameter remains large during the slow-roll epoch for a broad range of the free parameter ${\mathrm{{\rm Y}}}_0$, as indicated by our data analysis.

1. Introduction

It is well-known that the inflation paradigm provides a compelling mechanism to explain the initial seeds of large-scale structure formation [1,2,3,4,5]. The long-standing puzzles of the hot Big Bang model, including the horizon, flatness, and monopole problems can be addressed effectively within this framework [6,7,8,9,10]. Warm inflation is an interesting alternative to standard cold inflation, characterized by the absence of a separate reheating phase [11,12,13,14,15]. Instead, during the slow-roll phase, the inflaton field decays into radiation or light fields continuously [16]. Accelerated expansion at early times is generally described within the framework of quantum field theory (QFT), typically involving scalar fields [6,7,8,9,10]. Perturbations of the inflaton play a dominant role in generating the primordial fluctuations required for large-scale structure formation [1,2,3,4,5]. Warm inflation was introduced as a multi-field inflationary scenario [16] involving a thermal bath generated by radiation fields during the accelerated expansion epoch (see recent reviews in Refs. [17,18]). The interaction between the inflaton and other light (radiation) fields is significant throughout the slow-roll period. Particle production occurs continuously during the expansion, resulting in a subdominant radiation energy density that decreases more slowly than the inflaton energy density. Inflation ends when the radiation and inflaton energy densities become comparable, at which point the universe smoothly transitions into a radiation-dominated epoch. The backreaction from the radiation sector can modify the effective potential and potentially spoil the slow-roll conditions, making warm inflation model-building more subtle. Axion–gauge field configurations provide a promising setup for warm inflation [19,20], as the shift symmetry of the axion field protects the potential against thermal corrections. In this work, we study a warm inflation model where the standard Chern–Simons interaction between the axion inflaton and gauge fields, representing the radiation sector, leads to a cubic form of the dissipation coefficient, $\mathrm{{\rm Y}}={\mathrm{{\rm Y}}}_0{T}^3$ [20,21]. At the microphysical level, the axion couples to gauge fields through the Chern–Simons term $\mathcal{L}\supset (\varphi /f)F\tilde{F}$, which induces dissipation after integrating out the light gauge sector in a thermal bath. In the minimal setup this yields $\mathrm{{\rm Y}}\propto T^3$ with an overall amplitude collected in ${\mathrm{{\rm Y}}}_0$; see Refs. [20,21]. In what follows we restrict to the regime where this derivation applies, $T/H\gtrsim 10$ and $Q\gtrsim 10$, which we check along the background evolution. Using a logamediate form of the scale factor, we analyze this model in detail. The effective potential of the logamediate model has been studied in the context of dark energy [22], and such potentials also appear in supergravity, Kaluza–Klein theories, and superstring models [23]. Notably, logamediate models can produce either blue or red tilted power spectra [24], a distinctive feature. We find a region of parameter space in the logamediate warm axion inflation model that is compatible with observational data. To analyze the model, we modify the CAMB code to directly perform parameter estimation and find the best-fit values consistent with current cosmological observations.

Relative to earlier warm-axion studies, we work with the logamediate expansion ansatz as a reconstruction device and then constrain the pair $(\lambda ,{\mathrm{{\rm Y}}}_0)$ directly with Planck 2018 TT,TE,EE+lensing. Throughout we keep the thermal regime $T>H$ and strong dissipation $Q\gg 1$ explicit and verify them a posteriori in the background solutions. This clarifies the domain where the minimal form $\mathrm{{\rm Y}}={\mathrm{{\rm Y}}}_0{T}^3$ is reliable and highlights the observational viability of the axion warm–inflation mechanism within the logamediate class.

2. Logamediate Warm Inflation

The logamediate inflation model, originally studied by Barrow [25], is characterized by the scale factor

$$a\left(t\right)=a_{0}exp\left(A{[lnt]}^{\lambda }\right),$$

(1)

where $A>0$ and $\lambda >1$ are constants. Notably, for $\lambda =1$, this reduces to the power-law inflation model, $a\left(t\right)\sim t^A$ [26]. This class of scale factors has been considered in various scalar-tensor theories [27]. Traditionally, inflationary models are studied by choosing a specific form of the potential and constraining its parameters using observational data. Alternatively, one may start with a parametrized form of the scale factor, as in the logamediate case, and derive the resulting inflationary observables by constraining the phase space of its free parameters [28,29,30]. In this work, we adopt the latter approach and explore the inflationary dynamics resulting from Equation (1), which contains two primary free parameters: A and $\lambda$. In the context of warm inflation, where particle production occurs during the slow-roll phase, the presence of a thermal bath modifies both the background and perturbative dynamics [31]. At the background level, the total energy conservation equation can be split into two parts using a phenomenological interaction term:

$$\begin{array}{c}\hfill {\dot{\rho }}_{\varphi }+3H({\rho }_{\varphi }+P_{\varphi })=-\mathrm{{\rm Y}}{\dot{\varphi }}^2,\\ \hfill {\dot{\rho }}_{\gamma }+4H{\rho }_{\gamma }=\mathrm{{\rm Y}}{\dot{\varphi }}^2,\end{array}$$

(2)

where dots denote derivatives with respect to time, and $\mathrm{{\rm Y}}$ is the dissipation coefficient responsible for converting scalar field energy into radiation during inflation. These equations lead to a modified Klein–Gordon equation for the inflation:

$$\ddot{\varphi }+3H(1+Q)\dot{\varphi }+V^{\prime }=0,$$

(3)

where $Q=\mathrm{{\rm Y}}/3H$ is the dissipation ratio, and primes denote derivatives with respect to $\varphi$. In the strong dissipation regime $Q\gg 1$, this parameter plays a critical role in both the background evolution and the spectrum of perturbations. We consider the specific case $\mathrm{{\rm Y}}={\mathrm{{\rm Y}}}_0{T}^3$, motivated by quantum field theory in thermal backgrounds [31]. Thus, our model has a two-dimensional parameter space defined by $(\lambda ,{\mathrm{{\rm Y}}}_0)$.

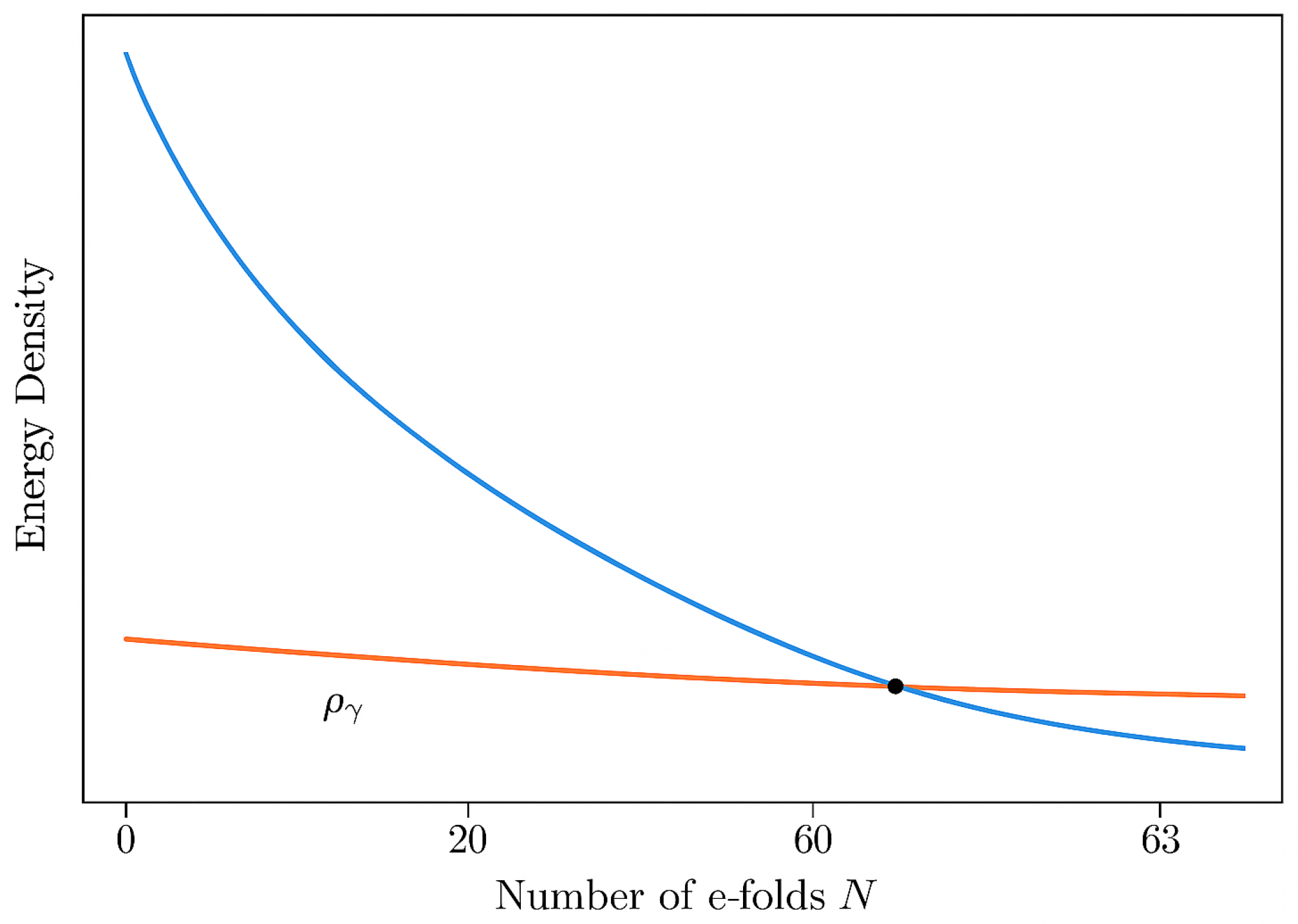
2.1. Background Evolution and Radiation Domination

To demonstrate the graceful exit from inflation in our warm logamediate scenario, we numerically solve the full background equations governing the evolution of the inflaton and radiation energy. The governing equations are:

$$\begin{array}{cc}\hfill {\dot{\rho }}_{\varphi }& =-3H(1+Q){\dot{\varphi }}^2,\\ \hfill {\dot{\rho }}_{\gamma }& =3HQ{\dot{\varphi }}^2-4H{\rho }_{\gamma },\end{array}$$

(4)

as well as inflaton evolution (3).

In Figure 1, we show the evolution of ${\rho }_{\varphi }$ and ${\rho }_{\gamma }$ as functions of the number of e-folds N. The inflaton energy density decreases monotonically, approximately exponentially, throughout inflation, while the radiation energy density remains nearly constant with a slight decline. Crucially, both energy densities converge at $N\approx 60$, after which radiation becomes the dominant component. This indicates a natural and continuous transition from the inflationary phase to a radiation-dominated universe, without the need for a separate reheating mechanism For the background solutions entering the parameter inference we integrate Equations (2)–(4) exactly, without slow-roll or strong-dissipation approximations, and verify that $T/H>10$ and $Q>10$ until $N\simeq 60$. 1

2.2. Perturbation

In the slow-roll regime, the inflaton’s dynamics are governed by

$$3H(1+Q)\dot{\varphi }\simeq -V^{\prime },4{\rho }_{\gamma }\simeq 3Q{\dot{\varphi }}^2,$$

(5)

and the Hubble parameter satisfies

$$H^2={\displaystyle \frac{V}{3M_P^2}},{\rho }_{\gamma }=C_{\gamma }{T}^4,Q={\displaystyle \frac{\mathrm{{\rm Y}}}{3H}},\mathrm{{\rm Y}}={\mathrm{{\rm Y}}}_0{T}^3.$$

(6)

By solving the background equations under these assumptions, one can derive the time evolution of the inflaton, expressed in terms of the incomplete gamma function $\Gamma (a,x)$ [32,33]. The number of e-folds between two times $t_1$ and t is given by

$$N={\int }_{t_1}^{t}Hdt=A\left[{(lnt)}^{\lambda }-{(ln{t}_1)}^{\lambda }\right],$$

(7)

with

$$H={\displaystyle \frac{\dot{a}}{a}}={\displaystyle \frac{A\lambda }{t}}{(lnt)}^{\lambda -1},\epsilon =-{\displaystyle \frac{\dot{H}}{H^2}}={\displaystyle \frac{{(lnt)}^{1-\lambda }}{A\lambda }}.$$

Assuming that inflation ends when $\epsilon =1$, we find the logarithmic time during inflation:

$$lnt={\left({\displaystyle \frac{N}{A}}+{\left(A\lambda \right)}^{{\displaystyle \frac{\lambda }{1-\lambda }}}\right)}^{{\displaystyle \frac{1}{\lambda }}}.$$

(8)

In the strong dissipation regime $Q\gg 1$, where $\mathrm{{\rm Y}}\propto T^3$, thermal fluctuations dominate over quantum ones. The resulting curvature power spectrum acquires a growing mode [34], leading to

$${\Delta }_{\mathcal{R}}^2\approx {\displaystyle \frac{\sqrt{3}}{4{\pi }^{3/2}}}{\displaystyle \frac{H^{3}T}{{\dot{\varphi }}^2}}{\left({\displaystyle \frac{Q}{Q_3}}\right)}^9{Q}^{1/2},$$

(9)

where $Q_3=7.3$ is a numerical factor determined by matching solutions in different regimes [20].

For completeness, the expression above follows from solving the coupled Langevin system for the inflaton and radiation fluctuations in the thermal, strongly dissipative regime. Modes freeze out at $k_F\simeq \sqrt{3HQ}$, and matching the sub-horizon stochastic solution to the growing mode at $k\sim k_F$ yields the enhancement factor $Q^{9/2}$. The numerical constant $Q_3\simeq 7.3$ encodes the fit to the exact solution in this regime, as reported in Refs. [20,34]. In our parameter scans we enforce $T>H$ and $Q\gg 1$ so that this formula is used only within its domain of validity. 2

Using the derived expressions for T and Q, and substituting for $lnt$ in terms of N, we obtain the scalar power spectrum as

$${\Delta }_{\mathcal{R}}^2\propto {\displaystyle \frac{{\left(\frac{N}{A}+{\left(A\lambda \right)}^{\frac{\lambda }{1-\lambda }}\right)}^{\frac{3(1-\lambda )}{8\lambda }}}{exp{\left[{\left(\frac{N}{A}+{\left(A\lambda \right)}^{\frac{\lambda }{1-\lambda }}\right)}^{\frac{1}{\lambda }}\right]}^{27/4}}}.$$

(10)

The scalar spectral index is defined as

$$n_s-1={\displaystyle \frac{dln{\Delta }_{\mathcal{R}}^2}{dlnk}}={\displaystyle \frac{dln{\Delta }_{\mathcal{R}}^2}{dN}}.$$

(11)

This leads to

$$n_s-1={\displaystyle \frac{3(1-\lambda )}{8A\lambda }}{\left({\displaystyle \frac{N}{A}}+{\left(A\lambda \right)}^{{\displaystyle \frac{\lambda }{1-\lambda }}}\right)}^{-1}-{\displaystyle \frac{27}{4A\lambda }}{\left({\displaystyle \frac{N}{A}}+{\left(A\lambda \right)}^{{\displaystyle \frac{\lambda }{1-\lambda }}}\right)}^{{\displaystyle \frac{1-\lambda }{\lambda }}}.$$

(12)

In the regime of interest, the second term dominates, and we approximate

$$n_s-1\simeq -{\displaystyle \frac{27}{4A\lambda }}{\left({\displaystyle \frac{N}{A}}+{\left(A\lambda \right)}^{{\displaystyle \frac{\lambda }{1-\lambda }}}\right)}^{{\displaystyle \frac{1-\lambda }{\lambda }}}.$$

(13)

Assuming sub-Planckian temperatures, tensor perturbations are unaffected and follow the standard expression from cold inflation [35]:

$${\Delta }_h^2={\displaystyle \frac{2}{{\pi }^2}}{\displaystyle \frac{H^2}{M_P^2}},r={\displaystyle \frac{{\Delta }_h^2}{{\Delta }_{\mathcal{R}}^2}}.$$

(14)

Thus, the tensor-to-scalar ratio is given by

$$r={\displaystyle \frac{8{\left(3Q_3\right)}^9{\left(A\lambda \right)}^{19/8}{\left(4C_{\gamma }\right)}^{65/18}}{\sqrt{\pi }·6^{57/8}{M}_P^{65/4}{\mathrm{{\rm Y}}}_0^{21/2}}}exp\left[{\left({\displaystyle \frac{N}{A}}+{\left(A\lambda \right)}^{{\displaystyle \frac{\lambda }{1-\lambda }}}\right)}^{19/4\lambda }\right]{\left({\displaystyle \frac{N}{A}}+{\left(A\lambda \right)}^{{\displaystyle \frac{\lambda }{1-\lambda }}}\right)}^{{\displaystyle \frac{19(1-\lambda )}{8\lambda }}}.$$

(15)

Assuming $A=1$, $N=60$, $Q_3=7.3$, and $C_{\gamma }=70$ [36], the above expression simplifies to

$$r={\displaystyle \frac{1.14\times {10}^{27}·{\lambda }^{19/8}}{{\mathrm{{\rm Y}}}_0^{21/2}}}exp\left[{\left(60+{\lambda }^{{\displaystyle \frac{\lambda }{1-\lambda }}}\right)}^{19/4\lambda }\right]{\left(60+{\lambda }^{{\displaystyle \frac{\lambda }{1-\lambda }}}\right)}^{{\displaystyle \frac{19(1-\lambda )}{8\lambda }}}.$$

(16)

In the next section, we will analyze the observational constraints on the model, focusing on the scalar spectral index $n_s$ and the scalar amplitude $A_s$ as functions of the free parameters $\lambda$ and ${\mathrm{{\rm Y}}}_0$. We do not impose the tensor-to-scalar ratio r as a constraint, since it is typically suppressed in the strong dissipation regime and easily satisfies current observational bounds.

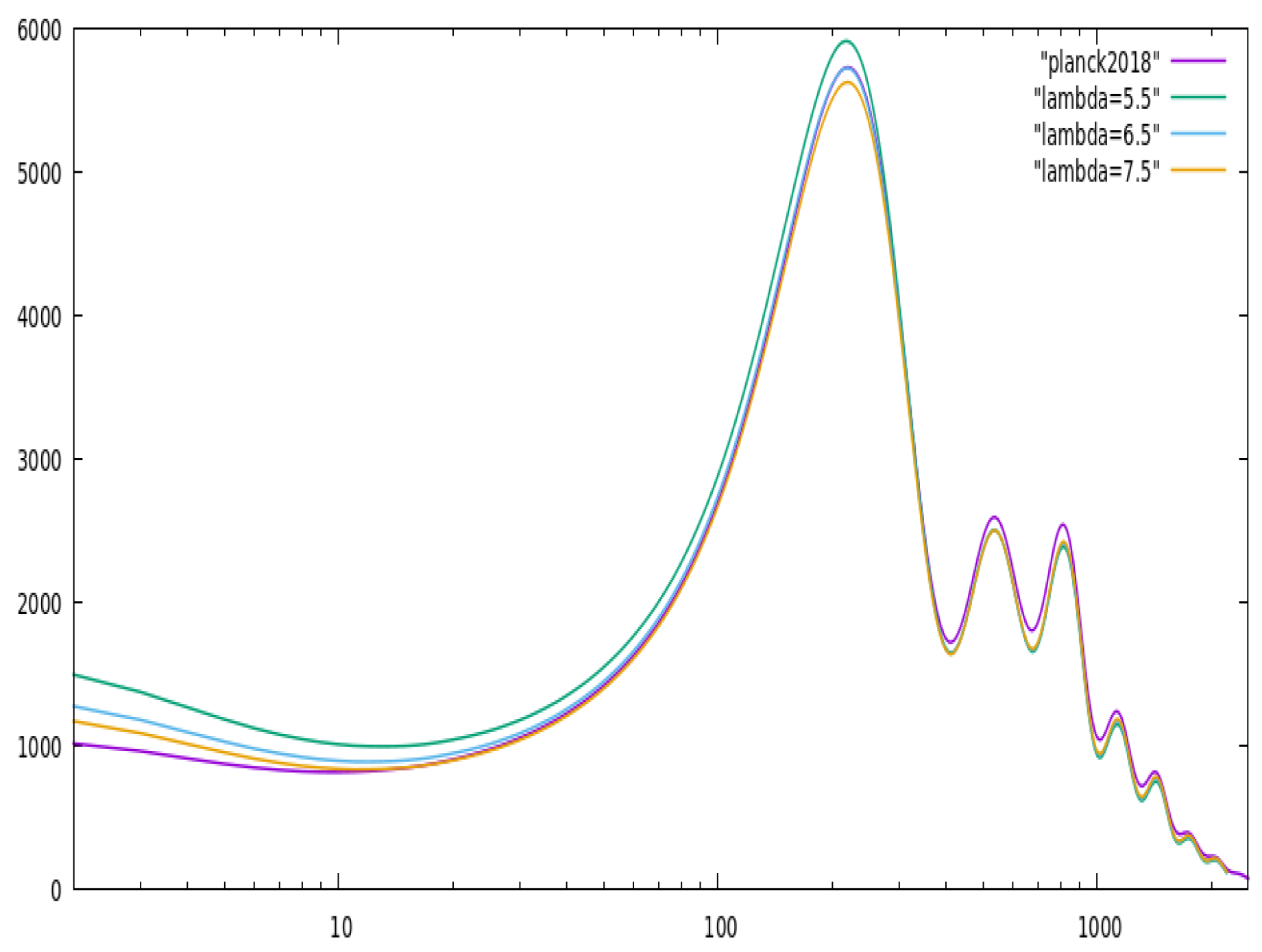
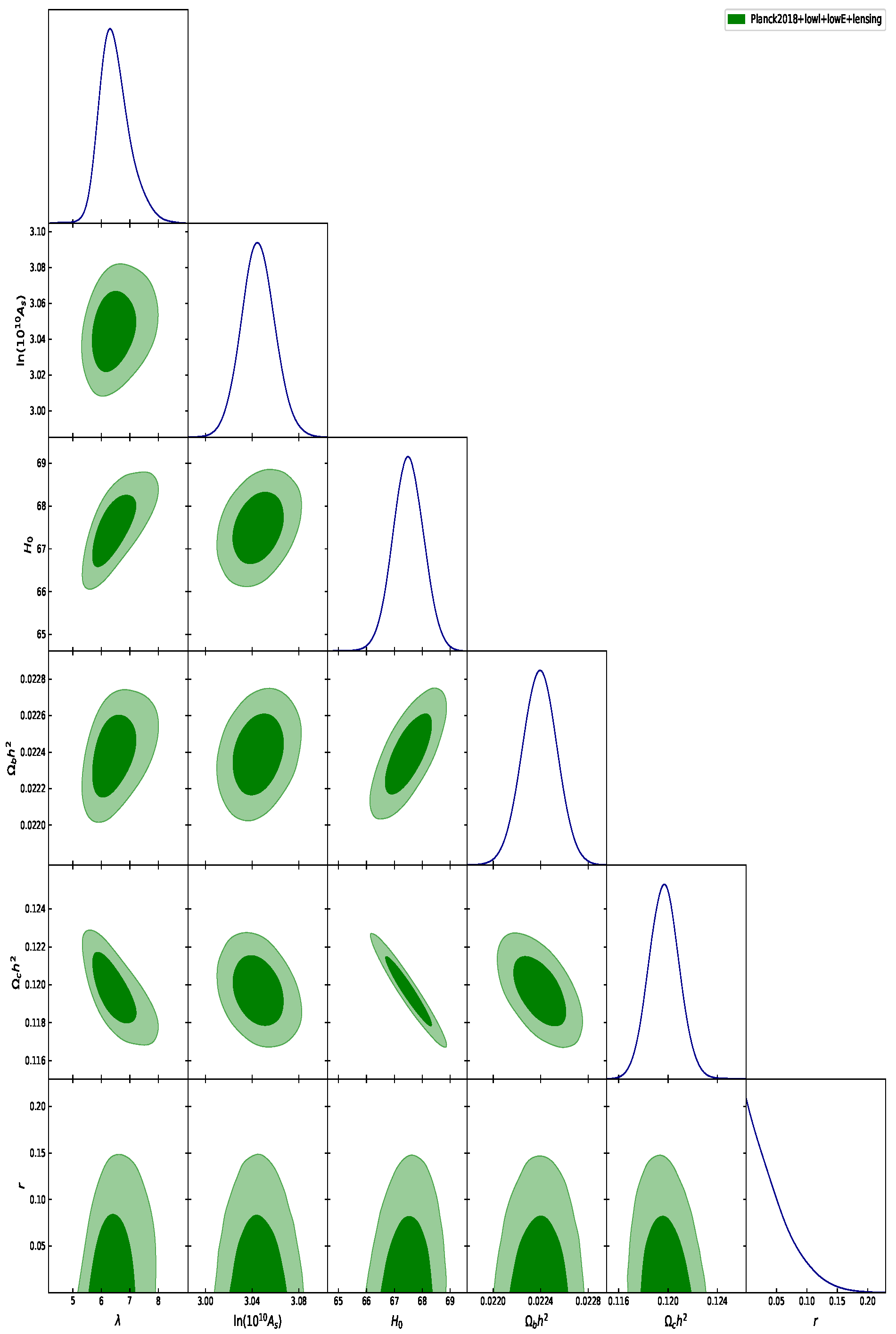
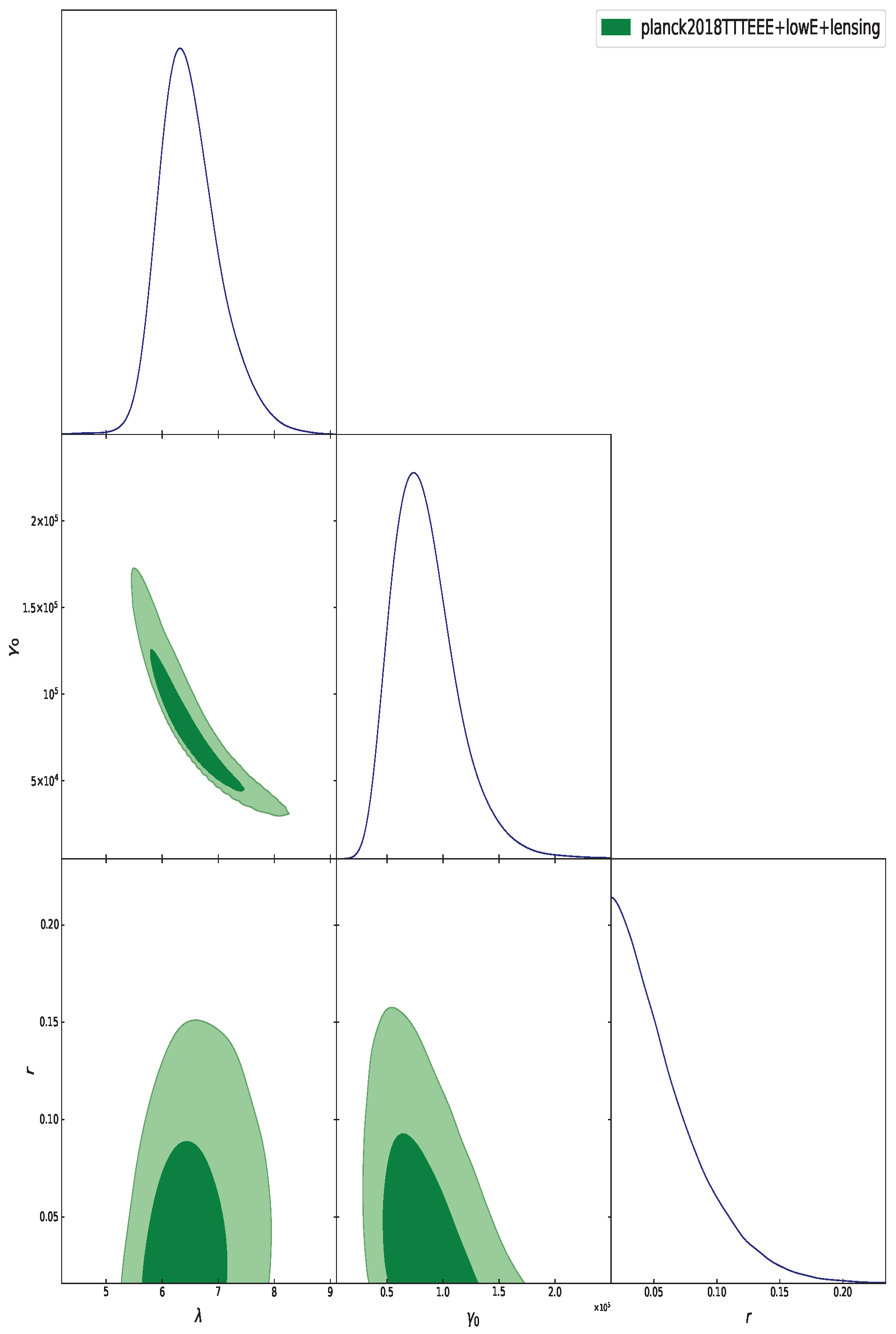
3. Methodology and Observational Data

The final goal of this article is to constrain the parameters of our model, as well as the late-time cosmological parameters, with a particular focus on the $\Lambda$CDM model. In this section, we describe the data and analysis methods used. In the likelihood we keep the late-time sector identical to the baseline $\Lambda$CDM model. Our warm-logamediate dynamics only determine the primordial amplitude $A_s$ and tilt $n_s$ at $N=60$ via Equations (10)–(13); no extra relativistic species, isocurvature modes, or late-time parameters are introduced beyond the standard six of $\Lambda$CDM.

We use the most recent publicly available measurements of the Cosmic Microwave Background (CMB), released by the Planck team as Planck 2018 data. Specifically, we utilize the temperature power spectrum $\left(TT\right)$, the polarization power spectrum $\left(EE\right)$, the temperature-polarization cross-correlation spectrum $\left(TE\right)$, and the low-ℓ polarization likelihood $\left(lowE\right)$ [37,38].

To derive constraints on the cosmological parameters, we employ a Markov Chain Monte Carlo (MCMC) analysis using the publicly available CosmoMC code [39]. Theoretical predictions are generated using the CAMB Boltzmann integrator [40].

We analyze the parameter dependence of the warm inflation model on inflationary observables. In particular, we consider the scalar spectral index $n_s$ and the scalar amplitude $A_s$ as functions of the model parameters $\lambda$ and A. In Figure 2, we plot the CMB power spectrum for fixed A and $N=60$, while varying $\lambda$.

As seen in Figure 2, the power spectrum is highly sensitive to the parameter $\lambda$, but only weakly dependent on A, which we fix at 1. A value of $\lambda =6.5$ provides a good fit to Planck 2018 data.

Using CosmoMC, we constrain the model and cosmological parameters for warm axion inflation and estimate posterior probability distributions with marginalized central values and standard deviations. As a baseline, we adopt the standard $\Lambda$CDM parametrization, which includes the following:

• ${\Omega }_b{h}^2$: current baryon density,
• ${\Omega }_c{h}^2$: current cold dark matter density,
• $\theta$: the angular size of the sound horizon at recombination,
• $\tau$: optical depth to reionization.

Figure 3 displays the posterior distributions. The likelihoods used include Planck $TT+TE+EE$, $low-\ell$, $lowE$, lensing, and joint analysis likelihoods. We used the GetDist package (included in CosmoMC) for post-processing and marginalization.

Table 1. Marginalized values and 68%/95% limits for model and cosmological parameters in the $\Lambda$CDM model.

Parameter	68% Limits	95% Limits
${\Omega }_b{h}^2$	$0.02239\pm 0.00015$	$0.02239\pm 0.00029$
${\Omega }_c{h}^2$	$0.1197\pm 0.0012$	$0.{1197}_{-0.0024}^{+0.0025}$
$100{\theta }_{MC}$	$1.04095\pm 0.00031$	$1.{04095}_{-0.00061}^{+0.00060}$
$\tau$	$0.0551\pm 0.0076$	$0.055\pm 0.015$
$ln\left({10}^{10}{A}_s\right)$	$3.045\pm 0.015$	$3.{045}_{-0.028}^{+0.029}$
$H_0$	$67.49\pm 0.56$	$67.5\pm 1.1$
$\lambda$	$6.{48}_{-0.61}^{+0.40}$	$6.{48}_{-0.97}^{+1.2}$
r	$<0.0536$	$<0.116$

summarizes the parameter constraints. All parameters are consistent with Planck 2018 $\Lambda$CDM values within 1$\sigma$ or 2$\sigma$. A positive correlation is observed between $\lambda$ and several cosmological parameters.

We further constrain the dissipation coefficient ${\mathrm{{\rm Y}}}_0$ using Table 1 and Equation (16). Figure 4 shows the joint posterior distributions of $\lambda$, r, and ${\mathrm{{\rm Y}}}_0$. A positive correlation between ${\mathrm{{\rm Y}}}_0$ and r is found, supporting a good fit to Planck 2018 data.

Using MCMC analysis, we constrain ${\mathrm{{\rm Y}}}_0$ and $\lambda$ directly from the data, which results in an upper bound on r as a derived quantity (

Table 2. Marginalized values and upper limits for r and ${\mathrm{{\rm Y}}}_0$ with $1\sigma$ and $2\sigma$ errors.

Parameter	68% Limits	95% Limits
$\lambda$	$6.{48}_{-0.61}^{+0.40}$	$6.{48}_{-0.97}^{+1.2}$
r	$<0.0536$	$<0.116$
${\mathrm{{\rm Y}}}_0$	$(0.9_{-0.4}^{+0.2})\times {10}^5$	$(0.9_{-0.5}^{+0.6})\times {10}^5$

).

4. Conclusions

In this work, we studied the logamediate solution of cosmic expansion in the context of warm axion inflation and analyzed its observational viability with Planck 2018 data. By adopting the cubic temperature dependence of the dissipation coefficient, $\mathrm{{\rm Y}}={\mathrm{{\rm Y}}}_0{T}^3$, we explored the strong dissipative regime and constrained the free parameters of the model using MCMC methods with CosmoMC. Our statistical analysis shows that values around

• $\lambda =6.{48}_{-0.61}^{+0.40}$ (68% C.L.), $6.{48}_{-0.97}^{+1.2}$ (95% C.L.),
• ${\mathrm{{\rm Y}}}_0=(0.9_{-0.4}^{+0.2})\times {10}^5$ (68% C.L.), $(0.9_{-0.5}^{+0.6})\times {10}^5$ (95% C.L.),

provide a good fit to Planck 2018 data, yielding a spectral index $n_s$ in agreement with observations and an upper bound on the tensor-to-scalar ratio r well below current limits.

We also examined the background dynamics, showing that the inflaton energy density decreases while the radiation density remains nearly constant and eventually dominates near $N\approx 60$. This demonstrates a continuous transition from inflation to a radiation-dominated universe, without the need for a separate reheating phase. However, we emphasize that the exact evolution of the slow-roll parameter $ϵ\left(N\right)$ in the logamediate framework does not naturally reach unity and then exceed it for $\lambda >1$. As noted in the manuscript, this limitation reflects an intrinsic property of the logamediate scale factor, and a complete resolution of the graceful exit problem requires further investigation.

Despite this theoretical limitation, the observational analysis carried out here remains consistent and reliable. The parameter space of the logamediate warm axion inflation model is well constrained and compatible with Planck data. Future work will focus on extending the formalism to properly account for the end of inflation and to incorporate updated numerical treatments of the warm inflation power spectrum. In addition, it would be interesting to examine the UV consistency of this setup in light of swampland conjectures; we leave this to future work. It was shown that the model Taken together, these results provide a consistent and testable warm–inflation scenario that matches current observations.