Hydrodynamics of Two-Dimensional CFTs
Abstract
1. Introduction
In conformal field theory, what dynamical regime and corresponding effective field theory description looks like gravity with a negative cosmological constant?
Is the fluid/gravity correspondence controlled by a geometric action on the coadjoint orbit of some diffeomorphism group?
(Claim) The Virasoro geometric action is an effective field theory describing the hydrodynamical regime of CFTs in 2d.
2. Hydrodynamics from Virasoro Geometric Action
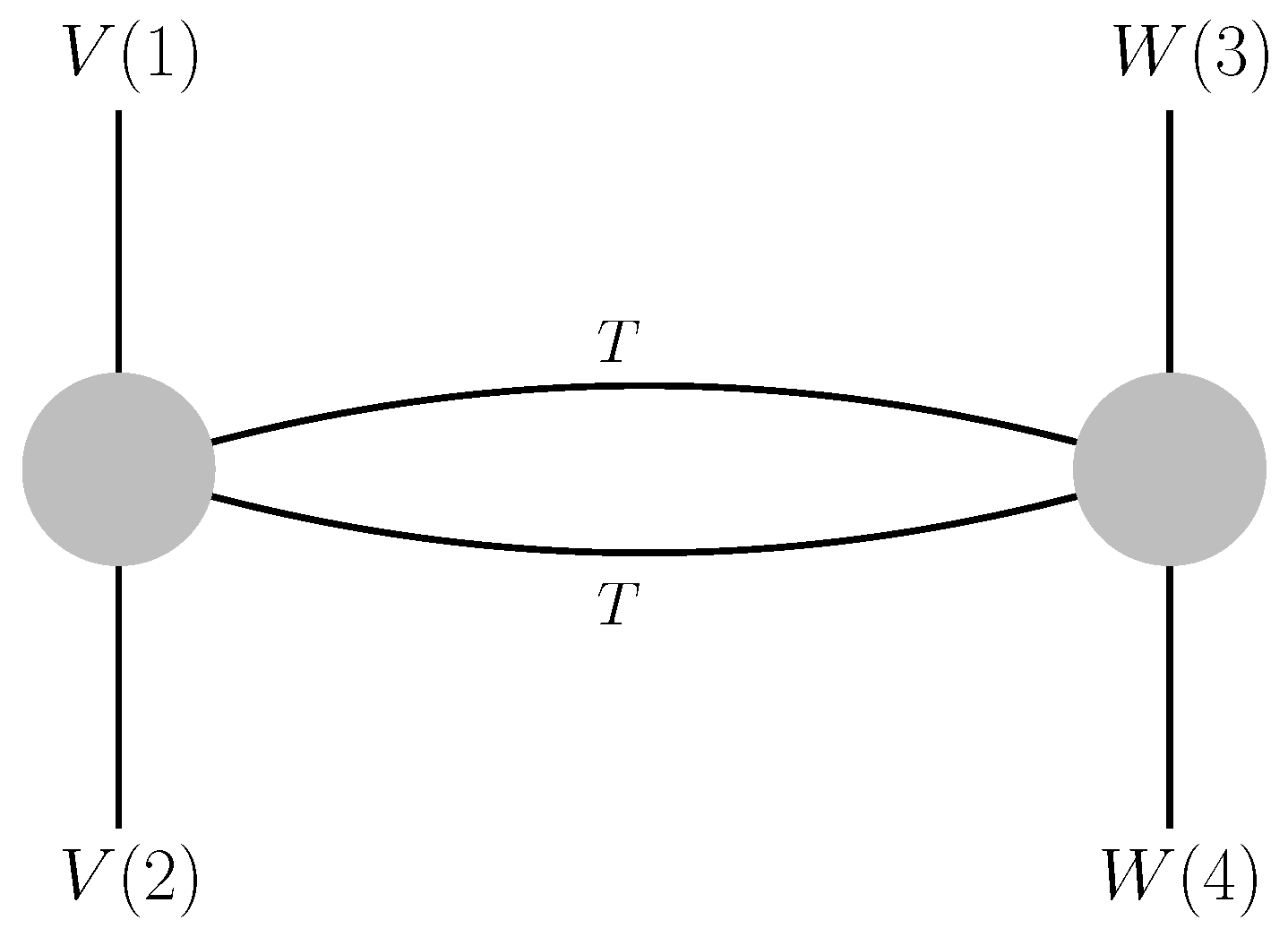
3. Reparametrization Theory Revisited
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Hydrodynamics of CFT2
Appendix A.1. Hydrodynamical Predictions
Appendix A.2. Agreement with CFT2 Result
References
- Maldacena, J.M. The Large N limit of superconformal field theories and supergravity. Adv. Theor. Math. Phys. 1998, 2, 231–252. [Google Scholar] [CrossRef]
- Gubser, S.S.; Klebanov, I.R.; Polyakov, A.M. Gauge theory correlators from noncritical string theory. Phys. Lett. B 1998, 428, 105–114. [Google Scholar] [CrossRef]
- Witten, E. Anti-de Sitter space and holography. Adv. Theor. Math. Phys. 1998, 2, 253–291. [Google Scholar] [CrossRef]
- Birmingham, D.; Sachs, I.; Solodukhin, S.N. Conformal field theory interpretation of black hole quasinormal modes. Phys. Rev. Lett. 2002, 88, 151301. [Google Scholar] [CrossRef]
- Policastro, G.; Son, D.T.; Starinets, A.O. From AdS/CFT correspondence to hydrodynamics. J. High Energy Phys. 2002, 2002, 43. [Google Scholar] [CrossRef]
- Policastro, G.; Son, D.T.; Starinets, A.O. From AdS/CFT correspondence to hydrodynamics. 2. Sound waves. J. High Energy Phys. 2002, 2002, 54. [Google Scholar] [CrossRef]
- Baier, R.; Romatschke, P.; Son, D.T.; Starinets, A.O.; Stephanov, M.A. Relativistic viscous hydrodynamics, conformal invariance, and holography. J. High Energy Phys. 2008, 2008, 100. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Hubeny, V.E.; Minwalla, S.; Rangamani, M. Nonlinear Fluid Dynamics from Gravity. J. High Energy Phys. 2008, 2008, 45. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Loganayagam, R.; Mandal, I.; Minwalla, S.; Sharma, A. Conformal Nonlinear Fluid Dynamics from Gravity in Arbitrary Dimensions. J. High Energy Phys. 2008, 2008, 116. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Hubeny, V.E.; Loganayagam, R.; Mandal, G.; Minwalla, S.; Morita, T.; Rangamani, M.; Reall, H.S. Local Fluid Dynamical Entropy from Gravity. J. High Energy Phys. 2008, 2008, 55. [Google Scholar] [CrossRef][Green Version]
- Bhattacharyya, S.; Minwalla, S.; Wadia, S.R. The Incompressible Non-Relativistic Navier-Stokes Equation from Gravity. J. High Energy Phys. 2009, 2009, 59. [Google Scholar] [CrossRef]
- Rangamani, M. Gravity and Hydrodynamics: Lectures on the fluid-gravity correspondence. Class. Quant. Grav. 2009, 26, 224003. [Google Scholar] [CrossRef]
- Hubeny, V.E.; Minwalla, S.; Rangamani, M. The fluid/gravity correspondence. arXiv 2011, arXiv:1107.5780. [Google Scholar] [PubMed]
- Dubovsky, S.; Hui, L.; Nicolis, A.; Son, D.T. Effective field theory for hydrodynamics: Thermodynamics, and the derivative expansion. Phys. Rev. D 2012, 85, 085029. [Google Scholar] [CrossRef]
- Bhattacharya, J.; Bhattacharyya, S.; Rangamani, M. Non-dissipative hydrodynamics: Effective actions versus entropy current. J. High Energy Phys. 2013, 2013, 153. [Google Scholar] [CrossRef]
- Haehl, F.M.; Loganayagam, R.; Rangamani, M. Adiabatic hydrodynamics: The eightfold way to dissipation. J. High Energy Phys. 2015, 2015, 60. [Google Scholar] [CrossRef]
- Haehl, F.M.; Loganayagam, R.; Rangamani, M. Topological sigma models & dissipative hydrodynamics. J. High Energy Phys. 2016, 2016, 39. [Google Scholar] [CrossRef]
- Crossley, M.; Glorioso, P.; Liu, H. Effective field theory of dissipative fluids. J. High Energy Phys. 2017, 2017, 95. [Google Scholar] [CrossRef]
- Haehl, F.M.; Loganayagam, R.; Rangamani, M. Two roads to hydrodynamic effective actions: A comparison. arXiv 2017, arXiv:1701.07896. [Google Scholar] [CrossRef]
- Haehl, F.M.; Loganayagam, R.; Rangamani, M. Effective Action for Relativistic Hydrodynamics: Fluctuations, Dissipation, and Entropy Inflow. J. High Energy Phys. 2018, 2018, 194. [Google Scholar] [CrossRef]
- Campoleoni, A.; Ciambelli, L.; Marteau, C.; Petropoulos, P.M.; Siampos, K. Two-dimensional fluids and their holographic duals. Nucl. Phys. B 2019, 946, 114692. [Google Scholar] [CrossRef]
- Adami, H.; Parvizi, A.; Sheikh-Jabbari, M.M.; Taghiloo, V.; Yavartanoo, H. Hydro & thermo dynamics at causal boundaries, examples in 3d gravity. J. High Energy Phys. 2023, 2023, 38. [Google Scholar] [CrossRef]
- Arnold, V.I. Sur la géométrie différentielle des groupes de lie de dimension infinie et ses applications à l’hydrodynamique des fluides parfaits. Ann. L’Institut Fourier 1966, 16, 319–361. [Google Scholar] [CrossRef]
- Arnold, V.I. Hamiltonian nature of the euler equations in the dynamics of a rigid body and of an ideal fluid. In Vladimir I. Arnold-Collected Works: Hydrodynamics, Bifurcation Theory, and Algebraic Geometry 1965–1972; Springer: Berlin/Heidelberg, Germany, 2014; pp. 175–178. [Google Scholar]
- Ebin, D.G.; Marsden, J. Groups of diffeomorphisms and the motion of an incompressible fluid. Ann. Math. 1970, 92, 102–163. [Google Scholar] [CrossRef]
- Arnold, V.I.; Khesin, B. Topological Methods in Hydrodynamics; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Marsden, J.E.; Ratiu, T.S.; Weinstein, A.D. Semidirect products and reduction in mechanics. Trans. Am. Math. Soc. 1984, 281, 147–177. [Google Scholar] [CrossRef]
- Marsden, J.E.; Ratiu, T.S.; Weinstein, A.D. Reduction and hamiltonian structures on duals of semidirect product lie algebras. Contemp. Math. 1984, 28, 55–100. [Google Scholar]
- Holm, D.D.; Marsden, J.E.; Ratiu, T.S. The euler–poincaré equations and semidirect products with applications to continuum theories. Adv. Math. 1998, 137, 1–81. [Google Scholar] [CrossRef]
- Khesin, B.; Misiołek, G.; Modin, K. Geometric hydrodynamics and infinite-dimensional newton’s equations. Bull. Am. Math. Soc. 2021, 58, 377–442. [Google Scholar] [CrossRef]
- Penna, R.F. BMS3 invariant fluid dynamics at null infinity. Class. Quant. Grav. 2018, 35, 044002. [Google Scholar] [CrossRef]
- Carrillo-González, M.; Penna, R.F. Asymptotic symmetries of three dimensional gravity and the membrane paradigm. J. High Energy Phys. 2019, 2019, 125. [Google Scholar] [CrossRef]
- Donnelly, W.; Freidel, L.; Moosavian, S.F.; Speranza, A.J. Gravitational edge modes, coadjoint orbits, and hydrodynamics. J. High Energy Phys. 2021, 2021, 8. [Google Scholar] [CrossRef]
- Kirillov, A.A. Lectures on the Orbit Method; American Mathematical Society: Providence, RI, USA, 2004. [Google Scholar]
- Alekseev, A.; Shatashvili, S.L. Path Integral Quantization of the Coadjoint Orbits of the Virasoro Group and 2D Gravity. Nucl. Phys. 1989, B323, 719–733. [Google Scholar] [CrossRef]
- Alekseev, A.; Shatashvili, S.L. From geometric quantization to conformal field theory. Commun. Math. Phys. 1990, 128, 197–212. [Google Scholar] [CrossRef]
- Rai, B.; Rodgers, V.G.J. From Coadjoint Orbits to Scale Invariant WZNW Type Actions and 2-D Quantum Gravity Action. Nucl. Phys. B 1990, 341, 119–133. [Google Scholar] [CrossRef]
- Delius, G.W.; van Nieuwenhuizen, P.; Rodgers, V.G.J. The Method of Coadjoint Orbits: An Algorithm for the Construction of Invariant Actions. Int. J. Mod. Phys. A 1990, 5, 3943–3983. [Google Scholar] [CrossRef]
- Aratyn, H.; Nissimov, E.; Pacheva, S.; Zimerman, A.H. Symplectic actions on coadjoint orbits. Phys. Lett. B 1990, 240, 127–132. [Google Scholar] [CrossRef]
- Barnich, G.; Gonzalez, H.A.; Salgado-Rebolledo, P. Geometric actions for three-dimensional gravity. Class. Quant. Grav. 2018, 35, 014003. [Google Scholar] [CrossRef]
- Barnich, G.; Nguyen, K.; Ruzziconi, R. Geometric action for extended Bondi-Metzner-Sachs group in four dimensions. J. High Energy Phys. 2022, 2022, 154. [Google Scholar] [CrossRef]
- Cotler, J.; Jensen, K. A theory of reparameterizations for AdS3 gravity. J. High Energy Phys. 2019, 2019, 79. [Google Scholar] [CrossRef]
- Haehl, F.M.; Rozali, M. Effective Field Theory for Chaotic CFTs. J. High Energy Phys. 2018, 2018, 118. [Google Scholar] [CrossRef]
- Haehl, F.M.; Reeves, W.; Rozali, M. Reparametrization modes, shadow operators, and quantum chaos in higher-dimensional CFTs. J. High Energy Phys. 2019, 2019, 102. [Google Scholar] [CrossRef]
- Anous, T.; Haehl, F.M. On the Virasoro six-point identity block and chaos. J. High Energy Phys. 2020, 2020, 2. [Google Scholar] [CrossRef]
- Nguyen, K. Reparametrization modes in 2d CFT and the effective theory of stress tensor exchanges. J. High Energy Phys. 2021, 2021, 29. [Google Scholar] [CrossRef]
- Nguyen, K. Virasoro blocks and the reparametrization formalism. J. High Energy Phys. 2023, 2023, 143. [Google Scholar] [CrossRef]
- Jensen, K. Chaos in AdS2 Holography. Phys. Rev. Lett. 2016, 117, 111601. [Google Scholar] [CrossRef]
- Mandal, G.; Nayak, P.; Wadia, S.R. Coadjoint orbit action of Virasoro group and two-dimensional quantum gravity dual to SYK/tensor models. J. High Energy Phys. 2017, 2017, 46. [Google Scholar] [CrossRef]
- Barnich, G.; Oblak, B. Holographic positive energy theorems in three-dimensional gravity. Class. Quant. Grav. 2014, 31, 152001. [Google Scholar] [CrossRef][Green Version]
- Ferrara, S.; Grillo, A.F.; Parisi, G.; Gatto, R. The shadow operator formalism for conformal algebra. Vacuum expectation values and operator products. Lett. Nuovo Cim. 1972, 4, 115–120. [Google Scholar] [CrossRef]
- Kadanoff, L.P.; Martin, P.C. Hydrodynamic equations and correlation functions. Ann. Phys. 1963, 24, 419–469. [Google Scholar] [CrossRef]
- Kovtun, P. Lectures on hydrodynamic fluctuations in relativistic theories. J. Phys. A 2012, 45, 473001. [Google Scholar] [CrossRef]
- Ramirez, D.M. Chaos and pole skipping in CFT2. J. High Energy Phys. 2021, 2021, 6. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, K. Hydrodynamics of Two-Dimensional CFTs. Universe 2025, 11, 402. https://doi.org/10.3390/universe11120402
Nguyen K. Hydrodynamics of Two-Dimensional CFTs. Universe. 2025; 11(12):402. https://doi.org/10.3390/universe11120402
Chicago/Turabian StyleNguyen, Kevin. 2025. "Hydrodynamics of Two-Dimensional CFTs" Universe 11, no. 12: 402. https://doi.org/10.3390/universe11120402
APA StyleNguyen, K. (2025). Hydrodynamics of Two-Dimensional CFTs. Universe, 11(12), 402. https://doi.org/10.3390/universe11120402




