Newtonian Fractional-Dimension Gravity and the Mass-Dimension Field Equation
Abstract
1. Introduction
2. Revised NFDG Computations
3. NFDG Mass-Dimension Field Equation
4. NFDG and Galactic Data Fitting
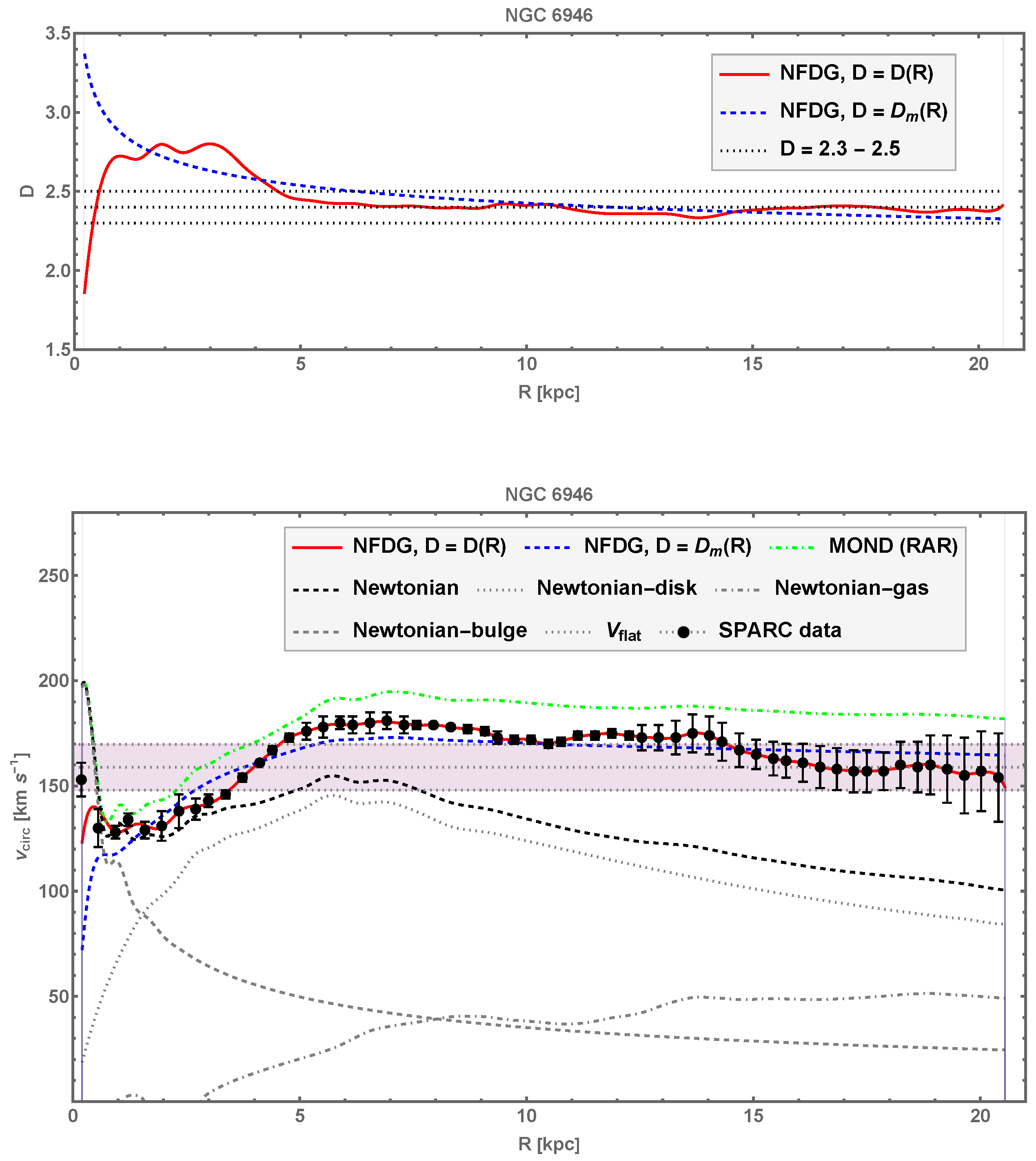
4.1. NGC 6946
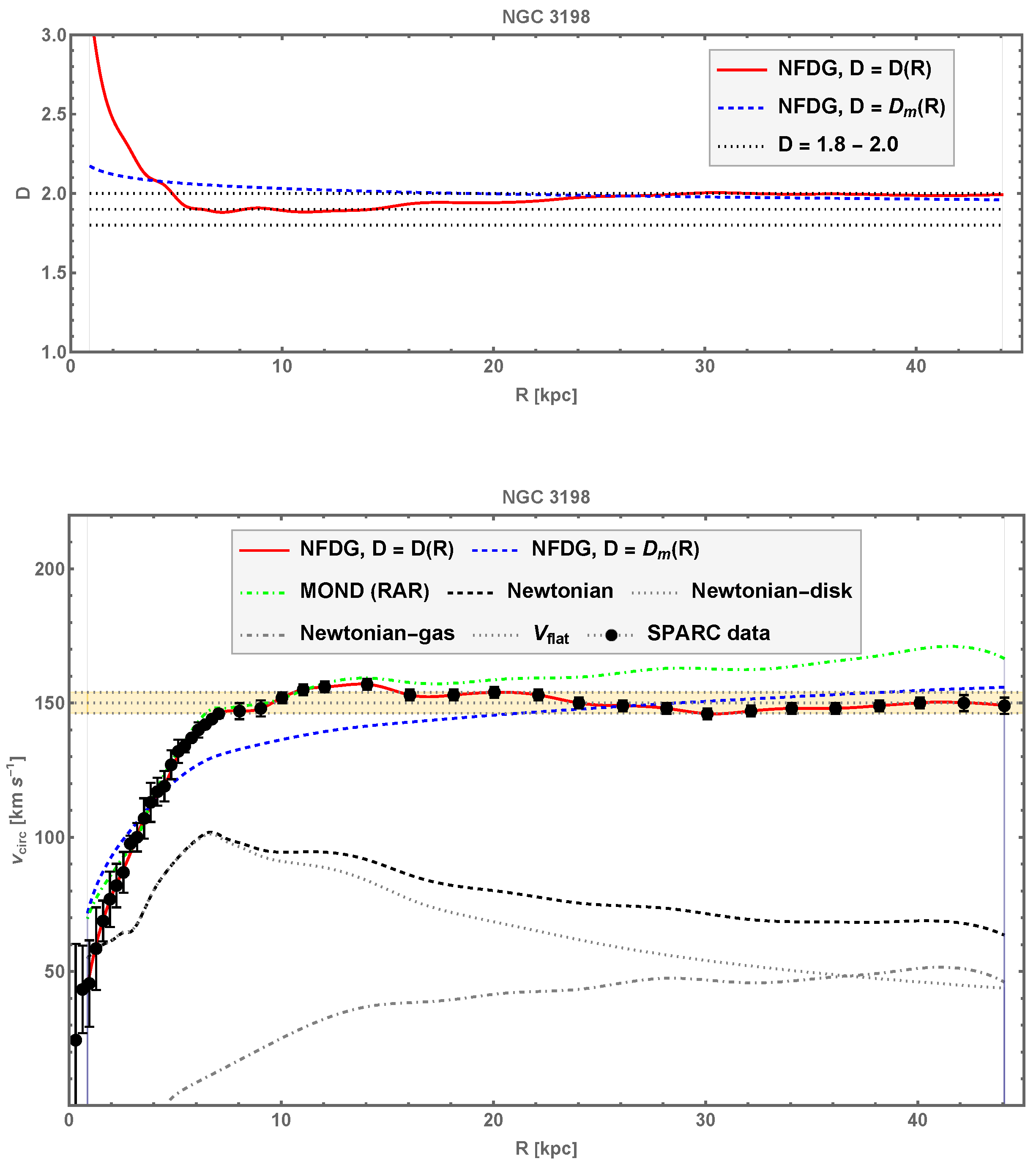
4.2. NGC 3198
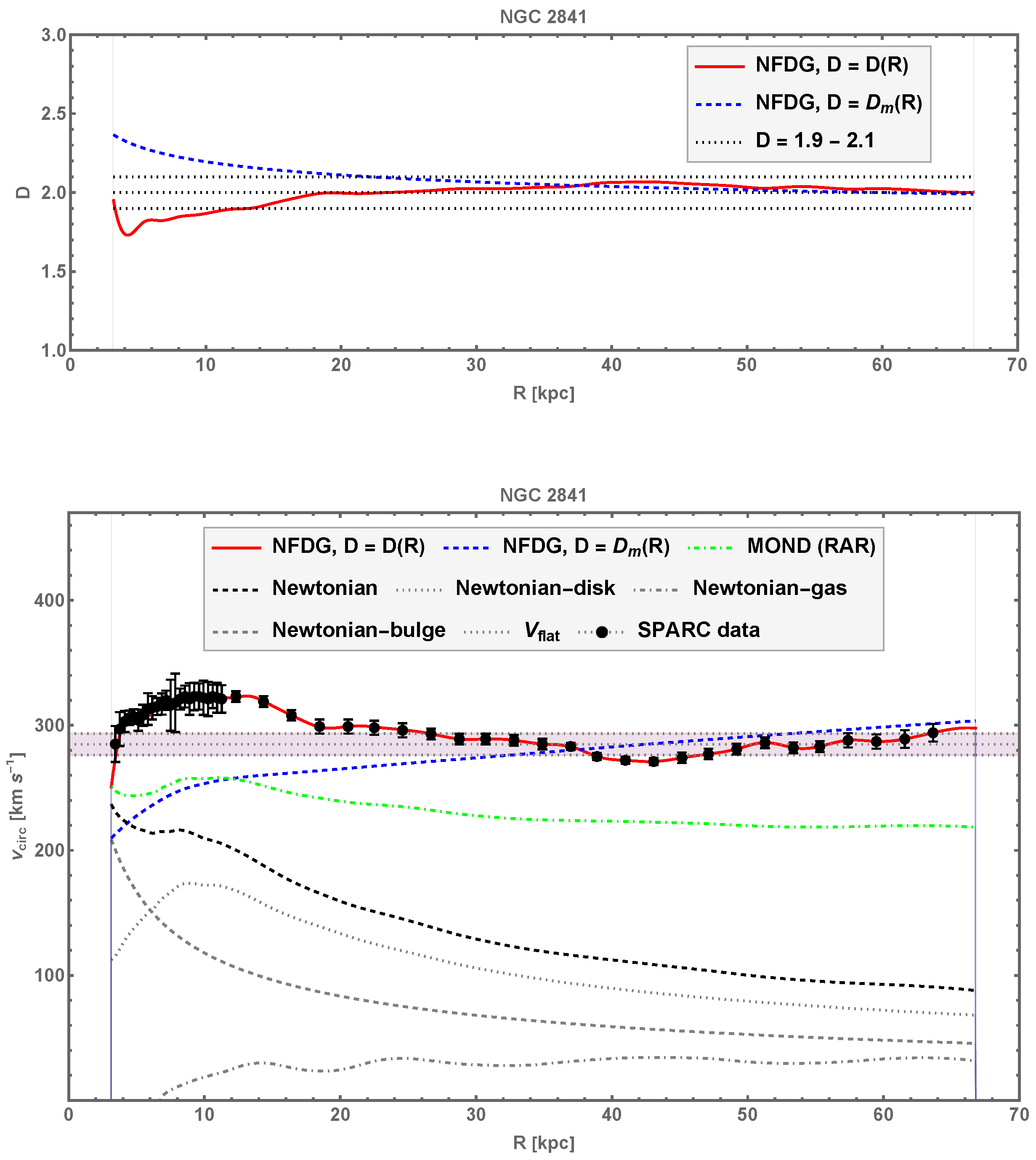
4.3. NGC 2841
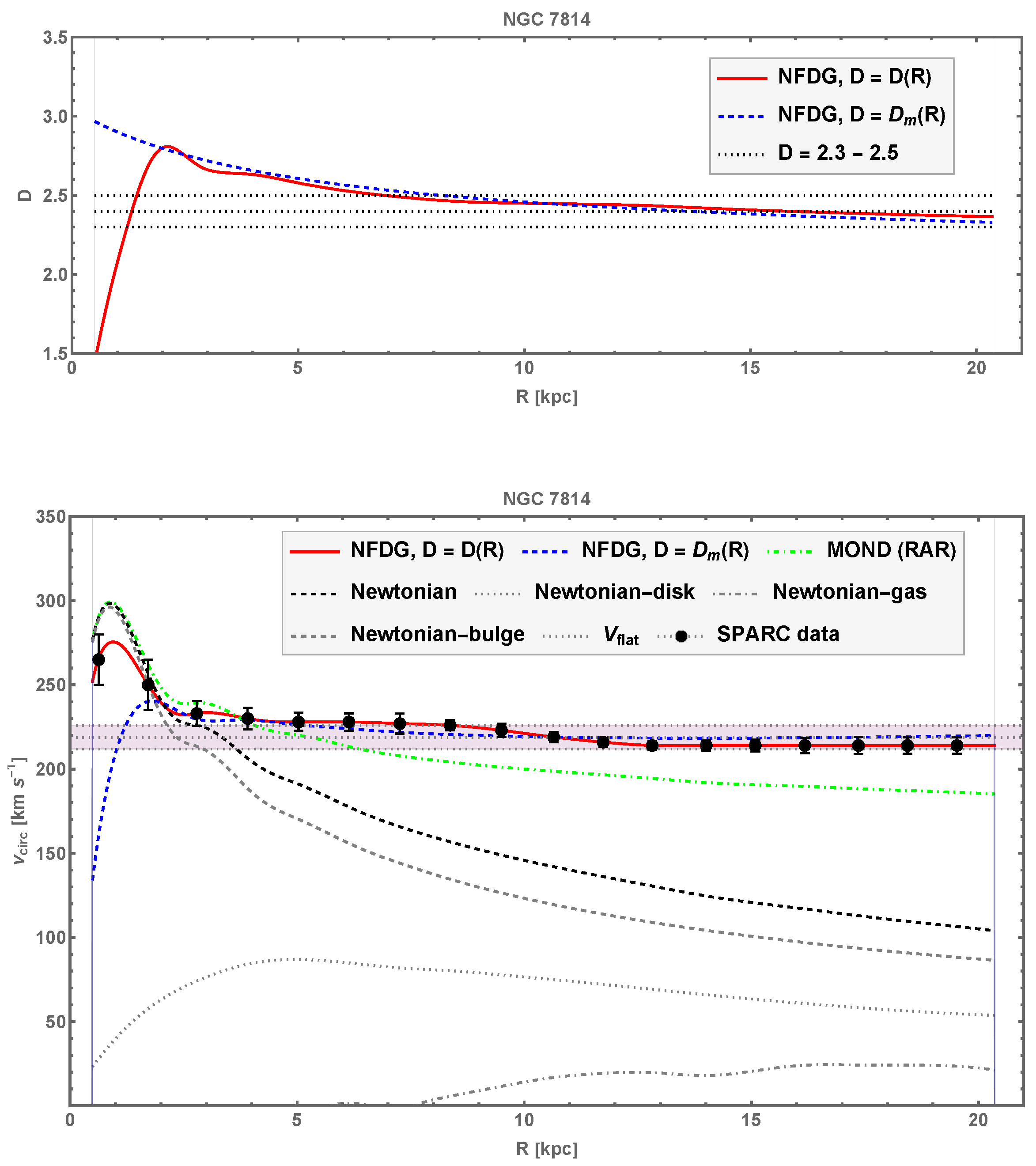
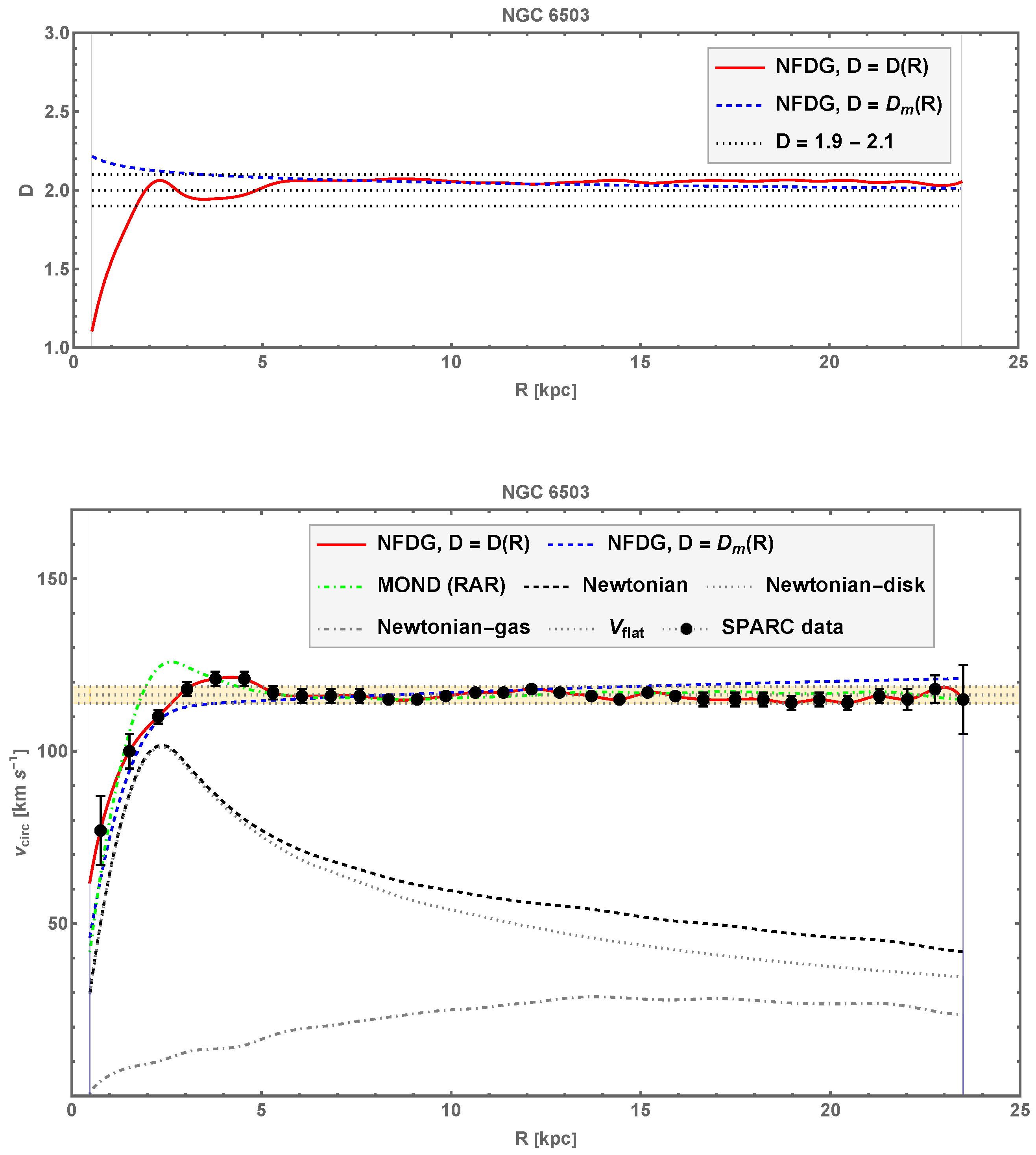
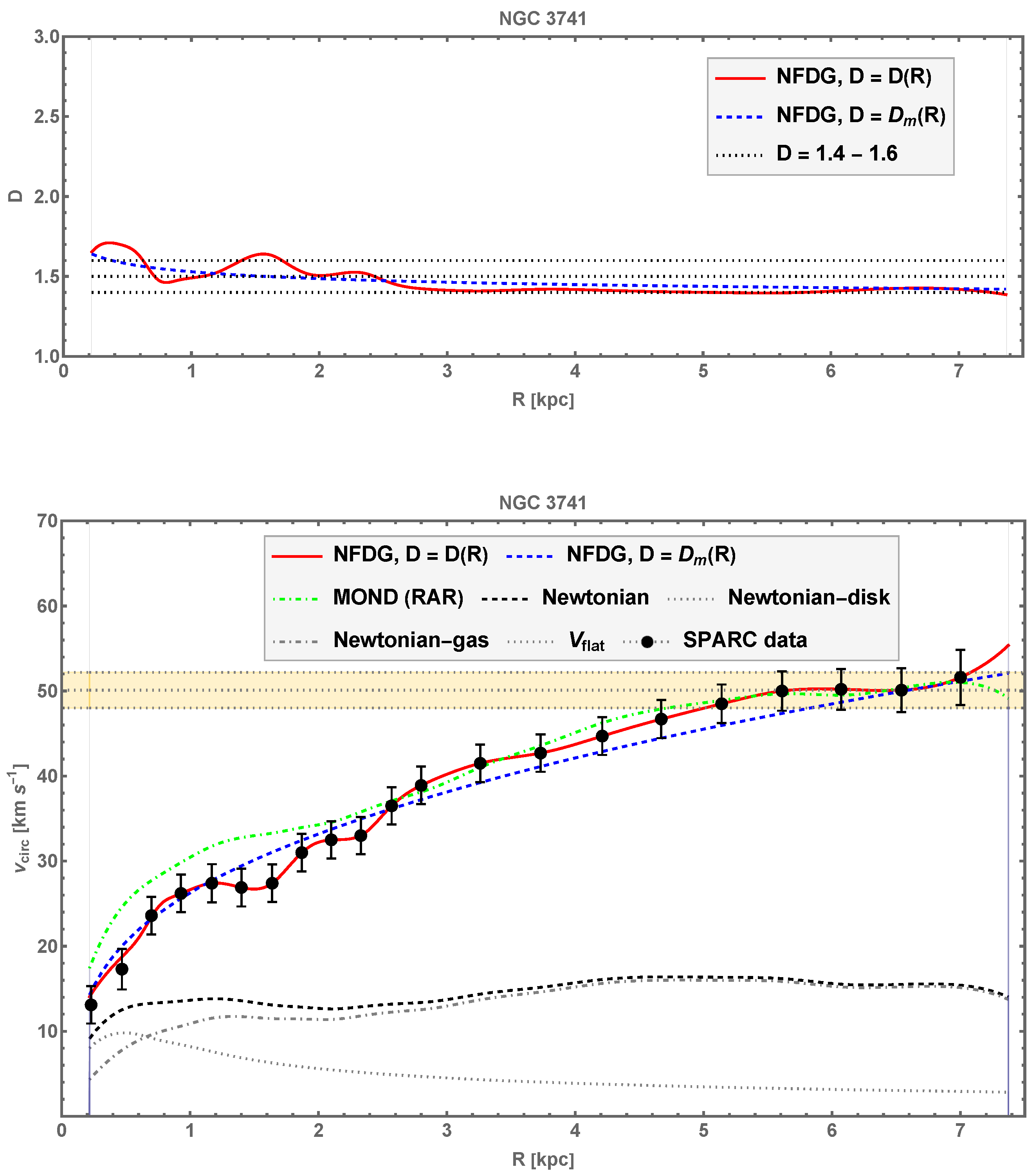
4.4. NGC 7814, NGC 6503, NGC 3741
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | A general overview of Newtonian Fractional-Dimension Gravity can also be found in the NFDG website [7], together with updated analyses of all the galaxies studied with NFDG methods. |
| 2 | This follows from the fundamental Equation (1) in paper IV [4] for spherically symmetric functions, originally introduced by Stillinger [47] and Svozil [48], adapted to an axially symmetric function in a dimensional metric space , i.e., |
References
- Varieschi, G.U. Newtonian Fractional-Dimension Gravity and MOND. Found. Phys. 2020, 50, 1608–1644, Erratum in Found. Phys. 2021, 51, 41.. [Google Scholar] [CrossRef]
- Varieschi, G.U. Newtonian Fractional-Dimension Gravity and Disk Galaxies. Eur. Phys. J. Plus 2021, 136, 183. [Google Scholar] [CrossRef]
- Varieschi, G.U. Newtonian Fractional-Dimension Gravity and Rotationally Supported Galaxies. Mon. Not. Roy. Astron. Soc. 2021, 503, 1915–1931. [Google Scholar] [CrossRef]
- Varieschi, G.U. Relativistic Fractional-Dimension Gravity. Universe 2021, 7, 387. [Google Scholar] [CrossRef]
- Varieschi, G.U. Newtonian fractional-dimension gravity and the external field effect. Eur. Phys. J. Plus 2022, 137, 1217. [Google Scholar] [CrossRef]
- Varieschi, G.U. Newtonian Fractional-Dimension Gravity and Galaxies without Dark Matter. Universe 2023, 9, 246. [Google Scholar] [CrossRef]
- Varieschi, G.U. Newtonian Fractional-Dimension Gravity (NFDG). 2020. Available online: https://gvarieschi.lmu.build/NFDG2020.html (accessed on 10 November 2025).
- Milgrom, M. A Modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys. J. 1983, 270, 365–370. [Google Scholar] [CrossRef]
- Milgrom, M. A Modification of the Newtonian dynamics: Implications for galaxies. Astrophys. J. 1983, 270, 371–383. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics: Implications for galaxy systems. Astrophys. J. 1983, 270, 384–389. [Google Scholar] [CrossRef]
- Famaey, B.; McGaugh, S. Modified Newtonian Dynamics (MOND): Observational Phenomenology and Relativistic Extensions. Living Rev. Rel. 2012, 15, 10. [Google Scholar] [CrossRef]
- Mannheim, P.D.; Kazanas, D. Exact Vacuum Solution to Conformal Weyl Gravity and Galactic Rotation Curves. Astrophys. J. 1989, 342, 635–638. [Google Scholar] [CrossRef]
- Mannheim, P.D.; Kazanas, D. Newtonian limit of conformal gravity and the lack of necessity of the second order Poisson equation. Gen. Rel. Grav. 1994, 26, 337–361. [Google Scholar] [CrossRef]
- Mannheim, P.D. Alternatives to dark matter and dark energy. Prog. Part. Nucl. Phys. 2006, 56, 340–445. [Google Scholar] [CrossRef]
- Moffat, J.W. Scalar-tensor-vector gravity theory. J. Cosmol. Astropart. Phys. 2006, 03, 004. [Google Scholar] [CrossRef]
- Calcagni, G. Geometry and field theory in multi-fractional spacetime. J. High Energy Phys. 2012, 01, 065. [Google Scholar] [CrossRef]
- Calcagni, G. Fractal universe and quantum gravity. Phys. Rev. Lett. 2010, 104, 251301. [Google Scholar] [CrossRef]
- Calcagni, G. Quantum field theory, gravity and cosmology in a fractal universe. J. High Energy Phys. 2010, 03, 120. [Google Scholar] [CrossRef]
- Calcagni, G. Multi-scale gravity and cosmology. J. Cosmol. Astropart. Phys. 2013, 12, 041. [Google Scholar] [CrossRef]
- Calcagni, G.; De Felice, A. Dark energy in multifractional spacetimes. Phys. Rev. D 2020, 102, 103529. [Google Scholar] [CrossRef]
- Calcagni, G. Multifractional theories: An updated review. Mod. Phys. Lett. A 2021, 36, 2140006. [Google Scholar] [CrossRef]
- Calcagni, G. Classical and quantum gravity with fractional operators. Class. Quant. Grav. 2021, 38, 165005. [Google Scholar] [CrossRef]
- Calcagni, G.; Varieschi, G.U. Gravitational potential and galaxy rotation curves in multi-fractional spacetimes. J. High Energy Phys. 2022, 08, 024. [Google Scholar] [CrossRef]
- Clifton, T.; Ferreira, P.G.; Padilla, A.; Skordis, C. Modified Gravity and Cosmology. Phys. Rept. 2012, 513, 1–189. [Google Scholar] [CrossRef]
- Saridakis, E.N.; Lazkoz, R.; Salzano, V.; Vargas Moniz, P.; Capozziello, S.; Jiménez, J.B.; De Laurentis, M.; Olmo, G.J.; Akrami, Y.; Bahamonde, S.; et al. Modified Gravity and Cosmology. An Update by the CANTATA Network; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar] [CrossRef]
- Garrett, K.; Duda, G. Dark Matter: A Primer. Adv. Astron. 2011, 2011, 968283. [Google Scholar] [CrossRef]
- Will, C.M. The Confrontation between General Relativity and Experiment. Living Rev. Rel. 2014, 17, 4. [Google Scholar] [CrossRef]
- Giusti, A. MOND-like Fractional Laplacian Theory. Phys. Rev. D 2020, 101, 124029. [Google Scholar] [CrossRef]
- Giusti, A.; Garrappa, R.; Vachon, G. On the Kuzmin model in fractional Newtonian gravity. Eur. Phys. J. Plus 2020, 135, 798. [Google Scholar] [CrossRef]
- Benetti, F.; Lapi, A.; Gandolfi, G.; Salucci, P.; Danese, L. Dark Matter in Fractional Gravity. I. Astrophysical Tests on Galactic Scales. Astrophys. J. 2023, 949, 65. [Google Scholar] [CrossRef]
- Benetti, F.; Lapi, A.; Gandolfi, G.; Haridasu, B.S.; Danese, L. Dark Matter in Fractional Gravity II: Tests in Galaxy Clusters. Universe 2023, 9, 329. [Google Scholar] [CrossRef]
- Benetti, F.; Lapi, A.; Gandolfi, G.; Butt, M.A.; Boumechta, Y.; Haridasu, B.S.; Baccigalupi, C. Dark Matter in Fractional Gravity III: Dwarf Galaxies Kinematics. Universe 2023, 9, 478. [Google Scholar] [CrossRef]
- Llanes-Estrada, F.J. Elongated Gravity Sources as an Analytical Limit for Flat Galaxy Rotation Curves. Universe 2021, 7, 346. [Google Scholar] [CrossRef]
- Moradpour, H.; Jalalzadeh, S.; Javaherian, M. Fractional stars. Astrophys. Space Sci. 2024, 369, 98. [Google Scholar] [CrossRef]
- Pascoli, G. A comparative study of MOND and MOG theories versus the κ-model: An application to galaxy clusters. Can. J. Phys. 2024, 102, 69–84. [Google Scholar] [CrossRef]
- Pascoli, G. The κ-Model under the Test of the SPARC Database. Universe 2024, 10, 151. [Google Scholar] [CrossRef]
- Pascoli, G.; Pernas, L. Is Dark Matter a Misinterpretation of a Perspective Effect? Symmetry 2024, 16, 937. [Google Scholar] [CrossRef]
- Baryshev, Y.; Teerikorpi, P. Discovery of Cosmic Fractals; World Scientific: River Edge, NJ, USA, 2002. [Google Scholar]
- Mandelbrot, B. The Fractal Geometry of Nature—Revised and Enlarged Edition; W. H. Freeman and Comp.: New York, NY, USA, 1983. [Google Scholar]
- Nottale, L. Scale Relativity and Fractal Space-Time; Imp. Coll. Press: London, UK, 2011. [Google Scholar]
- Calcagni, G. Multifractional theories: An unconventional review. J. High Energy Phys. 2017, 03, 138. [Google Scholar] [CrossRef]
- Falconer, K.J. The Geometry of Fractal Sets; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Barnsley, M. Fractals Everywhere: New Edition; Academic Press: San Diego, CA, USA, 1993. [Google Scholar]
- Lelli, F.; McGaugh, S.S.; Schombert, J.M. SPARC: Mass Models for 175 Disk Galaxies with Spitzer Photometry and Accurate Rotation Curves. Astron. J. 2016, 152, 157. [Google Scholar] [CrossRef]
- Li, P.; Lelli, F.; McGaugh, S.; Schombert, J. Fitting the radial acceleration relation to individual SPARC galaxies. Astron. Astrophys. 2018, 615, A3. [Google Scholar] [CrossRef]
- Li, P.; McGaugh, S.S.; Lelli, F.; Schombert, J.M.; Pawlowski, M.S. Incorporating baryon-driven contraction of dark matter halos in rotation curve fits. Astron. Astrophys. 2022, 665, A143. [Google Scholar] [CrossRef]
- Stillinger, F.H. Axiomatic basis for spaces with noninteger dimension. J. Math. Phys. 1977, 18, 1224–1234. [Google Scholar] [CrossRef]
- Svozil, K. Quantum field theory on fractal spacetime: A new regularisation method. J. Phys. Math. Gen. 1987, 20, 3861–3875. [Google Scholar] [CrossRef]
- Palmer, C.; Stavrinou, P. Equations of motion in a non-integer-dimensional space. J. Phys. Math. Gen. 2004, 37, 6987–7003. [Google Scholar] [CrossRef]
- Binney, J.; Tremaine, S. Galactic Dynamics: Second Edition; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Cohl, H.S.; Kalnins, E.G. Fourier and Gegenbauer expansions for a fundamental solution of the Laplacian in the hyperboloid model of hyperbolic geometry. J. Phys. Math. Gen. 2012, 45, 145206. [Google Scholar] [CrossRef]
- NIST Digital Library of Mathematical Functions. Release 1.2.4 of 2025-03-15. Olver, F.W.J., Olde Daalhuis, A.B., Lozier, D.W., Schneider, B.I., Boisvert, R.F., Clark, C.W., Miller, B.R., Saunders, B.V., Cohl, H.S., McClain, M.A., Eds.; Available online: https://dlmf.nist.gov/ (accessed on 10 November 2025).
- Tarasov, V.E. Fractional Dynamics Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Tarasov, V.E. Anisotropic fractal media by vector calculus in non-integer dimensional space. J. Math. Phys. 2014, 55, 083510. [Google Scholar] [CrossRef]
- Tarasov, V.E. Vector calculus in non-integer dimensional space and its applications to fractal media. Commun. Nonlinear Sci. Numer. Simul. 2015, 20, 360–374. [Google Scholar] [CrossRef]
- Lelli, F.; (Arcetri Astrophysical Observatory (INAF), Florence, Italy). Private communication, 2024.
- Chae, K.H.; Lelli, F.; Desmond, H.; McGaugh, S.S.; Li, P.; Schombert, J.M. Testing the Strong Equivalence Principle: Detection of the External Field Effect in Rotationally Supported Galaxies. Astrophys. J. 2020, 904, 51. [Google Scholar] [CrossRef]
- Li, P.; Lelli, F.; McGaugh, S.; Schombert, J. A comprehensive catalog of dark matter halo models for SPARC galaxies. Astrophys. J. Suppl. 2020, 247, 31. [Google Scholar] [CrossRef]
- Sancisi, R. The Visible Matter—Dark Matter Coupling 2003. Available online: http://arxiv.org/abs/astro-ph/0311348 (accessed on 10 November 2025).
- Mathematica, Version 14.2. Mathematica. Wolfram Research Inc.: Champaign, IL, USA, 2024. Available online: https://www.wolfram.com/mathematica (accessed on 10 November 2025).
- McGaugh, S.; Lelli, F.; Schombert, J. Radial Acceleration Relation in Rotationally Supported Galaxies. Phys. Rev. Lett. 2016, 117, 201101. [Google Scholar] [CrossRef]
- Lelli, F.; McGaugh, S.S.; Schombert, J.M.; Pawlowski, M.S. One Law to Rule Them All: The Radial Acceleration Relation of Galaxies. Astrophys. J. 2017, 836, 152. [Google Scholar] [CrossRef]
- Sanders, R.H.; McGaugh, S.S. Modified Newtonian Dynamics as an Alternative to Dark Matter. Annu. Rev. Astron. Astr. 2002, 40, 263–317. [Google Scholar] [CrossRef]
- Gentile, G.; Famaey, B.; de Blok, W.J.G. THINGS about MOND. Astron. Astrophys. 2011, 527, A76. [Google Scholar] [CrossRef]
- Gentile, G.; Jozsa, G.I.G.; Serra, P.; Heald, G.H.; de Blok, W.J.G.; Fraternali, F.; Patterson, M.T.; Walterbos, R.A.M.; Oosterloo, T. HALOGAS: Extraplanar gas in NGC 3198. Astron. Astrophys. 2013, 554, A125. [Google Scholar] [CrossRef]
- Begeman, K.G.; Broeils, A.H.; Sanders, R.H. Extended rotation curves of spiral galaxies: Dark haloes and modified dynamics. Mon. Not. Roy. Astron. Soc. 1991, 249, 523. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Varieschi, G.U. Newtonian Fractional-Dimension Gravity and the Mass-Dimension Field Equation. Universe 2025, 11, 388. https://doi.org/10.3390/universe11120388
Varieschi GU. Newtonian Fractional-Dimension Gravity and the Mass-Dimension Field Equation. Universe. 2025; 11(12):388. https://doi.org/10.3390/universe11120388
Chicago/Turabian StyleVarieschi, Gabriele U. 2025. "Newtonian Fractional-Dimension Gravity and the Mass-Dimension Field Equation" Universe 11, no. 12: 388. https://doi.org/10.3390/universe11120388
APA StyleVarieschi, G. U. (2025). Newtonian Fractional-Dimension Gravity and the Mass-Dimension Field Equation. Universe, 11(12), 388. https://doi.org/10.3390/universe11120388





