1. Introduction
A renewal of interest in studying black holes (BHs) came from the direct detection of gravitational waves by Laser Interferometer Gravitational-Wave Observatory (LIGO) detectors from two merging stellar mass BH systems [
1] in 2016 that opened a new era of possibilities in astronomy, astrophysics and gravitational theories. One of the routes for the understanding of gravity and its relation with the other fundamental interactions, namely the hierarchy problem, considers that the universe is somewhat embedded and evolves in a higher-dimensional space-time. This is not a new idea. Most of these models have been Kaluza–Klein and/or string inspired, such as the seminal works of Arkani-Hamed, Dvali, and Dimopolous (ADD) [
2] with a six-dimensional bulk for large extra dimensions where only the sub millimeter gravity accessed and the other gauge interactions remain confined in the four-dimensional space-time. With the use of the Israel–Lanczos junction condition [
3], the popular Randall–Sundrum model [
4,
5] attracted much attention, specifically model II [
5] that proposed an infinite five-dimensional model that shared similarities with a four-dimensional model that appealed to the holographic AdS/CFT conjecture [
6]. In model II, the so-called three-brane is embedded in a five-dimensional anti-de Sitter (AdS5) space-time focused on an explanation of the behavior of gravity. Another popular high-dimensional model relies on the Dvali–Gabadadze–Porrati [
7] model that considers the 3 + 1 Minkowski space-time embedded in a flat five-dimensional bulk. One common characteristic of these models and variants is that the embedding is not completely defined. Thus, in such models, the embedding is static, i.e., it is fixed to a boundary and/or specific conditions are needed to obtain its dynamics. The extrinsic curvature does not exert any dynamical influence on the relation of the bulk and the embedded space-time and is commonly replaced by those conditions.
Our present work is essentially based on previous communications [
8,
9,
10] that proposed a five-dimensional model using dynamical embedding using the Nash embedding theorem [
11,
12] to investigate possible physical consequences of the perturbations of the geometry in embedded spaces. This present framework is different from the standard braneworld models since the extrinsic curvature exerts a fundamental role leading to a dynamical embedding rather than static embedding. Then, we propose a model-independent formulation, avoiding referring to this model as a braneworld model considering all the differences between the formulations. In fact, standard braneworld models may be described as a particular case of the covariant-independent approach presented in this paper and may be regarded as a family of stable perturbations of a given locally embedded background space-time.
Due to the fact that BHs turned out to be one of the crucial elements to understand the behavior of gravity, the study of exact solutions provides an important test for alternative theories of gravity [
13,
14,
15,
16,
17,
18,
19]. In previous communications, we explored a four-dimensional spherically symmetric geometry embedded in a five-dimensional bulk. For such geometry, we found that a higher space for embedding with a bulk larger than 5 is a must due to strong restrictions on the embedding itself [
20]. In this case, the Newtonian limit could not be correctly obtained. We obtained similar results with a classical thermodynamic analysis for the before-mentioned geometry in which global stability was not a preferred state [
21]. Moreover, the analysis of the quasinormal frequencies of the BHs produced using the Wentzel, Kramers, and Brillouin (WKB) approximation [
22] also indicated serious constraints on embedding models in five dimensions, and the correct analysis of spherically symmetric geometry in an embedded space should be made at least with a six-dimensional bulk. This was effectively implemented in Ref. [
23] in which, besides the extrinsic curvature, we had the influence of the torsion vector
as a gauge group of rotations
in the extra dimensions. As a result, we obtained the correct embedding for a spherically symmetric metric producing a lukewarm BH and the appearance of an emergent cosmological constant
.
BHs are true accelerators of cosmic particles, capable of generating cosmic rays with unimaginable energies. To explain this phenomenon, some fundamental processes are evoked and take place in the vicinity of black holes, collisional processes [
24,
25] or those related to particle decay [
26] both arising from a process of harnessing gravitational energyor accelerating processes related to electromagnetic fields from the relationship between BHs and plasma structures, such as accretion disks and jets [
27,
28,
29]. From a broader perspective, BHs are perfect cosmic laboratories for testing fundamental theories, such as the theory of general relativity, but they also serve to scrutinize astrophysical phenomena that are still poorly understood. In astronomy, for example, understanding the behavior of galactic black holes is the same as understanding the formation properties of the host galaxy [
30,
31]. The gravitational influence of these BHs affects star formation and galactic dynamics. The interplay between these supermassive BHs and the surrounding gas can influence the formation and evolution of galaxies, regulating the rate of star formation and the distribution of matter. Also noteworthy is the case of stellar mass BHs, born from the collapse of massive stars, which provide insights into the process of stellar formation and evolution. The observation of gamma ray burst data associated with the multimessenger astronomy of gravitational wave emission can be a good way to link the way particles accelerate at the edge of stellar BHs. For instance, in both the stellar and galactic cases, the acceleration of particles near black holes can lead to the appearance of UHECRs, which have energies much higher than any particle that can be produced in terrestrial accelerators [
25,
32,
33,
34,
35,
36,
37].
Investigating the origin of these particles and how they propagate through space is one of the main focuses of astroparticle physics. These cosmic messengers can come from gamma-ray bursts and other extreme phenomena in the universe, but in particular, they can be accelerated at the edge of BHs. The most standard way to understand this is through the acceleration of particles in accretion disks. In these disks, particles are accelerated to speeds close to that of light, thanks to intense electric fields, modulated by the powerful magnetic fields present in the region. This acceleration is the main mechanism for the production of cosmic rays. Another way comes from the fact that many black holes, especially supermassive ones, launch jets of high-energy particles in opposite directions. These jets are composed of matter accelerated to speeds close to that of light and can extend for millions of light-years. It is worth noting, however, that the energies of UHECRs that exceed the Greisen–Zatsepin–Kuzmin (GZK) limit denote energy sources that are not yet understood [
27,
32,
34,
38]. A deep understanding of the spectrum beyond GZK can provide important contributions to the link between the phenomenon described here (the acceleration of particles at the edge of black holes from the collisional BSW effect) and the observation of UHECRs. By describing a collisional mechanism for extracting gravitorotational energy from a black hole, the BSW effect suggests that these objects are not only sinks of matter but can also be sources of energy.
In this paper, we maintain the same five-dimensional bulk with a different metric. We investigate some consequences of a vacuum solution of an embedded four-dimensional model of an axially symmetric gravitational field for a rotating BH to obtain a model for the final fate of the gravitational collapse. In the second section, we make highlights of a mathematical review on embeddings and the general mechanism to obtain the induced field equations in four-dimensional space-time starting from a five-dimensional bulk. The third section focuses on an analysis of the line element of the generic extension of the Kerr metric known as the Gürses–Gürsey metric [
39], where we obtain the metric’s singularity and horizons. In the fourth section, we discuss the geodesic of test particles and collision effects. In the final section, we present our final remarks and prospects.
2. Highlights on Embeddings and Induced Field Equations
To study the physics of embeddings, we simplify our analyses, starting from a classical approach. Mainly motivated from the hierarchy problem of fundamental interactions, the “not-so-new" physical problems such as dark matter and dark energy problems suggest that something is missing in the LHS of Einstein’s equations. To solve these issues, embeddings may provide a viable direction to follow. We adopt dynamical embedding to differ from popular braneworld models, where the perturbations are triggered from the confined sources and the brane is generated by a scalar field coupled to gravity that needs a sophisticated mechanism to localize matter on the brane. Generally speaking, in these models, a common practice is to rely on junction conditions that replace the extrinsic curvature by the energy–momentum tensor of the confined sources. In fact, braneworld models may be described as a particular case of the covariant-independent approach presented in this paper.
The general solution for embedding between geometries is credit to J. Nash [
11]. The Nash theorem proposes that a stable embedding with a regular map
(
) occurs by means of a smooth and differentiable process. This makes it possible for any embedded metric geometry to be generated continuously through a sequence of small metric orthogonal perturbations such as
where
is the perturbed metric and
is the extrinsic curvature. The
y parameter is an arbitrary spatial coordinate wherein orthogonal perturbations are driven. The overbar sign indicates a background (non-perturbed) quantity.
By definition, written in the Gaussian frame
, the extrinsic curvature is given by
which tells us how normal unitary vector
in the embedded space deviates from the tangent plane. As a result, the embedded geometry bends. This characteristic sounds interesting to investigate physical problems in cosmology and astrophysics with strong gravitational sources. Then, we investigated the extrinsic curvature per se as an orthogonal complement to the tangent component of the gravitational field,
. Concerning notation, capital Latin indices are fixed to 5. Small-case Latin indices refer to the only one extra dimension fixed to 1. All Greek indices refer to the embedded space-time running from 1 to 4.
From Equation (
1), one obtains Nash’s deformation formula given by
This is the core of Nash’s embedding theorem published in 1954 applied to non-Euclidean metrics [
11] and in 1956 to Riemannian metrics [
12] and later extended to pseudo-Riemanian manifolds by Greene [
40]. This is a key condition for the perturbations of an embedded space inside the bulk. It also imposes a geometric constraint on the deformations of the embedded space. In this framework, these deformations are not arbitrary and can be generated by perturbations along the direction
orthogonal to the embedded space
by the Lie transport of the Gaussian frame
that gives
where we define a differentiable and regular map by
. In Equation (
5), the independent unit vector field,
, is orthogonal to
and is not affected by perturbations in that direction. This mechanism avoids possible coordinate gauges that may lead to false perturbations. The perturbed coordinate
defines a coordinate chart between the bulk and the embedded space-time. Equations (
4) and (
5) link the freedom of perturbations of the embedded space-time to the bulk once the extra dimensions do not share the same diffeomorphism invariance of the embedded space. In five dimensions, this process is simplified and just one deformation parameter suffices to locally deform the embedded background in the same way as conducted in Equations (
4) and (
5).
In the present application, we adopt a five-dimensional bulk,
, wherein a smaller space,
, is isometrically embedded. Then, one defines chart
and the bulk metric
as
Consequently, gravitational action
S can be defined with confined matter fields as
where
is a fundamental energy scale on the embedded space, and the curly
denotes the five-dimensional Ricci scalar of the bulk. The Lagrangian
denotes the bulk source Lagrangian.
One important aspect of the embedding is the Gauss and Codazzi equations given by
where
denotes the five-dimensional Riemann tensor, and
is the four-dimensional Riemann tensor. The semicolon sign in Equation (
9) represents the ordinary covariant derivative with respect to the metric
and
. These equations reflect the integrability conditions for the embedding to assure the relation of the bulk with the embedded space. The Nash deformation formula in Equation (
3) guarantees the dynamics of the embedded space by solving Equations (
8) and (
9). The bulk Lagrangian source
is somewhat independent of the embedding. Since only gravity should access the bulk by the geometrical constraint of Equation (
3),
is confined as
from the generic components of
of the energy–momentum tensor of the bulk. The components
,
, and
define the energy–momentum of the tangent (tensor), vector, and scalar components of
.
and
G denote the matter gauge fields and the gravitational Newtonian constant, respectively.
As a common practice, the variation in the Einstein–Hilbert action in Equation (
7) with respect to the bulk metric
gives higher-dimensional Einstein equations written as
where
is the energy scale parameter and
is the energy–momentum tensor for the bulk, and the five-dimensional bulk with constant curvature whose related Riemann tensor is
where
denotes the bulk metric components in arbitrary coordinates and constant curvature
is either zero (flat bulk) or it can have positive (deSitter) or negative (anti-deSitter) cosmological constant
. For a flat bulk, one obtains the four non-perturbed induced gravitational field equations from a five-dimensional bulk as [
8,
9,
10,
41,
42]
where
denotes the four-dimensional Einstein tensor and
is the deformation tensor. The non-perturbed extrinsic term
in Equation (
12) is given by
where we denote the mean curvature by
and
and the Gaussian curvature by
. By direct derivation, Equation (
14) is conserved in the sense that
3. A Gürses–Gürsey Metric Embedded in Five-Dimensions
In the present application, we are interested in realizing how the extrinsic effect unfolds in this gravitational system. Then, we consider a vacuum solution of a four-dimensional axially symmetric gravitational field. In Boyer–Lindquist coordinates, we start with a generic extension of the Kerr metric, i.e., the line element of the Gürses–Gürsey metric [
39] written as
where we have introduced the notation
,
and
at the scale
, in which
J is the angular momentum and
m is a rotating mass. The function
is an arbitrary function of the radial coordinate
r. In principle, it should absorb a non-trivial effect from extrinsic geometry as a result of the embedding. In other words, we should calculate Equation (
13) to realize how the extrinsic effects propagate in the main field equation, i.e., Equation (
12). Clearly, when
, one obtains the standard Kerr solution, and fixing
and
, we recover the standard Schwarzchild metric. Thus, the solution of Equation (
13) can be generically written as
where
is a generic coordinate function.
Taking Equations (
17) and (
13), one obtains (with no sum for
)
where we can identify
and we can write the quantity
in terms of
as
As
is a conserved quantity, we can find six equations regarding
. After carrying out a calculation, one finds only two independent equations
and the relations
where
and
are generic functions from the direct integration of the functions in
. Hence, calculating
quantities, taking into account that
and
, we write
as
Assuming the simplest isotropic solution when
, one obtains
In order to determinate the function
, we insert Equation (
19) into the scalar gravitational equation of Equation (
12). In vacuum, with
, we rewrite Equation (
12) contracted with
in a more convenient form as
where we define the extrinsic scalar as
. Thus, using Equations (
16) and (
19), we calculate Equation (
21) and obtain the radial equation for the function
as
For the choice
, we obtain the solution
where the
parameter is regarded as a relic from extrinsic geometry, and
and
are integration constants.
To find the horizons
of the metric in Equation (
16), we start calculating the component
. Then, we obtain the related inner and outer horizons given by
By the condition
, we obtain the inner and outer ergospheres as
where we appropriately choose
and
.
When extrinsic curvature vanishes, setting
, in the previous results, then we recover the standard Kerr horizons. A real physical curvature singularity is seen in the Kretschmann scalar
at
but it remains finite at
. A singular ring is found at
and this result is independent of the presence of extrinsic curvature. Moreover, an important remark is that the zero mass limit of Equation (
23) does not lead to a flat Minkowski space of the metric in Equation (
16). In order to study a real solution, the radial coordinate is assumed to have one asymptotic region corresponding to
, but at this limit, the horizons
become singular and so is the metric in Equation (
16). Clearly, this can be avoided when imposing the boundary
and Equation (
23) that results in the simpler form
As a result, the inner and outer horizons are now given by
Moreover, the inner and outer ergospheres are
When extrinsic curvature vanishes, setting
, in the previous results, then the standard Kerr horizons and ergospheres are recovered again. In this case,
is referred as a tidal “extrinsic charge” in resemblance to Kerr–Newman solutions.
Using the free open-source SageMath [
43], we obtain
Figure 1 and
Figure 2. In
Figure 1, we propose an ansatz to constrain the
dimensionless tidal “extrinsic charge” that should have a cosmological magnitude, as defined in Ref. ([
44]), given by
where
is the dimensionless Hubble factor and
denotes the current cosmological parameter for matter density content adopting the baseline mean values of 68% intervals of base-
CDM model from Planck TT,TE,EE+lowE+lensing [
45]. Thus, one obtains
and we use it as a reference value.
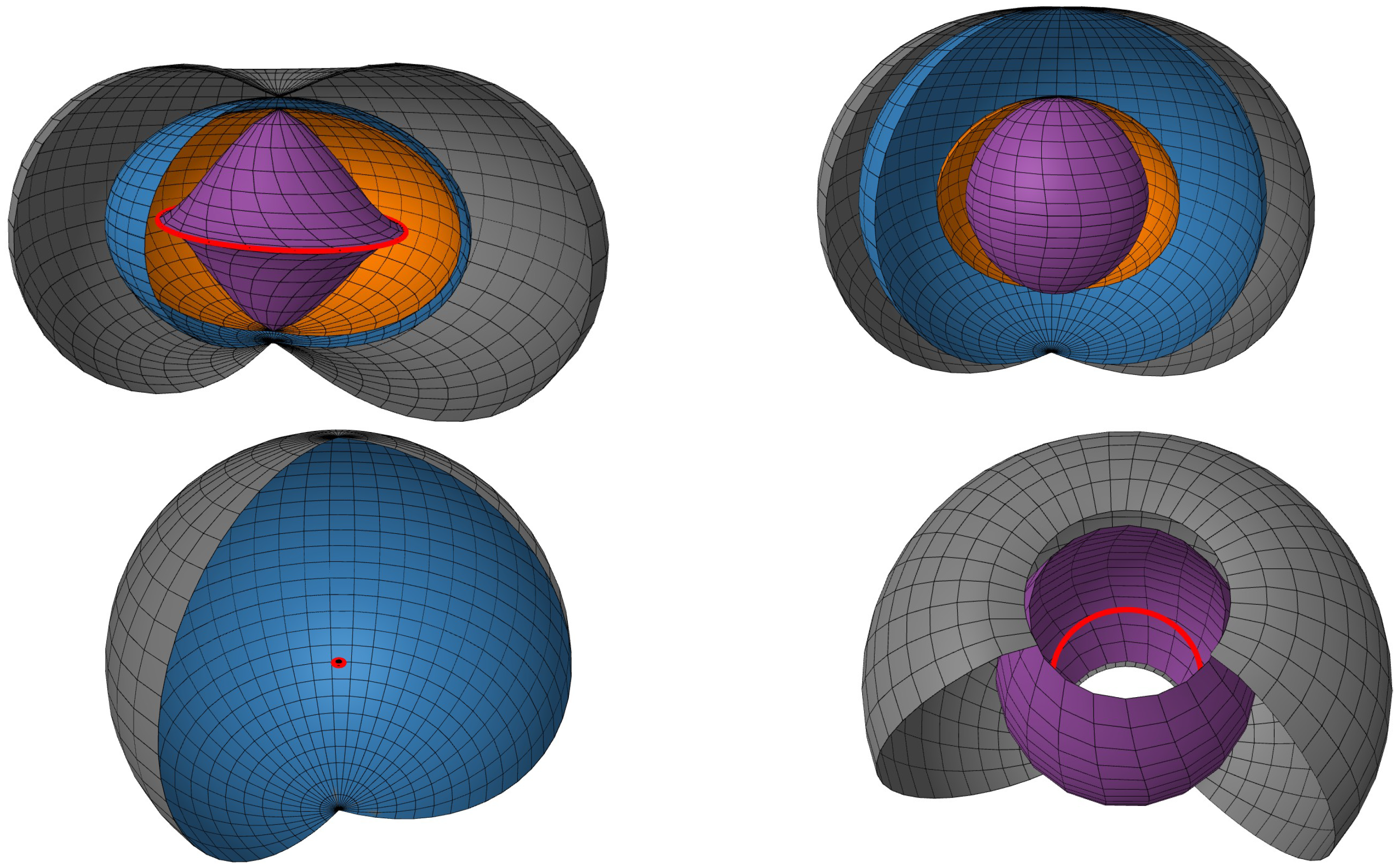
In
Figure 1, we present Gürses–Gürsey surfaces in the upper right and bottom panels. Fixing the values of
and
, for the optimal mass
, the ring singularity is naked and is shielded by the inner ergosphere. The curvature singularity lies at the kink in the inner ergosurface on the inside. The outer and inner ergosphere and horizons and singular ring are represented as grey, lilac, blue, orange, and red colors, respectively. For masses less than 2.4, the geometry is progressively “mutilated”, i.e., all horizons and ergospheres cease to converge to the ring singularity. On the other hand, regarding masses higher than 2.4, the inner horizon and inner ergosphere become progressively smaller up to being shielded by the ring singularity covered by the outer ergosphere and outer horizon. Just for the sake of comparison, Kerr surfaces are represented in the upper left panel. The overall pattern is similar to that described in the case of the Gürses–Gürsey metric. The difference lies in the fact that the masses in Kerr surfaces are lower to maintain the Kerr geometry. Thus, the reference values of mass is fixed at
but masses less than or higher than 1 progressively generate smaller inner horizons and ergospheres up to the ring singularity.
In
Figure 2, we compare images with relativistic aberration added to the accretion disk around BHs changed by extrinsic curvature relaxing to different values of
.The optimal mass value is
for all cases. Scale
a is fixed as
, and from left to right in the upper and bottom panels, we have the results for
, respectively. We found that higher values of the extrinsic term lead to the enlargement of the photon rings but also with an increase in the BH’s inner shadow. It is important to point out that the increase in the shadow comes from an increase in the inner horizons until the image of the disk’s underside vanishes. The upper left panel shows a lower value of
and the photon ring is not visible.
4. Geodesic of Test Particles and Collisional Effects
Once the properties of these BHs have been obtained with this approach, we analyze the geodesics of colliding classical charged particles at the BH stable orbits. For simplicity, we consider that particle geodesics do not present backreaction effects. It appears from the results that charged particles can be accelerated to ultrahigh energies in marginally bound orbits near extreme rotating embedded BHs in the presence of magnetic fields. Such a result can help us to understand, for example, high-energy astrophysical phenomena associated with BHs in the universe, in particular, the origin and mechanisms within the acceleration of UHECRs. The sources of UHECRs are still a subject of discussion and BHs are potential particle acceleration sources [
46,
47,
48].
Suppose that the described BH is surrounded by collisional particles along its possible stable orbits. When considering the motion of particles only under the action of gravity, the conserved quantities along geodesics are the energy and the angular momentum, represented, respectively, by the free-test particle energy in terms of the four-momentum
as
and the free-test particle angular momentum per unit rest mass
Such conserved quantities are respectively associated to Killing vectors
and
. Assuming the properties and symmetries presented here are similar to those of a Kerr or a Kerr–Newman BH, we can envisage that when particles are crossing the ergosphere, they acquire negative energy as ascertained by an observer at infinity [
49]. In this framework, the scattering process of colliding particles near the horizon of an extremal BH (
) can extract mass and angular momentum from the hole, reaching arbitrarily high center-of-mass energy, i.e., a particular case of the so-called Bañados–Silk–West (BSW) effect [
50]. Particle geodesics determined by an effective potential enables the determination of energy and angular momentum values in which the particles may escape to infinity [
51,
52]. Additionally, when magnetic fields are present and when a charged particle orbits the ISCO of the embedded BH of Equation (
16), an incoming particle can collide, leading to the expelling of the charged particle to infinity, even if
[
47], where
is the rotational astrophysical limit, a.k.a. the Thorne Limit [
53]. In this case, the presence of magnetic fields may change the frame-dragging aspects of the space-time near the ISCO, permitting the BSW effect for arbitrary values of
a.
Consider now two particles, each one with mass
, one of them at the ISCO and the other coming from infinity, with energies
and
and different angular momenta
and
. In this case, the center-of-mass energy (normalized by the particle mass
) of the two-particle system is given by [
50]
where
and
are the four velocities (
, where
is the proper time) of each particle. The four-momentum of the particle reads
, where
is the electromagnetic four-potential and
q is the charge of the particle. From the Lorentz gauge
, the only nonzero component of the four-potential is
, where
B is the uniform magnetic field present in the system. Therefore, the conserved quantities in Equations (
30) and (
31) are written, normalized by the particle mass
, as
Considering the conserved quantities in (
33) and (
34) (
) and the normalization condition
, we have the following system of equations:
where
is the normalized magnetic field strength. Here, we considered for simplicity only equatorial motions (i.e.,
).
The center-of-mass collision energy of two particles is calculated from Equation (
32).
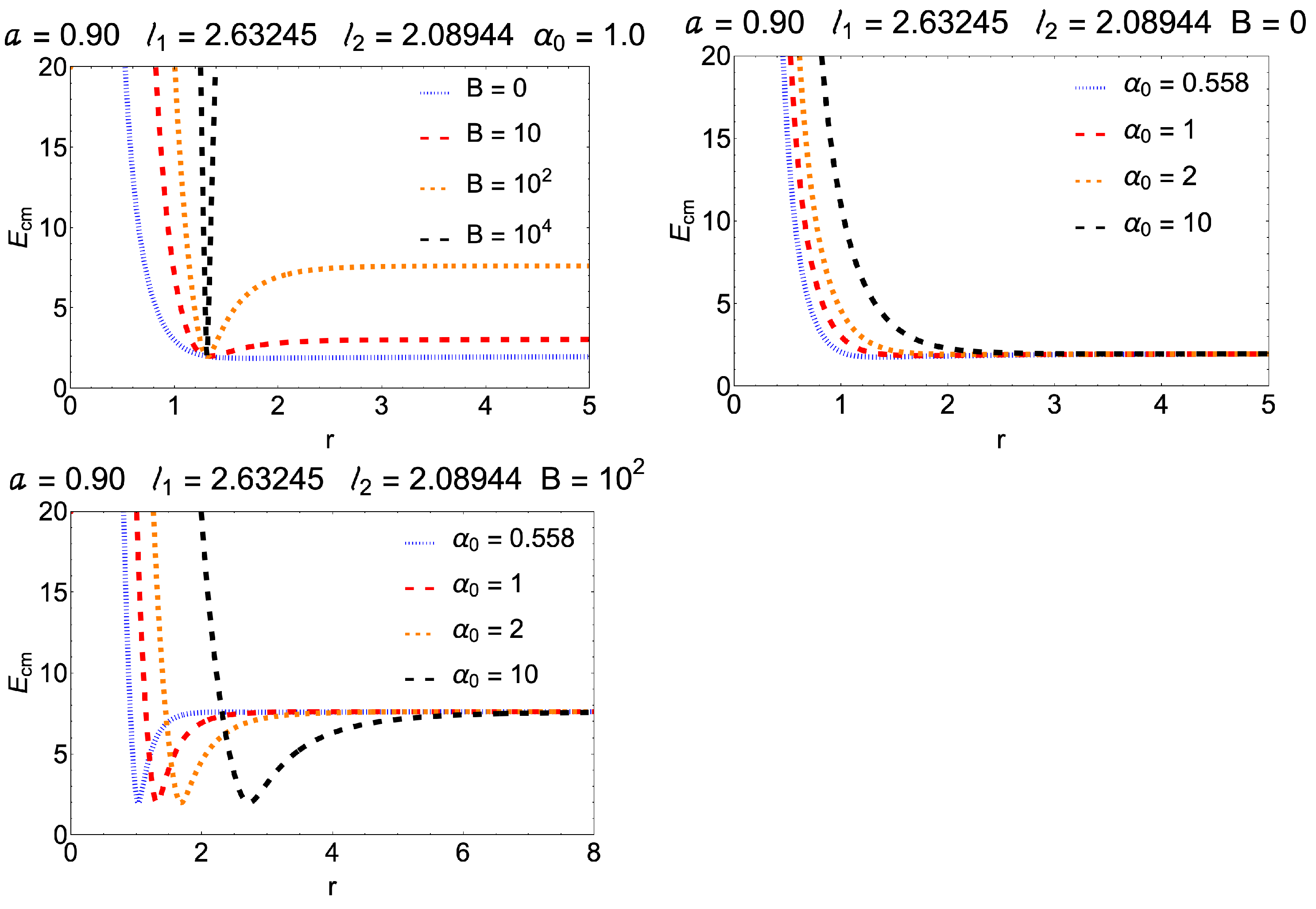
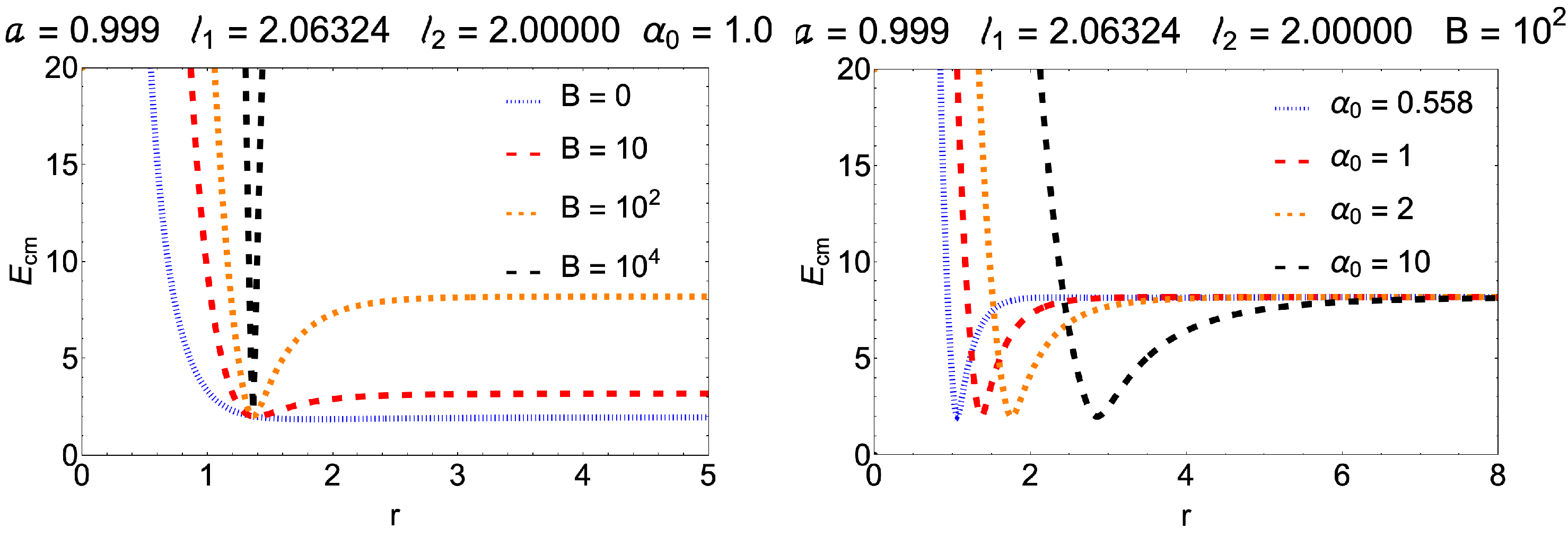
Figure 3 and
Figure 4 show the results of the
for a set of possible particle angular momenta for BH spins of order
and BH spins in a near-extremal (
) regime. Here, we use the permitted range
[
50] for the particle angular momenta. The results presented point to the possibility of particles being expelled to infinity at positions slightly shifted from the BH ISCO which depends on the intensity of
B and also on the intensity of
. For a fixed value of spin, say
, larger “extrinsic charge” values
cause accelerations to infinity, even at points relatively far from the event horizon. When the magnetic field is turned on, this effect becomes even more effective. The higher the values of
, the greater the chances that the particles will be expelled at positions far from the ISCO. For instance, when
, the ISCO is located at
. For the extreme value of
, in the presence of magnetic fields, the particle is expelled at
, far from the ISCO.