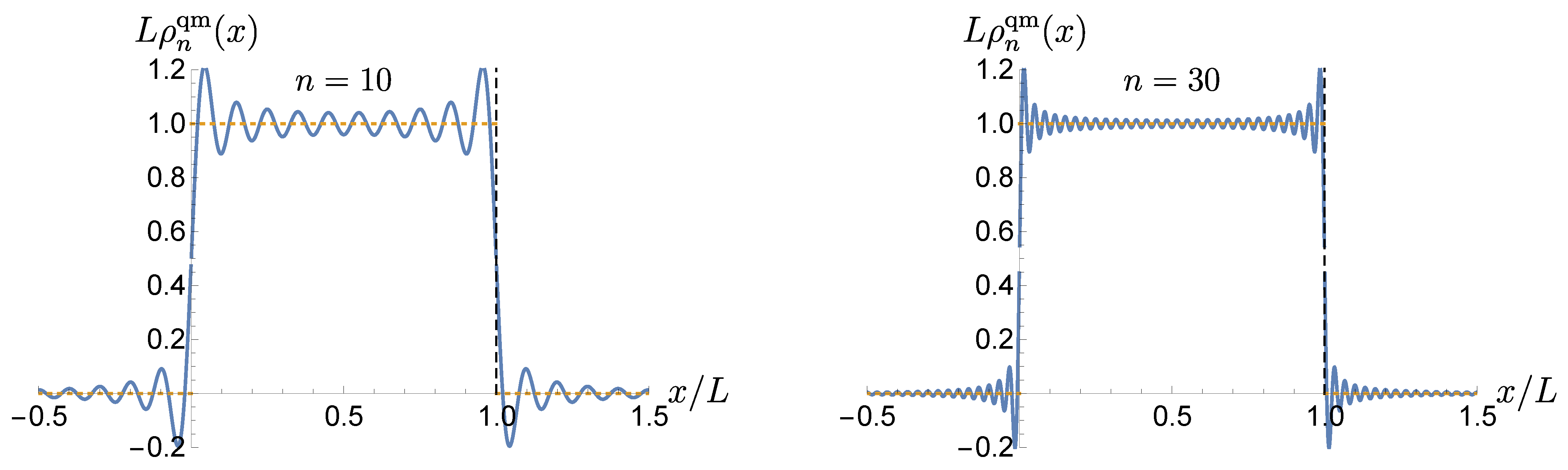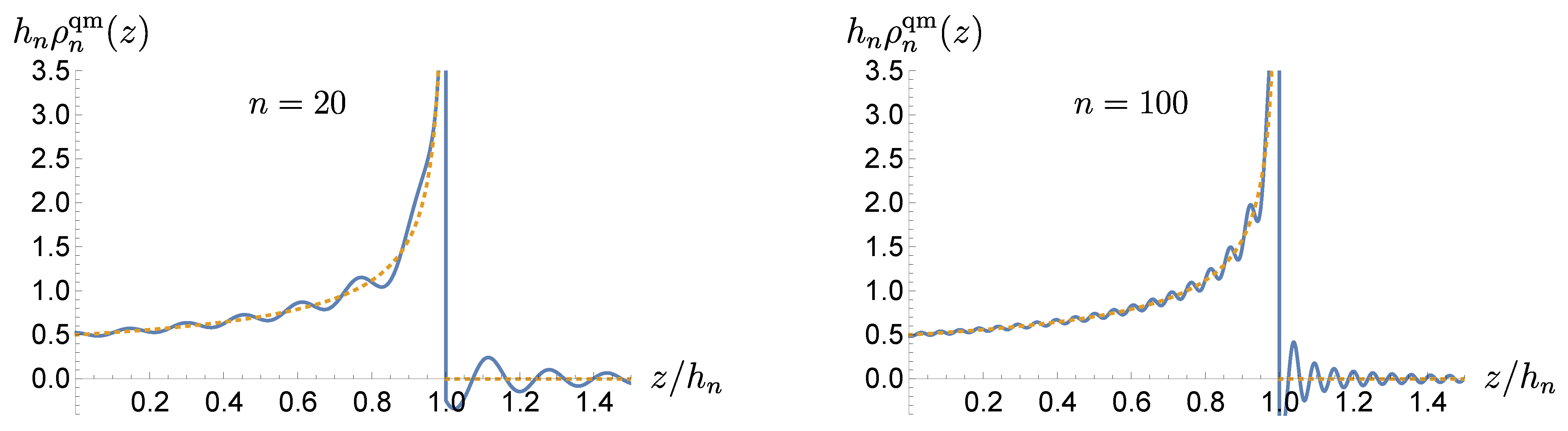1. Introduction
In general, the correspondence principle states that the predictions of a new physical theory becomes identical to the predictions of an old theory in the appropriate limit. For example, the correspondence principle is accomplished by special relativity, which reduces to the Newtonian prediction for velocities much smaller than the speed of light in a vacuum. Also, the general theory of relativity reduces to the Newtonian gravitation for weak gravitational fields. In a similar fashion, one expects the predictions of quantum mechanics to reproduce those of classical mechanics in some limit; however, such quantum-to-classical correspondence is more subtle, such that there is no agreement after a century of discussion. The main difficulty is perhaps that the conceptual frameworks of these theories are fundamentally different. This led Einstein to assert, as subtly discussed in his famous letters with Born, that quantum formalism is inadequate for providing a complete description of reality [
1].
In the literature, one can find various approaches to discussing the quantum-to-classical correspondence [
2,
3,
4,
5,
6], all of them rooted in either (i) Planck’s limit
or (ii) Bohr’s correspondence principle
[
7]. The former was introduced to show that the Planck energy density for black-body radiation reduces to the Rayleigh–Jeans law as
, and the latter was introduced to show that the transition frequency between neighboring energy levels in the hydrogen atom tends to the classical orbital frequency of the electron as
. As pointed out by Liboff, these two formulations are not universally equivalent [
8]. On the other hand, since these statements of the correspondence principle were introduced before the development of modern quantum mechanics, it was not clear how they should be applied to the wave function or matrix elements of an operator. Some methods addressing the quantum-to-classical correspondence in the context of modern quantum theory include the WKB method, the path integral formulation and Ehrenfest’s theorem. In Ref. [
9], we discussed in detail why these approaches are not universally reliable for investigating the classical limit of quantum mechanics, since, at the end, all of them require a very narrowly peaked probability density.
The quantum–classical correspondence has also been discussed using the Wigner phase-space formulation of quantum mechanics [
10]. This seems to be a natural framework to tackle this problem since both theories can be expressed in terms of a joint position–momentum distribution. Indeed, as shown in Ref. [
11] for a quantum harmonic oscillator, the classical limit of the Wigner function for highly excited states (i.e., coherent and WKB states) yields the microcanonical ensemble. Other important analyses of the quantum–classical correspondence in the framework of the Wigner function are presented in references [
12,
13,
14].
On the other side, a simpler and often more intuitive approach for visualizing the quantum–classical correspondence in periodic systems involves a direct comparison of the probability densities in either position or momentum spaces [
15,
16,
17,
18,
19]. Of course, such correspondence does not arise pointwise since the quantum distribution is highly oscillatory for
while the classical distribution is smooth between the turning points. Instead, as is widely accepted [
8], the correspondence should be understood in a locally averaged sense. The analytical evaluation of local averages is rather difficult in the position space and it can be performed only for the infinite square well potential [
15], whose quantum distribution is mathematically simple enough. This problem was invoked by Einstein to illustrate his concerns on the completeness of quantum mechanics, concluding that, despite the emergence of the classical distribution, it requires speaking of an ensemble and tells nothing on the individual particle [
1]
In recent papers, we reformulated the method to evaluate the local average of a quantum distribution based on two reasonable simple assumptions: (i) the system is periodic and (ii) the quantum distribution rapidly oscillates for high quantum numbers around the classical distribution [
20,
21,
22]. Periodicity allows us to express the classical and quantum distributions in Fourier series, and the local averaging process in position space implies that the quantum Fourier coefficient asymptotically approaches the classical Fourier coefficient. This simple procedure renders, at first order of approximation, the exact classical probability density for intricate periodic quantum systems, such as the nonrelativistic [
20] and relativistic [
23] harmonic oscillator, the hydrogen atom [
22] and the quantum bouncer [
9]. However, the analysis of the subdominant terms of the asymptotic distribution remains open. These terms, being nonvanishing, can be interpreted as a residual quantum behavior at the macroscopic scale. Physically, this means that the convergence in distribution does not produce the exact classical results but a macroscopic quantum distribution that consists of the classical distribution plus small oscillations around it. This analysis is far from trivial and, in this paper, we aim to fill this gap. In particular, we will focus on the quantum corrections to the quantum bouncer. As mentioned, in Ref. [
9], we computed the exact classical limit of this system and envisaged the emergence of the quantum corrections, which were not discussed nor computed there. Here, we shall present a full theory to investigate the quantum corrections in general, which are to be applied to this particular system. We choose this system because, apart from its importance from the quantum–mechanical side (which implies that the macroscopic description of a system emerges from quantum mechanics), it also has profound implications from the gravitational point of view, as we shall discuss in the following.
The universality of free fall (UFF), often referred to as the weak equivalence principle, states that every test body (being small enough to neglect the effects of gravity gradients) experiences the same acceleration in a gravitational field, regardless of their mass or internal composition. It constitutes one of the logical foundations of general relativity [
24]. The UFF also represents a profound difference between the classical and quantum domains since the dynamics of quantum particles are mass-dependent and thus not satisfying the essence of the weak equivalence principle [
25]. The validity of the UFF requires the Eötvös parameter to be zero for any couple of test bodies freely falling in the presence of a gravity field [
26,
27]. Classical and quantum experiments performed to constrain the value of this parameter have been reported, the former with an astonishing precision [
27,
28], highly overcoming that of the second ones [
29,
30,
31], though there are proposals to dramatically improve the precision of quantum tests [
32]. The validity of the UFF in quantum mechanics has also been studied theoretically, yielding many different conclusions by means of different approaches [
33,
34,
35]. Other authors have discussed the relevance of this subject as well [
36,
37]. In this paper, we demonstrate that the UFF is an emergent phenomenon. Following the method that we introduced, we show that the macroscopic behavior of the quantum bouncer implies, at first order of approximation, the validity of the UFF. However, the quantum corrections indicate that, even at the macroscopic scale, there is a residual mass-dependent quantum–mechanical behavior, which implies that the UFF is not universal at all but an emergent phenomenon in the classical world.
The remainder of this paper is organized as follows. In
Section 2, we introduce the method in a pedagogical fashion. For the sake of clarity, we first discuss what the classical probability density means and then we reformulate the local averages in the Fourier space. As a guiding model, in
Section 3, we apply the method to the infinite square well potential. Next, in
Section 4, we show that, for a particle bouncing under a gravity field, in the limit of a high quantum number, the leading term correctly reproduces the classical distribution. We discuss in detail the sub-leading terms, which are interpreted as quantum corrections. Finally, in
Section 5, we summarize our results and provide some context for the relevance of our findings.
3. A Guiding Model: The Infinite Square Well Potential
Consider the simplest bound-state problem in quantum theory: a point particle in one dimension confined between perfectly reflecting walls at
and
. This potential, although simple, has been used to model real quantum well systems that can be created in the laboratory, e.g., it provides physical realizations of atomic mirrors [
41]. Classically, the particle moves with the same speed
v at every position inside the well because there are no forces acting there. Using the expression (
3) for the classical probability density, with
we obtain
where
is the Heaviside step function defined by
for
and
for
. Therefore, the classical probability density of finding the particle at
x is constant inside the box and there is no preferable position for finding a classical particle. The quantum-mechanical problem is quite different. In this case, the normalized eigenfunctions
satisfying Dirichlet boundary conditions on the walls and energy eigenvalues
can be written as
In
Figure 2, we plot the dimensionless classical probability density (
11) and the dimensionless quantum probability density
for the excited energy eigenstate with
and for a high-energy eigenstate with
. The former case suggests that the probability of finding the particle near to the walls is nearly zero. Also, there are specific points, the nodes, in which the probability of finding the particle is zero. Clearly, this situation cannot be interpreted in terms of classical physics since it implies that the particle accelerates and decelerates continuously, even in the absence of forces inside the box. In the latter case, we observe that the classical distribution
does not follow the quantum distribution
but instead follows the local average. This can be understood as follows. In a high-energy eigenstate (
), the wavelength is very short and hence, at every point inside the box, there are effectively a peak and a node. So, as
n is increased, peaks and nodes get closer and closer to each other and the quantum distribution appears to become a constant equal to the average of the peak and the node, i.e., equal to
, which is the classical distribution, thus losing any information regarding the nodes, but this is indeed true only in the formal limit
. This naive conclusion is reached when averaging over an oscillation solely, but this is not the case, since, as discussed in the previous section, the quantum-to-classical transition should be understood in a distributional sense, and hence information regarding the nodes must survive in the limiting process, as we shall see in the following. Now, let us derive this result in an analytical fashion by using the mathematical formulation introduced in
Section 2.2. Fourier expanding the quantum probability density
, as defined in Equation (
6), gives the Fourier coefficients
where
. Of course, by inverse Fourier transforming this expression, we go back to the sinusoidal quantum probability density. Now, we look for the asymptotic behavior of the Fourier coefficient (
13) in the limit
. We have to carry this out with some care. For large
n, this expression can be written as the geometric series
which is valid over the compact domain
in order to guarantee its convergence. This imposes a restriction upon the Fourier variable
p, namely
, where
is the momentum defined by Equation (
12). This restriction, which emerges from the mathematical structure of the quantum Fourier coefficient, is indeed physical since it is also consistent with the condition imposed by the energy surface in the classical case. Therefore, though in the quantum regime the momentum can reach any value, once we fix the (high) energy of the system to obtain the asymptotic behavior of the Fourier coefficient for
, the possible values for the momentum become restricted. This subtle fact was not considered in Ref. [
20] and we shall explore its consequences in the following.
Keeping the leading order terms up to
in Equation (
14), we obtain
for
. Therefore, the asymptotic behavior of the quantum probability density in position space is obtained by Fourier transforming Equation (
15) as defined in Equation (
6). We obtain
where
. This integral is quite simple. The result is
where Si is the sine integral, defined as
. Note that, in Equation (
17),
x is not restricted to being between 0 and
L, as in the original classical and quantum distributions. In
Figure 3, we plot the asymptotic distribution (
17) for different values of
n. Taking
, we can see that the macroscopic distribution
exhibits oscillations around the classical distribution inside the quantum well and around zero outside. As we increase
n, for example, up to
, the amplitude of the oscillations decreases in both regions. As discussed above, in the formal limit
, we obtain a smooth distribution, i.e., without the small oscillations. This can be seen by using the asymptotic expansion
[
42], such that the limit
upon Equation (
17) produces
which is exactly the smooth classical probability density. Note that the oscillatory behavior of the macroscopic distribution vanishes only in the formal limit
. In a realistic classical situation, the value of
n is given by
, where
(
) is the classical energy (momentum), and hence the small oscillations around the classical distribution survive. For example, for a thermal Neutron with
J trapped in a 1 mm box, we obtain
. For the even more classical case of a particle with mass 1 g moving at 1 m/s inside a 1 cm box, one obtains
. Therefore, the small quantum oscillations that we can see in
Figure 3 are due to the small values of
n that we are using there compared with the realistic value of
. Therefore, macroscopically, such oscillations are strongly suppressed.
As a consistency check, let us evaluate the expectation value of
by using the classical, quantum and asymptotic probability densities. The classical expectation value is a simple task, with the result
. The quantum expectation value can also be computed in a closed form, and it can be expressed in terms of the generalized hypergeometric function
as
For the sake of comparison, we now evaluate the expectation value by using the asymptotic distribution (
17). Keeping terms up to order
, we obtain
and this result can also be obtained by power expanding the exact quantum result (
19) in inverse powers of the quantum number
n. Once again, one can further see that the formal limit
applied on Equation (
20) yields the exact classical result. In a realistic case, the additional term in Equation (
20) is present and can be interpreted as a residual quantum behavior at the macroscopic level.
4. The Quantum Bouncer: Exact Result and Quantum Corrections
The quantum bouncer, which is the problem of a particle bouncing on a perfectly reflecting surface under the influence of gravity, is described by a constant field force with the appropriate boundary condition at the ground level [
43]. Strikingly, the GRANIT experiment conducted at the Institute Laue-Langevin [
44] and the qBOUNCE collaboration [
45] have observed the gravitational quantum states of ultracold neutrons bounded by the Earth’s gravitational field. In these experiments, neutrons do not bounce smoothly but at certain well-defined quantized heights, in agreement with the predictions of quantum mechanics. UCNs bridge the gap between gravity experiments at short distances and the precise measurement techniques of quantum mechanics. Due to this, they have been used to perform weak equivalence principle tests as well as probing the Newton’s inverse square law of gravity at short distances [
45,
46].
All the basics of the quantum bouncer were introduced in Ref. [
9]. Here, we just summarize the required results in the presence of the linearized potential energy
where
g is the gravitational acceleration,
m is the gravitational mass and the vertical position
z is measured from the ground level
. Assuming that the particle is initially at rest and dropped from a height
h, the classical probability density is found to be
Clearly, the probability density blows up as
since the particle spends a relatively longer time near
h. It is worth pointing out that the function
does not depend on the mass of the particle, in contrast with the expressions for the classical distributions for the harmonic oscillator [
20] and the hydrogen atom [
22]. This is a direct consequence of the universality of free fall, often referred to as the weak equivalence principle, which is exactly true in classical mechanics.
The associated quantum mechanical problem, the so-called quantum bouncer, is more intricate. The normalized solution to the Schrödinger equation that satisfies the boundary condition
(i.e., the ground is impenetrable) and decays as
z goes to infinity is [
47,
48,
49]
where
is the Airy function [
50],
is the
n-th zero of the Airy function
and
is the gravitational length. The resulting quantized energies are given by
with
.
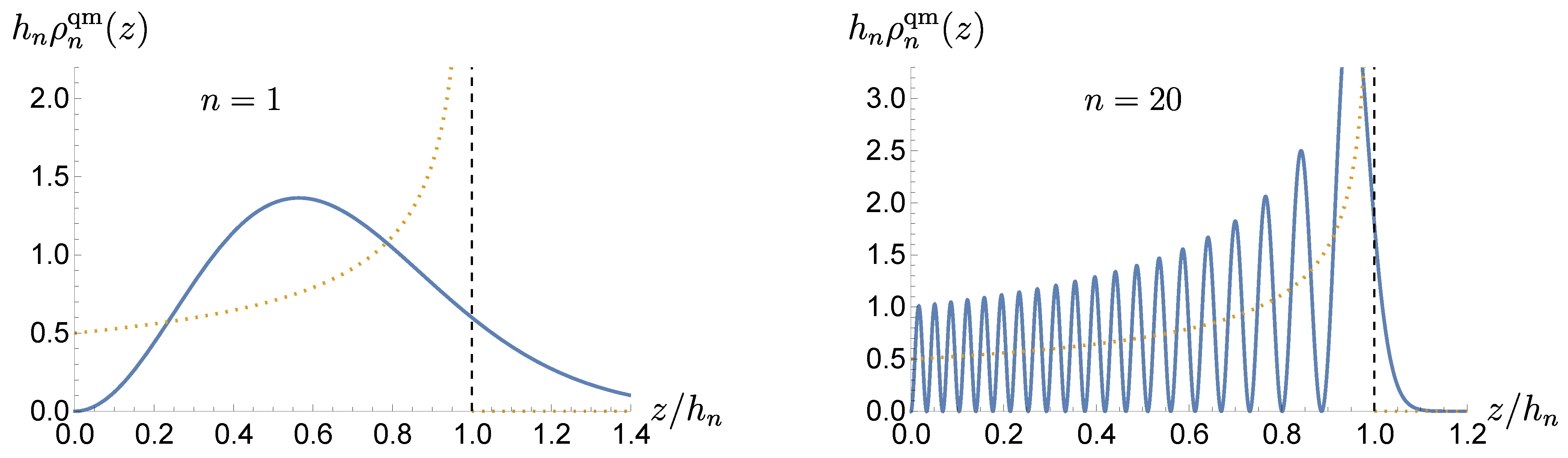
In
Figure 4, we superimpose the normalized quantum probability density
(continuous blue line) with the normalized classical distribution
(dashed yellow line) as a function of the normalized distance
and for different values of
n, namely for the ground state
and for the excited state with
. Here,
determines the turning point. As in the case of the infinite square well potential, the quantum probability density for the
n-th eigenstate rapidly oscillates around the smooth classical distribution for
.
We now proceed to the evaluation of the Fourier coefficient
, which is given by
As far as we know, the exact analytical evaluation of this integral has not been reported yet. However, for the purposes of this paper, we only require its asymptotic behavior for
. To achieve this, we use the method of Albright [
50], as some basic primitives of the Airy functions allow us to express the Fourier coefficient (
24) as a series in inverse powers of
. The details of the calculations are relegated to
Appendix A, and here we only present the final results. Let us only retain the dominant terms. For the sake of simplicity, we split the Fourier coefficient (
24) as the sum of two terms, i.e.,
. The leading term
is found to be
where
, and
is the error function defined by Equation (
A11) [
42]. The sub-leading term is given by
Now, we have to inverse Fourier transform these coefficients to obtain the asymptotic form of the quantum probability density in position space. It can also be written as the sum of two terms, namely
, where
and
are the Fourier transformations of Equations (
25) and (
26), respectively. To perform this, we have to take some care, since while the exact Fourier coefficient (
24) is valid for
, the approximate expressions (
25) and (
26) are not. This situation is similar to the case of the Fourier coefficient for the infinite square well potential: while the exact coefficient (
13) is valid for
, the asymptotic coefficient (
15) is valid for
. To clearly see this point, one can inverse Fourier transform the leading order term (
25) over
and obtain the exact classical result
However, if the sub-leading term (
26) is Fourier-transformed in a similar fashion, the corresponding integral does not converge. This is not surprising at all since, as discussed, the application of the method of Albright to compute the asymptotics of the quantum Fourier coefficient (
24) has a definite domain of validity, something like what happens with the infinite square well potential. Recall that, in order to properly obtain an expansion of the quantum Fourier coefficient (
13), we restricted the Fourier variable
p to the domain
, where
is the momentum of the particle. In the quantum bouncer case, we have a similar situation, since our expression for the Fourier coefficient is valid over a finite domain solely, since we truncate the series when using the method of Albright. Such analysis is still absent in the literature and we estimate it from a numerical analysis in
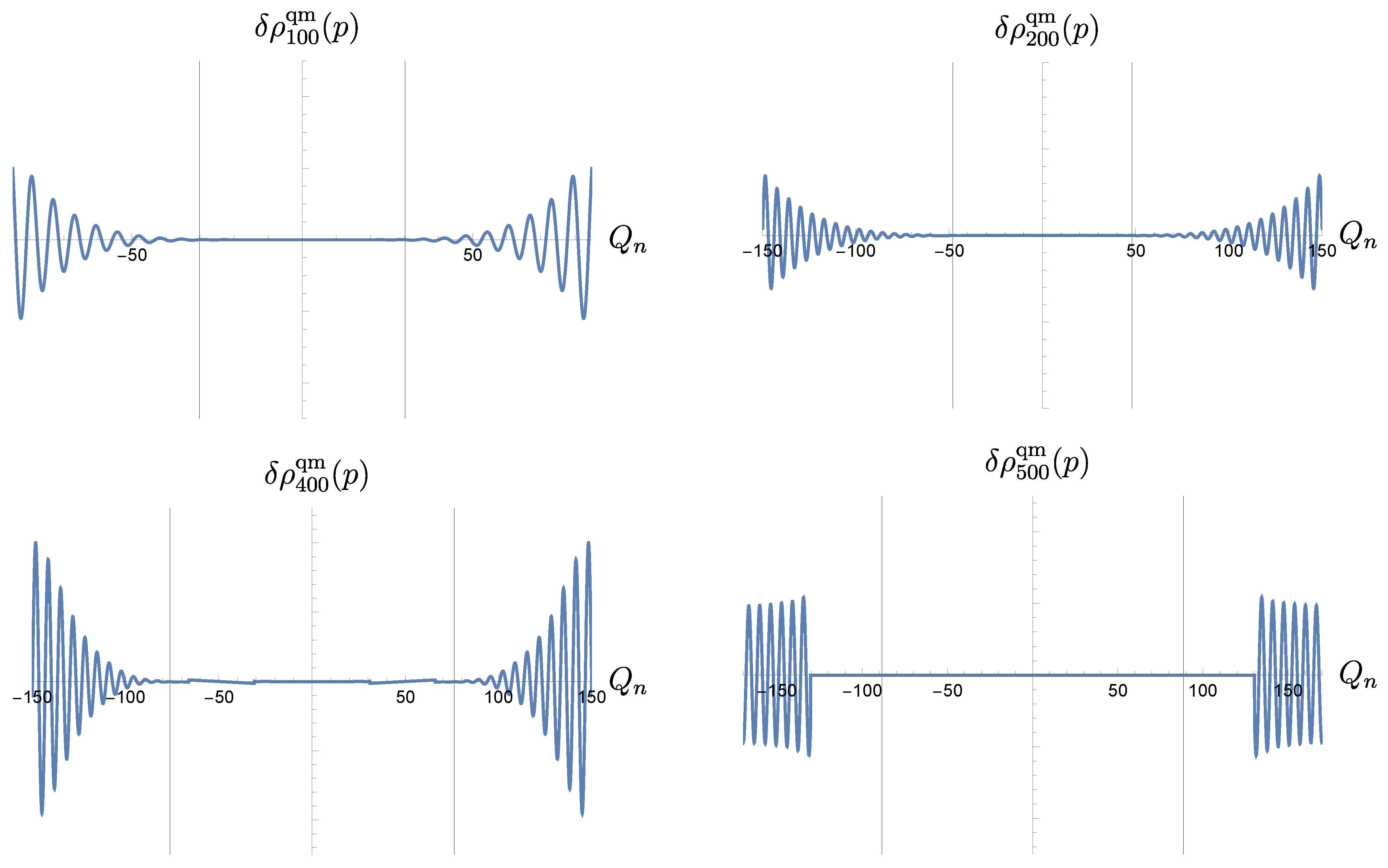
Appendix B. Indeed, numerically, we determine the domain over the Fourier variable
to be
, where
is the
n-th zero of the Airy function. We are now ready to evaluate the inverse Fourier transform, which should be performed over the finite interval
. To keep close contact with the exact classical limit, we express the integral as follows
and use the identity
such that
The last integral can be approximated as follows. First, we take the real part explicitly:
where
,
and
and
are the Fresnel integrals.
Now, for
, the integrand is highly oscillatory. In addition, the interval of integration (for large
x) give us a way to approximate the integral since one can consider the asymptotic behavior of the Fresnel integrals for large arguments. Keeping the leading contribution, we obtain
and therefore
This expression gives the exact classical probability density with small oscillations around it. This is clearly seen from the asymptotic behavior of the Fresnel integrals for large arguments, i.e.,
for
. As in the quantum well case, the formal limit
yields the exact smooth classical probability distribution
, given by Equation (
22). Finite values of
n retain the small oscillations, which we interpret as a residual quantum behavior at the macroscopic scale.
In all of the above, we have taken for definiteness and made some important approximations based on this assumption. Now, we shall better justify our choice. For a particle freely falling from a height h, the principal quantum can be estimated from . Since we are assuming that , one can use the approximate expression for the zeros of the Airy function and therefore . For reference, for a Cs atom, one finds μm such that, if released from 1 mm, the corresponding quantum number is . For the much lighter Na atom, one finds μm, which produces . To obtain smaller values for n, the gravitational length must be larger, and this is achieved with lighter particles. For example, the gravitational length for a neutron is μm, which leads to . These estimations justify our analysis of the above.
So far, we have studied only the physics arising from the leading order term of the quantum Fourier coefficient and showed the emergence of the exact classical probability distribution plus small quantum corrections with an amplitude driven by
. Now, we have to investigate the sub-leading term arising from the quantum Fourier coefficient
given by Equation (
26). In addition, since the quantum correction arising from
decays as
, we will keep terms up to this order in the following. The inverse Fourier transformation of Equation (
26) then reads as
where we have neglected the term decaying as
. Retaining the most important contributions, we obtain
which decays as
, i.e., faster than the correction arising in Equation (
31). However, it is worth to mention that this term provides small oscillations beyond the classical turning point, which do not arise in Equation (
31).
All of the above tell us that the asymptotic form of the quantum probability density in position space is
where we have power-expanded the Fresnel integrals in Equation (30) up to the first-order correction. The next-order expansion is smaller than those of Equation (
33). In
Figure 5, we plot the asymptotic distribution (
34) for
(left panel) and
(right panel). We observe that the asymptotic distribution exhibits small oscillations around the smooth classical probability density. In these cases, the small oscillations are observable due to the small value of
n that we are using, but they are strongly suppressed in a realistic situation.
To validate our results, we now evaluate some expectation values. For example, the classical expectation value of
, with
, is
The expectation value can be computed easily by using the asymptotic probability density
. Using the standard procedure to regularize infinite trigonometric integrals, we obtain
such that the final result becomes
Clearly, the second term can be interpreted as a quantum correction at the macroscopic level. For the sake of comparison, we have to evaluate the quantum expectation value and then power-expand the result up to
. To our knowledge, a closed-form expression for the quantum expectation value has not been reported yet. However, with the method of Albright, we can obtain an asymptotic expression for the expectation value, i.e.,
and, performing the summations, we retrieve exactly the asymptotic expectation value given by Equation (
37).
5. Conclusions
Classical and quantum descriptions of single-particle systems are fundamentally different: while the former tells us the exact position and momentum of a particle, the latter gives us the probability of finding the particle at some position or bearing some momentum. This makes the analysis of the quantum–classical correspondence difficult. There are traditional methods that address such correspondence, for example, the WKB method and the Ehrenfest’s theorem; however, these are not universally reliable for investigating the classical limit in a general way. Also, the correspondence has been discussed in the language of the theory of distributions. By direct comparison of the classical and quantum probability densities, one realizes that the classical behavior emerges as a coarse-grained description of the quantum system. Therefore, since the correspondence is not pointwise, one expects the emergence of remnants of the quantum behavior at the macroscopic level as small oscillations enveloping the classical distribution.
The distributional quantum-to-classical convergence means that the quantum distribution, if averaged locally over a finite interval, approaches the classical distribution provided that the quantum number is large. This is formally expressed by Equation (
5). The evaluation of Equation (
5) is impractical in most cases (except for the infinite square well potential, since the quantum distribution is sinusoidal); however, it can be carried out in a simpler fashion when transformed to the Fourier space. In short, the convergence in distribution (
5) is expressed in Fourier space by Equation (
9), i.e., the quantum Fourier coefficient approaches the classical Fourier coefficient when the quantum number is large, but sub-leading quantum corrections emerge. In order to demonstrate the applicability of this method, we initially addressed the problem of a particle in a box. To this end, we compute an exact quantum Fourier coefficient (
13), which is valid for any value of the momentum (Fourier variable), and then compute its asymptotic behavior for
, which naturally restricts the domain of the Fourier variable (which, in this case, is dictated by the convergence of a geometric series). Finally, by inverse Fourier transforming the asymptotic quantum Fourier coefficient, we obtain Equation (
17), which is the emergent macroscopic distribution in position space, i.e., the locally averaged quantum distribution.
Figure 3 shows the macroscopic distribution. As expected, it behaves as the classical distribution plus small oscillations whose amplitude decreases as
with
. As a consistency check, we evaluated the exact expectation value of
(with
) and demonstrated its consistency with the one computed when evaluated by using the macroscopic distribution. Our result implies that, at the macroscopic scale, all happens as if the quantum behavior is hidden, leaving us with an apparent world described consistently in a classical language.
The validity of the universality of free fall is one of the cornerstones of general relativity and one may ask if it emerges or not from the quantum behavior at high energies. Its validity in the classical domain is widely accepted, but the mass-dependent quantum dynamics explicitly break it. All of these factors motivate the analysis of the macroscopic behavior of the quantum bouncer: a particle bouncing on a perfectly reflecting surface under the influence of gravity. In this paper, we have also studied this problem following the program described above. The first step is the computation of the exact quantum Fourier coefficient (
24). The integral cannot be evaluated in an analytical fashion. However, using the method of Albright, we obtained an asymptotic expression for
, whose leading and sub-leading terms are given by Equations (
25) and (
26), respectively. The validity of these expressions was verified by comparing the asymptotics of the quantum Fourier coefficient (
25) + (
26) versus the exact result (
24) computed numerically. This analysis also gave the domain of validity of our expansion. Finally, by inverse Fourier transforming the Fourier coefficient in the corresponding compact domain, we obtained the macroscopic distribution, given by Equation (
34). In
Figure 5, we superimposed the smooth classical distribution with our macroscopic distribution and reach similar conclusions as those of the particle in a box: for
, the macroscopic distribution behaves as the classical distribution plus small oscillations, which we interpret as quantum corrections at the macroscopic level. All in all, our results indicate that the universality of free fall is an emergent phenomenon since quantum mechanics imply a remnant mass-dependent quantum behavior even at macroscopic scales.
We close by commenting on a possible generalization of this work. As discussed, the Wigner phase-space formulation of quantum mechanics provides a natural framework in which the quantum–classical correspondence can be studied in a common language: joint position–momentum distributions. The method that we introduced works in the position space, where one can directly visualize the distributional convergence of the probability densities. However, it is natural to wonder whether such a procedure can be extended to the phase-space probability distribution. We have left this problem for a future investigation.