Different Aspects of Entropic Cosmology

Abstract

We provide a short review of the recent developments in entropic cosmology based on two thermodynamic laws of the apparent horizon, namely the first and the second laws of thermodynamics. The first law essentially provides the change in entropy of the apparent horizon during the cosmic evolution of the universe; in particular, it is expressed by $TdS=-d\left(\rho V\right)+WdV$ (where W is the work density and other quantities have their usual meanings). In this way, the first law actually links various theories of gravity with the entropy of the apparent horizon. This leads to a natural question—“What is the form of the horizon entropy corresponding to a general modified theory of gravity?”. The second law of horizon thermodynamics states that the change in total entropy (the sum of horizon entropy + matter fields’ entropy) with respect to cosmic time must be positive, where the matter fields behave like an open system characterised by a non-zero chemical potential. The second law of horizon thermodynamics importantly provides model-independent constraints on entropic parameters. Finally, we discuss the standpoint of entropic cosmology on inflation (or bounce), reheating and primordial gravitational waves from the perspective of a generalised entropy function.

1. Introduction

The benchmark of Bekenstein–Hawking entropy connects two apparently different sectors, namely gravity and thermodynamics, on equal footing. In particular, the black hole horizon exhibits thermal behaviour whereby the entropy of the horizon scales by the area of the horizon and the surface gravity fixes the corresponding temperature [1,2,3,4]. In the cosmological context, there exists an apparent horizon that is a marginally trapped surface with vanishing expansion that divides the observable universe from the unobservable universe. Similar to black hole thermodynamics, the cosmic horizon is generally considered to exhibit thermal behaviour [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25], and one can motivate it using the following arguments:

• During the cosmic evolution of the universe, the matter fields inside of the horizon show a flux from inside to outside the horizon (the flux is outward in nature during the accelerating stage), which results in a decrease in the matter fields’ entropy. This violates the second law of thermodynamics, which states that the change in total entropy must be positive. Therefore, the cosmic horizon should be incorporated with entropy to manage the increase in total entropy (the sum of horizon entropy + matter fields’ entropy).
• The cosmological field equations are time-reversal-symmetric; thus, they always come with a contracting solution, along with an expanding one. However, our observational data indicate that the universe is expanding. Therefore, the natural question that comes to mind is “Why does the universe always choose the expanding solution?”. In order to answer this question, we need to associate thermal behaviour with the cosmic horizon. Then, the second law of horizon thermodynamics actually disagrees the contracting solution in order to achieve a positive change in total entropy.

Consequently, the subject of “entropic cosmology” has gained a lot of interest, in which the cosmic horizon is associated with entropy that follows the following thermodynamic law [5,6,7,8,19]:

$$\begin{array}{c}\hfill T_{\mathrm{h}}d{S}_{\mathrm{h}}=-d\left(\rho V\right)+{\displaystyle \frac{1}{2}}\left(\rho -p\right)dV\end{array}$$

(1)

where V is the volume enclosed by the apparent horizon expressed by $R_{\mathrm{h}}=1/H$ (with H being the Hubble parameter of the universe); moreover, $T_{\mathrm{h}}$ and $S_{\mathrm{h}}$ are the temperature and entropy of the horizon, respectively (and the other quantities have their usual meanings). We now assume that the universe is homogeneous and isotropic, owing to which the total energy inside the apparent horizon is expressed as $U=\rho V$; otherwise, if $\rho$ depends on spatial coordinates, then the energy inside the horizon should be expressed by the integral (over the volume of the horizon) of $U=\int \rho dV$. Here, $T_{\mathrm{h}}$ is fixed by the surface gravity of the apparent horizon, which, in the case of the spatially flat Friedmann–Lemaître–Robertson–Walker (FLRW) metric, turns out to be

$$\begin{array}{c}\hfill T_{\mathrm{h}}={\displaystyle \frac{H}{2\pi }}\left|1+{\displaystyle \frac{\dot{H}}{2H^2}}\right|.\end{array}$$

(2)

At this stage, we would like to mention that the microscopic origin of horizon entropy (and its associated temperature) is still a debatable topic and needs further investigation (see [26,27] for some progress in this regard). Together with Equation (1) (which is the first law of horizon thermodynamics in cosmology), the second law states that [20]

$$\begin{array}{c}\hfill d\left(S_{\mathrm{h}}+S_{\mathrm{m}}\right)>0,\end{array}$$

(3)

where $S_{\mathrm{m}}$ represents the entropy of the matter fields inside of the horizon. With a specific form of horizon entropy, the first law of horizon thermodynamics (along with the local conservation law of the matter fields) leads to the cosmological field equation; for instance, the Bekenstein–Hawking-like entropy of the cosmic horizon provides the usual FLRW equations of Einstein gravity from Equation (1). However, for a different form of horizon entropy (compared to Bekenstein–Hawking-like horizon entropy), we end up with the following modified cosmological field equations:

$$\begin{array}{c}\hfill \dot{H}\left({\displaystyle \frac{\partial S_{\mathrm{h}}}{\partial S}}\right)=-4\pi G\left(\rho +p\right)\end{array}$$

(4)

and

$$\begin{array}{c}\hfill \int \left({\displaystyle \frac{\partial S_{\mathrm{h}}}{\partial S}}\right)d\left(H^2\right)={\displaystyle \frac{8\pi G}{3}}\rho +{\displaystyle \frac{\mathrm{\Lambda }}{3}},\end{array}$$

(5)

where $S=\pi /\left(G{H}^2\right)$ is the Bekenstein–Hawking entropy (clearly, for $S_{\mathrm{h}}\equiv S$, one obtains the usual FLRW equations). Such a modified cosmic scenario has some interesting cosmological consequences starting from inflation (or bounce) to the dark energy era [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,28,29,30,31,32,33,34,35,36,37,38,39]. Some variants of Bekenstein–Hawking entropy are Tsallis entropy [40], Rényi entropy [41], Barrow entropy [42], Sharma–Mittal entropy [43], Kaniadakis entropy [44], loop quantum gravity entropy [45], etc. The important point is that all of these entropies share some common features; for example, they all vanish at the limit of $S\to 0$, and they show monotonically increasing behaviour with respect to the Bekenstein–Hawking entropy variable (S). One more reason for interest in entropic cosmology is that it is related to the holographic cosmology initiated by Witten and Susskind [46,47,48]. In particular, entropic cosmology proves to be equivalent to the generalised holographic scenario with suitable holographic cut-offs [49,50]. The significant contributions of holographic cosmology (or, equivalently, entropic cosmology) corresponding to the aforementioned entropies explain the dark energy era of our universe, namely holographic dark energy (HDE) [51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69].

Based on the above arguments, some immediate questions that arise include the following:

• What is the form of the horizon entropy that leads to the cosmological field equations for a general modified theory of gravity from Equation (1)?
• Does there exist any generalised entropy that can generalise all the known entropies proposed so far (like Tsallis entropy, Rényi entropy, Barrow entropy, Sharma–Mittal entropy, Kaniadakis entropy, etc.)? This question is well motivated, as all these entropies share some common properties, as mentioned above.
• If a generalised form of entropy exists, then what are the constraints on the generalised entropic parameters coming from the second law of horizon thermodynamics? Furthermore, what is the standpoint of generalised entropy on primordial gravitational waves? Does the constraint coming from the primordial gravitational waves match that based on the second law of horizon thermodynamics?

The present article, based on some of our previous works [19,20,24,25,28,33], provides a brief review, answering the above questions. We follow the $\left(-,+,+,+,\dots .\right)$ signature of a spatially flat $(n+1)$ dimensional spacetime metric, and we take $G=c=ħ=1$, where G is the Newton’s constant, c is the speed of light and ħ is Planck’s constant.

2. First Law of Horizon Thermodynamics: Consistent Entropy for a General Modified Theory of Gravity

The question that we encounter in this section is the following: What is the form of entropy that, based on the thermodynamic law (1), can produce the cosmological field equations for a general modified theory of gravity [19]?

The FLRW equations for a general modified theory of gravity in $(n+1)$ dimensional spacetime can be expressed as

$$\begin{array}{cc}\hfill H^2=& {\displaystyle \frac{16\pi }{n(n-1)}}(\rho +{\rho }_{\mathrm{c}})\mathrm{and}\dot{H}=-{\displaystyle \frac{8\pi }{(n-1)}}(\rho +{\rho }_{\mathrm{c}}+p+p_{\mathrm{c}}),\hfill \end{array}$$

(6)

where ${\rho }_{\mathrm{c}}$ and $p_{\mathrm{c}}$ represent the modifications compared to Einstein gravity. Owing to such modifications, we can expect that the corresponding horizon entropy for a general modified gravity theory will take the following form:

$$\begin{array}{c}\hfill S_{\mathrm{h}}={\displaystyle \frac{A}{4}}+S_{\mathrm{c}}\left(A\right),\end{array}$$

(7)

where the suffix ‘h’ represents horizon’ entropy. Here, $A=n{\mathrm{\Omega }}_n{R_{\mathrm{h}}}^{n-1}$ represents the area of the apparent horizon in $n+1$ dimensional spacetime, and $S_{\mathrm{c}}$ is a function of A. In particular, the horizon entropy for a general theory of gravity is considered to be corrected over that in the case of Einstein gravity, namely Equation (7). The correction ($S_{\mathrm{c}}$) explicitly depends on the modification of gravitational action, which we need to find in such a way that the following thermodynamic law holds with $E=\rho V$ and $W={\displaystyle \frac{1}{2}}\left(\rho -p\right)$:

$$\begin{array}{c}\hfill T_{\mathrm{h}}d{S}_{\mathrm{h}}=-dE+WdV.\end{array}$$

(8)

By using $S_{\mathrm{h}}={\displaystyle \frac{A}{4}}+S_{\mathrm{c}}$, the above equation can be equivalently written as

$$\begin{array}{c}\hfill T_{\mathrm{h}}{\displaystyle \frac{d{S}_{\mathrm{c}}}{dt}}={\displaystyle \frac{d}{dt}}\left({\rho }_{\mathrm{c}}V\right)-W_{\mathrm{c}}{\displaystyle \frac{dV}{dt}}+\left[-{\displaystyle \frac{d}{dt}}\left(\rho V+{\rho }_{\mathrm{c}}V\right)+{\displaystyle \frac{1}{2}}\left(\rho +{\rho }_{\mathrm{c}}-p-p_{\mathrm{c}}\right){\displaystyle \frac{dV}{dt}}-T{\displaystyle \frac{d}{dt}}\left({\displaystyle \frac{A}{4}}\right)\right],\end{array}$$

(9)

where $W_{\mathrm{c}}={\displaystyle \frac{1}{2}}\left({\rho }_{\mathrm{c}}-p_{\mathrm{c}}\right)$. With $R_{\mathrm{h}}={\displaystyle \frac{1}{H}}$ in combination with Equation (2), we obtain

$$\begin{array}{c}\hfill {\displaystyle \frac{d{S}_{\mathrm{c}}}{dt}}=-2\pi n{\mathrm{\Omega }}_n\left({\rho }_{\mathrm{c}}+p_{\mathrm{c}}\right){R_{\mathrm{h}}}^n,\end{array}$$

(10)

upon the integration of which, we obtain

$$\begin{array}{c}\hfill S_{\mathrm{c}}=2\pi n{\mathrm{\Omega }}_n\int {R_{\mathrm{h}}}^{n-2}\left({\displaystyle \frac{{\rho }_{\mathrm{c}}+p_{\mathrm{c}}}{\dot{H}}}\right)d{R}_{\mathrm{h}}.\end{array}$$

(11)

Equation (11) argues that $S_{\mathrm{c}}$ should be a function of only $R_{\mathrm{h}}$ (or, equivalently, the area of the horizon), as $d{R}_{\mathrm{h}}$ is the only differential present in the rhsof the above expression. In general, the integration into Equation (11) should be realized by specifying the scale factor ($a=a\left(t\right)$) as a function of the cosmological time (t). In particular, if we consider a specific scale factor, then $H\left(t\right)$ and, consequently, $R_{\mathrm{h}}$ are also expressed as a function of t, and as a result, the integrand in Equation (11) can be expressed in terms of $R_{\mathrm{h}}$. Then, Equation (11) can be integrated to yield $S_{\mathrm{c}}=S_{\mathrm{c}}\left(R_{\mathrm{h}}\right)$. With the above form of $S_{\mathrm{c}}$, Equation (7) provides the full entropy corresponding to a general modified theory of gravity as

$$\begin{array}{c}\hfill S_{\mathrm{h}}={\displaystyle \frac{A}{4}}+2\pi n{\mathrm{\Omega }}_n\int {R_{\mathrm{h}}}^{n-2}\left({\displaystyle \frac{{\rho }_{\mathrm{c}}+p_{\mathrm{c}}}{\dot{H}}}\right)d{R}_{\mathrm{h}},\end{array}$$

(12)

It can be observed that for ${\rho }_{\mathrm{c}}=p_{\mathrm{c}}=0$, i.e., for Einstein’s theory of gravity, the entropy from Equation (12) becomes $S_{\mathrm{h}}=A/4$, as per our expectation. Moreover, for $\rho =p=0$, i.e., without any matter fields, Equation (6) yields $\left({\rho }_{\mathrm{c}}+p_{\mathrm{c}}\right)/\dot{H}=-8\pi /(n-1)$, which immediately yields to $S_{\mathrm{h}}=0$ from Equation (12). However, this is expected, as there is no flux of matter fields from inside to outside of the horizon for $\rho =p=0$ or, equivalently, there is no information loss associated with the horizon.

Below, we present some specific examples of gravity theories and determine the respective entropy from Equation (12).

• For $(n+1)$ dimensional GB gravity, where the FLRW equations are expressed as

  $$\begin{array}{ccc}\hfill H^2+\lambda (n-2)(n-3)H^4& =& {\displaystyle \frac{16\pi }{n(n-1)}}\rho ,\hfill \\ \hfill \left[1+2\lambda (n-2)(n-3)H^2\right]\dot{H}& =& -{\displaystyle \frac{8\pi }{(n-1)}}\left(\rho +p\right),\hfill \end{array}$$

  (13)

  with $\lambda$ being the GB parameter, the corresponding horizon entropy from Equation (12) is expressed as

  $$\begin{array}{c}\hfill S_{\mathrm{h}}={\displaystyle \frac{A}{4}}\left\{1+{\displaystyle \frac{2\lambda (n-1)(n-2)}{{R_{\mathrm{h}}}^2}}\right\}.\end{array}$$

  (14)
• For $(3+1)$ dimensional $f\left(Q\right)$ gravity theory, the FLRW equations are expressed as

  $$\begin{array}{ccc}\hfill H^2& =& {\displaystyle \frac{1}{6f_{\mathrm{Q}}}}\left(\rho +{\displaystyle \frac{f}{2}}\right),\hfill \\ \hfill \dot{H}& =& -{\displaystyle \frac{1}{2f_{\mathrm{Q}}}}\left({\displaystyle \frac{\rho }{2}}+{\displaystyle \frac{f}{2}}+12H^2{f}_{\mathrm{QQ}}\dot{H}-{\displaystyle \frac{f}{4}}+{\displaystyle \frac{p}{2}}-\dot{H}{f}_{\mathrm{Q}}\right),\hfill \end{array}$$

  (15)

  where $f_{\mathrm{Q}}$ and $f_{\mathrm{QQ}}$ represent the first and second derivatives of $f\left(Q\right)$ (with respect to the variable (Q)), respectively. Clearly, in this case, one requires a certain form of $f\left(Q\right)$, which is taken to be a power law type, i.e., $f\left(Q\right)=Q^n$ (with n being a constant). Such a form of $f\left(Q\right)$, along with Equation (12), leads to the following entropy corresponding to the $(3+1)$ dimensional $f\left(Q\right)$ gravity:

  $$\begin{array}{c}\hfill S_{\mathrm{h}}={\displaystyle \frac{A}{4}}\left[1-32\pi \left\{1+{\displaystyle \frac{n(1-2n)}{(2-n)}}{\left({\displaystyle \frac{6\pi }{A}}\right)}^{n-1}\right\}\right].\end{array}$$

  (16)

It can be noted that in both GB gravity and $f\left(Q\right)$ gravity theories, the integration of Equation (12) can be performed without specifying the scale factor ($a=a\left(t\right)$). This may not be the case when the gravitational field equations contain higher derivatives of the Hubble parameter; for instance, in the $F\left(R\right)$ gravity theory, where the FLRW equations contain $\stackrel{⃛}{H}$, one needs to specify the scale factor ($a\left(t\right)$) to perform the integration and to determine $S_{\mathrm{h}}$ (corresponding to $F\left(R\right)$ gravity) from Equation (12) [19]. On other hand, it is well known that a $F\left(R\right)$ theory can be recast as a scalar-tensor theory through the conformal transformation of the spacetime metric, where the scalar potential depends on the form of $F\left(R\right)$ under consideration. However, it was pointed out in [19] that such a mathematical equivalence between $F\left(R\right)$ and scalar-tensor theory is spoiled from the perspective of the entropy of the apparent horizon.

At this stage it deserves mentioning that the determination of the horizon entropy from the thermodynamic law (1) encounters a problem. In particular, it requires the quantity $\left(1+{\displaystyle \frac{\dot{H}}{2H^2}}\right)$ to be positive; otherwise, the entropy (particularly for Einstein gravity) turns out to be negative, which is impossible. The condition, namely $1+{\displaystyle \frac{\dot{H}}{2H^2}}<0$, may occur during the reheating process, where the EoS parameter of the matter field ($\omega =p/\rho$) is larger than $1/3$. Then, one may argue that for such a reheating era, where $\omega >1/3$, there exists no such entropy (of the horizon) that connects the FLRW Equation (6) with the thermodynamic law (1). In order to resolve this issue, the following modified thermodynamic law was proposed in the context of cosmology [19]:

$$\begin{array}{c}\hfill T_{\mathrm{h}}d{S}_{\mathrm{h}}^{\left(m\right)}=-dE+\rho dV,\end{array}$$

(17)

where $T_{\mathrm{h}}$ is shown in Equation (2) and the superfix ‘m’ stands for the ‘modified’ thermodynamic law. Such a modified thermodynamic law, indeed, resolves the aforementioned problem [19] and, thus, is considered to be more general than the previous law (1) which is a limiting case of the modified thermodynamics for $p=-\rho$.

This modified thermodynamic law surely affects the horizon entropy compared to that of the previous law. For instance,

• In the case of $(n+1)$ dimensional Einstein gravity, the modified thermodynamic law (17) leads to the corresponding horizon entropy, which is expressed as

  $$\begin{array}{c}\hfill S_{\mathrm{h}}^{\left(m\right)}={\displaystyle \frac{n(n-1)}{4}}{\mathrm{\Omega }}_n\int {\displaystyle \frac{{R_{\mathrm{h}}}^{n-2}}{\left|1+\frac{\dot{H}}{2H^2}\right|}}d{R}_{\mathrm{h}},\end{array}$$

  (18)

  which, for a constant EoS parameter for the matter field, i.e., for a constant of $\omega =p/\rho$, results in the following form:

  $$\begin{array}{c}\hfill S_{\mathrm{h}}^{\left(m\right)}\left(\mathrm{constant}\omega \right)={\displaystyle \frac{A}{\left|4-n-n\omega \right|}}.\end{array}$$

  (19)
  Equation (19) clearly indicates that $S_{\mathrm{h}}^{\left(m\right)}$ explicitly depends on the value of $\omega$. Therefore, in this modified thermodynamic law, the form of entropy corresponding to Einstein’s gravity changes with the evolution era of the universe. This is unlike the previous case, where the horizon entropy for Einstein’s gravity is given by $A/4$, which does not change in its form with the evolution of the universe.

  $$\begin{array}{c}\hfill \begin{array}{cc}{S}_{\mathrm{h}}^{\left(m\right)}\left(\mathrm{constant}\omega \right)={\displaystyle \frac{A}{4}}\hfill & \mathrm{during\; inflation\; when}\omega =-1,\hfill \\ S_{\mathrm{h}}^{\left(m\right)}\left(\mathrm{constant}\omega \right)={\displaystyle \frac{A}{\left|4-n\right|}},\hfill & \mathrm{during\; matter-dominated\; era\; when}\omega =0,\hfill \\ S_{\mathrm{h}}^{\left(m\right)}\left(\mathrm{constant}\omega \right)={\displaystyle \frac{A}{4\left|1-n/3\right|}},\hfill & \mathrm{during\; radiation\; era\; when}\omega =1/3,\hfill \end{array}\end{array}$$
• For $(n+1)$ dimensional GB gravity theory, the required entropy corresponding to (17) is expressed as

  $$\begin{array}{c}\hfill S_{\mathrm{h}}^{\left(m\right)}={\displaystyle \frac{A}{4}}\left\{1+{\displaystyle \frac{2\alpha }{{R_{\mathrm{h}}}^2}}\left({\displaystyle \frac{n-1}{n-3}}\right)\right\},\end{array}$$

  (20)

  when $H=\mathrm{constant}$, and

  $$\begin{array}{c}\hfill S_{\mathrm{h}}^{\left(m\right)}=\left({\displaystyle \frac{1}{\left|1-1/\left(2h_0\right)\right|}}\right){\displaystyle \frac{A}{4}}\left\{1+{\displaystyle \frac{2\alpha }{{R_{\mathrm{h}}}^2}}\left({\displaystyle \frac{n-1}{n-3}}\right)\right\}\end{array}$$

  (21)

  when $H=h_0/t$, with $A=n{\mathrm{\Omega }}_n{R_{\mathrm{h}}}^{n-1}$ representing the area of the apparent horizon.
• For a general modified theory of gravity, the corresponding horizon entropy coming from the modified thermodynamic law (17) is obtained as

  $$\begin{array}{c}\hfill S_{\mathrm{h}}^{\left(m\right)}={\displaystyle \frac{n(n-1){\mathrm{\Omega }}_n}{4}}\int {\displaystyle \frac{{R_{\mathrm{h}}}^{n-2}}{\left|1+\frac{\dot{H}}{2H^2}\right|}}d{R}_{\mathrm{h}}+2\pi n{\mathrm{\Omega }}_n\int {R_{\mathrm{h}}}^{n-2}\left({\displaystyle \frac{{\rho }_{\mathrm{c}}+p_{\mathrm{c}}}{\dot{H}\left|1+\frac{\dot{H}}{2H^2}\right|}}\right)d{R}_{\mathrm{h}},\end{array}$$

  (22)
  The above expressions of horizon entropy (for different gravity theories) arising from the modified thermodynamic law (17) are proven to exist, irrespective of whether $\left(1+{\displaystyle \frac{\dot{H}}{2H^2}}\right)$ is positive or negative.

3. Second Law of Horizon Thermodynamics

Until now, we have used only the first law of thermodynamics of the apparent horizon. However, in the context of horizon thermodynamics, a consistent cosmology also demands the validity of the second law of thermodynamics, i.e., the change in total entropy (which is the sum of the horizon entropy and the entropy of the matter fields) with cosmic time should be positive [20].

$$\begin{array}{c}\hfill {\dot{S}}_{\mathrm{h}}+{\dot{S}}_{\mathrm{m}}>0.\end{array}$$

(23)

Equation (1) immediately yields the change in horizon entropy as

$$\begin{array}{c}\hfill {\dot{S}}_{\mathrm{h}}={\displaystyle \frac{8\pi }{H^3}}\left(\rho +p\right).\end{array}$$

(24)

Besides the thermodynamics of the apparent horizon governed by Equation (1), we also need to consider the thermodynamics of the matter fields. In particular, the matter fields inside the apparent horizon obey the following thermodynamic law:

$$\begin{array}{c}\hfill T_{\mathrm{m}}d{S}_{\mathrm{m}}=d\left(\rho V\right)+pdV-\mu dN,\end{array}$$

(25)

where $T_{\mathrm{m}}$ and $S_{\mathrm{m}}$ represent the temperature and the entropy of the matter fields, respectively; note that $T_{\mathrm{m}}$, in general, is different than the horizon temperature. The matter fields exhibit a flux through the horizon, which is either outward or inward, depending on the background cosmic era of the universe. Owing to this flux, the matter fields behave like an open system, where $\mu$ (in Equation (25)) is the chemical potential and $dN$ represents the change in particle number (within time $dt$) inside of the horizon. Due to $V={\displaystyle \frac{4\pi }{3H^3}}$, the above expression takes the following form:

$$\begin{array}{c}\hfill T_{\mathrm{m}}{\dot{S}}_{\mathrm{m}}=-{\displaystyle \frac{4\pi }{H^2}}\left(\rho +p\right)\left\{1+{\displaystyle \frac{\dot{H}}{H^2}}\right\}-\mu \dot{N}.\end{array}$$

(26)

For the purpose of $\dot{N}$, we need to understand that the speed of the formation of the apparent horizon is different than the comoving expansion speed of the universe. Actually, the speed of the formation of the apparent horizon turns out to be $v_{\mathrm{h}}=-\dot{H}/H^2$, while the comoving speed of the universe at a physical distance of d from an observer is expressed as $v_{\mathrm{c}}=Hd$. Therefore, $v_{\mathrm{c}}=1$ at the apparent horizon (i.e., at $d=1/H$). Therefore, $v_{\mathrm{c}}>v_{\mathrm{h}}$ when the universe undergoes an accelerating era, while for a decelerating era, we have $v_{\mathrm{c}}<v_{\mathrm{h}}$. Hence, we calculate

$$\begin{array}{c}\hfill V_{\mathrm{c}}(t+dt)-V(t+dt)={\displaystyle \frac{4\pi }{3}}{\left({\displaystyle \frac{1}{H}}-{\displaystyle \frac{\dot{H}}{H^2}}dt\right)}^3-{\displaystyle \frac{4\pi }{3}}{\left({\displaystyle \frac{1}{H}}+dt\right)}^3={\displaystyle \frac{4\pi }{H^2}}\left(1-ϵ\right)dt,\end{array}$$

(27)

with $ϵ=-\dot{H}/H^2$, which represents the gap between the comoving volume and the volume enclosed by the horizon. Therefore, we can write

$$\begin{array}{c}\hfill {\displaystyle \frac{dN}{dt}}=-{\displaystyle \frac{\rho }{u}}{\displaystyle \frac{d}{dt}}\left[V_{\mathrm{c}}(t+dt)-V(t+dt)\right],\end{array}$$

(28)

where u is the energy per particle. The above expression, along with Equation (27), immediately results in

$$\begin{array}{c}\hfill \mu \dot{N}=-{\displaystyle \frac{4\pi \rho }{H^2}}\left(1-ϵ\right).\end{array}$$

(29)

To arrive at Equation (29), we used $\mu \equiv {\displaystyle \frac{\partial }{\partial N}}\left(\mathrm{total}\mathrm{energy}\right)=u$. Plugging this into Equation (26) yields

$$\begin{array}{c}\hfill T_{\mathrm{m}}{\dot{S}}_{\mathrm{m}}=-{\displaystyle \frac{4\pi }{H^2}}\left(\rho +p\right)\left\{1+{\displaystyle \frac{\dot{H}}{H^2}}\right\}+{\displaystyle \frac{4\pi \rho }{H^2}}\left(1-ϵ\right).\end{array}$$

(30)

Equations (24) and (30) provide the change in horizon entropy, as well the change in matter fields’ entropy (with respect to the cosmic time). These immediately determine the change in total entropy as

$$\begin{array}{c}\hfill T_{\mathrm{h}}{\displaystyle \frac{d{S}_{\mathrm{h}}}{dt}}+T_{\mathrm{m}}{\displaystyle \frac{d{S}_{\mathrm{m}}}{dt}}=-2\pi \left(\rho +p\right)\left({\displaystyle \frac{\dot{H}}{H^4}}\right)+{\displaystyle \frac{4\pi \rho }{H^2}}\left(1-ϵ\right),\end{array}$$

(31)

We can eliminate $\rho$ and p from the above expression by using the Friedmann Equations (4) and (5). As a result, we obtain

$$\begin{array}{c}\hfill T_{\mathrm{h}}{\displaystyle \frac{d{S}_{\mathrm{h}}}{dt}}+T_{\mathrm{m}}{\displaystyle \frac{d{S}_{\mathrm{m}}}{dt}}={\displaystyle \frac{{ϵ}^2}{2G}}\left({\displaystyle \frac{\partial S_{\mathrm{h}}}{\partial S}}\right)-{\displaystyle \frac{3(ϵ-1)}{2G}}{\displaystyle \frac{1}{H^2}}\int \left({\displaystyle \frac{\partial S_{\mathrm{h}}}{\partial S}}\right)d\left(H^2\right).\end{array}$$

(32)

Equation (32) indicates that the total change in entropy depends on the following two factors: (a) the background cosmic evolution of the universe (through the Hubble parameter) and (b) the form of the horizon entropy under consideration (through $S_{\mathrm{h}}$). Below, we consider some specific forms of horizon entropy and establish the constraints on the corresponding entropic parameters in order to validate the second law of horizon thermodynamics during a wide range of cosmic eras.

• For Tsallis entropy ($S_{\mathrm{h}}\equiv S_{\mathrm{T}}=S^{\delta }$, where the suffix ‘T’ stands for Tsallis entropy and $S={\displaystyle \frac{\pi }{G{H}^2}}$ is the Bekenstein–Hawking entropy), the change in total entropy from Equation (32) is expressed as

  $$\begin{array}{c}\hfill T_{\mathrm{h}}\left({\displaystyle \frac{d{S}_{\mathrm{T}}}{dt}}\right)+T_{\mathrm{m}}\left({\displaystyle \frac{d{S}_{\mathrm{m}}}{dt}}\right)=\left({\displaystyle \frac{\delta }{2G}}\right){\left({\displaystyle \frac{\pi }{G{H}^2}}\right)}^{\delta -1}\left\{{ϵ}^2-{\displaystyle \frac{3\left(ϵ-1\right)}{\left(2-\delta \right)}}\right\}.\end{array}$$

  (33)
  • During inflation, $ϵ\simeq 0$; thus, in order to have in order for $T_{\mathrm{h}}{\dot{S}}_{\mathrm{T}}+T_{\mathrm{m}}{\dot{S}}_{\mathrm{m}}>0$ from Equation (33), the Tsallis exponent has to fulfill the following condition:

    $$\begin{array}{c}\hfill 0<\delta <2.\end{array}$$

    (34)
  • During the reheating stage, $ϵ={\displaystyle \frac{3}{2}}\left(1+{\omega }_0\right)$, where ${\omega }_0$ is the effective EoS parameter; thus, Equation (33) leads to the following constraint on $\delta$ to satisfy $T_{\mathrm{h}}{\dot{S}}_{\mathrm{T}}+T_{\mathrm{m}}{\dot{S}}_{\mathrm{m}}>0$, as the EoS parameter may vary within the range of ${\omega }_0=[0,1]$:

    $$\begin{array}{c}\hfill 0<\delta <{\displaystyle \frac{5}{4}}.\end{array}$$

    (35)
  • During the radiation era, the changes in the matter fields’ entropy and the horizon entropy are expressed as

    $$\begin{array}{c}\hfill {\dot{S}}_{\mathrm{m}}\propto {\displaystyle \frac{3}{a^3{H}^2}}\left(ϵ-1\right),\end{array}$$

    (36)

    and

    $$\begin{array}{c}\hfill {\dot{S}}_{\mathrm{T}}={\displaystyle \frac{4\pi }{GH}}\left({\displaystyle \frac{\delta }{2-\delta }}\right){\left({\displaystyle \frac{\pi }{G{H}^2}}\right)}^{\delta -1},\end{array}$$

    (37)

    respectively. Clearly, ${\dot{S}}_{\mathrm{m}}>0$, as during the radiation era, $ϵ$ is larger than unity; moreover, the positivity of ${\dot{S}}_{\mathrm{T}}$ leads to

    $$\begin{array}{c}\hfill 0<\delta <2.\end{array}$$

    (38)
  Because $\delta$ remains constant with the cosmic expansion of the universe, all the above constraints on $\delta$ during different cosmic eras are simultaneously fulfilled if the following condition is met:

  $$\begin{array}{c}\hfill 0<\delta <\mathrm{Min}\left[2,{\displaystyle \frac{5}{4}},2\right]={\displaystyle \frac{5}{4}}.\end{array}$$

  (39)
  Here, it can be noted that such a range of $\delta$ also covers the case of Bekenstein–Hawking entropy, where $\delta =1$, i.e., Bekenstein–Hawking entropy also fulfills the requirement of the second law of horizon thermodynamics.

Following the above procedure, one can determine the constraints on entropic parameters for other forms of the horizon entropy. Here, we present a list for several forms of $S_{\mathrm{h}}$ [20]:

• For Rényi entropy, $S_{\mathrm{h}}\equiv S_{\mathrm{R}}={\displaystyle \frac{1}{\alpha }}ln\left(1+\alpha S\right)$ (with $\alpha$ being the parameter), and the constraint on the Rényi exponent, from an inflation- to radiation-dominated era, followed by a reheating stage, is expressed as follows:

  $$\begin{array}{c}\hfill \alpha >{\displaystyle \frac{G{H}_{\mathrm{I}}^2}{\pi }},\end{array}$$

  (40)

  where $H_{\mathrm{I}}$ is the Hubble scale during inflation.
• For Kaniadakis entropy, $S_{\mathrm{h}}\equiv S_{\mathrm{K}}={\displaystyle \frac{1}{K}}\sinh \left(KS\right)$,and the second law of horizon thermodynamics is fulfilled from the inflation → reheating → radiation era if the Kaniadakis exponent obeys the following constraint:

  $$\begin{array}{c}\hfill -1.4\left({\displaystyle \frac{G{H}_{\mathrm{I}}^2}{\pi }}\right)\lesssim K\lesssim 1.4\left({\displaystyle \frac{G{H}_{\mathrm{I}}^2}{\pi }}\right).\end{array}$$

  (41)
• The four-parameter generalised entropy given by

  $$\begin{array}{c}\hfill S_{\mathrm{h}}\equiv S_{\mathrm{g}}\left[{\alpha }_{+},{\alpha }_{-},\beta ,\gamma \right]={\displaystyle \frac{1}{\gamma }}\left[{\left(1+{\displaystyle \frac{{\alpha }_{+}}{\beta }}S\right)}^{\beta }-{\left(1+{\displaystyle \frac{{\alpha }_{-}}{\beta }}S\right)}^{-\beta }\right],\end{array}$$

  (42)

  is the minimal version of generalised entropy that is able to generalise all the known entropies proposed so far. The parameters should lie within the following constraints in order to validate the second law of horizon thermodynamics:

  $$\begin{array}{c}\hfill {\displaystyle \frac{{\alpha }_{\pm }}{\beta }}>{\displaystyle \frac{G{H}_{\mathrm{I}}^2}{\pi }},0<\beta <{\displaystyle \frac{5}{4}}\mathrm{and}\gamma >0.\end{array}$$

  (43)

Importantly, the above ranges provide model-independent constraints on entropic parameters (for different entropy functions of the apparent horizon) directly from the second law of horizon thermodynamics during a wide range of cosmic eras of the universe.

4. Generalised Entropy Functions

As mentioned in Equations (4) and (5), different forms of horizon entropy ($S_{\mathrm{h}}$) lead to different cosmological scenarios. In this regard, several entropies have been proposed, like Tsallis entropy [40], Rényi entropy [41], Barrow entropy [42], Sharma–Mittal entropy [43], Kaniadakis entropy [44], loop quantum gravity entropy [45], etc. However, irrespective of the form, $S_{\mathrm{h}}$ maintains some common properties, including the following:

• $S_{\mathrm{h}}$ is a monotonically increasing function of the Bekenstein–Hawking entropy variable ($S=A/\left(4G\right)$, where $A=4\pi R_{\mathrm{h}}^2$ denotes the area of the apparent horizon);
• $S_{\mathrm{h}}$ goes to zero in the limit of $S\to 0$, which can be thought of as equivalent to the third law of thermodynamics.

Such common properties indicate that there should exist some generalised form of entropy (with few parameters) that can generalise all the known entropies proposed so far at suitable representatives of the entropic parameters. Motivated by this idea, a few parameter-dependent generalised entropy functions (both singular and on-singular) have been proposed, which are able to generalise known entropies, like Tsallis entropy, Rényi entropy, Barrow entropy, Sharma–Mittal entropy, Kaniadakis entropy and loop quantum gravity entropy. Initially, six-parameter and three-parameter generalised entropies were proposed in [23], taking the forms of

$$\begin{array}{c}\hfill S_6({\alpha }_{\pm },{\beta }_{\pm },{\gamma }_{\pm })={\displaystyle \frac{1}{{\alpha }_{+}+{\alpha }_{-}}}\left[{\left(1+{\displaystyle \frac{{\alpha }_{+}}{{\beta }_{+}}}{S}^{{\gamma }_{+}}\right)}^{{\beta }_{+}}-{\left(1+{\displaystyle \frac{{\alpha }_{-}}{{\beta }_{-}}}{S}^{{\gamma }_{-}}\right)}^{-{\beta }_{-}}\right],\end{array}$$

(44)

and

$$\begin{array}{c}\hfill S_3(\alpha ,\beta ,\gamma )={\displaystyle \frac{1}{\gamma }}\left[{\left(1+{\displaystyle \frac{\alpha }{\beta }}S\right)}^{\beta }-1\right],\end{array}$$

(45)

respectively, where the respective entropic parameters are shown in brackets. However, after the introduction of this proposal, it was soon realized that the minimum number of parameters required in a generalised entropy function that can generalise all the aforementioned entropies is equal to four. Consequently, the four-parameter generalised entropy is expressed as

$$\begin{array}{c}\hfill S_4({\alpha }_{\pm },\beta ,\gamma )={\displaystyle \frac{1}{\gamma }}\left[{\left(1+{\displaystyle \frac{{\alpha }_{+}}{\beta }}S\right)}^{\beta }-{\left(1+{\displaystyle \frac{{\alpha }_{-}}{\beta }}S\right)}^{-\beta }\right],\end{array}$$

(46)

where $\left\{{\alpha }_{\pm },\beta ,\gamma \right\}$ are the parameters that are considered to be positive in order to make $S_4$ a monotonically increasing function with respect to S.

All the above entropies $\left\{S_6,S_4,S_3\right\}$ possesses a singularity in a different type of cosmological scenario, particularly in bouncing contexts, as Bekenstein–Hawking entropy, itself, diverges in bouncing scenarios (at the instant of bounce). Such diverging behaviour is common to all known entropies (like Tsallis entropy, Rényi entropy, Barrow entropy, Sharma–Mittal entropy, Kaniadakis entropy and loop quantum gravity entropy). To resolve this issue, a singular-free generalised entropy containing five parameters taking the form of

$$\begin{array}{c}\hfill S_5({\alpha }_{\pm },\beta ,\gamma ,ϵ)={\displaystyle \frac{1}{\gamma }}\left[{\left\{1+{\displaystyle \frac{1}{ϵ}}tanh\left({\displaystyle \frac{ϵ{\alpha }_{+}}{\beta }}S\right)\right\}}^{\beta }-{\left\{1+{\displaystyle \frac{1}{ϵ}}tanh\left({\displaystyle \frac{ϵ{\alpha }_{-}}{\beta }}S\right)\right\}}^{-\beta }\right],\end{array}$$

(47)

was proposed in [25], which turns out to be singular-free due to the presence of a hyperbolic function and is able to generalise all the entropies known so far. The minimum parameters required for a singular-free entropy that is also able to generalise all the known entropies is equal to five. Therefore, the minimal constructions of a generalised version of entropy are expressed by the four-parameter [24] and five-parameter [25] generalised entropy—based on universe’s evolution, in particular, whether the universe passes through a non-singular bounce (or not) during its cosmic evolution respectively. Various representatives of $\left\{S_6,S_4,S_3,S_5\right\}$ and their convergence to the known entropies are schematically shown in

Table 1. Schematic table summarizing various representatives of generalised entropies and their convergence to known entropies. Here, $S_{\mathrm{T}}=\mathrm{Tsallis}\mathrm{entropy}$, $S_{\mathrm{B}}=\mathrm{Barrow}\mathrm{entropy}$, $S_{\mathrm{R}}=\mathrm{R}é\mathrm{nyi}\mathrm{entropy}$, $S_{\mathrm{SM}}=\mathrm{Sharma}-\mathrm{Mittal}\mathrm{entropy}$, $S_{\mathrm{K}}=\mathrm{Kaniadakis}\mathrm{entropy}$ and $S_{\mathrm{q}}=\mathrm{loop}\mathrm{quantum}\mathrm{gravity}\mathrm{entropy}$.

$S_3$	$\gamma =\alpha$	$S_{\mathrm{SM}}$	$S_4$	${\alpha }_{-}=0,{\alpha }_{+}=\gamma$	$S_{\mathrm{SM}}$
	$\alpha \to \infty$	$S_{\mathrm{T}},S_{\mathrm{B}}$		${\alpha }_{+}\to \infty ,{\alpha }_{-}=0$	$S_{\mathrm{T}},S_{\mathrm{B}}$
	$\alpha ,\beta \to 0$ with ${\displaystyle \frac{\alpha }{\beta }}$ finite	$S_{\mathrm{R}}$		${\alpha }_{-}=0,{\alpha }_{+}=\gamma ,\beta \to 0$ with ${\displaystyle \frac{{\alpha }_{+}}{\beta }}$ finite	$S_{\mathrm{R}}$
	$\beta \to \infty ,\gamma =\alpha$	$S_{\mathrm{q}}$		$\beta \to \infty ,{\alpha }_{-}=0,{\alpha }_{+}=\gamma$	$S_{\mathrm{q}}$
				$\beta \to \infty ,{\alpha }_{+}={\alpha }_{-}$	$S_{\mathrm{K}}$
$S_5$	$ϵ,{\alpha }_{-}\to 0,{\alpha }_{+}=\gamma$	$S_{\mathrm{SM}}$	$S_6$	${\alpha }_{-}=0,{\alpha }_{+}={\gamma }_{+}{\beta }_{+}$	$S_{\mathrm{SM}}$
	$ϵ\to 0,{\alpha }_{-}=0,{\alpha }_{+}\to \infty ,\gamma ={\left({\displaystyle \frac{{\alpha }_{+}}{\beta }}\right)}^{\beta }$	$S_{\mathrm{T}},S_{\mathrm{B}}$		${\alpha }_{+}={\alpha }_{-}\to 0,{\gamma }_{+}={\gamma }_{-}$	$S_{\mathrm{T}},S_{\mathrm{B}}$
	$ϵ,\beta \to 0,{\alpha }_{-}=0,{\alpha }_{+}=\gamma$ with ${\displaystyle \frac{{\alpha }_{+}}{\beta }}$ finite	$S_{\mathrm{R}}$		${\alpha }_{+},{\beta }_{+}\to 0,{\gamma }_{+}=1$ with ${\displaystyle \frac{{\alpha }_{+}}{{\beta }_{+}}}$ finite	$S_{\mathrm{R}}$
	$ϵ,{\alpha }_{-}\to 0,\beta \to \infty ,{\alpha }_{+}=\gamma$	$S_{\mathrm{q}}$		${\beta }_{+}\to \infty ,{\alpha }_{-}=0,{\gamma }_{+}=1$	$S_{\mathrm{q}}$
	$ϵ\to 0,\beta \to \infty ,{\alpha }_{+}={\alpha }_{-}$	$S_{\mathrm{K}}$		${\beta }_{\pm }\to 0,{\alpha }_{+}={\alpha }_{-},{\gamma }_{\pm }=1$	$S_{\mathrm{K}}$

. The widespread application of generalised entropies to cosmology and black holes is addressed in [24,25,28,29,30,31,33,34].

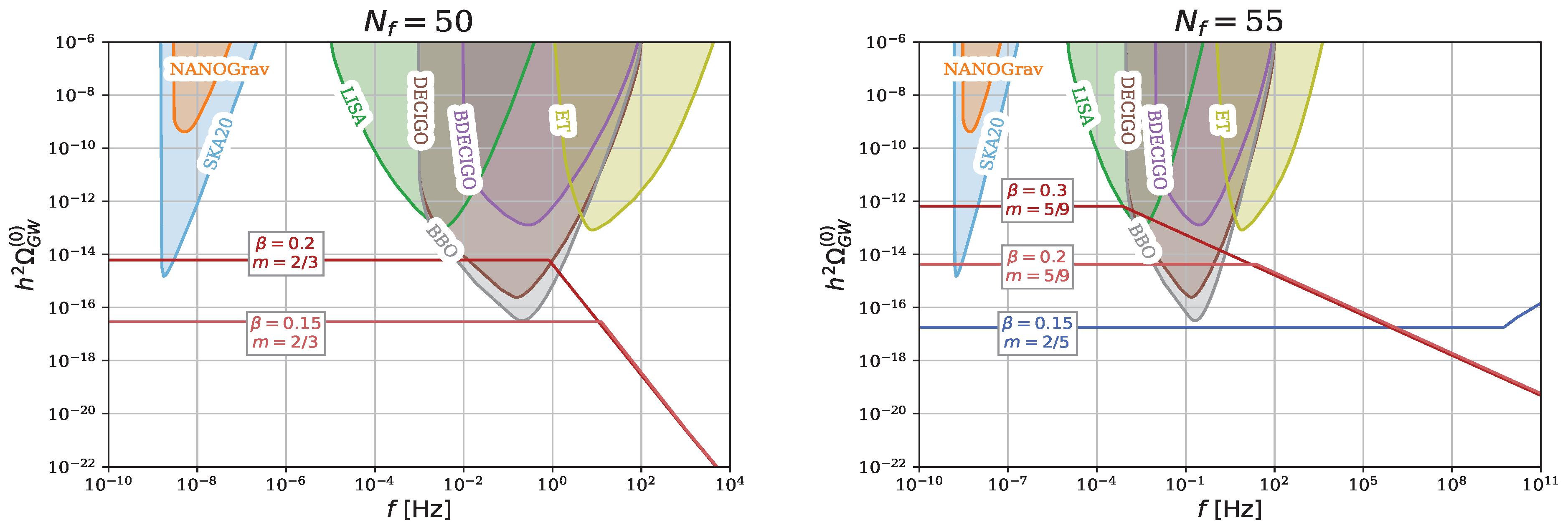
5. Primordial Gravitational Waves (GWs) in Entropic Cosmology

In this section, we discuss primordial GWs generated during inflation in the context of entropic cosmology when the entropy of the apparent horizon is expressed by the four-parameter generalised entropy ($S_{\mathrm{g}}$) that was been recently proposed in [24]. In particular,

$$\begin{array}{c}\hfill S_{\mathrm{g}}\left[{\alpha }_{+},{\alpha }_{-},\beta ,\gamma \right]={\displaystyle \frac{1}{\gamma }}\left[{\left(1+{\displaystyle \frac{{\alpha }_{+}}{\beta }}S\right)}^{\beta }-{\left(1+{\displaystyle \frac{{\alpha }_{-}}{\beta }}S\right)}^{-\beta }\right],\end{array}$$

(48)

where ${\alpha }_{\pm }$, $\beta$ and $\gamma$ are entropic parameters that are assumed to be positive. During the early stage of the universe, we assume that matter fields are absent; then, the FLRW equation corresponding to $S_{\mathrm{g}}$ results in a constant Hubble parameter (this statement is also true for other forms of horizon entropy). This, in turn, leads to eternal inflation, which has no exit mechanism; moreover, the primordial curvature perturbation is exactly scale-invariant, which is inconsistent with the Planck data. Thus, in order to support viable inflation, one may consider that the entropic parameters are not strictly constant; rather, they slowly vary with time. The following choices are available in this regard [24]:

$$\begin{array}{c}\hfill \gamma \left(N\right)=\exp \left[{\int }_{N_{\mathrm{f}}}^N\sigma \left(N\right)dN\right]\mathrm{with}\sigma \left(N\right)={\sigma }_0+{\mathrm{e}}^{-\left(N_{\mathrm{f}}-N\right)},\end{array}$$

(49)

which the other parameters (${\alpha }_{\pm }$, $\beta$) remain constant. Here, ${\sigma }_0$ is a constant, and N denotes the e-folding number, with $N_{\mathrm{f}}$ being the total e-folding number of the inflationary era. With varying $\gamma \left(N\right)$, the FLRW equation becomes

$$\begin{array}{c}\hfill -\left({\displaystyle \frac{2\pi }{G}}\right)\left[{\displaystyle \frac{{\alpha }_{+}{\left(1+\frac{{\alpha }_{+}}{\beta }S\right)}^{\beta -1}+{\alpha }_{-}{\left(1+\frac{{\alpha }_{-}}{\beta }S\right)}^{-\beta -1}}{{\left(1+\frac{{\alpha }_{+}}{\beta }S\right)}^{\beta }-{\left(1+\frac{{\alpha }_{-}}{\beta }S\right)}^{-\beta }}}\right]{\displaystyle \frac{1}{H^3}}{\displaystyle \frac{dH}{dN}}=\sigma \left(N\right),\end{array}$$

(50)

which, when solved for the Hubble parameter ($H=H\left(N\right)$), yields

$$\begin{array}{c}\hfill H\left(N\right)=4\pi M_{\mathrm{Pl}}\sqrt{{\displaystyle \frac{{\alpha }_{+}}{\beta }}}\left[{\displaystyle \frac{2^{1/\left(2\beta \right)}exp\left[-\frac{1}{2\beta }{\int }^N\sigma \left(N\right)dN\right]}{{\left\{1+\sqrt{1+4{\left({\alpha }_{+}/{\alpha }_{-}\right)}^{\beta }exp\left[-2{\int }^N\sigma \left(N\right)dN\right]}\right\}}^{1/\left(2\beta \right)}}}\right],\end{array}$$

(51)

where ${\int }_0^N\sigma \left(N\right)dN=N{\sigma }_0+{\mathrm{e}}^{-(N_{\mathrm{f}}-N)}-{\mathrm{e}}^{-N_{\mathrm{f}}}$. The above form of $H\left(N\right)$ is compatible with quasi-dS inflation with an exit at $N=N_{\mathrm{f}}$; moreover, the primordial curvature perturbation and the tensor-to-scalar ratio are compatible with the Planck data [70] for a suitable range of entropic parameters [24].

After inflation ends, the universe enters a reheating phase when the energy density corresponding to $S_{\mathrm{g}}$ decays to relativistic particles. Here, we consider a perturbative reheating scenario, which is generally parametrized by a constant EoS parameter (${\omega }_{\mathrm{eff}}$). Therefore, the Hubble parameter during the reheating stage is expressed as

$$\begin{array}{c}\hfill H\left(N\right)=H_{\mathrm{f}}\exp \left[-\left(N-N_{\mathrm{f}}\right)/m\right],\end{array}$$

(52)

where $H_{\mathrm{f}}$ is the Hubble parameter at the end of inflation (note: $H\left(N\right)$ is continuous at the junction of $N=N_{\mathrm{f}}$) and m is an exponent related to the reheating EoS parameter by ${\omega }_{\mathrm{eff}}=-1+2/\left(3m\right)$. The above Hubble parameter during reheating should be a solution of the Equation (50); this is possible for the following form of $\sigma \left(N\right)$ [28] during the reheating stage:

$$\begin{array}{c}\hfill \sigma \left(N\right)=\left({\displaystyle \frac{2\pi }{G}}\right){\displaystyle \frac{e^{2\left(N-N_{\mathrm{f}}\right)/m}}{m{H}_{\mathrm{f}}^2}}\left[{\displaystyle \frac{{\alpha }_{+}{\zeta }_{+}^{\beta -1}+{\alpha }_{-}{\zeta }_{-}^{-\beta -1}}{{\zeta }_{+}^{\beta }-{\zeta }_{-}^{-\beta }}}\right],\end{array}$$

(53)

where

$$\begin{array}{c}\hfill {\zeta }_{\pm }=1+{\displaystyle \frac{\pi {\alpha }_{\pm }}{\beta G{H}_{\mathrm{f}}^2}}{e}^{2\left(N-N_{\mathrm{f}}\right)/m}.\end{array}$$

Thus, as a whole, $\sigma \left(N\right)$ has the form of Equation (49) during inflation and that of Equation (53) during the reheating stage. Consequently, the e-folds for the reheating and the corresponding reheating temperature are expressed as

$$\begin{array}{c}\hfill N_{\mathrm{re}}={\displaystyle \frac{2m}{\left(2m-1\right)}}\left\{61.6-{\displaystyle \frac{1}{4\beta }}ln\left[{\displaystyle \frac{\beta {\mathrm{e}}^{-\left(1+{\sigma }_0{N}_{\mathrm{f}}\right)}{\left\{1+\sqrt{1+{\mathrm{e}}^{2\left(1+{\sigma }_0{N}_{\mathrm{f}}\right)}\left[{\left(\frac{1+{\sigma }_0}{2\beta }\right)}^2-1\right]}\right\}}^2}{{\left(16{\pi }^2{\alpha }_{+}/3\beta \right)}^{\beta }\left\{1+{\sigma }_0+2\beta \right\}}}\right]-N_{\mathrm{f}}\right\}\end{array}$$

(54)

and

$$\begin{array}{c}\hfill T_{\mathrm{re}}=H_{\mathrm{i}}{\left({\displaystyle \frac{43}{11g_{\mathrm{re}}}}\right)}^{1/3}\left({\displaystyle \frac{T_0}{k/a_0}}\right)e^{-\left(N_{\mathrm{f}}+N_{\mathrm{re}}\right)},\end{array}$$

(55)

respectively. Reheating phenomenology requires $N_{\mathrm{re}}>0$ and $T_{\mathrm{re}}>T_{\mathrm{BBN}}\approx {10}^{-2}\mathrm{GeV}$. The following ranges of the entropic parameters lead to a viable phenomenology during inflation, as well as during reheating [28]:

Having set the background evolution, we now address the spectrum of primordial GWs generated during inflation in the context of generalised entropic cosmology [33]. If $h_{ij}(t,\overrightarrow{x})$ is the tensor perturbation characterising GWs over a spatially flat FLRW spacetime, then the spacetime metric can be expressed as

$$\begin{array}{c}\hfill d{s}^2=-d{t}^2+a^2\left(t\right)\left[\left({\delta }_{ij}+h_{ij}\right)d{x}^{i}d{x}^j\right].\end{array}$$

(56)

Upon quantizing $h_{ij}(t,\overrightarrow{x})$, we can write the mode expansion as

$$\begin{array}{c}\hfill {\widehat{h}}_{ij}(t,\overrightarrow{x})=\sum _{\lambda =+,\times }\int {\displaystyle \frac{d^3\overrightarrow{k}}{{\left(2\pi \right)}^{3/2}}}\left[{\widehat{a}}_k^{\lambda }{ϵ}_{ij}^{\lambda }\left(\overrightarrow{k}\right)h(k,t){\mathrm{e}}^{i\overrightarrow{k}.\overrightarrow{x}}+c.c.\right],\end{array}$$

(57)

where $\lambda =+,\times$ denotes two types of polarisations of the GWs; ${ϵ}_{ij}^{\lambda }\left(\overrightarrow{k}\right)$ represents the polarisation tensor, and ${\widehat{a}}_k$ (${\widehat{a}}_k^{+}$) represents the annihilation (creation) operators that satisfy the usual commutation rules. Moreover, from the transverse condition of GWs, i.e., due to ${\partial }_i{h}^{ij}=0$, one immediately obtains $k^i{ϵ}_{ij}^{\lambda }\left(\overrightarrow{k}\right)=0$. The Fourier mode ($h(k,t)$) obeys the following condition:

$$\begin{array}{c}\hfill \ddot{h}(k,t)+3H\dot{h}(k,t)+{\displaystyle \frac{k^2}{a^2}}h(k,t)=0.\end{array}$$

(58)

As described above, the background Hubble parameter is almost constant during inflation; thus, Equation (58) is solved for $h(k,t)$ during the same period as follows:

$$\begin{array}{c}\hfill h(k,\eta )=-\sqrt{{\displaystyle \frac{2}{k}}}\left({\displaystyle \frac{H_{\mathrm{i}}}{M_{\mathrm{Pl}}}}\right)\eta e^{-ik\eta }\left(1-{\displaystyle \frac{i}{k\eta }}\right),\end{array}$$

(59)

where $H_{\mathrm{i}}$ is the constant Hubble parameter during inflation and can be obtained from Equation (51) at $N=0$. For the post-inflationary evolution, let us introduce the transfer function ($\chi (k,\eta )$) as

$$h(k,\eta )=\left[\underset{\left|k\eta \right|\ll 1}{lim}h(k,\eta )\right]\chi (k,\eta )=i\sqrt{{\displaystyle \frac{2}{k^3}}}\left({\displaystyle \frac{H_{\mathrm{i}}}{M_{\mathrm{Pl}}}}\right)\chi (k,\eta ),$$

(60)

in terms of which Equation (58) takes the following form:

$$\ddot{\chi }(k,t)+3H\dot{\chi }(k,t)+{\displaystyle \frac{k^2}{a^2}}\chi (k,t)=0.$$

(61)

During the reheating stage, $H\propto A^{-{\displaystyle \frac{3}{2}}(1+w_{\mathrm{eff}})}$ (where $A=a/a_{\mathrm{f}}$ is the rescaled scale factor; note that $A=1$ at the end of inflation); consequently, Equation (61) is solved as follows:

$${\chi }^{\mathrm{RH}}(k,A)=A^{-{\displaystyle \frac{3+3w_{\mathrm{eff}}}{4}}}\left[C\left(k\right)J_{\nu }\left({\displaystyle \frac{2k/k_{\mathrm{re}}}{1+3w_{\mathrm{eff}}}}{\left({\displaystyle \frac{A}{A_{\mathrm{re}}}}\right)}^{{\displaystyle \frac{1+3w_{\mathrm{eff}}}{2}}}\right)+D\left(k\right)J_{-\nu }\left({\displaystyle \frac{2k/k_{\mathrm{re}}}{1+3w_{\mathrm{eff}}}}{\left({\displaystyle \frac{A}{A_{\mathrm{re}}}}\right)}^{{\displaystyle \frac{1+3w_{\mathrm{eff}}}{2}}}\right)\right],$$

(62)

where $\nu =(1-3m)/(2+2m)$ and $k_{\mathrm{re}}$ represent the modes that re-enter the horizon at the end of reheating. Moreover, $C\left(k\right)$ and $D\left(k\right)$ are the integration constants, which can be determined from the continuity condition of the transfer function at the junction between inflation and reheating, as expressed by

$$\chi (k,A=1)=1\mathrm{and}{\displaystyle \frac{d\chi }{dA}}{|}_{A=1}=0$$

(63)

respectively. Furthermore, the transfer function during radiation follows from Equation (58) by using $H\propto A^{-2}$ and is expressed as

$$\begin{array}{ccc}\hfill {\chi }^{\mathrm{RD}}(k,A)& =& {\displaystyle \frac{e^{-ib(A-A_{\mathrm{re}})}}{2A}}\left[\left(A_{\mathrm{re}}-{\displaystyle \frac{1}{ib}}\right){\chi }^{\mathrm{RH}}(k,A_{\mathrm{re}})-\left({\displaystyle \frac{A_{\mathrm{re}}}{ib}}\right){\displaystyle \frac{d{\chi }^{\mathrm{RH}}(k,A_{\mathrm{re}})}{dA}}\right]\hfill \\ & +& {\displaystyle \frac{e^{ib(A-A_{\mathrm{re}})}}{2A}}\left[\left(A_{\mathrm{re}}+{\displaystyle \frac{1}{ib}}\right){\chi }^{\mathrm{RH}}(k,A_{\mathrm{re}})+\left({\displaystyle \frac{A_{\mathrm{re}}}{ib}}\right){\displaystyle \frac{d{\chi }^{\mathrm{RH}}(k,A_{\mathrm{re}})}{dA}}\right].\hfill \end{array}$$

(64)

where ${\chi }^{\mathrm{RH}}(k,A_{\mathrm{re}})$ represents the transfer function at the end of reheating; thus, $\chi (k,A)$ becomes continuous at the junction between reheating and radiation occurring at $A=A_{\mathrm{re}}$.

The current dimensionless energy density parameter (${\mathrm{\Omega }}_{\mathrm{GW}}^{\left(0\right)}\left(k\right)$) (i.e., in the present epoch) is expressed as

$$\begin{array}{c}\hfill {\mathrm{\Omega }}_{\mathrm{GW}}^{\left(0\right)}\left(k\right)h^2={\displaystyle \frac{1}{6{\pi }^2}}{\left({\displaystyle \frac{g_{r,0}}{g_{r,eq}}}\right)}^{1/3}{\mathrm{\Omega }}_{\mathrm{R}}{h}^2{\left({\displaystyle \frac{H_{\mathrm{i}}}{M_{\mathrm{Pl}}}}\right)}^2\left\{A^2{\left|{\displaystyle \frac{d{\chi }^{\mathrm{RD}}(k,A)}{dA}}\right|}^2+b^2{A}^2{\left|{\chi }^{\mathrm{RD}}(k,A)\right|}^2\right\},\end{array}$$

(65)

where ${\mathrm{\Omega }}_{\mathrm{R}}$ denotes the present-day dimensionless energy density of radiation, and $g_{r,eq}$ and $g_{r,0}$ represent the number of relativistic degrees of freedom at matter–radiation equality and today, respectively. The above solutions of $\chi (k,A)$ lead to the following forms of ${\mathrm{\Omega }}_{\mathrm{GW}}^{\left(0\right)}\left(k\right)$ for different modes:

• For the modes that re-enter the horizon during the radiation era, i.e., for $k<k_{\mathrm{re}}$ (where $k_{\mathrm{re}}$ represents the mode that re-enters the horizon at the end of reheating),

  $${\mathrm{\Omega }}_{\mathrm{GW}}^{\left(0\right)}\left(k\right)h^2\simeq \left({\displaystyle \frac{1}{6{\pi }^2}}\right){\mathrm{\Omega }}_{\mathrm{R}}{h}^2{\left({\displaystyle \frac{H_{\mathrm{i}}}{M_{\mathrm{Pl}}}}\right)}^2,$$

  (66)

  where we assumed that $g_{r,0}=g_{r,eq}$.
• For the modes that re-enter the horizon during the reheating stage, i.e., for $k_{\mathrm{re}}<k<k_{\mathrm{f}}$ (where $k_{\mathrm{f}}$ is the mode that re-enters the horizon at the end of inflation),

  $${\mathrm{\Omega }}_{\mathrm{GW}}^{\left(0\right)}\left(k\right)h^2\simeq \left({\displaystyle \frac{1}{6{\pi }^2}}\right){\mathrm{\Omega }}_{\mathrm{R}}{h}^2{\left({\displaystyle \frac{H_{\mathrm{i}}}{M_{\mathrm{Pl}}}}\right)}^2{\left(1+3w_{\mathrm{eff}}\right)}^{{\displaystyle \frac{4}{1+3w_{\mathrm{eff}}}}}{\left({\displaystyle \frac{\Gamma (1-\nu )}{\sqrt{\pi }}}\right)}^2{\left({\displaystyle \frac{k}{k_{\mathrm{re}}}}\right)}^{2\left({\displaystyle \frac{3w_{\mathrm{eff}}-1}{3w_{\mathrm{eff}}+1}}\right)},$$

  (67)

  where, once again, we assume that $g_{r,0}=g_{r,eq}$.

As a whole, Equations (66) and (67) clearly demonstrate that the GWs today have a flat spectrum for the modes that re-enter the horizon during the radiation-dominated era, while the spectrum is tilted over the modes that re-enter the horizon during the reheating era. The amount of such tilt is expressed as

$$\begin{array}{c}\hfill n_{\mathrm{GW}}=2\left({\displaystyle \frac{3w_{\mathrm{eff}}-1}{3w_{\mathrm{eff}}+1}}\right)={\displaystyle \frac{2(1-2m)}{1-m}},\end{array}$$

(68)

which is blue for $m<{\displaystyle \frac{1}{2}}$ and red for $m>{\displaystyle \frac{1}{2}}$. In Figure 1, the GW spectra of today are plotted for a set of values of the entropic parameters ($\beta$, ${\sigma }_0$ and m), as well as for two different inflationary e-folding numbers, namely $N_{\mathrm{f}}=50$ and 55. The set of values of the entropic parameters is consistent with their viable ranges listed in

Table 2. Viable ranges of entropic parameters from both the inflation and reheating phenomenology for three different choices of $N_{\mathrm{f}}$. Here, it is important to mention that ${\omega }_{\mathrm{eff}}$ needs to be greater than $1/3$ for $N_{\mathrm{f}}\gtrsim 57$.

Viable Choice of ${\mathit{N}}_{\mathbf{f}}$	Viable Range of ${\mathit{\sigma }}_0$	Viable Range of $\mathit{\beta }$	Viable Range of ${\left(\frac{{\mathit{\alpha }}_{+}}{{\mathit{\alpha }}_{-}}\right)}^{\mathit{\beta }}$	Reheating EoS
(1) Set-1: $N_{\mathrm{f}}=50$	${\sigma }_0=[0.0127,0.0166]$	(a) $0.05<\beta <0.10$	$2\times {10}^5<{\left({\displaystyle \frac{{\alpha }_{+}}{{\alpha }_{-}}}\right)}^{\beta }<8.5\times {10}^5$	${\displaystyle \frac{1}{3}}<w_{\mathrm{eff}}<1$
		(b) $0.10<\beta <0.35$	$7.5<{\left({\displaystyle \frac{{\alpha }_{+}}{{\alpha }_{-}}}\right)}^{\beta }<2\times {10}^5$	$-{\displaystyle \frac{1}{3}}<w_{\mathrm{eff}}<{\displaystyle \frac{1}{3}}$
(2) Set-2: $N_{\mathrm{f}}=55$	${\sigma }_0=[0.0129,0.0166]$	(a) $0.06<\beta <0.22$	$4\times {10}^4<{\left({\displaystyle \frac{{\alpha }_{+}}{{\alpha }_{-}}}\right)}^{\beta }<5\times {10}^5$	${\displaystyle \frac{1}{3}}<w_{\mathrm{eff}}<1$
		(b) $0.22<\beta <0.40$	$7.5<{\left({\displaystyle \frac{{\alpha }_{+}}{{\alpha }_{-}}}\right)}^{\beta }<4\times {10}^4$	$-{\displaystyle \frac{1}{3}}<w_{\mathrm{eff}}<{\displaystyle \frac{1}{3}}$
(3) Set-3: $N_{\mathrm{f}}=60$	${\sigma }_0=[0.0130,0.0166]$	(a) $0.08<\beta <0.40$	$7.5<{\left({\displaystyle \frac{{\alpha }_{+}}{{\alpha }_{-}}}\right)}^{\beta }<3\times {10}^5$	${\displaystyle \frac{1}{3}}<w_{\mathrm{eff}}<1$

. The figures clearly illustrate the qualitative features discussed herein. Therefore, if the future, observatories can detect the signals of primordial GWs. In such cases, our theoretical expectation determined in the present work may represent a possible tool for the measurement of the generalised entropic parameters.

6. Non-Singular Bounce in Entropic Cosmology

In order to have a bounce in entropic cosmology, the entropy of the apparent horizon itself needs to be non-singular at the instance of the vanishing Hubble parameter ($H=0$). This is unlike to four-parameter generalised entropy (or even other known entropies proposed so far, like Tsallis entropy, Renyi entropy, etc.), which becomes singular at $H=0$. In the spirit of addressing a non-singular bounce, a new singular-free entropy function was recently proposed in [25], as expressed by

$$\begin{array}{c}\hfill S_{\mathrm{ns}}\left[{\alpha }_{\pm },\beta ,\gamma ,ϵ\right]={\displaystyle \frac{1}{\gamma }}\left[{\left\{1+{\displaystyle \frac{1}{ϵ}}tanh\left({\displaystyle \frac{ϵ{\alpha }_{+}}{\beta }}S\right)\right\}}^{\beta }-{\left\{1+{\displaystyle \frac{1}{ϵ}}tanh\left({\displaystyle \frac{ϵ{\alpha }_{-}}{\beta }}S\right)\right\}}^{-\beta }\right],\end{array}$$

(69)

where ${\alpha }_{\pm }$, $\beta$, $\gamma$ and $ϵ$ are parameters that are considered to be positive, $S=\pi /\left(G{H}^2\right)$ symbolizes Bekenstein–Hawking entropy and the suffix ‘ns’ stands for ‘non-singular’. Below, use the following notation:

$$\begin{array}{c}\hfill {\chi }_{\pm }=1+{\displaystyle \frac{1}{ϵ}}tanh\left({\displaystyle \frac{ϵ{\alpha }_{\pm }}{\beta }}S\right).\end{array}$$

Note the due to the hyperbolic nature of the tan, the above form of entropy remains finite at the instance of $H=0$, (i.e., at the time of bounce). However, $S_{\mathrm{ns}}$ with constant parameters does not provide a viable cosmology; thus, we consider the $\gamma$ parameter to vary with time, while all other parameters remain fixed, i.e.,

$$\begin{array}{c}\hfill \gamma =\gamma \left(N\right),\end{array}$$

(70)

with N being the e-fold number of the universe. As an effect of $\gamma =\gamma \left(N\right)$, the modified Friedmann equations corresponding to the $S_{\mathrm{ns}}$ are expressed as

$$\begin{array}{c}\hfill \left[{\displaystyle \frac{{\alpha }_{+}{\mathrm{sech}}^2\left(\frac{ϵ{\alpha }_{+}}{\beta }S\right){\chi }_{+}^{\beta -1}+{\alpha }_{-}{\mathrm{sech}}^2\left(\frac{ϵ{\alpha }_{-}}{\beta }S\right){\chi }_{-}^{-\beta -1}}{{\chi }_{+}^{\beta }-{\chi }_{-}^{-\beta }}}\right]dS={\displaystyle \frac{{\gamma }^{\prime }\left(N\right)}{\gamma \left(N\right)}}dN\end{array}$$

where an overprime denotes ${\displaystyle \frac{d}{d\eta }}$. Integrating the above equation, one obtains

$$\begin{array}{c}\hfill tanh\left({\displaystyle \frac{ϵ\pi \alpha }{\beta G{H}^2}}\right)={\left\{{\displaystyle \frac{\gamma \left(N\right)+\sqrt{{\gamma }^2\left(N\right)+4}}{2}}\right\}}^{1/\beta }-1.\end{array}$$

(71)

where we take ${\alpha }_{+}={\alpha }_{-}=\alpha$ (without losing any generality) in order to extract an explicit solution of $H\left(N\right)$ that depends on the explicit form of $\gamma \left(N\right)$. In the following, we consider two symmetric bounce cases, namely exponential bounce and quasi-matter bounce cases, and determine the associated form of $\gamma \left(N\right)$ using Equation (71).

• The scale factor,

  $$\begin{array}{c}\hfill a\left(t\right)=\exp \left(a_0{t}^2\right),\end{array}$$

  (72)

  describes the exponential bounce, where the bounce happens at $t=0$. Herem $a_0$ is a constant with a mass dimension of [+2], which is actually related to the entropic parameters of $S_{\mathrm{ns}}$; thus, without losing any generality, we take $a_0={\displaystyle \frac{ϵ\pi \alpha }{4G\beta }}$. Such an exponential bounce can be achieved from singular-free entropic cosmology, provided the $\gamma \left(N\right)$ is expressed as

  $$\begin{array}{c}\hfill \gamma \left(N\right)={\left\{1+{\displaystyle \frac{1}{ϵ}}tanh\left({\displaystyle \frac{1}{N}}\right)\right\}}^{\beta }-{\left\{1+{\displaystyle \frac{1}{ϵ}}tanh\left({\displaystyle \frac{1}{N}}\right)\right\}}^{-\beta }.\end{array}$$

  (73)
• Quasi-matter bounce is described by the following scale factor:

  $$\begin{array}{c}\hfill a\left(t\right)={\left[1+a_0{\left({\displaystyle \frac{t}{t_0}}\right)}^2\right]}^n,\end{array}$$

  (74)

  where n, $a_0$ and $t_0$ are connected to the entropic parameters. In particular, one may take $n=\sqrt{\alpha }$, $a_0={\displaystyle \frac{\pi }{4\beta }}$ and $t_0=\sqrt{G/ϵ}$, with G being the gravitational constant. Consequently, $\gamma \left(N\right)$ that leads to such quasi-matter bounce is expressed as

  $$\begin{array}{c}\hfill \gamma \left(N\right)={\left\{1+{\displaystyle \frac{1}{ϵ}}tanh\left[{\mathrm{e}}^{-N/\sqrt{\alpha }}{\left({\mathrm{e}}^{N/\sqrt{\alpha }}-1\right)}^{{\displaystyle \frac{1}{2}}}\right]\right\}}^{\beta }-{\left\{1+{\displaystyle \frac{1}{ϵ}}tanh\left[{\mathrm{e}}^{-N/\sqrt{\alpha }}{\left({\mathrm{e}}^{N/\sqrt{\alpha }}-1\right)}^{{\displaystyle \frac{1}{2}}}\right]\right\}}^{-\beta }.\end{array}$$

  (75)

At this stage, it deserves mentioning that the comoving Hubble radius in the case of exponential bounce monotonically decreases with time and asymptotically goes to zero at both sides of the bounce. This results in the fact that the primordial perturbation modes are generated near the bounce where all the modes lie in the sub-Hubble regime; moreover, the perturbation modes in the distant past remain outside of the Hubble radius. As a result, exponential bounce suffers from a horizon problem. This is unlike quasi-matter bounce, where the comoving Hubble radius monotonically increases with cosmic time and eventually diverges in the asymptotic regime. Thus, the perturbation modes generate and lie in the sub-Hubble regime in the distant past, far away from the bounce. This resolves the horizon problem in this case. Moreover, quasi-matter bounce also leads to viable observable quantities consistent with the Planck data [25].

7. Brief Discussion on Future Perspectives

In Section 2, we discussed how a gravity theory is linked with a specific form of horizon entropy through the first law of horizon thermodynamics. Therefore, it is important to understand the gravity theory corresponding to four-parameter generalised entropy. This is important because four-parameter generalised entropy is able to generalise all the known entropies; thus, the theory of gravity equivalent to such a generalised entropy must have rich consequences in the context of cosmology, as well as in black hole physics. It is evident from Section 5 that the theoretical expectation of GW spectra based on four-parameter generalised entropy does not intersect with the sensitivity curve of NANOGrav. This may indicate that the standard inflationary evolution may not be the full story of the early universe. Thus, a modified inflationary evolution—for instance, a short deceleration epoch inside inflation—may be required to corroborate the theoretical GW spectra with NANOGrav data. The aspect of the generalised entropy in such a modified cosmic evolution and its consistency with NANOGrav data have significance in their own right. Apart from the early universe scenario, there are few unsolvable issues of entropic cosmology yet to be solved in the context of the dark energy era. For instance, (a) Can we obtain a viable reason from entropic cosmology regarding the cosmic transition of the universe from standard deceleration to late-time acceleration?; (b) What is the view of entropic cosmology on the Hubble tension issue, as well as on the LCDM epoch?, etc. Moreover, with development of entropic cosmology, black holes and compact objects remain to be studied, which are obtained with entropic modification of FLRW equations. These issues are timely and will, perhaps, be studied in the future.