Characterisation of the Atmosphere in Very High Energy Gamma-Astronomy for Imaging Atmospheric Cherenkov Telescopes
Abstract
1. Introduction
2. Atmospheric Monitoring Strategies and Instruments for Imaging Atmospheric Cherenkov Telescopes
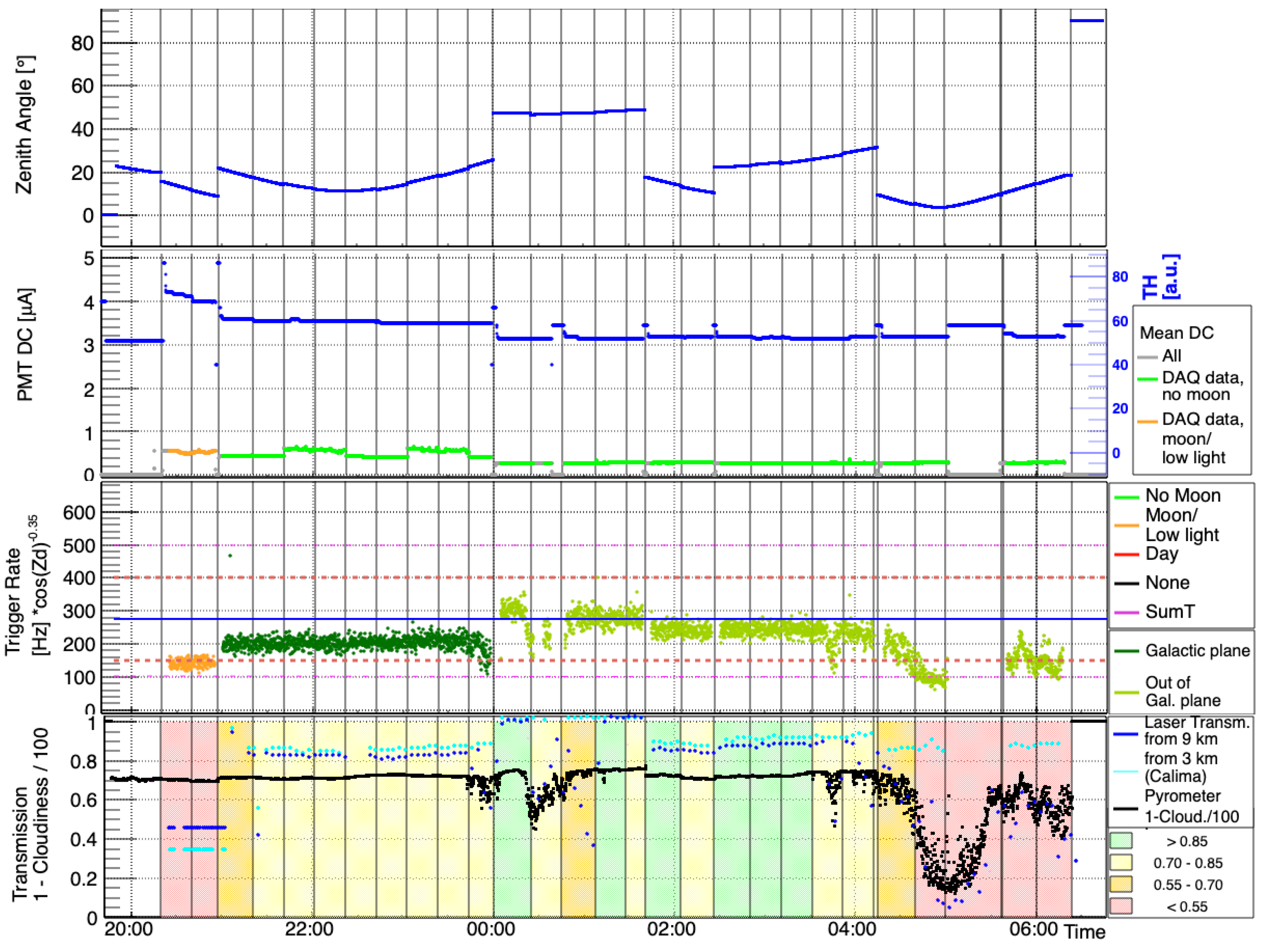
2.1. MAGIC Optical LIDAR
2.2. CTAO FRAM
3. Results and Discussion
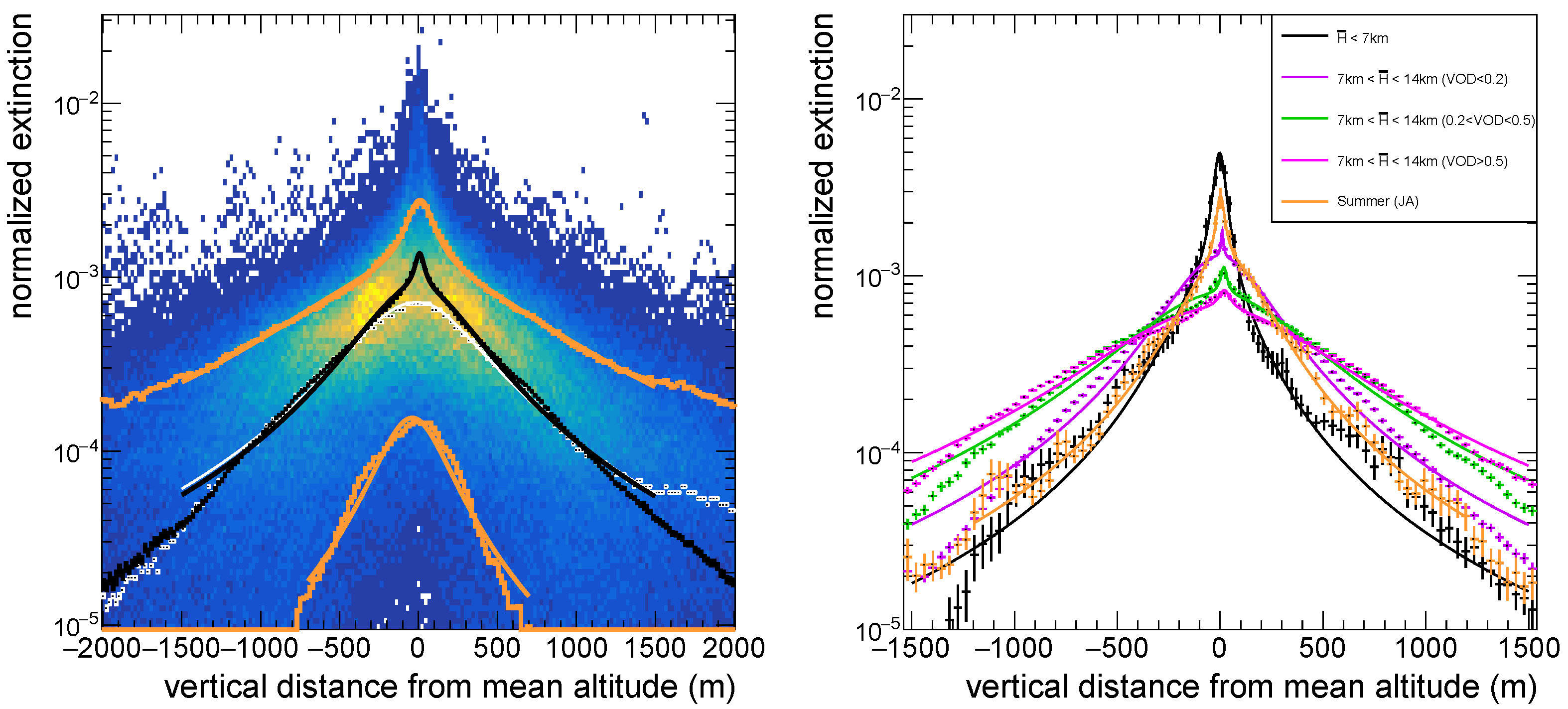
3.1. Atmospheric Aerosol Transmission Profiles Measured by the MAGIC LIDAR
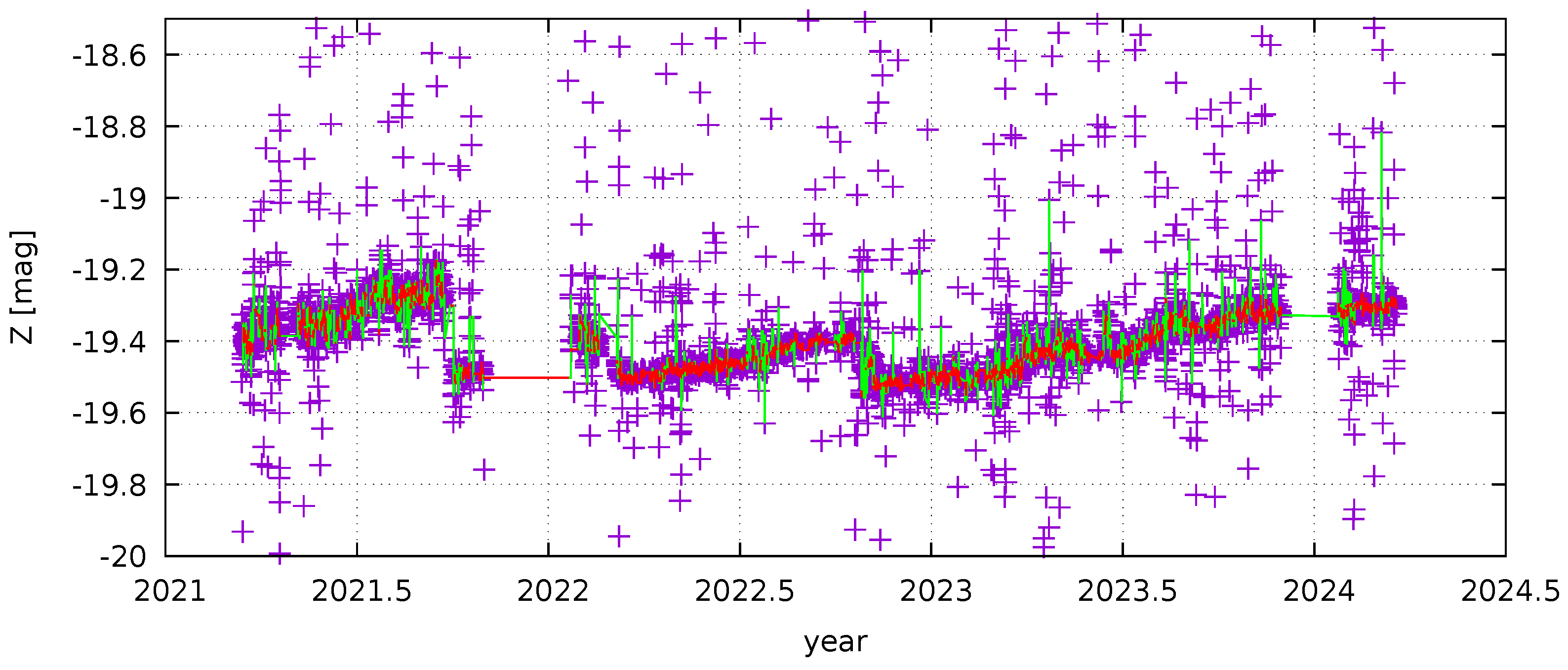
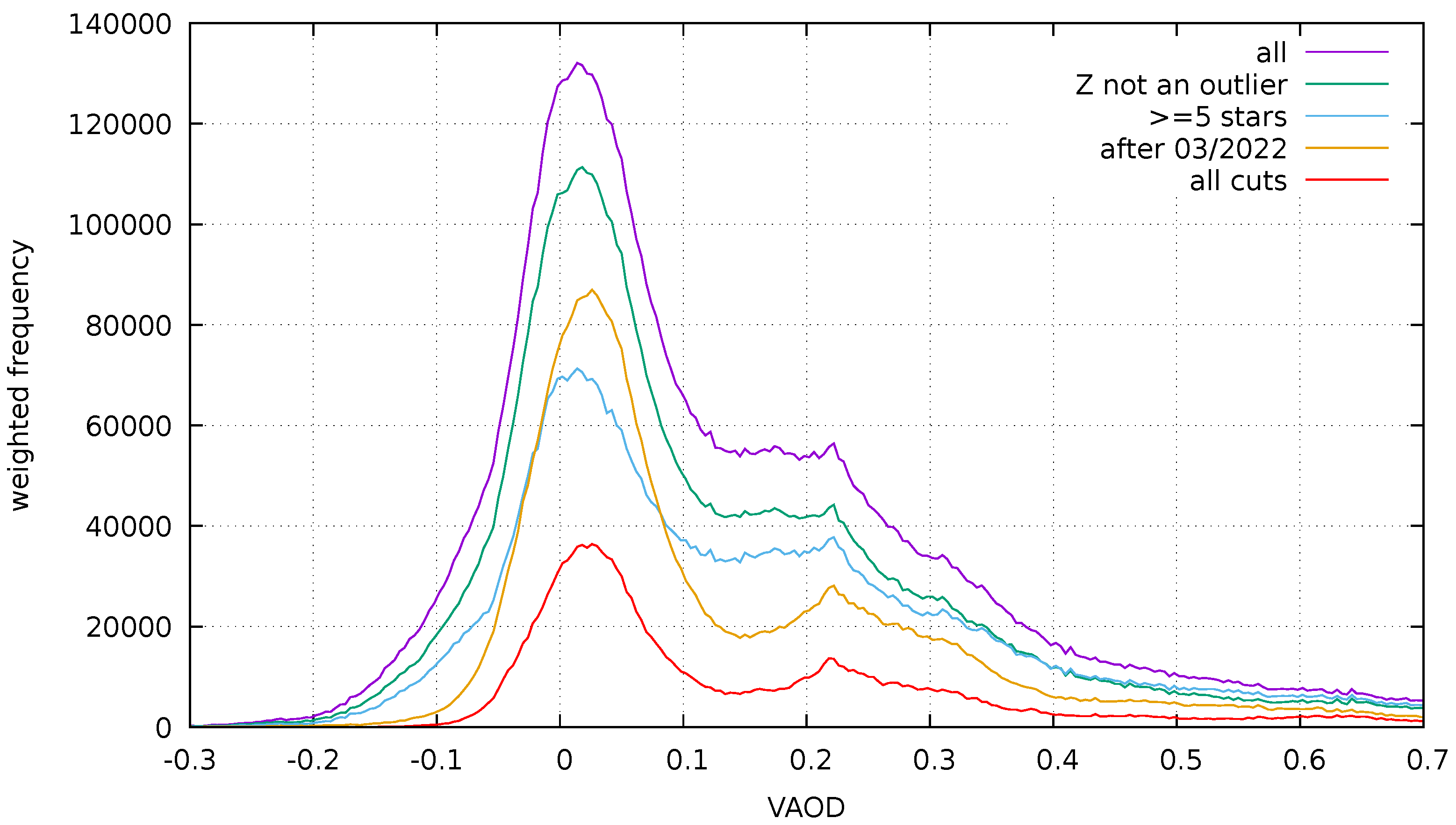
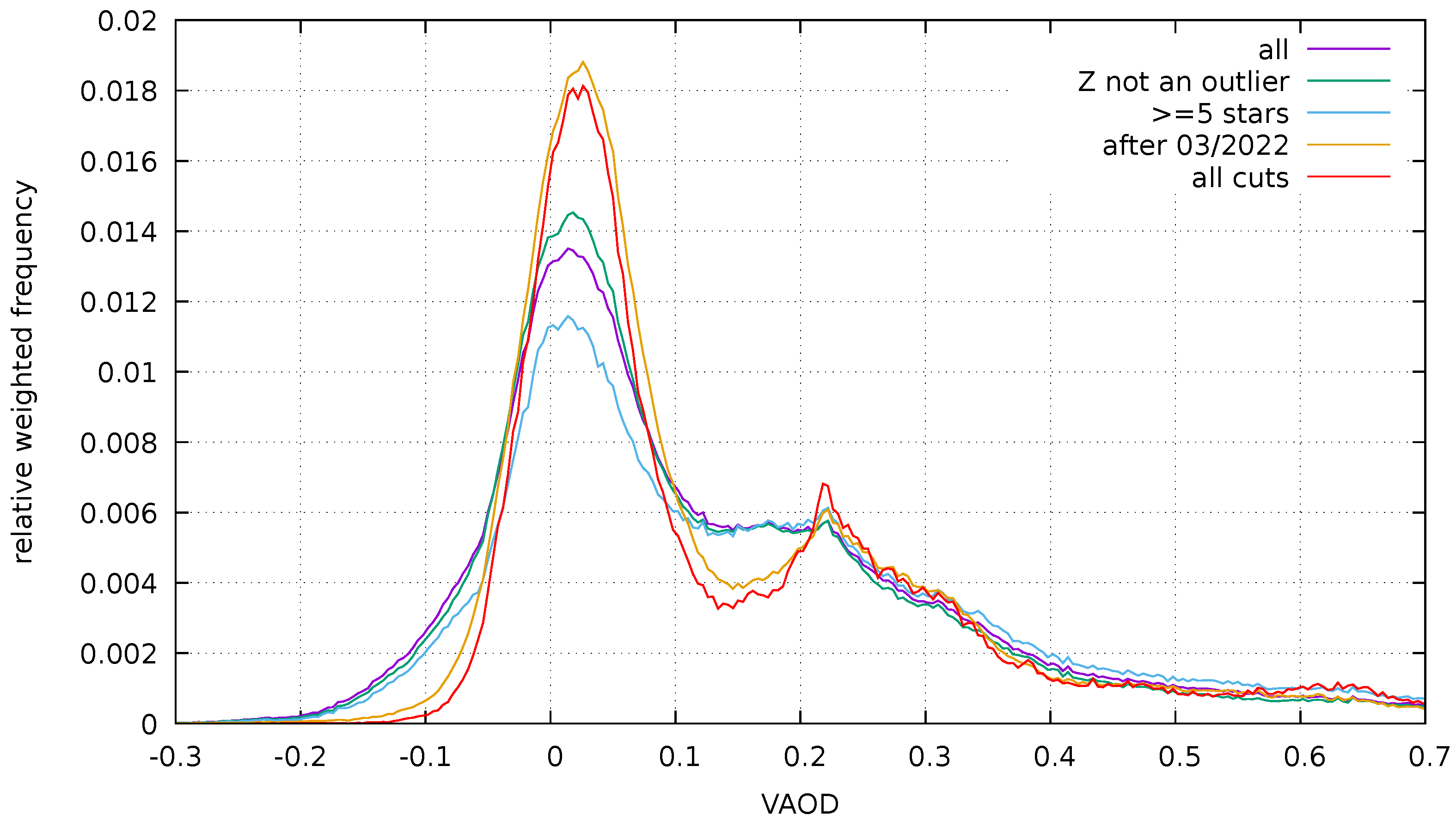
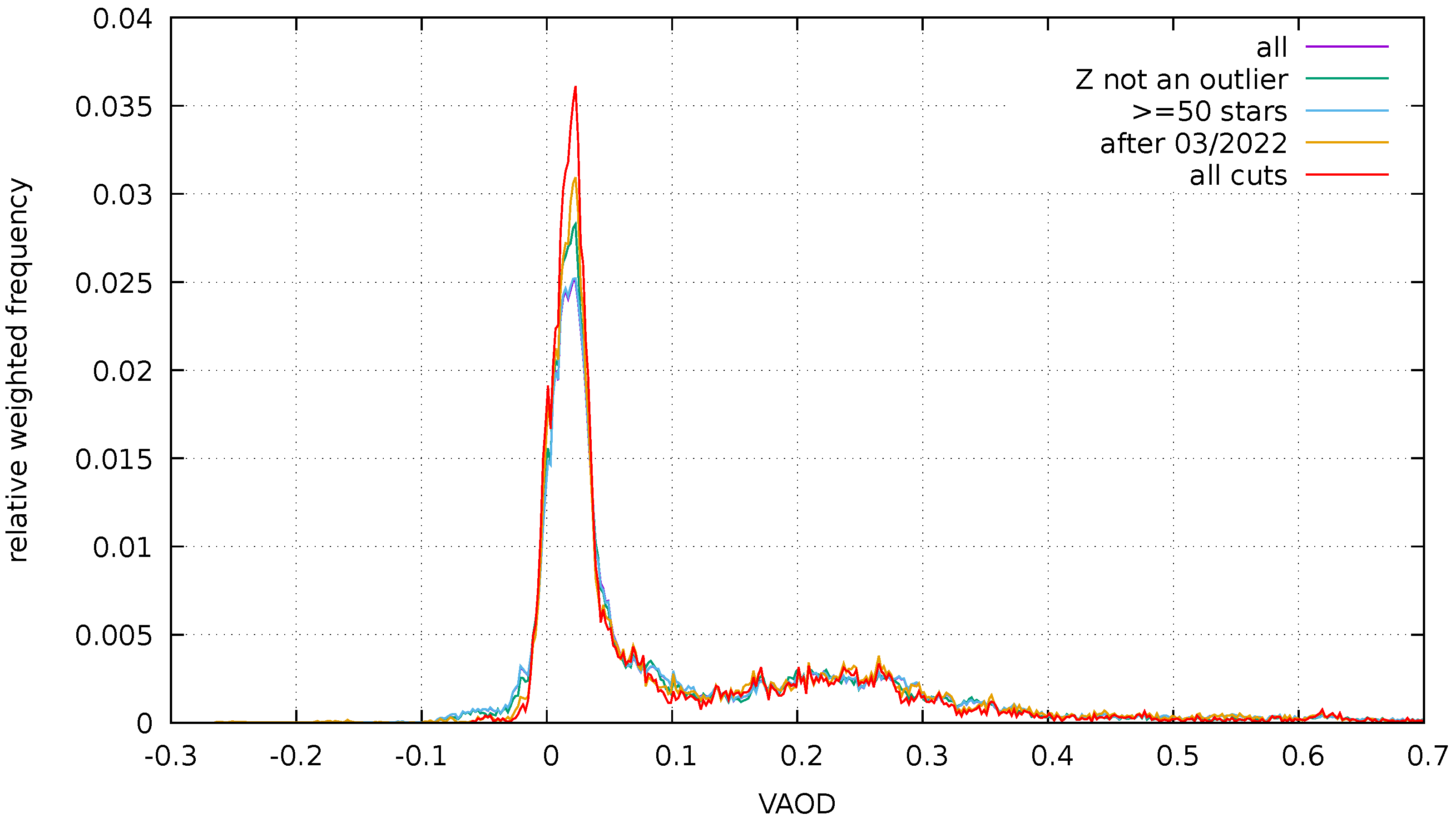
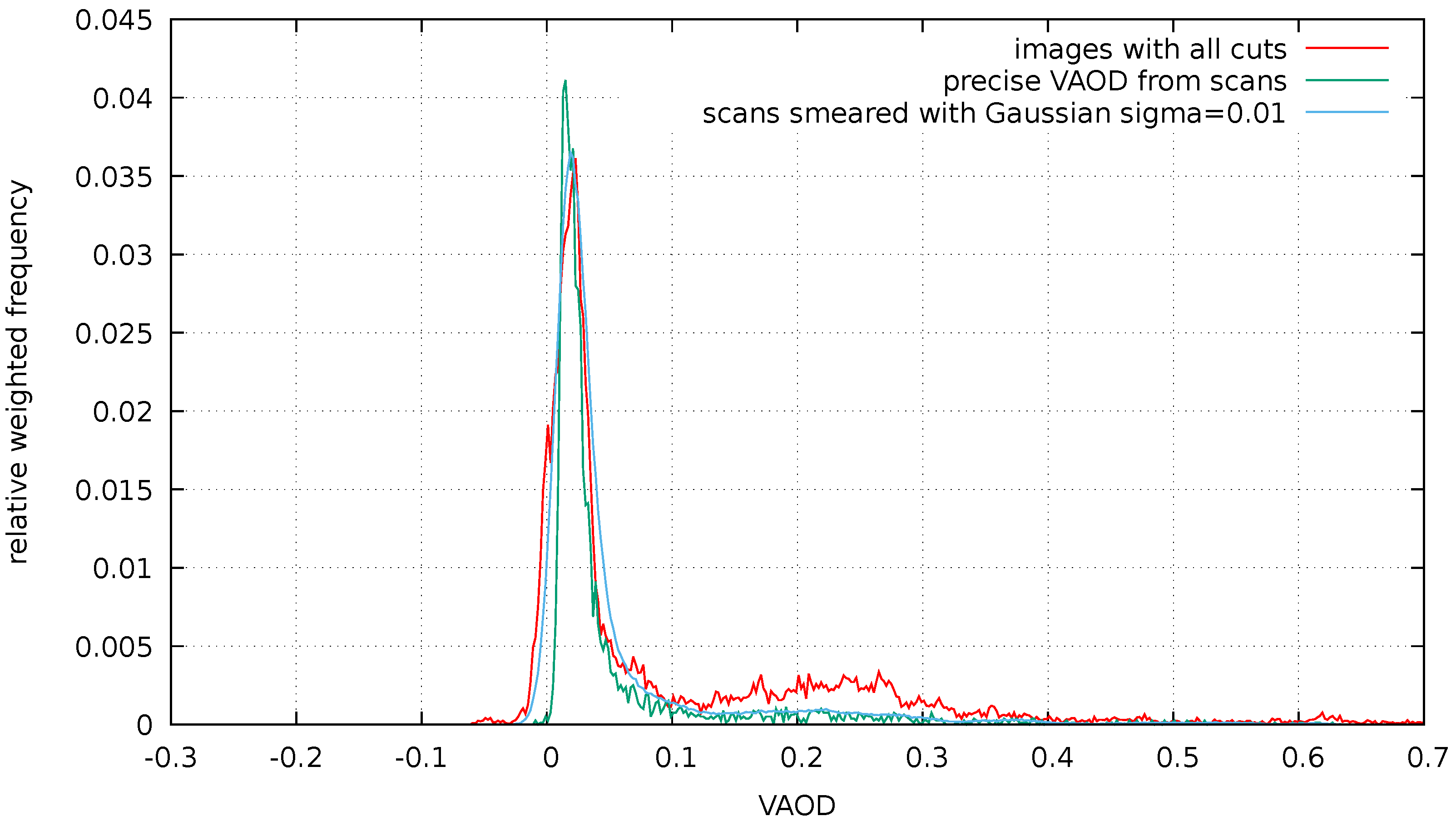
3.2. FRAM Aerosol Optical Depth Maps
4. Conclusions and Future Perspectives
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AGN | Active Galactic Nucleus |
| AOD | Aerosol Optical Depth |
| CCD | Charge Coupled Device |
| CTAO | Cherenkov Telescope Array Observatory |
| FoV | Field of view |
| FRAM | F/Photometric Robotic Telescope |
| GRB | Gamma-ray burst |
| HPD | Hybrid photodetector |
| IACT | Imaging Atmospheric Cherenkov Telescope |
| IRF | Instrument response function |
| LIDAR | LIght Detection And Ranging |
| LIV | Lorenz Invariance Violation |
| MAGIC | Major Atmospheric Gamma Imaging Cherenkov |
| MC | Monte Carlo |
| MWL | Multiwavelength |
| OB | Observation block |
| ORM | Observatorio del Roque de los Muchachos |
| PSF | Point spread function |
| QE | Quantum efficiency |
| STI | Stable Time Interval |
| ToO | Target of Opportunity |
| VAOD | Vertical aerosol optical depth |
| VHE | Very High Energy |
References
- Hinton, J.A.; Hofmann, W. Teraelectronvolt Astronomy. Annu. Rev. Astron. Astrophys. 2009, 47, 523–565. [Google Scholar] [CrossRef]
- Acharya, B.S.; Agudo, I.; Samarai, I.A.; Alfaro, R.; Alfaro, J.; Alispach, C.; Alves Batista, R.; Amans, J.P.; Amato, E.; Ambrosi, G. Science with the Cherenkov Telescope Array; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2017; Volume 1709, p. 213. [Google Scholar]
- Sobczyńska, D.; Bednarek, W. The impact of clouds on image parameters in IACT at very high energies. Eur. Phys. J. Web Conf. 2015, 89, 03009. [Google Scholar] [CrossRef]
- Aleksić, J.; Ansoldi, S.; Antonelli, L.A.; Antoranz, P.; Babic, A.; Bangale, P.; Barceló, M.; Barrio, J.A.; Becerra González, J.; Bednarek, W.; et al. The major upgrade of the MAGIC telescopes, Part II: A performance study using observations of the Crab Nebula. Astropart. Phys. 2016, 72, 76–94. [Google Scholar] [CrossRef]
- Ahnen, M.L.; Ansoldi, S.; Antonelli, L.A.; Arcaro, C.; Babić, A.; Banerjee, B.; Bangale, P.; Barres de Almeida, U.; Barrio, J.A.; Becerra González, J.; et al. Performance of the MAGIC telescopes under moonlight. Astropart. Phys. 2017, 94, 29–41. [Google Scholar] [CrossRef]
- Schmuckermaier, F.; Gaug, M.; Fruck, C.; Moralejo, A.; Hahn, A.; Dominis Prester, D.; Dorner, D.; Font, L.; Mićanović, S.; Mirzoyan, R.; et al. Correcting Imaging Atmospheric Cherenkov Telescope data with atmospheric profiles obtained with an elastic light detecting and ranging system. Astron. Astrophys. 2023, 673, A2. [Google Scholar] [CrossRef]
- Manganaro, M.; Dominis Prester, D. Highlights of the Magic Florian Goebel Telescopes in the Study of Active Galactic Nuclei. Universe 2024, 10, 80. [Google Scholar] [CrossRef]
- Aartsen, M.G.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Al Samarai, I.; Altmann, D.; Andeen, K. Multimessenger observations of a flaring blazar coincident with high-energy neutrino IceCube-170922A. Science 2018, 361, eaat1378. [Google Scholar] [CrossRef]
- Addazi, A.; Alvarez-Muniz, J.; Alves Batista, R.; Amelino-Camelia, G.; Antonelli, V.; Arzano, M.; Asorey, M.; Atteia, J.L.; Bahamonde, S.; Bajardi, F.; et al. Quantum gravity phenomenology at the dawn of the multi-messenger era-A review. Prog. Part. Nucl. Phys. 2022, 125, 103948. [Google Scholar] [CrossRef]
- Acciari, V.A.; Ansoldi, S.; Antonelli, L.A.; Arbet Engels, A.; Baack, D.; Babić, A.; Banerjee, B.; Barres de Almeida, U.; Barrio, J.A.; Becerra González, J.; et al. Unraveling the Complex Behavior of Mrk 421 with Simultaneous X-Ray and VHE Observations during an Extreme Flaring Activity in 2013 April. Astrophys. J. Suppl. Ser. 2020, 248, 29. [Google Scholar] [CrossRef]
- Domínguez, A.; Primack, J.R.; Rosario, D.J.; Prada, F.; Gilmore, R.C.; Faber, S.M.; Koo, D.C.; Somerville, R.S.; Pérez-Torres, M.A.; Pérez-González, P.; et al. Extragalactic background light inferred from AEGIS galaxy-SED-type fractions. Mon. Not. R. Astron. Soc. 2011, 410, 2556–2578. [Google Scholar] [CrossRef]
- Ulrich, M.H.; Maraschi, L.; Urry, C.M. Variability of Active Galactic Nuclei. Annu. Rev. Astron. Astrophys. 1997, 35, 445–502. [Google Scholar] [CrossRef]
- Pecimotika, M.; Dominis Prester, D.; Hrupec, D.; Mićanović, S.; Pavletić, L.; Sitarek, J. Performance and systematic uncertainties of CTA-North in conditions of reduced atmospheric transmission. J. Cosmol. Astropart. Phys. 2023, 2023, 011. [Google Scholar] [CrossRef]
- Sobczyńska, D.; Adamczyk, K.; Sitarek, J.; Szanecki, M. An analysis method for data taken by Imaging Air Cherenkov Telescopes at very high energies under the presence of clouds. Astropart. Phys. 2020, 120, 102450. [Google Scholar] [CrossRef]
- Żywucka, N.; Sitarek, J.; Sobczyńska, D.; Pecimotika, M.; Hrupec, D.; Dominis Prester, D.; Pavletić, L.; Mićanović, S. A novel image-correction method for cloud-affected observations with Imaging Atmospheric Cherenkov Telescopes. Astron. Astrophys. 2024, 685, A165. [Google Scholar] [CrossRef]
- Fruck, C.; Gaug, M.; Hahn, A.; Acciari, V.; Besenrieder, J.; Dominis Prester, D.; Dorner, D.; Fink, D.; Font, L.; Mićanović, S.; et al. Characterizing the aerosol atmosphere above the Observatorio del Roque de los Muchachos by analysing seven years of data taken with an GaAsP HPD-readout, absolutely calibrated elastic LIDAR. Mon. Not. R. Astron. Soc. 2022, 515, 4520–4550. [Google Scholar] [CrossRef]
- Holch, T.L.; Leuschner, F.; Schäfer, J.; Steinmassl, S. Assessing aerosol induced errors in Monte Carlo based air-shower reconstruction for atmospheric Cherenkov detectors. J. Phys. Conf. Ser. 2022, 2398, 012017. [Google Scholar] [CrossRef]
- Bregeon, J.; Compin, M.; Rivoire, S.; Sanguillon, M.; Vasileiadis, G. An elastic lidar system for the H.E.S.S. Experiment. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2016, 819, 60–66. [Google Scholar] [CrossRef]
- Will, M. Atmospheric Monitoring at the Site of the MAGIC Telescopes. EPJ Web Conf. 2017, 144, 01002. [Google Scholar] [CrossRef]
- Connolly, M. Aerosols and the Imaging Atmospheric Cherenkov Technique. Ph.D. Thesis, National University of Ireland, Galway, Ireland, 2018. [Google Scholar]
- Hahn, J.; de los Reyes, R. Atmospheric monitoring in H.E.S.S. EPJ Web Conf. 2015, 89, 02002. [Google Scholar] [CrossRef]
- Hahn, J.; de los Reyes, R.; Bernlöhr, K.; Krüger, P.; Lo, Y.T.E.; Chadwick, P.M.; Daniel, M.K.; Deil, C.; Gast, H.; Kosack, K.; et al. Impact of aerosols and adverse atmospheric conditions on the data quality for spectral analysis of the H.E.S.S. telescopes. Astropart. Phys. 2014, 54, 25–32. [Google Scholar] [CrossRef]
- Ballester, O.; Blanch, O.; Boix, J.; Bregeon, J.; Brun, P.; Çolak, S.M.; Doro, M.; Da Deppo, V.; Font, L.; Gabella, O.; et al. Raman LIDARs for the atmospheric calibration along the line-of-sight of CTA. In Proceedings of the 36th International Cosmic Ray Conference (ICRC2019), Madison, WI, USA, 24 July–1 August 2019; Volume PoS(ICRC2019)814. [Google Scholar]
- Vasileiadis, G.; Brun, P.; Gabella, O.; Rivoire, S.; Avdikos, G.; Louridas, A.; Georgoussis, G.; Papayannis, A. Design and Development of a Raman Lidar for Cherenkov Gamma Array Experiments. Eur. Phys. J. Web Conf. 2020, 237, 07006. [Google Scholar] [CrossRef]
- Živec, M.; Ballester, O.; Blanch, O.; Boix, J.; Calisse, P.G.; Campoy Ordaz, A.; Doro, M.; Font, L.; Garcia, R.; Gaug, M.; et al. Observation of the Cumbre Vieja volcano plume above the Observatorio del Roque de los Muchachos with the Barcelona Raman LIDAR. J. Phys. Conf. Ser. 2022, 2398, 012013. [Google Scholar] [CrossRef]
- Ebr, J.; Karpov, S.; Eliášek, J.; Blažek, J.; Cunniffe, R.; Ebrová, I.; Janeček, P.; Jelínek, M.; Juryšek, J.; Mandát, D.; et al. A New Method for Aerosol Measurement Using Wide-field Photometry. Astron. J. 2021, 162, 6. [Google Scholar] [CrossRef]
- Gaug, M.; Hahn, A.; Acciari, V.; Besenrieder, J.; Dominis Prester, D.; Dorner, D.; Fink, D.; Font, L.; Fruck, C.; Mićanović, S.; et al. Seven years of quasi-continuous LIDAR data. J. Phys. Conf. Ser. 2022, 2398, 012010. [Google Scholar] [CrossRef]
- Stefanik, S.; Nosek, D.; de los Reyes, R.; Gaug, M.; Travnicek, P. Atmospheric monitoring and inter-calibration of the telescope optical throughput efficiencies using the trigger rates of the Cherenkov Telescope Array. Astropart. Phys. 2019, 109, 12–24. [Google Scholar] [CrossRef]
- Mandat, D.; Pech, M. All Sky Camera for CTA Site characterization. Eur. Phys. J. Web Conf. 2017, 144, 01005. [Google Scholar] [CrossRef]
- Adam, J.; Buss, J.; Brügge, K.; Nöthe, M.; Rhode, W. Cloud Detection and Prediction with All Sky Cameras. Eur. Phys. J. Web Conf. 2017, 144, 01004. [Google Scholar] [CrossRef]
- Saito, T.Y.; Bernardini, E.; Bose, D.; Fonseca, M.V.; Lorenz, E.; Mannheim, K.; Mirzoyan, R.; Orito, R.; Schweizer, T.; Shayduk, M.; et al. Very high QE HPDs with a GaAsP photocathode for the MAGIC telescope project. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2009, 610, 258–261. [Google Scholar] [CrossRef]
- Fruck, C. The Galactic Center Resolved with MAGIC and a New Technique for Atmospheric Calibration. Ph.D. Thesis, Technische Universität München, Garching, Germany, 2015. [Google Scholar]
- Pérez-Ramírez, D.; Aceituno, J.; Ruiz, B.; Olmo, F.; Alados-Arboledas, L. Development and calibration of a star photometer to measure the aerosol optical depth: Smoke observations at a high mountain site. Atmos. Environ. 2008, 42, 2733–2738. [Google Scholar] [CrossRef]
- Baibakov, K.; O’Neill, N.T.; Ivanescu, L.; Duck, T.J.; Perro, C.; Herber, A.; Schulz, K.H.; Schrems, O. Synchronous polar winter starphotometry and lidar measurements at a High Arctic station. Atmos. Meas. Tech. 2015, 8, 3789–3809. [Google Scholar] [CrossRef]
- Aab, A.; Abreu, P.; Aglietta, M.; Albury, J.M.; Allekotte, I.; Almela, A.; Alvarez-Muñiz, J.; Alves Batista, R.; Anastasi, G.A.; Anchordoqui, L.; et al. The FRAM robotic telescope for atmospheric monitoring at the Pierre Auger Observatory. J. Instrum. 2021, 16, P06027. [Google Scholar] [CrossRef]
- Janeček, P.; Prouza, M.; Ebr, J. FRAM for CTA. EPJ Web Conf. 2015, 89, 03006. [Google Scholar] [CrossRef]
- Dorner, D.; Nilsson, K.; Bretz, T. A method to correct IACT data for atmospheric absorption due to the Saharan Air Layer. Astron. Astrophys. 2009, 493, 721–725. [Google Scholar] [CrossRef]
- Sobczyńska, D.; Bednarek, W. Influence of clouds on the parameters of images measured by IACT at very high energies. J. Phys. G Nucl. Part. Phys. 2014, 41, 125201. [Google Scholar] [CrossRef]
- Klett, J.D. Stable analytical inversion solution for processing lidar returns. Appl. Opt. 1981, 20, 211–220. [Google Scholar] [CrossRef] [PubMed]
- Negi, S.; Ebr, J.; Karpov, S.; Eliášek, J. Improved Point Spread Function Correction for Aerosol Measurements Using Wide-field Stellar Photometry. J. Phys. Conf. Ser. 2022, 2398, 012019. [Google Scholar] [CrossRef]
- Janeček, P.; Ebr, J.; Blažek, J.; Prouza, M.; Mašek, M.; Eliášek, J. FRAM for the Cherenkov Telescope Array: An update. Eur. Phys. J. Web Conf. 2017, 144, 01012. [Google Scholar] [CrossRef]
- Høg, E.; Fabricius, C.; Makarov, V.V.; Urban, S.; Corbin, T.; Wycoff, G.; Bastian, U.; Schwekendiek, P.; Wicenec, A. The Tycho-2 catalogue of the 2.5 million brightest stars. Astron. Astrophys. 2000, 355, L27–L30. [Google Scholar]
- Vallenari, A.; Brown, A.G.A.; Prusti, T.; de Bruijne, J.H.J.; Arenou, F.; Babusiaux, C.; Biermann, M.; Creevey, O.L.; Ducourant, C. Gaia Data Release 3. Summary of the content and survey properties. Astron. Astrophys. 2023, 674, A1. [Google Scholar] [CrossRef]



| Case | C | |||||
|---|---|---|---|---|---|---|
| (m) | (m) | (1) | (m) | (m) | (1) | |
| Mean | 7 | 36 | 0.95 | −8 | 394 | 1.12 |
| Median | −26 | 448 | 0. | n.a. | n.a. | 1.00 |
| 5% Quantile | −41 | 238 | 0. | n.a. | n.a. | 0.12 |
| 95% Quantile | 10 | 100. | 0.82 | −32 | 815 | 3.2 |
| Case | C | |||||
|---|---|---|---|---|---|---|
| (m) | (m) | (1) | (m) | (m) | (1) | |
| Low clouds | −2 | 35 | 0.53 | −46 | 210 | 0.98 |
| Medium-altitude clouds, VOD < 0.2 | 10 | 7 | 0.99 | −2 | 266 | 1.08 |
| Medium-altitude clouds, 0.2 < VOD < 0.5 | 18 | 19 | 0.98 | −12 | 473 | 1.18 |
| Medium-altitude clouds, VOD > 0.5 | 20 | 35 | 0.98 | −22 | 589 | 1.22 |
| Summer clouds (July, August) | 1 | 24 | 0.87 | 24 | 226 | 0.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dominis Prester, D.; Ebr, J.; Gaug, M.; Hahn, A.; Babić, A.; Eliášek, J.; Janeček, P.; Karpov, S.; Kolarek, M.; Manganaro, M.; et al. Characterisation of the Atmosphere in Very High Energy Gamma-Astronomy for Imaging Atmospheric Cherenkov Telescopes. Universe 2024, 10, 349. https://doi.org/10.3390/universe10090349
Dominis Prester D, Ebr J, Gaug M, Hahn A, Babić A, Eliášek J, Janeček P, Karpov S, Kolarek M, Manganaro M, et al. Characterisation of the Atmosphere in Very High Energy Gamma-Astronomy for Imaging Atmospheric Cherenkov Telescopes. Universe. 2024; 10(9):349. https://doi.org/10.3390/universe10090349
Chicago/Turabian StyleDominis Prester, Dijana, Jan Ebr, Markus Gaug, Alexander Hahn, Ana Babić, Jiří Eliášek, Petr Janeček, Sergey Karpov, Marta Kolarek, Marina Manganaro, and et al. 2024. "Characterisation of the Atmosphere in Very High Energy Gamma-Astronomy for Imaging Atmospheric Cherenkov Telescopes" Universe 10, no. 9: 349. https://doi.org/10.3390/universe10090349
APA StyleDominis Prester, D., Ebr, J., Gaug, M., Hahn, A., Babić, A., Eliášek, J., Janeček, P., Karpov, S., Kolarek, M., Manganaro, M., & Mirzoyan, R. (2024). Characterisation of the Atmosphere in Very High Energy Gamma-Astronomy for Imaging Atmospheric Cherenkov Telescopes. Universe, 10(9), 349. https://doi.org/10.3390/universe10090349







