Supernova Neutrinos: Flavour Conversion Mechanisms and New Physics Scenarios
Abstract
1. Introduction
2. Supernova Neutrino: Emission Phases and Spectra
- During the initial collapse phase, preceding the core bounce, a small amount of electron neutrinos is primarily emitted due to processes like beta decay and electron capture.
- Following the core bounce, approximately 25 milliseconds later, there is a rapid increase in the flux of electron neutrinos known as the “neutronization burst” phase. During this phase, small amounts of electron antineutrinos and other neutrino flavours are also emitted, although their contribution is negligible compared to the flux of electron neutrinos.
- Subsequently, the “accretion phase” ensues, lasting for approximately a few hundred milliseconds. As the shockwave stalls, matter accumulates onto the core over several hundred milliseconds. During this phase, the star undergoes cooling by emitting neutrinos and antineutrinos of all flavours. Typically, there is an excess of electron neutrinos compared to other species, with a discernible hierarchy in average energies: .
- Finally, the “Kelvin–Helmholtz cooling phase” begins, wherein the proto-neutron star at the core cools down by emitting neutrinos over a period of around ten seconds. In this phase, the hierarchy of average energy among neutrino flavours is observed to be less pronounced.
3. Neutrino Propagation: Equations of Motion
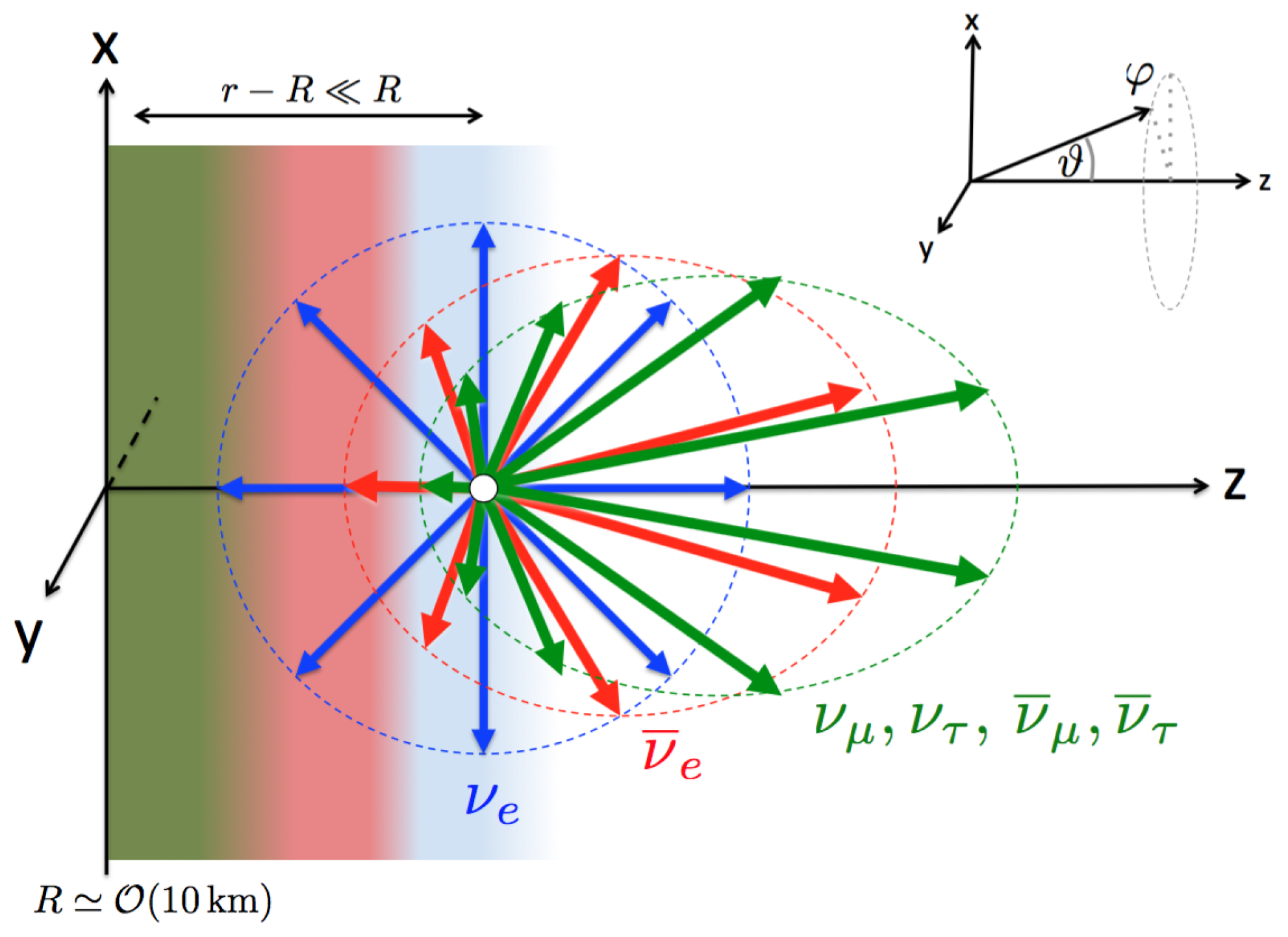
4. Neutrino Flavour Conversions inside a Supernova
4.1. Matter-Induced Resonant Flavour Conversions
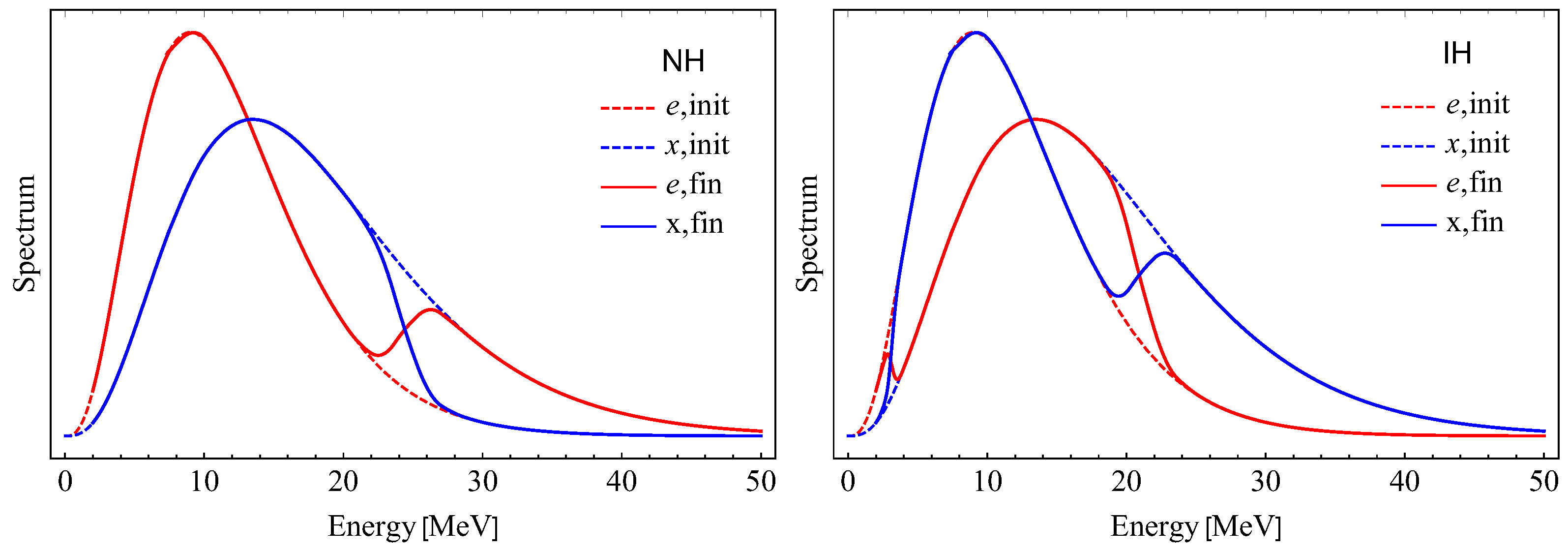
4.2. Slow Collective Flavour Conversions
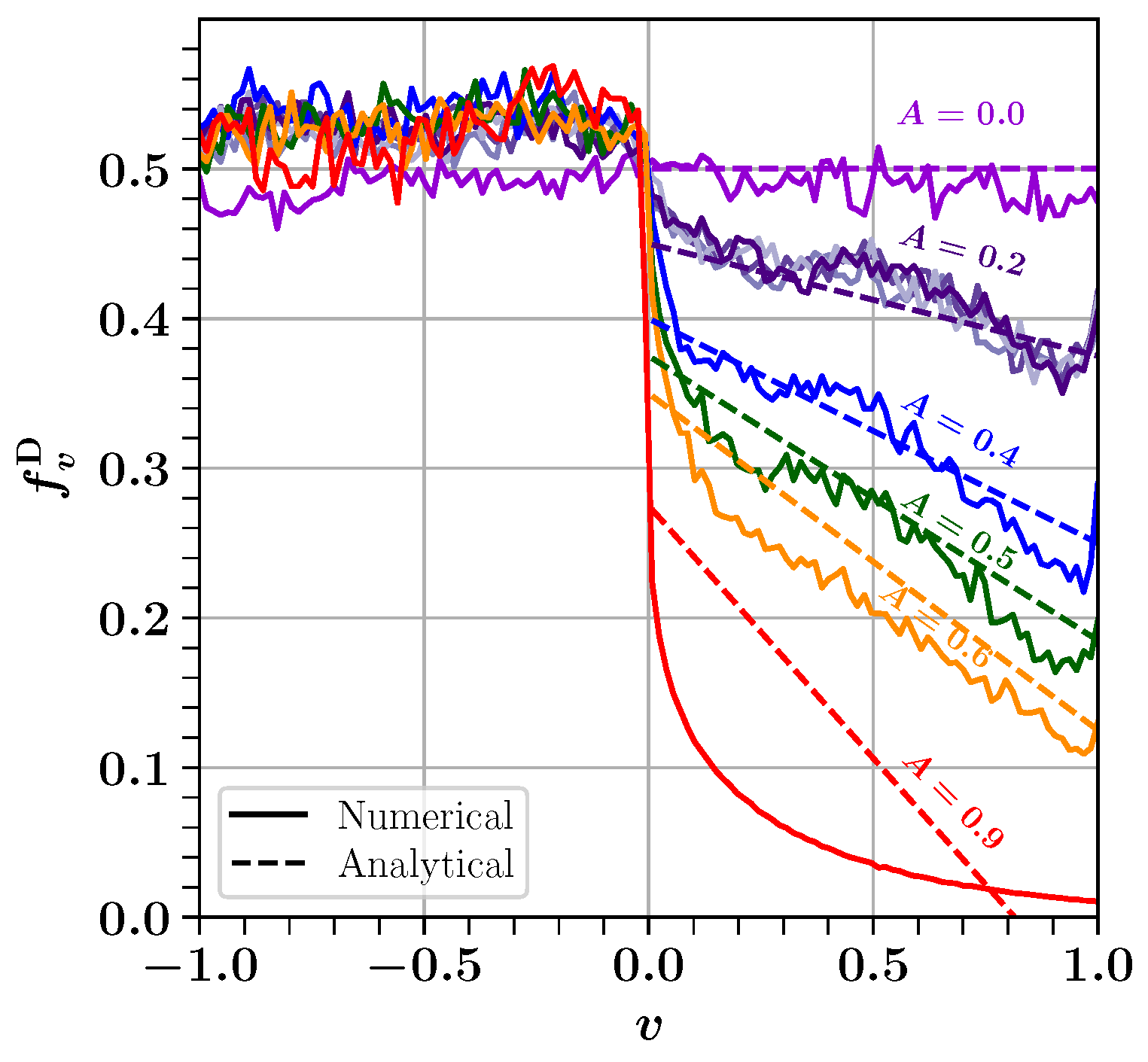
4.3. Fast Collective Flavour Conversions
4.4. A Comment on Mean-Field Approximation vs. Many-Body Effects
5. New Physics from Supernova Neutrinos
- It can affect the net luminosity and average energy of the emitted neutrinos and hence the duration of the neutrino emission phase.
- It can affect the shape/normalisation of the emitted neutrino spectra.
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SN | supernova |
| MSW | Mikheyev–Smirnov–Wolfenstein |
| CC | charged current |
| NC | neutral current |
| ELN | electron lepton number |
| μLN | muon lepton number |
| τLN | tau lepton number |
| SM | Standard Model |
| NSI | non-standard interactions |
| NSSI | non-standard self-interactions |
| LNV | lepton-number violation |
References
- Hirata, K.; Kajita, T.; Koshiba, M.; Nakahata, M.; Oyama, Y.; Sato, N.; Suzuki, A.; Takita, M.; Totsuka, Y.; Kifune, T.; et al. Observation of a Neutrino Burst from the Supernova SN 1987a. Phys. Rev. Lett. 1987, 58, 1490–1493. [Google Scholar] [CrossRef] [PubMed]
- Hirata, K.S.; Kajita, T.; Koshiba, M.; Nakahata, M.; Oyama, Y.; Sato, N.; Suzuki, A.; Takita, M.; Totsuka, Y.; Kifune, T.; et al. Observation in the Kamiokande-II Detector of the Neutrino Burst from Supernova SN 1987a. Phys. Rev. D 1988, 38, 448–458. [Google Scholar] [CrossRef] [PubMed]
- Bionta, R.M.; Blewitt, G.; Bratton, C.B.; Casper, D.; Ciocio, A.; Claus, R.; Cortez, B.; Crouch, M.; Dye, S.T.; Errede, S.; et al. Observation of a Neutrino Burst in Coincidence with Supernova SN 1987a in the Large Magellanic Cloud. Phys. Rev. Lett. 1987, 58, 1494. [Google Scholar] [CrossRef] [PubMed]
- Bratton, C.B.; Casper, D.; Ciocio, A.; Claus, R.; Crouch, M.; Dye, S.T.; Errede, S.; Gajewski, W.; Goldhaber, M.; Haines, T.J.; et al. Angular Distribution of Events From Sn1987a. Phys. Rev. D 1988, 37, 3361. [Google Scholar] [CrossRef] [PubMed]
- Alekseev, E.N.; Alekseeva, L.N.; Krivosheina, I.V.; Volchenko, V.I. Detection of the Neutrino Signal From SN1987A in the LMC Using the Inr Baksan Underground Scintillation Telescope. Phys. Lett. B 1988, 205, 209–214. [Google Scholar] [CrossRef]
- Bethe, H.A. Supernova mechanisms. Rev. Mod. Phys. 1990, 62, 801–866. [Google Scholar] [CrossRef]
- Mezzacappa, A. Ascertaining the core collapse supernova mechanism: The State of the Art and the Road Ahead. Ann. Rev. Nucl. Part. Sci. 2005, 55, 467–515. [Google Scholar] [CrossRef]
- Raffelt, G.G. Stars as Laboratories for Fundamental Physics; The University of Chicago Press: Chicago, IL, USA, 1996. [Google Scholar]
- Kotake, K.; Sato, K.; Takahashi, K. Explosion mechanism, neutrino burst, and gravitational wave in core-collapse supernovae. Rep. Prog. Phys. 2006, 69, 971–1144. [Google Scholar] [CrossRef]
- Woosley, S.; Janka, T. The physics of core-collapse supernovae. Nat. Phys. 2005, 1, 147. [Google Scholar] [CrossRef]
- Janka, H.T.; Langanke, K.; Marek, A.; Martinez-Pinedo, G.; Mueller, B. Theory of Core-Collapse Supernovae. Phys. Rep. 2007, 442, 38–74. [Google Scholar] [CrossRef]
- Janka, H.T. Explosion Mechanisms of Core-Collapse Supernovae. Ann. Rev. Nucl. Part. Sci. 2012, 62, 407–451. [Google Scholar] [CrossRef]
- Mirizzi, A.; Tamborra, I.; Janka, H.T.; Saviano, N.; Scholberg, K.; Bollig, R.; Hudepohl, L.; Chakraborty, S. Supernova Neutrinos: Production, Oscillations and Detection. Riv. Nuovo Cim. 2016, 39, 1–112. [Google Scholar] [CrossRef]
- Burrows, A.; Vartanyan, D. Core-Collapse Supernova Explosion Theory. Nature 2021, 589, 29–39. [Google Scholar] [CrossRef] [PubMed]
- Baade, W.; Zwicky, F. On Super-novae. Proc. Natl. Acad. Sci. USA 1934, 20, 254–259. [Google Scholar] [CrossRef] [PubMed]
- Brown, G.E.; Bethe, H.A.; Baym, G. Supernova theory. Nucl. Phys. 1982, A375, 481–532. [Google Scholar] [CrossRef]
- Burrows, A. Neutrinos From Supernova Explosions. Ann. Rev. Nucl. Part. Sci. 1990, 40, 181–212. [Google Scholar] [CrossRef]
- Colgate, S.A.; White, R.H. The Hydrodynamic Behavior of Supernovae Explosions. Astrophys. J. 1966, 143, 626. [Google Scholar] [CrossRef]
- Bethe, H.A.; Wilson, J.R. Revival of a stalled supernova shock by neutrino heating. Astrophys. J. 1985, 295, 14–23. [Google Scholar] [CrossRef]
- Mikheev, S.P.; Smirnov, A.Y. Resonance Amplification of Oscillations in Matter and Spectroscopy of Solar Neutrinos. Sov. J. Nucl. Phys. 1985, 42, 913–917. [Google Scholar]
- Wolfenstein, L. Neutrino Oscillations in Matter. Phys. Rev. 1978, D17, 2369–2374. [Google Scholar] [CrossRef]
- Kuo, T.K.; Pantaleone, J.T. Nonadiabatic Neutrino Oscillations in Matter. Phys. Rev. 1989, D39, 1930. [Google Scholar] [CrossRef] [PubMed]
- Dighe, A.S.; Smirnov, A.Y. Identifying the neutrino mass spectrum from the neutrino burst from a supernova. Phys. Rev. 2000, D62, 033007. [Google Scholar] [CrossRef]
- Pantaleone, J.T. Neutrino oscillations at high densities. Phys. Lett. 1992, B287, 128–132. [Google Scholar] [CrossRef]
- Pantaleone, J.T. Neutrino flavor evolution near a supernova’s core. Phys. Lett. 1995, B342, 250–256. [Google Scholar] [CrossRef]
- Kostelecky, V.A.; Samuel, S. Selfmaintained coherent oscillations in dense neutrino gases. Phys. Rev. 1995, D52, 621–627. [Google Scholar] [CrossRef] [PubMed]
- Samuel, S. Bimodal coherence in dense selfinteracting neutrino gases. Phys. Rev. 1996, D53, 5382–5393. [Google Scholar] [CrossRef] [PubMed]
- Duan, H.; Fuller, G.M.; Qian, Y.Z. Collective neutrino flavor transformation in supernovae. Phys. Rev. 2006, D74, 123004. [Google Scholar] [CrossRef]
- Duan, H.; Fuller, G.M.; Carlson, J.; Qian, Y.Z. Simulation of Coherent Non-Linear Neutrino Flavor Transformation in the Supernova Environment. 1. Correlated Neutrino Trajectories. Phys. Rev. 2006, D74, 105014. [Google Scholar] [CrossRef]
- Duan, H.; Fuller, G.M.; Carlson, J.; Qian, Y.Z. Coherent Development of Neutrino Flavor in the Supernova Environment. Phys. Rev. Lett. 2006, 97, 241101. [Google Scholar] [CrossRef]
- Hannestad, S.; Raffelt, G.G.; Sigl, G.; Wong, Y.Y.Y. Self-induced conversion in dense neutrino gases: Pendulum in flavour space. Phys. Rev. 2006, D74, 105010, Erratum in Phys. Rev. D 2007, 76, 029901. [Google Scholar] [CrossRef]
- Duan, H.; Fuller, G.M.; Carlson, J.; Qian, Y.Z. Analysis of Collective Neutrino Flavor Transformation in Supernovae. Phys. Rev. 2007, D75, 125005. [Google Scholar] [CrossRef]
- Duan, H.; Fuller, G.M.; Qian, Y.Z. Collective Neutrino Oscillations. Ann. Rev. Nucl. Part. Sci. 2010, 60, 569–594. [Google Scholar] [CrossRef]
- Sawyer, R.F. Speed-up of neutrino transformations in a supernova environment. Phys. Rev. 2005, D72, 045003. [Google Scholar] [CrossRef]
- Sawyer, R.F. The multi-angle instability in dense neutrino systems. Phys. Rev. D 2009, 79, 105003. [Google Scholar] [CrossRef]
- Sawyer, R.F. Neutrino cloud instabilities just above the neutrino sphere of a supernova. Phys. Rev. Lett. 2016, 116, 081101. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, S.; Hansen, R.S.; Izaguirre, I.; Raffelt, G. Self-induced neutrino flavor conversion without flavor mixing. JCAP 2016, 1603, 042. [Google Scholar] [CrossRef]
- Dasgupta, B.; Mirizzi, A.; Sen, M. Fast neutrino flavor conversions near the supernova core with realistic flavor-dependent angular distributions. JCAP 2017, 1702, 019. [Google Scholar] [CrossRef]
- Dasgupta, B.; Sen, M. Fast Neutrino Flavor Conversion as Oscillations in a Quartic Potential. Phys. Rev. 2018, D97, 023017. [Google Scholar] [CrossRef]
- Shalgar, S.; Tamborra, I. Dispelling a myth on dense neutrino media: Fast pairwise conversions depend on energy. JCAP 2021, 01, 014. [Google Scholar] [CrossRef]
- Tamborra, I.; Shalgar, S. New Developments in Flavor Evolution of a Dense Neutrino Gas. Ann. Rev. Nucl. Part. Sci. 2021, 71, 165–188. [Google Scholar] [CrossRef]
- Richers, S.; Sen, M. Fast Flavor Transformations. In Handbook of Nuclear Physics; Tanihata, I., Toki, H., Kajino, T., Eds.; Springer: Singapore, 2022; pp. 1–17. [Google Scholar] [CrossRef]
- Horiuchi, S.; Kneller, J.P. What can be learned from a future supernova neutrino detection? J. Phys. 2018, G45, 043002. [Google Scholar] [CrossRef]
- Fiorillo, D.F.G.; Heinlein, M.; Janka, H.T.; Raffelt, G.; Vitagliano, E.; Bollig, R. Supernova simulations confront SN 1987A neutrinos. Phys. Rev. D 2023, 108, 083040. [Google Scholar] [CrossRef]
- Li, S.W.; Beacom, J.F.; Roberts, L.F.; Capozzi, F. Old Data, New Forensics: The First Second of SN 1987A Neutrino Emission. Phys. Rev. D 2024, 109, 083025. [Google Scholar] [CrossRef]
- Abe, K.; Bronner, C.; Hayato, Y.; Hiraide, K.; Ikeda, M.; Imaizumi, S.; Kameda, J.; Kanemura, Y.; Kataoka, Y.; Miki, S.; et al. First gadolinium loading to Super-Kamiokande. Nucl. Instrum. Meth. A 2022, 1027, 166248. [Google Scholar] [CrossRef]
- Abe, S.; Asami, S.; Eizuka, M.; Futagi, S.; Gando, A.; Gando, Y.; Gima, T.; Goto, A.; Hachiya, T.; Hata, K.; et al. Search for supernova neutrinos and constraint on the galactic star formation rate with the KamLAND data. Astrophys. J. 2022, 934, 85. [Google Scholar] [CrossRef]
- Köpke, L.; IceCube Collaboration. Supernova Neutrino Detection with IceCube. J. Phys. Conf. Ser. 2011, 309, 012029. [Google Scholar] [CrossRef]
- Abi, B.; Acciarri, R.; Acero, M.A.; Adamov, G.; Adams, D.; Adinolfi, M.; Ahmad, Z.; Ahmed, J.; Alion, T.; Monsalve, S.A.; et al. Deep Underground Neutrino Experiment (DUNE), Far Detector Technical Design Report, Volume II: DUNE Physics. arXiv 2020, arXiv:2002.03005. [Google Scholar]
- Abe, K.; Abe, K.; Aihara, H.; Aimi, A.; Akutsu, R.; Andreopoulos, C.; Anghel, I.; Anthony, L.H.; Antonova, M.; Ashida, Y.; et al. Hyper-Kamiokande Design Report. arXiv 2018, arXiv:1805.04163. [Google Scholar]
- An, F.; An, G.; An, Q.; Antonelli, V.; Baussan, E.; Beacom, J.; Bezrukov, L.; Blyth, S.; Brugnera, R.; Avanzini, M.B.; et al. Neutrino Physics with JUNO. J. Phys. G 2016, 43, 030401. [Google Scholar] [CrossRef]
- Pattavina, L.; Ferreiro Iachellini, N.; Tamborra, I. Neutrino observatory based on archaeological lead. Phys. Rev. D 2020, 102, 063001. [Google Scholar] [CrossRef]
- Chakraborty, S.; Hansen, R.S.; Izaguirre, I.; Raffelt, G. Self-induced flavor conversion of supernova neutrinos on small scales. JCAP 2016, 1601, 028. [Google Scholar] [CrossRef]
- Fuller, G.M.; Haxton, W.C.; Grohs, E.B. Chapter 8: Neutrinos in Stellar Astrophysics. In The Encyclopedia of Cosmology; World Scientific: Singapore, 2023; pp. 367–431. [Google Scholar] [CrossRef]
- Volpe, M.C. Neutrinos from dense environments: Flavor mechanisms, theoretical approaches, observations, and new directions. arXiv 2023, arXiv:2301.11814. [Google Scholar]
- Capozzi, F.; Saviano, N. Neutrino Flavor Conversions in High-Density Astrophysical and Cosmological Environments. Universe 2022, 8, 94. [Google Scholar] [CrossRef]
- Burrows, A. On detecting stellar collapse with neutrinos. ApJ 1984, 283, 848–852. [Google Scholar] [CrossRef]
- Keil, M.T.; Raffelt, G.G.; Janka, H.T. Monte Carlo study of supernova neutrino spectra formation. Astrophys. J. 2003, 590, 971–991. [Google Scholar] [CrossRef]
- Tamborra, I.; Muller, B.; Hudepohl, L.; Janka, H.T.; Raffelt, G. High-resolution supernova neutrino spectra represented by a simple fit. Phys. Rev. D 2012, 86, 125031. [Google Scholar] [CrossRef]
- Bollig, R.; Janka, H.T.; Lohs, A.; Martinez-Pinedo, G.; Horowitz, C.J.; Melson, T. Muon Creation in Supernova Matter Facilitates Neutrino-driven Explosions. Phys. Rev. Lett. 2017, 119, 242702. [Google Scholar] [CrossRef]
- Raffelt, G.; Sigl, G.; Stodolsky, L. Quantum statistics in particle mixing phenomena. Phys. Rev. D 1992, 45, 1782–1788. [Google Scholar] [CrossRef]
- Raffelt, G.; Sigl, G.; Stodolsky, L. NonAbelian Boltzmann equation for mixing and decoherence. Phys. Rev. Lett. 1993, 70, 2363–2366, Erratum in Phys. Rev. Lett. 2007, 98, 069902. [Google Scholar] [CrossRef]
- Dolgov, A.D. Neutrinos in the Early Universe. Sov. J. Nucl. Phys. 1981, 33, 700–706. [Google Scholar]
- Barbieri, R.; Dolgov, A. Neutrino oscillations in the early universe. Nucl. Phys. B 1991, 349, 743–753. [Google Scholar] [CrossRef]
- Sigl, G.; Raffelt, G. General kinetic description of relativistic mixed neutrinos. Nucl. Phys. B 1993, 406, 423–451. [Google Scholar] [CrossRef]
- Kuo, T.K.; Pantaleone, J.T. Neutrino Oscillations in Matter. Rev. Mod. Phys. 1989, 61, 937. [Google Scholar] [CrossRef]
- Available online: http://www.nu-fit.org/?q=node/8 (accessed on 1 April 2024).
- Esteban, I.; Gonzalez-Garcia, M.C.; Maltoni, M.; Martinez-Soler, I.; Schwetz, T. Updated fit to three neutrino mixing: Exploring the accelerator-reactor complementarity. JHEP 2017, 01, 087. [Google Scholar] [CrossRef]
- Fuller, G.M.; Mayle, R.W.; Wilson, J.R.; Schramm, D.N. Resonant neutrino oscillations and stellar collapse. APJ 1987, 322, 795–803. [Google Scholar] [CrossRef]
- Lunardini, C.; Smirnov, A.Y. Probing the neutrino mass hierarchy and the 13 mixing with supernovae. JCAP 2003, 0306, 009. [Google Scholar] [CrossRef]
- Dighe, A.S.; Keil, M.T.; Raffelt, G.G. Detecting the neutrino mass hierarchy with a supernova at IceCube. JCAP 2003, 0306, 005. [Google Scholar] [CrossRef]
- Dighe, A.S.; Keil, M.T.; Raffelt, G.G. Identifying earth matter effects on supernova neutrinos at a single detector. JCAP 2003, 0306, 006. [Google Scholar] [CrossRef]
- Dighe, A.S.; Kachelriess, M.; Raffelt, G.G.; Tomas, R. Signatures of supernova neutrino oscillations in the earth mantle and core. JCAP 2004, 0401, 004. [Google Scholar] [CrossRef]
- Barger, V.; Huber, P.; Marfatia, D. Supernova neutrinos can tell us the neutrino mass hierarchy independently of flux models. Phys. Lett. 2005, B617, 167–173. [Google Scholar] [CrossRef]
- Fogli, G.L.; Lisi, E.; Mirizzi, A.; Montanino, D. Revisiting nonstandard interaction effects on supernova neutrino flavor oscillations. Phys. Rev. 2002, D66, 013009. [Google Scholar] [CrossRef]
- Schirato, R.C.; Fuller, G.M. Connection between supernova shocks, flavor transformation, and the neutrino signal. arXiv 2002, arXiv:astro-ph/0205390. [Google Scholar]
- Takahashi, K.; Sato, K.; Dalhed, H.E.; Wilson, J.R. Shock propagation and neutrino oscillation in supernova. Astropart. Phys. 2003, 20, 189–193. [Google Scholar] [CrossRef]
- Fogli, G.L.; Lisi, E.; Montanino, D.; Mirizzi, A. Analysis of energy and time dependence of supernova shock effects on neutrino crossing probabilities. Phys. Rev. 2003, D68, 033005. [Google Scholar] [CrossRef]
- Fogli, G.L.; Lisi, E.; Mirizzi, A.; Montanino, D. Probing supernova shock waves and neutrino flavor transitions in next-generation water-Cerenkov detectors. JCAP 2005, 0504, 002. [Google Scholar] [CrossRef]
- Tomas, R.; Kachelriess, M.; Raffelt, G.; Dighe, A.; Janka, H.T.; Scheck, L. Neutrino signatures of supernova shock and reverse shock propagation. JCAP 2004, 0409, 015. [Google Scholar] [CrossRef]
- Dasgupta, B.; Dighe, A. Phase effects in neutrino conversions during a supernova shock wave. Phys. Rev. 2007, D75, 093002. [Google Scholar] [CrossRef]
- Galais, S.; Kneller, J.; Volpe, C.; Gava, J. Shockwaves in Supernovae: New Implications on the Diffuse Supernova Neutrino Background. Phys. Rev. 2010, D81, 053002. [Google Scholar] [CrossRef]
- Friedland, A.; Mukhopadhyay, P. Near-critical supernova outflows and their neutrino signatures. Phys. Lett. B 2022, 834, 137403. [Google Scholar] [CrossRef]
- Radice, D.; Abdikamalov, E.; Ott, C.D.; Mösta, P.; Couch, S.M.; Roberts, L.F. Turbulence in Core-Collapse Supernovae. J. Phys. G 2018, 45, 053003. [Google Scholar] [CrossRef]
- Fogli, G.L.; Lisi, E.; Mirizzi, A.; Montanino, D. Damping of supernova neutrino transitions in stochastic shock-wave density profiles. JCAP 2006, 06, 012. [Google Scholar] [CrossRef]
- Friedland, A.; Gruzinov, A. Neutrino signatures of supernova turbulence. arXiv 2006, arXiv:astro-ph/0607244. [Google Scholar]
- Kneller, J.P.; Volpe, C. Turbulence effects on supernova neutrinos. Phys. Rev. D 2010, 82, 123004. [Google Scholar] [CrossRef]
- Borriello, E.; Chakraborty, S.; Janka, H.T.; Lisi, E.; Mirizzi, A. Turbulence patterns and neutrino flavor transitions in high-resolution supernova models. JCAP 2014, 1411, 030. [Google Scholar] [CrossRef]
- Lund, T.; Kneller, J.P. Combining collective, MSW, and turbulence effects in supernova neutrino flavor evolution. Phys. Rev. D 2013, 88, 023008. [Google Scholar] [CrossRef]
- Kneller, J.P.; Kabadi, N.V. Sensitivity of neutrinos to the supernova turbulence power spectrum: Point source statistics. Phys. Rev. D 2015, 92, 013009. [Google Scholar] [CrossRef]
- Patton, K.M.; Kneller, J.P.; McLaughlin, G.C. Stimulated neutrino transformation through turbulence on a changing density profile and application to supernovae. Phys. Rev. D 2015, 91, 025001. [Google Scholar] [CrossRef]
- Yang, Y.; Kneller, J.P. Neutrino Flavour Evolution Through Fluctuating Matter. J. Phys. G 2018, 45, 045201. [Google Scholar] [CrossRef]
- Kneller, J.P.; de los Reyes, M. The effect of core-collapse supernova accretion phase turbulence on neutrino flavor evolution. J. Phys. G 2017, 44, 084008. [Google Scholar] [CrossRef]
- Abbar, S. Turbulence Fingerprint on Collective Oscillations of Supernova Neutrinos. Phys. Rev. D 2021, 103, 045014. [Google Scholar] [CrossRef]
- Mukhopadhyay, M.; Sen, M. On probing turbulence in core-collapse supernovae in upcoming neutrino detectors. JCAP 2024, 03, 040. [Google Scholar] [CrossRef]
- Lunardini, C.; Smirnov, A.Y. Neutrinos from SN1987A, earth matter effects and the LMA solution of the solar neutrino problem. Phys. Rev. D 2001, 63, 073009. [Google Scholar] [CrossRef]
- Lunardini, C.; Smirnov, A.Y. Supernova neutrinos: Earth matter effects and neutrino mass spectrum. Nucl. Phys. B 2001, 616, 307–348. [Google Scholar] [CrossRef]
- Mirizzi, A.; Raffelt, G.G.; Serpico, P.D. Earth matter effects in supernova neutrinos: Optimal detector locations. JCAP 2006, 05, 012. [Google Scholar] [CrossRef]
- Dasgupta, B.; Dighe, A.; Mirizzi, A. Identifying neutrino mass hierarchy at extremely small theta(13) through Earth matter effects in a supernova signal. Phys. Rev. Lett. 2008, 101, 171801. [Google Scholar] [CrossRef] [PubMed]
- Borriello, E.; Chakraborty, S.; Mirizzi, A.; Serpico, P.D.; Tamborra, I. (Down-to-)Earth matter effect in supernova neutrinos. Phys. Rev. D 2012, 86, 083004. [Google Scholar] [CrossRef]
- Hajjar, R.; Mena, O.; Palomares-Ruiz, S. Earth tomography with supernova neutrinos at future neutrino detectors. Phys. Rev. D 2023, 108, 083011. [Google Scholar] [CrossRef]
- Raffelt, G.; Sarikas, S.; de Sousa Seixas, D. Axial Symmetry Breaking in Self-Induced Flavor Conversion of Supernova Neutrino Fluxes. Phys. Rev. Lett. 2013, 111, 091101, Erratum in Phys. Rev. Lett. 2014, 113, 239903. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, S.; Fischer, T.; Mirizzi, A.; Saviano, N.; Tomas, R. No collective neutrino flavor conversions during the supernova accretion phase. Phys. Rev. Lett. 2011, 107, 151101. [Google Scholar] [CrossRef]
- Dasgupta, B.; Mirizzi, A. Temporal Instability Enables Neutrino Flavor Conversions Deep Inside Supernovae. Phys. Rev. D 2015, 92, 125030. [Google Scholar] [CrossRef]
- Raffelt, G.G.; Smirnov, A.Y. Adiabaticity and spectral splits in collective neutrino transformations. Phys. Rev. 2007, D76, 125008. [Google Scholar] [CrossRef]
- Raffelt, G.G.; Smirnov, A.Y. Self-induced spectral splits in supernova neutrino fluxes. Phys. Rev. 2007, D76, 081301, Erratum in Phys. Rev. D 2008, 77, 029903. [Google Scholar] [CrossRef]
- Fogli, G.L.; Lisi, E.; Marrone, A.; Mirizzi, A. Collective neutrino flavor transitions in supernovae and the role of trajectory averaging. JCAP 2007, 0712, 010. [Google Scholar] [CrossRef]
- Fogli, G.L.; Lisi, E.; Marrone, A.; Mirizzi, A.; Tamborra, I. Low-energy spectral features of supernova (anti)neutrinos in inverted hierarchy. Phys. Rev. 2008, D78, 097301. [Google Scholar] [CrossRef]
- Dasgupta, B.; Dighe, A.; Raffelt, G.G.; Smirnov, A.Y. Multiple Spectral Splits of Supernova Neutrinos. Phys. Rev. Lett. 2009, 103, 051105. [Google Scholar] [CrossRef] [PubMed]
- Dasgupta, B.; Dighe, A.; Mirizzi, A.; Raffelt, G.G. Spectral split in prompt supernova neutrino burst: Analytic three-flavor treatment. Phys. Rev. 2008, D77, 113007. [Google Scholar] [CrossRef]
- Dasgupta, B.; Dighe, A. Collective three-flavor oscillations of supernova neutrinos. Phys. Rev. 2008, D77, 113002. [Google Scholar] [CrossRef]
- Friedland, A. Self-refraction of supernova neutrinos: Mixed spectra and three-flavor instabilities. Phys. Rev. Lett. 2010, 104, 191102. [Google Scholar] [CrossRef] [PubMed]
- Choubey, S.; Dasgupta, B.; Dighe, A.; Mirizzi, A. Signatures of collective and matter effects on supernova neutrinos at large detectors. arXiv 2010, arXiv:1008.0308. [Google Scholar]
- Banerjee, A.; Dighe, A.; Raffelt, G. Linearized flavor-stability analysis of dense neutrino streams. Phys. Rev. 2011, D84, 053013. [Google Scholar] [CrossRef]
- Izaguirre, I.; Raffelt, G.; Tamborra, I. Fast Pairwise Conversion of Supernova Neutrinos: A Dispersion-Relation Approach. Phys. Rev. Lett. 2017, 118, 021101. [Google Scholar] [CrossRef] [PubMed]
- Capozzi, F.; Dasgupta, B.; Lisi, E.; Marrone, A.; Mirizzi, A. Fast flavor conversions of supernova neutrinos: Classifying instabilities via dispersion relations. Phys. Rev. 2017, D96, 043016. [Google Scholar] [CrossRef]
- Capozzi, F.; Raffelt, G.; Stirner, T. Fast Neutrino Flavor Conversion: Collective Motion vs. Decoherence. JCAP 2019, 09, 002. [Google Scholar] [CrossRef]
- Yi, C.; Ma, L.; Martin, J.D.; Duan, H. The dispersion relation of the fast neutrino oscillation wave. arXiv 2019, arXiv:1901.01546. [Google Scholar] [CrossRef]
- Abbar, S.; Duan, H. Fast neutrino flavor conversion: Roles of dense matter and spectrum crossing. arXiv 2017, arXiv:1712.07013v1. [Google Scholar] [CrossRef]
- Dasgupta, B. Collective Neutrino Flavor Instability Requires a Crossing. Phys. Rev. Lett. 2022, 128, 081102. [Google Scholar] [CrossRef] [PubMed]
- Morinaga, T. Fast neutrino flavor instability and neutrino flavor lepton number crossings. arXiv 2021, arXiv:2103.15267. [Google Scholar] [CrossRef]
- Chakraborty, M.; Chakraborty, S. Three flavor neutrino conversions in supernovae: Slow & fast instabilities. JCAP 2020, 2001, 005. [Google Scholar] [CrossRef]
- Capozzi, F.; Chakraborty, M.; Chakraborty, S.; Sen, M. Fast flavor conversions in supernovae: The rise of mu-tau neutrinos. Phys. Rev. Lett. 2020, 125, 251801. [Google Scholar] [CrossRef]
- Shalgar, S.; Tamborra, I. Three flavor revolution in fast pairwise neutrino conversion. Phys. Rev. D 2021, 104, 023011. [Google Scholar] [CrossRef]
- Capozzi, F.; Chakraborty, M.; Chakraborty, S.; Sen, M. Supernova fast flavor conversions in 1+1D: Influence of mu-tau neutrinos. Phys. Rev. D 2022, 106, 083011. [Google Scholar] [CrossRef]
- Capozzi, F.; Dasgupta, B.; Mirizzi, A.; Sen, M.; Sigl, G. Collisional triggering of fast flavor conversions of supernova neutrinos. Phys. Rev. Lett. 2019, 122, 091101. [Google Scholar] [CrossRef] [PubMed]
- Shalgar, S.; Tamborra, I. A change of direction in pairwise neutrino conversion physics: The effect of collisions. Phys. Rev. D 2021, 103, 063002. [Google Scholar] [CrossRef]
- Martin, J.D.; Carlson, J.; Cirigliano, V.; Duan, H. Fast flavor oscillations in dense neutrino media with collisions. Phys. Rev. D 2021, 103, 063001. [Google Scholar] [CrossRef]
- Sasaki, H.; Takiwaki, T. A detailed analysis of the dynamics of fast neutrino flavor conversions with scattering effects. PTEP 2022, 2022, 073E01. [Google Scholar] [CrossRef]
- Sigl, G. Simulations of fast neutrino flavor conversions with interactions in inhomogeneous media. Phys. Rev. D 2022, 105, 043005. [Google Scholar] [CrossRef]
- Shalgar, S.; Tamborra, I. Neutrino flavor conversion, advection, and collisions: Toward the full solution. Phys. Rev. D 2023, 107, 063025. [Google Scholar] [CrossRef]
- Hansen, R.S.L.; Shalgar, S.; Tamborra, I. Enhancement or damping of fast neutrino flavor conversions due to collisions. Phys. Rev. D 2022, 105, 123003. [Google Scholar] [CrossRef]
- Padilla-Gay, I.; Tamborra, I.; Raffelt, G.G. Neutrino fast flavor pendulum. II. Collisional damping. Phys. Rev. D 2022, 106, 103031. [Google Scholar] [CrossRef]
- Akaho, R.; Liu, J.; Nagakura, H.; Zaizen, M.; Yamada, S. Collisional and fast neutrino flavor instabilities in two-dimensional core-collapse supernova simulation with Boltzmann neutrino transport. Phys. Rev. D 2024, 109, 023012. [Google Scholar] [CrossRef]
- Fiorillo, D.F.G.; Padilla-Gay, I.; Raffelt, G.G. Collisions and collective flavor conversion: Integrating out the fast dynamics. Phys. Rev. D 2024, 109, 063021. [Google Scholar] [CrossRef]
- Shalgar, S.; Tamborra, I. Do Neutrinos Become Flavor Unstable Due to Collisions with Matter in the Supernova Decoupling Region? arXiv 2023, arXiv:2307.10366. [Google Scholar] [CrossRef]
- Johns, L. Collisional Flavor Instabilities of Supernova Neutrinos. Phys. Rev. Lett. 2023, 130, 191001. [Google Scholar] [CrossRef] [PubMed]
- Johns, L.; Xiong, Z. Collisional instabilities of neutrinos and their interplay with fast flavor conversion in compact objects. Phys. Rev. D 2022, 106, 103029. [Google Scholar] [CrossRef]
- Xiong, Z.; Wu, M.R.; Martínez-Pinedo, G.; Fischer, T.; George, M.; Lin, C.Y.; Johns, L. Evolution of collisional neutrino flavor instabilities in spherically symmetric supernova models. Phys. Rev. D 2023, 107, 083016. [Google Scholar] [CrossRef]
- Lin, Y.C.; Duan, H. Collision-induced flavor instability in dense neutrino gases with energy-dependent scattering. Phys. Rev. D 2023, 107, 083034. [Google Scholar] [CrossRef]
- Xiong, Z.; Johns, L.; Wu, M.R.; Duan, H. Collisional flavor instability in dense neutrino gases. Phys. Rev. D 2023, 108, 083002. [Google Scholar] [CrossRef]
- Liu, J.; Nagakura, H.; Akaho, R.; Ito, A.; Zaizen, M.; Yamada, S. Universality of the neutrino collisional flavor instability in core-collapse supernovae. Phys. Rev. D 2023, 108, 123024. [Google Scholar] [CrossRef]
- Kato, C.; Nagakura, H.; Johns, L. Collisional flavor swap with neutrino self-interactions. arXiv 2023, arXiv:2309.02619. [Google Scholar] [CrossRef]
- Abbar, S.; Volpe, M.C. On Fast Neutrino Flavor Conversion Modes in the Nonlinear Regime. Phys. Lett. 2019, B790, 545–550. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Dasgupta, B. Fast Flavor Depolarization of Supernova Neutrinos. Phys. Rev. Lett. 2021, 126, 061302. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Dasgupta, B. Late-time behavior of fast neutrino oscillations. Phys. Rev. D 2020, 102, 063018. [Google Scholar] [CrossRef]
- Wu, M.R.; George, M.; Lin, C.Y.; Xiong, Z. Collective fast neutrino flavor conversions in a 1D box: Initial conditions and long-term evolution. Phys. Rev. D 2021, 104, 103003. [Google Scholar] [CrossRef]
- Richers, S.; Willcox, D.E.; Ford, N.M.; Myers, A. Particle-in-cell Simulation of the Neutrino Fast Flavor Instability. Phys. Rev. D 2021, 103, 083013. [Google Scholar] [CrossRef]
- Richers, S.; Willcox, D.; Ford, N. Neutrino fast flavor instability in three dimensions. Phys. Rev. D 2021, 104, 103023. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Dasgupta, B. Elaborating the Ultimate Fate of Fast Collective Neutrino Flavor Oscillations. arXiv 2022, arXiv:2205.05129. [Google Scholar] [CrossRef]
- Zaizen, M.; Nagakura, H. Simple method for determining asymptotic states of fast neutrino-flavor conversion. Phys. Rev. D 2023, 107, 103022. [Google Scholar] [CrossRef]
- Cornelius, M.; Shalgar, S.; Tamborra, I. Perturbing fast neutrino flavor conversion. JCAP 2024, 02, 038. [Google Scholar] [CrossRef]
- Johns, L.; Nagakura, H.; Fuller, G.M.; Burrows, A. Fast oscillations, collisionless relaxation, and spurious evolution of supernova neutrino flavor. Phys. Rev. D 2020, 102, 103017. [Google Scholar] [CrossRef]
- Xiong, Z.; Qian, Y.Z. Stationary solutions for fast flavor oscillations of a homogeneous dense neutrino gas. Phys. Lett. B 2021, 820, 136550. [Google Scholar] [CrossRef]
- Abbar, S.; Capozzi, F. Suppression of fast neutrino flavor conversions occurring at large distances in core-collapse supernovae. JCAP 2022, 03, 051. [Google Scholar] [CrossRef]
- Richers, S.; Duan, H.; Wu, M.R.; Bhattacharyya, S.; Zaizen, M.; George, M.; Lin, C.Y.; Xiong, Z. Code comparison for fast flavor instability simulations. Phys. Rev. D 2022, 106, 043011. [Google Scholar] [CrossRef]
- Nagakura, H.; Zaizen, M. Time-Dependent and Quasisteady Features of Fast Neutrino-Flavor Conversion. Phys. Rev. Lett. 2022, 129, 261101. [Google Scholar] [CrossRef] [PubMed]
- Zaizen, M.; Nagakura, H. Characterizing quasisteady states of fast neutrino-flavor conversion by stability and conservation laws. Phys. Rev. D 2023, 107, 123021. [Google Scholar] [CrossRef]
- Fiorillo, D.F.G.; Raffelt, G.G. Flavor solitons in dense neutrino gases. Phys. Rev. D 2023, 107, 123024. [Google Scholar] [CrossRef]
- Abbar, S.; Wu, M.R.; Xiong, Z. Physics-informed neural networks for predicting the asymptotic outcome of fast neutrino flavor conversions. Phys. Rev. D 2024, 109, 043024. [Google Scholar] [CrossRef]
- Abbar, S.; Harada, A.; Nagakura, H. Machine Learning-Based Detection of Non-Axisymmetric Fast Neutrino Flavor Instabilities in Core-Collapse Supernovae. arXiv 2024, arXiv:2401.10915. [Google Scholar]
- Fiorillo, D.F.G.; Raffelt, G.G.; Sigl, G. Inhomogeneous Kinetic Equation for Mixed Neutrinos: Tracing the Missing Energy. arXiv 2024, arXiv:2401.05278. [Google Scholar]
- Fiorillo, D.F.G.; Raffelt, G. Fast flavor conversions at the edge of instability. arXiv 2024, arXiv:2403.12189. [Google Scholar]
- Xiong, Z.; Wu, M.R.; George, M.; Lin, C.Y. Robust integration of fast flavor conversions in classical neutrino transport. arXiv 2024, arXiv:2403.17269. [Google Scholar]
- Johns, L.; Nagakura, H.; Fuller, G.M.; Burrows, A. Neutrino oscillations in supernovae: Angular moments and fast instabilities. Phys. Rev. D 2020, 101, 043009. [Google Scholar] [CrossRef]
- Padilla-Gay, I.; Tamborra, I.; Raffelt, G.G. Neutrino Flavor Pendulum Reloaded: The Case of Fast Pairwise Conversion. Phys. Rev. Lett. 2022, 128, 121102. [Google Scholar] [CrossRef] [PubMed]
- Fiorillo, D.F.G.; Raffelt, G.G. Slow and fast collective neutrino oscillations: Invariants and reciprocity. Phys. Rev. D 2023, 107, 043024. [Google Scholar] [CrossRef]
- Tamborra, I.; Huedepohl, L.; Raffelt, G.; Janka, H.T. Flavor-dependent neutrino angular distribution in core-collapse supernovae. Astrophys. J. 2017, 839, 132. [Google Scholar] [CrossRef]
- Tamborra, I.; Hanke, F.; Janka, H.T.; Mueller, B.; Raffelt, G.G.; Marek, A. Self-sustained asymmetry of lepton-number emission: A new phenomenon during the supernova shock-accretion phase in three dimensions. Astrophys. J. 2014, 792, 96. [Google Scholar] [CrossRef]
- Dasgupta, B.; Mirizzi, A.; Sen, M. Simple method of diagnosing fast flavor conversions of supernova neutrinos. Phys. Rev. 2018, D98, 103001. [Google Scholar] [CrossRef]
- Glas, R.; Janka, H.T.; Capozzi, F.; Sen, M.; Dasgupta, B.; Mirizzi, A.; Sigl, G. Fast Neutrino Flavor Instability in the Neutron-star Convection Layer of Three-dimensional Supernova Models. Phys. Rev. D 2020, 101, 063001. [Google Scholar] [CrossRef]
- Nagakura, H.; Johns, L. Constructing angular distributions of neutrinos in core-collapse supernovae from zeroth and first moments calibrated by full Boltzmann neutrino transport. Phys. Rev. D 2021, 103, 123025. [Google Scholar] [CrossRef]
- Abbar, S. Searching for Fast Neutrino Flavor Conversion Modes in Core-collapse Supernova Simulations. JCAP 2020, 05, 027. [Google Scholar] [CrossRef]
- Abbar, S.; Capozzi, F.; Glas, R.; Janka, H.T.; Tamborra, I. On the characteristics of fast neutrino flavor instabilities in three-dimensional core-collapse supernova models. Phys. Rev. D 2021, 103, 063033. [Google Scholar] [CrossRef]
- Capozzi, F.; Abbar, S.; Bollig, R.; Janka, H.T. Fast neutrino flavor conversions in one-dimensional core-collapse supernova models with and without muon creation. arXiv 2020, arXiv:2012.08525. [Google Scholar] [CrossRef]
- Nagakura, H.; Johns, L. New method for detecting fast neutrino flavor conversions in core-collapse supernova models with two-moment neutrino transport. Phys. Rev. D 2021, 104, 063014. [Google Scholar] [CrossRef]
- Nagakura, H.; Johns, L.; Burrows, A.; Fuller, G.M. Where, when, and why: Occurrence of fast-pairwise collective neutrino oscillation in three-dimensional core-collapse supernova models. Phys. Rev. D 2021, 104, 083025. [Google Scholar] [CrossRef]
- Ehring, J.; Abbar, S.; Janka, H.T.; Raffelt, G.; Tamborra, I. Fast neutrino flavor conversion in core-collapse supernovae: A parametric study in 1D models. Phys. Rev. D 2023, 107, 103034. [Google Scholar] [CrossRef]
- Abbar, S.; Nagakura, H. Detecting fast neutrino flavor conversions with machine learning. Phys. Rev. D 2024, 109, 023033. [Google Scholar] [CrossRef]
- Froustey, J.; Richers, S.; Grohs, E.; Flynn, S.D.; Foucart, F.; Kneller, J.P.; McLaughlin, G.C. Neutrino fast flavor oscillations with moments: Linear stability analysis and application to neutron star mergers. Phys. Rev. D 2024, 109, 043046. [Google Scholar] [CrossRef]
- Dasgupta, B.; O’Connor, E.P.; Ott, C.D. The Role of Collective Neutrino Flavor Oscillations in Core-Collapse Supernova Shock Revival. Phys. Rev. 2012, D85, 065008. [Google Scholar] [CrossRef]
- Ehring, J.; Abbar, S.; Janka, H.T.; Raffelt, G.; Tamborra, I. Fast Neutrino Flavor Conversions Can Help and Hinder Neutrino-Driven Explosions. Phys. Rev. Lett. 2023, 131, 061401. [Google Scholar] [CrossRef] [PubMed]
- Fujimoto, S.i.; Nagakura, H. Explosive nucleosynthesis with fast neutrino-flavour conversion in core-collapse supernovae. Mon. Not. R. Astron. Soc. 2022, 519, 2623–2629. [Google Scholar] [CrossRef]
- Xiong, Z.; Sieverding, A.; Sen, M.; Qian, Y.Z. Potential Impact of Fast Flavor Oscillations on Neutrino-driven Winds and Their Nucleosynthesis. Astrophys. J. 2020, 900, 144. [Google Scholar] [CrossRef]
- Fischer, T.; Guo, G.; Langanke, K.; Martinez-Pinedo, G.; Qian, Y.Z.; Wu, M.R. Neutrinos and nucleosynthesis of elements. Prog. Part. Nucl. Phys. 2024, 137, 104107. [Google Scholar] [CrossRef]
- Balantekin, A.B.; Cervia, M.J.; Patwardhan, A.V.; Surman, R.; Wang, X. Collective neutrino oscillations and heavy-element nucleosynthesis in supernovae: Exploring potential effects of many-body neutrino correlations. arXiv 2023, arXiv:2311.02562. [Google Scholar] [CrossRef]
- Friedland, A.; Mukhopadhyay, P.; Patwardhan, A.V. Successful νp-process in neutrino-driven outflows in core-collapse supernovae. arXiv 2023, arXiv:2312.03208. [Google Scholar]
- Sen, M. New Aspects of Supernova Neutrino Flavor Conversions: In the Standard Model and Beyond. Ph.D. Thesis, Tata Institute of Fundamental Research, Mumbai, India, 2018. [Google Scholar]
- Friedland, A.; Lunardini, C. Do many particle neutrino interactions cause a novel coherent effect? JHEP 2003, 10, 043. [Google Scholar] [CrossRef]
- Friedland, A.; Lunardini, C. Neutrino flavor conversion in a neutrino background: Single particle versus multiparticle description. Phys. Rev. D 2003, 68, 013007. [Google Scholar] [CrossRef]
- Balantekin, A.B.; Pehlivan, Y. Neutrino-Neutrino Interactions and Flavor Mixing in Dense Matter. J. Phys. G 2007, 34, 47–66. [Google Scholar] [CrossRef]
- Pehlivan, Y.; Balantekin, A.B.; Kajino, T.; Yoshida, T. Invariants of Collective Neutrino Oscillations. Phys. Rev. D 2011, 84, 065008. [Google Scholar] [CrossRef]
- Volpe, C.; Väänänen, D.; Espinoza, C. Extended evolution equations for neutrino propagation in astrophysical and cosmological environments. Phys. Rev. D 2013, 87, 113010. [Google Scholar] [CrossRef]
- Väänänen, D.; Volpe, C. Linearizing neutrino evolution equations including neutrino-antineutrino pairing correlations. Phys. Rev. D 2013, 88, 065003. [Google Scholar] [CrossRef]
- Serreau, J.; Volpe, C. Neutrino-antineutrino correlations in dense anisotropic media. Phys. Rev. D 2014, 90, 125040. [Google Scholar] [CrossRef]
- Birol, S.; Pehlivan, Y.; Balantekin, A.B.; Kajino, T. Neutrino Spectral Split in the Exact Many Body Formalism. Phys. Rev. D 2018, 98, 083002. [Google Scholar] [CrossRef]
- Patwardhan, A.V.; Cervia, M.J.; Baha Balantekin, A. Eigenvalues and eigenstates of the many-body collective neutrino oscillation problem. Phys. Rev. D 2019, 99, 123013. [Google Scholar] [CrossRef]
- Cervia, M.J.; Patwardhan, A.V.; Balantekin, A.B.; Coppersmith, t.S.N.; Johnson, C.W. Entanglement and collective flavor oscillations in a dense neutrino gas. Phys. Rev. D 2019, 100, 083001. [Google Scholar] [CrossRef]
- Rrapaj, E. Exact solution of multiangle quantum many-body collective neutrino-flavor oscillations. Phys. Rev. C 2020, 101, 065805. [Google Scholar] [CrossRef]
- Roggero, A. Entanglement and many-body effects in collective neutrino oscillations. Phys. Rev. D 2021, 104, 103016. [Google Scholar] [CrossRef]
- Patwardhan, A.V.; Cervia, M.J.; Balantekin, A.B. Spectral splits and entanglement entropy in collective neutrino oscillations. Phys. Rev. D 2021, 104, 123035. [Google Scholar] [CrossRef]
- Patwardhan, A.V.; Cervia, M.J.; Rrapaj, E.; Siwach, P.; Balantekin, A.B. Many-Body Collective Neutrino Oscillations: Recent Developments. In Handbook of Nuclear Physics; Tanihata, I., Toki, H., Kajino, T., Eds.; Springer: Singapore, 2023; pp. 1–16. [Google Scholar] [CrossRef]
- Raffelt, G.G. Particle physics from stars. Ann. Rev. Nucl. Part. Sci. 1999, 49, 163–216. [Google Scholar] [CrossRef]
- Ellis, J.R.; Olive, K.A. Constraints on Light Particles From Supernova Sn1987a. Phys. Lett. B 1987, 193, 525. [Google Scholar] [CrossRef]
- Raffelt, G.; Seckel, D. Bounds on Exotic Particle Interactions from SN 1987a. Phys. Rev. Lett. 1988, 60, 1793. [Google Scholar] [CrossRef] [PubMed]
- Turner, M.S. Axions from SN1987A. Phys. Rev. Lett. 1988, 60, 1797–1800. [Google Scholar] [CrossRef]
- Burrows, A.; Ressell, M.T.; Turner, M.S. Axions and SN1987A: Axion trapping. Phys. Rev. D 1990, 42, 3297–3309. [Google Scholar] [CrossRef] [PubMed]
- Dolan, M.J.; Ferber, T.; Hearty, C.; Kahlhoefer, F.; Schmidt-Hoberg, K. Revised constraints and Belle II sensitivity for visible and invisible axion-like particles. JHEP 2017, 12, 094, Erratum in JHEP 2021, 03, 190. [Google Scholar] [CrossRef]
- Chang, J.H.; Essig, R.; McDermott, S.D. Supernova 1987A Constraints on Sub-GeV Dark Sectors, Millicharged Particles, the QCD Axion, and an Axion-like Particle. JHEP 2018, 09, 051. [Google Scholar] [CrossRef]
- Carenza, P.; Fischer, T.; Giannotti, M.; Guo, G.; Martínez-Pinedo, G.; Mirizzi, A. Improved axion emissivity from a supernova via nucleon-nucleon bremsstrahlung. JCAP 2019, 10, 016, Erratum in JCAP 2020, 05, E01. [Google Scholar] [CrossRef]
- Carenza, P.; Fore, B.; Giannotti, M.; Mirizzi, A.; Reddy, S. Enhanced Supernova Axion Emission and its Implications. Phys. Rev. Lett. 2021, 126, 071102. [Google Scholar] [CrossRef]
- Lucente, G.; Carenza, P.; Fischer, T.; Giannotti, M.; Mirizzi, A. Heavy axion-like particles and core-collapse supernovae: Constraints and impact on the explosion mechanism. JCAP 2020, 12, 008. [Google Scholar] [CrossRef]
- Calore, F.; Carenza, P.; Giannotti, M.; Jaeckel, J.; Lucente, G.; Mirizzi, A. Supernova bounds on axionlike particles coupled with nucleons and electrons. Phys. Rev. D 2021, 104, 043016. [Google Scholar] [CrossRef]
- Caputo, A.; Raffelt, G. Astrophysical Axion Bounds: The 2024 Edition. In Proceedings of the 1st Training School of the COST Action COSMIC WISPers (CA21106), Lecce, Italy, 11–14 September 2023. [Google Scholar] [CrossRef]
- Rrapaj, E.; Reddy, S. Nucleon-nucleon bremsstrahlung of dark gauge bosons and revised supernova constraints. Phys. Rev. C 2016, 94, 045805. [Google Scholar] [CrossRef]
- Chang, J.H.; Essig, R.; McDermott, S.D. Revisiting Supernova 1987A Constraints on Dark Photons. JHEP 2017, 01, 107. [Google Scholar] [CrossRef]
- Sung, A.; Guo, G.; Wu, M.R. Supernova Constraint on Self-Interacting Dark Sector Particles. Phys. Rev. D 2021, 103, 103005. [Google Scholar] [CrossRef]
- Caputo, A.; Millar, A.J.; O’Hare, C.A.J.; Vitagliano, E. Dark photon limits: A handbook. Phys. Rev. D 2021, 104, 095029. [Google Scholar] [CrossRef]
- Cerdeño, D.G.; Cermeño, M.; Farzan, Y. Constraints from the duration of supernova neutrino burst on on-shell light gauge boson production by neutrinos. Phys. Rev. D 2023, 107, 123012. [Google Scholar] [CrossRef]
- Farzan, Y. Bounds on the coupling of the Majoron to light neutrinos from supernova cooling. Phys. Rev. D 2003, 67, 073015. [Google Scholar] [CrossRef]
- Brune, T.; Päs, H. Massive Majorons and constraints on the Majoron-neutrino coupling. Phys. Rev. D 2019, 99, 096005. [Google Scholar] [CrossRef]
- Heurtier, L.; Zhang, Y. Supernova Constraints on Massive (Pseudo)Scalar Coupling to Neutrinos. JCAP 2017, 02, 042. [Google Scholar] [CrossRef]
- Diamond, M.; Fiorillo, D.F.G.; Marques-Tavares, G.; Vitagliano, E. Axion-sourced fireballs from supernovae. Phys. Rev. D 2023, 107, 103029, Erratum in Phys. Rev. D 2023, 108, 049902. [Google Scholar] [CrossRef]
- Antel, C.; Battaglieri, M.; Beacham, J.; Boehm, C.; Buchmüller, O.; Calore, F.; Carenza, P.; Chauhan, B.; Cladè, P.; Coloma, P.; et al. Feebly-interacting particles: FIPs 2022 Workshop Report. Eur. Phys. J. C 2023, 83, 1122. [Google Scholar] [CrossRef]
- Caputo, A.; Raffelt, G.; Vitagliano, E. Muonic boson limits: Supernova redux. Phys. Rev. D 2022, 105, 035022. [Google Scholar] [CrossRef]
- Caputo, A.; Raffelt, G.; Vitagliano, E. Radiative transfer in stars by feebly interacting bosons. JCAP 2022, 08, 045. [Google Scholar] [CrossRef]
- Fiorillo, D.F.G.; Vitagliano, E. Self-interacting dark sectors in supernovae are fluid. arXiv 2024, arXiv:2404.07714. [Google Scholar]
- Bollig, R.; DeRocco, W.; Graham, P.W.; Janka, H.T. Muons in Supernovae: Implications for the Axion-Muon Coupling. Phys. Rev. Lett. 2020, 125, 051104, Erratum in Phys. Rev. Lett. 2021, 126, 189901. [Google Scholar] [CrossRef] [PubMed]
- Croon, D.; Elor, G.; Leane, R.K.; McDermott, S.D. Supernova Muons: New Constraints on Z’ Bosons, Axions and ALPs. JHEP 2021, 01, 107. [Google Scholar] [CrossRef]
- Fiorillo, D.F.G.; Raffelt, G.G.; Vitagliano, E. Strong Supernova 1987A Constraints on Bosons Decaying to Neutrinos. Phys. Rev. Lett. 2023, 131, 021001. [Google Scholar] [CrossRef] [PubMed]
- Caputo, A.; Janka, H.T.; Raffelt, G.; Vitagliano, E. Low-Energy Supernovae Severely Constrain Radiative Particle Decays. Phys. Rev. Lett. 2022, 128, 221103. [Google Scholar] [CrossRef] [PubMed]
- Mastrototaro, L.; Mirizzi, A.; Serpico, P.D.; Esmaili, A. Heavy sterile neutrino emission in core-collapse supernovae: Constraints and signatures. JCAP 2020, 01, 010. [Google Scholar] [CrossRef]
- Carenza, P.; Lucente, G.; Mastrototaro, L.; Mirizzi, A.; Serpico, P.D. Comprehensive constraints on heavy sterile neutrinos from core-collapse supernovae. Phys. Rev. D 2024, 109, 063010. [Google Scholar] [CrossRef]
- Brdar, V.; de Gouvêa, A.; Li, Y.Y.; Machado, P.A.N. Neutrino magnetic moment portal and supernovae: New constraints and multimessenger opportunities. Phys. Rev. D 2023, 107, 073005. [Google Scholar] [CrossRef]
- Raffelt, G.G.; Zhou, S. Supernova bound on keV-mass sterile neutrinos reexamined. Phys. Rev. D 2011, 83, 093014. [Google Scholar] [CrossRef]
- Argüelles, C.A.; Brdar, V.; Kopp, J. Production of keV Sterile Neutrinos in Supernovae: New Constraints and Gamma Ray Observables. Phys. Rev. D 2019, 99, 043012. [Google Scholar] [CrossRef]
- Syvolap, V.; Ruchayskiy, O.; Boyarsky, A. Resonance production of keV sterile neutrinos in core-collapse supernovae and lepton number diffusion. Phys. Rev. D 2022, 106, 015017. [Google Scholar] [CrossRef]
- Suliga, A.M.; Tamborra, I.; Wu, M.R. Tau lepton asymmetry by sterile neutrino emission–Moving beyond one-zone supernova models. JCAP 2019, 12, 019. [Google Scholar] [CrossRef]
- Chen, Y.M.; Sen, M.; Tangarife, W.; Tuckler, D.; Zhang, Y. Core-collapse supernova constraint on the origin of sterile neutrino dark matter via neutrino self-interactions. JCAP 2022, 11, 014. [Google Scholar] [CrossRef]
- Suliga, A.M.; Tamborra, I.; Wu, M.R. Lifting the core-collapse supernova bounds on keV-mass sterile neutrinos. JCAP 2020, 08, 018. [Google Scholar] [CrossRef]
- Tamborra, I.; Raffelt, G.G.; Hudepohl, L.; Janka, H.T. Impact of eV-mass sterile neutrinos on neutrino-driven supernova outflows. JCAP 2012, 1201, 013. [Google Scholar] [CrossRef]
- Franarin, T.; Davis, J.H.; Fairbairn, M. Prospects for detecting eV-scale sterile neutrinos from a galactic supernova. JCAP 2018, 09, 002. [Google Scholar] [CrossRef]
- Tang, J.; Wang, T.; Wu, M.R. Constraining sterile neutrinos by core-collapse supernovae with multiple detectors. JCAP 2020, 10, 038. [Google Scholar] [CrossRef]
- Esteban-Pretel, A.; Tomas, R.; Valle, J.W.F. Probing non-standard neutrino interactions with supernova neutrinos. Phys. Rev. D 2007, 76, 053001. [Google Scholar] [CrossRef]
- Esteban-Pretel, A.; Tomas, R.; Valle, J.W.F. Interplay between collective effects and non-standard neutrino interactions of supernova neutrinos. Phys. Rev. D 2010, 81, 063003. [Google Scholar] [CrossRef]
- Blennow, M.; Mirizzi, A.; Serpico, P.D. Nonstandard neutrino-neutrino refractive effects in dense neutrino gases. Phys. Rev. 2008, D78, 113004. [Google Scholar] [CrossRef]
- Das, A.; Dighe, A.; Sen, M. New effects of non-standard self-interactions of neutrinos in a supernova. JCAP 2017, 1705, 051. [Google Scholar] [CrossRef]
- Dighe, A.; Sen, M. Nonstandard neutrino self-interactions in a supernova and fast flavor conversions. Phys. Rev. 2018, D97, 043011. [Google Scholar] [CrossRef]
- Shalgar, S.; Tamborra, I.; Bustamante, M. Core-collapse supernovae stymie secret neutrino interactions. Phys. Rev. D 2021, 103, 123008. [Google Scholar] [CrossRef]
- Fiorillo, D.F.G.; Raffelt, G.G.; Vitagliano, E. Large Neutrino Secret Interactions Have a Small Impact on Supernovae. Phys. Rev. Lett. 2024, 132, 021002. [Google Scholar] [CrossRef] [PubMed]
- Chang, P.W.; Esteban, I.; Beacom, J.F.; Thompson, T.A.; Hirata, C.M. Toward Powerful Probes of Neutrino Self-Interactions in Supernovae. Phys. Rev. Lett. 2023, 131, 071002. [Google Scholar] [CrossRef] [PubMed]
- Carpio, J.A.; Kheirandish, A.; Murase, K. Time-delayed neutrino emission from supernovae as a probe of dark matter-neutrino interactions. JCAP 2023, 04, 019. [Google Scholar] [CrossRef]
- Das, A.; Sen, M. Boosted dark matter from diffuse supernova neutrinos. Phys. Rev. D 2021, 104, 075029. [Google Scholar] [CrossRef]
- Lin, Y.H.; Wu, W.H.; Wu, M.R.; Wong, H.T.K. Searching for Afterglow: Light Dark Matter Boosted by Supernova Neutrinos. Phys. Rev. Lett. 2023, 130, 111002. [Google Scholar] [CrossRef] [PubMed]
- Das, A.; Herbermann, T.; Sen, M.; Takhistov, V. Energy-dependent Boosted Dark Matter from Diffuse Supernova Neutrino Background. arXiv 2024, arXiv:2403.15367. [Google Scholar]
- Kernan, P.J.; Krauss, L.M. Yet another paper on SN1987A: Large angle oscillations and the electron-neutrino mass. Nucl. Phys. B 1995, 437, 243–256. [Google Scholar] [CrossRef]
- Pompa, F.; Capozzi, F.; Mena, O.; Sorel, M. Absolute ν Mass Measurement with the DUNE Experiment. Phys. Rev. Lett. 2022, 129, 121802. [Google Scholar] [CrossRef]
- Hansen, R.S.L.; Lindner, M.; Scholer, O. Timing the neutrino signal of a Galactic supernova. Phys. Rev. D 2020, 101, 123018. [Google Scholar] [CrossRef]
- Linzer, N.B.; Scholberg, K. Triangulation Pointing to Core-Collapse Supernovae with Next-Generation Neutrino Detectors. Phys. Rev. D 2019, 100, 103005. [Google Scholar] [CrossRef]
- Serpico, P.D.; Chakraborty, S.; Fischer, T.; Hudepohl, L.; Janka, H.T.; Mirizzi, A. Probing the neutrino mass hierarchy with the rise time of a supernova burst. Phys. Rev. 2012, D85, 085031. [Google Scholar] [CrossRef]
- Brdar, V.; Xu, X.J. Timing and multi-channel: Novel method for determining the neutrino mass ordering from supernovae. JCAP 2022, 08, 067. [Google Scholar] [CrossRef]
- Frieman, J.A.; Haber, H.E.; Freese, K. Neutrino Mixing, Decays and Supernova Sn1987a. Phys. Lett. B 1988, 200, 115–121. [Google Scholar] [CrossRef]
- Iváñez Ballesteros, P.; Volpe, M.C. SN1987A and neutrino non-radiative decay. Phys. Lett. B 2023, 847, 138252. [Google Scholar] [CrossRef]
- de Gouvêa, A.; Martinez-Soler, I.; Sen, M. Impact of neutrino decays on the supernova neutronization-burst flux. Phys. Rev. D 2020, 101, 043013. [Google Scholar] [CrossRef]
- Pal, P.B.; Wolfenstein, L. Radiative Decays of Massive Neutrinos. Phys. Rev. D 1982, 25, 766. [Google Scholar] [CrossRef]
- Barbieri, R.; Mohapatra, R.N. Limit on the Magnetic Moment of the Neutrino from Supernova SN 1987a Observations. Phys. Rev. Lett. 1988, 61, 27. [Google Scholar] [CrossRef]
- Lim, C.S.; Marciano, W.J. Resonant Spin - Flavor Precession of Solar and Supernova Neutrinos. Phys. Rev. D 1988, 37, 1368–1373. [Google Scholar] [CrossRef]
- Akhmedov, E.K. Resonant Amplification of Neutrino Spin Rotation in Matter and the Solar Neutrino Problem. Phys. Lett. B 1988, 213, 64–68. [Google Scholar] [CrossRef]
- Ando, S.; Sato, K. A Comprehensive study of neutrino spin flavor conversion in supernovae and the neutrino mass hierarchy. JCAP 2003, 10, 001. [Google Scholar] [CrossRef][Green Version]
- Akhmedov, E.K.; Fukuyama, T. Supernova prompt neutronization neutrinos and neutrino magnetic moments. JCAP 2003, 12, 007. [Google Scholar] [CrossRef]
- Jana, S.; Porto-Silva, Y.P.; Sen, M. Exploiting a future galactic supernova to probe neutrino magnetic moments. JCAP 2022, 09, 079. [Google Scholar] [CrossRef]
- de Gouvea, A.; Shalgar, S. Effect of Transition Magnetic Moments on Collective Supernova Neutrino Oscillations. JCAP 2012, 10, 027. [Google Scholar] [CrossRef]
- Abbar, S. Collective Oscillations of Majorana Neutrinos in Strong Magnetic Fields and Self-induced Flavor Equilibrium. Phys. Rev. D 2020, 101, 103032. [Google Scholar] [CrossRef]
- Giunti, C.; Studenikin, A. Neutrino electromagnetic interactions: A window to new physics. Rev. Mod. Phys. 2015, 87, 531. [Google Scholar] [CrossRef]
- Wolfenstein, L. Different Varieties of Massive Dirac Neutrinos. Nucl. Phys. B 1981, 186, 147–152. [Google Scholar] [CrossRef]
- Martinez-Soler, I.; Perez-Gonzalez, Y.F.; Sen, M. Signs of pseudo-Dirac neutrinos in SN1987A data. Phys. Rev. D 2022, 105, 095019. [Google Scholar] [CrossRef]
- Sen, M. Constraining pseudo-Dirac neutrinos from a galactic core-collapse supernova. arXiv 2022, arXiv:2205.13291. [Google Scholar]
- Guzzo, M.M.; Nunokawa, H.; Tomas, R. Testing the principle of equivalence by supernova neutrinos. Astropart. Phys. 2002, 18, 277–286. [Google Scholar] [CrossRef]
- Mukhopadhyay, M.; Lunardini, C.; Timmes, F.X.; Zuber, K. Presupernova neutrinos: Directional sensitivity and prospects for progenitor identification. Astrophys. J. 2020, 899, 153. [Google Scholar] [CrossRef]
- Reddy, S.; Zhou, D. Dark lepton superfluid in protoneutron stars. Phys. Rev. D 2022, 105, 023026. [Google Scholar] [CrossRef]
- Ghosh, M.; Grossman, Y.; Tangarife, W.; Xu, X.J.; Yu, B. Neutrino forces in neutrino backgrounds. JHEP 2023, 02, 092. [Google Scholar] [CrossRef]
- Chakraborty, S.; Mirizzi, A.; Sigl, G. Testing Lorentz invariance with neutrino bursts from supernova neutronization. Phys. Rev. 2013, D87, 017302. [Google Scholar] [CrossRef]
- Dasgupta, B.; Fischer, T.; Horiuchi, S.; Liebendorfer, M.; Mirizzi, A.; Sagert, I.; Schaffner-Bielich, J. Detecting the QCD phase transition in the next Galactic supernova neutrino burst. Phys. Rev. D 2010, 81, 103005. [Google Scholar] [CrossRef]
- Beacom, J.F. The Diffuse Supernova Neutrino Background. Ann. Rev. Nucl. Part. Sci. 2010, 60, 439–462. [Google Scholar] [CrossRef]
- De Gouvêa, A.; Martinez-Soler, I.; Perez-Gonzalez, Y.F.; Sen, M. Fundamental physics with the diffuse supernova background neutrinos. Phys. Rev. D 2020, 102, 123012. [Google Scholar] [CrossRef]
- Ando, S.; Ekanger, N.; Horiuchi, S.; Koshio, Y. Diffuse neutrino background from past core-collapse supernovae. arXiv 2023, arXiv:2306.16076. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sen, M. Supernova Neutrinos: Flavour Conversion Mechanisms and New Physics Scenarios. Universe 2024, 10, 238. https://doi.org/10.3390/universe10060238
Sen M. Supernova Neutrinos: Flavour Conversion Mechanisms and New Physics Scenarios. Universe. 2024; 10(6):238. https://doi.org/10.3390/universe10060238
Chicago/Turabian StyleSen, Manibrata. 2024. "Supernova Neutrinos: Flavour Conversion Mechanisms and New Physics Scenarios" Universe 10, no. 6: 238. https://doi.org/10.3390/universe10060238
APA StyleSen, M. (2024). Supernova Neutrinos: Flavour Conversion Mechanisms and New Physics Scenarios. Universe, 10(6), 238. https://doi.org/10.3390/universe10060238






