Lorentzian Quantum Cosmology from Effective Spin Foams
Abstract
1. Introduction
2. The Cosmological Ball and Shell Model with Effective Spin Foams
2.1. Effective Spin Foam Models
2.2. The Discretization
2.3. Regular and Irregular Light Cone Structure
2.4. The Regge Action
2.5. Critical Points of the Action
2.6. Discrete Area Spectra
2.7. The Path Integral Measure
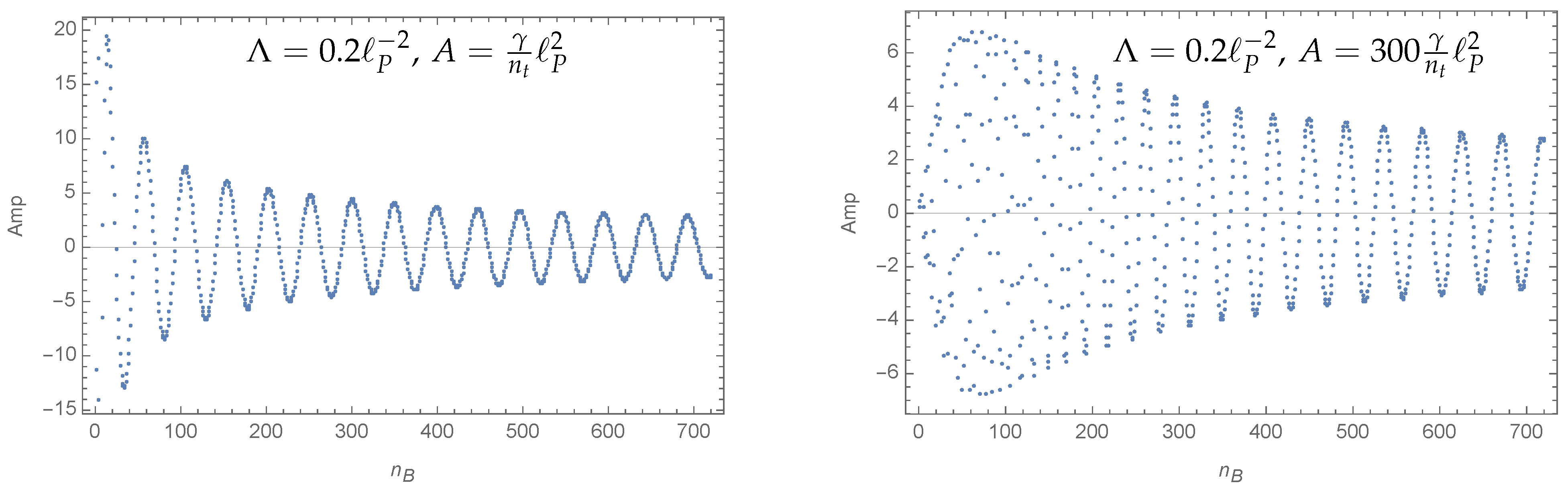
2.8. The Spin Foam Sum
3. Acceleration Operators for Series Convergence
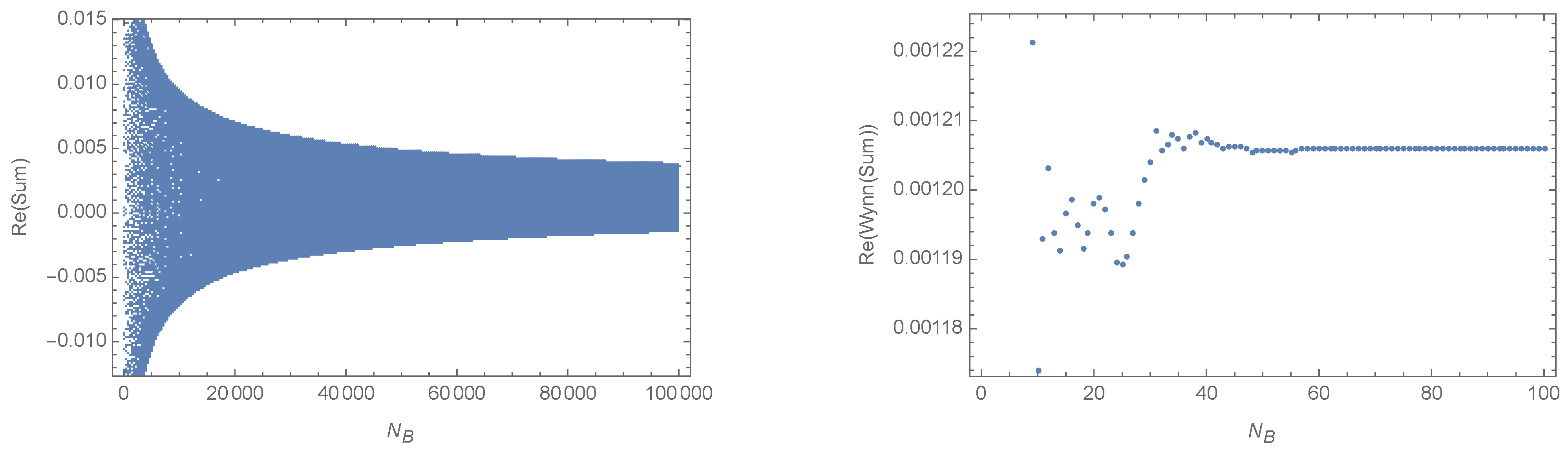
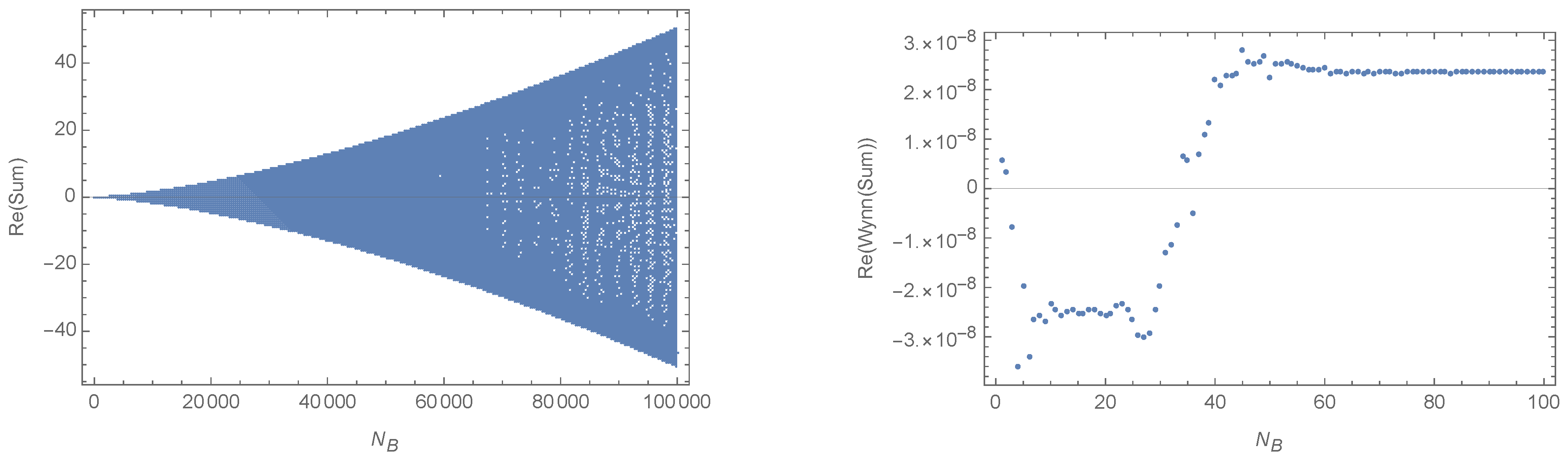
3.1. Shanks Transform and Wynn’s Epsilon Algorithm
3.2. Applications
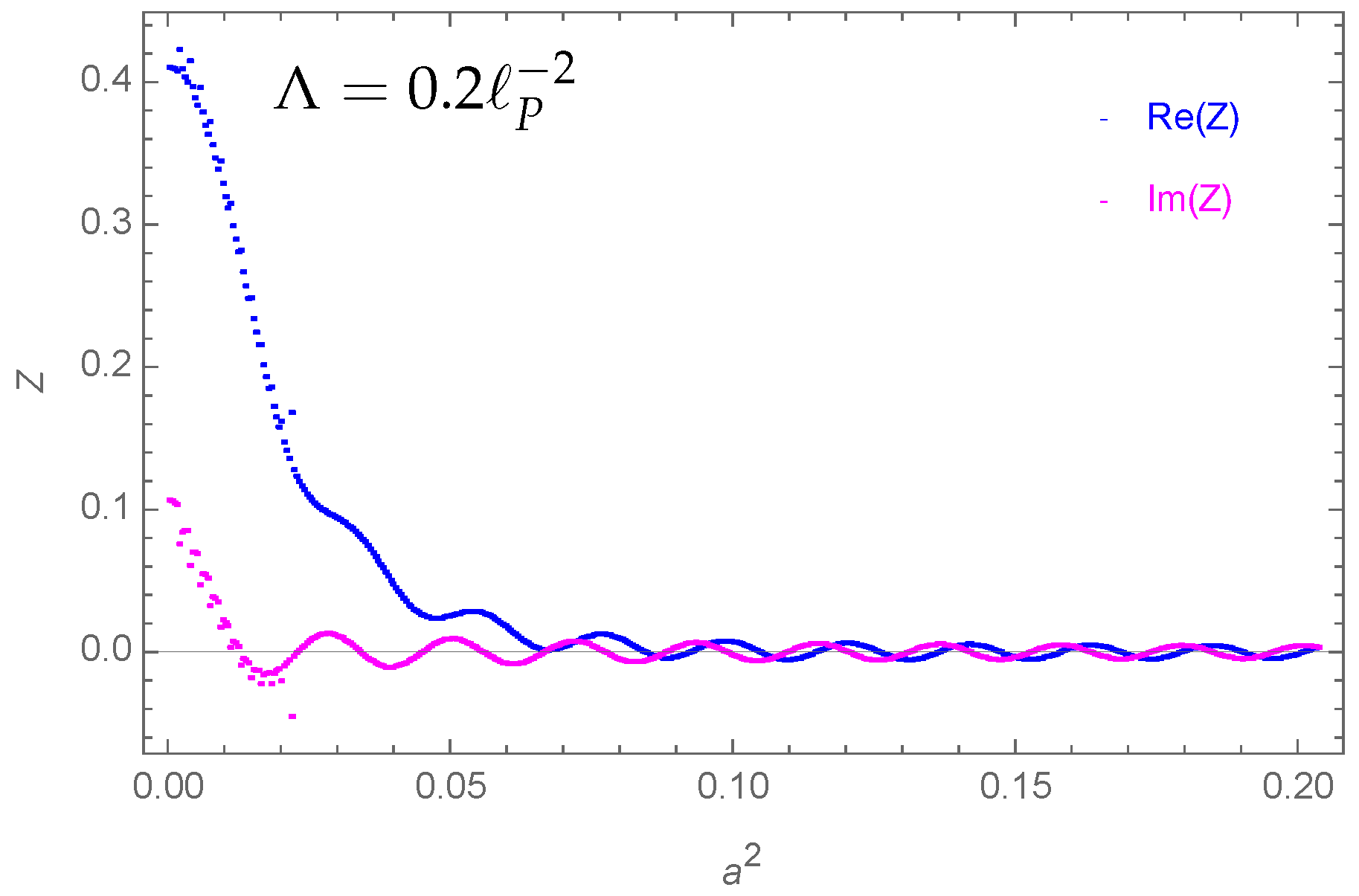
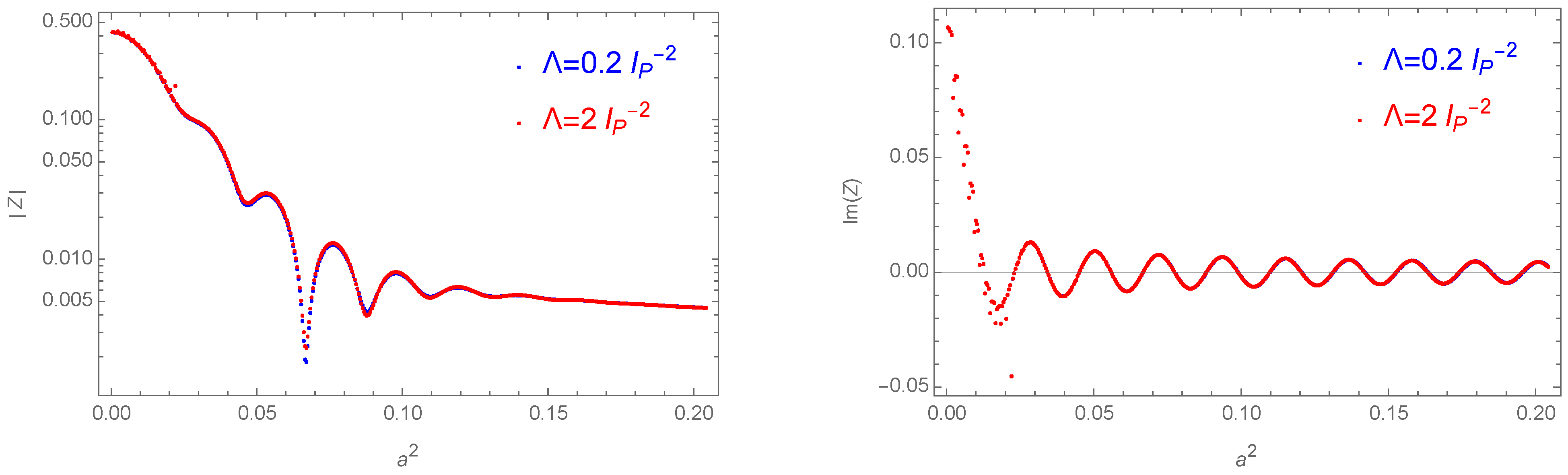
4. Results
4.1. The Shell Model—Examples with a Lorentzian Saddle Point
- The difference between including and excluding the hinge irregular region is relatively small; e.g., the absolute values of the differences in the spin foam sum for the first example below are of the order of ; for the second example, ; and for the third example, . We will show here the version where we include the hinge irregular region into the path integral. There would not be a visible difference in the plots for the alternative choice.
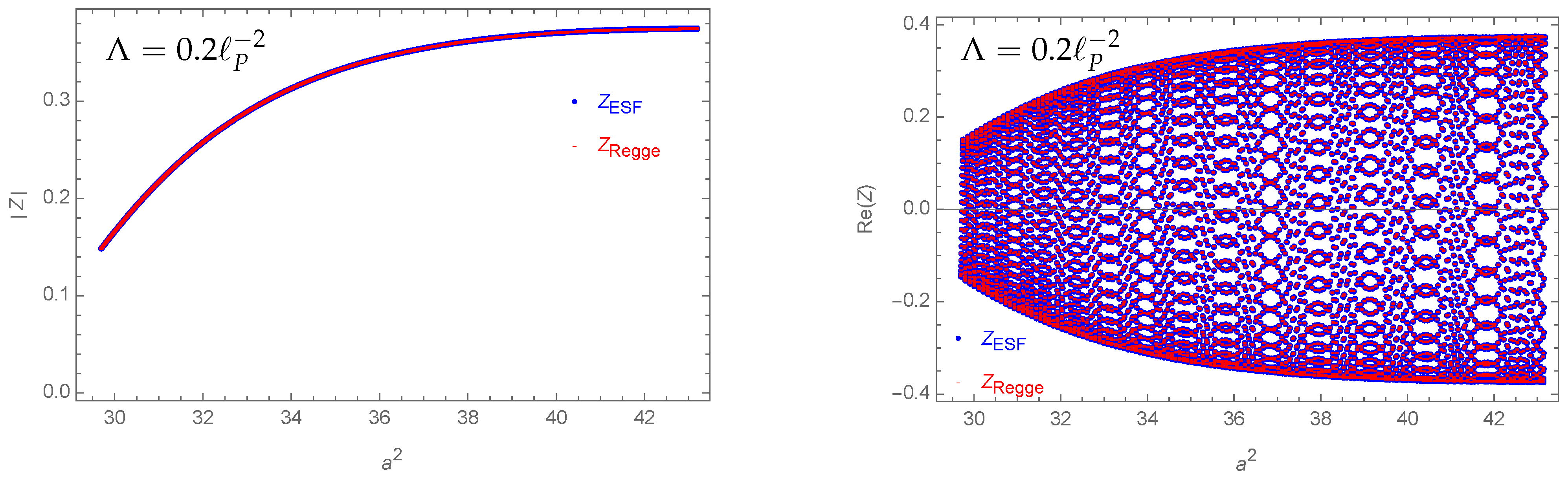
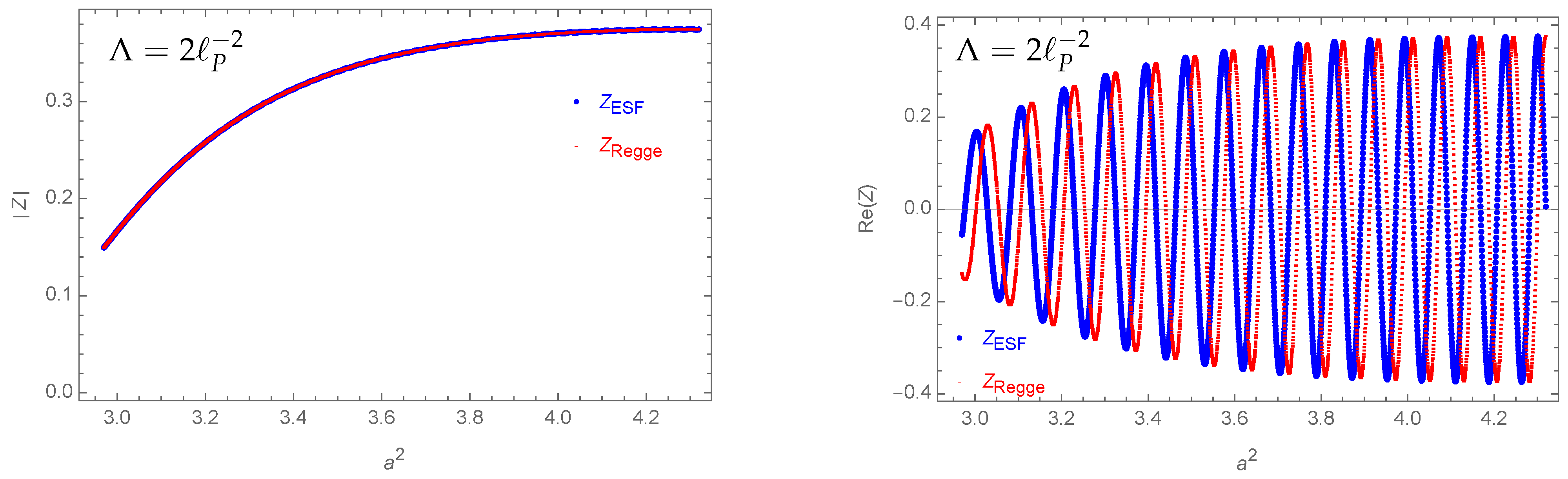
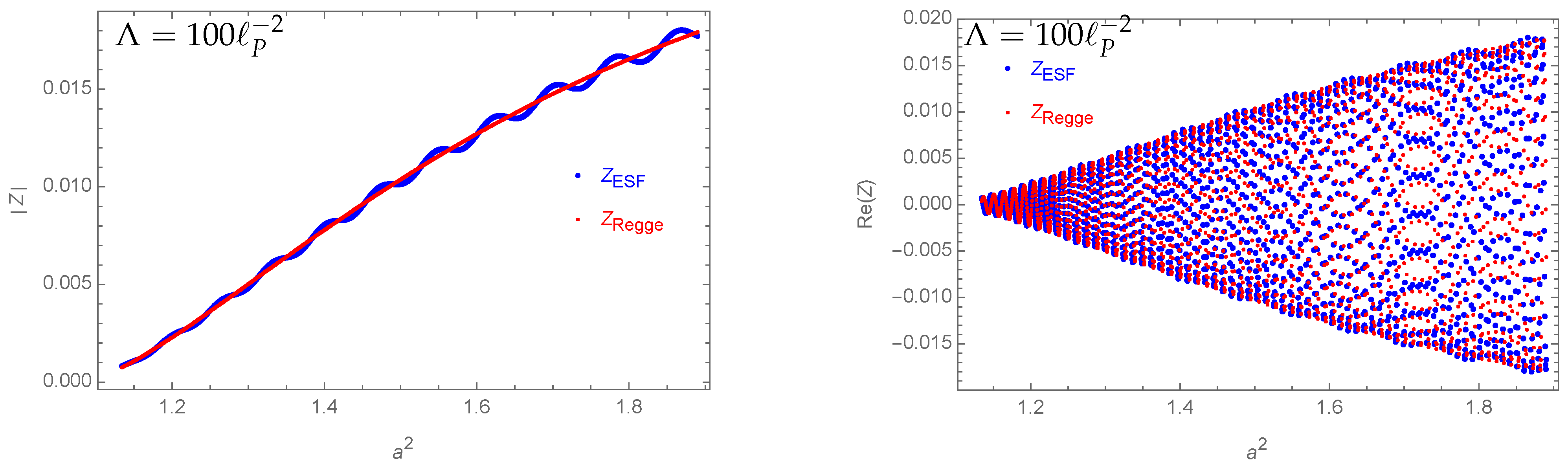
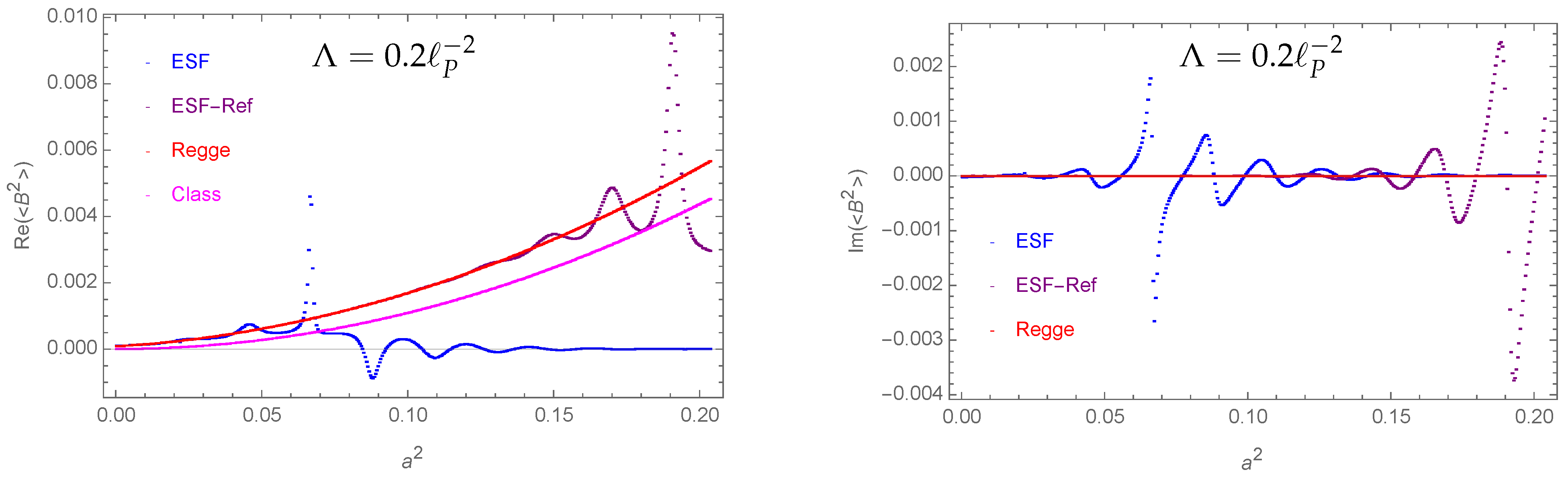
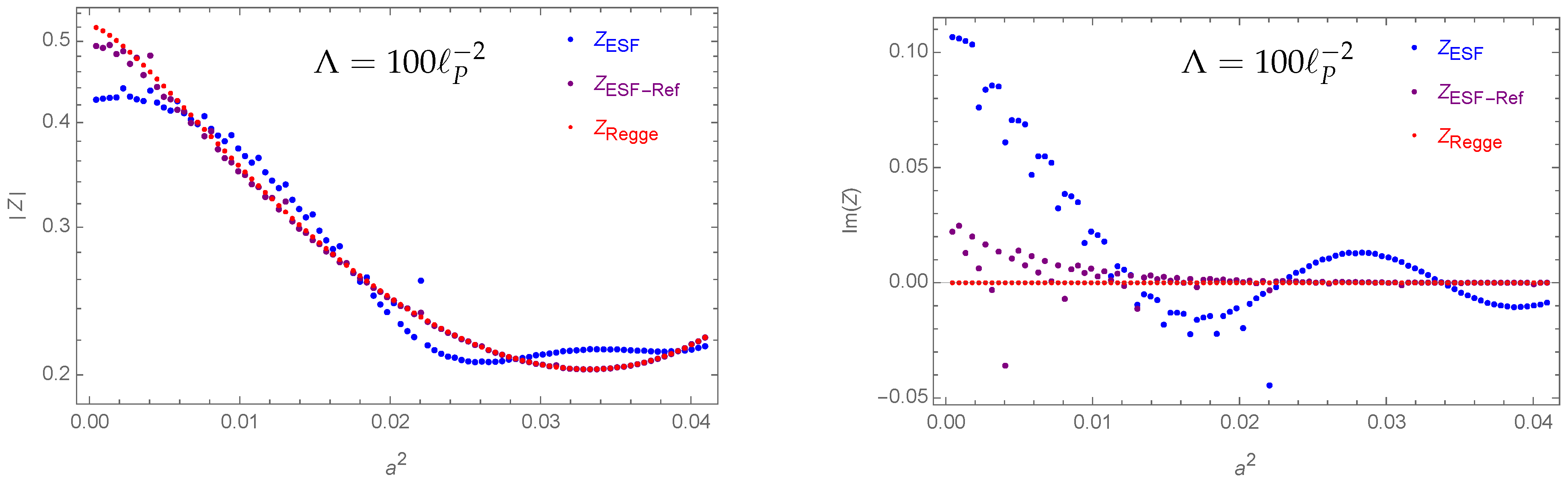
- The difference between Regge path integrals and effective spin foam sums is relatively small (e.g., see Figure 5).
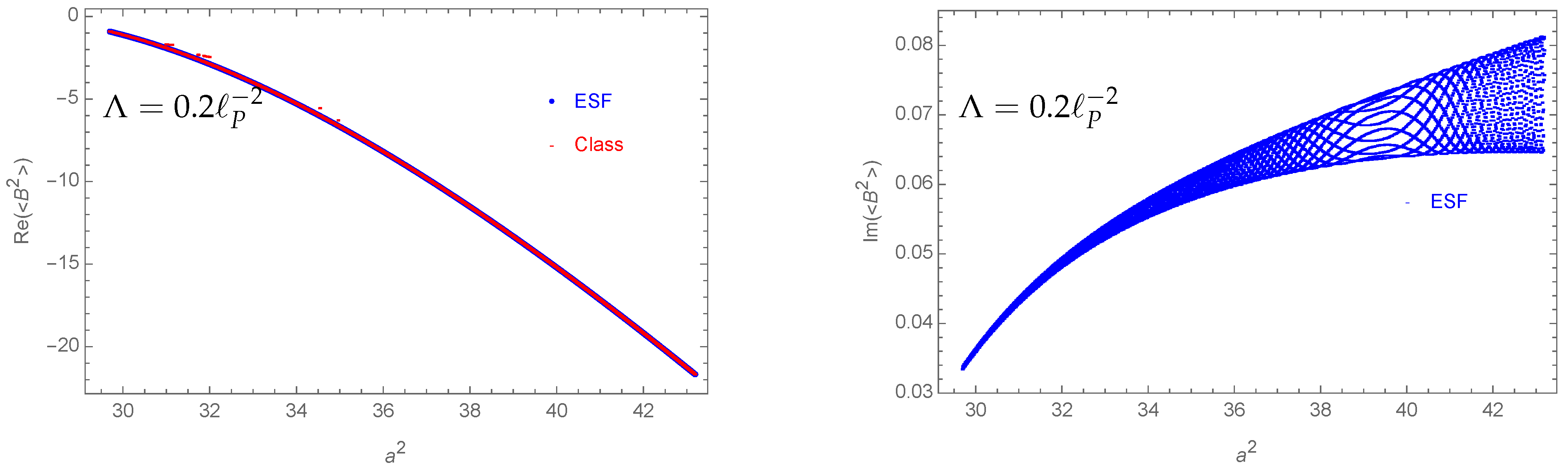
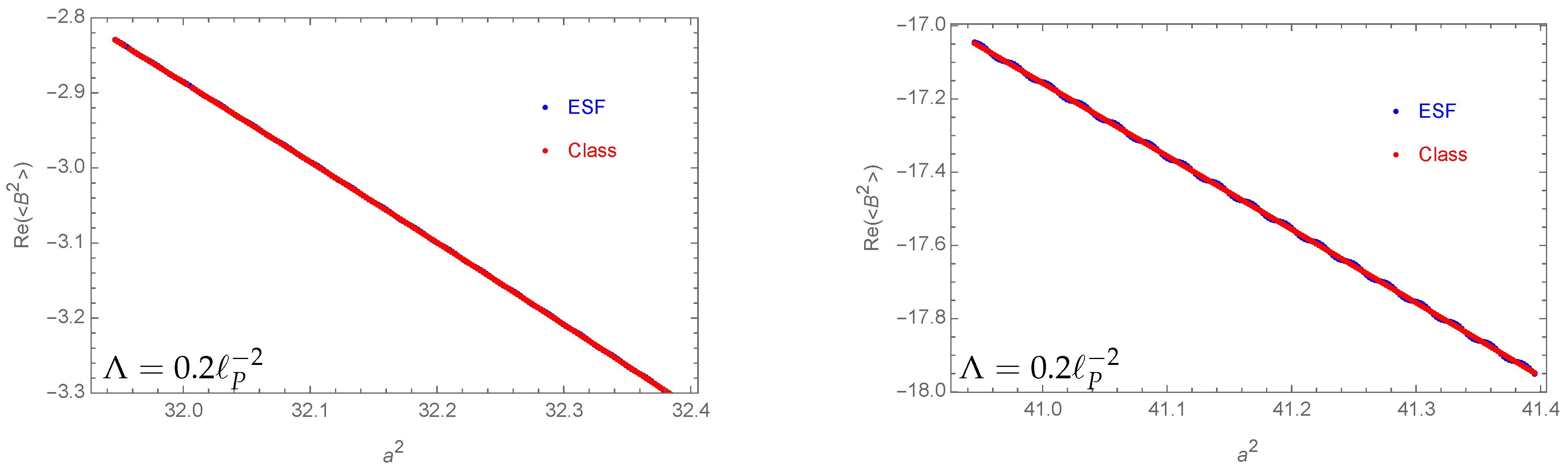
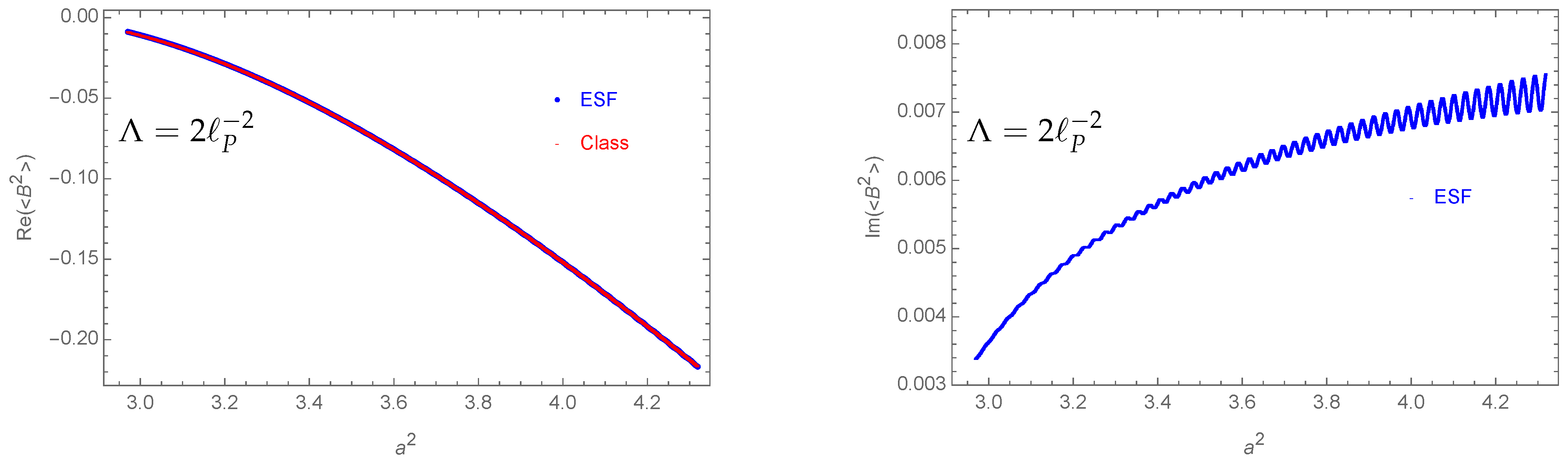
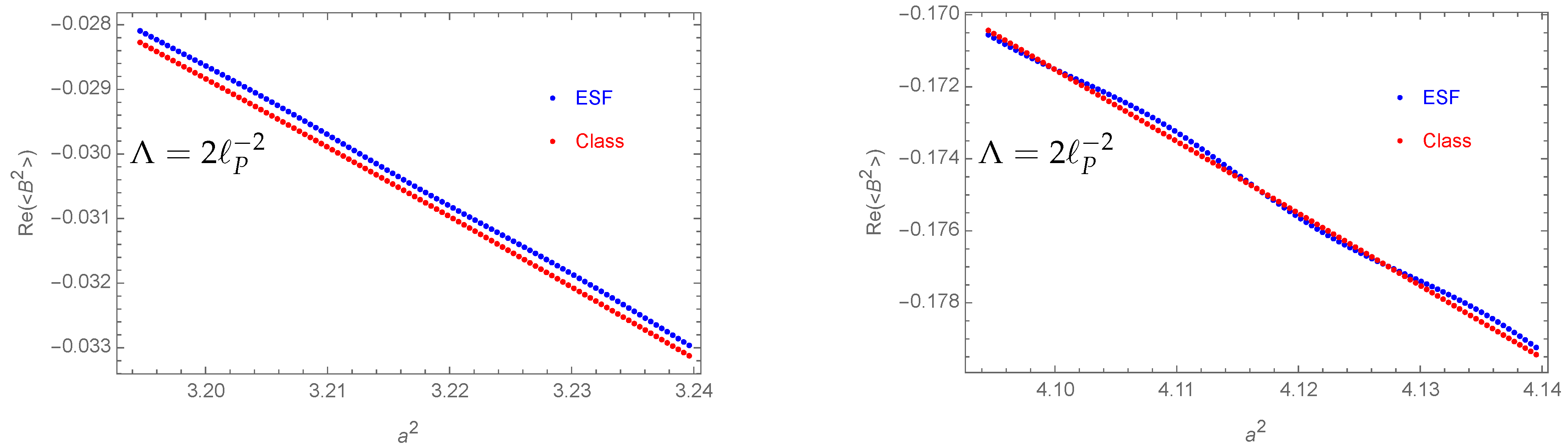
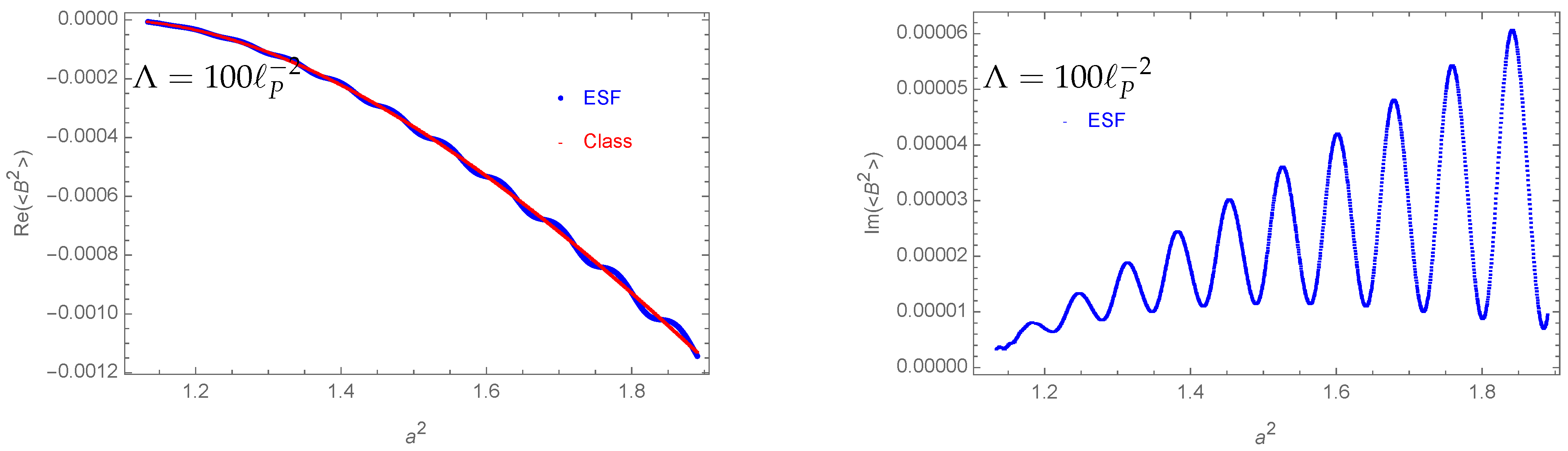
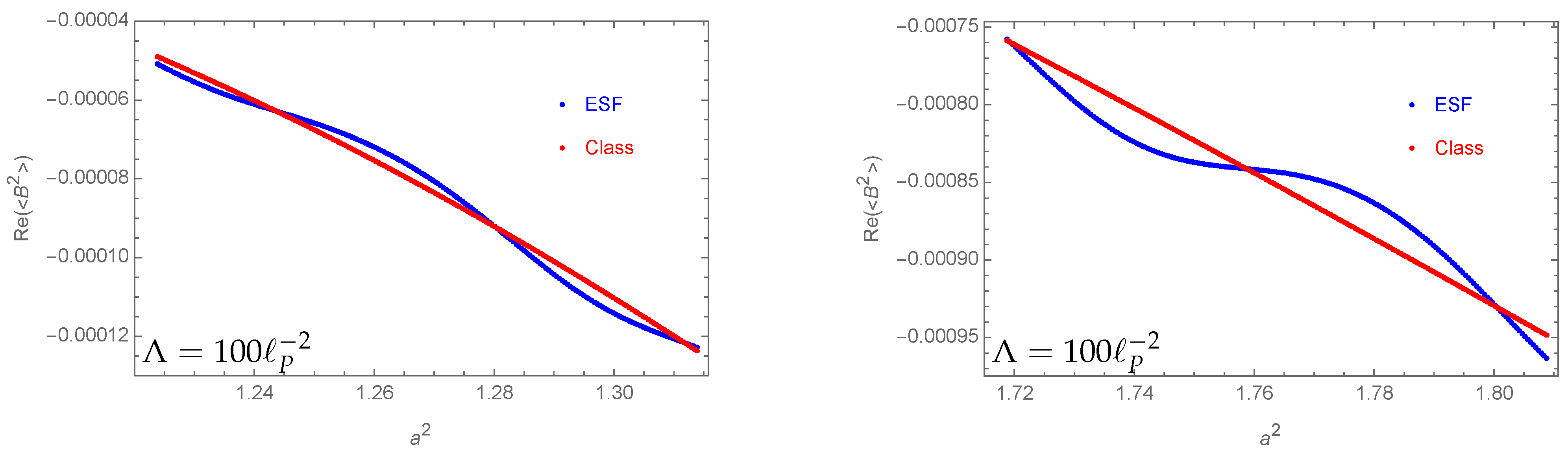
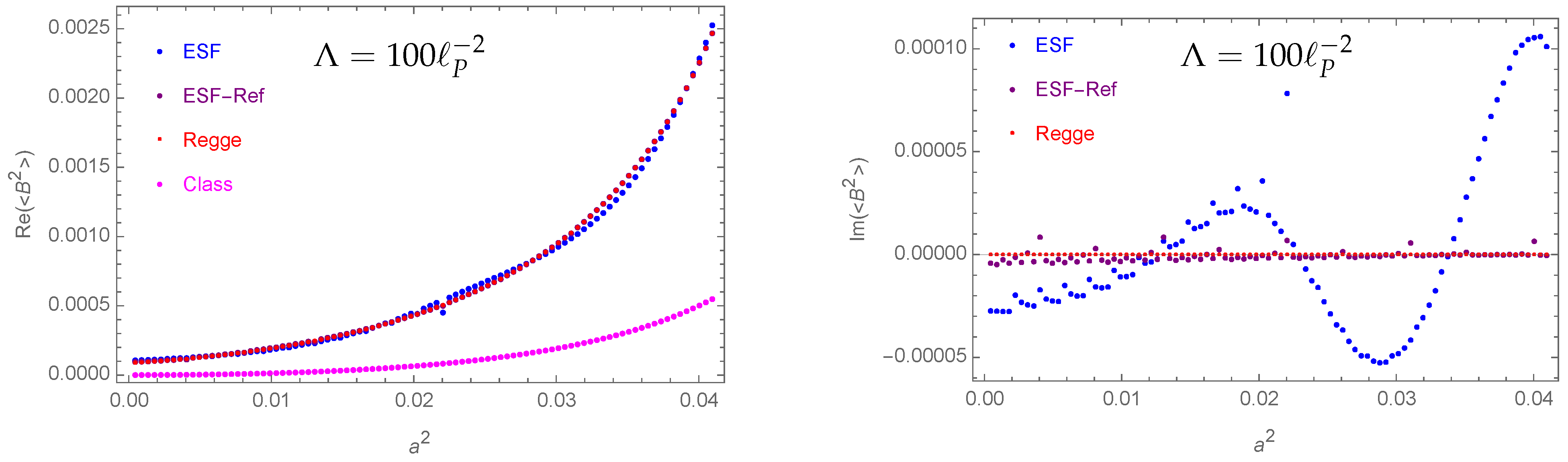
- The expectation value for the bulk area squared is well approximated by its classical value (e.g., see Figure 6).
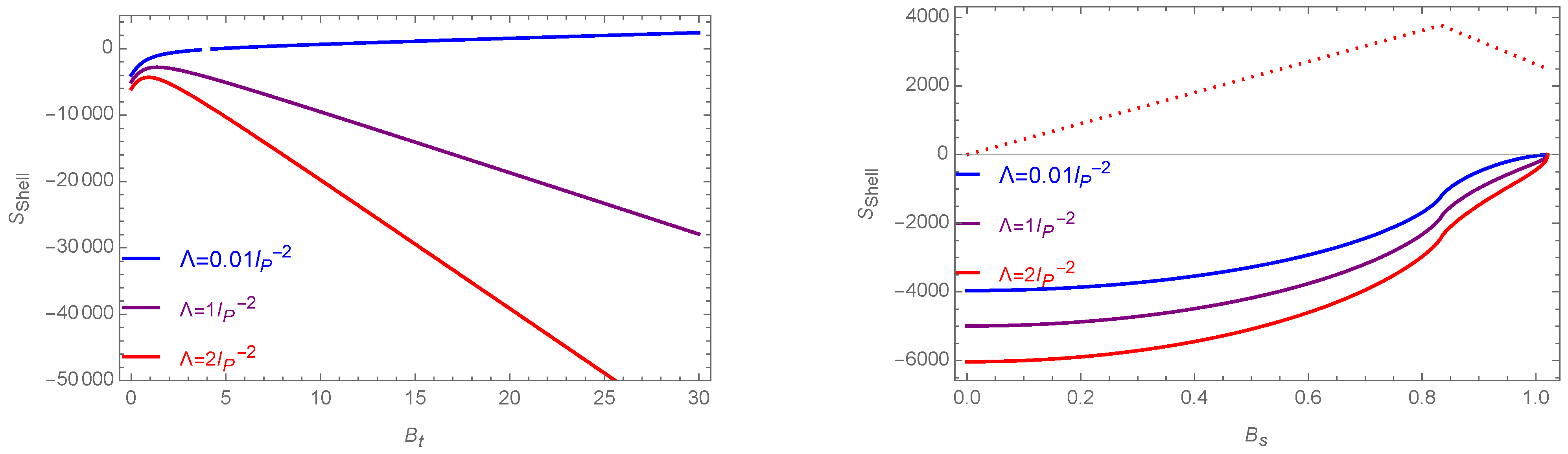
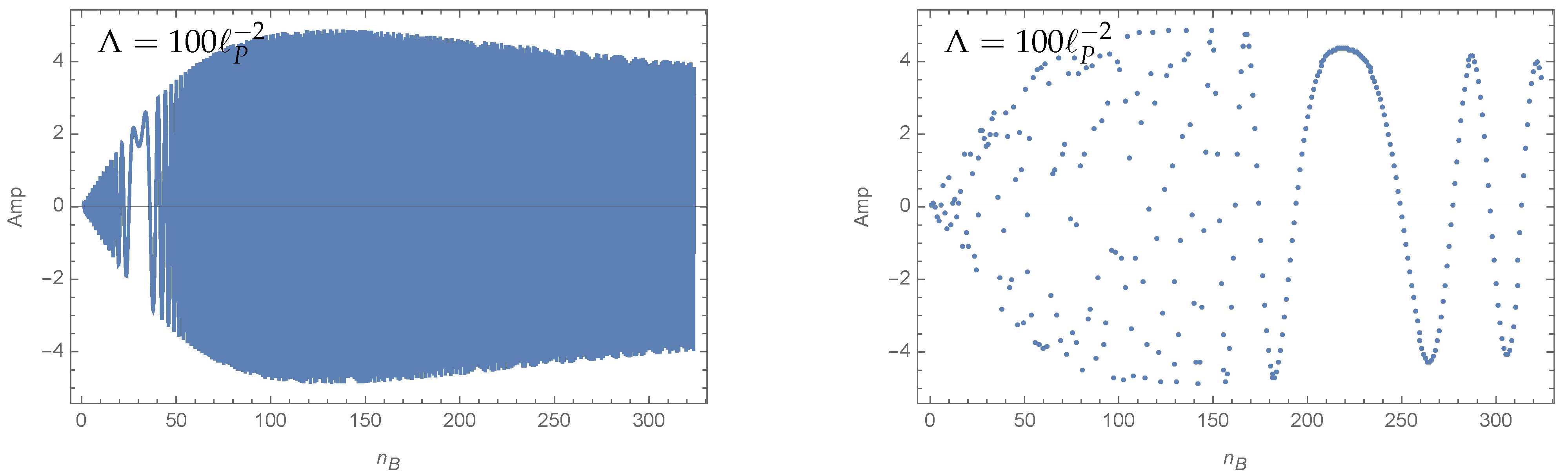
- Larger deviations can be found for large values of the cosmological constant (see Figures 13 and 14).
4.2. The Ball Model–Examples with a Euclidean Saddle Point
5. Discussion
- We provided heuristic arguments for the choice of a discrete area spectrum in (8) in the symmetry-reduced model. A similar issue appears for loop quantum cosmology [94]. It would be desirable to have a more rigorous derivation of the spectrum in symmetry-reduced models. One way to achieve this is to allow for more inhomogeneous bulk variables and to then integrate out the inhomogeneities and, in this way, to define an effective model for only symmetry-reduced configurations, that is, to implement a coarse graining and renormalization process [76,84,108,109].
- We only considered one time step. With the shell model, we can easily incorporate more time steps, in both the Euclidean and Lorentzian regime. We found that, for both the Lorentzian and Euclidean regime, the deviations between Regge integral and spin foam sum got stronger with larger differences between the initial and final scale factor. It will be interesting to see whether we arrive at the same conclusion if we incorporate more time steps, and how, e.g., the threshold value beyond which we see strong deviations in the Euclidean regime changes.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Regge Actions for the Ball and Shell Model
| 1 | |
| 2 | The smaller the parameter, the stronger the suppression. |
| 3 | |
| 4 | These frusta can be subdivided into 4-simplices, but this introduces additional edge lengths. In this model, we fix these additional edge lengths by demanding that the frusta are piecewise flat building blocks [48]. Frusta, which, however, have a cubic instead of a tetrahedral base, have also been used in [84] in the context of restricted spin foam models. |
| 5 | |
| 6 | In case the triangulation has a boundary, one has a (Gibbons–Hawking–York) boundary term [89]. This boundary term has the same structure as the bulk term; the only difference is that the deficit angles are replaced by extrinsic curvature angles. The latter are computed in the same way as the deficit angles; one only needs to replace the flat angle with the flat half-angle, or some other choice if one considers corners. |
| 7 | See [23] for an extensive discussion on the analytical continuation of this action and the resulting Riemann surface. |
| 8 | In the continuum model, one finds two Euclidean critical values for a positive imaginary lapse. These two values correspond to an evolution that remains in one hemisphere of the de Sitter sphere and an evolution that crosses the equator and therefore involves both hemispheres. Using only one time step in the discrete model, we only see the first case; to see the second solution, one needs at least two time steps. |
| 9 | In the continuum, one again finds two solutions corresponding to the solution not crossing or crossing the equator of the Lorentzian de Sitter space. Discretely (with only one time step), we only find the solution that does not cross the equator. |
| 10 | One actually has only for space-like areas in a space-like tetrahedron. For space-like areas in a time-like tetrahedron, one rather has and the condition [43]. The equidistant spectrum is a compromise, where we do not need to distinguish between these two types of space-like areas. |
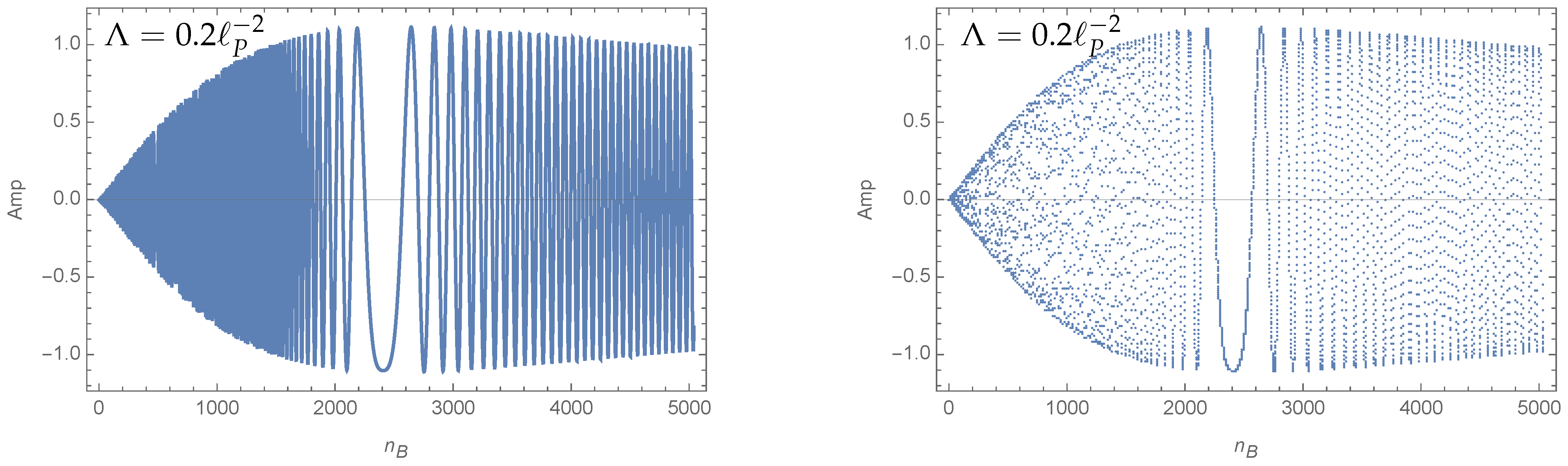
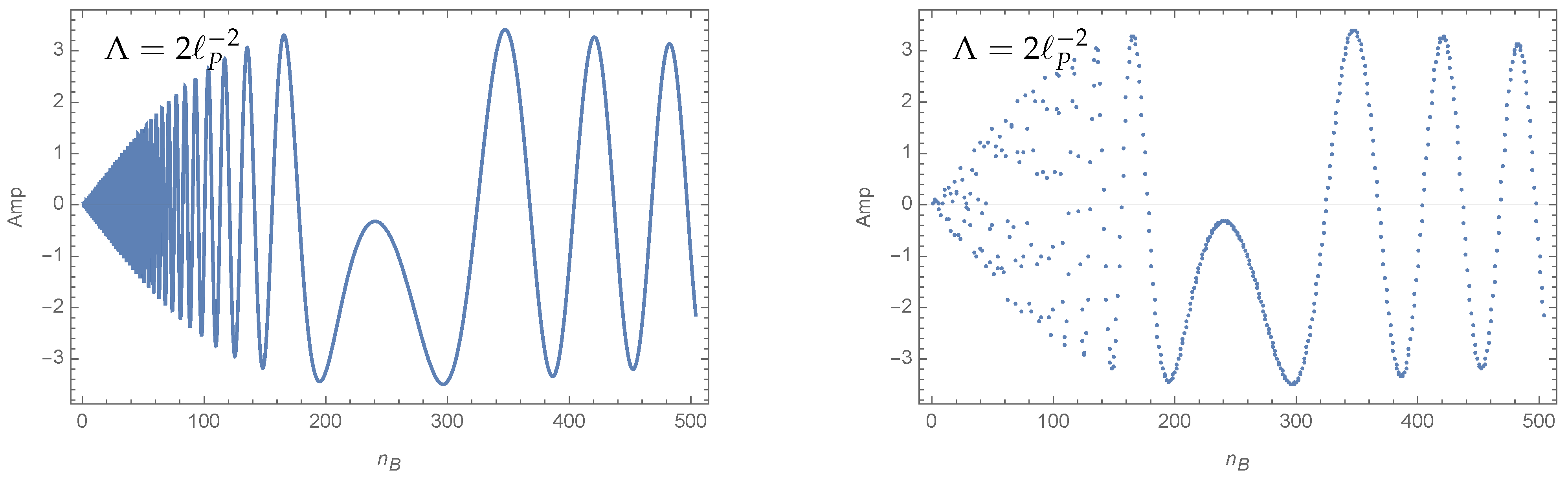
| 11 | We observed that an action that asymptotes to a quadratic growth in the summation variable might be harder to treat. The reasons are pseudo saddle points, which can appear because of the interplay between the frequency of the oscillations in the amplitude and the discretization of the variable, which defines the density with which the amplitude is probed. See Figure 12 for an example of a pseudo saddle point. With a quadratic growth of the action in the summation variable, such pseudo saddle points will appear and can lead to the partial sums exhibiting a staircase like behavior, that is, oscillating around one value for a certain range of the cut-off, but then suddenly changing to oscillations around another value if this cut-off crosses a threshold value corresponding to a pseudo saddle point. Such a behavior is not well approximated by series of the form (16), and Wynn’s epsilon algorithm has to be expected to fail in capturing the infinite sum. |
| 12 | The path integral includes a priori integrals over the scale factors at each time step and over a lapse at each time step. After a variable transformation, the action can be made to be quadratic in a variable related to the scale factors, and this variable can be integrated out. The lapse variables are gauge-fixed, leaving only a global lapse parameter to be integrated over. |
| 13 | The discrete analytical continuation can be uniquely specified if one provides the function values for positive real integers and positive imaginary integers. Trying different choices for the values of the function for positive imaginary integers, we always found directions in the positive complex half-plane in which the discrete analytical continuation diverges. |
| 14 | In the plots, we translate again the boundary areas to scale factors squared by comparing the three volumes in the simplicial model with the three volumes of the spatial hypersurfaces in the mini-superspace model (see [48]). |
| 15 | There is no classical solution, but we do have a saddle point along Euclidean data. We refer to the position of this saddle point as “classical value”. |
| 16 | See Note 11. |
| 17 | See Note 11. |
| 18 | |
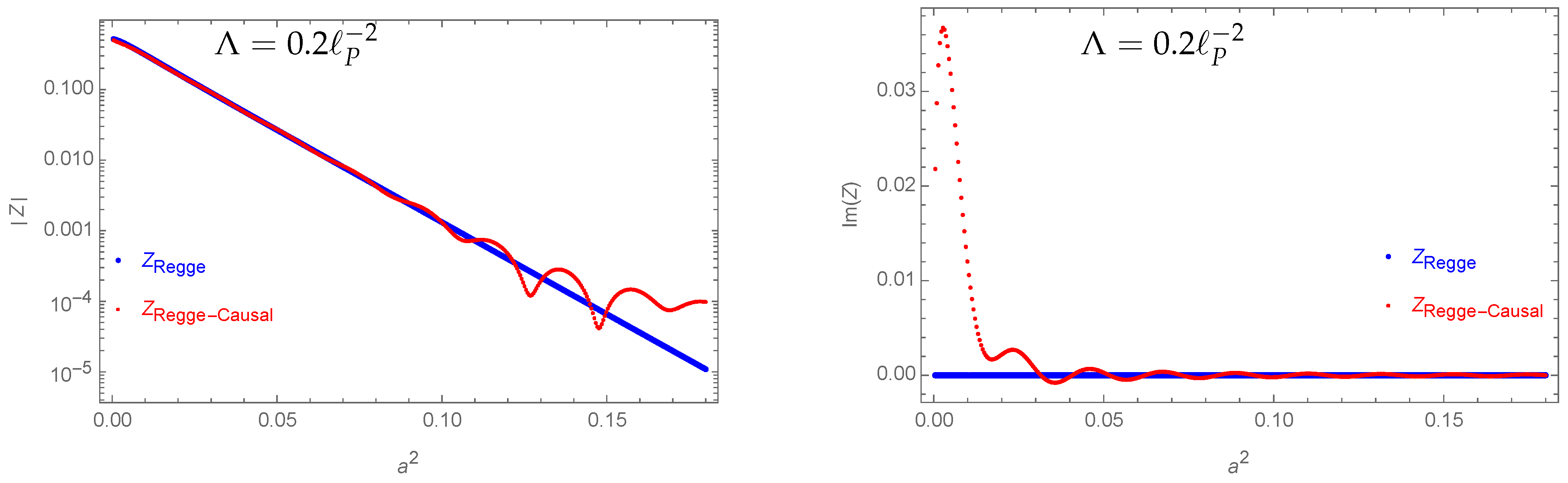
| 19 | Here, we find that the cases with Euclidean critical points lead to an exponentially suppressed amplitude (consistent with [8,23]). Note that we decided to sum over the hinge irregular configurations with a choice of (complex) Regge action, leading to exponentially suppressed amplitudes. We expect to find a different result if we implement the opposite choice. Finding an exponentially suppressed amplitude is compatible with the findings of [105], which apply a saddle point approximation for the one-simplex amplitude expressed as an integral over continuous parameters. On the other hand, [40] does find a non-suppressed amplitude for a discretization given by one (not further subdivided) simplex. The reason is the so-called vector geometries, which are thought to describe degenerate configurations [106]. It is still open whether such vector geometries should be allowed in the spin foam path, integral or not [107]. |
References
- de Boer, J.; Dittrich, B.; Eichhorn, A.; Giddings, S.B.; Gielen, S.; Liberati, S.; Livine, E.R.; Oriti, D.; Papadodimas, K.; Pereira, A.D.; et al. Frontiers of Quantum Gravity: Shared challenges, converging directions. arXiv 2022, arXiv:2207.10618. [Google Scholar]
- Ambjorn, J.; Loll, R. Nonperturbative Lorentzian quantum gravity, causality and topology change. Nucl. Phys. B 1998, 536, 407–434. [Google Scholar] [CrossRef]
- Ambjorn, J.; Jurkiewicz, J.; Loll, R. A Nonperturbative Lorentzian path integral for gravity. Phys. Rev. Lett. 2000, 85, 924–927. [Google Scholar] [CrossRef] [PubMed]
- Ambjorn, J.; Jurkiewicz, J.; Loll, R. Dynamically triangulating Lorentzian quantum gravity. Nucl. Phys. B 2001, 610, 347–382. [Google Scholar] [CrossRef]
- Engle, J.; Livine, E.; Pereira, R.; Rovelli, C. LQG vertex with finite Immirzi parameter. Nucl. Phys. B 2008, 799, 136. [Google Scholar] [CrossRef]
- Freidel, L.; Krasnov, K. A New Spin Foam Model for 4d Gravity. Class. Quant. Grav. 2008, 25, 125018. [Google Scholar] [CrossRef]
- Perez, A. The Spin Foam Approach to Quantum Gravity. Living Rev. Rel. 2013, 16, 3. [Google Scholar] [CrossRef] [PubMed]
- Feldbrugge, J.; Lehners, J.L.; Turok, N. Lorentzian quantum cosmology. Phys. Rev. D 2017, 95, 103508. [Google Scholar] [CrossRef]
- Asante, S.K.; Dittrich, B.; Padua-Arg uelles, J. Effective spin foam models for Lorentzian quantum gravity. Class. Quant. Grav. 2021; in press. [Google Scholar] [CrossRef]
- Ito, Y.; Kadoh, D.; Sato, Y. Tensor network approach to 2D Lorentzian quantum Regge calculus. Phys. Rev. D 2022, 106, 106004. [Google Scholar] [CrossRef]
- Gibbons, G.W.; Hawking, S.W.; Perry, M.J. Path Integrals and the Indefiniteness of the Gravitational Action. Nucl. Phys. B 1978, 138, 141–150. [Google Scholar] [CrossRef]
- Lefschetz, S. Applications of Algebraic Topology, Graphs and Networks, the Picard-Lefschetz Theory and Feynman Integrals; Applied Mathematical Sciences; Springer: Berlin, Germany; New York, NY, USA, 1975; Volume 16. [Google Scholar]
- Vassiliev, V.A. Applied Picard-Lefschetz Theory; Mathematical Surveys and Monographs; AMS: Providence, RI, USA, 2002; Volume 97. [Google Scholar]
- Witten, E. Analytic Continuation Of Chern-Simons Theory. AMS/IP Stud. Adv. Math. 2011, 50, 347–446. [Google Scholar]
- Witten, E. A New Look At The Path Integral Of Quantum Mechanics. arXiv 2010, arXiv:1009.6032. [Google Scholar] [CrossRef]
- Tanizaki, Y.; Koike, T. Real-time Feynman path integral with Picard–Lefschetz theory and its applications to quantum tunneling. Annals Phys. 2014, 351, 250–274. [Google Scholar] [CrossRef]
- Cristoforetti, M.; Di Renzo, F.; Scorzato, L.; AuroraScience Collaboration. New approach to the sign problem in quantum field theories: High density QCD on a Lefschetz thimble. Phys. Rev. D 2012, 86, 074506. [Google Scholar] [CrossRef]
- Bongiovanni, L. Numerical methods for the sign problem in Lattice Field Theory. arXiv 2016, arXiv:1603.06458. [Google Scholar]
- Alexandru, A.; Basar, G.; Bedaque, P.F.; Warrington, N.C. Complex Paths Around The Sign Problem. Rev. Mod. Phys. 2022, 94, 015006. [Google Scholar] [CrossRef]
- Fujisawa, G.; Nishimura, J.; Sakai, K.; Yosprakob, A. Backpropagating Hybrid Monte Carlo algorithm for fast Lefschetz thimble calculations. arXiv 2022, arXiv:2112.10519. [Google Scholar] [CrossRef]
- Han, M.; Huang, Z.; Liu, H.; Qu, D.; Wan, Y. Spinfoam on a Lefschetz thimble: Markov chain Monte Carlo computation of a Lorentzian spinfoam propagator. Phys. Rev. D 2021, 103, 084026. [Google Scholar] [CrossRef]
- Jia, D. Complex, Lorentzian, and Euclidean simplicial quantum gravity: Numerical methods and physical prospects. Class. Quantum Gravity 2022, 39, 065002. [Google Scholar] [CrossRef]
- Asante, S.K.; Dittrich, B.; Padua-Arg uelles, J. Complex actions and causality violations: Applications to Lorentzian quantum cosmology. Class. Quantum Gravity 2023, 40, 105005. [Google Scholar] [CrossRef]
- Rovelli, C. Quantum Gravity; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar] [CrossRef]
- Thiemann, T. Modern Canonical Quantum General Relativity; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar] [CrossRef]
- Bojowald, M. Loop quantum cosmology. Living Rev. Relativ. 2005, 8, 11. [Google Scholar] [CrossRef] [PubMed]
- Ashtekar, A.; Singh, P. Loop Quantum Cosmology: A Status Report. Class. Quantum Gravity 2011, 28, 213001. [Google Scholar] [CrossRef]
- Banerjee, K.; Calcagni, G.; Martin-Benito, M. Introduction to loop quantum cosmology. SIGMA 2012, 8, 016. [Google Scholar] [CrossRef]
- Agullo, I.; Singh, P. Loop Quantum Cosmology. Living Rev. Relativ. 2008, 11, 1–131. [Google Scholar]
- Bojowald, M. Critical evaluation of common claims in loop quantum cosmology. Universe 2020, 6, 36. [Google Scholar] [CrossRef]
- Bojowald, M. Noncovariance of “covariant polymerization” in models of loop quantum gravity. Phys. Rev. D 2021, 103, 126025. [Google Scholar] [CrossRef]
- Brunnemann, J.; Fleischhack, C. On the configuration spaces of homogeneous loop quantum cosmology and loop quantum gravity. arXiv 2007, arXiv:0709.1621. [Google Scholar]
- Brunnemann, J.; Koslowski, T.A. Symmetry Reduction of Loop Quantum Gravity. Class. Quantum Gravity 2011, 28, 245014. [Google Scholar] [CrossRef]
- Bianchi, E.; Rovelli, C.; Vidotto, F. Towards Spinfoam Cosmology. Phys. Rev. D 2010, 82, 084035. [Google Scholar] [CrossRef]
- Dona, P.; Frisoni, P. How-to Compute EPRL Spin Foam Amplitudes. Universe 2022, 8, 208. [Google Scholar] [CrossRef]
- Asante, S.K.; Dittrich, B.; Haggard, H.M. Effective Spin Foam Models for Four-Dimensional Quantum Gravity. Phys. Rev. Lett. 2020, 125, 231301. [Google Scholar] [CrossRef] [PubMed]
- Asante, S.K.; Dittrich, B.; Haggard, H.M. Discrete gravity dynamics from effective spin foams. Class. Quantum Gravity 2021, 38, 145023. [Google Scholar] [CrossRef]
- Bianchi, E.; Krajewski, T.; Rovelli, C.; Vidotto, F. Cosmological constant in spinfoam cosmology. Phys. Rev. D 2011, 83, 104015. [Google Scholar] [CrossRef]
- Vidotto, F. Many-nodes/many-links spinfoam: The homogeneous and isotropic case. Class. Quantum Gravity 2011, 28, 245005. [Google Scholar] [CrossRef]
- Gozzini, F.; Vidotto, F. Primordial Fluctuations From Quantum Gravity. Front. Astron. Space Sci. 2021, 7, 629466. [Google Scholar] [CrossRef]
- Frisoni, P.; Gozzini, F.; Vidotto, F. Markov chain Monte Carlo methods for graph refinement in spinfoam cosmology. Class. Quantum Gravity 2023, 40, 105001. [Google Scholar] [CrossRef]
- Weniger, E.J. Nonlinear sequence transformations for the acceleration of convergence and the summation of divergent series. Comput. Phys. Rep. 1989, 10, 189. [Google Scholar] [CrossRef]
- Conrady, F.; Hnybida, J. A spin foam model for general Lorentzian 4-geometries. Class. Quantum Gravity 2010, 27, 185011. [Google Scholar] [CrossRef]
- Rovelli, C.; Smolin, L. Discreteness of area and volume in quantum gravity. Nucl. Phys. B 1995, 442, 593–622, Erratum in Nucl. Phys. B 1995, 456, 753–754. [Google Scholar] [CrossRef]
- Ashtekar, A.; Lewandowski, J. Quantum theory of geometry. 1: Area operators. Class. Quantum Gravity 1997, 14, A55–A82. [Google Scholar] [CrossRef]
- Gielen, S.; Oriti, D.; Sindoni, L. Cosmology from Group Field Theory Formalism for Quantum Gravity. Phys. Rev. Lett. 2013, 111, 031301. [Google Scholar] [CrossRef]
- Gielen, S.; Oriti, D.; Sindoni, L. Homogeneous cosmologies as group field theory condensates. J. High Energy Phys. 2014, 6, 013. [Google Scholar] [CrossRef]
- Dittrich, B.; Gielen, S.; Schander, S. Lorentzian quantum cosmology goes simplicial. Class. Quantum Gravity 2022, 39, 035012. [Google Scholar] [CrossRef]
- Regge, T. General Relativity Without Coordinates. Nuovo Cim. 1961, 19, 558. [Google Scholar] [CrossRef]
- Dittrich, B.; Ryan, J.P. Phase space descriptions for simplicial 4d geometries. Class. Quantum Gravity 2011, 28, 065006. [Google Scholar] [CrossRef]
- Dittrich, B.; Ryan, J.P. Simplicity in simplicial phase space. Phys. Rev. D 2010, 82, 064026. [Google Scholar] [CrossRef]
- Dittrich, B.; Ryan, J.P. On the role of the Barbero-Immirzi parameter in discrete quantum gravity. Class. Quantum Gravity 2013, 30, 095015. [Google Scholar] [CrossRef]
- Dittrich, B. Modified Graviton Dynamics From Spin Foams: The Area Regge Action. arXiv 2021, arXiv:2105.10808. [Google Scholar]
- Dittrich, B.; Kogios, A. From spin foams to area metric dynamics to gravitons. Class. Quantum Gravity 2023, 40, 095011. [Google Scholar] [CrossRef]
- Borissova, J.N.; Dittrich, B. Towards effective actions for the continuum limit of spin foams. Class. Quantum Gravity 2023, 40, 105006. [Google Scholar] [CrossRef]
- Dittrich, B.; Padua-Arg uelles, J. Twisted geometries are area-metric geometries. arXiv 2023, arXiv:2302.11586. [Google Scholar] [CrossRef]
- Dittrich, B.; Speziale, S. Area-angle variables for general relativity. New J. Phys. 2008, 10, 083006. [Google Scholar] [CrossRef]
- Asante, S.K.; Simão, J.D.; Steinhaus, S. Spin-foams as semiclassical vertices: Gluing constraints and a hybrid algorithm. Phys. Rev. D 2023, 107, 046002. [Google Scholar] [CrossRef]
- Han, M.; Liu, H.; Qu, D. Complex critical points in Lorentzian spinfoam quantum gravity: 4-simplex amplitude and effective dynamics on double-Δ3 complex. arXiv 2023, arXiv:2301.02930. [Google Scholar] [CrossRef]
- Asante, S.K.; Dittrich, B.; Girelli, F.; Riello, A.; Tsimiklis, P. Quantum geometry from higher gauge theory. Class. Quantum Gravity 2020, 37, 205001. [Google Scholar] [CrossRef]
- Baratin, A.; Freidel, L. Hidden Quantum Gravity in 4-D Feynman diagrams: Emergence of spin foams. Class. Quantum Gravity 2007, 24, 2027–2060. [Google Scholar] [CrossRef]
- Baratin, A.; Freidel, L. A 2-categorical state sum model. J. Math. Phys. 2015, 56, 011705. [Google Scholar] [CrossRef]
- Simão, J.D.; Steinhaus, S. Asymptotic analysis of spin-foams with timelike faces in a new parametrization. Phys. Rev. D 2021, 104, 126001. [Google Scholar] [CrossRef]
- Dona, P.; Han, M.; Liu, H. Spinfoams and high performance computing. arXiv 2022, arXiv:2212.14396. [Google Scholar]
- Barrett, J.W.; Rocek, M.; Williams, R.M. A Note on area variables in Regge calculus. Class. Quant. Grav. 1999, 16, 1373. [Google Scholar] [CrossRef]
- Asante, S.K.; Dittrich, B.; Haggard, H.M. The Degrees of Freedom of Area Regge Calculus: Dynamics, Non-metricity, and Broken Diffeomorphisms. Class. Quantum Gravity 2018, 35, 135009. [Google Scholar] [CrossRef]
- Bahr, B.; Rabuffo, G.; Steinhaus, S. Renormalization of symmetry restricted spin foam models with curvature in the asymptotic regime. Phys. Rev. D 2018, 98, 106026. [Google Scholar] [CrossRef]
- Bahr, B.; Dittrich, B. Regge calculus from a new angle. New J. Phys. 2010, 12, 033010. [Google Scholar] [CrossRef]
- Fairbairn, W.J.; Meusburger, C. Quantum deformation of two four-dimensional spin foam models. J. Math. Phys. 2012, 53, 022501. [Google Scholar] [CrossRef]
- Dupuis, M.; Girelli, F. Observables in Loop Quantum Gravity with a cosmological constant. Phys. Rev. D 2014, 90, 104037. [Google Scholar] [CrossRef]
- Haggard, H.M.; Han, M.; Kamiński, W.; Riello, A. SL(2,C) Chern–Simons theory, a non-planar graph operator, and 4D quantum gravity with a cosmological constant: Semiclassical geometry. Nucl. Phys. B 2015, 900, 1–79. [Google Scholar] [CrossRef]
- Dittrich, B. (3 + 1)-dimensional topological phases and self-dual quantum geometries encoded on Heegaard surfaces. J. High Energy Phys. 2017, 5, 123. [Google Scholar] [CrossRef]
- Han, M. Four-dimensional spinfoam quantum gravity with a cosmological constant: Finiteness and semiclassical limit. Phys. Rev. D 2021, 104, 104035. [Google Scholar] [CrossRef]
- Bahr, B.; Dittrich, B. Improved and Perfect Actions in Discrete Gravity. Phys. Rev. D 2009, 80, 124030. [Google Scholar] [CrossRef]
- Breaking and restoring of diffeomorphism symmetry in discrete gravity. AIP Conf. Proc. 2009, 1196, 10.
- Asante, S.K.; Dittrich, B.; Steinhaus, S. Spin foams, Refinement limit and Renormalization. arXiv 2022, arXiv:2211.09578. [Google Scholar]
- Dittrich, B. Diffeomorphism symmetry in quantum gravity models. Adv. Sci. Lett. 2009, 2, 151. [Google Scholar] [CrossRef]
- Bahr, B.; Dittrich, B. (Broken) Gauge Symmetries and Constraints in Regge Calculus. Class. Quantum Gravity 2009, 26, 225011. [Google Scholar] [CrossRef]
- Hartle, J.B. Simplicial minisuperspace I. General discussion. J. Math. Phys. 1985, 26, 804–814. [Google Scholar] [CrossRef]
- Hartle, J.B. Simplicial minisuperspace. II. Some classical solutions on simple triangulations. J. Math. Phys. 1986, 27, 287–295. [Google Scholar] [CrossRef]
- Hartle, J.B. Simplicial minisuperspace. III. Integration contours in a five-simplex model. J. Math. Phys. 1989, 30, 452–460. [Google Scholar] [CrossRef]
- Collins, P.A.; Williams, R.M. Dynamics of the Friedmann Universe Using Regge Calculus. Phys. Rev. D 1973, 7, 965–971. [Google Scholar] [CrossRef]
- Liu, R.G.; Williams, R.M. Regge calculus models of the closed vacuum Λ–FLRW universe. Phys. Rev. D 2016, 93, 024032. [Google Scholar] [CrossRef]
- Bahr, B.; Kloser, S.; Rabuffo, G. Towards a Cosmological subsector of Spin Foam Quantum Gravity. Phys. Rev. D 2017, 96, 086009. [Google Scholar] [CrossRef]
- Jordan, S.; Loll, R. Causal Dynamical Triangulations without Preferred Foliation. Phys. Lett. B 2013, 724, 155–159. [Google Scholar] [CrossRef]
- Jordan, S.; Loll, R. De Sitter Universe from Causal Dynamical Triangulations without Preferred Foliation. Phys. Rev. D 2013, 88, 044055. [Google Scholar] [CrossRef]
- Sorkin, R. Time Evolution Problem in Regge Calculus. Phys. Rev. D 1975, 12, 385–396, Erratum in Phys. Rev. D 1981, 23, 565–565. [Google Scholar] [CrossRef]
- Sorkin, R.D. Lorentzian angles and trigonometry including lightlike vectors. arXiv 2019, arXiv:1908.10022. [Google Scholar]
- Hartle, J.B.; Sorkin, R. Boundary Terms in the Action for the Regge Calculus. Gen. Rel. Grav. 1981, 13, 541–549. [Google Scholar] [CrossRef]
- Dittrich, B.; Jacobson, T.; Padua-Arg uelles, J. De Sitter horizon entropy from a simplicial Lorentzian path integral. arXiv 2024, arXiv:2403.02119. [Google Scholar]
- Dorronsoro, J.D.; Halliwell, J.J.; Hartle, J.B.; Hertog, T.; Janssen, O. Real no-boundary wave function in Lorentzian quantum cosmology. Phys. Rev. D 2017, 96, 043505. [Google Scholar] [CrossRef]
- Bojowald, M. Loop quantum cosmology. Living Rev. Rel. 2008, 11, 4. [Google Scholar] [CrossRef] [PubMed]
- Ashtekar, A.; Pawlowski, T.; Singh, P. Quantum Nature of the Big Bang: Improved dynamics. Phys. Rev. D 2006, 74, 084003. [Google Scholar] [CrossRef]
- Beetle, C.; Engle, J.S.; Hogan, M.E.; Mendonça, P. Diffeomorphism invariant cosmological sector in loop quantum gravity. Class. Quantum Gravity 2017, 34, 225009. [Google Scholar] [CrossRef]
- Schmidt, J.R. On the numerical solution of linear simultaneous equations by an iterative method. Philos. Mag. 1941, 32, 369. [Google Scholar] [CrossRef]
- Shanks, D. Non-linear transformations of divergent and slowly convergent sequences. J. Math. Phys. 1955, 34, 1. [Google Scholar] [CrossRef]
- Wynn, P. On a device for computing the em(Sn) transformation. Math. Tables Aids Comput. 1956, 10, 91. [Google Scholar] [CrossRef]
- Wynn, P. A note on programming repeated applications of the ϵ-algorithm. R.F.T.I.—Chiffres 1965, 8, 23. [Google Scholar]
- Aitken, A. On Bernoulli’s Numerical Solution of Algebraic Equations. Proc. R. Soc. Edinb. 1927, 46, 289–305. [Google Scholar] [CrossRef]
- Donà, P.; Frisoni, P. Summing bulk quantum numbers with Monte Carlo in spin foam theories. Phys. Rev. D 2023, 107, 106008. [Google Scholar] [CrossRef]
- Hartle, J.B.; Hawking, S.W. Wave Function of the Universe. Phys. Rev. D 1983, 28, 2960–2975. [Google Scholar] [CrossRef]
- Duffin, R.J. Basic properties of discrete analytic functions. Duke Math. J. 1956, 23, 335. [Google Scholar] [CrossRef]
- Borissova, J.; Dittrich, B.; Qu, D.; Schiffer, M. Spikes and spines in 3D Lorentzian simplicial quantum gravity. arXiv 2024, arXiv:2406.19169. [Google Scholar]
- Borissova, J.; Dittrich, B.; Qu, D.; Schiffer, M. Spikes and spines in 4D Lorentzian simplicial quantum gravity. arXiv, 2024; to appear. [Google Scholar]
- Han, M.; Liu, H. Analytic Continuation of Spin foam Models. arXiv 2021, arXiv:2104.06902. [Google Scholar]
- Barrett, J.W.; Dowdall, R.J.; Fairbairn, W.J.; Hellmann, F.; Pereira, R. Lorentzian spin foam amplitudes: Graphical calculus and asymptotics. Class. Quantum Gravity 2010, 27, 165009. [Google Scholar] [CrossRef]
- Engle, J. A spin-foam vertex amplitude with the correct semiclassical limit. Phys. Lett. B 2013, 724, 333–337. [Google Scholar] [CrossRef][Green Version]
- Dittrich, B. From the discrete to the continuous: Towards a cylindrically consistent dynamics. New J. Phys. 2012, 14, 123004. [Google Scholar] [CrossRef]
- Dittrich, B. The continuum limit of loop quantum gravity—A framework for solving the theory. arXiv 2014, arXiv:1409.1450. [Google Scholar]
- Bahr, B.; Dittrich, B.; Steinhaus, S. Perfect discretization of reparametrization invariant path integrals. Phys. Rev. D 2011, 83, 105026. [Google Scholar] [CrossRef]
- Dittrich, B.; Steinhaus, S. Path integral measure and triangulation independence in discrete gravity. Phys. Rev. D 2012, 85, 044032. [Google Scholar] [CrossRef]
- Borissova, J.N.; Dittrich, B. Lorentzian quantum gravity via Pachner moves: One-loop evaluation. arXiv 2023, arXiv:2303.07367. [Google Scholar] [CrossRef]
- Dittrich, B.; Hohn, P.A. From covariant to canonical formulations of discrete gravity. Class. Quantum Gravity 2010, 27, 155001. [Google Scholar] [CrossRef]
- Dittrich, B.; Hoehn, P.A. Constraint analysis for variational discrete systems. J. Math. Phys. 2013, 54, 093505. [Google Scholar] [CrossRef]
- Dittrich, B.; Padua-Argüelles, J. Bianchi I quantum cosmology from effective spin foams. arXiv, 2023; to appear. [Google Scholar]
- Genz, A.C. A nonlinear method for the acceleration of the convergence of multidimensional squences. J. Comput. Appl. Math. 1977, 3, 181. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dittrich, B.; Padua-Argüelles, J. Lorentzian Quantum Cosmology from Effective Spin Foams. Universe 2024, 10, 296. https://doi.org/10.3390/universe10070296
Dittrich B, Padua-Argüelles J. Lorentzian Quantum Cosmology from Effective Spin Foams. Universe. 2024; 10(7):296. https://doi.org/10.3390/universe10070296
Chicago/Turabian StyleDittrich, Bianca, and José Padua-Argüelles. 2024. "Lorentzian Quantum Cosmology from Effective Spin Foams" Universe 10, no. 7: 296. https://doi.org/10.3390/universe10070296
APA StyleDittrich, B., & Padua-Argüelles, J. (2024). Lorentzian Quantum Cosmology from Effective Spin Foams. Universe, 10(7), 296. https://doi.org/10.3390/universe10070296






