Effects of Impurities and Deformations on Electronic Effective Mass in Quantum Revival Time within the Infinite Square Well

Abstract

Quantum revival phenomena, wherein the wave function of a quantum system periodically returns to its initial state after evolving in time, are investigated in this study. Focusing on electrons confined within a quantum box with an impurity, both weak- and strong-coupling regimes are explored, revealing intricate relationships between impurity parameters and temporal dynamics. This investigation considers the influence of impurity position, impurity strength, and external factors such as aluminum concentration, temperature and hydrostatic pressure on classical periods and revival times. Through analytical derivations and graphical analyses, this study elucidates the sensitivity of quantum revivals to these parameters, providing valuable insights into the fundamental aspects of quantum mechanics. While no specific physical applications are discussed, the findings offer implications for quantum heat engines and other quantum-based technologies, emphasizing the importance of understanding quantum revivals in confined quantum systems.

1. Introduction

Quantum revival refers to a phenomenon in which the wave function of a quantum system periodically returns to its initial state after evolving in time [1]. It arises in systems that are confined or periodic in nature, such as particles in a box or atoms in an optical lattice [2,3]. It is characterized by the recurrence of interference patterns in the probability density of finding the system in different states. Quantum revival is a fundamental aspect of quantum mechanics with applications in various fields, including quantum information processing [4,5] and condensed matter physics [6]. As is well known, it has counterparts in other branches of physics. One notable example is in the study of wave phenomena, where similar periodic behaviors can be observed. For instance, in classical wave physics, phenomena such as wave interference and diffraction can lead to periodic patterns in the intensity or amplitude of waves [7]. Additionally, in certain systems in classical mechanics, such as periodic mechanical oscillators or coupled pendulums, there can be periodic recurrences of specific states or motions due to the system’s inherent periodicity. While the underlying principles may differ between classical and quantum systems, the concept of periodic recurrence is a common thread across various branches of physics.

The time of quantum revival may be relevant not only for studies of electronic properties in quantum devices [8] but also for the study of quantum thermal machines [9]. The effects of topological defects on quantum revivals have been addressed in [10,11,12]. Recently, it was shown that the influence of spiral dislocation gives rise to a non-null revival time in the harmonic oscillator [13]. Additionally, the classical periods and revival times of electron currents in several bulk nanostructured semiconductor materials were computed in [14]. The hallmark concept of periodic collapse and revival of coherence in a room-temperature ensemble of quantum dots is demonstrated in [15]. Quantum revivals within relativistic theory can be explored in [16], and further investigations concerning exact quantum revivals for the Dirac equation are detailed in [17].

Speaking of another topic of great current interest, in article [18], the authors investigated the impacts due to impurity in the quasi-static thermodynamics of thermal machines, with the quantum system of a particle in a box as the working substance. However, quantum thermodynamics aims to consider, in addition to thermal and quantum fluctuations, those due to processes with finite time. We will not delve into these investigations at the moment, but rather focus on a fundamental aspect of quantum mechanics, which is quantum revival. Inspired by these works, in this contribution, we investigate the classical periods and revival times for the system mentioned at the beginning of this paragraph. Furthermore, we explore the impact of deformations on the electronic effective mass on these quantities, that is, we consider electrons in $GaAs/G{a}_{1-x}A{l}_{x}As$ [19]. Effects of hydrostatic pressure, temperature and aluminum concentration warrant attention due to pronounced modifications in physical quantities in electronic systems [20,21,22].

This paper is divided as follows: in Section 2, we present the studied model and the eigenenergies for the electron in the impurity-doped box. In Section 3, we present its effective mass as a function of temperature, hydrostatic pressure and aluminum concentration. In Section 4, we calculate the revival times and perform graphical analyses to observe the effects of impurity position in the box and the effects of deformations in the effective mass on these times. Section 5 contains the conclusions of the work.

2. The Hamiltonian Model and the Eigenenergies

The Hamiltonian describing a particle of mass m confined within a 1-D infinite square well (ISW) of length L, featuring an impurity situated at position $pL$ ($0\le p\le 1$) inside the well, is expressed as follows:

$$\begin{array}{ccc}\hfill H& =& H_0+H^{\prime },\hfill \\ \hfill \mathrm{where},H_0& =& -\frac{{\hslash }^2}{2m}{\nabla }^2+V\left(x\right),V\left(x\right)=\left\{\begin{array}{cc}0\hfill & \mathrm{for}0\le x\le L\hfill \\ \infty \hfill & \mathrm{otherwise}\hfill \end{array}\right.,\hfill \\ \hfill \mathrm{and}{H}^{\prime }& =& -\lambda \delta (x-pL).\hfill \end{array}$$

(1)

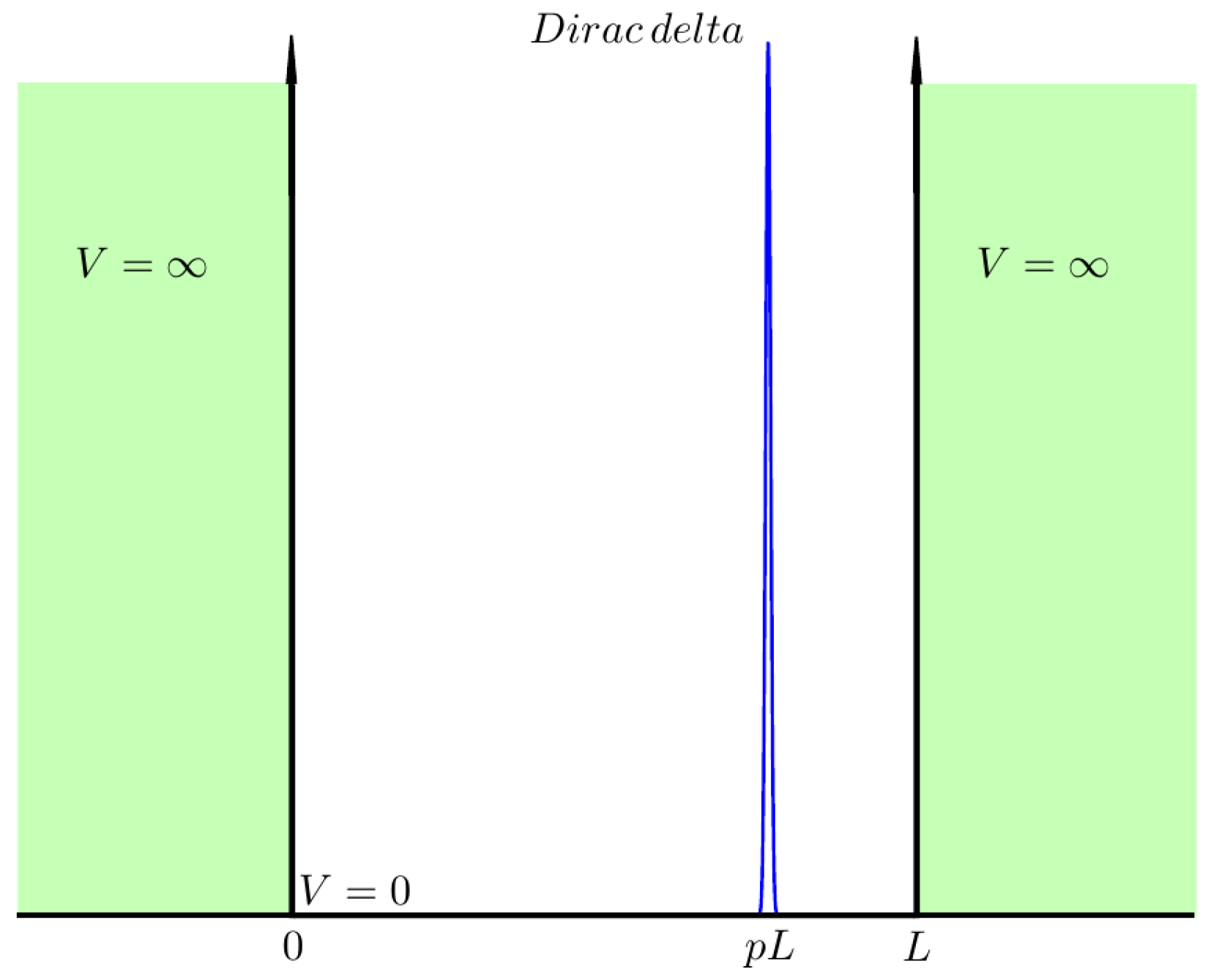
Here, $H_0$ represents the Hamiltonian of the particle within the ISW, governed by the kinetic energy term and the potential energy function $V\left(x\right)$, which is zero within the well and infinite elsewhere. The additional term $H^{\prime }$ introduces the effect of the impurity, modeled as a delta function potential with strength denoted by $\lambda$. The parameter p determines the precise location of the impurity within the well. A negative $\lambda$ implies a repulsive impurity, behaving akin to a barrier, while a positive $\lambda$ denotes an attractive impurity, creating a well-like potential. The schematic representation of the ISW potential featuring a repulsive impurity is depicted in Figure 1. In this section, we will present the eigenvalues in four cases, leaving the details for Appendix A.

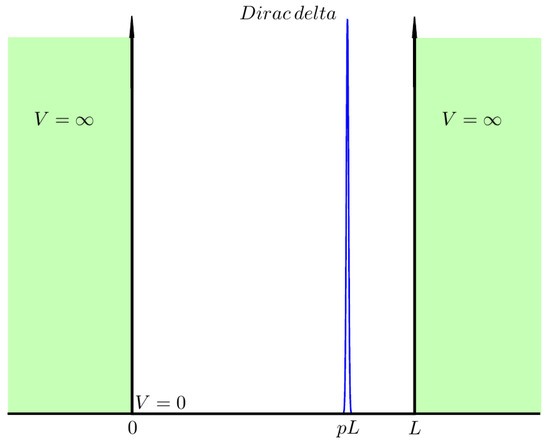
Figure 1. One-dimensional infinite square well with a Dirac delta barrier representing the potential induced by an impurity.

The first-order corrections to the energy eigenvalues caused by either attractive or repulsive $\delta$ function impurities are

$$E_{n,w}^{\left(1\right)}=\frac{{\hslash }^2}{2m{L}^2}\left(n^2{\pi }^2-4\frac{sin\left(n\pi p\right)}{f}\right).$$

(2)

The eigenenergies up to the second-order correction will be given by

$$E_{n,w}^{\left(2\right)}=\frac{{\hslash }^2}{2m{L}^2}\left(n^2{\pi }^2-4\frac{sin\left(n\pi p\right)}{f}\right)-2\frac{{\hslash }^2{\left(sin\left(n\pi p\right)\right)}^4\left(1+2n\pi \left(1-2p\right)cot\left(n\pi p\right)\right)}{m{L}^2{n}^2{\pi }^2{f}^2}.$$

(3)

The parameter f is a dimensionless parameter representing the strength of the impurity, given by $f=\frac{{\hslash }^2}{m\lambda L}$. These two cases hold for $f\ge \left|0.5\right|$.

For the strong-coupling case, $f\ll 0.1$, a perturbative approach is employed to determine the energy eigenvalue by applying perturbation up to the first order in the strength parameter, giving rise to two possible eigenenergies:

$$E_{n,str}^{\left(a\right)}=\frac{{\hslash }^2}{2m{L}^2}\left(\frac{n^2{\pi }^2}{p^2}+\frac{nf\pi }{p^3}\right)$$

(4)

and

$$E_{n,str}^{\left(b\right)}=\frac{{\hslash }^2}{2m{L}^2}\left(\frac{n^2{\pi }^2}{{(1-p)}^2}+\frac{nf\pi }{{(1-p)}^3}\right).$$

(5)

In what follows, we will consider the particle mass m given by the electronic effective mass denoted as $m_{\mathrm{eff}}(x,P,T)$, which depends on the aluminum concentration in the material, hydrostatic pressure and temperature. Details regarding its dependence on these physical quantities for the material $GaAs/G{a}_{1-x}A{l}_{x}As$ will be presented subsequently.

3. Effects of Hydrostatic Pressure, Temperature and Al Concentration on the Effective Electron Mass

The effective mass of an electron in a material is as real as its mass in a vacuum [23]. In this way, we consider a case for electrons on $GaAs/G{a}_{1-x}A{l}_{x}As$. The effective mass of electrons in the conduction band, which is assumed to be dependent on x (aluminum concentration), P (hydrostatic pressure) and T (temperature), and can be expressed as [19]

$$\begin{array}{c}\hfill m_{eff}\left(x,P,T\right)=m_0{\left\{1+\left(\frac{28900-6290x}{3}\right)\left[\frac{2}{E_g^{\Gamma }\left(x,P,T\right)}+\frac{1}{E_g^{\Gamma }\left(x,P,T\right)+314-66x}\right]+\zeta \left(x\right)\right\}}^{-1},\end{array}$$

(6)

where $m_e=9.11\times {10}^{-31}$ Kg is the electron mass in a vacuum,

$$\begin{array}{c}\hfill \zeta \left(x\right)=-3.950+0.488x+4.938x^2,\end{array}$$

(7)

and

$$\begin{array}{c}\hfill E_g^{\Gamma }\left(x,P,T\right)={\lambda }_1+{\lambda }_{2}x+{\lambda }_3{x}^2+aP-\frac{b{T}^2}{T_0+T},\end{array}$$

(8)

with ${\lambda }_1=1519$ meV, ${\lambda }_2=1360$ meV, ${\lambda }_3=220$ meV, $a=107$ meV/GPa, $b=0.5405$ meV/K and $T_0=204$ K.

These deformations in the effective mass of the electron in this material will be considered in the subsequent analyses. In the following, we will denote $m_{eff}(x,P,T)$ as $m_{eff}$ for the purpose of simplifying notation.

4. Quantum Revivals

Quantum revivals manifest when the wave function regains its initial configuration, marking what is termed a “revival” moment. The theory we consider assumes that the index n is discrete. Additionally, it is assumed that the wavefunction expansion is strongly weighted around a central value $n_1$ for the quantum number n [24]. It is shown in Ref. [25] that classical periods and quantum revival time are defined in terms of the energy difference between two adjacent states. The following correspondence is used for the first order: the first discrete derivative can be approximated by the second-order centered finite difference as

$$\frac{dE}{dn}\approx \frac{E_{n+1}-E_{n-1}}{2\Delta n}.$$

Consequently, in quantum systems characterized by a single quantum number n, the energy eigenvalues can be expanded around it, yielding the energy expressed as a Taylor series:

$$E_n\approx E_{n_1}+{\left(\frac{dE}{dn}\right)}_{n=n_1}(n-n_1)+\frac{1}{2}{\left(\frac{d^{2}E}{d{n}^2}\right)}_{n=n_1}{(n-n_1)}^2+\dots$$

(9)

This way, distinct time scales emerge [1,26]: the classical period is determined by

$$t=\frac{2\pi \hslash }{{\left(\frac{dE}{dn}\right)}_{n=n_1}}.$$

(10)

while the revival time is defined as

$$\tau =\frac{4\pi \hslash }{{\left(\frac{d^{2}E}{d{n}^2}\right)}_{n=n_1}}.$$

(11)

We could also include the third-order term which allows defining the quantum super-revival time. Let us set aside that case for now.

From these definitions, and considering the energies described above (Equations (2)–(5)), the classical periods and the revival times are obtained and described by the following:

$$t_{n,w}^{\left(1\right)}=4\frac{\pi m_{\mathit{eff}}{L}^2}{\hslash }{\left(2n{\pi }^2-4\frac{\pi pcos\left(n\pi p\right)}{f}\right)}^{-1},$$

(12)

$$\begin{array}{c}\hfill t_{n,w}^{\left(2\right)}=2\frac{{\pi }^3{m}_{\mathit{eff}}{L}^2{n}^3{f}^2}{\left(A_1+B_1+C_1-D_1+E_1\right)\hslash },\end{array}$$

(13)

with $A_1\equiv 4+{\pi }^4-8p\left(p-1/2\right){\pi }^2$, $B_1\equiv 2\left(\left(8p-2\right)sin\left(\pi p\right)+{\pi }^{2}p\right)\pi cos\left(\pi p\right)$, $C_1\equiv \left(-8+40p\left(p-1/2\right){\pi }^2\right){\left(cos\left(\pi p\right)\right)}^2$, $D_1\equiv 16sin\left(\pi p\right)\left(p-1/4\right)\pi {\left(cos\left(\pi p\right)\right)}^3$ and $E_1\equiv 4+{\pi }^4-8p\left(p-1/2\right){\pi }^2$,

$$\begin{array}{c}\hfill t_{n,str}^{\left(a\right)}=4\frac{\pi m_{\mathit{eff}}{L}^2}{\hslash }{\left(2\frac{n{\pi }^2}{p^2}+\frac{f\pi }{p^3}\right)}^{-1},\end{array}$$

(14)

$$\begin{array}{c}\hfill t_{n,str}^{\left(b\right)}=4\frac{\pi m_{\mathit{eff}}{L}^2}{\hslash }{\left(2\frac{n{\pi }^2}{{(1-p)}^2}+\frac{f\pi }{{(1-p)}^3}\right)}^{-1},\end{array}$$

(15)

$$\begin{array}{c}\hfill {\tau }_{n,w}^{\left(1\right)}=8\frac{\pi m_{\mathit{eff}}{L}^2}{\hslash }{\left(2{\pi }^2+4\frac{{\pi }^2{p}^{2}sin\left(n\pi p\right)}{f}\right)}^{-1},\end{array}$$

(16)

$$\begin{array}{c}\hfill {\tau }_{n,w}^{\left(2\right)}=4\frac{{\pi }^3{m}_{\mathit{eff}}{L}^2{n}^4{f}^2}{\left(A_2+B_2+C_2-D_2+E_2+F_2\right)\hslash }\end{array}$$

(17)

with

$$A_2\equiv -12+{\pi }^4{f}^2{n}^4+24p\left(p-1/3\right)n^2{\pi }^2,$$

$$B_2\equiv 2{\pi }^{4}sin\left(n\pi p\right)f{n}^4{p}^2,$$

$$C_2\equiv 80sin\left(n\pi p\right)\pi n\left(n^2{p}^2\left(p-1/2\right){\pi }^2-3/5p+1/10\right)cos\left(n\pi p\right),$$

$$D_2\equiv \left(24-120p\left(p-1/3\right)n^2{\pi }^2\right){\left(cos\left(n\pi p\right)\right)}^2,$$

$$E_2\equiv 128sin\left(n\pi p\right)\pi n\left(n^2{p}^2\left(p-1/2\right){\pi }^2-3/8p+1/16\right){\left(cos\left(n\pi p\right)\right)}^3,$$

$$F_2\equiv \left(-12+96p\left(p-1/3\right)n^2{\pi }^2\right){\left(cos\left(n\pi p\right)\right)}^4,$$

$$\begin{array}{c}\hfill {\tau }_{n,str}^{\left(a\right)}=4\frac{m_{\mathit{eff}}{L}^2{p}^2}{\pi \hslash }\end{array}$$

(18)

and

$$\begin{array}{c}\hfill {\tau }_{n,str}^{\left(b\right)}=4\frac{m_{\mathit{eff}}{L}^2{(1-p)}^2}{\pi \hslash }.\end{array}$$

(19)

In the case of weak coupling, the times depend both on this coupling and on the position of the impurity. This is not the case for strong coupling, which depends solely on the position of the impurity.

In the following analysis, we will graphically examine these times with respect to classical periods and revival times for an electron in the box without the delta potential and with the effective mass of electrons in GaAs at $x=T=P=0$, given by $m^{*}=0.067\times m_e$, where $m_e=9.11\times {10}^{-31}$ Kg is the electron mass in a vacuum. They are given, respectively, by the following:

$$T_0=2\frac{m^{*}{L}^2}{\pi \hslash n}$$

(20)

and

$${\tau }_0=4\frac{m^{*}{L}^2}{\pi \hslash }.$$

(21)

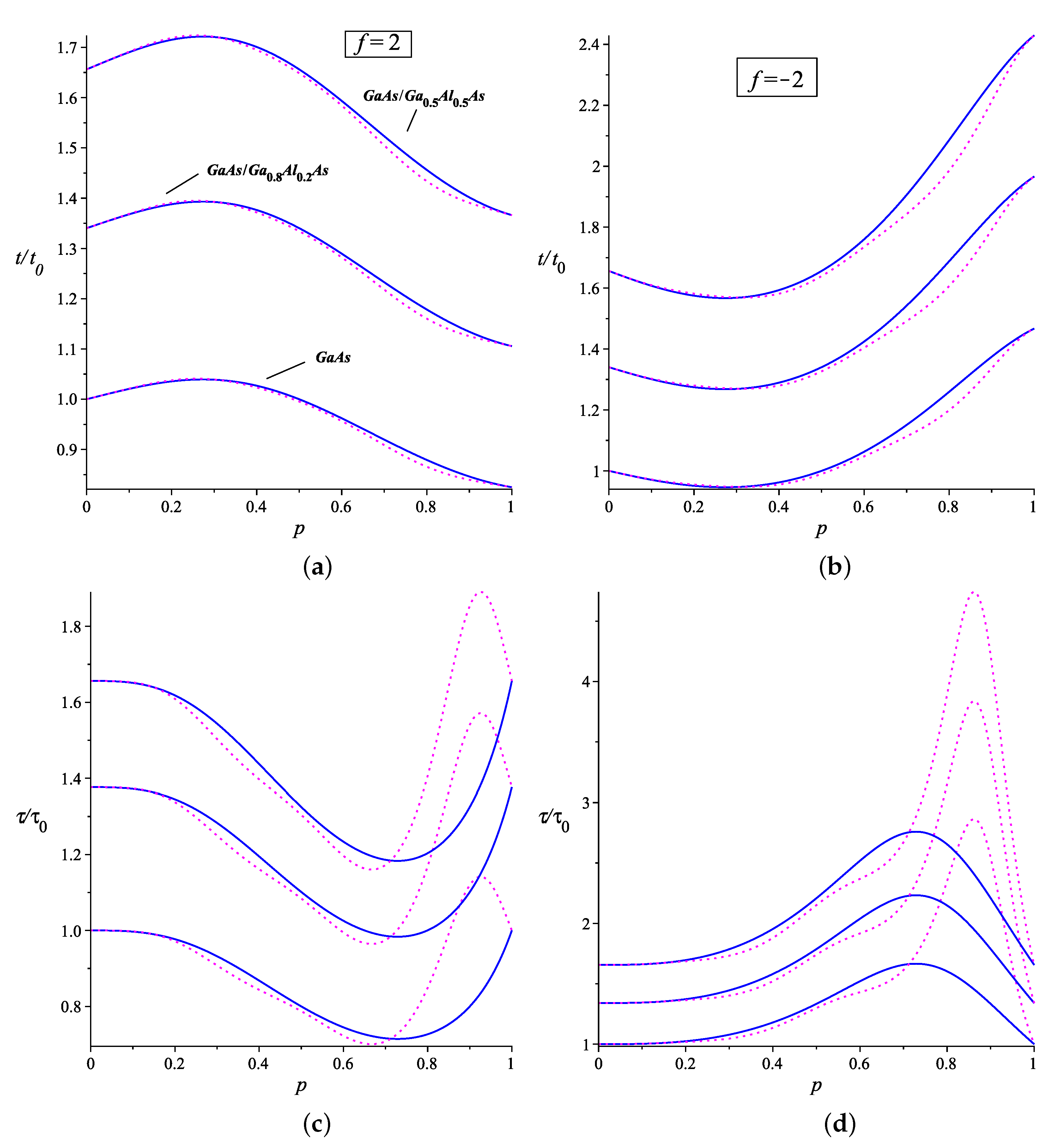
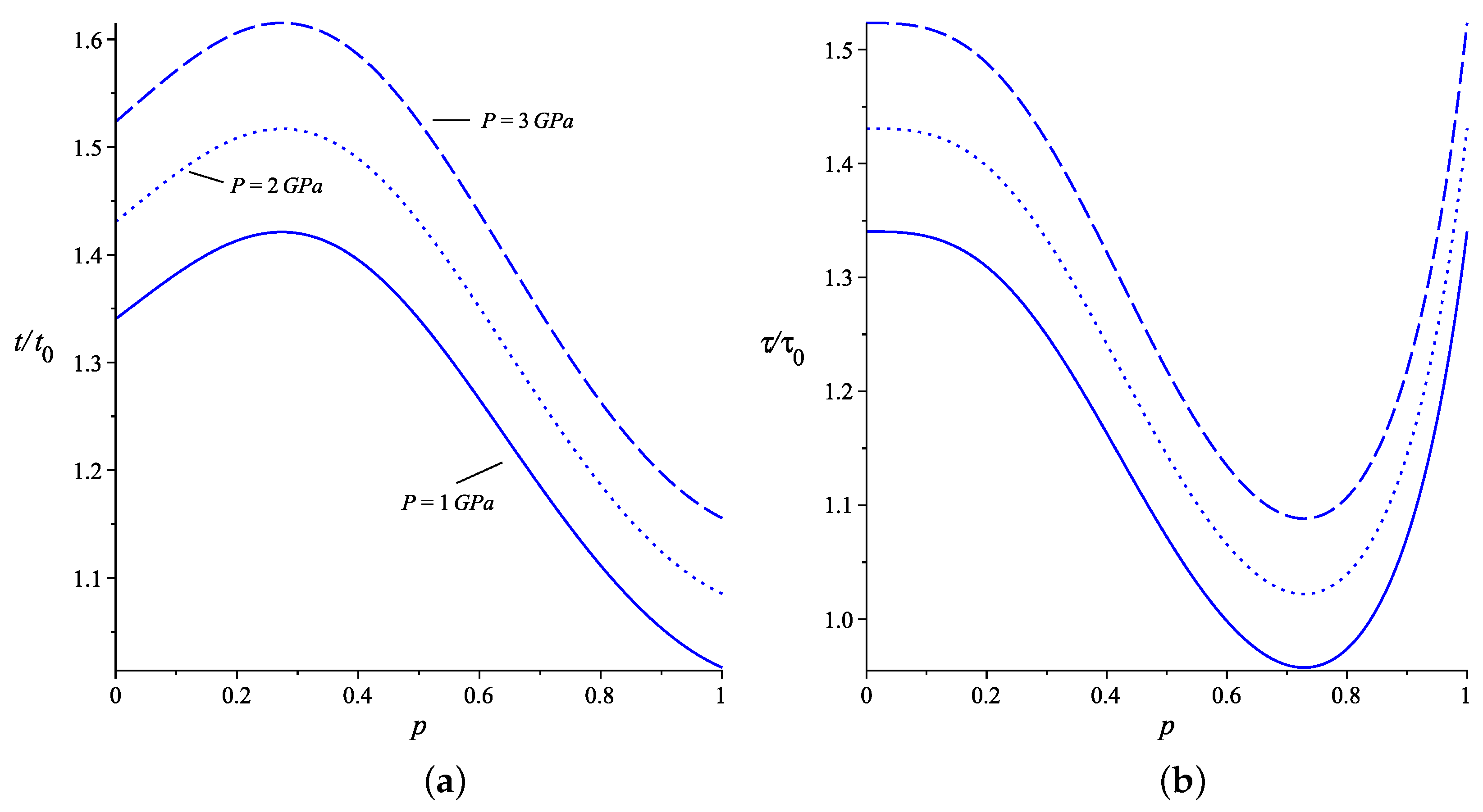
The energy levels are inversely proportional to the effective mass of the electron in the box. Therefore, any increase in its value results in increased calculated times, as they become proportional to it. We consider the case $n=1$, as this is the value of n for the largest values for these times. We analyze the classical periods and revival times versus the position of the impurity for the weak-coupling regime in Figure 2. As the concentration of Al increases, the profile of the graphs does not change, but the times are increased. The same occurs for an increase in hydrostatic pressure (see Figure 3). The effects of temperature on the effective mass are the least pronounced, so we will not plot them here. For $f=\pm 2$, the graphs show that the times behave non-monotonically as a function of the impurity’s position within the box and in the opposite way. For a classical period and $f=2$, the lowest value of time occurs when the impurity is close to the infinite wall on the right, while the highest value is near $p=0.3$. For $f=-2$, this behavior inverts. As for the revival time, the highest value occurs when the impurity approaches the infinite wall on the left, while the lowest value is near $p=0.7$. The inversion in this behavior is also observed for $f=-2$. Notice that the classical periods calculated from the energy derived from second-order perturbation theory deviate, in $0.6<p<1$, towards slightly smaller values compared to the case for first-order perturbation. For the revival time, there is a peak time near $p=0.9$, but perhaps this region may not represent a physical value to be observed. Including more terms in the expansion could correct this situation, but we leave this open-ended.

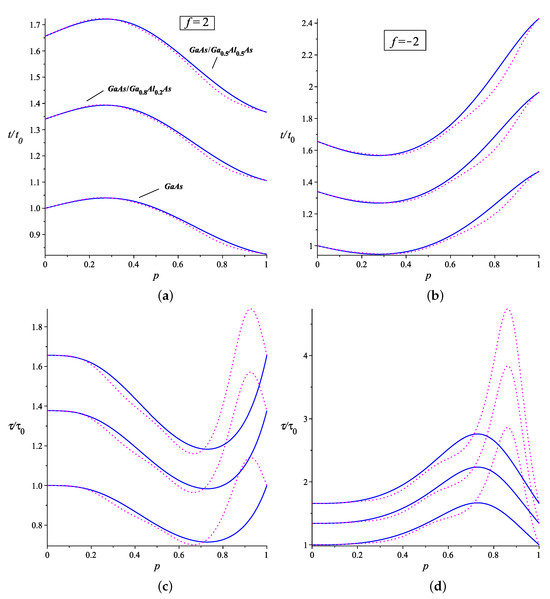
Figure 2. The plots show the changes in classical period (a,b) and revival times (c,d) versus the impurity position in the box, for weak coupling with an impurity. As the concentration of $Al$ increases, their profiles do not change, but the times shift to higher values. We considered $T=0.5$ K, $L=25$ nm and $n=1$. The blue solid lines take into account the first-order corrections to the energy eigenvalues, whereas the magenta dotted lines include corrections up to the second order.

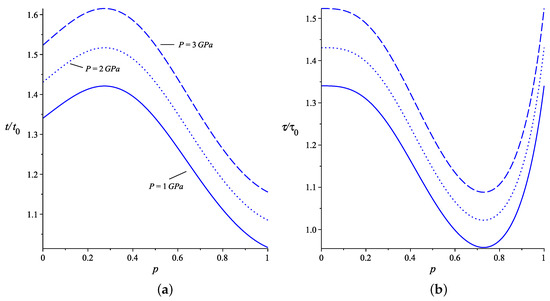
Figure 3. The plots show the changes in classical period (a), and revival times (b), versus the impurity position in the box for different hydrostatic pressure, for weak coupling with an impurity. As it increases, the times shift to higher values. We considered $GaAs/G{a}_{0.8}A{l}_{0.2}As$, with $f=2$, $T=0.5$ K, $L=25$ nm and $n=1$.

Turning our attention to the strong-coupling limit, for $f=\pm 0.01$, the times behave monotonically, but in opposite ways for the two distinct energy spectra, which depend on the chosen condition (see Figure 4). Where one reaches the highest time, the other reaches the lowest value, and vice versa. The times are the same for $p=0.5$. One additional detail is that changes in f do not affect these times. In the case of revival time, it does not depend on this parameter, while, for the classical period, it appears in a small term proportional to $p^3$, which will be irrelevant regardless of the value of f. Indeed, due to these details, both cases will behave similarly, proportional to $p^2$.

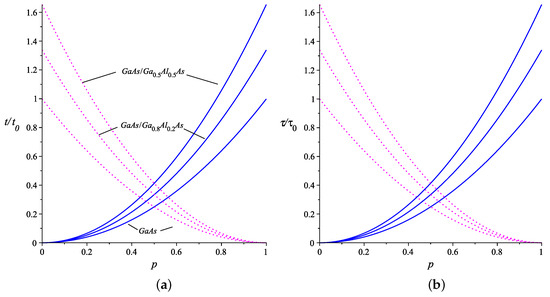
Figure 4. The plots show the changes in classical period (a), and revival times (b), versus the impurity position in the box for the strong coupling with an impurity. As the concentration of $Al$ increases, their profiles do not change, but the times shift to higher values. We considered $f=0.01$, $T=0.5$ K, $L=25$ nm and $n=1$. Solid blue lines are related to the eigenenergy (4) and dotted magenta lines to the eigenenergy (5).

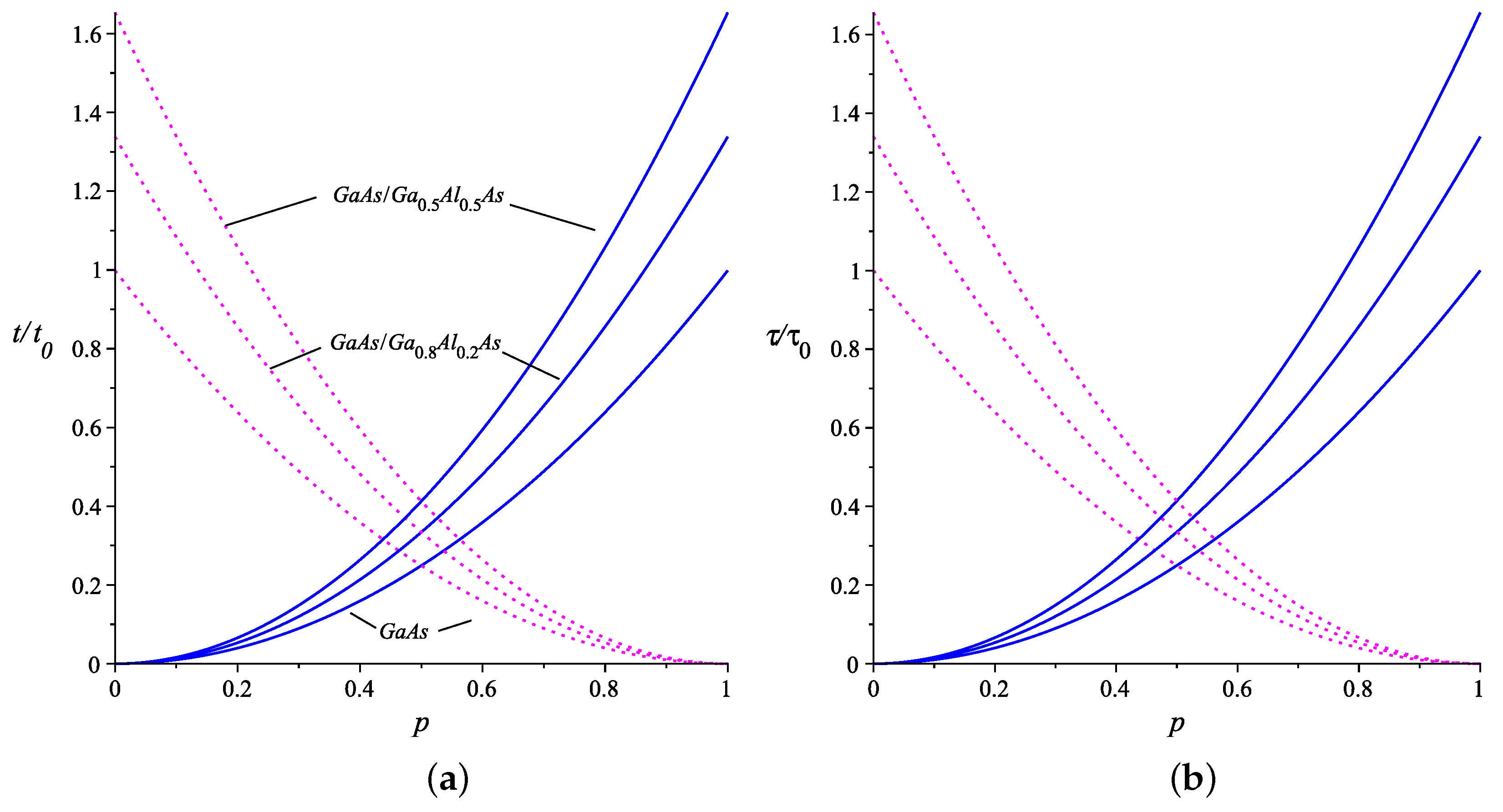
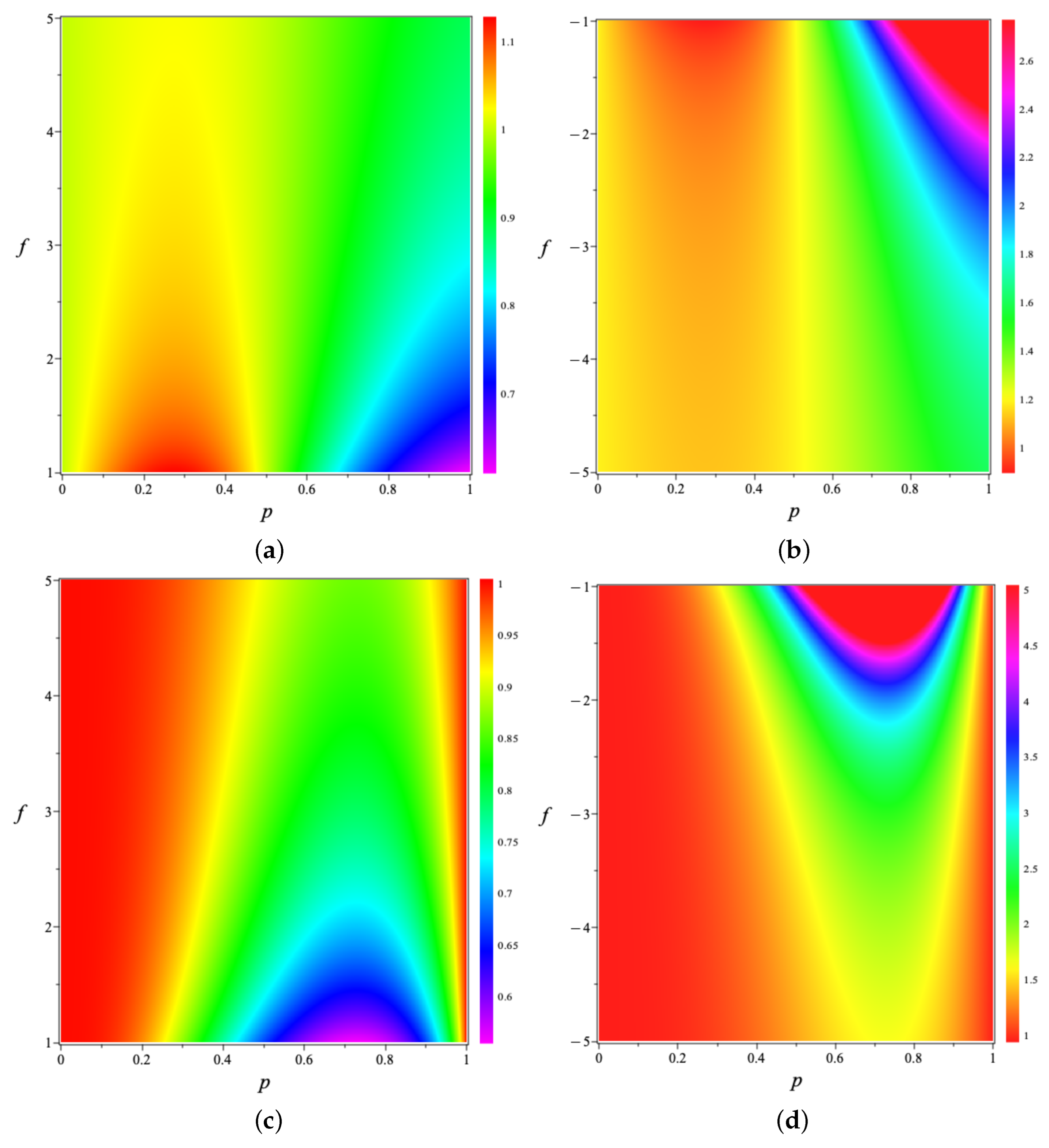
In Figure 5, we present a density plot of the calculated times for the first-order energy correction in the weak regime coupling with impurity. We show only the case for electrons in GaAs because altering the aluminum concentration, temperature and pressure results in an increase in effective mass, thereby increasing these times. For any other case, the profiles of these density plots remain the same. Firstly, we plotted the graphs for $f>\left|1\right|$ because, for f smaller than that up to $\left|0.5\right|$, the times have negative values and even divergences. Therefore, our study also suggests that the work [17] is better applied for values of this coupling constant $f>\left|1\right|$. As we can see, quantum revivals exhibit interesting behaviors for electrons in a quantum box, and the position of the impurity significantly affects them. From these plots, we observe that the classical periods and quantum revival times are either maximum or minimum in well-defined regions, depending on the values of f and p involved. In Figure 5a,c, which correspond to positive values of f, the orange regions indicate the maximum values of these times, while the purple regions indicate the minimum values. For negative f, Figure 5b,d, the red colors indicate the regions where the classical period and quantum revival times are maximum, while the orange regions indicate the minimum values for them.

Figure 5. The density plots of classical periods (a,b), and revival times (c,d), against the impurity position p and impurity strength f, in the weak-coupling regime. We consider $GaAs$. Changing the effective mass of the electron will keep their shapes consistent, but the color values will increase.

As mentioned, the aluminum concentration in the sample causes these times to increase, as does the increase in hydrostatic pressure. That is, raising the effective mass of the electron increases these times. They also depend on $L^2$, with L being the size of the box. We will not make a physical application here, but this study should be important and particularly relevant for the case of quantum heat engines based on this physical system as a working substance.

From an experimental standpoint, our work may extend beyond electronic systems, as exemplified by the case of a trapped, laser-cooled ion within the combined electrostatic harmonic potential of a Paul ion trap and a sinusoidal potential of an optical lattice [27]. This setup can simulate an infinite well with a $\mathsf{\delta }$ barrier [16]. In this particular case, the position of the impurity remains fixed. While this concept is proposed in work [18], it does not consider any time scale.

5. Concluding Remarks

In conclusion, the investigation presented in this work delves into the realm of quantum revivals in systems featuring confined quantum particles, particularly electrons in a quantum box with an impurity. By exploring both weak- and strong-coupling regimes, this study unveils intricate relationships between impurity position, impurity strength, and the resulting classical periods and revival times. Notably, the effective mass of the electron, influenced by factors such as aluminum concentration, temperature and hydrostatic pressure, plays a pivotal role in determining these temporal dynamics.

In the weak-coupling regime, the classical period and revival times exhibit nuanced behaviors as the impurity position varies within the box. Additionally, changes in aluminum concentration and hydrostatic pressure lead to shifts in these times, underlining the sensitivity of quantum revivals to external conditions. Similarly, in the strong-coupling limit, classical period and revival times display distinct trends depending on the chosen condition, emphasizing the complex interplay between impurity characteristics and temporal dynamics.

Moreover, the density plots provide insightful visualizations of these temporal phenomena, offering a comprehensive understanding of the intricate relationship between impurity parameters and quantum revival dynamics. What brought richness to the problem was the variation in the position of the impurity within the box, along with the deformations in the effective mass. This variation led to the results discussed based on the graphs investigated here. The maximum and minimum times were observed in regions of these graphs that showed the relationship between the position of the impurity and its intensity. This relationship should be used to optimize the system, depending on the desired application. Although no specific physical applications are discussed in this study, the findings hold potential implications for quantum heat engines and other quantum-based technologies, underscoring the relevance of understanding quantum revivals in confined quantum systems.

Overall, this investigation contributes valuable insights into the fundamental aspects of quantum mechanics, shedding light on the rich dynamics of quantum revivals and their dependence on impurity characteristics and external conditions. Future work perspectives include the need to investigate higher-dimensional systems, such as the use of electronic metamaterials [28], variable mass systems [29] and curvature effects [30], among other things. These aspects may lead to exploring the impacts of quantum revivals on optical and electronic properties [31], as well as investigating more elaborate versions of thermal machines with impurities beyond those discussed in [18], taking into account finite-time thermodynamics.