Abstract
We propose a novel dark-energy equation-of-state parametrization, with a single parameter that quantifies the deviation from CDM cosmology. We first confront the scenario with various datasets, from the Hubble function (OHD), Pantheon, baryon acoustic oscillations (BAO), and their joint observations, and we show that has a preference for a non-zero value, namely, a deviation from CDM cosmology is favored, although the zero value is marginally inside the 1 confidence level. However, we find that the present Hubble function value acquires a higher value, namely, Km s−1 Mpc−1, which implies that the tension can be partially alleviated. Additionally, we perform a cosmographic analysis, showing that the universe transits from deceleration to acceleration in the recent cosmological past; nevertheless, in the future, it will not result in a de Sitter phase since it exhibits a second transition from acceleration to deceleration. Finally, we perform the statefinder analysis. The scenario behaves similarly to the CDM paradigm at high redshifts, while the deviation becomes significant at late and recent times and especially in the future.
PACS:
98.80.-k; 95.36.+x; 98.80.Es
1. Introduction
The understanding of fundamental physics is challenged by the universe’s rapid expansion, which is the most exciting subject in modern cosmology. This phenomenon indicates that, contrary to popular belief, the cosmos is expanding faster with time. It was initially discovered in the late 20th century through observations of distant supernovae. Under the general relativistic framework, the first general class of explanation involves introducing new and exotic sectors in the universe content, under the umbrella term dark energy [1,2]. Extending the fundamental principles of gravity constitutes the second general class, in which case the cause of acceleration is of gravitational origin [3,4,5,6,7].
Nevertheless, at the phenomenological level, both approaches can be quantified through the (effective) dark-energy equation-of-state parameter . Thus, introducing various parametrizations of allows us to describe the universe’s evolution and confront with observational datasets to reveal the required dark-energy features to obtain agreement. Several researchers have embraced a phenomenological strategy for modeling the equation of state (EoS) parameter, representing it as a function of redshift, denoted as [8], or equivalently as a function of the cosmic scale factor [9,10]. This methodology streamlines the examination of dark energy (DE) dynamics and enables the exploration of physically significant functions. However, during data fitting, it becomes necessary to simplify the parameterization of the equation of state and subsequently restrict the evolution of based on the parameters we introduced in our parametrization. In particular, starting from the simple cosmological constant, a large number of parametrizations have been introduced in the literature, involving one parameter [11,12] or two parameters, such as the Chevallier–Polarski–Linder (CPL) parametrization [13,14], the linear parametrization [15,16,17], the logarithmic parametrization [18], the Jassal–Bagla–Padmanabhan parametrization (JBP) [19], the Barboza–Alcaniz (BA) parametrization [20], problem at low reshift [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50], etc. Additionally, note that one can impose the parametrization at the deceleration parameter level [51,52,53], at the equation-of-sate (EoS) parameter level [54], or even at the Hubble parameter level [55,56,57,58].
In the present manuscript, we propose a novel dark-energy equation-of-state parametrization, with a single parameter that quantifies the deviation from CDM cosmology. Additionally, under this scenario, dark energy behaves like a cosmological constant at high redshifts, while the deviation becomes significant at low and recent redshifts, especially in the future. Finally, for , we recover the CDM cosmology completely. As we will see, apart from being capable of fitting the data, the new parametrization can partially alleviate the tension too since it leads to a value in between the Planck one and the one from direct measurements [59,60]. Recently, several authors have conducted so many remarkable works regarding the measurements of obtained from cosmological probes for different redshifts, such as a bias-free cosmological analysis with quasars alleviating tension [61]; new statistical insights and cosmological constraints consisting of gamma-ray bursts, quasars, baryonic acoustic oscillations, and supernovae Ia [62]; reduced uncertainties up to on the Hubble constant and the matter density with the SNIa with a new statistical analysis [63]; on the Hubble constant tension in the SNIa Pantheon sample [64]; on the evolution of the Hubble constant with the SNIa Pantheon sample and baryon acoustic oscillations: a feasibility study for GRB-cosmology in 2030 [65]; and gravity in the Jordan frame as a paradigm for the Hubble tension, in which the authors provides a subsequent interpretation of the results through an effective Hubble constant that evolves with the redshift in a modified gravity theory in the Jordan frame [66].
The article is organized as follows. In Section 2, we present the novel dark-energy parametrization. Then, in Section 3, we perform a detailed confrontation with observations, namely, with Hubble function (OHD), Pantheon, and baryon acoustic oscillations (BAO) data. In Section 4, we perform a cosmographic analysis, and we apply the statefinder diagnostic. Finally, Section 5 is devoted to the conclusions. Lastly, the details of the various datasets and the corresponding fitting procedure are given in the Appendix A.
2. New Single-Parameter Equation-of-State Parametrization
In this section, we first briefly review the basic equations of any cosmological scenario, and then we introduce the new parametrization for the dark-energy equation of state, with just a single parameter. We consider the usual homogeneous and isotropic Friedmann–Robertson–Walker (FRW) metric
with the scale factor and K the spatial curvature parameter ( for spatially flat, open, and closed universe, respectively). Furthermore, we consider that the universe is filled with baryonic and dark matter, radiation, and effective dark-energy fluid. Hence, the Friedmann equations that determine the background evolution of the universe are
where G is the gravitational constant, and is the Hubble function, with dots marking time derivatives. The total energy density and pressure are thus given as and , where the subscripts stand respectively for radiation, baryon, cold dark matter, and dark energy. As usual, and without loss of generality, we focus on the spatially flat case, and therefore in the following we impose . Finally, assuming that the various sectors do not interact mutually, we deduce that they are separately conserved, following the conservation equations
where . In the above expression, we have introduced the equation-of-state parameter of each fluid as , which yields
We proceed by providing, for completeness, the evolution equations of the universe at the perturbation level. In the synchronous gauge, the perturbed metric reads as
with as the conformal time, and where and denote the unperturbed and the perturbed metric parts (with the trace). Perturbing additionally the universe fluids and transforming to the Fourier space, we finally extract [67,68,69]:
with primes denoting the conformal-time derivative and with denoting the conformal Hubble function, and where k is the mode wave number. Moreover, stands for the over density of the i-th fluid, marks the divergence of the i-th fluid velocity, and is the corresponding anisotropic stress. Lastly, is the adiabatic sound speed given as .
Let us now introduce the new dark-energy parametrization. As usual, knowing the equation of state of a fluid allows us to extract its time evolution by solving Equation (4). For radiation, we have , and thus we obtain (setting the scale factor at present to 1), while for the baryonic and dark matter, we have , which leads to and , where stands for the present density value of the i-th fluid. Concerning the equation-of-state parameter of the dark-energy sector, since it is unknown, as we mentioned in the Introduction, one can consider various parametrizations. Focusing on the barotropic fluid sub-class, we consider that it is a function of time only, or equivalently, of the scale factor a, i.e., . Hence, the solution of the EoS Equation (5) leads to
In this work, we consider a novel dark-energy equation-of-state parameter (5) as follows:
where is the single parameter. Hence, introducing for convenience the redshift z as the independent variable (where ), the above relation becomes
Relation (11) is the parametrization that we propose, and in the case , we recover the CDM concordance model, where and , but in the general case, the parameter quantifies the deviation from the CDM scenario. However, note that for general , for large redshifts, i.e., for , we acquire , which implies that the deviation from the CDM scenario disappears in this regime, and thus, the Big Bang nucleosynthesis bounds are immediately satisfied.
Inserting the above parametrization in the first Friedmann Equation (2), we obtain
where is the present value of the Hubble parameter, and where we have introduced the present values of the density parameters (hence, the present value of the total matter density parameter is ). This expression allows us to investigate the cosmological evolution in detail, and confront it with observational datasets. Actually, expression (12), which is a simple deviation from CDM cosmology only at small redshifts, while it recovers CDM scenario at high redshifts, was the motivation behind parametrization (10).
Lastly, from parametrization (11) and the corresponding Hubble function (12), we can straightforwardly calculate various quantities. In particular, the deceleration parameter is given by
while the higher-order cosmographic parameters [70] read as
Similarly, for the matter and dark-energy density parameters, we obtain
and
3. Observational Constraints
In the previous section, we proposed a new parametrization for the dark-energy equation of state, given by (11), which has a single parameter, namely, . In this section, we perform a detailed confrontation with various datasets [71,72,73,74,75], focusing on the bounds of . In particular, we will use data from (i) Hubble function observations (OHD) with 77 data points [76], (ii) Pantheon with 1048 data points [77], and (iii) baryon acoustic oscillations (BAO). The details of the datasets and the corresponding methodology are given in the Appendix A. In our analysis, we use the following priors: , , and .
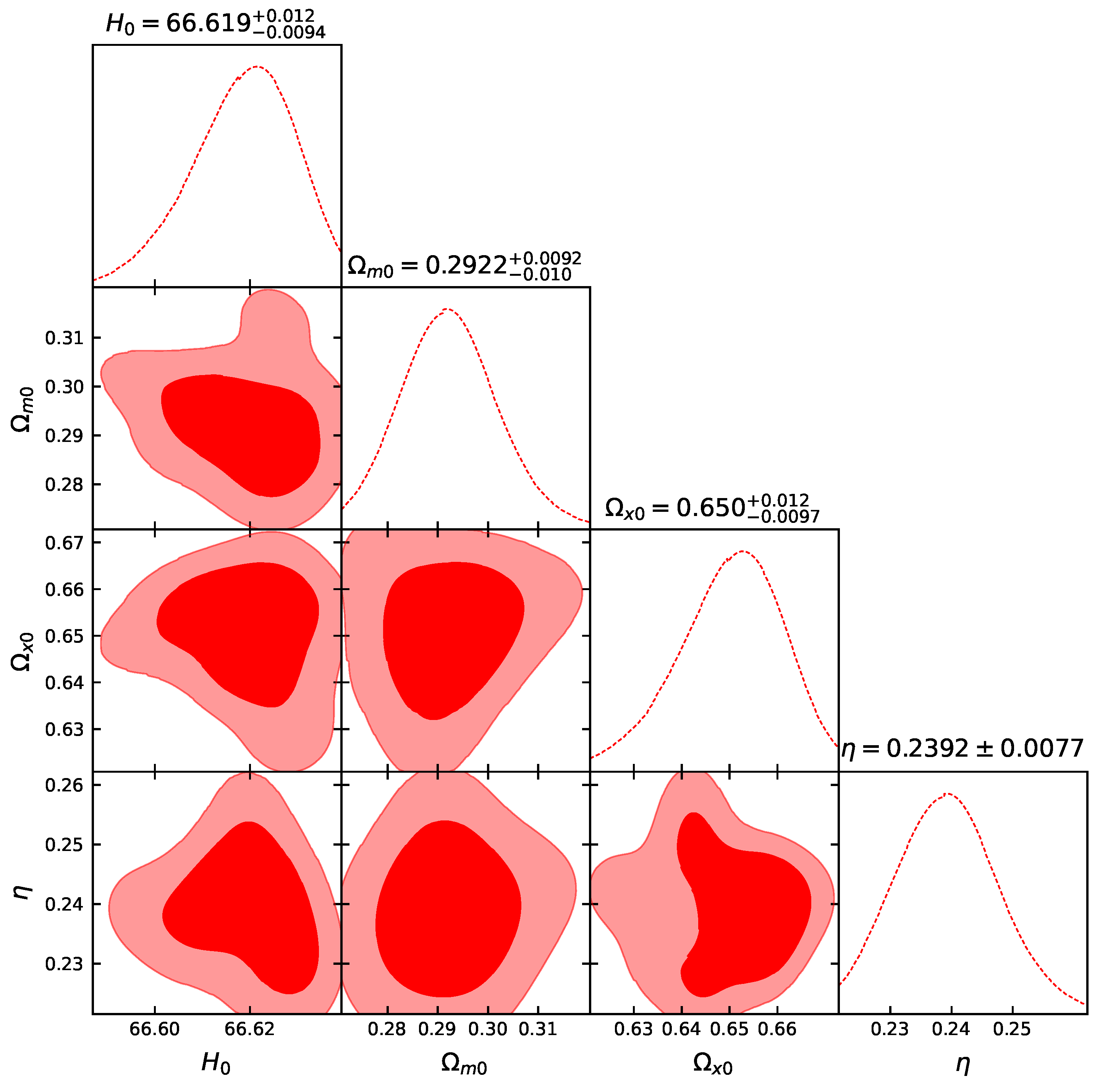
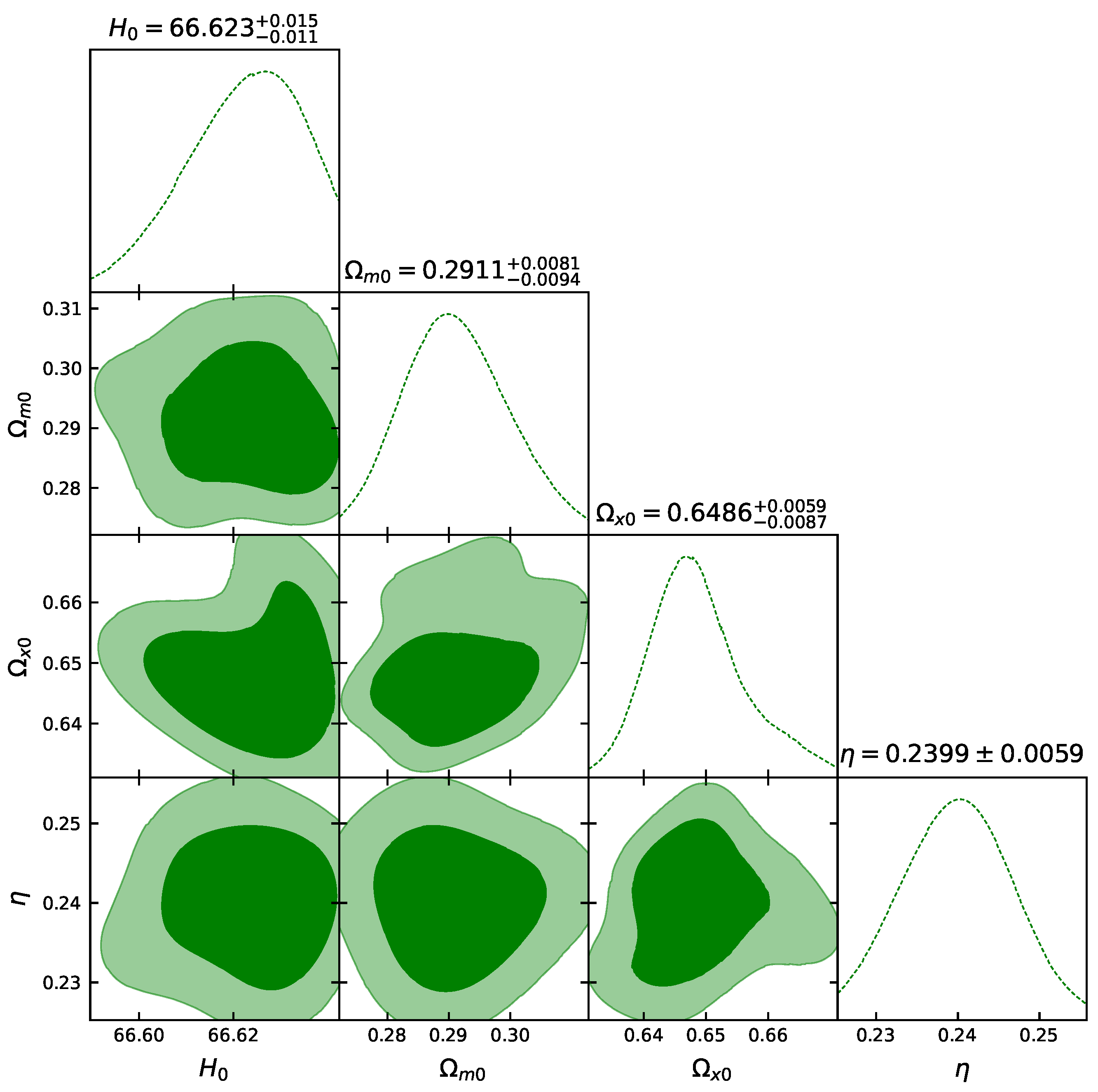
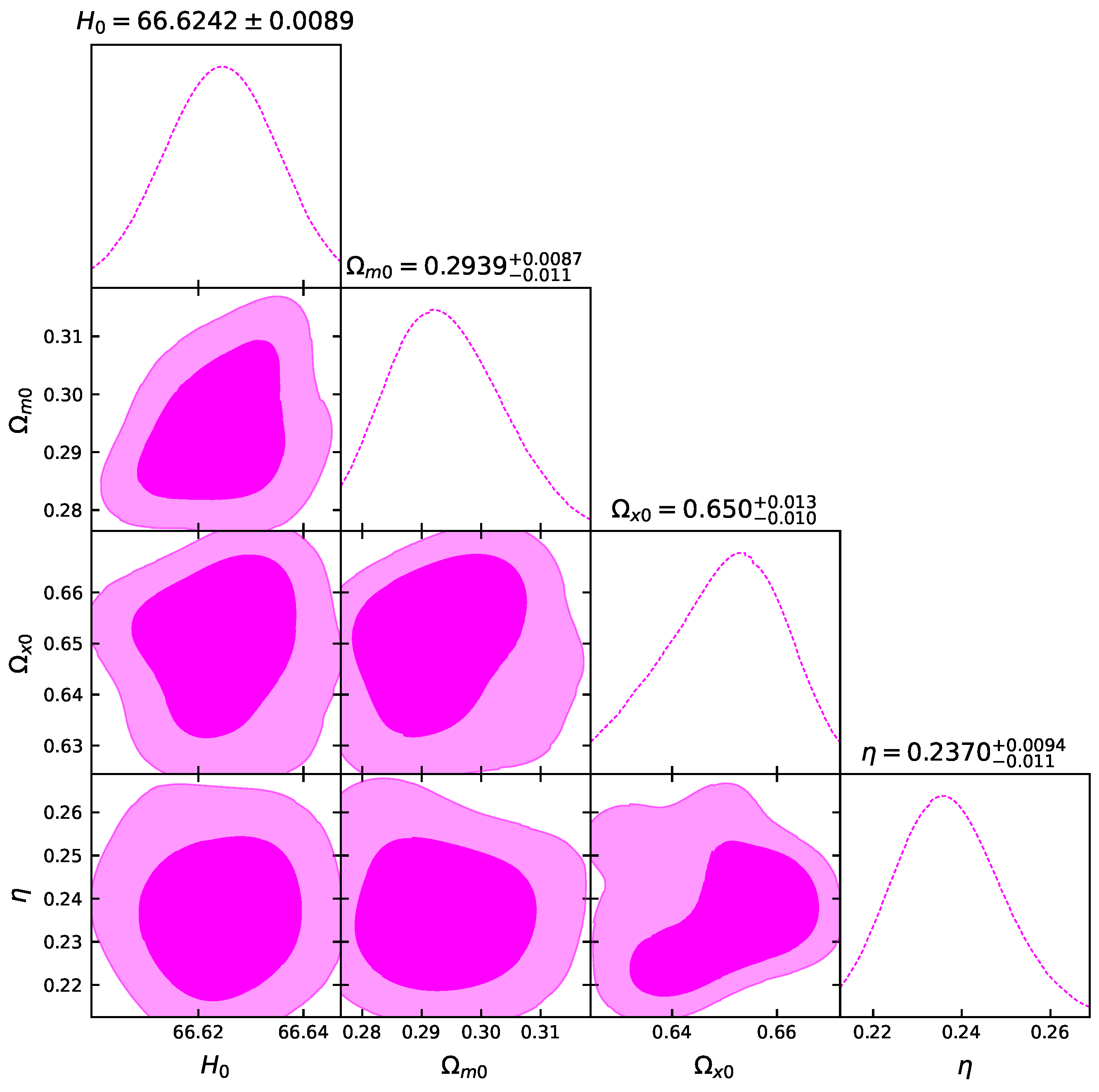
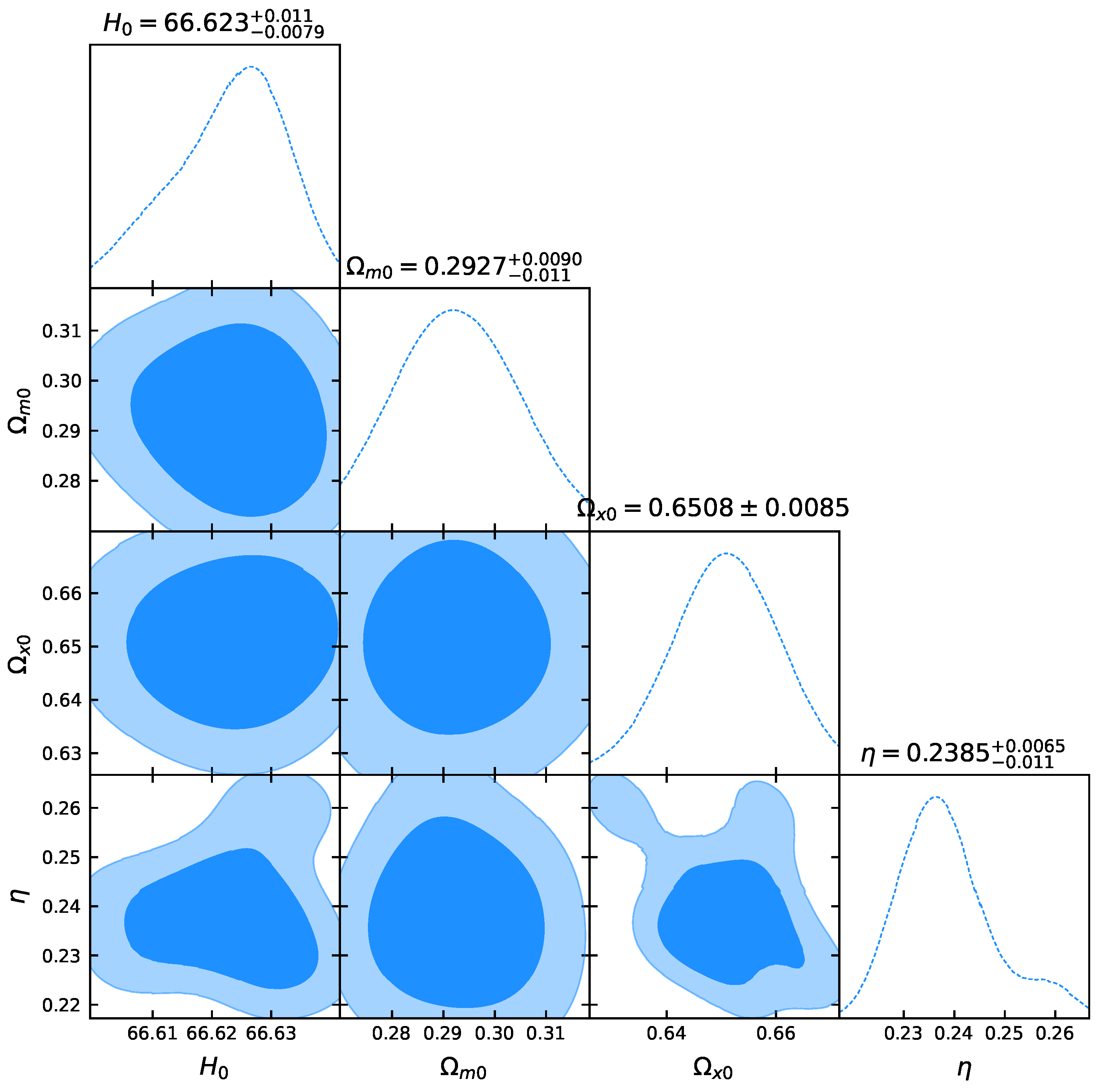
Let us now present the constraints we obtain after applying the above formalism and datasets in the Friedmann equations at hand, focusing on the new model parameter . In Figure 1, Figure 2, Figure 3 and Figure 4, we present the likelihood contours with and confidence levels, around the best-fit values. Additionally, in Table 1, we summarize the obtained results. Finally, in Table 2, we summarize other cosmological parameters, such as the density parameters and the deceleration parameter, the equation-of-state parameters, and the transition redshift.
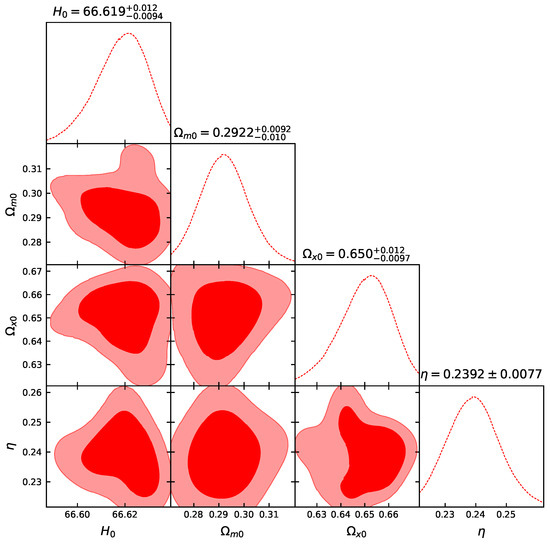
Figure 1.
The likelihood contours, with and confidence levels, for the dataset.
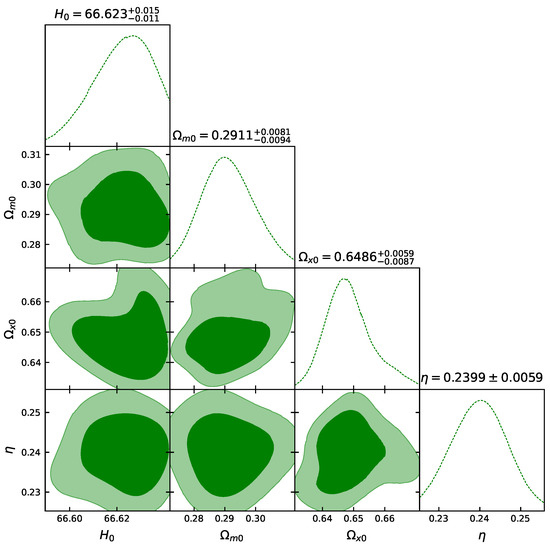
Figure 2.
The likelihood contours, with and confidence levels, for the dataset.
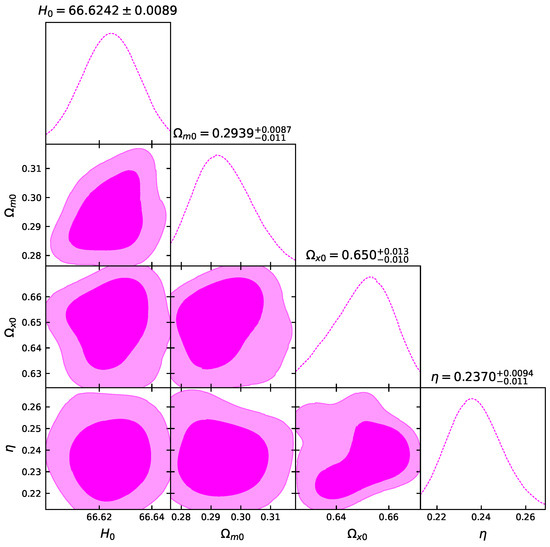
Figure 3.
The likelihood contours, with and confidence levels, for the data.
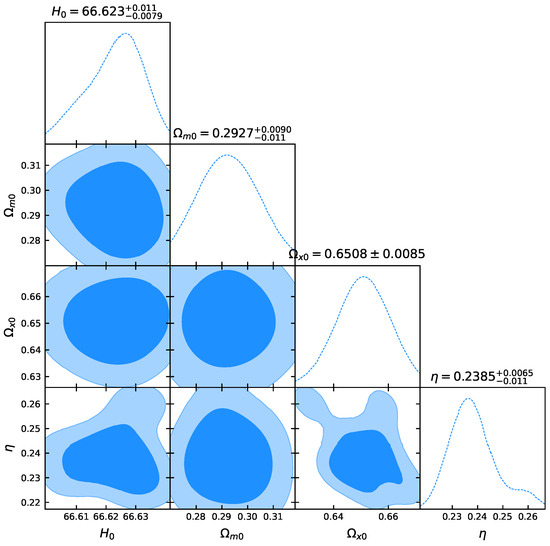
Figure 4.
The likelihood contours, with and confidence levels, for the data.

Table 1.
Summary of the observational constraints on the model parameters , , and from various datasets.

Table 2.
Summary of the constraints on the deceleration parameter q, the transition redshift and the current value of the dark-energy equation-of-state parameter .
As we observe, the new model parameter that quantifies the deviation from CDM cosmology has a preference for a non-zero value, although zero is marginally inside the 1 confidence level. Concerning , we observe that we obtain a higher value compared to the CDM scenario, although a bit lower than the direct measurements Km s−1 Mpc−1 at CL, based on the supernovae calibrated by Cepheids [59], which implies that the new dark-energy parametrization at hand can partially alleviate the tension. This is an additional result of the present work.
Figure 2 is plotted using the Pantheon dataset comprising 1048 data points, and a full covariance matrix is used. In the case of Figure 2, we notice that the shape of the contour is not oval, i.e., the posterior distribution for behaves as a bimodal distribution, and therefore we need to test the convergence for the Pantheon dataset. The Gelman–Rubin convergence test [78] is one of the statistical tools in Bayesian inference that is widely used to access the convergence of the chains. The test is based on the idea that multiple MCMC chains with different starting points should converge to the same posterior distribution if they have been run for long enough, that is, after several steps. Essentially, this test evaluates, for each parameter of the discussed model, the term called potential scale reduction , which is the ratio between the variance within a chain and the variance Var() among the chains:
Also, in the likelihood contour of the Pantheon dataset, there is a possibility of for the value and for the value within 100 steps of burn-in, which were used to run the MCMC chains.
The maximum Gelman–Rubin diagnostic across the model parameters is labeled as Max Gelman–Rubin in the header and is less than . Refs. [78,79] suggest that diagnostic values greater than for any of the model parameters should indicate non-convergence. The contour plots in the plane with and errors are given in Figure 2, and the corresponding best-fit values of , and for different datasets are given in Table 1.
4. Cosmographic Analysis and Statefinder Diagnostic
In this section, for completeness, we perform the cosmographic analysis of the cosmological scenario with the new dark-energy parametrization, and we apply the statefinder diagnostic. For simplicity, we neglect the radiation sector.
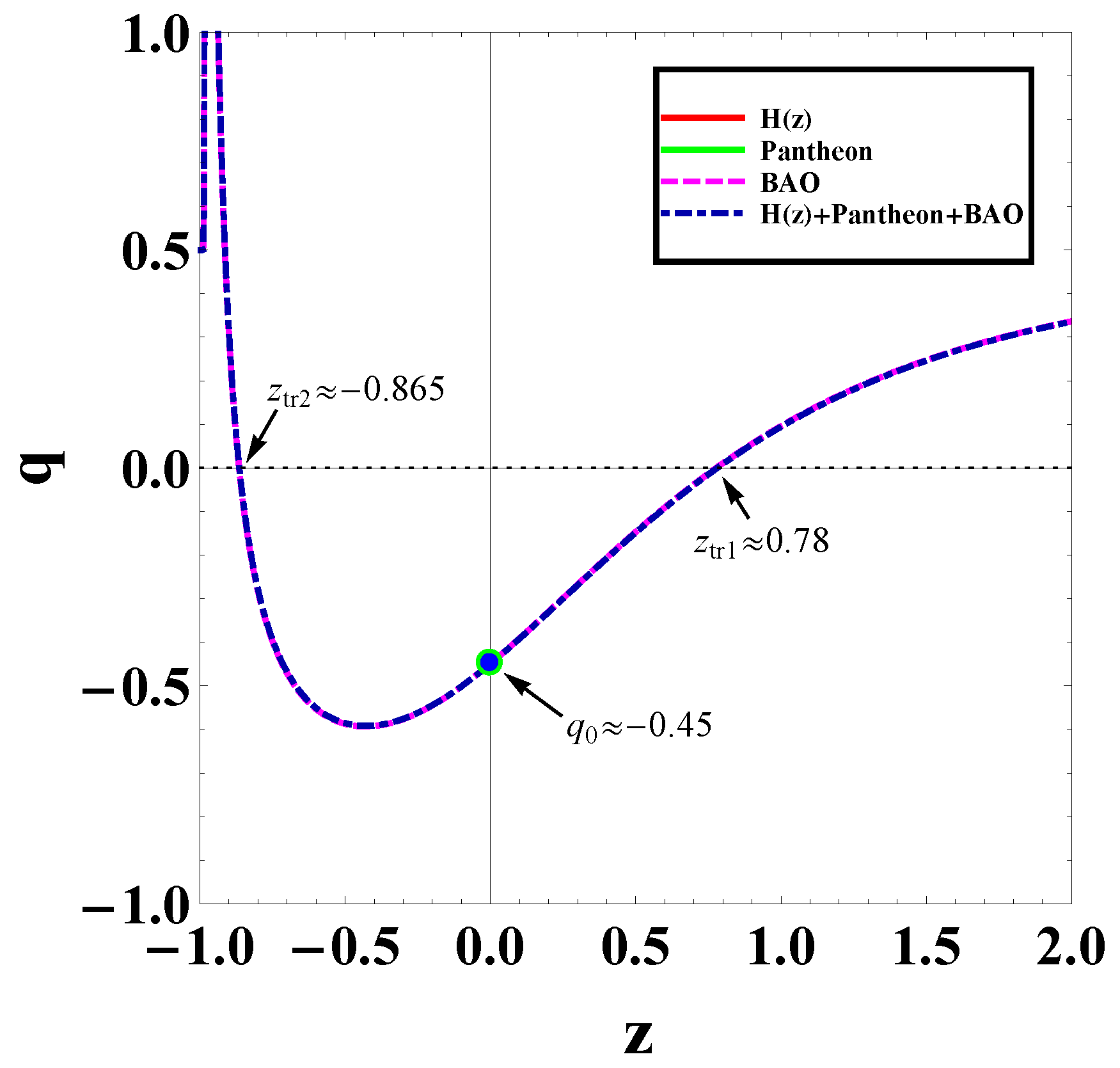
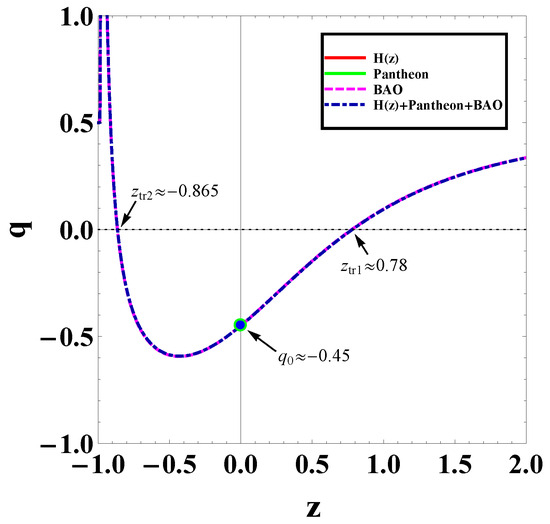
Let us start with the deceleration parameter given in (13). Using the best-fit values of the model parameters given in Table 1 and Table 2, we plot in Figure 5. As we can see, we obtain the transition from deceleration to acceleration at the transition redshift in agreement with observations. However, it is interesting to note that the novel parametrization at hand will lead to a second transition in the future, at redshift , from acceleration to deceleration (at around ).
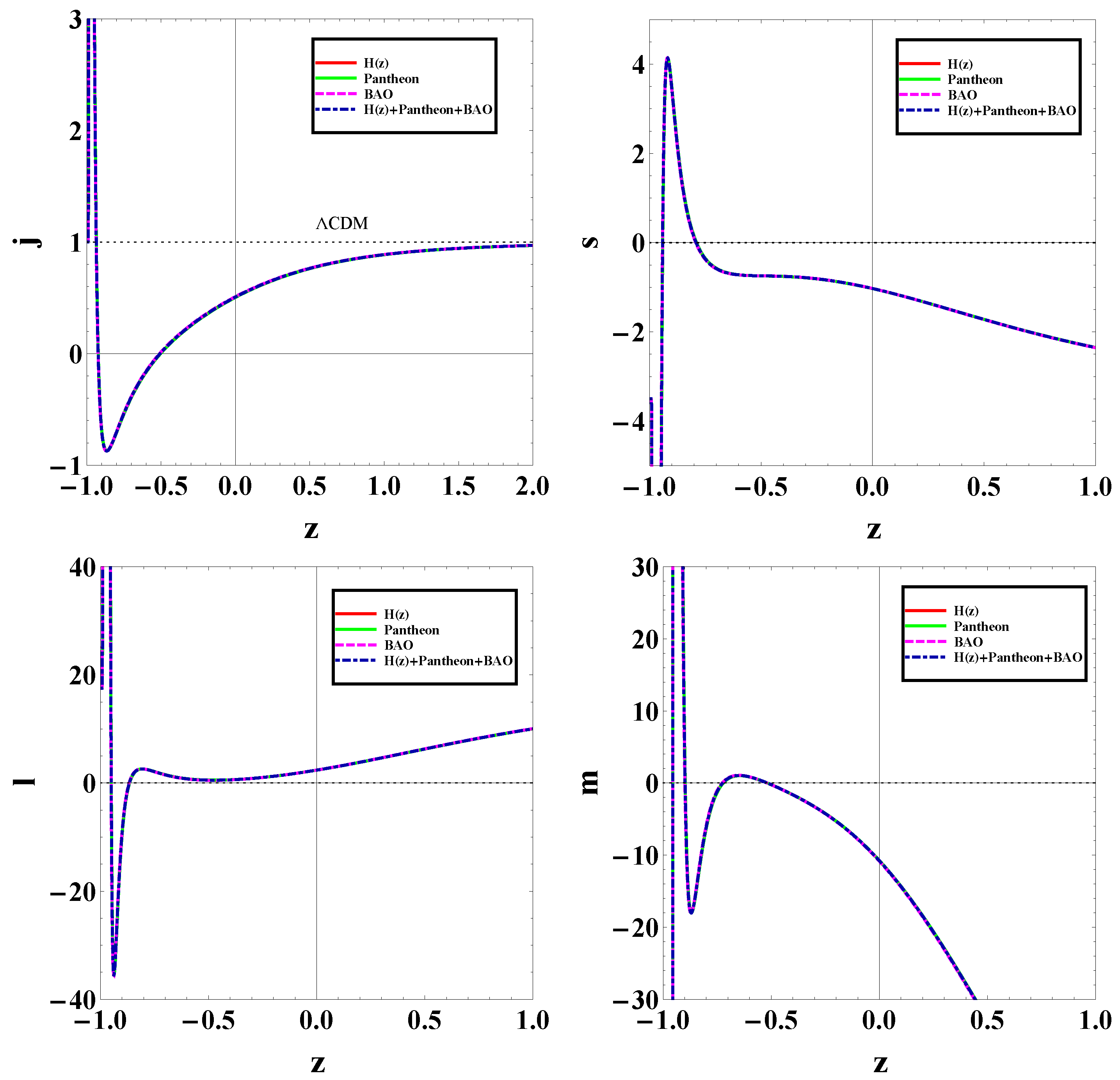
We proceed to the examination of the other cosmographic parameters given in Equations (14)–(17). In particular, we use the best-fit values of the model parameters given in Table 1 and Table 2, and in Figure 6, we present their evolution. Additionally, in Table 3 we summarize their values at present. Since in the CDM paradigm, the value of the jerk parameter is equal to unity (), the deviation from quantifies the deviation of a dark-energy scenario from the concordance model. Again, we find that the new proposed dark-energy parametrization behaves similarly to CDM scenario at high redshifts, while the deviation becomes more significant at late and recent times, and especially in the future. Finally, the same features can be obtained from the evolution of the snap s, lerk l, and m parameters.
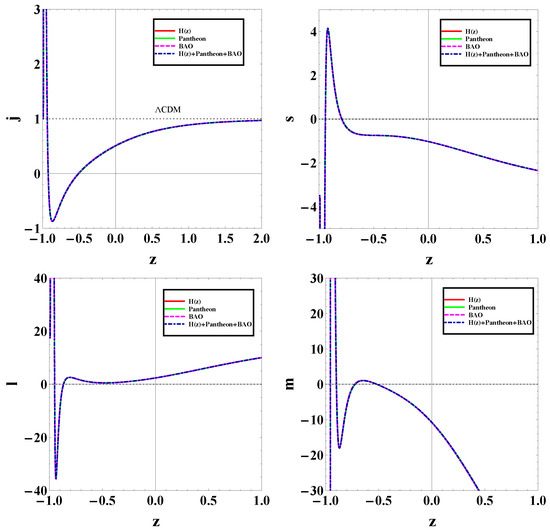

Table 3.
Summary of the constraints on the present values of the cosmographic parameters, namely jerk j, snap s, lerk l and m parameters, as well as on the present values of the statefinder diagnostic parameters r and .
Let us now come to the statefinder diagnostic, which is based on higher derivatives of the scale factor [80,81,82]. In particular, one introduces a pair of geometrical parameters in order to examine the dynamics of different dark-energy models [83,84]. The pair of parameters are defined as:
with . For our parametrization (9), the expression for r is found to be
where
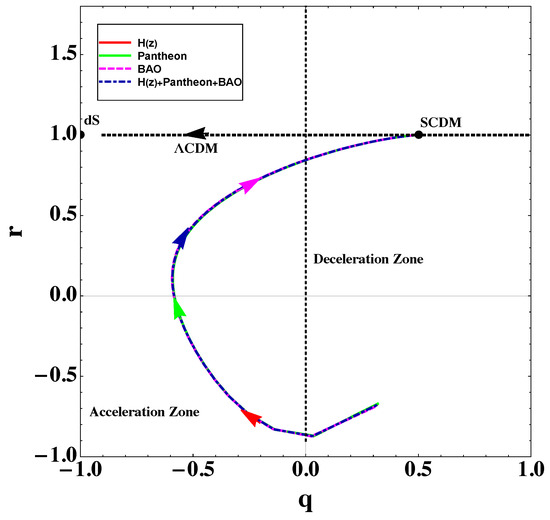
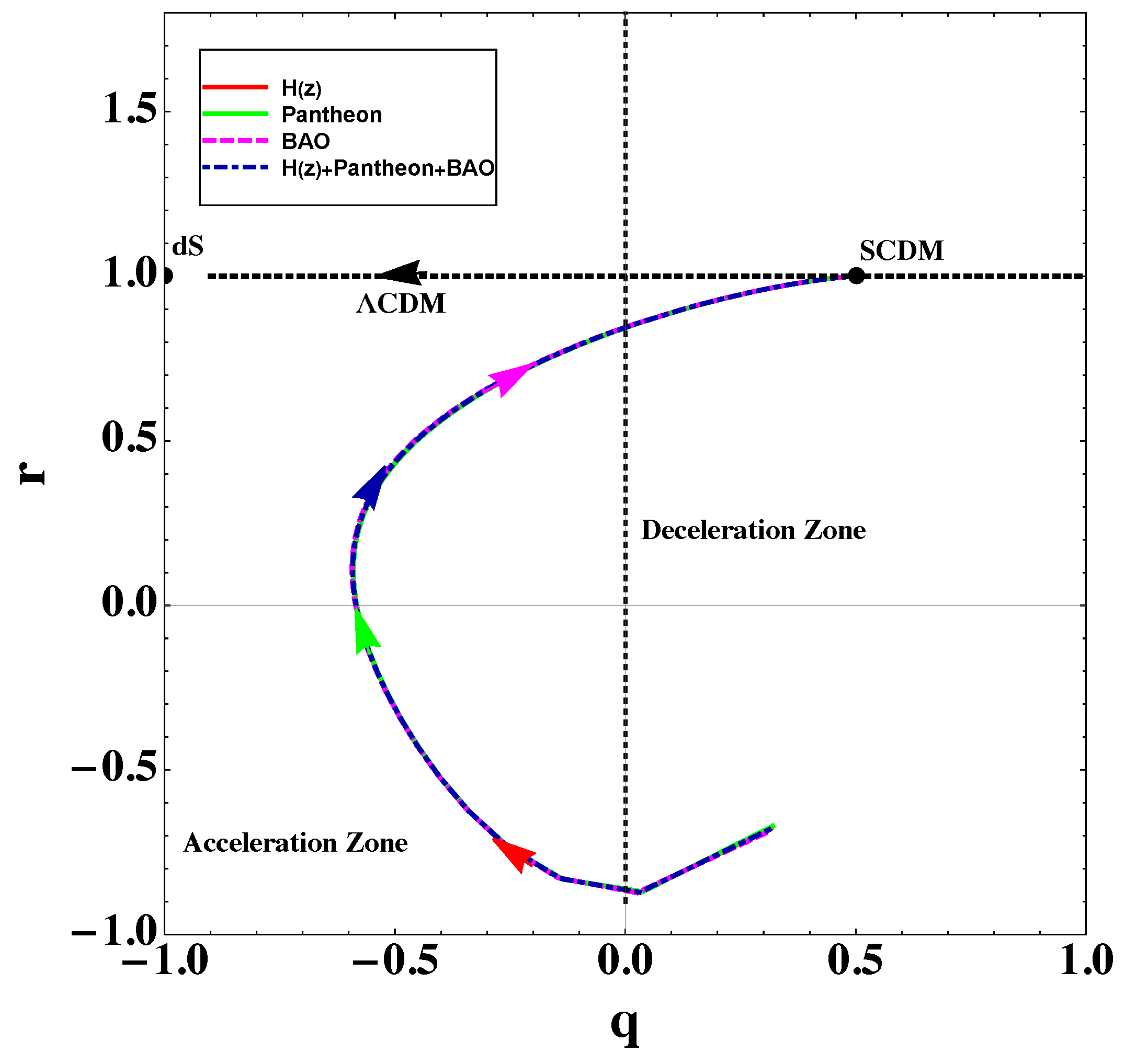
In Figure 7, we present trajectories for different observational datasets in the plane. As we can see, all trajectories start from the decelerating zone, enter into the accelerating zone behaving close to CDM at present, and in the far future, they converge to the CDM model without a cosmological constant (namely, the model) without resulting to the de Sitter () phase. The present values of parameters of the statefinder diagnostic are also given in Table 3. As we can see, the new parametrization at hand at high redshifts behaves like CDM, while the deviation appears at small redshifts and present time.
5. Conclusions
In this work, we proposed a novel dark-energy equation-of-state parametrization, with a single parameter that quantifies the deviation from CDM cosmology. Firstly, we confronted the scenario with various datasets, from the Hubble function (OHD), Pantheon dataset, baryon acoustic oscillations (BAO) observations, and their joint dataset, and we presented the corresponding likelihood contours. As we saw, the new model parameter has a preference for a non-zero value, namely, a deviation from CDM cosmology is favored, although the zero value is marginally inside the 1 confidence level. However, interestingly enough, we found that acquires a higher value compared to the CDM scenario, which implies that the new dark-energy parametrization at hand can partially alleviate the tension.
Additionally, we performed a cosmographic analysis, examining the cosmographic parameters, namely, deceleration q, jerk j, snap s, lerk l, and m parameters. As we showed, in the scenario at hand, the universe transits from deceleration to acceleration in the recent cosmological past; however, in the future it will not result in a de Sitter phase since a second transition (at ) will lead from acceleration to deceleration. Additionally, we found that the scenario behaves similarly to the CDM paradigm at high redshifts, while the deviation becomes significant at late and recent times (and thus, the tension is alleviated), and especially in the future.
Finally, we performed a statefinder diagnostic analysis. As we saw, all trajectories start from the decelerating zone, enter into the accelerating zone behaving close to CDM at the present time, while in the far future, they converge to deceleration without resulting in the de Sitter phase.
In summary, the new parametrization of the dark-energy equation of state with a single parameter is efficient in describing the data, as well as being able to alleviate the tension. Hence, it would be worthy to proceed to more detailed investigations, such as examining it at the perturbation level, and in particular, relating to the tension. Such an analysis will be performed in a separate project.
Author Contributions
Conceptualization, J.K.S.; methodology, J.K.S. and H.B.; software, P.S. and H.B.; validation, P.S., H.B. and S.M.; formal analysis, J.K.S., H.B. and E.N.S.; investigation, J.K.S. and E.N.S.; data curation, J.K.S. and H.B.; writing—original draft preparation, J.K.S. and E.N.S.; writing—review and editing, J.K.S. and E.N.S.; visualization, P.S. and H.B.; supervision, J.K.S. and E.N.S.; project administration, J.K.S. and E.N.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All data used in this work were taken from published papers of other groups, publicly available, and were given proper credits.
Acknowledgments
J. K. Singh wishes to thank M. Sami and S. G. Ghosh for the fruitful discussions. The authors also express their thanks to the referees for their valuable comments and suggestions.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Observational Data
In this appendix, we present the observational datasets we use in our analysis, and we provide the relevant methodology and the corresponding .
Appendix A.1. H(z) Data
In the case of observational Hubble data (OHD), the corresponding of the maximum likelihood analysis is given by
where is evaluated at redshift , while and represent the theoretical and observed values, and is the standard deviation. The detailed data, namely, the 77 points, are given in Table A1 below.

Table A1.
The 77 Hubble parameter data from measurements used in the present analysis in units of . Method (a) corresponds to the cosmic chronometric method, method (b) to the signal in the galaxy distribution, and method (c) to the signal in the forest distribution alone, or cross-correlated with .
Table A1.
The 77 Hubble parameter data from measurements used in the present analysis in units of . Method (a) corresponds to the cosmic chronometric method, method (b) to the signal in the galaxy distribution, and method (c) to the signal in the forest distribution alone, or cross-correlated with .
| z | (km/s/Mpc) | Method | Reference |
|---|---|---|---|
| 0.00 | 69.1 ± 1.3 | a | [85] |
| 0.07 | 70.4 ± 20 | a | [86] |
| 0.07 | 69.0 ± 19.6 | a | [86] |
| 0.09 | 70.4 ± 12.2 | a | [87] |
| 0.10 | 70.4 ± 12.2 | a | [86] |
| 0.120 | 68.6 ± 26.2 | a | [86] |
| 0.12 | 70.0 ± 26.7 | a | [85] |
| 0.170 | 83.0 ± 8 | a | [87] |
| 0.170 | 84.7 ± 8.2 | a | [87] |
| 0.179 | 76.5 ± 4 | a | [88] |
| 0.1791 | 75.0 ± 4 | a | [88] |
| 0.199 | 76.5 ± 5.1 | a | [88] |
| 0.1993 | 75.0 ± 5 | a | [88] |
| 0.200 | 72.9 ± 29.6 | a | [86] |
| 0.20 | 74.4 ± 30.2 | a | [86] |
| 0.24 | 81.5 ± 2.7 | b | [89] |
| 0.27 | 78.6 ± 14.3 | a | [87] |
| 0.280 | 88.8 ± 36.3 | a | [86] |
| 0.28 | 90.6 ± 37.3 | a | [85] |
| 0.35 | 84.4 ± 8.6 | b | [85] |
| 0.3519 | 83.0 ± 14 | a | [88] |
| 0.352 | 84.7 ± 14.3 | a | [88] |
| 0.38 | 81.5 ± 1.9 | b | [90] |
| 0.3802 | 83.0 ± 13.5 | a | [91] |
| 0.3802 | 84.7 ± 14.1 | a | [91] |
| 0.40 | 95.0 ± 17 | a | [87] |
| 0.40 | 96.9 ± 17.3 | a | [87] |
| 0.4004 | 77.0 ± 10.2 | a | [91] |
| 0.4004 | 78.6 ± 10.4 | a | [91] |
| 0.4247 | 87.1 ± 11.2 | a | [91] |
| 0.4247 | 88.9 ± 11.4 | a | [91] |
| 0.43 | 88.3 ± 3.8 | a | [85] |
| 0.44 | 84.3 ± 7.9 | a | [92] |
| 0.4497 | 92.8 ± 12.9 | a | [91] |
| 0.4497 | 94.7 ± 13.1 | a | [91] |
| 0.470 | 89.0 ± 34.0 | a | [93] |
| 0.47 | 90.8 ± 50.6 | a | [93] |
| 0.4783 | 80.0 ± 99.0 | a | [91] |
| 0.4783 | 82.5 ± 9.2 | a | [91] |
| 0.48 | 99.0 ± 63.2 | a | [93] |
| 0.51 | 90.8 ± 1.9 | b | [90] |
| 0.57 | 98.8 ± 3.4 | b | [86] |
| 0.593 | 104.0 ± 13.0 | a | [88] |
| 0.593 | 106.1 ± 13.3 | a | [88] |
| 0.60 | 89.7 ± 6.2 | a | [86] |
| 0.61 | 97.8 ± 2.1 | b | [90] |
| 0.64 | 98.82 ± 2.98 | b | [94] |
| 0.6797 | 92.0 ± 8 | a | [88] |
| 0.68 | 93.9 ± 8.1 | a | [88] |
| 0.73 | 99.3 ± 7.1 | a | [92] |
| 0.7812 | 105.0 ± 12 | a | [88] |
| 0.781 | 107.1 ± 12.2 | a | [88] |
| 0.875 | 127.6 ± 17.3 | a | [88] |
| 0.8754 | 125.0 ± 17 | a | [88] |
| 0.88 | 91.8 ± 40.8 | a | [95] |
| 0.880 | 90.0 ± 40 | a | [93] |
| 0.90 | 69.0 ± 12 | a | [87] |
| 0.90 | 119.4 ± 23.4 | a | [87] |
| 0.900 | 117.0 ± 23 | a | [87] |
| 1.037 | 157.2 ± 20.4 | a | [88] |
| 1.037 | 154.0 ± 20 | a | [88] |
| 1.30 | 171.4 ± 17.3 | a | [87] |
| 1.300 | 168.0 ± 17 | a | [87] |
| 1.363 | 160.0 ± 33.6 | a | [96] |
| 1.363 | 163.3 ± 34.3 | a | [96] |
| 1.430 | 177.0 ± 18 | a | [87] |
| 1.43 | 180.6 ± 18.3 | a | [87] |
| 1.530 | 140.0 ± 14 | a | [87] |
| 1.53 | 142.9 ± 14.2 | a | [87] |
| 1.750 | 202.0 ± 40 | a | [87] |
| 1.75 | 206.1 ± 40.8 | a | [87] |
| 1.965 | 186.5 ± 50.4 | a | [96] |
| 1.965 | 190.3 ± 51.4 | a | [96] |
| 2.30 | 228.0 ± 8.1 | c | [97] |
| 2.34 | 226.5 ± 7.1 | c | [97] |
| 2.36 | 230.6 ± 8.2 | c | [98] |
Appendix A.2. Pantheon Data
We use the latest published dataset for the supernovae type Pantheon sample, consisting of 1048 data points. In our analysis, we utilize these data points, which have been confirmed spectroscopically by SNe and cover the redshift range of . The function for the Pantheon dataset is taken as:
where and are the theoretical and observed distance modulus, and the standard deviation. The distance modulus is defined as
where m and M denote the apparent and absolute magnitudes. Additionally, the luminosity distance for the flat universe and the nuisance parameter are given by
and
respectively.
Appendix A.3. Baryon Acoustic Oscillations (BAO)
Concerning baryon acoustic oscillations (BAO), we use the data from the Sloan Digital Sky Survey () [99], Galaxy survey () [100], [101] and three parallel measurements from the survey [92]. In the BAO observations, the distance redshift ratio is
where is the redshift at the time of photon decoupling [102], and is the corresponding comoving sound horizon [103]. The dilation scale defined by Eisenstein et al. [104] is
where is the angular diameter distance, which essentially is a geometric mean of two transverse and one radial direction. The value of is given by [105]
where
and the inverse covariance matrix is
approaching the correlation coefficients available in [105,106].
Appendix A.4. Joint Analysis
In the case where some of the above datasets are used simultaneously, the corresponding arises from the sum of the separate ones. In particular, we will use the following combinations:
References
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1935. [Google Scholar] [CrossRef]
- Cai, Y.F.; Saridakis, E.N.; Setare, M.R.; Xia, J.Q. Quintom Cosmology: Theoretical implications and observations. Phys. Rep. 2010, 493, 1–60. [Google Scholar] [CrossRef]
- Felice, A.D.; Tsujikawa, S. f(R) theories. Living Rev. Relativ. 2010, 13, 3. [Google Scholar] [CrossRef]
- Capozziello, S.; Laurentis, M.D. Extended Theories of Gravity. Phys. Rep. 2011, 509, 167–321. [Google Scholar] [CrossRef]
- Cai, Y.F.; Capozziello, S.; Laurentis, M.D.; Saridakis, E.N. f(T) teleparallel gravity and cosmology. Rep. Prog. Phys. 2016, 79, 106901. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-Time Evolution. Phys. Rep. 2017, 692, 1–104. [Google Scholar] [CrossRef]
- Saridakis, E.N.; Lazkoz, R.; Salzano, V.; Moniz, P.V.; Capozziello, S.; Jiménez, J.B. Modified Gravity and Cosmology: An Update by the CANTATA Network; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Castillo-Santos, M.N.; Hernández-Almada, A.; García-Aspeitia, M.A.; Magaña, J. An exponential equation of state of dark energy in the light of 2018 CMB Planck data. Phys. Dark Univ. 2023, 40, 101225. [Google Scholar] [CrossRef]
- Liu, D.J.; Li, X.Z.; Hao, J.; Jin, X.H. Revisiting the parametrization of Equation of State of Dark Energy via SNIa Data. Mon. Not. R. Astron. Soc. 2008, 388, 275–281. [Google Scholar] [CrossRef]
- Perkovic, D.; Stefancic, H. Barotropic fluid compatible parametrizations of dark energy. Eur. Phys. J. C 2020, 80, 629. [Google Scholar] [CrossRef]
- Gong, Y.G.; Zhang, Y.Z. Probing the curvature and dark energy. Phys. Rev. D 2005, 72, 043518. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Valentino, E.D.; Saridakis, E.N.; Chakraborty, S. Observational constraints on one-parameter dynamical dark-energy parametrizations and the H0 tension. Phys. Rev. D 2019, 99, 043543. [Google Scholar] [CrossRef]
- Chevallier, M.; Polarski, D. Accelerating universes with scaling dark matter. Int. J. Mod. Phys. D 2001, 10, 213–223. [Google Scholar] [CrossRef]
- Linder, E.V. Exploring the expansion history of the universe. Phys. Rev. Lett. 2003, 90, 091301. [Google Scholar] [CrossRef]
- Cooray, A.R.; Huterer, D. Gravitational lensing as a probe of quintessence. Astrophys. J. 1999, 513, L95. [Google Scholar] [CrossRef]
- Astier, P. Can luminosity distance measurements probe the equation of state of dark energy. Phys. Lett. B 2001, 500, 8–15. [Google Scholar] [CrossRef]
- Weller, J.; Albrecht, A. Future supernovae observations as a probe of dark energy. Phys. Rev. D 2002, 65, 103512. [Google Scholar] [CrossRef]
- Efstathiou, G. Constraining the equation of state of the universe from distant type Ia supernovae and cosmic microwave background anisotropies. Mon. Not. R. Astron. Soc. 1999, 310, 842–850. [Google Scholar] [CrossRef]
- Jassal, H.K.; Bagla, J.S.; Padmanabhan, T. Observational constraints on low redshift evolution of dark energy: How consistent are different observations? Phys. Rev. D 2005, 72, 103503. [Google Scholar] [CrossRef]
- Barboza, E.M., Jr.; Alcaniz, J.S. A parametric model for dark energy. Phys. Lett. B 2008, 666, 415–419. [Google Scholar] [CrossRef]
- Banerjee, A.; Cai, H.; Heisenberg, L.; Colgáin, E.; Sheikh-Jabbari, M.M.; Yang, T. Hubble sinks in the low-redshift swampland. Phys. Rev. D 2021, 103, L081305. [Google Scholar] [CrossRef]
- Lee, B.H.; Lee, W.; Colgáin, E.; Sheikh-Jabbari, M.M.; Thakur, S. Is local H0 at odds with dark energy EFT? J. Cosmol. Astropart. Phys. 2022, 2022, 004. [Google Scholar]
- Ma, J.Z.; Zhang, X. Probing the dynamics of dark energy with novel parametrizations. Phys. Lett. B 2011, 699, 233–238. [Google Scholar] [CrossRef]
- Nesseris, S.; Perivolaropoulos, L. A Comparison of cosmological models using recent supernova data. Phys. Rev. D 2004, 70, 043531. [Google Scholar] [CrossRef]
- Linder, E.V.; Huterer, D. How many dark energy parameters? Phys. Rev. D 2005, 72, 043509. [Google Scholar] [CrossRef]
- Feng, B.; Li, M.; Piao, Y.S.; Zhang, X. Oscillating quintom and the recurrent universe. Phys. Lett. B 2006, 634, 101–105. [Google Scholar] [CrossRef]
- Zhao, G.B.; Xia, J.Q.; Li, H.; Tao, C.; Virey, J.M.; Zhu, Z.H.; Zhang, X. Probing for dynamics of dark energy and curvature of universe with latest cosmological observations. Phys. Lett. B 2007, 648, 8–13. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. The Oscillating dark energy: Future singularity and coincidence problem. Phys. Lett. B 2006, 637, 139–148. [Google Scholar] [CrossRef]
- Saridakis, E.N. Theoretical Limits on the Equation-of-State Parameter of Phantom Cosmology. Phys. Lett. B 2009, 676, 7–11. [Google Scholar] [CrossRef]
- Dutta, S.; Saridakis, E.N.; Scherrer, R.J. Dark energy from a quintessence (phantom) field rolling near potential minimum (maximum). Phys. Rev. D 2009, 79, 103005. [Google Scholar] [CrossRef]
- Lazkoz, R.; Salzano, V.; Sendra, I. Oscillations in the dark energy EoS: New MCMC lessons. Phys. Lett. B 2011, 694, 198. [Google Scholar] [CrossRef]
- Feng, L.; Lu, T. A new equation of state for dark energy model. J. Cosmol. Astropart. Phys. 2011, 2011, 034. [Google Scholar] [CrossRef]
- Saridakis, E.N. Phantom evolution in power-law potentials. Nucl. Phys. B 2009, 819, 116–126. [Google Scholar] [CrossRef]
- Felice, A.D.; Nesseris, S.; Tsujikawa, S. Observational constraints on dark energy with a fast varying equation of state. J. Cosmol. Astropart. Phys. 2012, 2012, 029. [Google Scholar] [CrossRef]
- Saridakis, E.N. Quintom evolution in power-law potentials. Nucl. Phys. B 2010, 830, 374–389. [Google Scholar] [CrossRef]
- Feng, C.J.; Shen, X.Y.; Li, P.; Li, X.Z. A New Class of Parametrization for Dark Energy without Divergence. J. Cosmol. Astropart. Phys. 2012, 2012, 023. [Google Scholar] [CrossRef]
- Basilakos, S.; Solá, J. Effective equation of state for running vacuum: ‘mirage’ quintessence and phantom dark energy. Mon. Not. R. Astron. Soc. 2014, 437, 3331–3342. [Google Scholar] [CrossRef]
- Pantazis, G.; Nesseris, S.; Perivolaropoulos, L. Comparison of thawing and freezing dark energy parametrizations. Phys. Rev. D 2016, 93, 103503. [Google Scholar] [CrossRef]
- Valentino, E.D.; Melchiorri, A.; Silk, J. Reconciling Planck with the local value of H0 in extended parameter space. Phys. Lett. B 2016, 761, 242–246. [Google Scholar] [CrossRef]
- Chávez, R.; Plionis, M.; Basilakos, S.; Terlevich, R.; Terlevich, E.; Melnick, J.; Bresolin, F.; González-Morán, A.L. Constraining the dark energy equation of state with HII galaxies. Mon. Not. R. Astron. Soc. 2016, 462, 2431–2439. [Google Scholar] [CrossRef]
- Zhao, G.B.; Raveri, M.; Pogosian, L.; Wang, Y.; Crittenden, R.G.; Handley, W.J.; Percival, W.J.; Beutler, F.; Brinkmann, J.; Zhang, H.; et al. Dynamical dark energy in light of the latest observations. Nat. Astron. 2017, 1, 627–632. [Google Scholar] [CrossRef]
- Yang, W.; Nunes, R.C.; Pan, S.; Mota, D.F. Effects of neutrino mass hierarchies on dynamical dark energy models. Phys. Rev. D 2017, 95, 103522. [Google Scholar] [CrossRef]
- Valentino, E.D.; Melchiorri, A.; Linder, E.V.; Silk, J. Constraining Dark Energy Dynamics in Extended Parameter Space. Phys. Rev. D 2017, 96, 023523. [Google Scholar] [CrossRef]
- Di Valentino, E. Crack in the cosmological paradigm. Nat. Astron. 2017, 1, 569–570. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Paliathanasis, A. Latest astronomical constraints on some nonlinear parametric dark energy models. Mon. Not. R. Astron. Soc. 2018, 475, 2605–2613. [Google Scholar] [CrossRef]
- Pan, S.; Saridakis, E.N.; Yang, W. Observational Constraints on Oscillating Dark-Energy Parametrizations. Phys. Rev. D 2018, 98, 063510. [Google Scholar] [CrossRef]
- Pan, S.; Yang, W.; Singha, C.; Saridakis, E.N. Observational constraints on sign-changeable interaction models and alleviation of the H0 tension. Phys. Rev. D 2019, 100, 083539. [Google Scholar] [CrossRef]
- Pan, S.; Yang, W.; Valentino, E.D.; Saridakis, E.N.; Chakraborty, S. Interacting scenarios with dynamical dark energy: Observational constraints and alleviation of the H0 tension. Phys. Rev. D 2019, 100, 103520. [Google Scholar] [CrossRef]
- Singh, J.K.; Balhara, H.; Bamba, K.; Jena, J. Bouncing cosmology in modified gravity with higher-order curvature terms. J. High Energy Phys. 2023, 3, 191. [Google Scholar] [CrossRef]
- Singh, J.K.; Shaily; Ram, S.; Santos, J.R.L.; Fortunato, J.A.S. The constrained cosmological model in Lyra geometry. Int. J. Mod. Phys. D 2023, 32, 2350040. [Google Scholar] [CrossRef]
- Cunha, J.V.; Lima, J.A.S. Transition Redshift: New Kinematic Constraints from Supernovae. Mon. Not. R. Astron. Soc. 2008, 390, 210–217. [Google Scholar] [CrossRef]
- Akarsu, O.; Dereli, T.; Kumar, S.; Xu, L. Probing kinematics and fate of the Universe with linearly time-varying deceleration parameter. Eur. Phys. J. Plus 2014, 129, 22. [Google Scholar] [CrossRef]
- Xu, L.; Lu, J. Cosmic constraints on deceleration parameter with Sne Ia and CMB. Mod. Phys. Lett. A 2009, 24, 369–376. [Google Scholar] [CrossRef]
- Colgáin, E.Ó.; Sheikh-Jabbari, M.M.; Yin, L. Can dark energy be dynamical? Phys. Rev. D 2021, 104, 023510. [Google Scholar] [CrossRef]
- Singh, J.K.; Bamba, K.; Nagpal, R.; Pacif, S.K.J. Bouncing cosmology in f(R,T) gravity. Phys. Rev. D 2018, 97, 123536. [Google Scholar] [CrossRef]
- Singh, J.K.; Nagpal, R. FLRW cosmology with EDSFD parametrization. Eur. Phys. J. C 2020, 80, 295. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Singular inflation from generalized equation of state fluids. Phys. Lett. B 2015, 747, 310–320. [Google Scholar] [CrossRef]
- Nagpal, R.; Singh, J.K.; Beesham, A.; Shabani, H. Cosmological aspects of a hyperbolic solution in f(R,T) gravity. Ann. Phys. 2019, 405, 234–255. [Google Scholar] [CrossRef]
- Abdalla, E.; Abellán, G.F.; Aboubrahim, A.; Agnello, A.; Akarsu, Ö.; Akrami, Y.; Alestas, G.; Aloni, D.; Amendola, L.; Pettorino, V.; et al. Cosmology intertwined: A review of the particle physics, astrophysics, and cosmology associated with the cosmological tensions and anomalies. J. High Energy Astrophys. 2022, 34, 49–211. [Google Scholar]
- Valentino, E.D.; Saridakis, E.; Riess, A. Cosmological tensions in the birthplace of the heliocentric model. Nat. Astron. 2022, 6, 1353–1355. [Google Scholar] [CrossRef]
- Lenart, A. Ł; Bargiacchi, G.; Dainotti, M.G.; Nagataki, S.; Capozziello, S. A Bias-free Cosmological Analysis with Quasars Alleviating H0 Tension. Astrophys. J. Suppl. Ser. 2023, 264, 46. [Google Scholar]
- Dainotti, M.G.; Bargiacchi, G.; Bogdan, M.; Capozziello, S.; Nagataki, S. Reduced uncertainties up to 43% on the Hubble constant and the matter density with the SNe Ia with a new statistical analysis. arXiv 2023, arXiv:2303.06974. [Google Scholar]
- Dainotti, M.G.; Simone, B.D.; Schiavone, T.; Montani, G.; Rinaldi, E.; Lambiase, G. On the Hubble constant tension in the SNe Ia Pantheon sample. Astrophys. J. 2021, 912, 150. [Google Scholar] [CrossRef]
- Schiavone, T.; Montani, G.; Dainotti, M.G.; Simone, B.D.; Rinaldi, E.; Lambiase, G. Running Hubble constant from the SNe Ia Pantheon sample? arXiv 2022, arXiv:2205.07033. [Google Scholar]
- Dainotti, M.G.; Simone, B.D.; Schiavone, T.; Montani, G.; Rinaldi, E.; Lambiase, G.; Bogdan, M.; Ugale, S. On the Evolution of the Hubble Constant with the SNe Ia Pantheon Sample and Baryon Acoustic Oscillations: A Feasibility Study for GRB-Cosmology in 2030. Galaxies 2022, 10, 24. [Google Scholar] [CrossRef]
- Schiavone, T.; Montani, G.; Bombacigno, F. f(R) gravity in the Jordan frame as a paradigm for the Hubble tension. Mon. Not. R. Astron. Soc. 2023, 522, L72–L77. [Google Scholar] [CrossRef]
- Mukhanov, V.F.; Feldman, H.A.; Brandenberger, R.H. Theory of cosmological perturbations. Phys. Rep. 1992, 215, 203–333. [Google Scholar] [CrossRef]
- Ma, C.P.; Bertschinger, E. Cosmological perturbation theory in the synchronous and conformal Newtonian gauges. Astrophys. J. 1995, 455, 7. [Google Scholar] [CrossRef]
- Malik, K.A.; Wands, D. Cosmological perturbations. Phys. Rep. 2009, 475, 1–51. [Google Scholar] [CrossRef]
- Bolotin, Y.L.; Cherkaskiy, V.A.; Ivashtenko, O.Y.; Konchatnyi, M.I.; Zazunov, L.G. Applied Cosmography: A Pedagogical Review. arXiv 2018, arXiv:1812.02394. [Google Scholar]
- Shaily; Singh, A.; Singh, J.K.; Ray, S. Late time phantom characteristic of the model in f (R, T) gravity with quadratic curvature term. arXiv arXiv:2402.01780.
- Singh, J.K.; Shaily; Balhara, H.; Bamba, K.; Jena, J. Cosmic analysis of a model in higher-order gravity theory. Astron. Comput. 2024, 46, 100790. [Google Scholar] [CrossRef]
- Singh, J.K.; Balhara, H.; Shaily; Singh, P. The constrained accelerating universe in f (R, T) gravity. Astron. Comput. 2024, 46, 100795. [Google Scholar]
- Balhara, H.; Singh, J.K.; Saridakis, E.N. Observational constraints and cosmographic analysis of f (T, TG) gravity and cosmology. arXiv 2024, arXiv:2312.17277. [Google Scholar]
- Riess, A.G.; Kirshner, R.P.; Schmidt, B.P.; Jha, S.; Challis, P.; Garnavich, P.M.; Esin, A.A.; Carpenter, C.; Grashius, R.; Schild, R.E.; et al. BV RI light curves for 22 type Ia supernovae. Astron. J. 1999, 117, 707–724. [Google Scholar] [CrossRef]
- Shaily; Zeyauddin, M.; Singh, J.K.; Santos, J.R.L. Dynamics of a hyperbolic solution in Scale-covariant theory. arXiv 2022, arXiv:2207.05076. [Google Scholar]
- Scolnic, D.M.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J.; Huber, M.E.; Kessler, R.; Narayan, G.; Riess, A.G.; et al. [Pan-STARRS1]. The Complete Light-curve Sample of Spectroscopically Confirmed SNe Ia from Pan-STARRS1 and Cosmological Constraints from the Combined Pantheon Sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- Gelman, A.; Rubin, D.B. Inference from Iterative Simulation Using Multiple Sequences. Stat. Sci. 1992, 7, 457–472. [Google Scholar] [CrossRef]
- Brooks, P.S.; Gelman, A. General methods for monitoring convergence of iterative simulations. J. Comput. Graph. Stat. 1998, 7, 434–455. [Google Scholar] [CrossRef]
- Sami, M.; Shahalam, M.; Skugoreva, M.; Toporensky, A. Cosmological dynamics of a nonminimally coupled scalar field system and its late time cosmic relevance. Phys. Rev. D 2012, 86, 103532. [Google Scholar] [CrossRef]
- Myrzakulov, R.; Shahalam, M. Statefinder hierarchy of bimetric and galileon models for concordance cosmology. J. Cosmol. Astropart. Phys. 2013, 2013, 047. [Google Scholar] [CrossRef]
- Rani, S.; Altaibayeva, A.; Shahalam, M.; Singh, J.K.; Myrzakulov, R. Constraints on cosmological parameters in power-law cosmology. J. Cosmol. Astropart. Phys. 2015, 2015, 031. [Google Scholar] [CrossRef]
- Sahni, V.; Saini, T.D.; Starobinsky, A.A.; Alam, U. JStatefinder—A new geometrical diagnostic of dark energy. J. Exp. Theor. Phys. Lett. 2003, 77, 201–206. [Google Scholar] [CrossRef]
- Alam, U.; Sahni, V.; Saini, T.D.; Starobinsky, A.A. Exploring the expanding universe and dark energy using the statefinder diagnostic. Mon. Not. R. Astron. Soc. 2003, 344, 1057–1074. [Google Scholar] [CrossRef]
- Farooq, O.; Madiyar, F.R.; Crandall, S.; Ratra, B. Hubble parameter measurement constraints on the redshift of the deceleration–acceleration transition, dynamical dark energy, and space curvature. Astrophys. J. 2017, 835, 26. [Google Scholar] [CrossRef]
- Zhang, M.-J.; Xia, J.-Q. Test of the cosmic evolution using Gaussian processes. J. Cosmol. Astropart. Phys. 2016, 2016, 005. [Google Scholar] [CrossRef]
- Simon, J.; Verde, L.; Jimenez, R. Constraints on the redshift dependence of the dark energy potential. Phys. Rev. D 2005, 71, 123001. [Google Scholar] [CrossRef]
- Moresco, M.; Cimatti, A.; Jimenez, R.; Pozzetti, L.; Zamorani, G.; Bolzonella, M.; Dunlop, J.; Lamareille, F.; Mignoli, M.; Welikala, N.; et al. Improved constraints on the expansion rate of the Universe up to z~1.1 from the spectroscopic evolution of cosmic chronometers. J. Cosmol. Astropart. Phys. 2012, 2012, 006. [Google Scholar] [CrossRef]
- Gaztanaga, E.; Cabre, A.; Hui, L. Clustering of luminous red galaxies—IV. Baryon acoustic peak in the line-of-sight direction and a direct measurement of H(z). Mon. Not. R. Astron. Soc. 2009, 399, 1663–1680. [Google Scholar] [CrossRef]
- Alam, S.; Ata, M.; Bailey, S.; Beutler, F.; Bizyaev, D.; Blazek, J.A.; Bolton, A.S.; Brownstein, J.R.; Burden, A.; Zhao, G.B.; et al. The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Cosmological analysis of the DR12 galaxy sample. Mon. Not. R. Astron. Soc. 2017, 470, 2617–2652. [Google Scholar] [CrossRef]
- Moresco, M.; Pozzetti, L.; Cimatti, A.; Jimenez, R.; Maraston, C.; Verde, L.; Thomas, D.; Citro, A.; Tojeiro, R.; Wilkinson, D. A 6% measurement of the Hubble parameter at z~0.45: Direct evidence of the epoch of cosmic re-acceleration. J. Cosmol. Astropart. Phys. 2016, 2016, 014. [Google Scholar] [CrossRef]
- Blake, C.; Brough, S.; Colless, M.; Contreras, C.; Couch, W.; Croom, S.; Croton, D.; Davis, T.M.; Drinkwater, M.J.; Yee, H.K.; et al. Energy Survey: Joint measurements of the expansion and growth history at z < 1. Mon. Not. R. Astron. Soc. 2012, 425, 405–414. [Google Scholar]
- Ratsimbazafy, A.L.; Loubser, S.I.; Crawford, S.M.; Cress, C.M.; Bassett, B.A.; Nichol, R.C.; Väisänen, P. Age-dating luminous red galaxies observed with the Southern African Large Telescope. Mon. Not. R. Astron. Soc. 2017, 467, 3239–3254. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, G.B.; Chuang, C.H.; Ross, A.J.; Percival, W.J.; Gil-Marín, H.; Cuesta, A.J.; Kitaura, F.S.; Rodriguez-Torres, S.; Zhu, F.; et al. The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Tomographic BAO analysis of DR12 combined sample in configuration space. Mon. Not. R. Astron. Soc. 2017, 469, 3762–3774. [Google Scholar] [CrossRef]
- Stern, D.; Jimenez, R.; Verde, L.; Kamionkowski, M.; Stanford, S.A. Cosmic chronometers: Constraining the equation of state of dark energy. I: H(z) measurements. J. Cosmol. Astropart. Phys. 2010, 2010, 008. [Google Scholar] [CrossRef]
- Moresco, M. Raising the bar: New constraints on the Hubble parameter with cosmic chronometers at z~2. Mon. Not. R. Astron. Soc. Lett. 2015, 450, L16–L20. [Google Scholar] [CrossRef]
- Delubac, T.; Bautista, J.E.; Rich, J.; Kirkby, D.; Bailey, S.; Font-Ribera, A.; Slosar, A.; Lee, K.; Pieri, M.M.; York, D.G.; et al. Baryon acoustic oscillations in the Lyα forest of BOSS DR11 quasars. Astron. Astrophys. 2015, 574, A59. [Google Scholar] [CrossRef]
- Font-Ribera, A.; Kirkby, D.; Miralda-Escudé, J.; Ross, N.P.; Slosar, A.; Rich, J.; Aubourg, É.; Bailey, S.; Bhardwaj, V.; York, D.G.; et al. Quasar-Lyman α forest cross-correlation from BOSS DR11: Baryon Acoustic Oscillations. J. Cosmol. Astropart. Phys. 2014, 2014, 027. [Google Scholar] [CrossRef]
- Padmanabhan, N.; Xu, X.; Eisenstein, D.J.; Scalzo, R.; Cuesta, A.J.; Mehta, K.T.; Kazin, E. A 2 per cent distance to z = 0.35 by reconstructing baryon acoustic oscillations—I. Methods and application to the Sloan Digital Sky Survey. Mon. Not. R. Astron. Soc. 2012, 427, 2132–2145. [Google Scholar] [CrossRef]
- Beutler, F.; Blake, C.; Colless, M.; Jones, D.H.; Staveley-Smith, L.; Campbell, L.; Parker, Q.; Saunders, W.; Watson, F. The 6dF Galaxy Survey: Baryon acoustic oscillations and the local Hubble constant. Mon. Not. R. Astron. Soc. 2011, 416, 3017–3032. [Google Scholar] [CrossRef]
- Anderson, L.; Aubourg, E.; Bailey, S.; Beutler, F.; Bhardwaj, V.; Blanton, M.; Zhao, G.-B.; BOSS Collaboration. The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: Baryon acoustic oscillations in the Data Releases 10 and 11 Galaxy samples. Mon. Not. R. Astron. Soc. 2014, 441, 24–62. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Zonca, A. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar]
- dos Santos, M.V.; Reis, R.R.; Waga, I. Constraining the cosmic deceleration-acceleration transition with type Ia supernova, BAO/CMB and H(z) data. J. Cosmol. Astropart. Phys. 2016, 2016, 066. [Google Scholar] [CrossRef]
- Eisenstein, D.J.; Zehavi, I.; Hogg, D.W.; Scoccimarro, R.; Blanton, M.R.; Nichol, R.C.; Scranton, R.; Seo, H.; Tegmark, M.; York, D.G. Detection of the baryon acoustic peak in the large-scale correlation function of SDSS luminous red galaxies. Astrophys. J. 2005, 633, 560. [Google Scholar] [CrossRef]
- Giostri, R.; dos Santos, M.V.; Waga, I.; Reis, R.R.R.; Calvao, M.O.; Lago, B.L. From cosmic deceleration to acceleration: New constraints from SN Ia and BAO/CMB. J. Cosmol. Astropart. Phys. 2012, 2012, 027. [Google Scholar] [CrossRef]
- Hinshaw, G.; Larson, D.; Komatsu, E.; Spergel, D.N.; Bennett, C.; Dunkley, J.; Nolta, M.R.; Halpern, M.; Hill, R.S.; Wright, E.L.; et al. Nine-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Cosmological parameter results. Astrophys. J. Suppl. Ser. 2013, 208, 19. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).