The Rotation of Classical Bulges in Barred Galaxies in the Presence of Gas
Abstract
1. Introduction
2. Simulation Setup
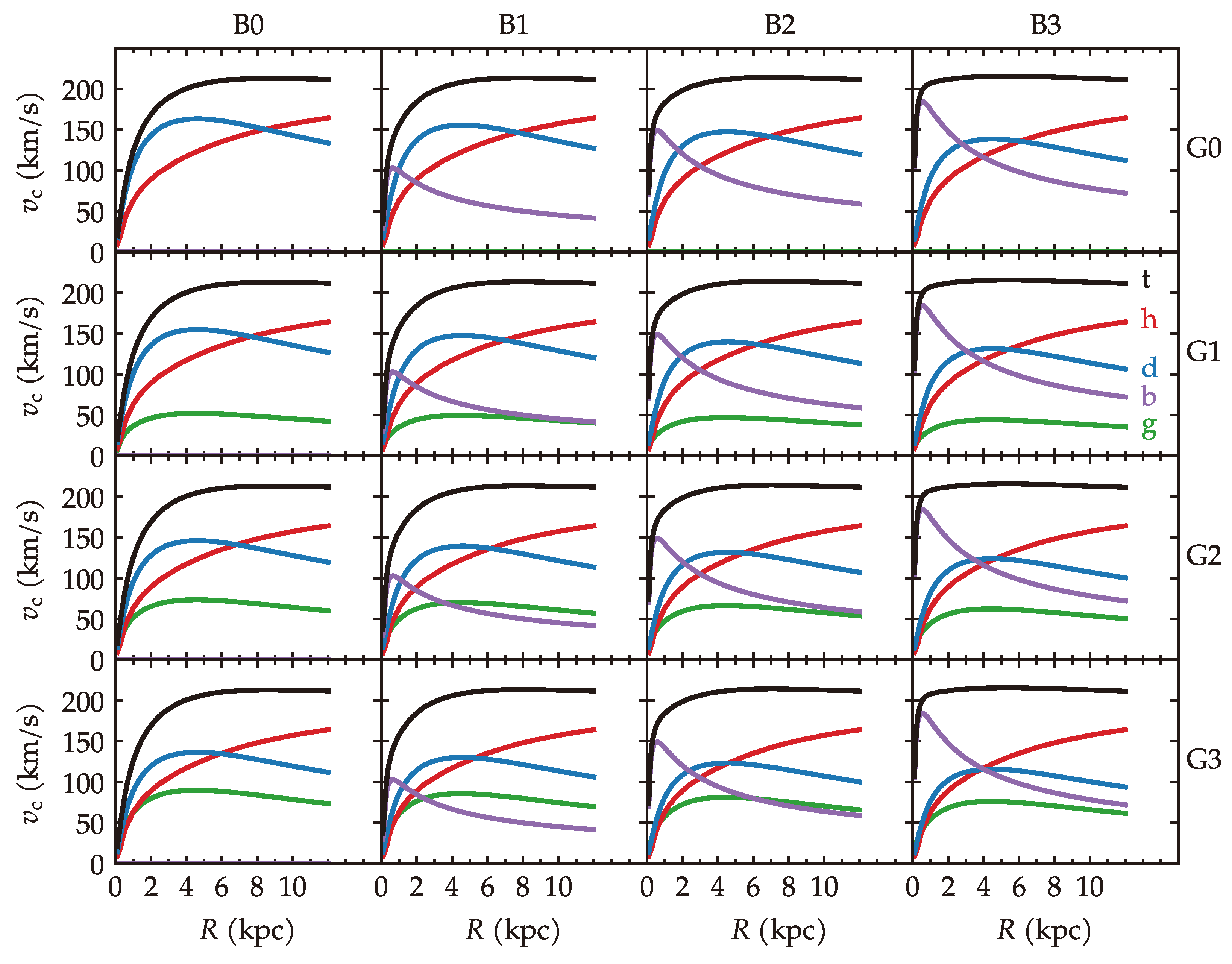
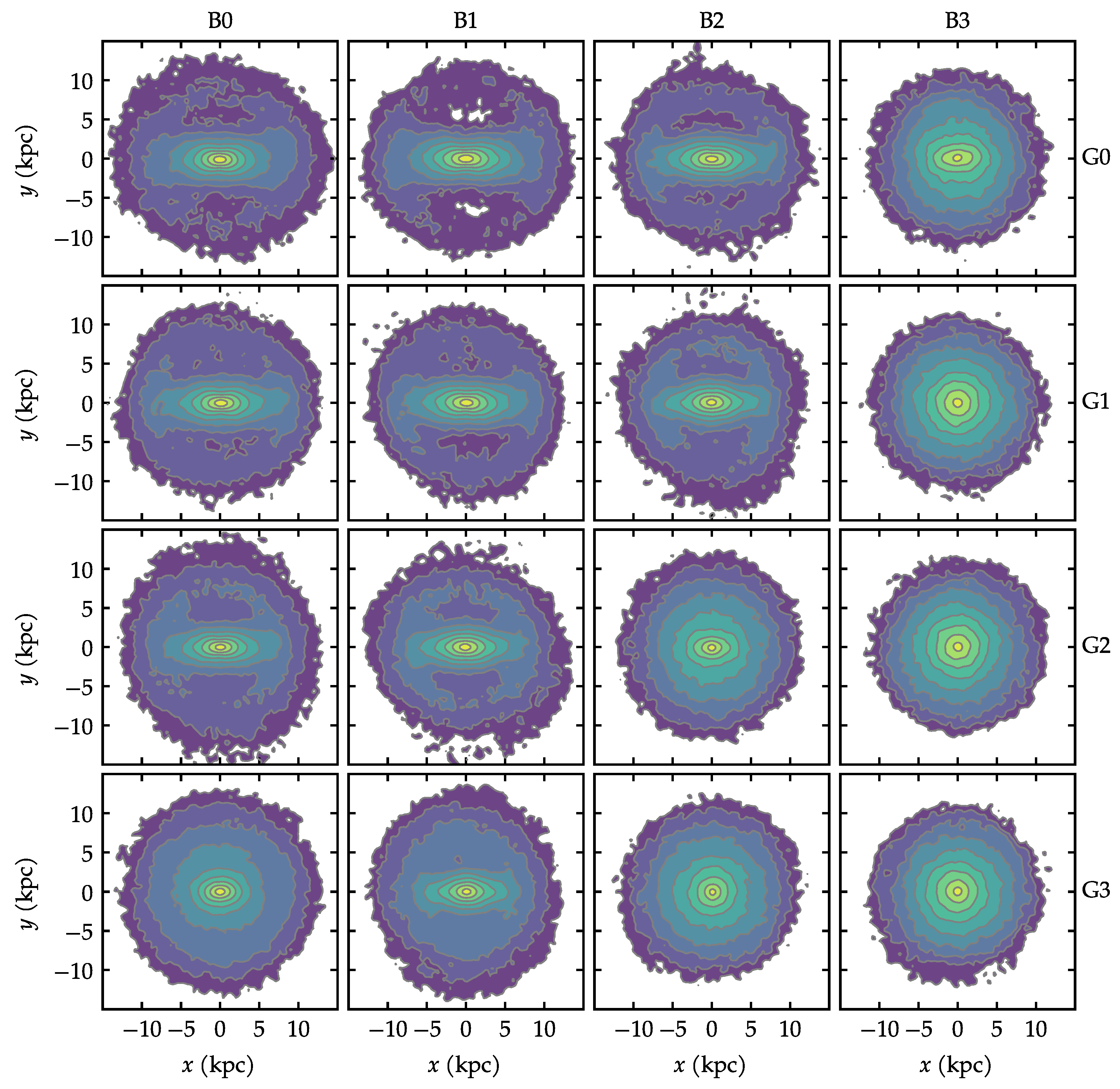
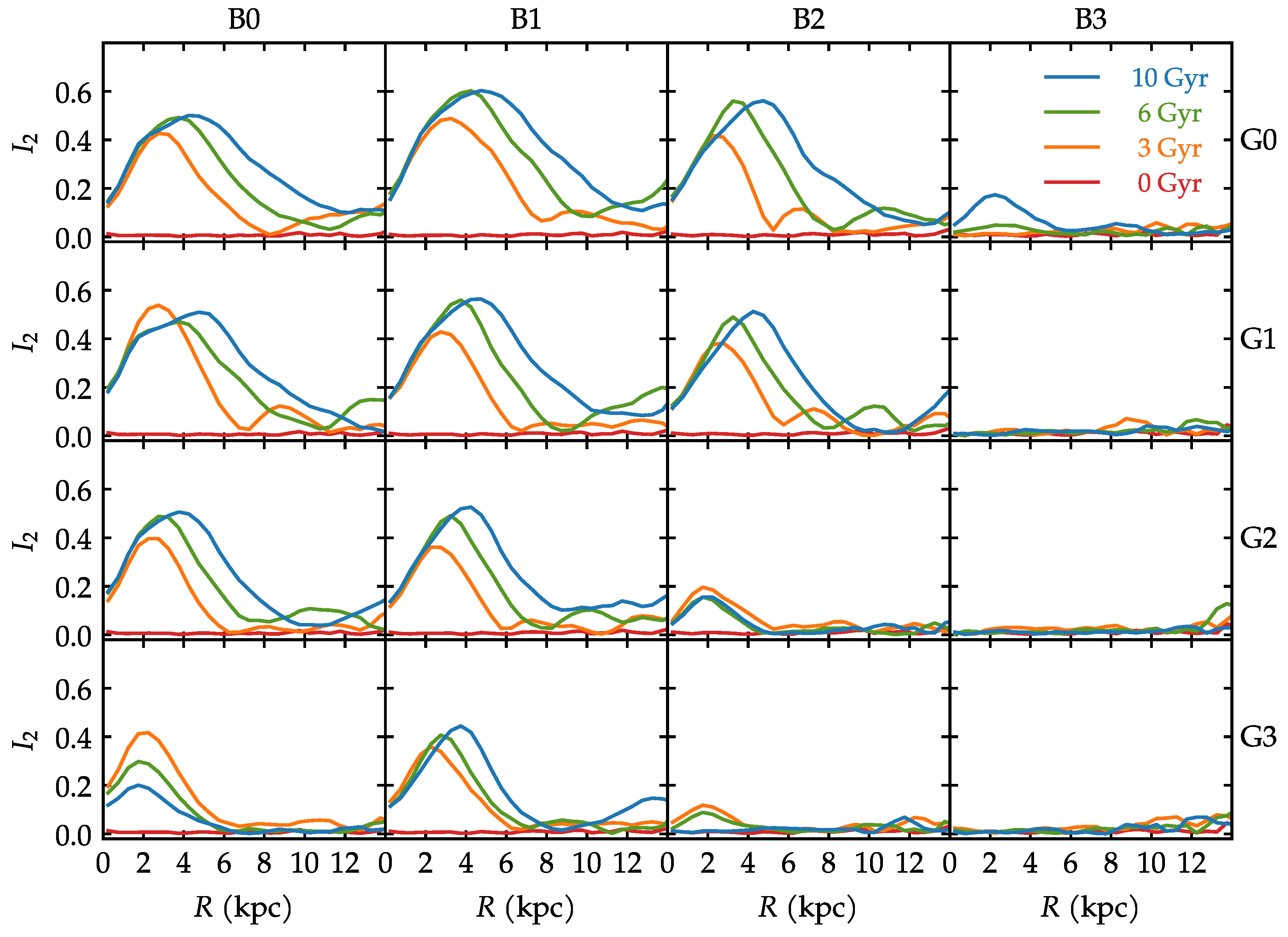
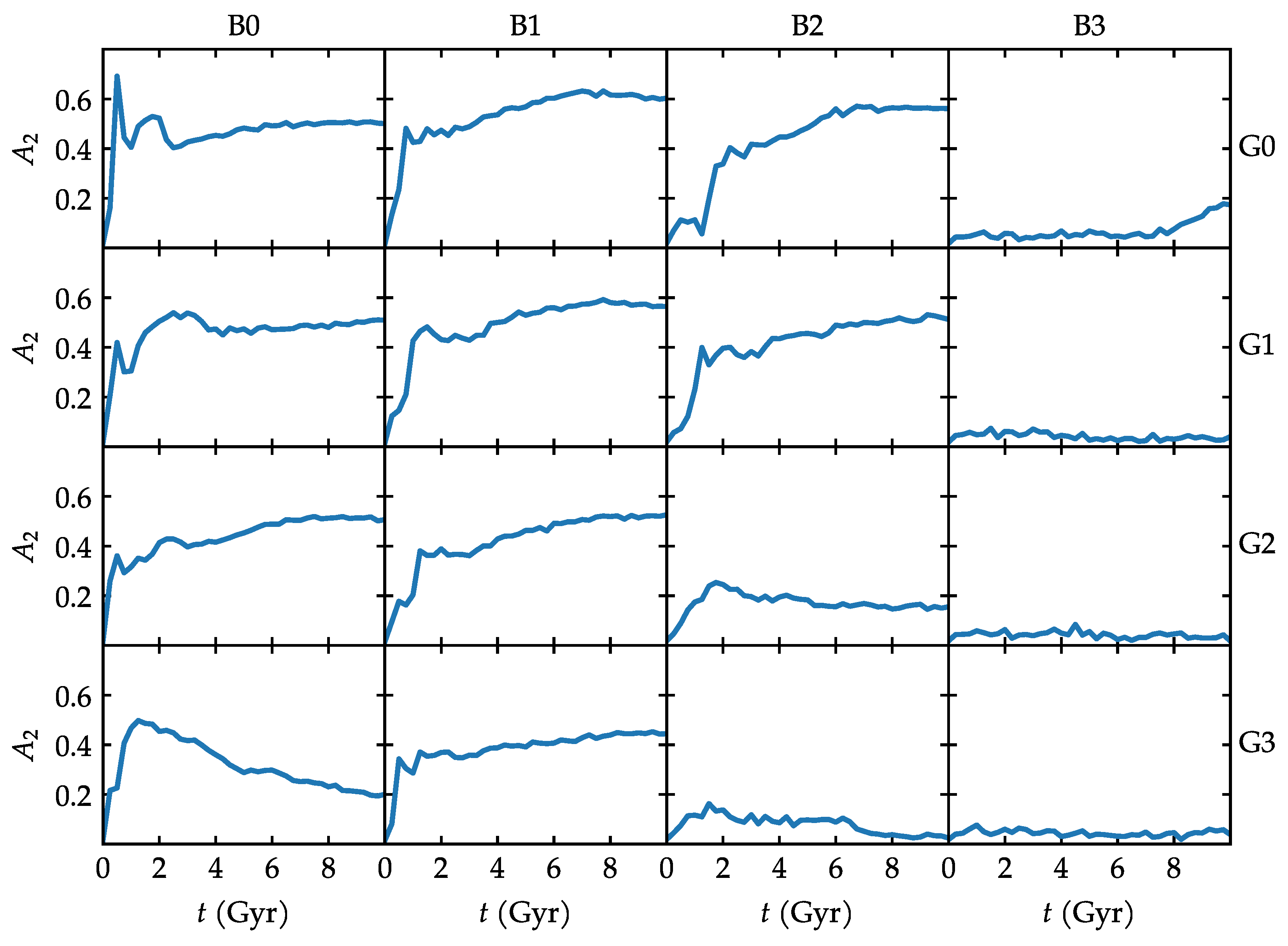
3. Results
3.1. Bar Evolution
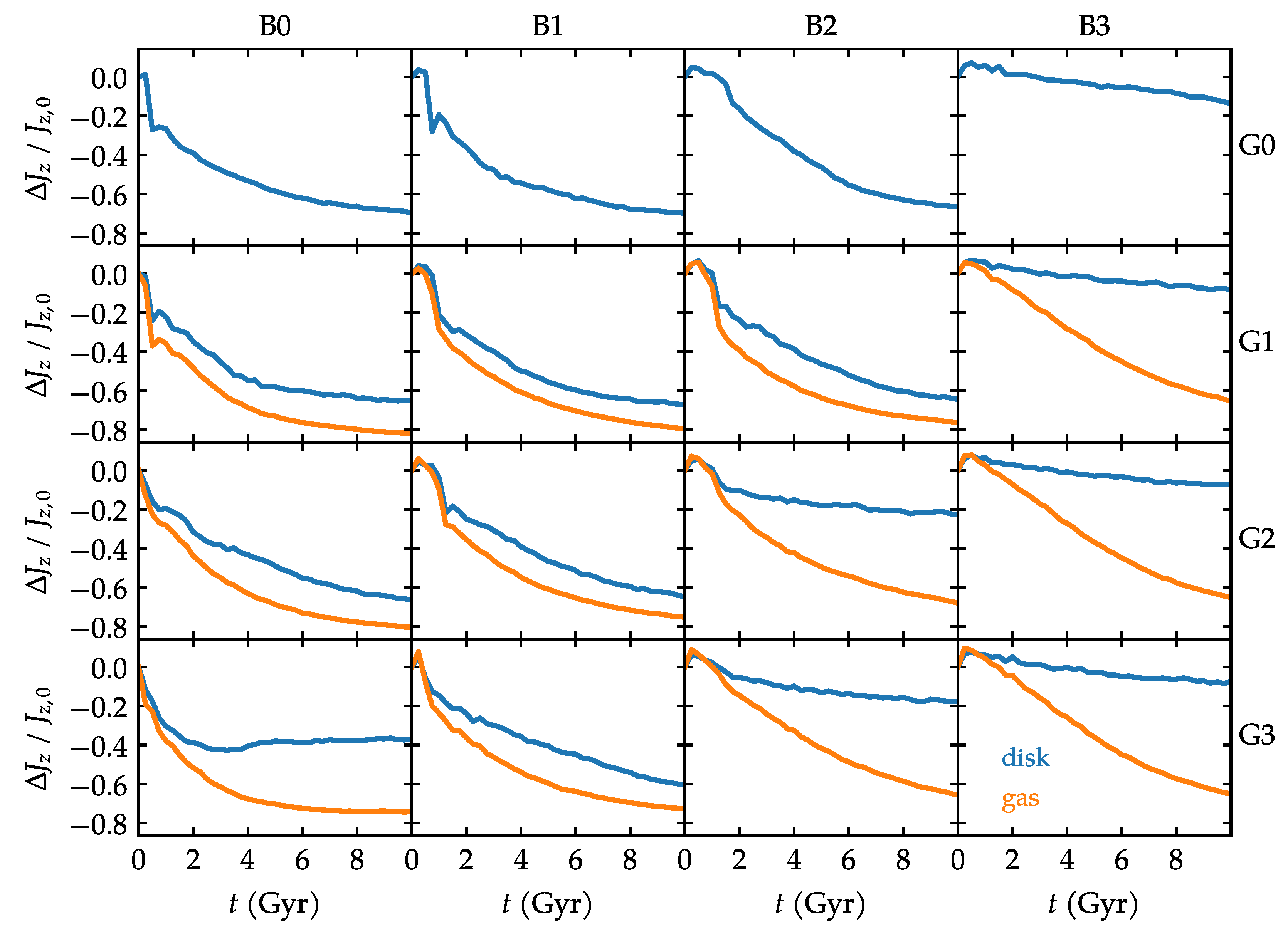
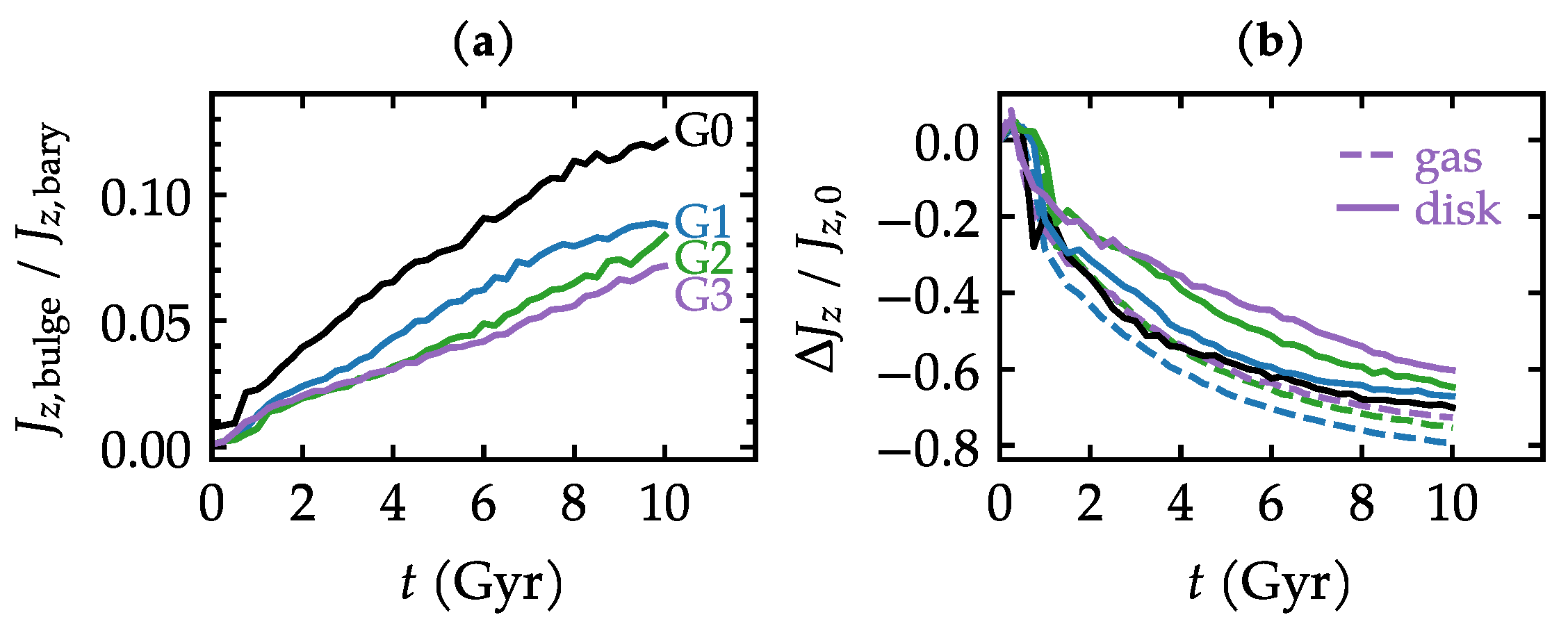
3.2. Angular Momentum
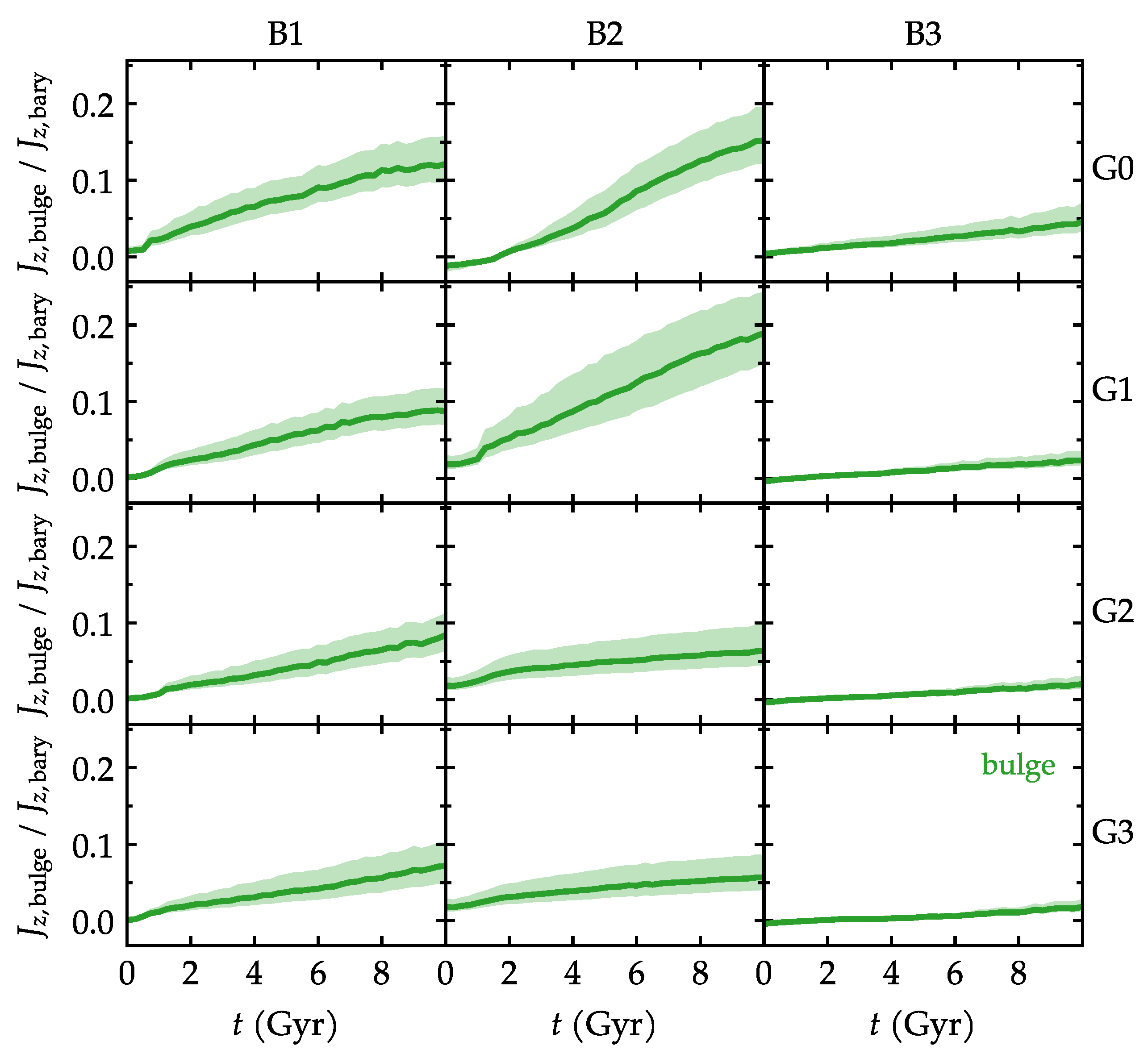
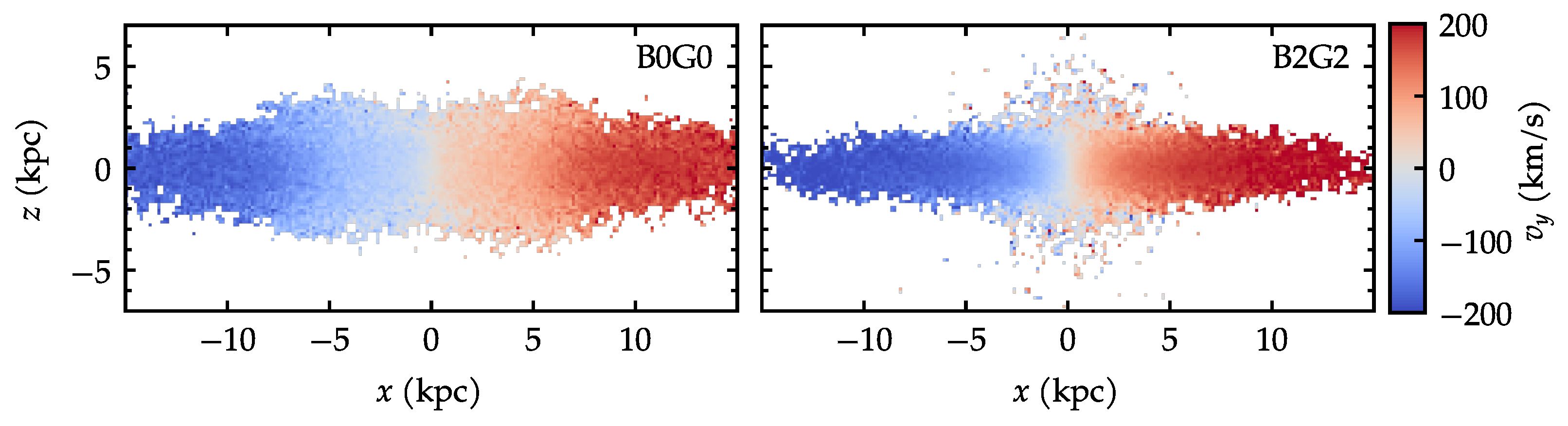
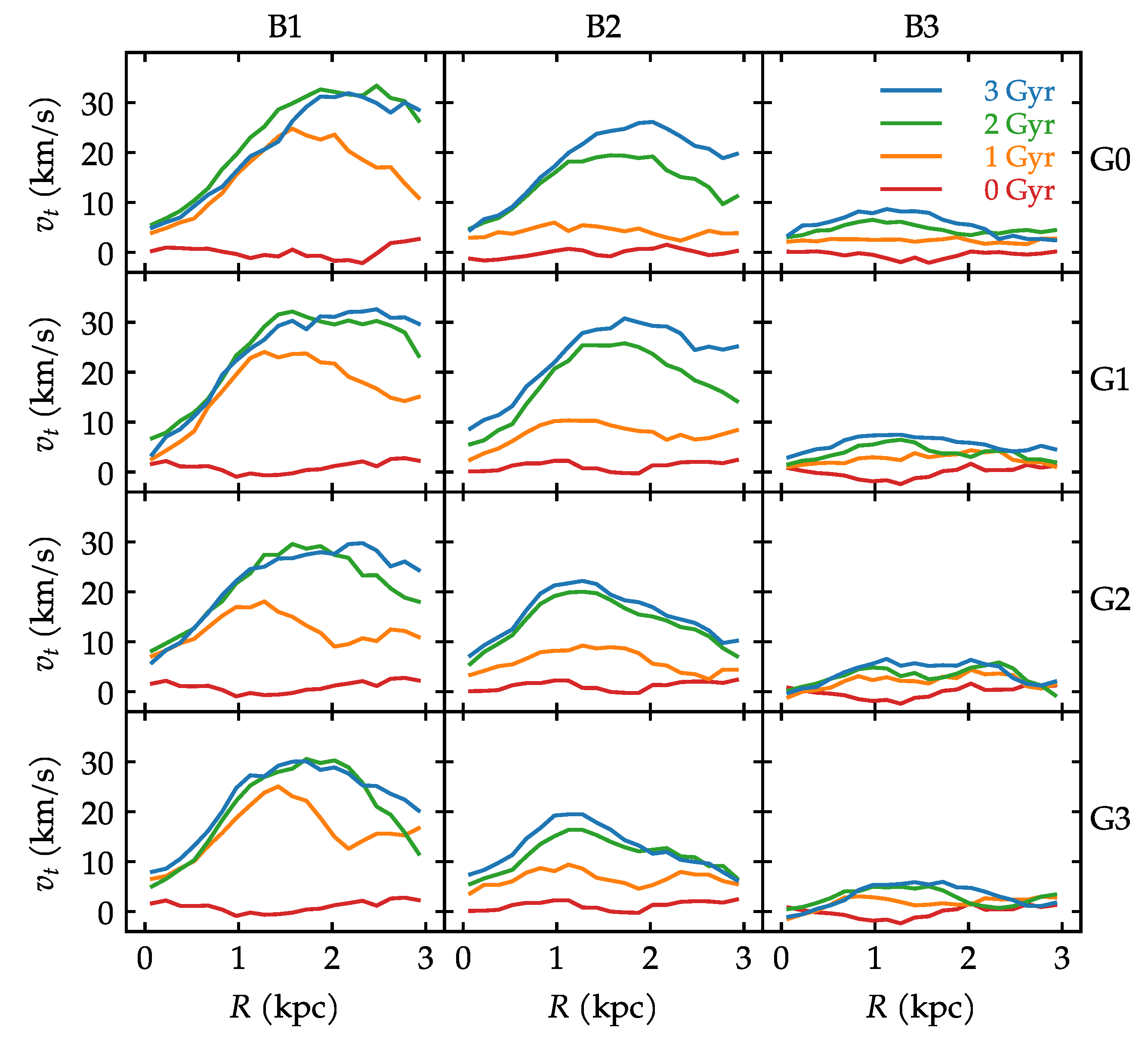
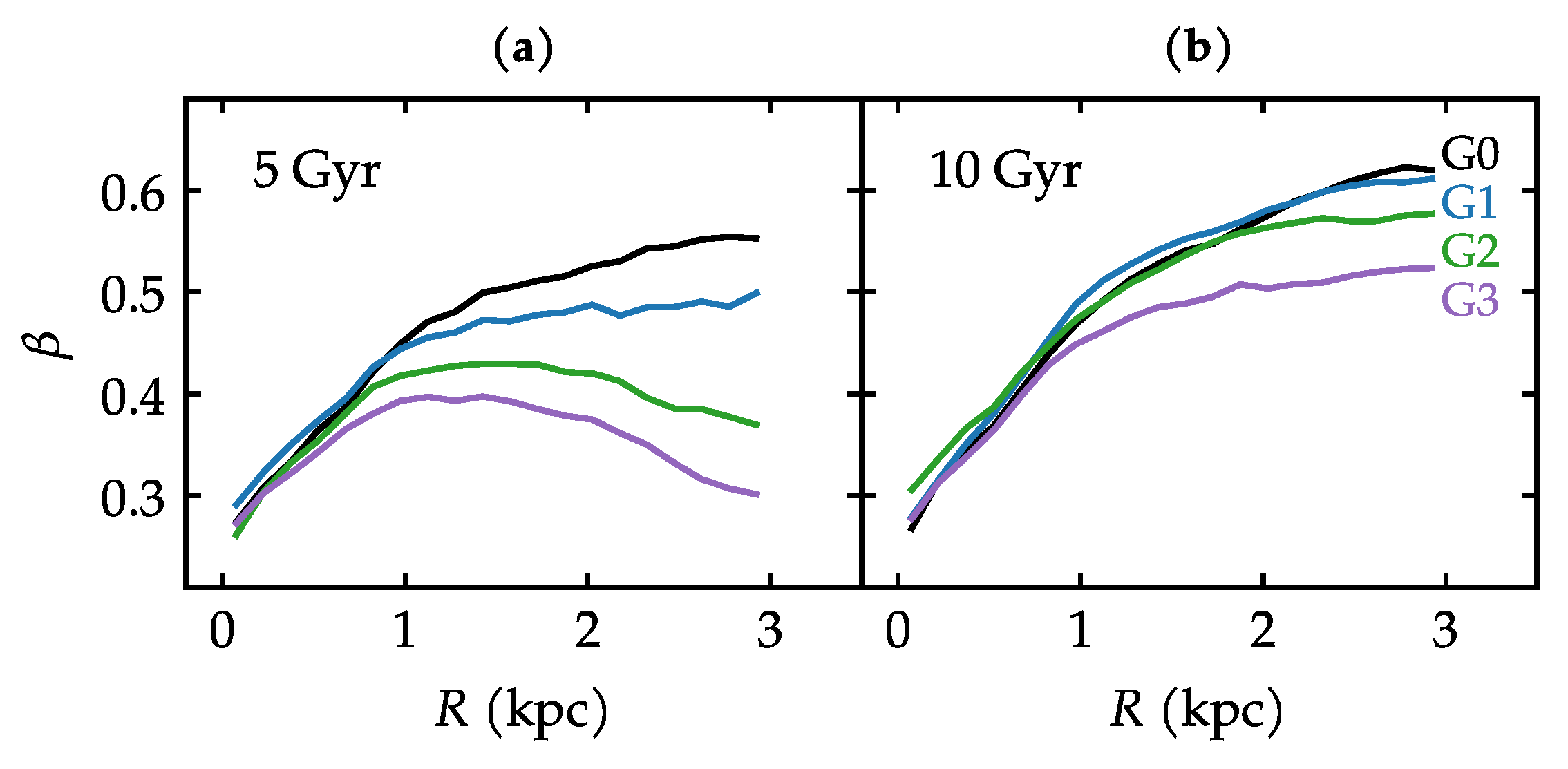
3.3. Bulge Kinematics
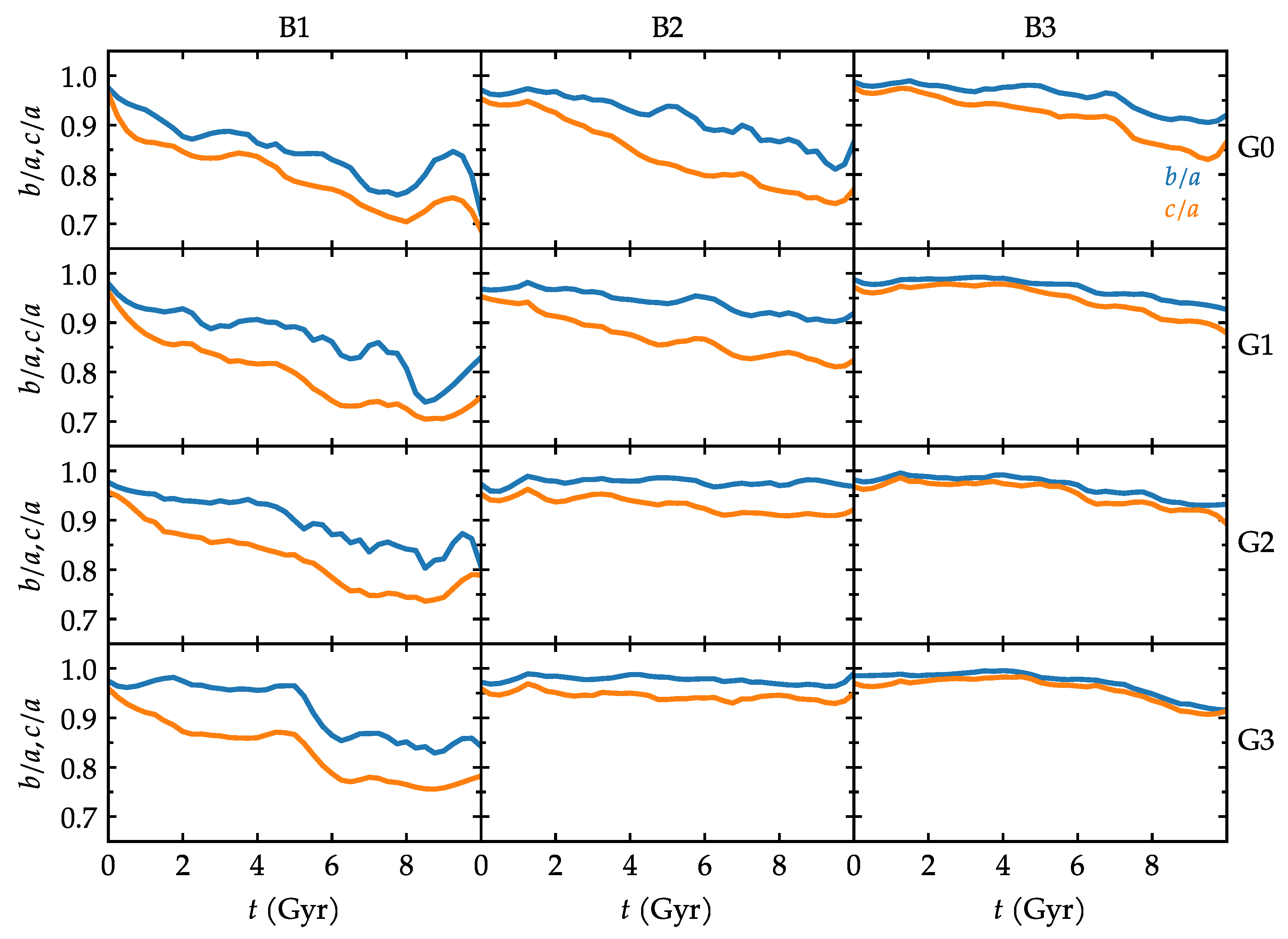
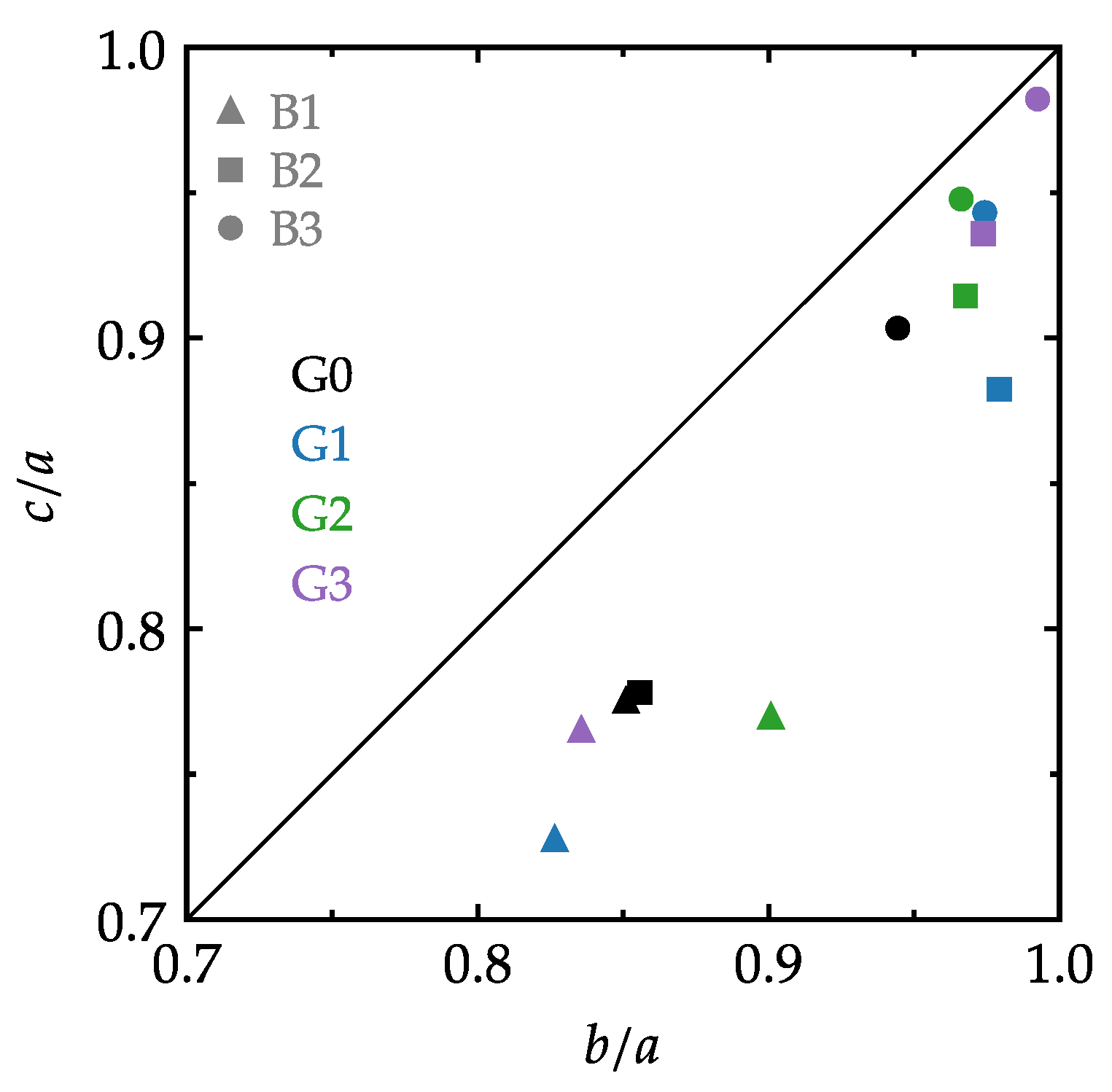
3.4. Bulge Shape
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Numerical Resolution
| Model | ||||||||
|---|---|---|---|---|---|---|---|---|
| () | () | () | () | |||||
| B3G3 | 1,000,000 | 140,000 | 60,000 | 200,000 | 9.0 | 1.8 | 2.6 | 0.6 |
| B3G3-em | 3,461,538 | 98,720 | 60,000 | 42,308 | 2.6 | 2.6 | 2.6 | 2.6 |
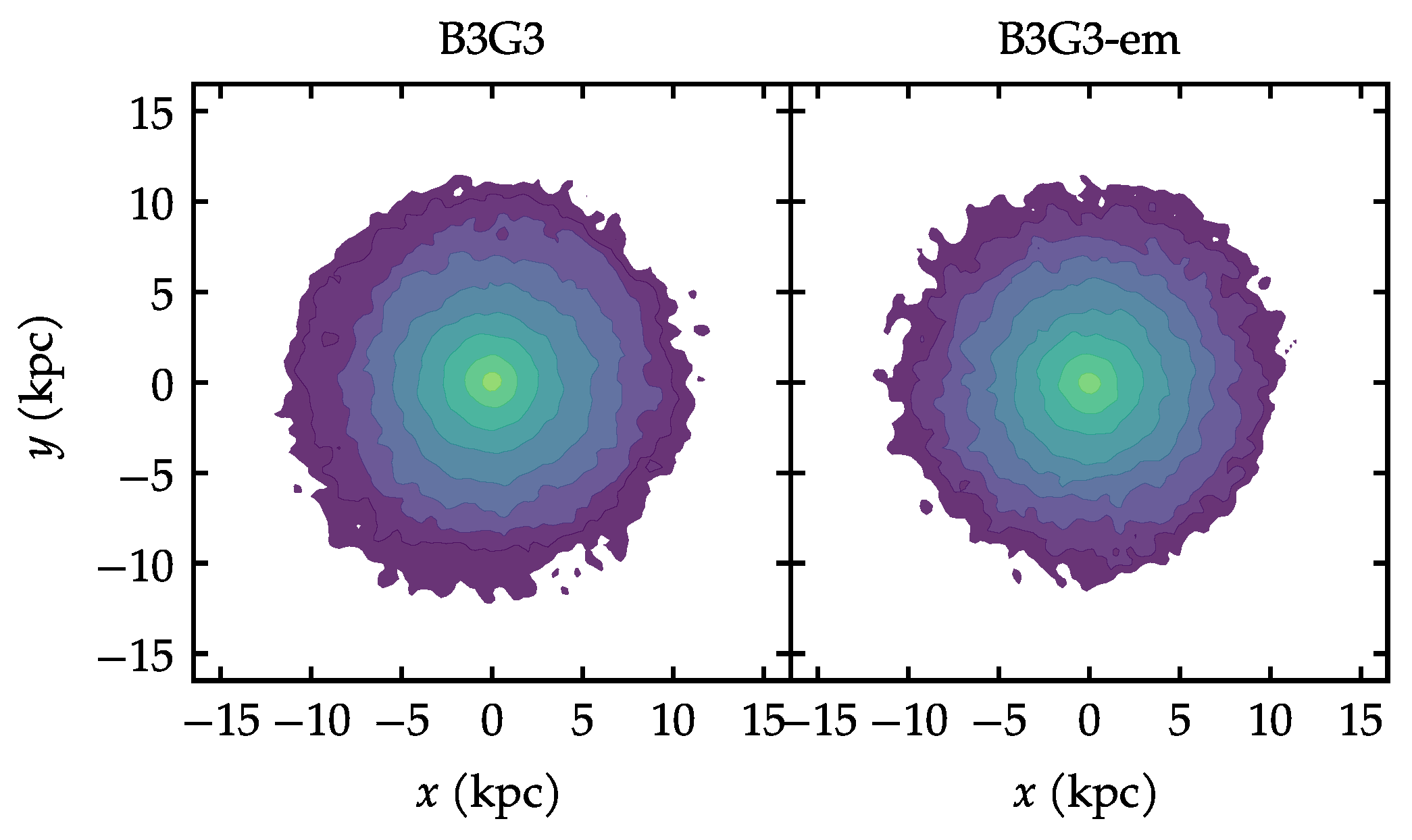
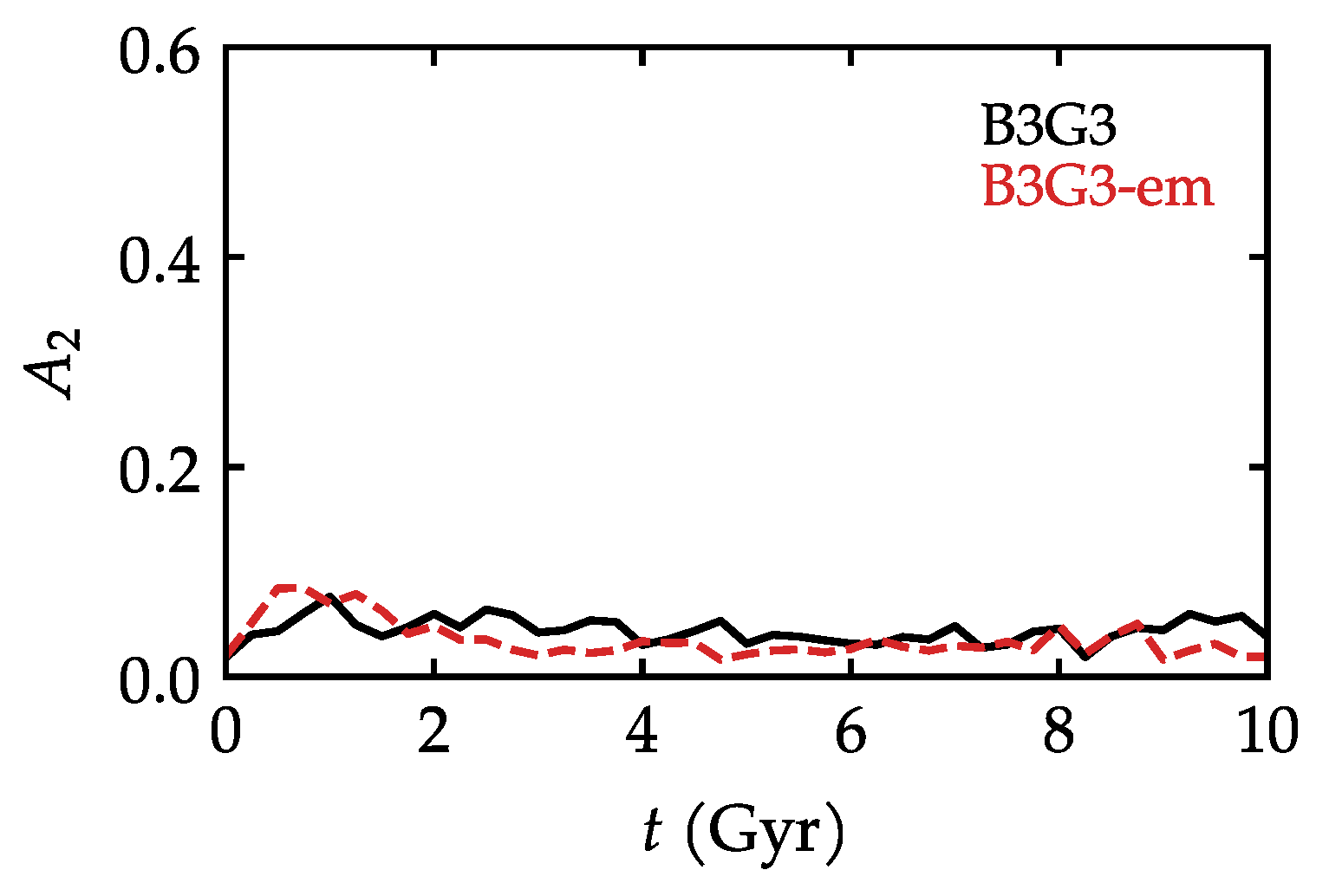
Appendix B. Resonances
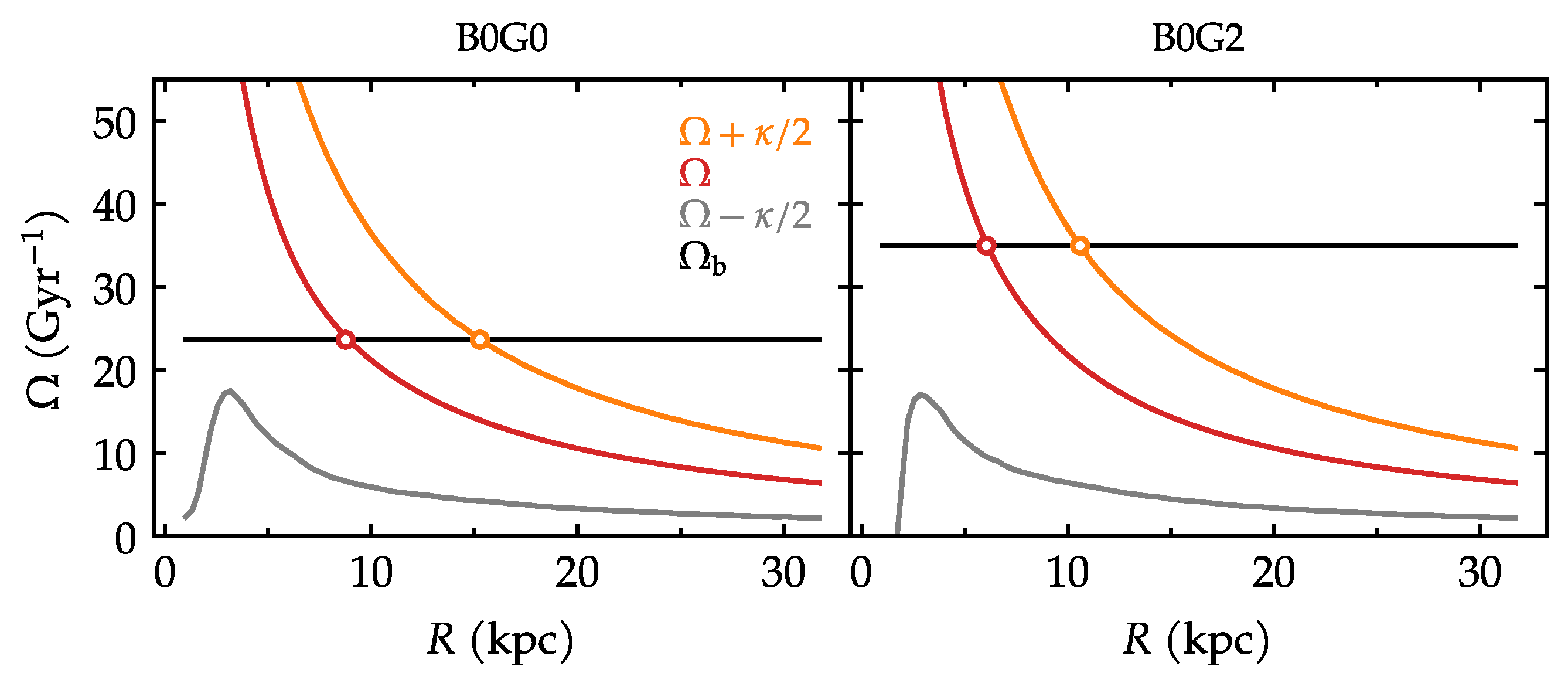
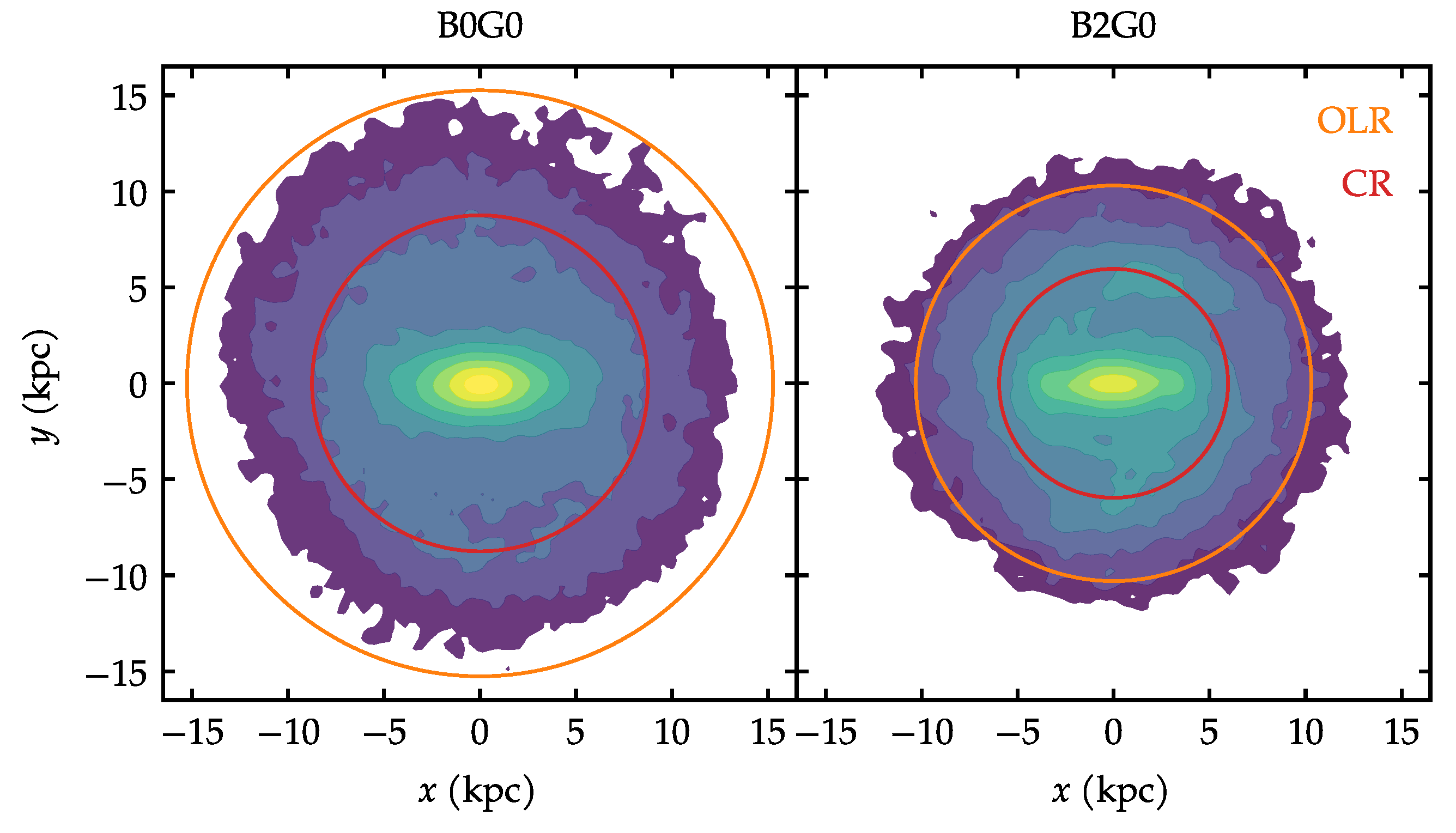

References
- Kormendy, J.; Kennicutt, R.C., Jr. Secular Evolution and the Formation of Pseudobulges in Disk Galaxies. Annu. Rev. Astron. Astrophys. 2004, 42, 603–683. [Google Scholar] [CrossRef]
- Gadotti, D.A. Structural properties of pseudo-bulges, classical bulges and elliptical galaxies: A Sloan Digital Sky Survey perspective. Mon. Not. R. Astron. Soc. 2009, 393, 1531–1552. [Google Scholar] [CrossRef]
- Ciambur, B.C.; Graham, A.W. Quantifying the (X/peanut)-shaped structure in edge-on disc galaxies: Length, strength, and nested peanuts. Mon. Not. R. Astron. Soc. 2016, 459, 1276–1292. [Google Scholar] [CrossRef]
- Savchenko, S.S.; Sotnikova, N.Y.; Mosenkov, A.V.; Reshetnikov, V.P.; Bizyaev, D.V. Measuring the X-shaped structures in edge-on galaxies. Mon. Not. R. Astron. Soc. 2017, 471, 3261–3272. [Google Scholar] [CrossRef]
- Athanassoula, E. Dynamical Evolution of Barred Galaxies. Celest. Mech. Dyn. Astron. 2005, 91, 9–31. [Google Scholar] [CrossRef]
- Martinez-Valpuesta, I.; Shlosman, I.; Heller, C. Evolution of Stellar Bars in Live Axisymmetric Halos: Recurrent Buckling and Secular Growth. Astrophys. J. 2006, 637, 214–226. [Google Scholar] [CrossRef]
- Okas, E.L. Anatomy of a buckling galactic bar. Astron. Astrophys. 2019, 629, A52. [Google Scholar] [CrossRef]
- Anderson, S.R.; Gough-Kelly, S.; Debattista, V.P.; Du, M.; Erwin, P.; Cuomo, V.; Caruana, J.; Hernquist, L.; Vogelsberger, M. The interplay between accretion, downsizing, and the formation of box/peanut bulges in TNG50. Mon. Not. R. Astron. Soc. 2024, 527, 2919–2939. [Google Scholar] [CrossRef]
- Hopkins, P.F.; Cox, T.J.; Younger, J.D.; Hernquist, L. How do Disks Survive Mergers? Astrophys. J. 2009, 691, 1168–1201. [Google Scholar] [CrossRef]
- Hopkins, P.F.; Bundy, K.; Croton, D.; Hernquist, L.; Keres, D.; Khochfar, S.; Stewart, K.; Wetzel, A.; Younger, J.D. Mergers and Bulge Formation in ΛCDM: Which Mergers Matter? Astrophys. J. 2010, 715, 202–229. [Google Scholar] [CrossRef]
- Menéndez-Delmestre, K.; Sheth, K.; Schinnerer, E.; Jarrett, T.H.; Scoville, N.Z. A Near-Infrared Study of 2MASS Bars in Local Galaxies: An Anchor for High-Redshift Studies. Astrophys. J. 2007, 657, 790–804. [Google Scholar] [CrossRef]
- Sheth, K.; Elmegreen, D.M.; Elmegreen, B.G.; Capak, P.; Abraham, R.G.; Athanassoula, E.; Ellis, R.S.; Mobasher, B.; Salvato, M.; Schinnerer, E.; et al. Evolution of the Bar Fraction in COSMOS: Quantifying the Assembly of the Hubble Sequence. Astrophys. J. 2008, 675, 1141–1155. [Google Scholar] [CrossRef]
- Saha, K.; Martinez-Valpuesta, I.; Gerhard, O. Spin-up of low-mass classical bulges in barred galaxies. Mon. Not. R. Astron. Soc. 2012, 421, 333–345. [Google Scholar] [CrossRef]
- Saha, K.; Gerhard, O.; Martinez-Valpuesta, I. Spin-up of massive classical bulges during secular evolution. Astron. Astrophys. 2016, 588, A42. [Google Scholar] [CrossRef]
- Lynden-Bell, D.; Kalnajs, A.J. On the generating mechanism of spiral structure. Mon. Not. R. Astron. Soc. 1972, 157, 1. [Google Scholar] [CrossRef]
- Kormendy, J. A morphological survey of bar, lens, and ring components in galaxies: Secular evolution in galaxy structure. Astrophys. J. 1979, 227, 714–728. [Google Scholar] [CrossRef]
- Sellwood, J.A. Galaxy models with live halos. Astron. Astrophys. 1980, 89, 296–307. [Google Scholar]
- Hernquist, L.; Weinberg, M.D. Bar-Spheroid Interaction in Galaxies. Astrophys. J. 1992, 400, 80. [Google Scholar] [CrossRef]
- Athanassoula, E.; Misiriotis, A. Morphology, photometry and kinematics of N -body bars—I. Three models with different halo central concentrations. Mon. Not. R. Astron. Soc. 2002, 330, 35–52. [Google Scholar] [CrossRef]
- Athanassoula, E. What determines the strength and the slowdown rate of bars? Mon. Not. R. Astron. Soc. 2003, 341, 1179–1198. [Google Scholar] [CrossRef]
- Weinberg, M.D.; Katz, N. The bar-halo interaction—II. Secular evolution and the religion of N-body simulations. Mon. Not. R. Astron. Soc. 2007, 375, 460–476. [Google Scholar] [CrossRef]
- Athanassoula, E.; Machado, R.E.G.; Rodionov, S.A. Bar formation and evolution in disc galaxies with gas and a triaxial halo: Morphology, bar strength and halo properties. Mon. Not. R. Astron. Soc. 2013, 429, 1949–1969. [Google Scholar] [CrossRef]
- Hernquist, L. An analytical model for spherical galaxies and bulges. Astrophys. J. 1990, 356, 359–364. [Google Scholar] [CrossRef]
- Hetznecker, H.; Burkert, A. The evolution of the dark halo spin parameters λ and λ’ in a ΛCDM universe: The role of minor and major mergers. Mon. Not. R. Astron. Soc. 2006, 370, 1905–1914. [Google Scholar] [CrossRef]
- Rodriguez-Gomez, V.; Genel, S.; Fall, S.M.; Pillepich, A.; Huertas-Company, M.; Nelson, D.; Pérez-Montaño, L.E.; Marinacci, F.; Pakmor, R.; Springel, V.; et al. Galactic angular momentum in the IllustrisTNG simulation—I. Connection to morphology, halo spin, and black hole mass. Mon. Not. R. Astron. Soc. 2022, 512, 5978–5994. [Google Scholar] [CrossRef]
- Springel, V.; Di Matteo, T.; Hernquist, L. Modelling feedback from stars and black holes in galaxy mergers. Mon. Not. R. Astron. Soc. 2005, 361, 776–794. [Google Scholar] [CrossRef]
- Springel, V. The cosmological simulation code GADGET-2. Mon. Not. R. Astron. Soc. 2005, 364, 1105–1134. [Google Scholar] [CrossRef]
- Machado, R.E.G.; Athanassoula, E. Loss of halo triaxiality due to bar formation. Mon. Not. R. Astron. Soc. 2010, 406, 2386–2404. [Google Scholar] [CrossRef]
- Kataria, S.K.; Das, M. A study of the effect of bulges on bar formation in disc galaxies. Mon. Not. R. Astron. Soc. 2018, 475, 1653–1664. [Google Scholar] [CrossRef]
- Iannuzzi, F.; Athanassoula, E. 2D kinematic signatures of boxy/peanut bulges. Mon. Not. R. Astron. Soc. 2015, 450, 2514–2538. [Google Scholar] [CrossRef]
- Collier, A.; Shlosman, I.; Heller, C. What makes the family of barred disc galaxies so rich: Damping stellar bars in spinning haloes. Mon. Not. R. Astron. Soc. 2018, 476, 1331–1344. [Google Scholar] [CrossRef]
- Berentzen, I.; Shlosman, I.; Jogee, S. Stellar Bar Evolution in Cuspy and Flat-cored Triaxial CDM Halos. Astrophys. J. 2006, 637, 582–597. [Google Scholar] [CrossRef]
- Villa-Vargas, J.; Shlosman, I.; Heller, C. Dark Matter Halos and Evolution of Bars in Disk Galaxies: Collisionless Models Revisited. Astrophys. J. 2009, 707, 218–232. [Google Scholar] [CrossRef]
- Collier, A.; Shlosman, I.; Heller, C. Dark matter bars in spinning haloes. Mon. Not. R. Astron. Soc. 2019, 488, 5788–5801. [Google Scholar] [CrossRef]
- Collier, A.; Shlosman, I.; Heller, C. Stellar bars in counter-rotating dark matter haloes: The role of halo orbit reversals. Mon. Not. R. Astron. Soc. 2019, 489, 3102–3115. [Google Scholar] [CrossRef]
- O’Neill, J.K.; Dubinski, J. Detailed comparison of the structures and kinematics of simulated and observed barred galaxies. Mon. Not. R. Astron. Soc. 2003, 346, 251–264. [Google Scholar] [CrossRef]
- Colín, P.; Valenzuela, O.; Klypin, A. Bars and Cold Dark Matter Halos. Astrophys. J. 2006, 644, 687–700. [Google Scholar] [CrossRef]
- Athanassoula, E. A bar in the inner halo of barred galaxies—I. Structure and kinematics of a representative model. Mon. Not. R. Astron. Soc. 2007, 377, 1569–1578. [Google Scholar] [CrossRef]
- Gonzalez, O.A.; Rejkuba, M.; Zoccali, M.; Valent, E.; Minniti, D.; Tobar, R. Reddening and metallicity maps of the Milky Way bulge from VVV and 2MASS. III. The first global photometric metallicity map of the Galactic bulge. Astron. Astrophys. 2013, 552, A110. [Google Scholar] [CrossRef]
- Zoccali, M.; Hill, V.; Lecureur, A.; Barbuy, B.; Renzini, A.; Minniti, D.; Gómez, A.; Ortolani, S. The metal content of bulge field stars from FLAMES-GIRAFFE spectra. I. Stellar parameters and iron abundances. Astron. Astrophys. 2008, 486, 177–189. [Google Scholar] [CrossRef]
- Zoccali, M.; Vasquez, S.; Gonzalez, O.A.; Valenti, E.; Rojas-Arriagada, A.; Minniti, J.; Rejkuba, M.; Minniti, D.; McWilliam, A.; Babusiaux, C.; et al. The GIRAFFE Inner Bulge Survey (GIBS). III. Metallicity distributions and kinematics of 26 Galactic bulge fields. Astron. Astrophys. 2017, 599, A12. [Google Scholar] [CrossRef]
- Ness, M.; Freeman, K.; Athanassoula, E.; Wylie-De-Boer, E.; Bland-Hawthorn, J.; Lewis, G.F.; Yong, D.; Asplund, M.; Lane, R.R.; Kiss, L.L.; et al. The Origin of the Split Red Clump in the Galactic Bulge of the Milky Way. Astrophys. J. 2012, 756, 22. [Google Scholar] [CrossRef]
- Springel, V.; Pakmor, R.; Pillepich, A.; Weinberger, R.; Nelson, D.; Hernquist, L.; Vogelsberger, M.; Genel, S.; Torrey, P.; Marinacci, F.; et al. First results from the IllustrisTNG simulations: Matter and galaxy clustering. Mon. Not. R. Astron. Soc. 2018, 475, 676–698. [Google Scholar] [CrossRef]
- Hopkins, P.F.; Wetzel, A.; Kereš, D.; Faucher-Giguère, C.A.; Quataert, E.; Boylan-Kolchin, M.; Murray, N.; Hayward, C.C.; Garrison-Kimmel, S.; Hummels, C.; et al. FIRE-2 simulations: Physics versus numerics in galaxy formation. Mon. Not. R. Astron. Soc. 2018, 480, 800–863. [Google Scholar] [CrossRef]
- Khoperskov, S.; Di Matteo, P.; Gerhard, O.; Katz, D.; Haywood, M.; Combes, F.; Berczik, P.; Gomez, A. The echo of the bar buckling: Phase-space spirals in Gaia Data Release 2. Astron. Astrophys. 2019, 622, L6. [Google Scholar] [CrossRef]
- Bennett, M.; Bovy, J.; Hunt, J.A.S. Exploring the Sgr-Milky Way-disk Interaction Using High-resolution N-body Simulations. Astrophys. J. 2022, 927, 131. [Google Scholar] [CrossRef]
- Dehnen, W.; Semczuk, M.; Schönrich, R. Measuring bar pattern speeds from single simulation snapshots. Mon. Not. R. Astron. Soc. 2023, 518, 2712–2718. [Google Scholar] [CrossRef]
- Binney, J.; Tremaine, S. Galactic Dynamics, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]





| Label | Bulge Fraction | Gas Fraction | ||||
|---|---|---|---|---|---|---|
| (%) | (%) | () | () | () | () | |
| B0G0 | 0 | 0 | 90 | 5.2 | 0 | 0 |
| B0G1 | 0 | 10 | 90 | 4.7 | 0 | 0.5 |
| B0G2 | 0 | 20 | 90 | 4.2 | 0 | 1 |
| B0G3 | 0 | 30 | 90 | 3.6 | 0 | 1.6 |
| B1G0 | 10 | 0 | 90 | 4.2 | 0.5 | 0 |
| B1G1 | 10 | 10 | 90 | 4.2 | 0.5 | 0.5 |
| B1G2 | 10 | 20 | 90 | 3.7 | 0.5 | 1 |
| B1G3 | 10 | 30 | 90 | 3.3 | 0.5 | 1.4 |
| B2G0 | 20 | 0 | 90 | 4.2 | 1 | 0 |
| B2G1 | 20 | 10 | 90 | 3.8 | 1 | 0.4 |
| B2G2 | 20 | 20 | 90 | 3.3 | 1 | 0.9 |
| B2G3 | 20 | 30 | 90 | 2.9 | 1 | 1.3 |
| B3G0 | 30 | 0 | 90 | 3.7 | 1.5 | 0 |
| B3G1 | 30 | 10 | 90 | 3.3 | 1.5 | 0.4 |
| B3G2 | 30 | 20 | 90 | 2.9 | 1.5 | 0.8 |
| B3G3 | 30 | 30 | 90 | 2.6 | 1.5 | 1.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Machado, R.E.G.; Sakamoto, K.R.; Wille, A.; Gonçalves, G.F. The Rotation of Classical Bulges in Barred Galaxies in the Presence of Gas. Universe 2024, 10, 223. https://doi.org/10.3390/universe10050223
Machado REG, Sakamoto KR, Wille A, Gonçalves GF. The Rotation of Classical Bulges in Barred Galaxies in the Presence of Gas. Universe. 2024; 10(5):223. https://doi.org/10.3390/universe10050223
Chicago/Turabian StyleMachado, Rubens E. G., Kenzo R. Sakamoto, Andressa Wille, and Gustavo F. Gonçalves. 2024. "The Rotation of Classical Bulges in Barred Galaxies in the Presence of Gas" Universe 10, no. 5: 223. https://doi.org/10.3390/universe10050223
APA StyleMachado, R. E. G., Sakamoto, K. R., Wille, A., & Gonçalves, G. F. (2024). The Rotation of Classical Bulges in Barred Galaxies in the Presence of Gas. Universe, 10(5), 223. https://doi.org/10.3390/universe10050223






