Abstract
This paper reviews the dynamics of a single isotropic and homogeneous scalar field in the context of cosmological models. A non-standard approach to the solution of the Einstein–Klein–Gordon equations is described which uses the scalar field as the evolution parameter for cosmic dynamics. General conclusions about the qualitative behaviour of the solutions can be drawn, and examples of how to obtain explicit solutions for some cosmological models of interest are given. For arbitrary potentials, analytical results can be obtained from the slow-roll approximation by using a series expansion for the Hubble parameter , from which a quantitative estimate for the number of e-folds of expansion is obtained. This approach is illustrated with the examples of quadratic potentials and hilltop models, with special consideration of Higgs-type potentials. The GUT-scale is shown to come out of such a model quite naturally. Finally, it is discussed how to find scalar potentials giving rise to a predetermined scalar-field behaviour and the associated evolution of the scale factor.
1. Introduction and motivation
Observations of variable stars, such as type Ia supernovae, and the distribution of galaxies in the universe, as well as the detailed maps of the Cosmic Microwave Background (CMB) made by the successive COBE, WMAP and PLANCK missions, have provided impressive amounts of data which allow us to trace the evolution of the universe over the last 13.8 billion years, back to a time at which the universe was more than 1000 times smaller in all directions [1,2,3]. What those studies have taught us is that for most of that past, the rate of cosmic expansion was determined by the density of massive matter in the universe. About one-seventh of that matter is of the baryonic type, mostly hydrogen and helium. The rest is of a different, unknown, but electrically neutral type; it is generally referred to as dark matter.
Surprisingly, however, since a little more than four billion years ago, the rate of cosmic expansion has become dominated by another source of energy density, which is not a kind of massive matter [4,5]. In view of its unknown nature, and as it makes its presence known exclusively via the accelerated rate of expansion of the universe, it is referred to as dark energy. In the context of General Relativity (GR), it can be parametrized by a cosmological constant. But, as there is presently no information on the evolution of dark energy from earlier times, it is impossible to say if it has always been really constant, or whether the dark energy density evolves itself over cosmological times. Another possible scenario would be for the cosmic expansion to be driven in part by one or more cosmic scalar fields, the energy of which can vary during the evolution of the universe. Such scenarios have been widely discussed, e.g., in the context of cosmic quintessence models [6,7].
Another epoch of accelerating expansion of the universe is thought to have taken place in a very early phase to explain the present homogeneity and isotropy of the cosmos, and in particular of the CMB, in which fluctuations are smaller than one part in . This era of cosmic inflation must have smoothed out any inhomogeneities in the distribution of matter and radiation in the part of the universe within our cosmic horizon [8,9,10,11,12]. Its origin is likewise to be traced to some source of cosmic vacuum energy for which a scalar field, referred to as the inflaton field, may have been responsible.
As the discovery of the Higgs particle has made clear, scalar fields also play an important role in particle physics, where the Brout–Englert–Higgs (BEH) field is responsible for the masses of weak vector bosons and charged leptons, and contributes to those of quarks. The mechanism behind the BEH effect is the non-zero vacuum expectation value (vev) acquired by the scalar field, which couples to particle fields with no mass to begin with. The vev of the scalar field is, however, temperature-dependent, and can therefore change over the life time of the universe. This suggests there may have been a period in the very early universe at extremely high temperature during which symmetry was not yet broken and leptons and vector bosons were all massless. Such a scenario then creates the problem, that the energy density of the BEH field at very early times would have been hugely different from the present (in which it contributes virtually nothing to the cosmic energy density). Presumably at that time, this energy density would have contributed to a very fast expansion of the universe. Indeed, models in which the standard-model BEH field is the source of inflation have been studied by various authors [13,14,15,16,17,18].
These considerations arising from both cosmology and particle physics make it desirable to develop a good understanding of the joint evolution of scalar fields and the expansion rate of the universe. There is, in fact, already a large literature on the subject; for an introduction, see, e.g., refs. [19,20] and references therein. In the following, we explore a non-standard approach to this topic based on earlier work [21,22,23]. This approach is useful in various contexts, not only to solve the equations of motion, but, for example, also to find the potential and the scale factor necessary to produce a certain prescribed evolution of the scalar field.
2. Modelling Cosmological Scalar Fields
We do not know how many fundamental scalar fields might contribute to the cosmic expansion. But, we can assume the combined potential of the scalars to form a landscape in which there is an effective potential with a well-defined minimum; if there would be a flat region near the minimum, this would give rise to massless or nearly massless (pseudo) Goldstone bosons, which we exclude. We also assume that any potential symmetries between the scalar fields are broken near the minimum. This implies that the effective scalar field fluctuates in a single direction in the scalar landscape. This assumption greatly facilitates our analysis. Another simplifying assumption, based on well-established observational evidence, is that the universe is taken to be spatially flat.
The resulting cosmological model is that of a single homogeneous scalar field in a homogeneous and isotropic universe, of which the scale factor evolves as determined by the Hubble parameter . The dynamics of these parameters is described by the Klein–Gordon equation in a homogeneous and isotropic space-time:
for the scalar field with potential , combined with the Einstein equation
where is the Planck length (in natural units with ). For periods of time in which the scalar field changes monotonically—e.g., during the period of an oscillation between two extreme values—the evolution of the Hubble parameter can be linked to that of the scalar field by considering it as an implicit function of time in terms of its dependence on the scalar field: . Such a point of view turns out to be remarkably fruitful [21,22,23]. First, note that
where the prime denotes differentiation with respect to the field . Differentiation of Equation (2) with respect to time with use of the KG equation then implies
Therefore, either the universe is static and flat and , or
It follows that Equation (2) can be cast in a form determining :
The points where this description can break down are critical points , where the evolution of the scalar field stops: ; at these points, and . Such points are classified as follows:
(a) End points of evolution occurring when
end points can be stable (in a minimum) or unstable (at a maximum or saddle point).
(b) Turning points, where
As in both cases , in case (a), the second derivative of the Hubble parameter must be finite: . In case (b), this quantity must diverge:
As an example, consider the case of a quadratic potential [23]
Then, the critical points are related by
Equation (11) defines a hyperbola, the shape of which is determined by the sign of the vacuum energy (Figure 1). For and positive H, there is a single branch with a minimum at . This minimum represents an endpoint of evolution corresponding to a de Sitter universe with a positive cosmological constant; for , the hyperbola degenerates into the asymptotic straight lines, and the end point of evolution becomes Minkowski space with . Finally, for , the critical curve is hyperbola with two branches, allowing the field to evolve from an expanding regime in which to the contracting regime ; the universe will then start to coalesce as soon as H crosses into negative values and total collapse becomes inevitable.
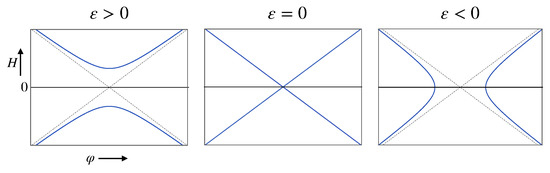
Figure 1.
Critical points of for scalar field with quadratic potential. Adapted from [23].
These scenarios are illustrated in Figure 2, showing some numerical solutions of Equation (6) for the case of the quadratic potential (10) with (Figure 2a) and (Figure 2b), respectively.
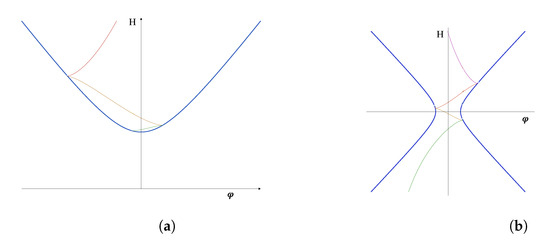
Figure 2.
Evolution curves for a quadratic potential with positive (a) and negative (b) vacuum energy. Adapted from [23].
3. An Exact Solution: Exponential Potentials
In some cases, Equation (6) can be solved exactly in analytical form. As a first step, it is convenient to renormalize the scalar field by
with the result that, upon switching the functional dependence of V and H, we obtain
For the case of non-negative definite potentials , the square root of this equation can be found by defining the function implicitly by
The function K then satisfies the differential equation [22]
As the left-hand side of this equation is odd in K, the two roots are related by ; this results in the same expression for H. Therefore, we can restrict ourselves without loss of generality to the positive sign on the right-hand side.
A particularly simple example arises for exponential potentials [24]
for which
For the special cases , the implicit solution is
The solutions vanishing at , i.e., , have been sketched in Figure 3.
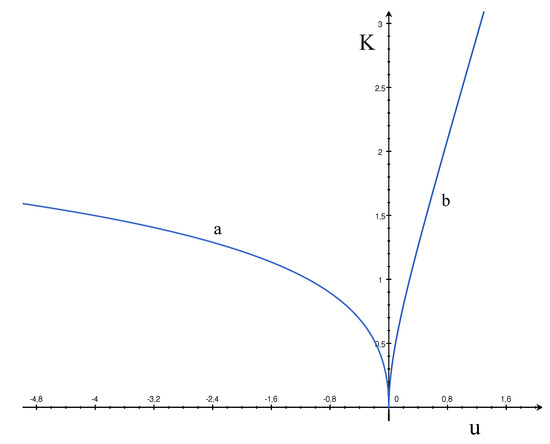
Figure 3.
for the exponential potential (16) with (a) and (b).
For general values of , the implicit solution of Equation (17) is
Substitution of this expression into the potential yield:
Together with the Expression (14), this determines the Hubble parameter as a function of K. Combining this with Equations (18) and (19), we obtain a full set of parametrized solutions .
4. Slow-Roll Approximation
For many scalar potentials, it is not possible to obtain exact solutions of Equation (6) in analytical form. Nevertheless, it is still possible to determine to what extent a certain potential can give rise to periods of accelerated expansion. Indeed, in such periods, the Hubble parameter is supposedly nearly constant, a condition leading to (quasi-)exponential expansion. The condition for changes in the Hubble parameter to be small compared to its value is given in terms of the dimensionless parameter by the inequality
Taking into account Equation (6), this implies
where equality in the second domain limit is reached for critical values such that . The domain of values where these inequalities hold is commonly referred to as the slow-roll region. For the case of the quadratic potential (10), the corresponding regime is sketched in Figure 4.
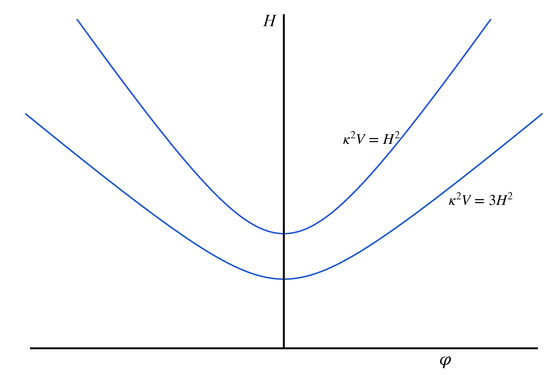
Figure 4.
The slow-roll regime for the quadratic potential (10).
The condition (21) is satisfied at or near critical points , where . This happens trivially at an end point of evolution provided , as
Such a scenario can account for late exponential expansion.
The condition (21) is also satisfied near turning points, where diverges. In this case, Equation (8) implies that near the critical point
As explained in [22] this naturally leads to an expansion of near a turning point in powers of . Therefore, we define a dimensionless field variable by
where the plus sign holds for a left turning point (where ), and the minus sign for a right turning point (where ). Now, expanding
Equation (6) then implies the identity
By substitution of (25) into the potential and comparison of powers of on both sides of the equation the coefficients can be determined.
It is then possible to establish the domain of -values where the inequality (22) is satisfied. This allows the computation of the number of N-folds of expansion created in the neighbourhood of a turning point:
Adding the branch descending from higher values of H and the one descending to lower values of H, we then arrive at the first approximation
where is the range over which the inequality (22) is satisfied.
To obtain a large number of e-folds from the combined left-moving and right-moving branches, it is therefore necessary that
5. Quadratic Potentials
As a typical example, consider the quadratic potential (10); substitution of the expansion (25) then results in
where
The evolution has a stable end point at if either (ending in a de Sitter universe) or (ending in a Minkowski universe). To determine what happens at turning points, compare (31) with (27) to establish that
The sign of is fixed by the sign of , which is determined by which branch of H is considered. For a left turning point, the inequality (22) implies
To this order in , the left inequality can be rewritten
In the limit , this reduces to , such that
For the number of e-folds, we then have
This does not become large for scalar values at or below the Planck scale , unless , when the evolution is already very close to the stable minimum of the potential, the eventual cosmological constant.
6. Hilltop Inflation
In a class of models of accelerated expansion which naturally give rise to large numbers of e-folds, the scalar field evolution starts at a maximum in the potential, a scenario known as hilltop inflation [25,26,27]. A simple example is the Higgs potential
Figure 5 shows the curve of critical points for a potential which has its true minimum at the Minkowski limit ; this happens if
The figure includes parts of a numerical solution of the evolution which comes close to the local maximum at . The local maximum itself is an end point in the sense of Equation (7), but an unstable end point, as the field will roll down as result of an arbitrary tiny fluctuation. For definiteness, we consider the scenario shown in Figure 5, where the scalar field starts at a small positive field value , and therefore, in the slow-roll approximation, it is parametrized as
In the neighbourhood of the local maximum, in the regime , Equation (37) reduces to that for the inverted quadratic potential corresponding to and . It then follows that the expansions (26) applies to
where . Therefore, to this approximation,
and the applicable range of -values is
The number of e-folds is then also estimated to be
where . Within the limit , the number of e-folds N can become arbitrarily large. For potentials which have an absolute Minkowski minimum, satisfying Equation (38), this becomes
A similar result was derived along a different route in ref. [27].
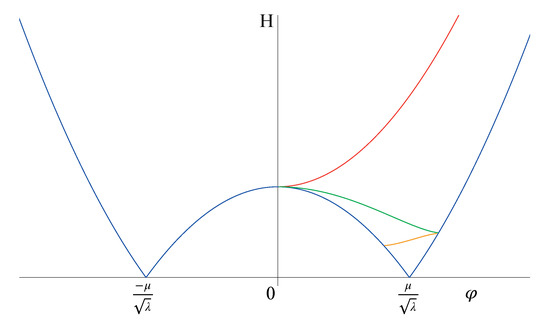
Figure 5.
Critical curve for the Higgs potential. The local maximum at is an unstable end point. Adapted from [23].
A question this scenario raises is how the scalar field happens to arrive at the maximum of the potential. One possibility is that it was caught in a local minimum of the potential before symmetry breaking, which, after a phase transition turned into a local maximum. However, another possibility is that it arrived at the maximum by direct dynamical evolution; remarkably, there is a simple analytical solution of the cosmological scalar field equations for Higgs-type potentials which leads to the unstable final state at the maximum of the potential [21,23]. This solution describes exponential roll-down
For large times , the scalar field (44) tends indeed to , implying that it ends at an end point of evolution. It follows from Equation (5) that
where h is a constant. The corresponding potential is found directly from Equation (6) and takes the form (37) with
The present cosmological energy density requires that the Minkowski limit (38) is realized to great accuracy; this observation imposes the relations
Given the scalar field (44) and the Hubble parameter (45), the evolution of the scale factor during this exponential decay phase can be straightforwardly computed to be [21]
An interesting feature of this solution is that, in addition to eventual exponential expansion with a Hubble constant h, it also describes an early phase of super-exponential expansion during a time , which leads to an additional number of e-folds determined by the initial scalar amplitude:
It follows that the initial value of the Hubble parameter is
This corresponds to the Planck energy if
In the standard scenario, the number of e-folds during inflation is required to be ; as in natural units , which is Planck time, this implies
fixing the time in which the scalar field rolls down to the unstable maximum at . How long it can stay there before rolling down to the minimal value (47) depends on the characteristics of the scalar fluctuations; using the results (43) and (46), the relation between the additional N-folds and the deviation from the exact maximum of the potential becomes
The scalar fluctuations near the minimum of the potential describe Higgs-type particles; their properties follow from the potential
which implies that for the mass of these Higgs particles in terms of the Planck mass is
In standard units, the Higgs mass then is of the order of the GUT scale GeV/. Note that we obtain this number without any input or extrapolation of standard model particle physics. Interestingly, the same energy range for hilltop models was found based on a completely independent comparison with the data of Planck, BICEP/Keck Array, and baryon acoustic oscillations in ref. [28].
7. Discussion
In this overview of isotropic and homogeneous cosmic scalar-field dynamics, we have shown how to solve the combined Einstein–Klein–Gordon field equations by using the field itself as a time variable. Considerable qualitative information is obtained from such a formulation, and in some interesting cases, the evolution of the field and the scale factor can be solved for exactly, without making use of approximations. Even when exact analytical solutions are difficult to obtain, the standard approximation procedure of slow-roll approximation can be used in analytical form by performing series expansion (26) to obtain expressions for the Hubble parameter and the number of e-folds in terms of the parameters of the potential. This was shown explicitly for the case of quadratic potentials, and in the scenario of hilltop inflation models. In the latter case, we also obtained the relation (53) between the number of e-folds and the deviation from the true (unstable) maximum of the potential.
In the analysis of cosmic scalar evolution presented here, the standard slow-roll parameters can be expressed (up to a factor of 2) as
Thus, they have a direct interpretation in terms of the relative slope and curvature of the Hubble parameter as a function of ; these quantities determine where quasi-exponential expansion is likely to occur. However, in our considerations we have not explicitly used a constraint on the parameter, as the series expansion (26) allows for direct estimation of the number of e-folds N given in (29). A discussion of the classification of inflationary models based explicitly on the interplay between the slow-roll parameters can be found in [29].
Finally, as was pointed out before in ref. [21], the descent of the scalar field from Planck-scale values to the local maximum of a Higgs-type potential includes a phase of super-exponential expansion which by itself can be sufficient to explain 60 e-folds of inflation. In this scenario, the Higgs field naturally gives rise to GUT-scale symmetry breaking.
Another advantage of our approach using the scalar field as the evolution parameter for the cosmic expansion is that one can perform reverse engineering of the potential. Namely, given the evolution of the scalar field , integration of the second Equation (5) allows us to determine the Hubble parameter ; substitution of this result into Equation (6) then directly gives the potential for which is the solution of Equation (1). An example of this procedure is the construction of the Higgs-type model (37) from the exponential decay of a scalar field; other examples can be found in ref. [23].
All of our analyses were performed in the context of canonical single-scalar field theories and their classical dynamics. An approach to multi-field dynamics was developed for example in [30], and non-linear scalar models were introduced in the context of k-essence dark energy in [31]. A general discussion of non-linear cosmological scalar field theories can be found in [32]. The UV-completion of cosmological field theories and its impact on predictions for inflation has been studied in [33].
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Fixsen, D.J.; Cheng, E.S.; Gales, J.M.; Mather, J.C.; Shafer, R.A.; Wright, E.L. The Cosmic Microwave Background Spectrum from the full COBE FIRAS Data Set. Astrophys. J. 1996, 473, 576. [Google Scholar] [CrossRef]
- Hinshaw, G. et al. [WMAP Collab] Nine-year WMAP observations: Final maps and results. Astrophys. J. 2013, 208, 19. [Google Scholar] [CrossRef]
- Aghanim, N. et al. [Planck Collab] Planck 2018 results I. Overview and the cosmological legacy of Planck. Astron. Astrophys. 2020, 641, A1. [Google Scholar]
- Betoule, M. et al. [SDDS-II and SNLS Collab] Improved cosmological constraints from a joint analysis of the SDSS-II and SNLS supernova samples. Astron. Astrophys. 2014, 568, A22. [Google Scholar] [CrossRef]
- Abbott, T.M.C. et al. [DES Collab] Dark Energy Survey Year 3 Results: Cosmological Constraints from Galaxy Clutering and Weak Lensing. arXiv 2022, arXiv:2105.13549. [Google Scholar]
- Wetterich, C. Cosmology and the fate of dilatation symmetry. Nucl. Phys. B 1988, 302, 668. [Google Scholar] [CrossRef]
- Zlatev, I.; Wang, L.; Steinhardt, P. Quintessence, Cosmic Coincidence, and the Cosmological Constant. Phys. Rev. Lett. 1999, 82, 896. [Google Scholar] [CrossRef]
- Starobinsky, A. A new type of isotropic cosmological models without singularity. Phys. Lett. B 1980, 91, 99. [Google Scholar] [CrossRef]
- Guth, A. Inflationary universe: A possible solution to the horizon and flatness problems. Phys. Rev. D 1981, 23, 347. [Google Scholar] [CrossRef]
- Albrecht, A.; Steinhardt, P. Cosmology for Grand Unified Theories with Radiatively Induced Symmetry Breaking. Phys. Rev. Lett. 1982, 48, 1220. [Google Scholar] [CrossRef]
- Linde, A. Chaotic inflation. Phys. Lett. B 1983, 129, 177. [Google Scholar] [CrossRef]
- Turner, M.S. Coherent scalar-field oscillations in an expanding universe. Phys. Rev. D 1983, 28, 1243. [Google Scholar] [CrossRef]
- Futamase, T.; Maeda, K.-I. Chaotic inflationary scenario in models having nonminimal coupling with curvature. Phys. Rev. D 1989, 39, 399. [Google Scholar] [CrossRef] [PubMed]
- Cervantes-Cota, J.L.; Dehnen, H. Induced gravity inflation in the standard model of particle physics. Nucl. Phys. B 1995, 442, 391. [Google Scholar] [CrossRef]
- Bezrukov, F.L.; Shaposhnikov, M. The standard model Higgs boson as the inflaton. Phys. Lett. B 2008, 659, 703. [Google Scholar] [CrossRef]
- Hamada, Y.; Kawai, H.; Oda, K.-Y.; Park, S.C. Higgs Inflation is Still Alive after the Results from BICEP2. Phys. Rev. Lett. 2014, 112, 241301. [Google Scholar] [CrossRef] [PubMed]
- Calmet, X.; Kuntz, I. Higgs Starobinsky Inflation. Eur. Phys. J. C 2016, 76, 289. [Google Scholar] [CrossRef]
- Ema, Y.; Mukaida, K.; Vis, J.V. Higgs Inflation as Nonlinear Sigma Model and Scalaron as its σ-meson. J. High Energy Phys. 2020, 11, 011. [Google Scholar] [CrossRef]
- Weinberg, S. Cosmology; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Martin, J.; Ringeval, C.; Vennin, V. Encyclopaedia Inflationaris. Phys. Dark Univ. 2014, 5–6, 75. [Google Scholar] [CrossRef]
- van Holten, J.W. Cosmological Higgs fields. Phys. Rev. Lett. 2002, 89, 201301. [Google Scholar] [CrossRef]
- van Holten, J.W. On single scalar field cosmology. arXiv 2013, arXiv:1301.1174v2. [Google Scholar]
- van Holten, J.W. Single scalar cosmology. Int. J. Mod. Phys. A 2013, 28, 1350132. [Google Scholar] [CrossRef]
- Halliwell, J.J. Scalar fields in cosmology with an exponential potential. Phys. Lett. B 1987, 185, 341. [Google Scholar] [CrossRef]
- Boubekeur, L.; Lyth, D. Hilltop Inflation. J. Cosmol. Astropart. Phys. 2005, 0507, 010. [Google Scholar] [CrossRef]
- Kallosh, R.; Linde, A. On hilltop and brane inflation after Planck. J. Cosmol. Astropart. Phys. 2019, 2019, 030. [Google Scholar] [CrossRef]
- Dimopoulos, K. An analytic treatment of quartic hilltop inflation. Phys. Lett. B 2020, 809, 135688. [Google Scholar] [CrossRef]
- Lillepalu, H.G.; Racioppi, A. Generalized hilltop inflation. Eur. Phys. J. Plus 2023, 138, 894. [Google Scholar] [CrossRef]
- Roest, D. Universality classes of inflation. J. Cosmol. Astropart. Phys. 2014, 01, 007. [Google Scholar] [CrossRef]
- Nibbelink, S.G.Ġ.; van Tent, B.J.W. Scalar perturbations during multiple-field slow-roll inflation. Class. Quantum Grav. 2002, 19, 613. [Google Scholar] [CrossRef]
- Armendáriz-Picón, C.; Damour, T.; Mukhanov, V. k-Inflation. Phys. Lett. B 1999, 458, 209–218. [Google Scholar] [CrossRef]
- van Holten, J.W.; Kerner, R. Time-reparametrization invariance and Hamilton-Jacobi approach to the cosmological σ-model. Fortschr. Phys. 2014, 62, 543. [Google Scholar] [CrossRef]
- Burgess, C.P.; Patil, A.P.; Trott, M. On the Predictiveness of Single-Field Inflationary Models. J. High Energy Phys. 2014, 1406, 010. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).