Abstract
We aim to constrain the stellar initial mass function (IMF) during the epoch of reionization. To this purpose, we build up a semi-empirical model for the reionization history of the Universe based on various ingredients: the latest determination of the UV galaxy luminosity function from JWST out to redshift ; data-inferred and simulation-driven assumptions on the redshift-dependent escape fraction of ionizing photons from primordial galaxies; a simple yet flexible parameterization of the IMF ∼ in terms of a high-mass end slope and a characteristic mass , below which a flattening or a bending sets in (allowing description of a variety of IMF shapes from the classic Salpeter to top-heavy ones); the PARSEC stellar evolution code to compute the UV and ionizing emission from different stars’ masses as a function of age and metallicity; and a few physical constraints related to stellar and galaxy formation in faint galaxies at the reionization redshifts. We then compare our model outcomes with the reionization observables from different astrophysical and cosmological probes and perform Bayesian inference on the IMF parameters via a standard MCMC technique. We find that the IMF slope is within the range from to , consistent with direct determination from star counts in the Milky Way, while appreciably flatter slopes are excluded at great significance. However, the bestfit value of the IMF characteristic mass ∼a few implies a suppression in the formation of small stellar masses at variance with the IMF in the local Universe. This may be induced by the thermal background of ∼20–30 K provided by CMB photons at the reionization redshifts. We check that our results are robust against different parameterizations for the redshift evolution of the escape fraction. Finally, we investigate the implications of our reconstructed IMF for the recent JWST detections of massive galaxies at and beyond the reionization epoch, showing that any putative tension with the standard cosmological framework is substantially alleviated.
1. Introduction
One of the very basic ingredients for understanding galaxy formation and evolution is constituted by the stellar initial mass function or IMF , which describes the distribution of stars’ masses per unit solar mass formed. Unfortunately, the IMF is largely uncertain, both from an observational and from a theoretical point of view (see [1,2,3] and references therein).
Based on direct star counts in the Milky Way and its satellite galaxies, the IMF shape has been historically characterized in terms of a power law at the high-mass end [4], going below into a flatter power law [5] or into a log-normal shape [6]. An exponential downturn has been also claimed to occur, especially for metal-poor stars [7,8]. Moreover, there is an ongoing debate in the literature on whether the IMF shape depends on the properties of the galactic environments where star formation proceeds. Redshift, age, metallicity, density/temperature of the interstellar medium, (specific) star formation rate (both volume and surface density), galaxy type, etc., have been proposed as relevant variables for determining the IMF based on theoretical modeling (e.g., [9,10,11,12,13]) and indirect observational evidences (e.g., [14,15,16,17,18]).
In the present work, we aim to provide constraints on the IMF during the epoch of reionization, i.e., a range of redshift z∼6–10 and galaxy properties (e.g., star formation rates yr−1, largely subsolar metallicity, etc.) unexplored so far. Reionization is the process through which the almost neutral intergalactic medium left over from recombination has transitioned again to an ionized state due to the radiation emitted (mainly) by faint primordial galaxies. The history of cosmic reionization that is inferred from cosmological data such as the electron scattering optical depth from the Planck mission [19] or other astrophysical probes [20,21,22,23,24,25,26,27,28,29] can set constraints on the level of the ionizing background from faint primordial galaxies. The background level depends mainly on the galaxy number density, on the escape fraction of ionizing photons from primordial galaxies, and on the IMF [30,31,32,33]. Given that the number density of faint galaxies in the reionization epoch has been constrained to a good accuracy thanks to HST and JWST surveys [34,35,36,37,38,39,40,41,42,43,44] (though an extrapolation to faint magnitudes is still required), and that the redshift-dependent escape fraction can be reasonably assessed via simulations [45,46,47,48,49,50] and indirectly inferred from data [51,52,53,54,55,56,57,58,59,60,61,62], the reionization observables can become a valuable probe for determining the stellar IMF.
Technically, we build a semi-empirical model of cosmic reionization by exploiting (i) robust measurements of the high-redshift UV luminosity functions for primordial galaxies out to redshift from recent JWST data; (ii) data-inferred or simulation-driven assumption on the redshift-dependent escape fraction of ionizing photons from primordial galaxies; (iii) a simple yet flexible parameterization of the IMF; (iv) the PARSEC stellar evolution code to compute the UV and ionizing emission from different stars’ masses as a function of age and metallicity; and (v) a few physical constraints related to stellar and galaxy formation in faint galaxies at the reionization redshifts. We then compare our model outcomes with the reionization observables and perform Bayesian inference on the IMF parameters.
2. Methods and Analysis
In this section, we introduce a basic semi-empirical model of reionization, describe the IMF parameterization, discuss galaxy-formation-informed constraints, and present the Bayesian MCMC framework exploited for parameter estimation.
2.1. Semi-Empirical Model of Reionization
We aim to construct a simple semi-empirical model of reionization along the lines pursued by [30,31,32,33]. To this purpose, we start from the updated determination of the UV luminosity functions calculated by [34,35,36,37,38,39,40,41,42,43,44] from HST and JWST data out to redshift . Specifically, in Figure 1, we illustrate the binned luminosity functions (filled circles) at ≈1600 Å in the redshift range z∼4–16 (color coded). We also display the corresponding double power law rendition (solid lines) in the following form:
where the redshift-dependent parameters , , , and have been determined by a simple fit to the data. Here, plays the role of an overall normalization, and are the slopes at the faint and bright ends, and is a characteristic magnitude describing the knee of the luminosity function, i.e., the transition between the two power laws. The luminosity function is well determined down to UV magnitude for z∼6–10, which constitutes the redshift range most relevant to our analysis, while the measurements at higher redshifts are more scattered and uncertain. The UV magnitude can be converted into monochromatic UV luminosity at 1600 Å as [erg s−1 Hz−1] .
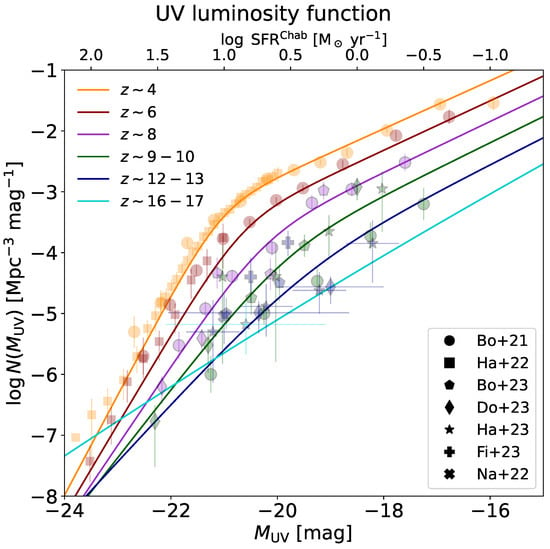
Figure 1.
The UV luminosity functions at redshifts (orange), 6 (brown), 8 (magenta), 9–10 (green), 12–13 (blue), and 16–17 (cyan). Data points are from [34,35] (circles), [36,37] (pentagons), [38,39] (stars), [40] (squares), [41,42] (diamonds), [43] (crosses), and [44] (pluses). Solid colored lines illustrate a double power law function fitted to the data (see text). The scale on the top axis refers to the SFR on adoption of a Chabrier IMF.
The intrinsic UV luminosity can be associated with the star formation rate (SFR) as SFR with the UV photons production efficiency depending on the IMF, on the age, and on the chemical composition [30,31,63,64,65]. For example, a reference value erg s−1 Hz−1 yr applies for a Chabrier IMF, age years, and sub-solar metallicity. This gives the relation log SFR [ yr−1] , which is adopted to build the scale of the top axis of Figure 1. Since most of the ionizing photons are produced in faint galaxies with SFR yr−1, dust absorption is not an issue, and related corrections of the UV luminosity functions can be neglected in the present context [32,33].
The cosmic UV luminosity density is obtained as follows:
where is a limiting magnitude such that, faintward of it, the luminosity function flattens or even bends down because galaxy formation becomes inefficient [66,67,68]. The quantity is uncertain since the UV luminosity function is observed only for magnitudes brighter than , but reionization studies indicate that must be appreciably fainter than this value [30,31,65]. In our analysis, it will be treated as a free parameter to be set by comparison with reionization observables. Our results are robust against the detailed shape of the luminosity function faintward of ∼. For example, instead of extrapolating it with a constant slope down to , one can adopt a smooth, progressive bending by multiplying Equation (1) by a factor for , as suggested by [69]. We have checked that, in the computation of the UV luminosity density, and hence in all our results, this produces a negligible impact.
The resulting UV luminosity density is shown in Figure 2 for three different values of . In particular, our result for agrees with the recent estimates from JWST data [36,37,38,39,41,42]. Note that the latter tends to be appreciably higher for than previous HST estimates [34,35]. This is evident when comparing the fit to JWST data by [41] (dot-dashed line) with the HST measurements by [40] (dotted line). Using a fainter enhances the UV luminosity density since this corresponds to adding galaxies with lower UV luminosity but much higher number density. The UV luminosity density can be expressed as a cosmic SFR density (i.e., the celebrated ‘Madau plot’) by assuming an IMF to compute . In particular, the right axis in Figure 2 shows the results when adopting a Chabrier IMF. In passing, we note that the classic fitting formula for designed by [64] to describe UV and IR data at (dashed line) substantially overestimates the recent JWST determinations for and thus cannot be used in the present context.
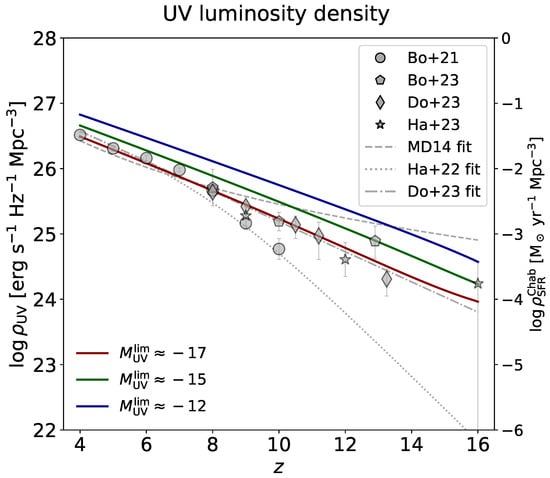
Figure 2.
The UV luminosity density as a function of redshift. Data points are from [34,35] (circles), [36,37] (pentagons), [38,39] (stars), [41,42] (diamonds). Solid colored lines illustrate the outcomes when integrating the UV luminosity function extrapolated down to magnitude limits (red), (green), and (blue). The scale on the right axis refers to the SFR density on adoption of a Chabrier IMF. The gray lines display the parameterization by [40] (dotted), [41] (dot-dashed), and [64] (dashed).
The cosmic ionization photon rate is given by the following [30,65,70,71]:
where is the production efficiency of ionizing photons (per unit SFR), is the average escape fraction from primordial galaxies, and is the ionization rate from active galactic nuclei (AGNs). It is worth discussing each of these quantities in turn. The ionizing photon production efficiency depends on the adopted IMF, age, metallicity, and other stellar population properties [31,65,70]. For example, a reference often adopted for a Chabrier IMF is ionizing photons s−1 yr.
The (spatially averaged) escape fraction from primordial galaxies is still very uncertain, with estimates spanning a range from a few to tens of percent [51,52,53,54,55,56,57,58]. Recent indirect observational estimates of the HI photoionization rate [31,59] and ionizing photon mean-free path [60], direct determinations in Lyman-break galaxies [61,62], and hydrodynamical radiative transfer simulations [49,50] suggest an increasing redshift dependence from a few percent at to about ten percent at z∼10, albeit with a variety of functional shapes. In this work, we stay agnostic and consider in our analysis the four different escape fraction parameterizations [45,46,47,48] that are reported in Figure 3. Note that the non-monotonic dependence of the green curve originates since this is not a fitting function but actually the result of a non-parametric Gaussian-processes-based reconstruction of by [48].
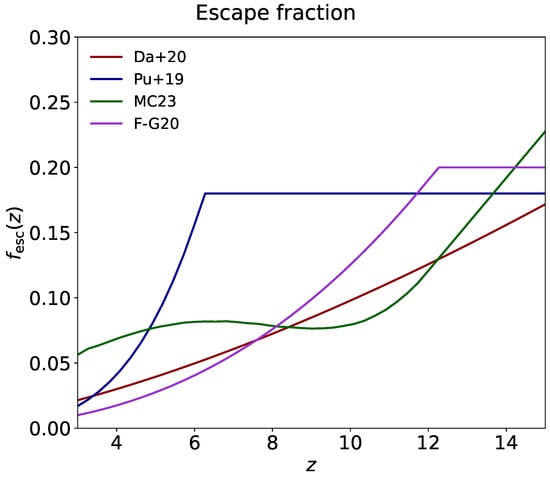
Figure 3.
The spatially averaged escape fraction of ionizing photons from primordial galaxies as a function of redshift. Colored lines refer to the four different parameterizations by [45] (red), [46] (blue), [47] (magenta), and [48] (green).
The AGN contribution in Equation (3) can be parameterized as follows [72]:
This expression relies on recent estimates of the bolometric AGN luminosity functions, which envisage a paucity of luminous quasars and a minor relevance of faint AGNs for , though the debate on the latter point is still open [72,73,74,75,76,77,78]. According to Equation (4), the AGN contribution to for is negligible with respect to primordial galaxies, even assuming ∼ [79,80].
We compute the hydrogen ionizing fraction as
expressing the interplay between ionization and recombination [81,82]. Here, is the mean co-moving hydrogen number density, and is the recombination timescale, which inversely depends on the redshift-dependent clumping factor provided by [83,84]. The electron scattering optical depth is given by
in terms of the Hubble rate and the number of free electrons . More details can be found in [32].
2.2. Initial Mass Function
Since our main aim is to constrain the shape of the IMF, we need an expression of it which is flexible yet does not involve too many parameters. To this purpose, we describe the IMF via a Larson [7] shape in terms of a power law index at high star masses and of a characteristic mass , below which the IMF flattens or even bends downwards. Plainly, the IMF normalization is derived from the condition , where and are the minimum and maximum star masses. The upper end is somewhat uncertain; however, for low-metallicity environments, there is observational evidence in local star-forming regions [85] and from the chemical enrichment in primordial galaxies [86] which suggests . However, such an outcome depends somewhat on the employed wind mass loss rates in high-mass stellar models in such a way that maximum star masses would still be viable. We adopt an effective upper star mass limit , but we have checked that the results of this work, which mainly concerns the UV and ionizing emission from massive stars (for which a rather flat luminosity vs. mass relation applies), are marginally impacted by such a value within the range 200–1000 .
The shape of the IMF for different values of the parameters and is illustrated in Figure 4. The index controls the power law behavior for large masses, and hence the relative number of high-mass stars, while the characteristic mass determines a smooth cutoff toward small stellar masses. Classic IMF shapes are easily reproduced with this parameterization. The Salpeter [4] IMF corresponds to and so that no flattening is present and the IMF is a simple power law. The Kroupa [5] and Chabrier [6] IMFs correspond to or and so that the slope of the IMF progressively flattens below , although no real cutoff is enforced. A top-heavy IMF can be obtained either with flat power law shapes and no cutoff so as to enhance the production of very massive stars or with a more canonical power law index and a cutoff below that strongly suppresses the formation of small/intermediate-mass stars.
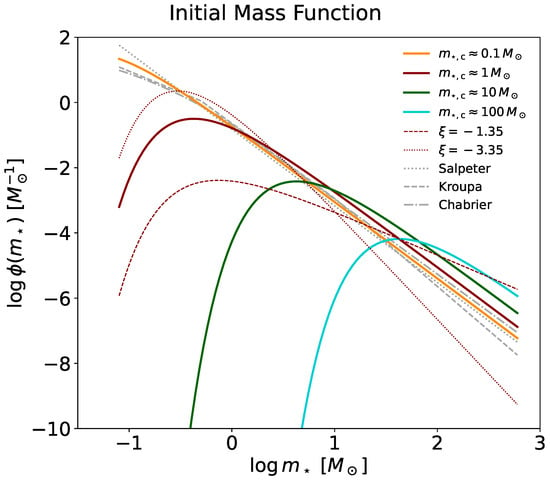
Figure 4.
The initial mass function (IMF) parameterized in terms of a Larson shape [7]. Solid lines refer to a slope and characteristic cutoff masses (orange), (red), (green), and (cyan). The case with is also plotted for different slopes: (red dashed) and (red dotted). The gray lines correspond to the Salpeter [4] (solid), the Kroupa [5] (dashed), and the Chabrier [6] (dot-dashed) IMFs.
The quantities and entered into Equation (3) crucially depend on the adopted IMF. We compute them by exploiting the PARSEC [86,87] stellar evolutionary code, in particular, its recent extension to high-mass stars [86]. The individual stellar tracks are used to compute the mean production rate of UV and ionizing photons, and then and are obtained by appropriately averaging these over the IMF. The outcome is illustrated in Figure 5, where and are plotted as a function of the characteristic mass of the IMF for different values of age, metallicity, and IMF slope.
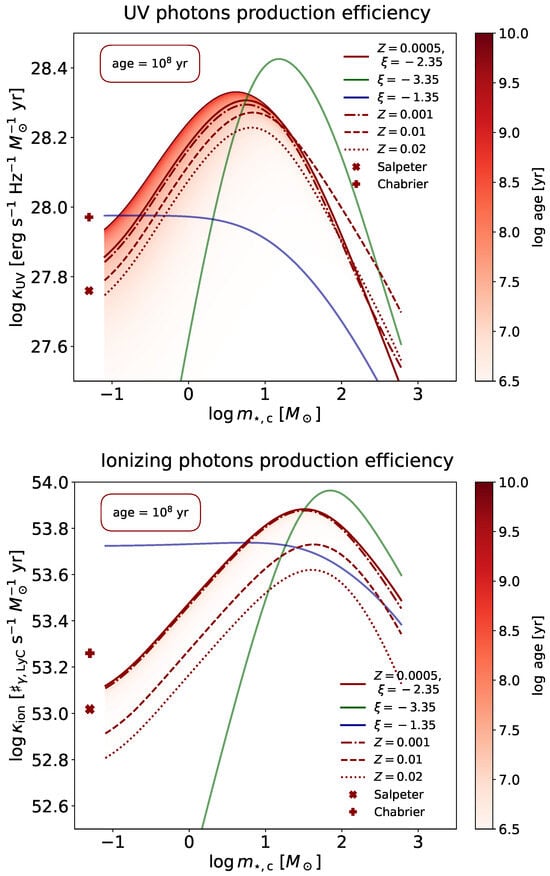
Figure 5.
The production efficiency of UV photons (top panel) and ionizing photons (bottom panel) as a function of the characteristic mass of the IMF. In both panels, the colored lines refer to an age of 100 Myr. The solid line is for an IMF slope and a metallicity . At fixed , the green line is for and the blue for . At fixed , the dot-dashed line is for , the dashed for , and the dotted for . The plus and cross display the reference values for the Salpeter and the Chabrier IMFs. Finally, at fixed and , the shaded area shows the effect of changing the age from 3 Myr to 10 Gyr.
The red solid line refers to a very low metal content , age of 100 Myr, and standard IMF slope . Increasing removes progressively star masses smaller than this value from the IMF, hence, weighting more intermediate- and/or high-mass stars. Therefore, the and follow a bell-shaped trend as a function of since they are maximized when has a value around the star masses, which are the most important contributors to the production of UV or ionizing photons. For , this occurs at around a few , while, for , it is at around a few tens of .
The red dot-dashed, dashed, and dotted curves show the effect of increasing the metallicity. This slightly shifts the peak of the curve toward higher and tends to appreciably reduce the production efficiency, especially in the case of ionizing photons. The red shaded area (as labeled in the color bar) displays the impact of the stellar population age. is mainly contributed by massive stars with very low age so it saturates after a few of years. is contributed also by intermediate-mass stars so it requires several of years to saturate. In the present context of faint galaxies in the reionization era, we can confidently exploit the results for low metallicities and age ≲ a few years.
The blue and green solid lines show, instead, the outcomes when varying the IMF slope. Flattening (steepening) the IMF slope smooths (exacerbates) the dependence of and on the IMF characteristic mass and decreases (increases) the maximal production efficiencies. This is particularly evident for since, e.g., adopting a very flat slope greatly under-weights the intermediate-mass stars that are significant contributors to the total UV photon production.
2.3. Constraints from Galaxy Formation
We now introduce three constraints related to galaxy and star formation in primordial galaxies that will help to break the degeneracies among, and hence better determine, the fitting parameters.
The first constraint concerns the link between the limiting UV magnitude and the minimum halo mass for galaxy formation . The rationale is that, for halo masses smaller than , galaxy formation is offset by various astrophysical processes [31,65,88,89]. This, in turn, must set since, at fainter magnitude, the UV luminosity function should not rise any longer, i.e., the number of faint galaxies must be appreciably reduced. We conservatively assume , which may be related to photo-suppression of star formation by the UV background [31].
To associate the UV magnitude and the host halo mass, we exploit an abundance matching technique [90,91,92,93], i.e., we require the cumulative number densities in galaxies and halos to match as follows:
which yields a relation . The integrand on the left-hand side is the CDM halo mass function by [94] computed via the COLOSSUS package [95]. The abundance matching outcome is plotted in Figure 6 for different redshifts (color coded) in the range relevant for reionization with the region below highlighted in gray shades.
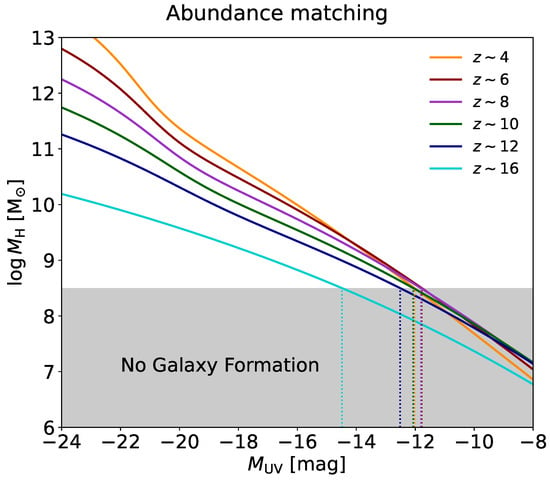
Figure 6.
The abundance matching relationship between the halo mass and the UV magnitude. Colored lines refer to different redshifts: (orange), 6 (brown), 8 (magenta), 10 (green), 12 (blue), and 16 (cyan). The shaded gray area illustrates the regions where galaxy formation is hindered (see text), corresponding to the UV magnitude limits highlighted by the dotted vertical lines.
Thus, we now require
meaning that, if galaxy formation is offset for halo masses , the UV luminosity function should flatten or even bend down for the correspondingly faint UV magnitudes . For redshifts z∼4–12, the resulting values of turn out to be around . Note that, in our Bayesian analysis below, we adopt a dex scatter around Equation (8) mainly related to uncertainties in the value (see [31,65]).
The second constraint involves the efficiency of galaxy formation expected in small halos. We can compute a cosmic-averaged star formation efficiency as the ratio between the co-moving density in stars and as a total number of baryons (integrated down to and down to the corresponding , respectively) as follows:
where is the cosmic baryon fraction, and is the IMF-averaged stellar mass-to-light ratio. The latter quantity can be computed via the PARSEC stellar evolution tracks after proper weighting over the adopted IMF and is displayed in Figure 7 as a function of the IMF parameters, metallicity, and age. The dependence on age is easy to understand; the mass-to-light ratio increases in older stellar populations since the UV luminosity from massive, short-living stars decreases as they progressively die, while the stellar mass is mostly contributed by the numerous low-mass, long-living stars. At a fixed age, increasing the IMF characteristic mass or flattening the IMF slope makes the decrease since low-mass stars are under-weighted. The dependence on metallicity is very weak.
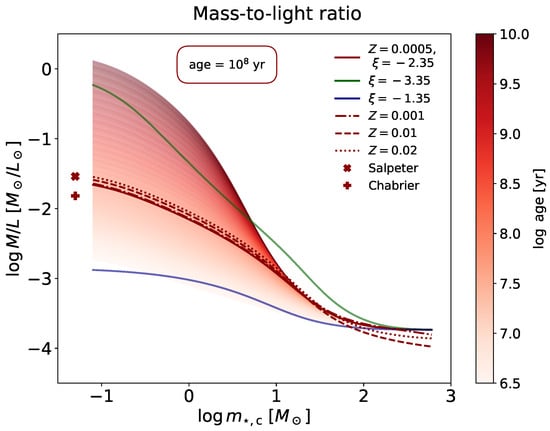
Figure 7.
The average as a function of the characteristic mass of the IMF. The colored lines refer to an age of 100 Myr. The solid line is for an IMF slope and a metallicity . At fixed , the green line is for and the blue for . At fixed , the dot-dashed line is for , the dashed for , and the dotted for . The plus and cross display the reference values for the Salpeter and the Chabrier IMFs. Finally, at fixed and , the shaded area shows the effect of changing the age from 3 Myr to 10 Gyr.
Constraints on come from abundance matching arguments involving the halo and the stellar mass functions [90,96]. In the local Universe, these are also consistent with independent observational determinations of the stellar mass vs. halo mass relation from satellite kinematics [97], galaxy rotation curves [98], and weak lensing [99]. In the present context, we are interested in a range of redshift and halo masses , where the abundance matching results must be somewhat extrapolated. However, the shape and evolution of the stellar mass vs. halo mass relation suggest that an upper limit can be safely adopted in small halos, though we allow for a rather large dispersion of dex around this value.
Finally, a third relevant constraint involves the characteristic mass of the IMF. During the reionization era at around , the CMB temperature can be as high as K. This provides a basic thermal background that can limit the fragmentation of gas clouds into small cores and the ensuing condensation into low-mass stars. A lower limit for the star masses can be obtained by considering the thermal Jeans mass as follows [10,12]:
where K is the present CMB temperature (a standard mean density of cm−3 is adopted). Note that such a value is a conservative lower limit in the sense that turbulent or magnetic pressure can lead to even larger values. We allow for a rather large dispersion of dex around such a value.
2.4. Bayesian Analysis
The discussion provided so far highlights that three parameters are relevant in our framework: the limiting UV magnitude , the IMF characteristic mass , and the IMF slope . We estimate these parameters via a Bayesian MCMC framework. Specifically, we adopt a standard log likelihood in terms of , where the sum is over different observables. For each of these, the is obtained in terms of the model and the data values with their uncertainties , summing over different redshifts (when applicable). Our overall data sample is fully reported in Table 1 and is constituted by observational measurements of the ionizing photon rate [20,21], the volume filling factor of ionized hydrogen [22,23,24,25,26,27,28,29], and the electron scattering optical depth [19].

Table 1.
Data considered for the Bayesian analysis of this work (see text for details).
We also include in the overall log likelihood the galaxy-formation-informed constraints discussed in Section 2.3: with and dex, to implement the relation between the limiting UV luminosity and minimum halo mass from Equation (8); with and dex, to implement the upper bound on the cosmic-averaged star formation efficiency from Equation (9); and with dex, to implement the lower bound on the characteristic mass of the IMF as provided by the thermal Jeans mass from Equation (10).
We adopt flat priors on the parameters , , and and then sample the parameter posterior distributions via the MCMC Python package emcee [100].
3. Results and Discussion
The results of our Bayesian analysis are displayed in Figure 8 and reported in Table 2. Specifically, in Figure 8, we illustrate the MCMC posterior distributions on the UV limiting magnitude , the IMF characteristic mass , and the IMF slope for the four different escape fraction prescriptions considered in this work (color coded). The crosses mark the bestfit values of the parameters, and the marginalized distributions are normalized to unity at their maximum. In Table 2, we summarize the marginalized posterior estimates of the parameters (median values, credible intervals, and bestfit values) together with the corresponding reduced of the fits.
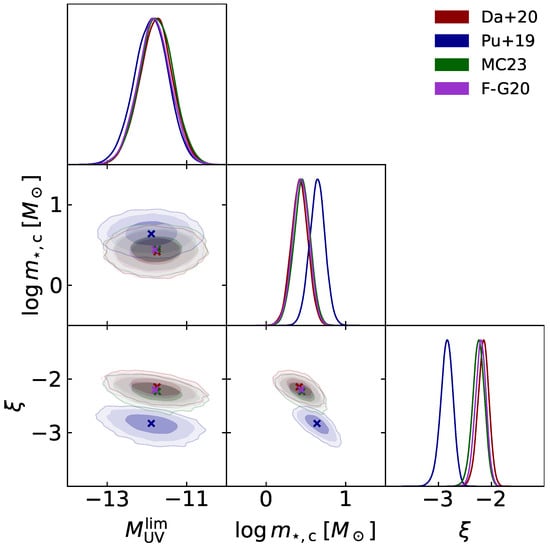
Figure 8.
MCMC posterior distributions of the limiting UV magnitude , on the characteristic cutoff mass of the IMF , and on the IMF slope . Colored contours/lines refer to each of the escape fraction parameterizations by [45] (red), [46] (blue), [48] (green), and [47] (magenta). The marginalized distributions are in arbitrary units (normalized to 1 at their maximum value).

Table 2.
Marginalized posterior estimates (median and confidence intervals and bestfit in square brackets) of the parameters from the MCMC analysis for the different escape fraction parameterizations (see text for details). Columns report the values of the limiting UV magnitude , the characteristic cutoff mass of the IMF, the IMF slope , and the reduced for the overall fit.
Pleasingly, the results for different escape fraction prescriptions are quite stable. This is due to the similarities of the escape fraction models illustrated in Figure 3 in the redshift range z∼6–10 where reionization data are available. Not surprisingly, the most variant results are for the escape fraction parameterization by [46], which implies that saturates to high values at , while the other escape fraction models envisage at those redshifts.
The bestfit values of the fitting parameter read for the UV limiting magnitude, a few for the IMF characteristic mass, and for the IMF slope. These are mainly determined by the need to have enough UV and ionizing photons to reproduce the reionization data but still meet the galaxy-formation-informed constraints described in Section 2.3. Remarkably, the IMF slope is, within uncertainties, consistent with the standard value of a Salpeter shape. Top-heavy IMFs with a flat slope are excluded at more than . This is because such slopes tend to largely overproduce ionizing photons, to the point of inducing a very early reionization history. The effects can be partly compensated only by changing to much brighter values that are actually inconsistent with the steep slope of the observed UV luminosity function at high redshift. However, the IMF is appreciably more top heavy than the classic Salpeter or Chabrier shapes in that star masses are appreciably suppressed. This may be related (but not exclusively) to the thermal Jeans limit from the hot CMB background.
In Figure 9, the best fit (solid lines) and the credible intervals (shaded areas) sampled from the posteriors are projected onto the reionization observables: the cosmic ionizing photon rate; the reionization history in terms of the redshift evolution of the volume filling factor for ionized hydrogen; and the electron scattering optical depth. The fits for all four escape fraction parameterizations are very good, as also testified by the reduced reported in Table 2. There is a slight preference for escape fraction models by [46,48] over the ones by [45,47]; however, the differences in and in the likelihood evidence are not statistically significant enough to draw definite conclusions. It is fair to say that all escape fraction models perform comparably well in fitting reionization observables.
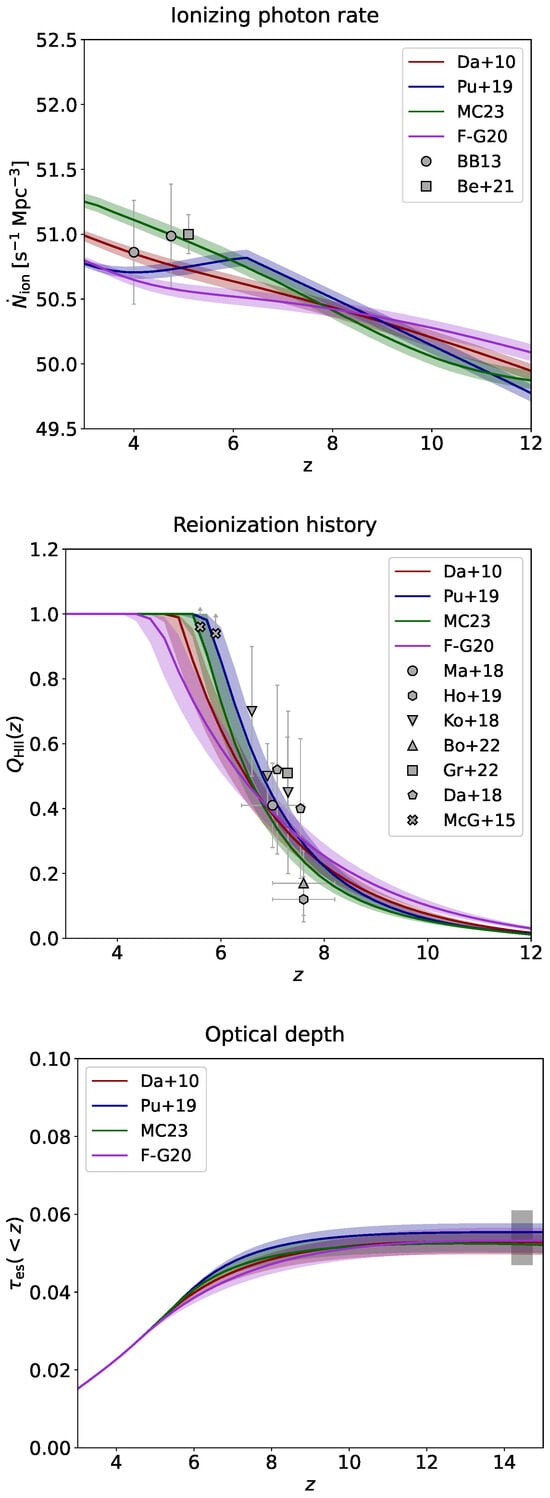
Figure 9.
Fits to the ionizing photon rate (top panel), reionization history in terms of the ionized hydrogen volume filling factor (middle panel), and optical depth for electron scattering (bottom panel). Colored lines illustrate the median, and the shaded areas show the credible interval from sampling the posterior distribution for each of the escape fraction parameterizations by [45] (red), [46] (blue), [48] (green), and [47] (magenta). Data are from [20] (circles) and [21] (squares) in the top panel; [25] (circles), [27] (hexagons), [22,26] (reversed triangles), [28] (triangles), [29] (squares), [24] (pentagons), and [23] (crosses) in the middle panel; [19] (gray shaded area) in the bottom panel.
Finally, in Figure 10, we display the reconstructed IMF for the different escape fraction models. Within confidence intervals, all IMFs are very similar, with a slope ∼ at high masses (slightly steeper ∼ for the [46] escape fraction), a maximum at around a few , and a cutoff at smaller mass, such that the number of stars with masses is suppressed by a factor of 100 or more with respect to a standard Salpeter or Chabrier shape. Comparing the overall shapes of the reconstructed IMF during the reionization epoch and the observed IMF in the local neighborhood leads to some physical conclusions. The IMF power law shape is the same and hence must originate by a fundamental process (e.g., turbulent fragmentation) in star-forming regions. The suppression in the formation of small stars, present at the reionization redshift but clearly at variance with the IMF in the local Universe, may be related to the vastly different environmental conditions (for example, the high thermal background provided by CMB photons in the reionization era).
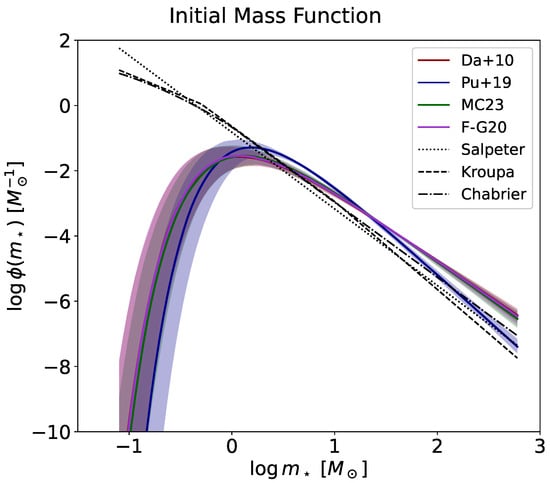
Figure 10.
IMF determination from our Bayesian analysis. Colored lines illustrate the median, and shaded areas show the credible interval from sampling the posterior distributions for each of the escape fraction parameterizations by [45] (red), [46] (blue), [48] (green), and [47] (magenta). The Salpeter (dotted), Kroupa (dashed), and Chabrier (dot-dashed) IMFs are also plotted for reference.
Clearly, such a reconstructed IMF with a paucity of small star masses below a few would have considerable consequences for the estimate of stellar masses from observed galaxy luminosities. This is particularly relevant in the light of the recent claims for substantial stellar masses estimated from JWST data at high redshift [44,101,102]. In particular, puzzling cases are constituted by the galaxies from the [101] sample, for which considerable stellar masses have been inferred from SED fitting to the JWST UV restframe photometry on adoption of a Salpeter IMF. Such galaxies have been shown to be marginally consistent with the standard CDM cosmology [103] in that, even assuming a maximal conversion of all the baryons into stars (star formation efficiency ), the stellar masses would correspond to extremely rare peaks in the density field.
Basically, the related argument is illustrated in Figure 11. Open symbols are the mass determinations from JWST data by [101] with a Salpeter IMF. The colored lines represent different peak heights in the density field as quantified by the ratio between the critical threshold for collapse and the mass variance of the field smoothed (with a top-hat filter in real space) on the mass scale at redshift z (typical peaks of the field should have ). In addition, solid lines assume a maximal star formation efficiency , while dotted ones refer to the typical value applying to local star-forming galaxies. It is seen that most of the galaxies, and especially the two most massive ones, are extremely improbable in the standard CDM cosmology, even assuming a maximal efficiency of star formation.
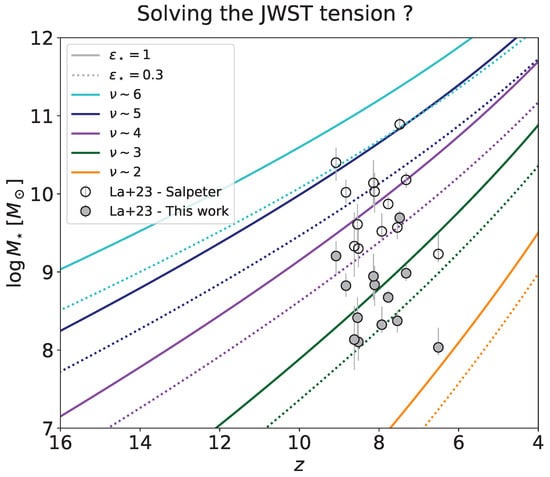
Figure 11.
Circles represent the estimate of stellar masses for the sample by [101] inferred either with a Salpeter IMF (empty symbols) or with the IMF reconstructed in this work (filled symbols) under the [48] escape fraction scenario. Colored lines illustrate the peak heights of the density field in terms of the ratio (orange), 3 (green), 4 (magenta), 5 (blue), and 6 (cyan). Solid lines assume a maximal star formation efficiency , while dotted ones refer to the typical value applying to local star-forming galaxies.
However, the situation improves substantially if we rely on the reconstructed IMF of this work. For the sake of simplicity, we exploit the outcomes for the escape fraction scenario by [48], but the results in the other cases are similar. At given UV luminosity and for the typical ages of the system at these high redshifts, the average ratios with our IMF are substantially reduced by a factor of with respect to the Salpeter one as a consequence of the paucity of small stars below the characteristic mass. Therefore, at a given observed UV luminosity, the estimated galaxy stellar masses are reduced by a correspondingly large factor. Most of the galaxies are brought to values and so are now in reasonable agreement with the CDM expectations, even assuming a standard value of the star formation efficiency . All in all, our reconstructed IMF appreciably alleviates the putative tension between JWST data and the standard cosmological framework.
4. Summary
In this paper, we have constrained the stellar initial mass function (IMF) during the epoch of reionization in the standard CDM cosmology.
To this purpose, we have built up a semi-empirical model for the reionization history of the Universe based on various ingredients: the latest determination of the UV galaxy luminosity function from JWST out to redshift ; data-inferred and simulation-driven assumptions on the redshift-dependent escape fraction of ionizing photons from primordial galaxies; a simple yet flexible parameterization of the IMF ∼ in terms of a slope at the high-mass end and of a characteristic mass , below which it flattens or bends downwards; the PARSEC stellar evolution code to compute the UV and ionizing emission from different stars’ masses as a function of age and metallicity; and a few physical constraints related to stellar and galaxy formation in faint galaxies at the reionization redshifts.
Our model has three main parameters: the limiting magnitude down to which the luminosity function is steeply increasing, the IMF slope , and characteristic mass . We have inferred these parameters via a standard MCMC technique, comparing our model outcomes with the reionization observables from different astrophysical and cosmological probes, including the cosmic ionizing photon rate, the redshift-dependent volume filling factor of ionized hydrogen, and the electron scattering optical depth from the Planck mission.
We have found that the IMF slope is within the range from to , consistent with direct determination from star counts in the Milky Way, while appreciably flatter slopes (hence, a strongly top-heavy IMF) are excluded at more than significance. The universality of the slope suggests that such a feature is originated by a fundamental process (e.g., turbulent fragmentation) in star-forming regions. On the other hand, the bestfit values of the IMF characteristic mass ∼a few implies a suppression in the formation of small stellar masses at variance with the local Universe. This occurrence may be related, though not exclusively, to the high thermal background of ∼20–30 K provided by CMB photons at the reionization redshifts. We have highlighted that such results are robust against different parameterizations for the redshift evolution of the escape fraction, which nevertheless remains the most uncertain ingredient in reionization studies. Observational campaigns and hydrodynamical simulations aimed at better reconstructing the escape fraction would be extremely welcome to strengthen the IMF constraints derived here.
Finally, we have investigated the implications of our reconstructed IMF for the recent JWST detections of massive galaxies at and beyond the reionization epoch. We have found that the stellar mass estimates from JWST data are considerably reduced when assuming the IMF from this work with respect to a Salpeter one. All in all, our reconstructed IMF substantially alleviates the tension of JWST data at high redshift with the standard cosmological framework.
Author Contributions
Conceptualization: A.L., G.G. and L.B.; methodology: A.L., G.G., A.B. and B.S.H.; validation: F.G., M.M., B.S.H., C.B., A.B. and L.D.; writing: A.L., G.G., L.B. and F.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially funded by the projects “Data Science methods for MultiMessenger Astrophysics & Multi-Survey Cosmology”, funded by the Italian Ministry of University and Research, Programmazione triennale 2021/2023 (DM no.2503, 9 December 2019), Programma Congiunto Scuole; EU H2020-MSCA-ITN-2019 no. 860744 BiD4BESt: “Big Data Applications for Black Hole Evolution Studies”; Italian Research Center of High-Performance Computing Big Data and Quantum Computing (ICSC), funded by the European Union—NextGenerationEU—and National Recovery and Resilience Plan (NRRP)—Mission 4 Component 2 within the activities of Spoke 3 (Astrophysics and Cosmos Observations); PRIN MUR 2022 project no. 20224JR28W “Charting Unexplored Avenues in Dark Matter”; INAF Large Grant 2022 funding scheme with the project “MeerKAT and LOFAR Team Up: a Unique Radio Window on Galaxy/AGN Co-Evolution”; INAF GO-GTO Normal 2023 funding scheme with the project “Serendipitous H-ATLAS-fields Observations of Radio Extragalactic Sources (SHORES)”.
Data Availability Statement
Data are contained within the article.
Acknowledgments
We acknowledge the three anonymous referees for their helpful comments and suggestions. We warmly thank M. Talia and G. Rodighiero for illuminating discussions about high-redshift UV/NIR dark galaxies and JWST data.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kroupa, P.; Jerabkova, T. A Universal Stellar Initial Mass Function? A Critical Look at Variations. Ann. Rev. Astron. Astrophys. 2010, 48, 339. [Google Scholar]
- Krumholz, M.R. The big problems in star formation: The star formation rate, stellar clustering, and the initial mass function. Phys. Rep. 2014, 539, 49. [Google Scholar] [CrossRef]
- Kroupa, P.; Jerabkova, T. The initial mass function of stars and the star-formation rates of galaxies. In Star-Formation Rates of Galaxies; Buat, V., Zezas, A., Eds.; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar] [CrossRef]
- Salpeter, E.E. The Luminosity Function and Stellar Evolution. Astrophys. J. 1955, 121, 161. [Google Scholar] [CrossRef]
- Kroupa, P. On the variation of the initial mass function. Mon. Not. R. Astron. Soc. 2001, 322, 231. [Google Scholar] [CrossRef]
- Chabrier, G. Galactic Stellar and Substellar Initial Mass Function. Publ. Astron. Soc. Pacific 2003, 115, 763. [Google Scholar] [CrossRef]
- Larson, R.B. Early star formation and the evolution of the stellar initial mass function in galaxies. Mon. Not. R. Astron. Soc. 1998, 301, 569. [Google Scholar] [CrossRef]
- Wise, J.H.; Abel, T.; Turk, M.J.; Norman, M.L.; Smith, B.D. The birth of a galaxy—II. The role of radiation pressure. Mon. Not. R. Astron. Soc. 2012, 427, 311. [Google Scholar] [CrossRef]
- Adams, F.C.; Fatuzzo, M. A Theory of the Initial Mass Function for Star Formation in Molecular Clouds. Astrophys. J. 1996, 464, 256. [Google Scholar] [CrossRef]
- Padoan, P.; Nordlund, A. The Stellar Initial Mass Function from Turbulent Fragmentation. Astrophys. J. 2002, 576, 870. [Google Scholar] [CrossRef]
- Weidner, C.; Kroupa, P. The Variation of Integrated Star Initial Mass Functions among Galaxies. Astrophys. J. 2005, 625, 754. [Google Scholar] [CrossRef]
- Hennebelle, P.; Chabrier, G. Analytical Theory for the Initial Mass Function. III. Time Dependence and Star Formation Rate. Astrophys. J. 2013, 770, 550. [Google Scholar] [CrossRef]
- Fontanot, F.; La Barbera, F.; De Lucia, G.; Pasquali, A.; Vazdekis, A. On the shape and evolution of a cosmic-ray-regulated galaxy-wide stellar initial mass function. Mon. Not. R. Astron. Soc. 2018, 479, 5678. [Google Scholar] [CrossRef]
- van Dokkum, P.G.; Conroy, C. A substantial population of low-mass stars in luminous elliptical galaxies. Nature 2010, 468, 940. [Google Scholar] [CrossRef]
- Martin-Navarro, I.; Vazdekis, A.; La Barbera, F.; Falcon-Barroso, J.; Lyubenova, M.; van de Ven, G.; Ferreras, I.; Sanchez, S.F.; Trager, S.C.; Garcia-Benito, R.; et al. IMF and Metallicity: A Tight Local Relation Revealed by the CALIFA Survey. Astrophys. J. 2015, 806, L31. [Google Scholar] [CrossRef]
- Cappellari, M. Structure and Kinematics of Early-Type Galaxies from Integral Field Spectroscopy. Ann. Rev. Astron. Astrophys. 2016, 54, 597. [Google Scholar] [CrossRef]
- Zhang, Z.-Y.; Romano, D.; Ivison, R.J.; Papadopoulos, P.P.; Matteucci, F. Stellar populations dominated by massive stars in dusty starburst galaxies across cosmic time. Nature 2018, 558, 260. [Google Scholar] [CrossRef]
- Li, J.; Liu, C.; Zhang, Z.-Y.; Tian, H.; Fu, X.; Li, J.; Yan, Z.-Q. Stellar initial mass function varies with metallicity and time. Nature 2023, 613, 460. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. [Planck Collaboration]. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Becker, G.D.; Bolton, J.S. New measurements of the ionizing ultraviolet background over 2 < z<5 and implications for hydrogen reionization. Mon. Not. R. Astron. Soc. 2013, 436, 1023. [Google Scholar]
- Becker, G.D.; D’Aloisio, A.; Christenson, H.M.; Zhu, Y.; Worseck, G.; Bolton, J.S. The mean free path of ionizing photons at 5<z<6: Evidence for rapid evolution near reionization. Mon. Not. R. Astron. Soc. 2021, 508, 1853–1869. [Google Scholar]
- Konno, A.; Ouchi, M.; Ono, Y.; Shimasaku, K.; Shibuya, T.; Furusawa, H.; Nakajima, K.; Naito, Y.; Momose, R.; Yuma, S.; et al. Accelerated Evolution of the Lyα Luminosity Function at z ≳ 7 Revealed by the Subaru Ultra-deep Survey for Lyα Emitters at z=7.3. Astrophys. J. 2014, 797, 16. [Google Scholar] [CrossRef]
- McGreer, I.D.; Mesinger, A.; D’Odorico, V. Model-independent evidence in favour of an end to reionization by z≈6. Mon. Not. R. Astron. Soc. 2015, 447, 499–505. [Google Scholar] [CrossRef]
- Davies, F.B.; Hennawi, J.F.; Banados, E.; Lukic, Z.; Decarli, R.; Fan, X.; Farina, E.P.; Mazzucchelli, C.; Rix, H.-W.; Venemans, B.P.; et al. Quantitative Constraints on the Reionization History from the IGM Damping Wing Signature in Two Quasars at z > 7. Astrophys. J. 2018, 864, 142. [Google Scholar] [CrossRef]
- Mason, C.A.; Treu, T.; Dijkstra, M.; Mesinger, A.; Trenti, M.; Pentericci, L.; de Barros, S.; Vanzella, E. The Universe Is Reionizing at z∼7: Bayesian Inference of the IGM Neutral Fraction Using Lyα Emission from Galaxies. Astrophys. J. 2018, 856, 2. [Google Scholar] [CrossRef]
- Konno, A.; Ouchi, M.; Shibuya, T.; Ono, Y.; Shimasaku, K.; Taniguchi, Y.; Nagao, T.; Kobayashi, M.A.R.; Kajisawa, M.; Kashikawa, N.; et al. SILVERRUSH. IV. Lyα luminosity functions at z = 5.7 and 6.6 studied with ∼1300 Lyα emitters on the 14–21 deg2 sky. Publ. Astron. Soc. Jpn. 2018, 70, S16. [Google Scholar] [CrossRef]
- Hoag, A.; Bradac, M.; Huang, K.; Mason, C.; Treu, T.; Schmidt, K.B.; Trenti, M.; Strait, V.; Lemaux, B.C.; Finney, E.Q.; et al. Constraining the Neutral Fraction of Hydrogen in the IGM at Redshift 7.5. Astrophys. J. 2019, 878, 12. [Google Scholar] [CrossRef]
- Bolan, P.; Lemaux, B.C.; Mason, C.; Bradac, M.; Treu, T.; Strait, V.; Pelliccia, D.; Pentericci, L.; Malkan, M. Inferring the IGM Neutral Fraction at z∼ 6–8 with Low-Luminosity Lyman Break Galaxies. arXiv 2021, arXiv:2111.14912. [Google Scholar]
- Greig, B.; Mesinger, A.; Davies, F.B.; Wang, F.; Yang, J.; Hennawi, J.F. IGM damping wing constraints on reionisation from covariance reconstruction of two z ≳ 7 QSOs. Mon. Not. R. Astron. Soc. 2022, 512, 5390–5403. [Google Scholar] [CrossRef]
- Robertson, B.E.; Ellis, R.S.; Furlanetto, S.R.; Dunlop, J.S. Cosmic reionization and early star-forming galaxies: A joint analysis of new constraints from Planck and Hubble Space Telescope. Astrophys. J. 2015, 802, L19. [Google Scholar] [CrossRef]
- Finkelstein, S.L.; D’Aloisio, A.; Paardekooper, J.-P.; Ryan, R., Jr.; Behroozi, P.; Finlator, K.; Livermore, R.; Upton Sanderbeck, P.R.; Dalla Vecchia, C.; Khochfar, S. Conditions for Reionizing the Universe with a Low Galaxy Ionizing Photon Escape Fraction. Astrophys. J. 2019, 879, 36. [Google Scholar] [CrossRef]
- Lapi, A.; Ronconi, T.; Boco, L.; Shankar, F.; Krachmalnicoff, N.; Baccigalupi, C.; Danese, L. Astroparticle Constraints from Cosmic Reionization and Primordial Galaxy Formation. Universe 2022, 8, 476. [Google Scholar] [CrossRef]
- Gandolfi, G.; Lapi, A.; Ronconi, T.; Danese, L. Astroparticle Constraints from the Cosmic Star Formation Rate Density at High Redshift: Current Status and Forecasts for JWST. Universe 2022, 8, 589. [Google Scholar] [CrossRef]
- Bouwens, R.J.; Oesch, P.A.; Stefanon, M.; Illingworth, G.; Labbé, I.; Reddy, N.; Atek, H.; Montes, M.; Naidu, R.; Nanayakkara, T.; et al. New Determinations of the UV Luminosity Functions from z 9 to 2 Show a Remarkable Consistency with Halo Growth and a Constant Star Formation Efficiency. Astron. J. 2021, 162, 47. [Google Scholar] [CrossRef]
- Oesch, P.A.; Bouwens, R.J.; Illingworth, G.D.; Labbé, I.; Stefanon, M. The Dearth of z∼10 Galaxies in All HST Legacy Fields—The Rapid Evolution of the Galaxy Population in the First 500 Myr. Astrophys. J. 2018, 855, 105. [Google Scholar] [CrossRef]
- Bouwens, R.; Illingworth, G.; Oesch, P.; Stefanon, M.; Naidu, R.; van Leeuwen, I.; Magee, D. UV luminosity density results at z > 8 from the first JWST/NIRCam fields: Limitations of early data sets and the need for spectroscopy. Mon. Not. R. Astron. Soc. 2023, 523, 1009. [Google Scholar] [CrossRef]
- Bouwens, R.J.; Stefanon, M.; Brammer, G.; Oesch, P.A.; Herard-Demanche, T.; Illingworth, G.D.; Matthee, J.; Naidu, R.P.; van Dokkum, P.G.; van Leeuwen, I.F. Evolution of the UV LF from z 15 to z 8 using new JWST NIRCam medium-band observations over the HUDF/XDF. Mon. Not. R. Astron. Soc. 2023, 523, 1036. [Google Scholar] [CrossRef]
- Harikane, Y.; Ouchi, M.; Oguri, M.; Ono, Y.; Nakajima, K.; Isobe, Y.; Umeda, H.; Mawatari, K.; Zhang, Y. A Comprehensive Study of Galaxies at z 9–16 Found in the Early JWST Data: Ultraviolet Luminosity Functions and Cosmic Star Formation History at the Pre-reionization Epoch. Astrophys. J. Suppl. 2023, 265, 5. [Google Scholar] [CrossRef]
- Harikane, Y.; Nakajima, K.; Ouchi, M.; Umeda, H.; Isobe, Y.; Ono, Y.; Xu, Y.; Zhang, Y. Pure Spectroscopic Constraints on UV Luminosity Functions and Cosmic Star Formation History From 25 Galaxies at zspec = 8.61–13.20 Confirmed with JWST/NIRSpec. arXiv 2023, arXiv:2304.06658. [Google Scholar]
- Harikane, Y.; Ono, Y.; Ouchi, M.; Liu, C.; Sawicki, M.; Shibuya, T.; Behroozi, P.S.; He, W.; Shimasaku, K.; Arnouts, S.; et al. GOLDRUSH. IV. Luminosity Functions and Clustering Revealed with 4,000,000 Galaxies at z∼ 2–7: Galaxy-AGN Transition, Star Formation Efficiency, and Implication for Evolution at z > 10. Astrophys. J. Suppl. 2023, 259, 20. [Google Scholar] [CrossRef]
- Donnan, C.T.; McLeod, D.J.; Dunlop, J.S.; McLure, R.J.; Carnall, A.C.; Begley, R.; Cullen, F.; Hamadouche, M.L.; Bowler, R.A.A.; Magee, D.; et al. The evolution of the galaxy UV luminosity function at redshifts z∼ 8–15 from deep JWST and ground-based near-infrared imaging. Mon. Not. R. Astron. Soc. 2023, 518, 6011. [Google Scholar] [CrossRef]
- Donnan, C.T.; McLeod, D.J.; McLure, R.J.; Dunlop, J.S.; Carnall, A.C.; Cullen, F.; Magee, D. The abundance of z ≳ 10 galaxy candidates in the HUDF using deep JWST NIRCam medium-band imaging. Mon. Not. R. Astron. Soc. 2023, 520, 4554. [Google Scholar] [CrossRef]
- Naidu, R.P.; Oesch, P.A.; van Dokkum, P.; Nelson, E.J.; Suess, K.A.; Brammer, G.; Whitaker, K.E.; Illingworth, G.; Bouwens, R.; Tacchella, S.; et al. Two Remarkably Luminous Galaxy Candidates at z≈ 10–12 Revealed by JWST. Astrophys. J. 2022, 940, L14. [Google Scholar] [CrossRef]
- Finkelstein, S.L.; Bagley, M.B.; Ferguson, H.C.; Wilkins, S.M.; Kartaltepe, J.S.; Papovich, C.; Yung, L.Y.A.; Haro, P.A.; Behroozi, P.; Dickinson, M.; et al. CEERS Key Paper. I. An Early Look into the First 500 Myr of Galaxy Formation with JWST. Astrophys. J. 2023, 946, L13. [Google Scholar] [CrossRef]
- Dayal, P.; Volonteri, M.; Choudhury, T.R.; Schneider, R.; Trebitsch, M.; Gnedin, N.Y.; Atek, H.; Hirschmann, M.; Reines, A. Reionization with galaxies and active galactic nuclei. Mon. Not. R. Astron. Soc. 2020, 495, 3065. [Google Scholar] [CrossRef]
- Puchwein, E.; Haardt, F.; Haehnelt, M.G.; Madau, P. Consistent modelling of the meta-galactic UV background and the thermal/ionization history of the intergalactic medium. Mon. Not. R. Astron. Soc. 2019, 485, 47. [Google Scholar] [CrossRef]
- Faucher-Giguère, C.-A. A cosmic UV/X-ray background model update. Mon. Not. R. Astron. Soc. 2020, 493, 1614. [Google Scholar] [CrossRef]
- Mitra, S.; Chatterjee, A. Non-parametric reconstruction of photon escape fraction from reionization. Mon. Not. R. Astron. Soc. 2023, 523, L35. [Google Scholar] [CrossRef]
- Kulkarni, G.; Keating, L.C.; Haehnelt, M.G.; Bosman, S.E.I.; Puchwein, E.; Chardin, J.; Aubert, D. Large Lyα opacity fluctuations and low CMB τ in models of late reionization with large islands of neutral hydrogen extending to z < 5.5. Mon. Not. R. Astron. Soc. 2019, 485, L24. [Google Scholar]
- Katz, H.; Saxena, A.; Rosdahl, J.; Kimm, T.; Blaizot, J.; Garel, T.; Michel-Dansac, L.; Haehnelt, M.; Ellis, R.S.; Pentericci, L.; et al. Two modes of LyC escape from bursty star formation: Implications for [CII] deficits and the sources of reionization. Mon. Not. R. Astron. Soc. 2023, 518, 270. [Google Scholar] [CrossRef]
- Paardekooper, J.-P.; Khochfar, S.; Dalla Vecchia, C. The First Billion Years project: The escape fraction of ionizing photons in the epoch of reionization. Mon. Not. R. Astron. Soc. 2015, 451, 2544. [Google Scholar] [CrossRef]
- Vanzella, E.; Nonino, M.; Cupani, G.; Castellano, M.; Sani, E.; Mignoli, M.; Calura, F.; Meneghetti, M.; Gilli, R.; Comastri, A.; et al. Direct Lyman continuum and Lyα escape observed at redshift 4. Mon. Not. R. Astron. Soc. 2018, 476, L15. [Google Scholar] [CrossRef]
- Alavi, A.; Colbert, J.; Teplitz, H.I.; Siana, B.; Scarlata, C.; Rutkowski, M.; Mehta, V.; Henry, A.; Dai, Y.S.; Haardt, F.; et al. Lyman Continuum Escape Fraction from Low-mass Starbursts at z = 1.3. Astrophys. J. 2020, 904, 59. [Google Scholar] [CrossRef]
- Smith, B.M.; Windhorst, R.A.; Cohen, S.H.; Koekemoer, A.M.; Jansen, R.A.; White, C.; Borthakur, S.; Hathi, N.; Jiang, L.; Rutkowski, M.; et al. The Lyman Continuum Escape Fraction of Galaxies and AGN in the GOODS Fields. Astrophys. J. 2020, 897, 41. [Google Scholar] [CrossRef]
- Izotov, Y.I.; Worseck, G.; Schaerer, D.; Guseva, N.G.; Chisholm, J.; Thuan, T.X.; Fricke, K.J.; Verhamme, A. Lyman continuum leakage from low-mass galaxies with M⋆<108 M⊙. Mon. Not. R. Astron. Soc. 2021, 503, 1734. [Google Scholar]
- Pahl, A.J.; Shapley, A.; Steidel, C.C.; Chen, Y.; Reddy, N.A. An uncontaminated measurement of the escaping Lyman continuum at z∼3. Mon. Not. R. Astron. Soc. 2021, 505, 2447. [Google Scholar] [CrossRef]
- Atek, H.; Furtak, L.J.; Oesch, P.; van Dokkum, P.; Reddy, N.; Contini, T.; Illingworth, G.; Wilkins, S. The star formation burstiness and ionizing efficiency of low-mass galaxies. Mon. Not. R. Astron. Soc. 2022, 511, 4464. [Google Scholar] [CrossRef]
- Naidu, R.P.; Matthee, J.; Oesch, P.A.; Conroy, C.; Sobral, D.; Pezzulli, G.; Hayes, M.; Erb, D.; Amorín, R.; Gronke, M.; et al. The synchrony of production and escape: Half the bright Lyα emitters at z ≈ 2 have Lyman continuum escape fractions ≈50%. Mon. Not. R. Astron. Soc. 2022, 510, 4582. [Google Scholar] [CrossRef]
- Khaire, V.; Srianand, R. New synthesis models of consistent extragalactic background light over cosmic time. Mon. Not. R. Astron. Soc. 2019, 484, 4174. [Google Scholar] [CrossRef]
- Cain, C.; D’Aloisio, A.; Gangolli, N.; Becker, G.D. A Short Mean Free Path at z = 6 Favors Late and Rapid Reionization by Faint Galaxies. Astrophys. J. 2021, 917, L37. [Google Scholar] [CrossRef]
- Steidel, C.C.; Bogosavljevic, M.; Shapley, A.E.; Reddy, N.A.; Rudie, G.C.; Pettini, M.; Trainor, R.F.; Strom, A.L. The Keck Lyman Continuum Spectroscopic Survey (KLCS): The Emergent Ionizing Spectrum of Galaxies at z∼3. Astrophys. J. 2018, 869, 123. [Google Scholar] [CrossRef]
- Fletcher, T.J.; Tang, M.; Robertson, B.E.; Nakajima, K.; Ellis, R.S.; Stark, D.P.; Inoue, A. The Lyman Continuum Escape Survey: Ionizing Radiation from [OIII]-strong Sources at a Redshift of 3.1. Astrophys. J. 2019, 878, 87. [Google Scholar] [CrossRef]
- Kennicutt, R.C.; Evans, N.J. Star Formation in the Milky Way and Nearby Galaxies. Annu. Rev. Astron. Astrophys. 2012, 50, 531–608. [Google Scholar] [CrossRef]
- Madau, P.; Dickinson, M. Cosmic Star-Formation History. Annu. Rev. Astron. Astrophys. 2014, 52, 415. [Google Scholar] [CrossRef]
- Cai, Z.; Lapi, A.; Bressan, A.; De Zotti, G.; Negrello, M.; Danese, L. A Physical Model for the Evolving Ultraviolet Luminosity Function of High Redshift Galaxies and their Contribution to the Cosmic Reionization. Astrophys. J. 2014, 785, 65. [Google Scholar] [CrossRef]
- Bose, S.; Deason, A.J.; Frenk, C.S. The Imprint of Cosmic Reionization on the Luminosity Function of Galaxies. Astrophys. J. 2018, 863, 123. [Google Scholar] [CrossRef]
- Romanello, M.; Menci, N.; Castellano, M. The Epoch of Reionization in Warm Dark Matter Scenarios. Universe 2021, 7, 365. [Google Scholar] [CrossRef]
- Munoz, J.B.; Qin, Y.; Mesinger, A.; Murray, S.G.; Greig, B.; Mason, C. The impact of the first galaxies on cosmic dawn and reionization. Mon. Not. R. Astron. Soc. 2022, 511, 3657–3681. [Google Scholar] [CrossRef]
- Bouwens, R.J.; Illingworth, G.; Ellis, R.S.; Oesch, P.A.; Stefanon, M. z∼2-9 galaxies magnified by the Hubble Frontier Field Clusters II: Luminosity functions and constraints on a faint end turnover. Astrophys. J. 2022, 940, 55. [Google Scholar] [CrossRef]
- Mao, J.; Lapi, A.; Granato, G.L.; de Zotti, G.; Danese, L. The Role of the Dust in Primeval Galaxies: A Simple Physical Model for Lyman Break Galaxies and Ly-α Emitters. Astrophys. J. 2007, 667, 655. [Google Scholar] [CrossRef][Green Version]
- Rutkowski, M.J.; Scarlata, C.; Haardt, F.; Siana, B.; Henry, A.; Rafelski, M.; Hayes, M.; Salvato, M.; Pahl, A.J.; Mehta, V.; et al. Lyman Continuum Escape Fraction of Star-forming Dwarf Galaxies at z∼1. Astrophys. J. 2016, 819, 81. [Google Scholar] [CrossRef]
- Shen, X.; Hopkins, P.F.; Faucher-Giguère, C.-A.; Alexander, D.M.; Richards, G.T.; Ross, N.P.; Hickox, R.C. The bolometric quasar luminosity function at z = 0–7. Mon. Not. R. Astron. Soc. 2020, 495, 3252–3275. [Google Scholar] [CrossRef]
- Shankar, F.; Mathur, S. On the Faint End of the High-Redshift Active Galactic Nucleus Luminosity Function. Astrophys. J. 2007, 660, 1051. [Google Scholar] [CrossRef]
- Giallongo, E.; Grazian, A.; Fiore, F.; Fontana, A.; Pentericci, L.; Vanzella, E.; Dickinson, M.; Kocevski, D.; Castellano, M.; Cristiani, S.; et al. Faint AGNs at z > 4 in the CANDELS GOODS-S field: Looking for contributors to the reionization of the Universe. Astron. Astrophys. 2015, 578, A83. [Google Scholar] [CrossRef]
- Ricci, F.; Marchesi, S.; Shankar, F.; La Franca, F.; Civano, F. Constraining the UV emissivity of AGN throughout cosmic time via X-ray surveys. Mon. Not. R. Astron. Soc. 2017, 465, 1915–1925. [Google Scholar] [CrossRef]
- Giallongo, E.; Grazian, A.; Fiore, F.; Kodra, D.; Urrutia, T.; Castellano, M.; Cristiani, S.; Dickinson, M.; Fontana, A.; Menci, N.; et al. Space Densities and Emissivities of Active Galactic Nuclei at z > 4. Astrophys. J. 2019, 884, 19. [Google Scholar] [CrossRef]
- Kulkarni, G.; Worseck, G.; Hennawi, J.F. Evolution of the AGN UV luminosity function from redshift 7.5. Mon. Not. R. Astron. Soc. 2019, 488, 1035–1065. [Google Scholar] [CrossRef]
- Ananna, T.T.; Urry, C.M.; Treister, E.; Hickox, R.C.; Shankar, F.; Ricci, C.; Cappelluti, N.; Marchesi, S.; Turner, T.J. Accretion History of AGNs. III. Radiative Efficiency and AGN Contribution to Reionization. Astrophys. J. 2020, 903, 85. [Google Scholar] [CrossRef]
- Grazian, A.; Giallongo, E.; Boutsia, K.; Cristiani, S.; Vanzella, E.; Scarlata, C.; Santini, P.; Pentericci, L.; Merlin, E.; Menci, N.; et al. The contribution of faint AGNs to the ionizing background at z > 4. Astron. Astrophys. 2018, 613, A44. [Google Scholar] [CrossRef]
- Romano, M. Lyman continuum escape fraction and mean free path of hydrogen ionizing photons for bright z∼4 QSOs from SDSS DR14. Astron. Astrophys. 2019, 632, A45. [Google Scholar] [CrossRef]
- Madau, P.; Haardt, F.; Rees, M.J. Radiative transfer in a clumpy Universe. III. The nature of cosmological ionizing sources. Astrophys. J. 1999, 514, 648. [Google Scholar] [CrossRef]
- Loeb, A.; Barkana, R. The Reionization of the Universe by the First Stars and Quasars. Annu. Rev. Astron. Astrophys. 2001, 39, 19–66. [Google Scholar] [CrossRef]
- Pawlik, A.H.; Schaye, J.; van Scherpenzeel, E. Keeping the Universe ionized: Photoheating and the clumping factor of the high-redshift intergalactic medium. Mon. Not. R. Astron. Soc. 2009, 394, 1812–1824. [Google Scholar] [CrossRef]
- Haardt, F.; Madau, P. Radiative Transfer in a Clumpy Universe. IV. New Synthesis Models of the Cosmic UV/X-Ray Background. Astrophys. J. 2012, 746, 125. [Google Scholar] [CrossRef]
- Schneider, F.R.N.; Ramírez-Agudelo, O.H.; Tramper, F.; Bestenlehner, J.M.; Castro, N.; Sana, H.; Evans, C.J.; Sabín-Sanjulián, C.; Simón-Díaz, S.; Langer, N.; et al. The VLT-FLAMES Tarantula Survey. XXIX. Massive star formation in the local 30 Doradus starburst. Astron. Astrophys. 2018, 618, A73. [Google Scholar] [CrossRef]
- Goswami, S.; Silva, L.; Bressan, A.; Grisoni, V.; Costa, G.; Marigo, P.; Granato, G.L.; Lapi, A.; Spera, M. Impact of very massive stars on the chemical evolution of extremely metal-poor galaxies. Astron. Astrophys. 2022, 663, A1. [Google Scholar] [CrossRef]
- Bressan, A.; Marigo, P.; Girardi, L.; Salasnich, B.; Dal Cero, C.; Rubele, S.; Nanni, A. PARSEC: Stellar tracks and isochrones with the PAdova and TRieste Stellar Evolution Code. Mon. Not. R. Astron. Soc. 2012, 427, 127. [Google Scholar] [CrossRef]
- Efstathiou, G. Suppressing the formation of dwarf galaxies via photoionization. Mon. Not. R. Astron. Soc. 1992, 256, 43. [Google Scholar] [CrossRef]
- Sobacchi, E.; Mesinger, A. How does radiative feedback from an ultraviolet background impact reionization? Mon. Not. R. Astron. Soc. 2013, 432, 3340. [Google Scholar] [CrossRef]
- Aversa, R.; Lapi, A.; De Zotti, G.; Danese, L. Black Hole and Galaxy Coevolution from Continuity Equation and Abundance Matching. Astrophys. J. 2015, 810, 74. [Google Scholar] [CrossRef]
- Moster, B.P.; Naab, T.; White, S.D.M. EMERGE—An empirical model for the formation of galaxies since z∼10. Mon. Not. R. Astron. Soc. 2018, 477, 1822. [Google Scholar] [CrossRef]
- Cristofari, P.; Ostriker, J.P. Abundance matching for low-mass galaxies in the CDM and FDM models. Mon. Not. R. Astron. Soc. 2019, 482, 4364. [Google Scholar] [CrossRef]
- Behroozi, P.; Wechsler, R.H.; Hearin, A.P.; Conroy, C. UNIVERSEMACHINE: The correlation between galaxy growth and dark matter halo assembly from z = 0–10. Mon. Not. R. Astron. Soc. 2020, 488, 3143. [Google Scholar] [CrossRef]
- Tinker, J.; Kravtsov, A.V.; Klypin, A.; Abazajian, K.; Warren, M.; Yepes, G.; Gottlober, S.; Holz, D.E. Toward a Halo Mass Function for Precision Cosmology: The Limits of Universality. Astrophys. J. 2008, 688, 709. [Google Scholar] [CrossRef]
- Diemer, B. COLOSSUS: A Python Toolkit for Cosmology, Large-scale Structure, and Dark Matter Halos. Astrophys. J. Suppl. Ser. 2018, 239, 35. [Google Scholar] [CrossRef]
- Moster, B.P.; Naab, T.; White, S.D.M. Galactic star formation and accretion histories from matching galaxies to dark matter haloes. Mon. Not. R. Astron. Soc. 2013, 428, 3121. [Google Scholar] [CrossRef]
- Lange, J.U.; van den Bosch, F.C.; Zentner, A.R.; Wang, K.; Villarreal, A.S. Updated results on the galaxy-halo connection from satellite kinematics in SDSS. Mon. Not. R. Astron. Soc. 2019, 487, 3112. [Google Scholar] [CrossRef]
- Lapi, A.; Salucci, P.; Danese, L. Precision Scaling Relations for Disk Galaxies in the Local Universe. Astrophys. J. 2018, 859, 2. [Google Scholar] [CrossRef]
- Mandelbaum, R.; Wang, W.; Zu, Y.; White, S.; Henriques, B.; More, S. Strong bimodality in the host halo mass of central galaxies from galaxy-galaxy lensing. Mon. Not. R. Astron. Soc. 2016, 457, 3002. [Google Scholar] [CrossRef]
- Foreman-Mackey, D.; Hogg, D.W.; Lang, D.; Goodman, J. emcee: The MCMC Hammer. Publ. Astron. Soc. Pac. 2013, 125, 306. [Google Scholar] [CrossRef]
- Labbe, I.; van Dokkum, P.; Nelson, E.; Bezanson, R.; Suess, K.A.; Leja, J.; Brammer, G.; Whitaker, K.; Mathews, E.; Stefanon, M.; et al. A population of red candidate massive galaxies 600 Myr after the Big Bang. Nature 2023, 616, 266. [Google Scholar] [CrossRef]
- Curtis-Lake, E.; Carniani, S.; Cameron, A.; Charlot, S.; Jakobsen, P.; Maiolino, R.; Bunker, A.; Witstok, J.; Smit, R.; Chevallard, J.; et al. Spectroscopic confirmation of four metal-poor galaxies at z = 10.3–13.2. Nature Astron. 2023, 7, 622. [Google Scholar] [CrossRef]
- Boylan-Kolchin, M. Stress testing ΛCDM with high-redshift galaxy candidates. Nature Astron. 2023, 7, 731. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).