A Critical Discussion on the H0 Tension †
Abstract
1. Introduction
2. A Summary of the CDM Model
- For an open Universe with , it is
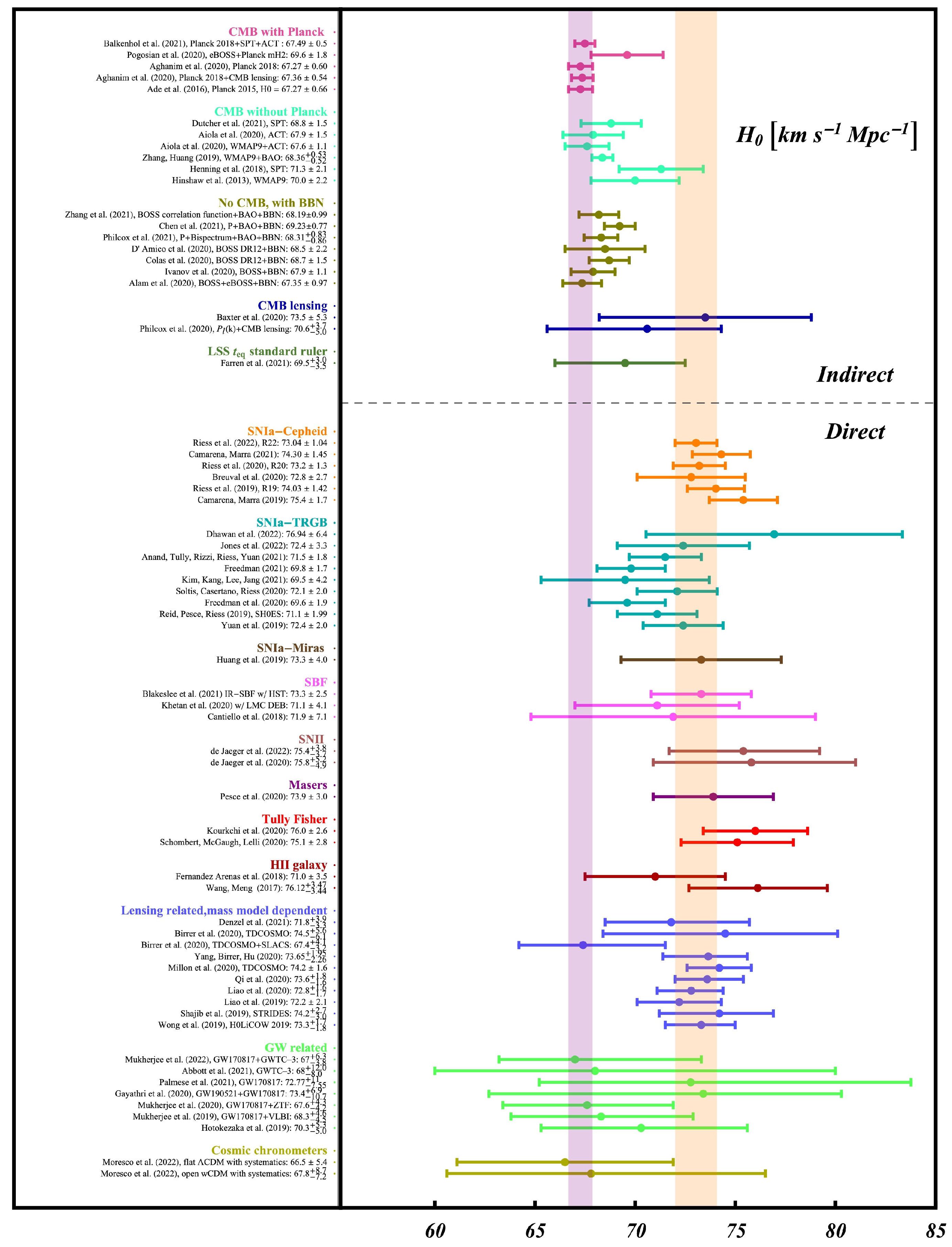
3. The Measurements and the Tension
3.1. Late and Early-Type Measurements
3.2. Overcoming the Tension
- Early Dark Energy, which behaves as a cosmological constant for , and then decades as fast as the radiation density (or even faster) at late times [50,52,231] via a slow-roll phase transition. While promising, this approach presents problems from both observational and theoretical perspectives [232]. Therefore, a modification has been proposed, called New Early Dark Energy, where instead of a slow phase transition, we have an almost instantaneous one [233]. This idea is similar to the aforementioned quintessence for late times.
- Extra relativistic degrees of freedom at the recombination, parameterized by the number of neutrino species, . According to our current understanding, for active massless neutrino families [234]. This number affects the inferred value of . Various models regarding further dark radiation have been proposed [235,236,237,238].
- Modifying the recombination history, by shifting the sound horizon for BAO at recombination. This can be achieved by either varying the early-time expansion history or by modifying the redshift of recombination. Various methods have been proposed to accomplish this, including exotic scenarios in the early Universe [239,240,241].
- A Running Vacuum model, linked to possibly Quantum Field Theory or String Theory, could be used to explain theoretically a possible phenomenological dependence of cosmological and gravitational constants with the cosmic time [258,259]. This kind of model can actually encompass different assumptions regarding the behavior of dark energy. It has also been successfully tested [260,261].
- The presence of local inhomogeneities that could affect the late-time measurements of , which may be either due to possible observational issues like incomplete sky sampling, astrophysical problems like incorrect modelling of the local structures, or a more fundamental nature, like the departure of the FLRW assumption at very small scales [262,263,264,265,266].
4. The Tension and the Look-Back Time
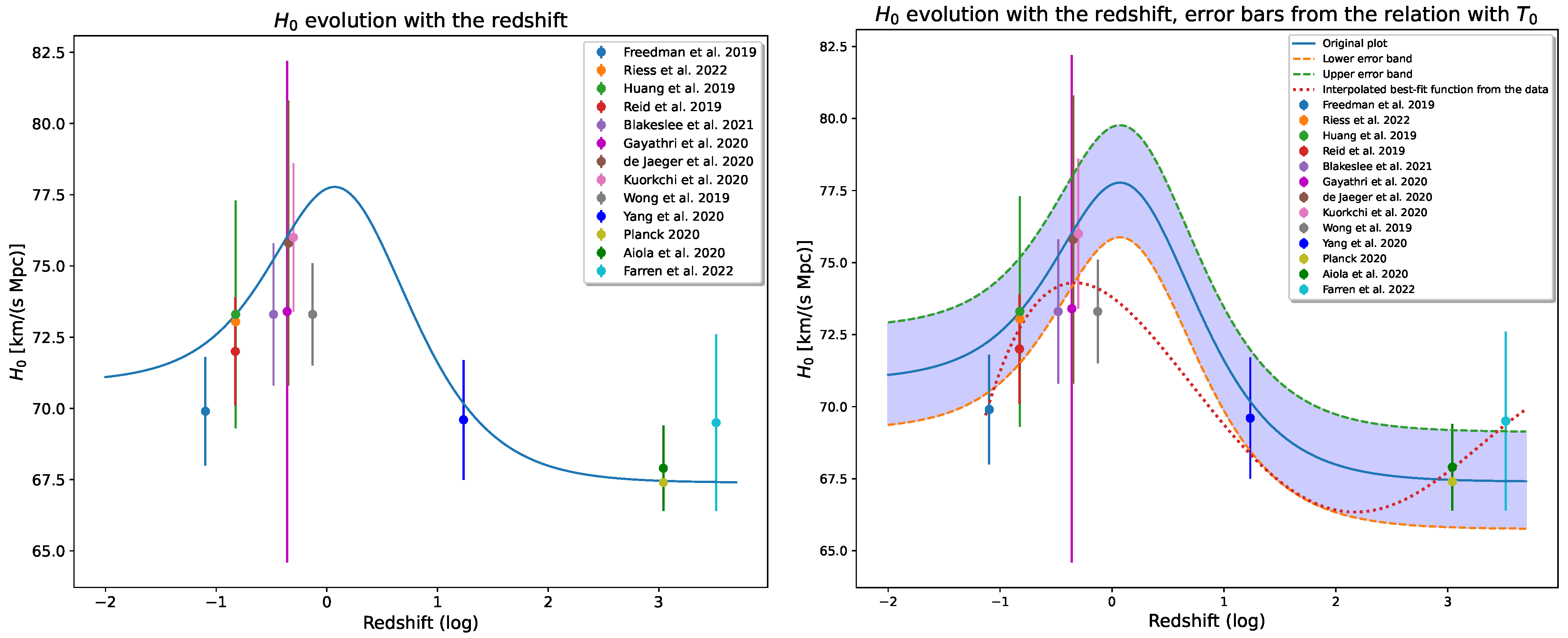
4.1. The Parameterization
- from the SH0ES collaboration, inferred by the cosmic distance ladder method considering Classical Cepheids + SNe Ia up to [24];
- from the Planck collaboration, obtained by the CMBR observations at [1];
- , obtained by using the TRGB as an anchor for SNe Ia instead of the Classical Cepheids, at [127];
- , derived from SNe Type II as the last step of the cosmological ladder, at [128];
- , derived from the Mira Variables employed as anchors of SNe Ia, at [276];
- , derived from the Tully-Fisher relation for spiral galaxies, at [129];
- , derived from the surface brightness fluctuations for the galaxies, at [130];
- , inferred from the Large Scale Structure standard ruler, and thus confronted to our computations at the redshift of equivalence [277];
- , inferred from the masers + SNe Ia and compared at [100];
- , derived from gravitational lensed quasars, confronted at [153];
- , which is a measurement provided by the CMBR independently from the Planck collaboration, and as such corresponding at the reionization epoch [159];
- , linked to the 21 cm absorption line and corresponding at the beginning of the so-called Cosmic Dawn, i.e., when the first stars formed (), in combination with CMBR data and considering a Chaplygin gas model for the dark sector [278];
- , deduced by gravitational waves, at [189].
4.2. A Variable from Late-Type Estimates
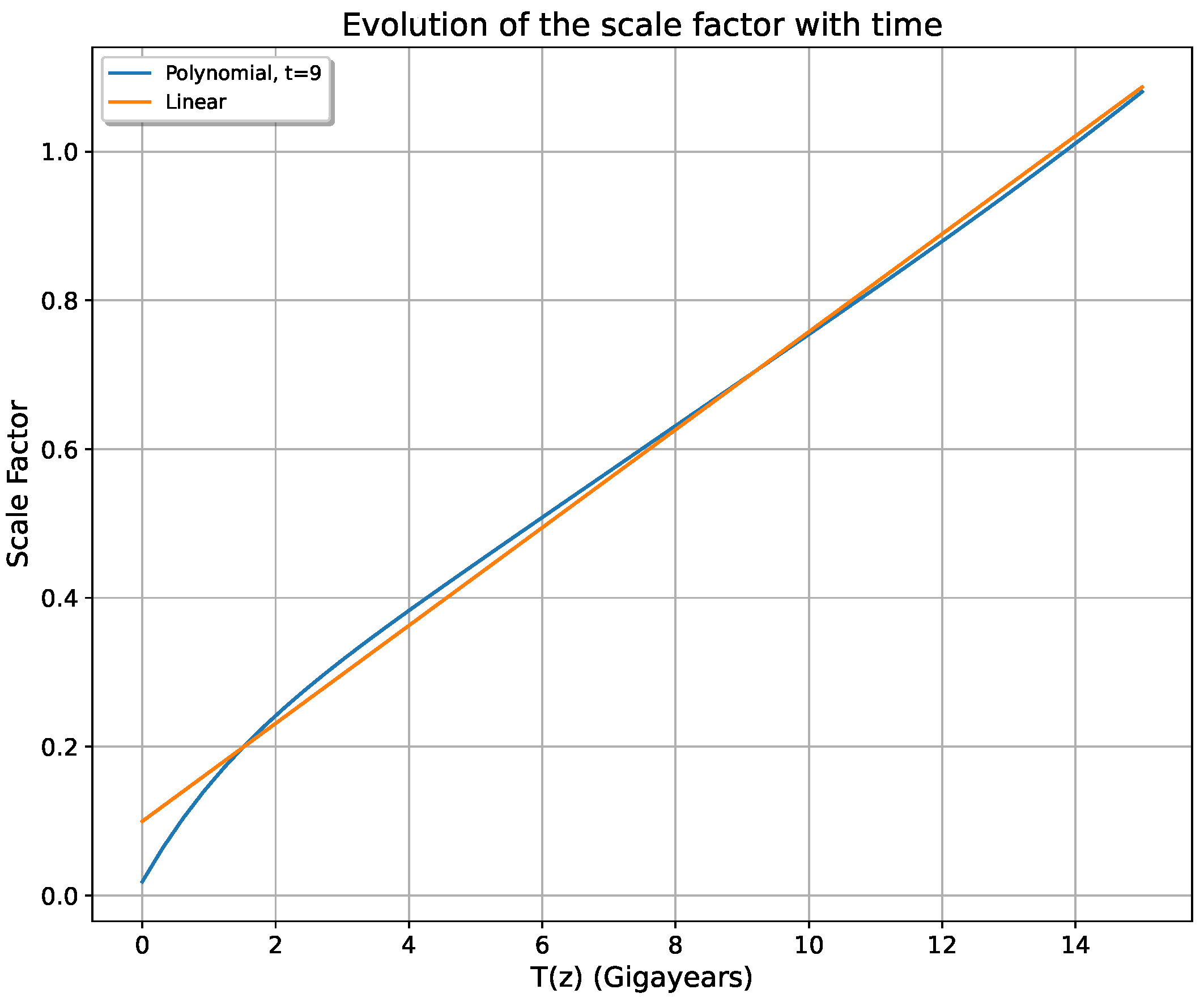
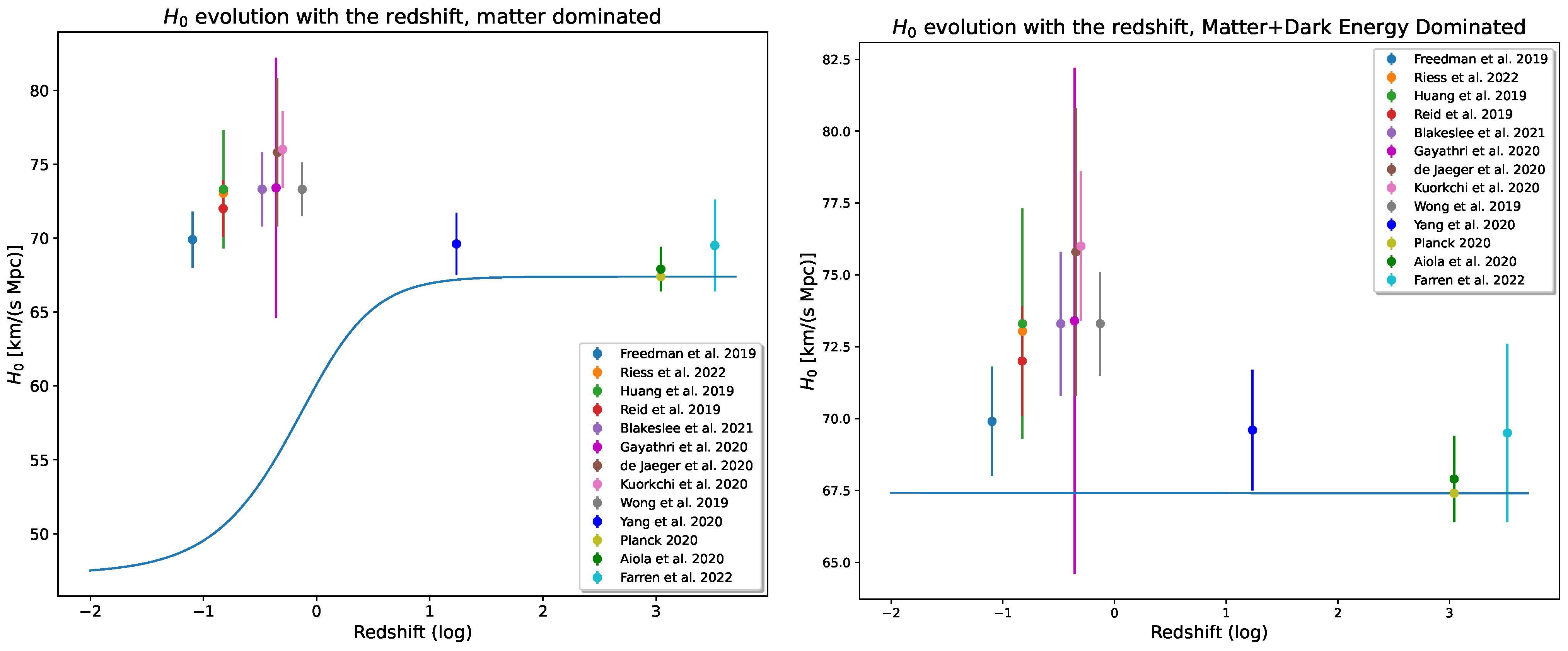
5. A Variable in CDM Model
6. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. Astron. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef]
- Weinberg, S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity; John Wiley and Sons: New York, NY, USA, 1972. [Google Scholar]
- Guth, A.H. Inflationary universe: A possible solution to the horizon and flatness problems. Phys. Lett. D 1981, 23, 347–356. [Google Scholar] [CrossRef]
- Starobinsky, A. Spectrum of relict gravitational radiation and the early state of the universe. J. Exp. Theor. Phys. Lett. 1979, 30, 682–685. [Google Scholar]
- Particle Data Group; Zyla, P.; Barnett, R.M.; Beringer, J.; Dahl, O.; Dwyer, D.A.; Groom, D.E.; Lin, C.J.; Lugovsky, K.S.; Pianori, E.; et al. Review of particle physics. Progr. Theor. Exp. Phys. 2020, 2020, 083C01. [Google Scholar]
- Particle Data Group; Workman, R.L.; Burkert, V.D.; Crede, V.; Klempt, E.; Thoma, U.; Tiator, L.; Agashe, K.; Aielli, G.; Allanach, B.C.; et al. Review of particle physics. Prog. Theor. Exp. Phys. 2022, 2022, 083C01. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Riess, A.G.; Strolger, L.G.; Casertano, S.; Ferguson, H.C.; Mobasher, B.; Gold, B.; Challis, P.J.; Filippenko, A.V.; Jha, S.; Li, W.; et al. New Hubble Space Telescope Discoveries of Type Ia Supernovae at z ≥ 1: Narrowing Constraints on the Early Behavior of Dark Energy. Astrophys. J. 2007, 659, 98–121. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Bahcall, N.A.; Ostriker, J.P.; Perlmutter, S.; Steinhardt, P.J. The Cosmic Triangle: Revealing the State of the Universe. Science 1999, 284, 1481–1488. [Google Scholar] [CrossRef]
- Spergel, D.N.; Verde, L.; Peiris, H.V.; Komatsu, E.; Nolta, M.R.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; et al. First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters. Astrophys. J. Suppl. Ser. 2003, 148, 175–194. [Google Scholar] [CrossRef]
- Schimd, C.; Tereno, I.; Uzan, J.P.; Mellier, Y.; van Waerbeke, L.; Semboloni, E.; Hoekstra, H.; Fu, L.; Riazuelo, A. Tracking quintessence by cosmic shear. Astron. Astrophys. 2006, 463, 405–421. [Google Scholar] [CrossRef]
- McDonald, P.; Seljak, U.; Burles, S.; Schlegel, D.J.; Weinberg, D.H.; Cen, R.; Shih, D.; Schaye, J.; Schneider, D.P.; Bahcall, N.A.; et al. The Lyα Forest Power Spectrum from the Sloan Digital Sky Survey. Astrophys. J. Suppl. Ser. 2006, 163, 80–109. [Google Scholar] [CrossRef]
- Bamba, K.; Capozziello, S.; Nojiri, S.; Odintsov, S.D. Dark energy cosmology: The equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155–228. [Google Scholar] [CrossRef]
- Joyce, A.; Jain, B.; Khoury, J.; Trodden, M. Beyond the cosmological standard model. Phys. Rep. 2015, 568, 1–98. [Google Scholar] [CrossRef]
- Abbott, T.M.C.; Allam, S.; Andersen, P.; Angus, C.; Asorey, J.; Avelino, A.; Avila, S.; Bassett, B.A.; Bechtol, K.; Bernstein, G.M.; et al. First Cosmology Results using Type Ia Supernovae from the Dark Energy Survey: Constraints on Cosmological Parameters. Astrophys. J. 2019, 872, L30. [Google Scholar] [CrossRef]
- Salucci, P.; Esposito, G.; Lambiase, G.; Battista, E.; Benetti, M.; Bini, D.; Boco, L.; Sharma, G.; Bozza, V.; Buoninfante, L.; et al. Einstein, Planck and Vera Rubin: Relevant Encounters Between the Cosmological and the Quantum Worlds. Front. Phys. 2021, 8, 579. [Google Scholar] [CrossRef]
- Zwicky, F. Die Rotverschiebung von extragalaktischen Nebeln. Helv. Phys. Acta 1933, 6, 110–127. [Google Scholar]
- Babcock, H.W. The rotation of the Andromeda Nebula. Lick Obs. Bull. 1939, 498, 41–51. [Google Scholar] [CrossRef]
- Rubin, V.C.; Ford, V.K. Rotation of the Andromeda Nebula from a Spectroscopic Survey of Emission Regions. Astrophys. J. 1970, 159, 379. [Google Scholar] [CrossRef]
- Schnee, R.W. Introduction to dark matter experiments. In Physics of the Large and the Small: TASI 2009; Csaki, C., Dodelso, S., Eds.; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2011; pp. 775–829. [Google Scholar] [CrossRef]
- Mitsou, V.A. Overview of searches for dark matter at the LHC. J. Phys. Conf. Ser. 2015, 651, 012023. [Google Scholar] [CrossRef]
- Aprile, E.; Aalbers, J.; Agostini, F.; Alfonsi, M.; Amaro, F.D.; Anthony, M.; Antunes, B.; Arneodo, F.; Balata, M.; Barrow, P.; et al. The XENON1T dark matter experiment. Eur. Phys. J. C 2017, 77, 881. [Google Scholar] [CrossRef]
- Riess, A.G.; Yuan, W.; Macri, L.M.; Scolnic, D.; Brout, D.; Casertano, S.; Jones, D.O.; Murakami, Y.; Anand, G.S.; Breuval, L.; et al. A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km/s/Mpc Uncertainty from the Hubble Space Telescope and the SH0ES Team. Astrophys. J. Lett. 2022, 934, L7. [Google Scholar] [CrossRef]
- Abdalla, E.; Abellán, G.F.; Aboubrahim, A.; Agnello, A.; Akarsu, Ö.; Akrami, Y.; Alestas, G.; Aloni, D.; Amendola, L.; Anchordoqui, L.A.; et al. Cosmology intertwined: A review of the particle physics, astrophysics, and cosmology associated with the cosmological tensions and anomalies. J. High Energy Astrophys. 2022, 34, 49–211. [Google Scholar] [CrossRef]
- Moresco, M.; Amati, L.; Amendola, L.; Birrer, S.; Blakeslee, J.P.; Cantiello, M.; Cimatti, A.; Darling, J.; Valle, M.D.; Fishbach, M.; et al. Unveiling the Universe with emerging cosmological probes. Living Rev. Relativ. 2022, 25, 6. [Google Scholar] [CrossRef]
- Capozziello, S. Curvature Quintessence. Int. J. Mod. Phys. D 2002, 11, 483–491. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59–144. [Google Scholar] [CrossRef]
- Capozziello, S.; Laurentis, M.D. Extended Theories of Gravity. Phys. Rep. 2011, 509, 167–321. [Google Scholar] [CrossRef]
- Capozziello, S.; Laurentis, M.D.; Odintsov, S.; Stabile, A. Hydrostatic equilibrium and stellar structure in f(R)-gravity. Phys. Rev. D 2011, 83, 064004. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.; Oikonomou, V. Modified gravity theories on a nutshell: Inflation, bounce and late-time evolution. Phys. Rep. 2017, 692, 1–104. [Google Scholar] [CrossRef]
- Felice, A.D.; Tsujikawa, S. f(R) Theories. Living Rev. Relativ. 2010, 13, 3. [Google Scholar] [CrossRef]
- Hu, W.; Sawicki, I. Models of f(R) Cosmic Acceleration that Evade Solar-System Tests. Phys. Rev. D 2007, 76, 064004. [Google Scholar] [CrossRef]
- Capozziello, S.; Cardone, V.F.; Troisi, A. Reconciling dark energy models with f(R) theories. Phys. Rev. D 2005, 71, 043503. [Google Scholar] [CrossRef]
- Oikonomou, V. Effects of a pre-inflationary de Sitter bounce on the primordial gravitational waves in f(R) gravity theories. Nucl. Phys. B 2022, 984, 115985. [Google Scholar] [CrossRef]
- Capozziello, S.; D’Agostino, R.; Luongo, O. Extended Gravity Cosmography. Int. J. Mod. Phys. D 2019, 28, 1930016. [Google Scholar] [CrossRef]
- Bajardi, F.; D’Agostino, R.; Benetti, M.; De Falco, V.; Capozziello, S. Early and late time cosmology: The f(R) gravity perspective. Eur. Phys. J. Plus 2022, 137, 1239. [Google Scholar] [CrossRef]
- Cai, Y.F.; Capozziello, S.; De Laurentis, M.; Saridakis, E.N. f(T) teleparallel gravity and cosmology. Rep. Prog. Phys. 2016, 79, 106901. [Google Scholar] [CrossRef] [PubMed]
- Benetti, M.; Capozziello, S.; Lambiase, G. Updating constraints on f(T) teleparallel cosmology and the consistency with big bang nucleosynthesis. Mon. Not. R. Astron. Soc. 2021, 500, 1795–1805. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.; Oikonomou, V. Integral F(R) gravity and saddle point condition as a remedy for the H0-tension. Nucl. Phys. B 2022, 980, 115850. [Google Scholar] [CrossRef]
- Spallicci, A.D.A.M.; Helayël-Neto, J.A.; López-Corredoira, M.; Capozziello, S. Cosmology and photon frequency shift induced by the Standard-Model Extension. Eur. Phys. J. C 2021, 81, 4. [Google Scholar] [CrossRef]
- Spallicci, A.D.A.M.; Sarracino, G.; Capozziello, S. Investigating dark energy by electromagnetic frequency shifts. Eur. Phys. J. Plus 2022, 137, 253. [Google Scholar] [CrossRef]
- Sarracino, G.; Spallicci, A.D.A.M.; Capozziello, S. Investigating dark energy by electromagnetic frequency shifts II: The Pantheon+ sample. Eur. Phys. J. Plus 2022, 137, 1386. [Google Scholar] [CrossRef]
- Capozziello, S.; Benetti, M.; Spallicci, A.D.A.M. Addressing the cosmological H0 tension by the Heisenberg uncertainty. Found. Phys. 2020, 50, 893. [Google Scholar] [CrossRef]
- Spallicci, A.D.A.M.; Benetti, M.; Capozziello, S. Heisenberg principle at cosmological scales. Found. Phys. 2022, 52, 23. [Google Scholar] [CrossRef]
- Bernal, J.L.; Verde, L.; Riess, A.G. The trouble with H0. J. Cosmol. Astropart. Phys. 2016, 2016, 019. [Google Scholar] [CrossRef]
- Mörtsell, E.; Dhawan, S. Does the Hubble constant tension call for new physics? J. Cosmol. Astropart. Phys. 2018, 2018, 025. [Google Scholar] [CrossRef]
- Vagnozzi, S.; Dhawan, S.; Gerbino, M.; Freese, K.; Goobar, A.; Mena, O. Constraints on the sum of the neutrino masses in dynamical dark energy models with w(z) ≤ −1 are tighter than those obtained in ΛCDM. Phys. Rev. D 2018, 98, 083501. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Valentino, E.D.; Nunes, R.C.; Vagnozzi, S.; Mota, D.F. Tale of stable interacting dark energy, observational signatures, and the H0 tension. J. Cosmol. Astropart. Phys. 2018, 2018, 019. [Google Scholar] [CrossRef]
- Poulin, V.; Smith, T.L.; Karwal, T.; Kamionkowski, M. Early Dark Energy can Resolve the Hubble Tension. Phys. Rev. Lett. 2019, 122, 221301. [Google Scholar] [CrossRef]
- Kreisch, C.D.; Cyr-Racine, F.Y.; Doré, O. Neutrino puzzle: Anomalies, interactions, and cosmological tensions. Phys. Rev. D 2020, 101, 103520. [Google Scholar] [CrossRef]
- Agrawal, P.; Cyr-Racine, F.Y.; Pinner, D.; Randall, L. Rock `n’ Roll Solutions to the Hubble Tension. Phys. Dark Universe 2023, 42, 101347. [Google Scholar] [CrossRef]
- Valentino, E.D.; Ferreira, R.Z.; Visinelli, L.; Danielsson, U. Late time transitions in the quintessence field and the H0 tension. Phys. Dark Universe 2019, 26, 100385. [Google Scholar] [CrossRef]
- Pan, S.; Yang, W.; Valentino, E.D.; Saridakis, E.N.; Chakraborty, S. Interacting scenarios with dynamical dark energy: Observational constraints and alleviation of the H0 tension. Phys. Rev. D 2019, 100, 103520. [Google Scholar] [CrossRef]
- Vagnozzi, S. New physics in light of the H0 tension: An alternative view. Phys. Rev. D 2020, 102, 023518. [Google Scholar] [CrossRef]
- Visinelli, L.; Vagnozzi, S.; Danielsson, U. Revisiting a Negative Cosmological Constant from Low-Redshift Data. Symmetry 2019, 11, 1035. [Google Scholar] [CrossRef]
- Knox, L.; Millea, M. Hubble constant hunter’s guide. Phys. Rev. D 2020, 101, 043533. [Google Scholar] [CrossRef]
- Valentino, E.D.; Melchiorri, A.; Mena, O.; Vagnozzi, S. Interacting dark energy in the early 2020s: A promising solution to the H0 and cosmic shear tensions. Phys. Dark Universe 2020, 30, 100666. [Google Scholar] [CrossRef]
- Valentino, E.D.; Melchiorri, A.; Mena, O.; Vagnozzi, S. Non-minimal dark sector physics and cosmological tensions. Phys. Rev. D 2020, 101, 063502. [Google Scholar] [CrossRef]
- Valentino, E.D.; Mukherjee, A.; Sen, A.A. Dark Energy with Phantom Crossing and the H0 Tension. Entropy 2021, 23, 404. [Google Scholar] [CrossRef]
- Smith, T.L.; Poulin, V.; Bernal, J.L.; Boddy, K.K.; Kamionkowski, M.; Murgia, R. Early dark energy is not excluded by current large-scale structure data. Phys. Rev. D 2021, 103, 123542. [Google Scholar] [CrossRef]
- Vagnozzi, S. Consistency tests of ΛCDM from the early integrated Sachs-Wolfe effect: Implications for early-time new physics and the Hubble tension. Phys. Rev. D 2021, 104, 063524. [Google Scholar] [CrossRef]
- Nunes, R.C.; Valentino, E.D. Dark sector interaction and the supernova absolute magnitude tension. Phys. Rev. D 2021, 104, 063529. [Google Scholar] [CrossRef]
- Cyr-Racine, F.Y.; Ge, F.; Knox, L. Symmetry of Cosmological Observables, a Mirror World Dark Sector, and the Hubble Constant. Phys. Rev. Lett. 2022, 128, 201301. [Google Scholar] [CrossRef]
- Anchordoqui, L.A.; Valentino, E.D.; Pan, S.; Yang, W. Dissecting the H0 and S8 tensions with Planck + BAO + supernova type Ia in multi-parameter cosmologies. J. High Energy Astrophys. 2021, 32, 28–64. [Google Scholar] [CrossRef]
- Poulin, V.; Smith, T.L.; Bartlett, A. Dark energy at early times and ACT data: A larger Hubble constant without late-time priors. Phys. Rev. D 2021, 104, 123550. [Google Scholar] [CrossRef]
- Alestas, G.; Camarena, D.; Valentino, E.D.; Kazantzidis, L.; Marra, V.; Nesseris, S.; Perivolaropoulos, L. Late-transition versus smooth H(z) deformation models for the resolution of the Hubble crisis. Phys. Rev. D 2022, 105, 063538. [Google Scholar] [CrossRef]
- Smith, T.L.; Lucca, M.; Poulin, V.; Abellan, G.F.; Balkenhol, L.; Benabed, K.; Galli, S.; Murgia, R. Hints of early dark energy in Planck, SPT, and ACT data: New physics or systematics? Phys. Rev. D 2022, 106, 043526. [Google Scholar] [CrossRef]
- Reeves, A.; Herold, L.; Vagnozzi, S.; Sherwin, B.D.; Ferreira, E.G.M. Restoring cosmological concordance with early dark energy and massive neutrinos? Mon. Not. R. Astron. Soc. 2023, 520, 3688–3695. [Google Scholar] [CrossRef]
- Poulin, V.; Smith, T.L.; Karwal, T. The Ups and Downs of Early Dark Energy solutions to the Hubble tension: A review of models, hints and constraints circa 2023. arXiv 2023, arXiv:2302.09032. [Google Scholar] [CrossRef]
- Demianski, M.; Piedipalumbo, E.; Sawant, D.; Amati, L. Cosmology with gamma-ray bursts I. The Hubble diagram through the calibrated Ep,i − Eiso correlation. Astron. Astrophys. 2017, 598, A112. [Google Scholar] [CrossRef]
- Lusso, E.; Piedipalumbo, E.; Risaliti, G.; Paolillo, M.; Bisogni, S.; Nardini, E.; Amati, L. Tension with the flat ΛCDM model from a high-redshift Hubble diagram of supernovae, quasars, and gamma-ray bursts. Astron. Astrophys. 2019, 628, L4. [Google Scholar] [CrossRef]
- Ryan, J.; Chen, Y.; Ratra, B. Baryon acoustic oscillation, Hubble parameter, and angular size measurement constraints on the Hubble constant, dark energy dynamics, and spatial curvature. Mon. Not. R. Astron. Soc. 2019, 488, 3844–3856. [Google Scholar] [CrossRef]
- Cao, S.; Ryan, J.; Ratra, B. Using Pantheon and DES supernova, baryon acoustic oscillation, and Hubble parameter data to constrain the Hubble constant, dark energy dynamics, and spatial curvature. Mon. Not. R. Astron. Soc. 2021, 504, 300–310. [Google Scholar] [CrossRef]
- Krishnan, C.; Colgáin, E.Ó.; Sheikh-Jabbari, M.; Yang, T. Running Hubble tension and a H0 diagnostic. Phys. Rev. D 2021, 103, 103509. [Google Scholar] [CrossRef]
- Colgáin, E.Ó.; Sheikh-Jabbari, M.; Yang, T. Elucidating cosmological model dependence with H0. Eur. Phys. J. C 2021, 81, 892. [Google Scholar] [CrossRef]
- Krishnan, C.; Mondol, R. H0 as a Universal FLRW Diagnostic. arXiv 2022, arXiv:2201.13384. [Google Scholar]
- Colgáin, E.Ó.; Sheikh-Jabbari, M.; Solomon, R.; Bargiacchi, G.; Capozziello, S.; Dainotti, M.; Stojkovic, D. Revealing intrinsic flat ΛCDM biases with standardizable candles. Phys. Rev. D 2022, 106, L041301. [Google Scholar] [CrossRef]
- Colgáin, E.Ó.; Sheikh-Jabbari, M.M.; Solomon, R.; Dainotti, M.G.; Stojkovic, D. Putting Flat ΛCDM In The (Redshift) Bin. arXiv 2022, arXiv:2206.11447. [Google Scholar]
- Colgáin, E.Ó.; Sheikh-Jabbari, M.M.; Solomon, R. High Redshift ΛCDM Cosmology: To Bin or not to Bin? arXiv 2022, arXiv:2211.02129. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Simone, B.D.; Schiavone, T.; Montani, G.; Rinaldi, E.; Lambiase, G. On the Hubble Constant Tension in the SNe Ia Pantheon Sample. Astrophys. J. 2021, 912, 150. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Simone, B.D.; Schiavone, T.; Montani, G.; Rinaldi, E.; Lambiase, G.; Bogdan, M.; Ugale, S. On the Evolution of the Hubble Constant with the SNe Ia Pantheon Sample and Baryon Acoustic Oscillations: A Feasibility Study for GRB-Cosmology in 2030. Galaxies 2022, 10, 24. [Google Scholar] [CrossRef]
- Dainotti, M.; De Simone, B.; Montani, G.; Schiavone, T.; Lambiase, G. The Hubble constant tension: Current status and future perspectives through new cosmological probes. arXiv 2023, arXiv:2301.10572. [Google Scholar]
- Schiavone, T.; Montani, G.; Dainotti, M.G.; De Simone, B.; Rinaldi, E.; Lambiase, G. Running Hubble constant from the SNe Ia Pantheon sample? arXiv 2022, arXiv:2205.07033. [Google Scholar]
- Schiavone, T.; Montani, G.; Bombacigno, F. f(R) gravity in the Jordan frame as a paradigm for the Hubble tension. Mon. Not. R. Astron. Soc. Lett. 2023, 522, L72–L77. [Google Scholar] [CrossRef]
- Malekjani, M.; Conville, R.M.; Colgáin, E.Ó.; Pourojaghi, S.; Sheikh-Jabbari, M.M. Negative Dark Energy Density from High Redshift Pantheon+ Supernovae. arXiv 2023, arXiv:2301.12725. [Google Scholar] [CrossRef]
- Gurzadyan, V.G.; Fimin, N.N.; Chechetkin, V.M. Cosmic voids and the kinetic analysis. Astron. Astrophys. 2022, 666, A149. [Google Scholar] [CrossRef]
- Hu, J.P.; Wang, F.Y. Hubble Tension: The Evidence of New Physics. Universe 2023, 9, 94. [Google Scholar] [CrossRef]
- Jia, X.A.; Hu, J.P.; Wang, F.Y. Evidence of a decreasing trend for the Hubble constant. Astron. Astrophys. 2023, 674, A45. [Google Scholar] [CrossRef]
- Capozziello, S.; Sarracino, G.; Spallicci, A.D.A.M. Questioning the H0 tension via the look-back time. Phys. Dark Universe 2023, 40, 101201. [Google Scholar] [CrossRef]
- Mecke, K.R.; Buchert, T.; Wagner, H. Robust morphological measures for large-scale structure in the Universe. Astron. Astrophys. 1994, 288, 697–704. [Google Scholar] [CrossRef]
- Yadav, J.K.; Bagla, J.S.; Khandai, N. Fractal dimension as a measure of the scale of homogeneity. Mon. Not. R. Astron. Soc. 2010, 405, 2009–2015. [Google Scholar] [CrossRef]
- Wiegand, A.; Buchert, T.; Ostermann, M. Direct Minkowski Functional analysis of large redshift surveys: A new high-speed code tested on the luminous red galaxy Sloan Digital Sky Survey-DR7 catalogue. Mon. Not. R. Astron. Soc. 2014, 443, 241–259. [Google Scholar] [CrossRef]
- Robertson, H.P. Kinematics and World-Structure. Astrophys. J. 1935, 82, 284. [Google Scholar] [CrossRef]
- Friedmann, A. Uber die Krummung des Raumes. Z. Fur Phys. 1922, 10, 377–386. [Google Scholar] [CrossRef]
- Hogg, D.W. Distance measures in cosmology. arXiv 1999, arXiv:astro-ph/9905116. [Google Scholar]
- Nemiroff, R.J.; Patla, B. Adventures in Friedmann cosmology: A detailed expansion of the cosmological Friedmann equations. Am. J. Phys. 2008, 76, 265–276. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Bowers, J.B.; Macri, L.; Zinn, J.C.; Scolnic, D. Cosmic Distances Calibrated to 1% Precision with Gaia EDR3 Parallaxes and Hubble Space Telescope Photometry of 75 Milky Way Cepheids Confirm Tension with ΛCDM. Astrophys. J. Lett. 2021, 908, L6. [Google Scholar] [CrossRef]
- Pietrzyński, G.; Graczyk, D.; Gallenne, A.; Gieren, W.; Thompson, I.B.; Pilecki, B.; Karczmarek, P.; Górski, M.; Suchomska, K.; Taormina, M.; et al. A distance to the Large Magellanic Cloud that is precise to one per cent. Nature 2019, 567, 200–203. [Google Scholar] [CrossRef]
- Reid, M.J.; Pesce, D.W.; Riess, A.G. An Improved Distance to NGC 4258 and Its Implications for the Hubble Constant. Astrophys. J. 2019, 886, L27. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.M.; Scolnic, D. Large Magellanic Cloud Cepheid Standards Provide a 1% Foundation for the Determination of the Hubble Constant and Stronger Evidence for Physics beyond ΛCDM. Astrophys. J. 2019, 876, 85. [Google Scholar] [CrossRef]
- Gaia Collaboration; Prusti, T.; de Bruijne, J.H.J.; Brown, A.G.A.; Vallenari, A.; Babusiaux, C.; Bailer-Jones, C.A.L.; Bastian, U.; Biermann, M.; Evans, D.W.; et al. The Gaia mission. Astron. Astrophys. 2016, 595, A1. [Google Scholar] [CrossRef]
- Gaia Collaboration; Brown, A.G.A.; Vallenari, A.; Prusti, T.; de Bruijne, J.H.J.; Mignard, F.; Drimmel, R.; Babusiaux, C.; Bailer-Jones, C.A.L.; Bastian, U.; et al. Gaia Data Release 1. Summary of the astrometric, photometric, and survey properties. Astron. Astrophys. 2016, 595, A2. [Google Scholar] [CrossRef]
- Gaia Collaboration; Brown, A.G.A.; Vallenari, A.; Prusti, T.; de Bruijne, J.H.J.; Babusiaux, C.; Bailer-Jones, C.A.L.; Biermann, M.; Evans, D.W.; Eyer, L.; et al. Gaia Data Release 2. Summary of the contents and survey properties. Astron. Astrophys. 2018, 616, A1. [Google Scholar] [CrossRef]
- Brown, A.G.A.; Vallenari, A.; Prusti, T.; de Bruijne, J.H.J.; Babusiaux, C.; Biermann, M.; Creevey, O.L.; Evans, D.W.; Eyer, L.; Hutton, A.; et al. Gaia Early Data Release 3. Astron. Astrophys. 2021, 650, C3. [Google Scholar] [CrossRef]
- Ripepi, V.; Clementini, G.; Molinaro, R.; Leccia, S.; Plachy, E.; Molnár, L.; Rimoldini, L.; Musella, I.; Marconi, M.; Garofalo, A.; et al. Gaia Data Release 3. Specific processing and validation of all sky RR Lyrae and Cepheid stars: The Cepheid sample. Astron. Astrophys. 2023, 674, A17. [Google Scholar] [CrossRef]
- Marconi, M.; Molinaro, R.; Bono, G.; Pietrzy’nski, G.; Gieren, W.; Pilecki, B.; Stellingwerf, R.F.; Graczyk, D.; Smolec, R.; Konorski, P.; et al. The Eclipsing Binary Cepheid OGLE-LMC-CEP-0227 in the Large Magellanic Cloud: Pulsation modelling of light and radial velocity curves. Astrophys. J. 2013, 768, L6. [Google Scholar] [CrossRef]
- Somma, G.D.; Marconi, M.; Molinaro, R.; Cignoni, M.; Musella, I.; Ripepi, V. An Extended Theoretical Scenario for Classical Cepheids. I. Modeling Galactic Cepheids in the Gaia Photometric System. Astrophys. J. Suppl. Ser. 2020, 247, 30. [Google Scholar] [CrossRef]
- De Somma, G.; Marconi, M.; Molinaro, R.; Cignoni, M.; Musella, I.; Ripepi, V. Gaia Parallaxes Versus Updated Pulsation Model Predictions. In Proceedings of the RR Lyrae/Cepheid 2019: Frontiers of Classical Pulsators; Astronomical Society of the Pacific Conference Series; Kinemuchi, K., Lovekin, C., Neilson, H., Vivas, K., Eds.; Astronomical Society of the Pacific: San Francisco, CA, USA, 2021; Volume 529, p. 27. [Google Scholar]
- Marconi, M.; Musella, I.; Fiorentino, G. Cepheid Pulsation Models at Varying Metallicity and ΔY/ΔZ. Astrophys. J. 2005, 632, 590–610. [Google Scholar] [CrossRef]
- Ripepi, V.; Catanzaro, G.; Molinaro, R.; Gatto, M.; De Somma, G.; Marconi, M.; Romaniello, M.; Leccia, S.; Musella, I.; Trentin, E.; et al. Cepheid metallicity in the Leavitt law (C-metall) survey—I. HARPS-N@TNG spectroscopy of 47 classical Cepheids and 1 BL Her variables. Mon. Not. R. Astron. Soc. 2021, 508, 4047–4071. [Google Scholar] [CrossRef]
- De Somma, G.; Marconi, M.; Molinaro, R.; Ripepi, V.; Leccia, S.; Musella, I. An Updated Metal-dependent Theoretical Scenario for Classical Cepheids. Astrophys. J. Suppl. Ser. 2022, 262, 25. [Google Scholar] [CrossRef]
- Breuval, L.; Riess, A.G.; Kervella, P.; Anderson, R.I.; Romaniello, M. An Improved Calibration of the Wavelength Dependence of Metallicity on the Cepheid Leavitt Law. Astrophys. J. 2022, 939, 89. [Google Scholar] [CrossRef]
- Meng, X.; Gao, Y.; Han, Z. SNe Ia as a cosmological probe. Int. J. Mod. Phys. D 2015, 24, 1530029. [Google Scholar] [CrossRef]
- Scolnic, D.; Brout, D.; Carr, A.; Riess, A.G.; Davis, T.M.; Dwomoh, A.; Jones, D.O.; Ali, N.; Charvu, P.; Chen, R.; et al. The Pantheon+ Analysis: The Full Data Set and Light-curve Release. Astrophys. J. 2022, 938, 113. [Google Scholar] [CrossRef]
- Brout, D.; Scolnic, D.; Popovic, B.; Riess, A.G.; Carr, A.; Zuntz, J.; Kessler, R.; Davis, T.M.; Hinton, S.; Jones, D.; et al. The Pantheon+ Analysis: Cosmological Constraints. Astrophys. J. 2022, 938, 110. [Google Scholar] [CrossRef]
- Scolnic, D.M.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J.; Huber, M.E.; Kessler, R.; Narayan, G.; Riess, A.G.; et al. The complete light-curve sample of spectroscopically confirmed SNe Ia from Pan-STARRS1 and cosmological constraints from the combined Pantheon sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- Hillebrandt, W.; Niemeyer, J.C. Type Ia Supernova Explosion Models. Annu. Rev. Astron. Astrophys. 2000, 38, 191–230. [Google Scholar] [CrossRef]
- Nomoto, K.; Thielemann, F.K.; Yokoi, K. Accreting white dwarf models for type I supern. III. Carbon deflagration supernovae. Astrophys. J. 1984, 286, 644–658. [Google Scholar] [CrossRef]
- Colgate, S.A.; McKee, C. Early Supernova Luminosity. Astrophys. J. 1969, 157, 623. [Google Scholar] [CrossRef]
- Carroll, S.M. The Cosmological Constant. Living Rev. Relativ. 2001, 4, 1. [Google Scholar] [CrossRef]
- Filippenko, A.V.; Richmond, M.W.; Matheson, T.; Shields, J.C.; Burbidge, E.M.; Cohen, R.D.; Dickinson, M.; Malkan, M.A.; Nelson, B.; Pietz, J.; et al. The Peculiar Type IA SN 1991T: Detonation of a White Dwarf? Astrophys. J. Lett. 1992, 384, L15. [Google Scholar] [CrossRef]
- Filippenko, A.V.; Richmond, M.W.; Branch, D.; Gaskell, M.; Herbst, W.; Ford, C.H.; Treffers, R.R.; Matheson, T.; Ho, L.C.; Dey, A.; et al. The Subluminous, Spectroscopically Peculiar Type 1a Supernova 1991bg in the Elliptical Galaxy NGC 4374. Astrophys. J. 1992, 104, 1543. [Google Scholar] [CrossRef]
- Khokhlov, A.M. Delayed detonation model for type IA supernovae. Astron. Astrophys. 1991, 245, 114–128. [Google Scholar]
- Phillips, M.M. The Absolute Magnitudes of Type IA Supernovae. Astrophys. J. Lett. 1993, 413, L105. [Google Scholar] [CrossRef]
- Salaris, M.; Cassisi, S. The “tip” of the red giant branch as a distance indicator: Results from evolutionary models. Mon. Not. R. Astron. Soc. 1997, 289, 406–414. [Google Scholar] [CrossRef]
- Freedman, W.L.; Madore, B.F.; Hatt, D.; Hoyt, T.J.; Jang, I.S.; Beaton, R.L.; Burns, C.R.; Lee, M.G.; Monson, A.J.; Neeley, J.R.; et al. The Carnegie-Chicago Hubble Program. VIII. An Independent Determination of the Hubble Constant Based on the Tip of the Red Giant Branch. Astrophys. J. 2019, 882, 34. [Google Scholar] [CrossRef]
- de Jaeger, T.; Stahl, B.E.; Zheng, W.; Filippenko, A.V.; Riess, A.G.; Galbany, L. A measurement of the Hubble constant from Type II supernovae. Mon. Not. R. Astron. Soc. 2020, 496, 3402–3411. [Google Scholar] [CrossRef]
- Kourkchi, E.; Tully, R.B.; Anand, G.S.; Courtois, H.M.; Dupuy, A.; Neill, J.D.; Rizzi, L.; Seibert, M. Cosmicflows-4: The Calibration of Optical and Infrared Tully-Fisher Relations. Astrophys. J. 2020, 896, 3. [Google Scholar] [CrossRef]
- Blakeslee, J.P.; Jensen, J.B.; Ma, C.P.; Milne, P.A.; Greene, J.E. The Hubble Constant from Infrared Surface Brightness Fluctuation Distances. Astrophys. J. 2021, 911, 65. [Google Scholar] [CrossRef]
- Uddin, S.A.; Burns, C.R.; Phillips, M.M.; Suntzeff, N.B.; Freedman, W.L.; Brown, P.J.; Morrell, N.; Hamuy, M.; Krisciunas, K.; Wang, L.; et al. Carnegie Supernova Project-I and -II: Measurements of H0 using Cepheid, TRGB, and SBF Distance Calibration to Type Ia Supernovae. arXiv 2023, arXiv:2308.01875. [Google Scholar]
- Cardona, W.; Kunz, M.; Pettorino, V. Determining H0 with Bayesian hyper-parameters. J. Cosmol. Astropart. Phys. 2017, 2017, 056. [Google Scholar] [CrossRef]
- Camarena, D.; Marra, V. Local determination of the Hubble constant and the deceleration parameter. Phys. Rev. Res. 2020, 2. [Google Scholar] [CrossRef]
- Dhawan, S.; Jha, S.W.; Leibundgut, B. Measuring the Hubble constant with Type Ia supernovae as near-infrared standard candles. Astron. Astrophys. 2018, 609, A72. [Google Scholar] [CrossRef]
- Burns, C.R.; Parent, E.; Phillips, M.M.; Stritzinger, M.; Krisciunas, K.; Suntzeff, N.B.; Hsiao, E.Y.; Contreras, C.; Anais, J.; Boldt, L.; et al. The Carnegie Supernova Project: Absolute Calibration and the Hubble Constant. Astrophys. J. 2018, 869, 56. [Google Scholar] [CrossRef]
- Follin, B.; Knox, L. Insensitivity of the distance ladder Hubble constant determination to Cepheid calibration modelling choices. Mon. Not. R. Astron. Soc. 2018, 477, 4534–4542. [Google Scholar] [CrossRef]
- Feeney, S.M.; Mortlock, D.J.; Dalmasso, N. Clarifying the Hubble constant tension with a Bayesian hierarchical model of the local distance ladder. Mon. Not. R. Astron. Soc. 2018, 476, 3861–3882. [Google Scholar] [CrossRef]
- Freedman, W.L.; Madore, B.F.; Hoyt, T.; Jang, I.S.; Beaton, R.; Lee, M.G.; Monson, A.; Neeley, J.; Rich, J. Calibration of the Tip of the Red Giant Branch. Astrophys. J. 2020, 891, 57. [Google Scholar] [CrossRef]
- Freedman, W.L. Measurements of the Hubble Constant: Tensions in Perspective. Astrophys. J. 2021, 919, 16. [Google Scholar] [CrossRef]
- Jang, I.S.; Lee, M.G. The Tip of the Red Giant Branch Distances to Typa Ia Supernova Host Galaxies. V. NGC 3021, NGC 3370, and NGC 1309 and the Value of the Hubble Constant. Astrophys. J. 2017, 836, 74. [Google Scholar] [CrossRef]
- Yuan, W.; Riess, A.G.; Macri, L.M.; Casertano, S.; Scolnic, D.M. Consistent Calibration of the Tip of the Red Giant Branch in the Large Magellanic Cloud on the Hubble Space Telescope Photometric System and a Redetermination of the Hubble Constant. Astrophys. J. 2019, 886, 61. [Google Scholar] [CrossRef]
- Kim, Y.J.; Kang, J.; Lee, M.G.; Jang, I.S. Determination of the Local Hubble Constant from Virgo Infall Using TRGB Distances. Astrophys. J. 2020, 905, 104. [Google Scholar] [CrossRef]
- Jones, D.O.; Mandel, K.S.; Kirshner, R.P.; Thorp, S.; Challis, P.M.; Avelino, A.; Brout, D.; Burns, C.; Foley, R.J.; Pan, Y.C.; et al. Cosmological Results from the RAISIN Survey: Using Type Ia Supernovae in the Near Infrared as a Novel Path to Measure the Dark Energy Equation of State. Astrophys. J. 2022, 933, 172. [Google Scholar] [CrossRef]
- Dhawan, S.; Goobar, A.; Johansson, J.; Jang, I.S.; Rigault, M.; Harvey, L.; Maguire, K.; Freedman, W.L.; Madore, B.F.; Smith, M.; et al. A Uniform Type Ia Supernova Distance Ladder with the Zwicky Transient Facility: Absolute Calibration Based on the Tip of the Red Giant Branch Method. Astrophys. J. 2022, 934, 185. [Google Scholar] [CrossRef]
- Scolnic, D.; Riess, A.G.; Wu, J.; Li, S.; Anand, G.S.; Beaton, R.; Casertano, S.; Anderson, R.; Dhawan, S.; Ke, X. CATS: The Hubble Constant from Standardized TRGB and Type Ia Supernova Measurements. Astrophys. J. Lett. 2023, 954, L31. [Google Scholar] [CrossRef]
- Khetan, N.; Izzo, L.; Branchesi, M.; Wojtak, R.; Cantiello, M.; Murugeshan, C.; Agnello, A.; Cappellaro, E.; Valle, M.D.; Gall, C.; et al. A new measurement of the Hubble constant using Type Ia supernovae calibrated with surface brightness fluctuations. Astron. Astrophys. 2021, 647, A72. [Google Scholar] [CrossRef]
- Cantiello, M.; Jensen, J.B.; Blakeslee, J.P.; Berger, E.; Levan, A.J.; Tanvir, N.R.; Raimondo, G.; Brocato, E.; Alexander, K.D.; Blanchard, P.K.; et al. A Precise Distance to the Host Galaxy of the Binary Neutron Star Merger GW170817 Using Surface Brightness Fluctuations. Astrophys. J. 2018, 854, L31. [Google Scholar] [CrossRef]
- de Jaeger, T.; Galbany, L.; Riess, A.G.; Stahl, B.E.; Shappee, B.J.; Filippenko, A.V.; Zheng, W. A 5% measurement of the Hubble-Lemaître constant from Type II supernovae. Mon. Not. R. Astron. Soc. 2022, 514, 4620–4628. [Google Scholar] [CrossRef]
- Schombert, J.; McGaugh, S.; Lelli, F. Using the Baryonic Tully-Fisher Relation to Measure H0. Astron. J. 2020, 160, 71. [Google Scholar] [CrossRef]
- Kourkchi, E.; Tully, R.B.; Courtois, H.M.; Dupuy, A.; Guinet, D. Cosmicflows-4: The baryonic Tully-Fisher relation providing ∼10000 distances. Mon. Not. R. Astron. Soc. 2022, 511, 6160–6178. [Google Scholar] [CrossRef]
- Bonvin, V.; Courbin, F.; Suyu, S.H.; Marshall, P.J.; Rusu, C.E.; Sluse, D.; Tewes, M.; Wong, K.C.; Collett, T.; Fassnacht, C.D.; et al. H0LiCOW V. New COSMOGRAIL time delays of HE 0435-1223: H0 to 3.8% precision from strong lensing in a flat ΛCDM model. Mon. Not. R. Astron. Soc. 2016, 465, 4914–4930. [Google Scholar] [CrossRef]
- Birrer, S.; Treu, T.; Rusu, C.E.; Bonvin, V.; Fassnacht, C.D.; Chan, J.H.H.; Agnello, A.; Shajib, A.J.; Chen, G.C.F.; Auger, M.; et al. Cosmographic analysis of the doubly imaged quasar SDSS 1206+332 and a new measurement of the Hubble constant. Mon. Not. R. Astron. Soc. 2019, 484, 4726–4753. [Google Scholar] [CrossRef]
- Wong, K.C.; Suyu, S.H.; Chen, G.C.F.; Rusu, C.E.; Millon, M.; Sluse, D.; Bonvin, V.; Fassnacht, C.D.; Taubenberger, S.; Auger, M.W.; et al. H0LiCOW-XIII. A 2.4 per cent measurement of H0 from lensed quasars: 5.3σ tension between early- and late-Universe probes. Mon. Not. R. Astron. Soc. 2019, 498, 1420–1439. [Google Scholar] [CrossRef]
- Millon, M.; Galan, A.; Courbin, F.; Treu, T.; Suyu, S.H.; Ding, X.; Birrer, S.; Chen, G.C.F.; Shajib, A.J.; Sluse, D.; et al. TDCOSMO. Astron. Astrophys. 2020, 639, A101. [Google Scholar] [CrossRef]
- Krishnan, C.; Mohayaee, R.; Colgáin, E.Ó.; Sheikh-Jabbari, M.M.; Yin, L. Does Hubble tension signal a breakdown in FLRW cosmology? Class. Quantum Gravity 2021, 38, 184001. [Google Scholar] [CrossRef]
- Verde, L.; Treu, T.; Riess, A.G. Tensions between the early and late Universe. Nat. Astron. 2019, 3, 891–895. [Google Scholar] [CrossRef]
- DiValentino, E. A combined analysis of the H0 late time direct measurements and the impact on the Dark Energy sector. Mon. Not. R. Astron. Soc. 2021, 502, 2065–2073. [Google Scholar] [CrossRef]
- Hinshaw, G.; Larson, D.; Komatsu, E.; Spergel, D.N.; Bennett, C.L.; Dunkley, J.; Nolta, M.R.; Halpern, M.; Hill, R.S.; Odegard, N.; et al. Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Parameter Results. Astrophys. J. Suppl. Ser. 2013, 208, 19. [Google Scholar] [CrossRef]
- Aiola, S.; Calabrese, E.; Maurin, L.; Naess, S.; Schmitt, B.L.; Abitbol, M.H.; Addison, G.E.; Ade, P.A.R.; Alonso, D.; Amiri, M.; et al. The Atacama Cosmology Telescope: DR4 maps and cosmological parameters. J. Cosmol. Astropart. Phys. 2020, 2020, 047. [Google Scholar] [CrossRef]
- Dutcher, D.; Balkenhol, L.; Ade, P.; Ahmed, Z.; Anderes, E.; Anderson, A.; Archipley, M.; Avva, J.; Aylor, K.; Barry, P.; et al. Measurements of the E-Mode Polarization and Temperature-E-Mode Correlation of the CMB from SPT-3G 2018 Data. Phys. Rev. D 2021, 104, 022003. [Google Scholar] [CrossRef]
- Eisenstein, D.J.; Zehavi, I.; Hogg, D.W.; Scoccimarro, R.; Blanton, M.R.; Nichol, R.C.; Scranton, R.; Seo, H.; Tegmark, M.; Zheng, Z.; et al. Detection of the Baryon Acoustic Peak in the Large-Scale Correlation Function of SDSS Luminous Red Galaxies. Astrophys. J. 2005, 633, 560–574. [Google Scholar] [CrossRef]
- Beutler, F.; Blake, C.; Colless, M.; Jones, D.H.; Staveley-Smith, L.; Campbell, L.; Parker, Q.; Saunders, W.; Watson, F. The 6dF Galaxy Survey: Baryon acoustic oscillations and the local Hubble constant. Mon. Not. R. Astron. Soc. 2011, 416, 3017–3032. [Google Scholar] [CrossRef]
- Blake, C.; Brough, S.; Colless, M.; Contreras, C.; Couch, W.; Croom, S.; Croton, D.; Davis, T.M.; Drinkwater, M.J.; Forster, K.; et al. The WiggleZ Dark Energy Survey: Joint measurements of the expansion and growth history at z < 1. Mon. Not. R. Astron. Soc. 2012, 425, 405–414. [Google Scholar] [CrossRef]
- du Mas des Bourboux, H.; Rich, J.; Font-Ribera, A.; de Sainte Agathe, V.; Farr, J.; Etourneau, T.; Goff, J.M.L.; Cuceu, A.; Balland, C.; Bautista, J.E.; et al. The Completed SDSS-IV Extended Baryon Oscillation Spectroscopic Survey: Baryon Acoustic Oscillations with Lyα Forests. Astrophys. J. 2020, 901, 153. [Google Scholar] [CrossRef]
- Alam, S.; Aubert, M.; Avila, S.; Balland, C.; Bautista, J.E.; Bershady, M.A.; Bizyaev, D.; Blanton, M.R.; Bovy, A.S.B.J.; Brinkmann, J.; et al. Completed SDSS-IV extended Baryon Oscillation Spectroscopic Survey: Cosmological implications from two decades of spectroscopic surveys at the Apache Point Observatory. Phys. Rev. D 2021, 103, 083553. [Google Scholar] [CrossRef]
- Cooke, R.J.; Pettini, M.; Steidel, C.C. One Percent Determination of the Primordial Deuterium Abundance. Astrophys. J. 2018, 855, 102. [Google Scholar] [CrossRef]
- Ivanov, M.M.; Simonović, M.; Zaldarriaga, M. Cosmological parameters from the BOSS galaxy power spectrum. J. Cosmol. Astropart. Phys. 2020, 2020, 042. [Google Scholar] [CrossRef]
- d’Amico, G.; Gleyzes, J.; Kokron, N.; Markovic, K.; Senatore, L.; Zhang, P.; Beutler, F.; Gil-Marín, H. The cosmological analysis of the SDSS/BOSS data from the Effective Field Theory of Large-Scale Structure. J. Cosmol. Astropart. Phys. 2020, 2020, 005. [Google Scholar] [CrossRef]
- Philcox, O.H.; Ivanov, M.M.; Simonović, M.; Zaldarriaga, M. Combining full-shape and BAO analyses of galaxy power spectra: A 1.6% CMB-independent constraint on H0. J. Cosmol. Astropart. Phys. 2020, 2020, 032. [Google Scholar] [CrossRef]
- Ivanov, M.M. Cosmological constraints from the power spectrum of eBOSS emission line galaxies. Phys. Rev. D 2021, 104, 103514. [Google Scholar] [CrossRef]
- Ivanov, M.M.; Philcox, O.H.; Simonović, M.; Zaldarriaga, M.; Nischimichi, T.; Takada, M. Cosmological constraints without nonlinear redshift-space distortions. Phys. Rev. D 2022, 105, 043531. [Google Scholar] [CrossRef]
- Philcox, O.H.; Ivanov, M.M. The BOSS DR12 Full-Shape Cosmology: Λ CDM Constraints from the Large-Scale Galaxy Power Spectrum and Bispectrum Monopole. Phys. Rev. D 2022, 105, 043517. [Google Scholar] [CrossRef]
- Chen, S.F.; Vlah, Z.; White, M. A new analysis of galaxy 2-point functions in the BOSS survey, including full-shape information and post-reconstruction BAO. J. Cosmol. Astropart. Phys. 2022, 2022, 008. [Google Scholar] [CrossRef]
- Brieden, S.; Gil-Marín, H.; Verde, L. Model-independent versus model-dependent interpretation of the SDSS-III BOSS power spectrum: Bridging the divide. Phys. Rev. D 2021, 104, L121301. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Sarracino, G.; Capozziello, S. Gamma-ray bursts, supernovae Ia, and baryon acoustic oscillations: A binned cosmological analysis. Publ. Astron. Soc. Jpn. 2022, 74, 1095–1113. [Google Scholar] [CrossRef]
- Bond, J.R.; Efstathiou, G. The statistics of cosmic background radiation fluctuations. Mon. Not. R. Astron. Soc. 1987, 226, 655–687. [Google Scholar] [CrossRef]
- Eisenstein, D.J.; Hu, W. Baryonic Features in the Matter Transfer Function. Astrophys. J. 1998, 496, 605–614. [Google Scholar] [CrossRef]
- Bashinsky, S.; Bertschinger, E. Position-Space Description of the Cosmic Microwave Background and Its Temperature Correlation Function. Phys. Rev. Lett. 2001, 87, 081301. [Google Scholar] [CrossRef] [PubMed]
- Bassett, B.A.; Hlozek, R. Baryon Acoustic Oscillations. arXiv 2009, arXiv:0910.5224. [Google Scholar]
- Dawson, K.S.; Schlegel, D.J.; Ahn, C.P.; Anderson, S.F.; Aubourg, É.; Bailey, S.; Barkhouser, R.H.; Bautista, J.E.; Beifiori, A.; Berlind, A.A.; et al. The Baryon Oscillation Spectroscopic Survey of SDSS-III. Astron. J. 2013, 145, 10. [Google Scholar] [CrossRef]
- Eisenstein, D.J.; Weinberg, D.H.; Agol, E.; Aihara, H.; Prieto, C.A.; Anderson, S.F.; Arns, J.A.; Aubourg, É.; Bailey, S.; Balbinot, E.; et al. SDSS-III: Massive Spectroscopic Surveys of the Distant Universe, the Milky Way Galaxy, and Extra-Solar Planetary Systems. Astron. J. 2011, 142, 72. [Google Scholar] [CrossRef]
- Dawson, K.S.; Kneib, J.P.; Percival, W.J.; Alam, S.; Albareti, F.D.; Anderson, S.F.; Armengaud, E.; Aubourg, É.; Bailey, S.; Bautista, J.E.; et al. The SDSS-IV extended Baryon Oscillation Spectroscopic Survey: Overview and Early Data. Astron. J. 2016, 151, 44. [Google Scholar] [CrossRef]
- Blanton, M.R.; Bershady, M.A.; Abolfathi, B.; Albareti, F.D.; Allende Prieto, C.; Almeida, A.; Alonso-García, J.; Anders, F.; Anderson, S.F.; Andrews, B.; et al. Sloan Digital Sky Survey IV: Mapping the Milky Way, Nearby Galaxies, and the Distant Universe. Astrophys. J. 2017, 154, 28. [Google Scholar] [CrossRef]
- Ross, A.J.; Samushia, L.; Howlett, C.; Percival, W.J.; Burden, A.; Manera, M. The clustering of the SDSS DR7 main Galaxy sample—I. A 4 per cent distance measure at z = 0.15. Mon. Not. R. Astron. Soc. 2015, 449, 835–847. [Google Scholar] [CrossRef]
- Aubourg, E.; Bailey, S.; Bautista, J.E.; Beutler, F.; Bhardwaj, V.; Bizyaev, D.; Blanton, M.; Blomqvist, M.; Bolton, A.S.; Bovy, J.; et al. Cosmological implications of baryon acoustic oscillation measurements. Phys. Rev. D 2015, 92, 123516. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; Adya, V.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Guidorzi, C.; Margutti, R.; Brout, D.; Scolnic, D.; Fong, W.; Alexander, K.D.; Cowperthwaite, P.S.; Annis, J.; Berger, E.; Blanchard, P.K.; et al. Improved Constraints on H0 from a Combined Analysis of Gravitational-wave and Electromagnetic Emission from GW170817. Astrophys. J. 2017, 851, L36. [Google Scholar] [CrossRef]
- Soares-Santos, M.; Palmese, A.; Hartley, W.; Annis, J.; Garcia-Bellido, J.; Lahav, O.; Doctor, Z.; Fishbach, M.; Holz, D.E.; Lin, H.; et al. First Measurement of the Hubble Constant from a Dark Standard Siren using the Dark Energy Survey Galaxies and the LIGO/Virgo Binary-Black-hole Merger GW170814. Astrophys. J. 2019, 876, L7. [Google Scholar] [CrossRef]
- Gayathri, V.; Healy, J.; Lange, J.; O’Brien, B.; Szczepanczyk, M.; Bartos, I.; Campanelli, M.; Klimenko, S.; Lousto, C.; O’Shaughnessy, R. Hubble Constant Measurement with GW190521 as an Eccentric Black Hole Merger. arXiv 2020, arXiv:2009.14247. [Google Scholar]
- Palmese, A.; Bom, C.R.; Mucesh, S.; Hartley, W.G. A Standard Siren Measurement of the Hubble Constant Using Gravitational-wave Events from the First Three LIGO/Virgo Observing Runs and the DESI Legacy Survey. Astrophys. J. 2023, 943, 56. [Google Scholar] [CrossRef]
- Jimenez, R.; Cimatti, A.; Verde, L.; Moresco, M.; Wandelt, B. The local and distant Universe: Stellar ages and H0. J. Cosmol. Astropart. Phys. 2019, 2019, 043. [Google Scholar] [CrossRef]
- Bernal, J.L.; Verde, L.; Jimenez, R.; Kamionkowski, M.; Valcin, D.; Wandelt, B.D. Trouble beyond H0 and the new cosmic triangles. Phys. Rev. D 2021, 103, 103533. [Google Scholar] [CrossRef]
- Boylan-Kolchin, M.; Weisz, D.R. Uncertain times: The redshift-time relation from cosmology and stars. Mon. Not. R. Astron. Soc. 2021, 505, 2764–2783. [Google Scholar] [CrossRef]
- Vagnozzi, S.; Pacucci, F.; Loeb, A. Implications for the Hubble tension from the ages of the oldest astrophysical objects. J. High Energy Astrophys. 2022, 36, 27–35. [Google Scholar] [CrossRef]
- Cimatti, A.; Moresco, M. Revisiting oldest stars as cosmological probes: New constraints on the Hubble constant. arXiv 2023, arXiv:2302.07899. [Google Scholar] [CrossRef]
- Boylan-Kolchin, M. Stress testing ΛCDM with high-redshift galaxy candidates. Nat. Astron. 2023, 7, 731–735. [Google Scholar] [CrossRef]
- Moresco, M.; Cimatti, A.; Jimenez, R.; Pozzetti, L.; Zamorani, G.; Bolzonella, M.; Dunlop, J.; Lamareille, F.; Mignoli, M.; Pearce, H.; et al. Improved constraints on the expansion rate of the Universe up to z∼ 1.1 from the spectroscopic evolution of cosmic chronometers. J. Cosmol. Astropart. Phys. 2012, 2012, 006. [Google Scholar] [CrossRef]
- Holsclaw, T.; Alam, U.; Sansó, B.; Lee, H.; Heitmann, K.; Habib, S.; Higdon, D. Nonparametric reconstruction of the dark energy equation of state. Phys. Rev. D 2010, 82, 103502. [Google Scholar] [CrossRef]
- Holsclaw, T.; Alam, U.; Sansó, B.; Lee, H.; Heitmann, K.; Habib, S.; Higdon, D. Nonparametric Dark Energy Reconstruction from Supernova Data. Phys. Rev. Lett. 2010, 105, 241302. [Google Scholar] [CrossRef]
- Bargiacchi, G.; Risaliti, G.; Benetti, M.; Capozziello, S.; Lusso, E.; Saccardi, A.; Signorini, M. Cosmography by orthogonalized logarithmic polynomials. Astron. Astrophys. 2021, 649, A65. [Google Scholar] [CrossRef]
- Amati, L.; Frontera, F.; Tavani, M.; in’t Zand, J.J.M.; Antonelli, A.; Costa, E.; Feroci, M.; Guidorzi, C.; Heise, J.; Masetti, N.; et al. Intrinsic spectra and energetics of BeppoSAX Gamma-Ray Bursts with known redshifts. Astron. Astrophys. 2002, 390, 81–89. [Google Scholar] [CrossRef]
- Ghirlanda, G.; Ghisellini, G.; Lazzati, D. The Collimation-corrected Gamma-Ray Burst Energies Correlate with the Peak Energy of Their νFν Spectrum. Astrophys. J. 2004, 616, 331–338. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Cardone, V.F.; Capozziello, S. A time-luminosity correlation for γ-ray bursts in the X-rays. Mon. Not. R. Astron. Soc. Lett. 2008, 391, L79–L83. [Google Scholar] [CrossRef]
- Kumar, P.; Zhang, B. The physics of gamma-ray bursts and relativistic jets. Phys. Rep. 2015, 561, 1–109. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Lenart, A.L.; Sarracino, G.; Nagataki, S.; Capozziello, S.; Fraija, N. The X-ray Fundamental Plane of the Platinum Sample, the Kilonovae, and the SNe Ib/c Associated with GRBs. Astrophys. J. 2020, 904, 97. [Google Scholar] [CrossRef]
- Cardone, V.F.; Capozziello, S.; Dainotti, M.G. An updated gamma-ray bursts Hubble diagram. Mon. Not. R. Astron. Soc. 2009, 400, 775–790. [Google Scholar] [CrossRef]
- Cardone, V.F.; Dainotti, M.G.; Capozziello, S.; Willingale, R. Constraining cosmological parameters by gamma-ray burst X-ray afterglow light curves. Mon. Not. R. Astron. Soc. 2010, 408, 1181–1186. [Google Scholar] [CrossRef]
- Amati, L.; D’Agostino, R.; Luongo, O.; Muccino, M.; Tantalo, M. Addressing the circularity problem in the Ep-Eiso correlation of gamma-ray bursts. Mon. Not. R. Astron. Soc. Lett. 2019, 486, L46–L51. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Lenart, A.L.; Chraya, A.; Sarracino, G.; Nagataki, S.; Fraija, N.; Capozziello, S.; Bogdan, M. The gamma-ray bursts fundamental plane correlation as a cosmological tool. Mon. Not. R. Astron. Soc. 2022, 518, 2201–2240. [Google Scholar] [CrossRef]
- Bargiacchi, G.; Dainotti, M.G.; Nagataki, S.; Capozziello, S. Gamma-ray bursts, quasars, baryonic acoustic oscillations, and supernovae Ia: New statistical insights and cosmological constraints. Mon. Not. R. Astron. Soc. 2023, 521, 3909–3924. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Nielson, V.; Sarracino, G.; Rinaldi, E.; Nagataki, S.; Capozziello, S.; Gnedin, O.Y.; Bargiacchi, G. Optical and X-ray GRB Fundamental Planes as cosmological distance indicators. Mon. Not. R. Astron. Soc. 2022, 514, 1828–1856. [Google Scholar] [CrossRef]
- Risaliti, G.; Lusso, E. A hubble diagram for quasars. Astrophys. J. 2015, 815, 33. [Google Scholar] [CrossRef]
- Risaliti, G.; Lusso, E. Cosmological Constraints from the Hubble Diagram of Quasars at High Redshifts. Nat. Astron. 2019, 3, 272–277. [Google Scholar] [CrossRef]
- Bargiacchi, G.; Benetti, M.; Capozziello, S.; Lusso, E.; Risaliti, G.; Signorini, M. Quasar cosmology: Dark energy evolution and spatial curvature. Mon. Not. R. Astron. Soc. 2022, 515, 1795–1806. [Google Scholar] [CrossRef]
- Lenart, A.L.; Bargiacchi, G.; Dainotti, M.G.; Nagataki, S.; Capozziello, S. A Bias-free Cosmological Analysis with Quasars Alleviating H 0 Tension. Astrophys. J. Suppl. Ser. 2023, 264, 46. [Google Scholar] [CrossRef]
- Risaliti, G.; Lusso, E.; Nardini, E.; Bargiacchi, G.; Bisogni, S.; Sacchi, A.; Signorini, M.; Trefoloni, B. Quasars as high-redshift standard candles. Astron. Nachrichten 2023, 344, e230054. [Google Scholar] [CrossRef]
- Signorini, M.; Risaliti, G.; Lusso, E.; Nardini, E.; Bargiacchi, G.; Sacchi, A.; Trefoloni, B. Quasars as standard candles. Astron. Astrophys. 2023, 676, A143. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Bargiacchi, G.; Lenart, A.Ł.; Nagataki, S.; Capozziello, S. Quasars: Standard Candles up to z = 7.5 with the Precision of Supernovae Ia. Astrophys. J. 2023, 950, 45. [Google Scholar] [CrossRef]
- Psaltis, D. Probes and Tests of Strong-Field Gravity with Observations in the Electromagnetic Spectrum. Living Rev. Relativ. 2008, 11, 9. [Google Scholar] [CrossRef]
- Feola, P.; Forteza, X.J.; Capozziello, S.; Cianci, R.; Vignolo, S. Mass-radius relation for neutron stars in f(R) = R + αR2 gravity: A comparison between purely metric and torsion formulations. Phys. Rev. D 2020, 101, 044037. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Ratra, B. Cosmology with a Time-Variable Cosmological “Constant”. Astrophys. J. Lett. 1988, 325, L17. [Google Scholar] [CrossRef]
- Ratra, B.; Peebles, P.J.E. Cosmological consequences of a rolling homogeneous scalar field. Phys. Rev. D 1988, 37, 3406–3427. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics Of Dark Energy. Int. J. Mod. Phys. D 2006, 15, 1753–1935. [Google Scholar] [CrossRef]
- Chevallier, M.; Polarski, D. Accelerating Universes with Scaling Dark Matter. Int. J. Mod. Phys. D 2001, 10, 213–223. [Google Scholar] [CrossRef]
- Linder, E.V. Exploring the Expansion History of the Universe. Phys. Rev. Lett. 2003, 90, 091301. [Google Scholar] [CrossRef]
- Piedipalumbo, E.; Scudellaro, P.; Esposito, G.; Rubano, C. A matter-dominated cosmological model with variable G and Λ and its confrontation with observational data. Gen. Relativ. Gravit. 2012, 44, 2477–2501. [Google Scholar] [CrossRef][Green Version]
- Bonometto, S.; Mezzetti, M.; Mainini, R. Strongly coupled dark energy with warm dark matter vs. LCDM. J. Cosmol. Astropart. Phys. 2017, 2017, 011. [Google Scholar] [CrossRef]
- Valentino, E.D.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the realm of the Hubble tension-a review of solutions. Class. Quantum Gravity 2021, 38, 153001. [Google Scholar] [CrossRef]
- Perivolaropoulos, L.; Skara, F. Challenges for ΛCDM: An update. New Astron. Rev. 2022, 95, 101659. [Google Scholar] [CrossRef]
- Schöneberg, N.; Abellán, G.F.; Sánchez, A.P.; Witte, S.J.; Poulin, V.; Lesgourgues, J. The H0 Olympics: A fair ranking of proposed models. Phys. Rep. 2022, 984, 1–55. [Google Scholar] [CrossRef]
- Karwal, T.; Kamionkowski, M. Dark energy at early times, the Hubble parameter, and the string axiverse. Phys. Rev. D 2016, 94, 103523. [Google Scholar] [CrossRef]
- Hill, J.C.; McDonough, E.; Toomey, M.W.; Alexander, S. Early dark energy does not restore cosmological concordance. Phys. Rev. D 2020, 102, 043507. [Google Scholar] [CrossRef]
- Niedermann, F.; Sloth, M.S. New early dark energy is compatible with current LSS data. Phys. Rev. D 2021, 103, 103537. [Google Scholar] [CrossRef]
- Mangano, G.; Miele, G.; Pastor, S.; Pinto, T.; Pisanti, O.; Serpico, P.D. Relic neutrino decoupling including flavour oscillations. Nucl. Phys. B 2005, 729, 221–234. [Google Scholar] [CrossRef]
- Jacques, T.D.; Krauss, L.M.; Lunardini, C. Additional light sterile neutrinos and cosmology. Phys. Rev. D 2013, 87, 083515. [Google Scholar] [CrossRef]
- Weinberg, S. Goldstone Bosons as Fractional Cosmic Neutrinos. Phys. Rev. Lett. 2013, 110, 241301. [Google Scholar] [CrossRef]
- Allahverdi, R.; Cicoli, M.; Dutta, B.; Sinha, K. Correlation between dark matter and dark radiation in string compactifications. J. Cosmol. Astropart. Phys. 2014, 2014, 002. [Google Scholar] [CrossRef]
- Valentino, E.D.; Giusarma, E.; Mena, O.; Melchiorri, A.; Silk, J. Cosmological limits on neutrino unknowns versus low redshift priors. Phys. Rev. D 2016, 93, 083527. [Google Scholar] [CrossRef]
- Hart, L.; Chluba, J. New constraints on time-dependent variations of fundamental constants using Planck data. Mon. Not. R. Astron. Soc. 2017, 474, 1850–1861. [Google Scholar] [CrossRef]
- Jedamzik, K.; Pogosian, L. Relieving the Hubble Tension with Primordial Magnetic Fields. Phys. Rev. Lett. 2020, 125, 181302. [Google Scholar] [CrossRef]
- Bose, B.; Lombriser, L. Easing cosmic tensions with an open and hotter universe. Phys. Rev. D 2021, 103, L081304. [Google Scholar] [CrossRef]
- Brevik, I.; Gorbunova, O. Dark energy and viscous cosmology. Gen. Relativ. Gravit. 2005, 37, 2039–2045. [Google Scholar] [CrossRef]
- Wang, D.; Yan, Y.J.; Meng, X.H. A new pressure-parametrization unified dark fluid model. Eur. Phys. J. C 2017, 77, 263. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Valentino, E.D.; Paliathanasis, A.; Lu, J. Challenging bulk viscous unified scenarios with cosmological observations. Phys. Rev. D 2019, 100, 103518. [Google Scholar] [CrossRef]
- da Silva, W.J.C.; Silva, R. Growth of matter perturbations in the extended viscous dark energy models. Eur. Phys. J. C 2021, 81, 403. [Google Scholar] [CrossRef]
- Khoury, J.; Weltman, A. Chameleon Fields: Awaiting Surprises for Tests of Gravity in Space. Phys. Rev. Lett. 2004, 93, 171104. [Google Scholar] [CrossRef] [PubMed]
- Khoury, J.; Weltman, A. Chameleon cosmology. Phys. Rev. D 2004, 69, 044026. [Google Scholar] [CrossRef]
- Vagnozzi, S.; Visinelli, L.; Brax, P.; Davis, A.C.; Sakstein, J. Direct detection of dark energy: The XENON1T excess and future prospects. Phys. Rev. D 2021, 104, 063023. [Google Scholar] [CrossRef]
- Cai, R.G.; Guo, Z.K.; Li, L.; Wang, S.J.; Yu, W.W. Chameleon dark energy can resolve the Hubble tension. Phys. Rev. D 2021, 103, L121302. [Google Scholar] [CrossRef]
- Benisty, D.; Davis, A.C. Dark energy interactions near the Galactic Center. Phys. Rev. D 2022, 105, 024052. [Google Scholar] [CrossRef]
- Haba, Z.; Stachowski, A.; Szydłowski, M. Dynamics of the diffusive DM-DE interaction–Dynamical system approach. J. Cosmol. Astropart. Phys. 2016, 2016, 024. [Google Scholar] [CrossRef]
- Koutsoumbas, G.; Ntrekis, K.; Papantonopoulos, E.; Saridakis, E.N. Unification of dark matter-dark energy in generalized Galileon theories. J. Cosmol. Astropart. Phys. 2018, 2018, 003. [Google Scholar] [CrossRef]
- Calogero, S.; Velten, H. Cosmology with matter diffusion. J. Cosmol. Astropart. Phys. 2013, 2013, 025. [Google Scholar] [CrossRef]
- Perez, A.; Sudarsky, D.; Wilson-Ewing, E. Resolving the H0 tension with diffusion. Gen. Relativ. Gravit. 2021, 53, 7. [Google Scholar] [CrossRef]
- Li, X.; Shafieloo, A. A Simple Phenomenological Emergent Dark Energy Model can Resolve the Hubble Tension. Astrophys. J. 2019, 883, L3. [Google Scholar] [CrossRef]
- Pan, S.; Yang, W.; Valentino, E.D.; Shafieloo, A.; Chakraborty, S. Reconciling H0 tension in a six parameter space? J. Cosmol. Astropart. Phys. 2020, 2020, 062. [Google Scholar] [CrossRef]
- Rezaei, M.; Naderi, T.; Malekjani, M.; Mehrabi, A. A Bayesian comparison between ΛCDM and phenomenologically emergent dark energy models. Eur. Phys. J. C 2020, 80, 374. [Google Scholar] [CrossRef]
- Solà, J. Cosmological constant and vacuum energy: Old and new ideas. J. Phys. Conf. Ser. 2013, 453, 012015. [Google Scholar] [CrossRef]
- Solà, J.; Gómez-Valent, A. The CDM cosmology: From inflation to dark energy through running Λ. Int. J. Mod. Phys. D 2015, 24, 1541003. [Google Scholar] [CrossRef]
- Peracaula, J.S.; de Cruz Pérez, J.; Gómez-Valent, A. Possible signals of vacuum dynamics in the Universe. Mon. Not. R. Astron. Soc. 2018, 478, 4357–4373. [Google Scholar] [CrossRef]
- Gómez-Valent, A.; Peracaula, J.S. Density perturbations for running vacuum: A successful approach to structure formation and to the σ8-tension. Mon. Not. R. Astron. Soc. 2018, 478, 126–145. [Google Scholar] [CrossRef]
- Camarena, D.; Marra, V. Impact of the cosmic variance on H0 on cosmological analyses. Phys. Rev. D 2018, 98, 023537. [Google Scholar] [CrossRef]
- Bengaly, C.A.P.; Andrade, U.; Alcaniz, J.S. How does an incomplete sky coverage affect the Hubble Constant variance? Eur. Phys. J. C 2019, 79, 768. [Google Scholar] [CrossRef]
- Krishnan, C.; Mohayaee, R.; Colgáin, E.O.; Sheikh-Jabbari, M.; Yin, L. Hints of FLRW breakdown from supernovae. Phys. Rev. D 2022, 105, 063514. [Google Scholar] [CrossRef]
- Kalbouneh, B.; Marinoni, C.; Bel, J. Multipole expansion of the local expansion rate. Phys. Rev. D 2023, 107, 023507. [Google Scholar] [CrossRef]
- Giani, L.; Howlett, C.; Said, K.; Davis, T.; Vagnozzi, S. An effective description of Laniakea: Impact on cosmology and the local determination of the Hubble constant. J. Cosmol. Astropart. Phys. 2024, 2024, 071. [Google Scholar] [CrossRef]
- Helayël-Neto, J.A.; Spallicci, A.D.A.M. Frequency variation for Vacuo Photon Propag. Standard-Model Extension. Eur. Phys. J. C 2019, 79, 590. [Google Scholar] [CrossRef]
- Bonetti, L.; dos Santos Filho, L.R.; Helayël-Neto, J.A.; Spallicci, A.D.A.M. Effective photon mass from Super and Lorentz symmetry breaking. Phys. Lett. B 2017, 764, 203. [Google Scholar] [CrossRef]
- Bonetti, L.; dos Santos Filho, L.R.; Helayël-Neto, J.A.; Spallicci, A.D.A.M. Photon sector analysis of Super and Lorentz symmetry breaking: Effective photon mass, bi-refringence and dissipation. Eur. Phys. J. C 2018, 78, 811. [Google Scholar] [CrossRef]
- Goldhaber, A.S.; Nieto, M.M. Photon and graviton mass limits. Rev. Mod. Phys. 2010, 82, 939. [Google Scholar] [CrossRef]
- Retinò, A.; Spallicci, A.D.A.M.; Vaivads, A. Solar wind test of the de Broglie-Proca massive photon with Cluster multi-spacecraft data. Astropart. Phys. 2016, 82, 49. [Google Scholar] [CrossRef]
- de Broglie, L. Nouvelles Recherches sur la Lumière; Actualités Scientifiques et Industrielles; Hermann & Cie: Paris, France, 1936; Volume 411. [Google Scholar]
- Proca, A. Sur les équations fondamentales des particules élémentaires. C. R. Acad. Sci. Paris 1936, 202, 1490. [Google Scholar]
- Kumar Aluri, P.; Cea, P.; Chingangbam, P.; Chu, M.C.; Clowes, R.G.; Hutsemékers, D.; Kochappan, J.P.; Lopez, A.M.; Liu, L.; Martens, N.C.M.; et al. Is the observable Universe consistent with the cosmological principle? Class. Quantum Gravity 2023, 40, 094001. [Google Scholar] [CrossRef]
- Krishnan, C.; Mondol, R.; Sheikh-Jabbari, M. Dipole cosmology: The Copernican paradigm beyond FLRW. J. Cosmol. Astropart. Phys. 2023, 2023, 020. [Google Scholar] [CrossRef]
- Huang, C.D.; Riess, A.G.; Yuan, W.; Macri, L.M.; Zakamska, N.L.; Casertano, S.; Whitelock, P.A.; Hoffmann, S.L.; Filippenko, A.V.; Scolnic, D. Hubble Space Telescope Observations of Mira Variables in the SN Ia Host NGC 1559: An Alternative Candle to Measure the Hubble Constant. Astrophys. J. 2020, 889, 5. [Google Scholar] [CrossRef]
- Farren, G.S.; Philcox, O.H.E.; Sherwin, B.D. Determining the Hubble constant without the sound horizon: Perspectives with future galaxy surveys. Phys. Rev. D 2022, 105, 063503. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Vagnozzi, S.; Valentino, E.D.; Mota, D.F.; Capozziello, S. Dawn of the dark: Unified dark sectors and the EDGES Cosmic Dawn 21-cm signal. J. Cosmol. Astropart. Phys. 2019, 2019, 044. [Google Scholar] [CrossRef]
- Bernardis, F.D.; Melchiorri, A.; Verde, L.; Jimenez, R. The cosmic neutrino background and the age of the Universe. J. Cosmol. Astropart. Phys. 2008, 2008, 020. [Google Scholar] [CrossRef][Green Version]
- Vandenberg, D.A.; Bolte, M.; Stetson, P.B. The Age of the Galactic Globular Cluster System. Annu. Rev. Astron. Astrophys. 1996, 34, 461–510. [Google Scholar] [CrossRef]
- Soderblom, D.R. The Ages of Stars. Annu. Rev. Astron. Astrophys. 2010, 48, 581–629. [Google Scholar] [CrossRef]
- Catelan, M. The ages of (the oldest) stars. Proc. Int. Astron. Union 2017, 13, 11–20. [Google Scholar] [CrossRef][Green Version]
- Valcin, D.; Bernal, J.L.; Jimenez, R.; Verde, L.; Wandelt, B.D. Inferring the age of the universe with globular clusters. J. Cosmol. Astropart. Phys. 2020, 2020, 002. [Google Scholar] [CrossRef]
- Sazhin, M.V.; Sazhina, O.S.; Chadayammuri, U. The Scale Factor in the Universe with Dark Energy. arXiv 2011, arXiv:astro-ph.CO/1109.2258. [Google Scholar] [CrossRef]
- Weinberg, E.J. Some problems with extended inflation. Phys. Rev. D 1989, 40, 3950–3959. [Google Scholar] [CrossRef]
- Califano, M.; de Martino, I.; Vernieri, D.; Capozziello, S. Exploiting the Einstein Telescope to solve the Hubble tension. Phys. Rev. D 2023, 107, 123519. [Google Scholar] [CrossRef]
- Califano, M.; de Martino, I.; Vernieri, D.; Capozziello, S. Constraining ΛCDM cosmological parameters with Einstein Telescope mock data. Mon. Not. R. Astron. Soc. 2022, 518, 3372–3385. [Google Scholar] [CrossRef]
- Laureijs, R.; Amiaux, J.; Arduini, S.; Auguères, J.L.; Brinchmann, J.; Cole, R.; Cropper, M.; Dabin, C.; Duvet, L.; Ealet, A.; et al. Euclid Definition Study Report. arXiv 2011, arXiv:astro-ph.CO/1110.3193. [Google Scholar]
- Scaramella, R.; Amiaux, J.; Mellier, Y.; Burigana, C.; Carvalho, C.S.; Cuillandre, J.C.; Silva, A.D.; Derosa, A.; Dinis, J.; Maiorano, E.; et al. Euclid preparation. I. The Euclid Wide Survey. Astron. Astrophys. 2022, 662, A112. [Google Scholar] [CrossRef]
- Blanchard, A.; Camera, S.; Carbone, C.; Cardone, V.F.; Casas, S.; Clesse, S.; Ilić, S.; Kilbinger, M.; Kitching, T.; Kunz, M.; et al. Euclid preparation. VII. Forecast validation for Euclid cosmological probes. Astron. Astrophys. 2020, 642, A191. [Google Scholar] [CrossRef]
- Frusciante, N.; Pace, F.; Cardone, V.F.; Casas, S.; Tutusaus, I.; Ballardini, M.; Bellini, E.; Benevento, G.; Bose, B.; Valageas, P.; et al. Euclid: Constraining linearly scale-independent modifications of gravity with the spectroscopic and photometric primary probes. arXiv 2023, arXiv:astro-ph.CO/2306.12368. [Google Scholar]
- Casas, S.; Cardone, V.F.; Sapone, D.; Frusciante, N.; Pace, F.; Parimbelli, G.; Archidiacono, M.; Koyama, K.; Tutusaus, I.; Camera, S.; et al. Euclid: Constraints on f(R) cosmologies from the spectroscopic and photometric primary probes. arXiv 2023, arXiv:astro-ph.CO/2306.11053. [Google Scholar]
- Bailey, A.C.; Vincenzi, M.; Scolnic, D.; Cuillandre, J.C.; Rhodes, J.; Hook, I.; Peterson, E.R.; Popovic, B. Type Ia supernova observations combining data from the Euclid mission and the Vera C. Rubin Observatory. Mon. Not. R. Astron. Soc. 2023, 524, 5432–5441. [Google Scholar] [CrossRef]
- Joudaki, S.; Blake, C.; Heymans, C.; Choi, A.; Harnois-Deraps, J.; Hildebrandt, H.; Joachimi, B.; Johnson, A.; Mead, A.; Parkinson, D.; et al. CFHTLenS revisited: Assessing concordance with Planck including astrophysical systematics. Mon. Not. R. Astron. Soc. 2016, 465, 2033–2052. [Google Scholar] [CrossRef]
- Abbott, T.; Aguena, M.; Alarcon, A.; Allam, S.; Alves, O.; Amon, A.; Andrade-Oliveira, F.; Annis, J.; Avila, S.; Bacon, D.; et al. Dark Energy Survey Year 3 results: Cosmological constraints from galaxy clustering and weak lensing. Phys. Rev. D 2022, 105, 023520. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Silk, J. Planck evidence for a closed Universe and a possible crisis for cosmology. Nat. Astron. 2019, 4, 196–203. [Google Scholar] [CrossRef]
- Challinor, A. CMB anisotropy science: A review. Proc. Int. Astron. Union 2012, 8, 42–52. [Google Scholar] [CrossRef]
- Schwarz, D.J.; Copi, C.J.; Huterer, D.; Starkman, G.D. CMB anomalies after Planck. Class. Quantum Gravity 2016, 33, 184001. [Google Scholar] [CrossRef]
- Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; Benabed, K.; et al. Planck2018 results: VII. Isotropy and statistics of the CMB. Astron. Astrophys. 2020, 641, A7. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Capozziello, S.; Sarracino, G.; De Somma, G. A Critical Discussion on the H0 Tension. Universe 2024, 10, 140. https://doi.org/10.3390/universe10030140
Capozziello S, Sarracino G, De Somma G. A Critical Discussion on the H0 Tension. Universe. 2024; 10(3):140. https://doi.org/10.3390/universe10030140
Chicago/Turabian StyleCapozziello, Salvatore, Giuseppe Sarracino, and Giulia De Somma. 2024. "A Critical Discussion on the H0 Tension" Universe 10, no. 3: 140. https://doi.org/10.3390/universe10030140
APA StyleCapozziello, S., Sarracino, G., & De Somma, G. (2024). A Critical Discussion on the H0 Tension. Universe, 10(3), 140. https://doi.org/10.3390/universe10030140







