Abstract
Physical laws manifest themselves through the amalgamation of mathematical symbols, numbers, functions, geometries, and relationships. These intricate combinations unfold within a mathematical model devised to capture and represent the “objective reality” of the system under examination. In this symbiotic relationship between physics and mathematics, the language of mathematics becomes a powerful tool for describing and predicting the behavior of the physical world. The language used and the associated concepts are in a perpetual state of evolution, mirroring the ongoing expansion of the phenomena accessible to our scientific understanding. In this contribution, written in honor of Richard Kerner, we delve into fundamental, at times seemingly elementary, elements of the mathematical language inherent to the physical sciences, guided by the overarching principles of symmetry and group theory. Our focus turns to the captivating realm of spheres, those strikingly symmetric entities that manifest prominently within our geometric landscape. By exploring the interplay between mathematical abstraction and the tangible beauty of symmetry, we seek to deepen our understanding of the underlying structures that govern our interpretation of the physical world.
MSC:
58D19; 58J70; 76M60; 52B15
1. Introduction
This contribution serves as a friendly tribute to Richard Kerner, a distinguished figure in the realm of theoretical and mathematical physics, whose methodologies consistently embody a harmonious blend of precision, intuition, and a poetic touch. Kerner’s ability to reveal the concealed facets of diverse phenomena, in the domains of general relativity and gauge theory (Kaluza–Klein, e.g., [1]), condensed matter (glasses, e.g., [2]), particle physics (quarks and ternary algebras, e.g., [3]), noncommutative geometric structures (e.g., [4]), and many others, is an attestation of his profound insights.
In each of his works, Kerner consistently imparts that distinct touch of originality, elevating his contributions beyond the ordinary. His dedication to unraveling the intricacies of the universe is reflected not only in the rigor of his approach but also in the elegance with which he brings to light the hidden dimensions of our physical reality. One of his latest publications, as referenced in [5], stands as a magisterial testament to his multifaceted talents.
This current contribution aligns seamlessly with the theme encapsulated in the title The Languages of Physics of the special issue in honor of Kerner. My focus will be directed towards the mathematical language of physics, emphasizing the inherent limitation in precision when scrutinized from the perspective of a physicist. Such models are transient rather than eternal, subject to the passage of (entropic) time and contingent upon the scale at which they operate. To align with experimental observations and predictions, these models often undergo modifications, sometimes requiring radical transformations. In the dynamic interplay between the modeler and the modeled object, a degree of probability emerges, representing the level of epistemic confidence in the model’s appropriateness [6].
This recognition of inherent uncertainty gives rise to the imperative of introducing some level of coarse-graining into the initial mathematical model, conceived to portray an ontic entity or fact. Take, for example, the inconceivability of irrational numbers in human perception, conceivability being here understood in terms of a measurable physical quantity. Yet physical laws, for several centuries now, have been articulated in terms of real numbers, denoted as , constructed from the abstract concept of limits (such as the limit of Cauchy sequences of rational numbers).
Nevertheless, these profoundly abstract mathematical concepts have evolved to such a degree of familiarity that they now stand as an indispensable foundation for formulating descriptions of our environment. Serving as a robust backdrop, they assist us in imposing structure and establishing a set of physical laws capable of navigating the intricacies of complexity and chaos. In our pursuit of order, we inevitably organize observations through the lens of symmetry.
Beneath the allure of this aesthetic concept lies the intricate framework of mathematics, particularly the concept of a group, with all its potential generalizations, deformations, approximations, and the inherent challenges of incompleteness and partial versions. It is within this mathematical tapestry that we find the tools and principles allowing us to not only conceptualize but also articulate the laws that govern the universe, providing a coherent and profound understanding of our complex reality.
In this contribution, which draws inspiration from a previous review [7] and recent lectures held in both Poland and Brazil, serving as a significant element within the thematic framework of the special issue titled “The Languages of Physics”, we harness the potency of the concept of symmetry to reexamine the first elements of the sequence of unit spheres, denoted as , and explore their profound physical implications across various domains of physics. This exploration extends into realms such as atomic, molecular, nuclear, particle, and condensed matter physics, shedding light on the intricate interplay between the mathematical abstraction of spheres and their tangible relevance in understanding the fundamental structures and behaviors that underpin the diverse facets of the physical world. In this regard, I cannot resist quoting the following excerpt from [8], translated from French.
From there comes her fascination for pieces, lids, and other wheels whose circular movement she perpetuates, immersed in a hypnotic contemplation that extracts her from the world and disconnects her from a reality that is too aggressive.
We do not aspire to introduce entirely original content in this paper. Rather, it is conceived as a fusion of fundamental (somewhat very basic) and advanced discussions on the mathematics of symmetry. Rather than striving to introduce entirely novel content, this article is crafted as a synthesis, merging fundamental (yet foundational) discussions with advanced insights into the mathematics of symmetry.
The journey begins with a recapitulation of essential concepts pertaining to groups and semi-groups (Section 2), followed by a freshman level reminder of algebraic and topological aspects of numbers (Section 3). We then show the significant role played by simple or semisimple Lie groups in elucidating symmetries across classical and quantum physics realms (Section 4).
The core of this presentation centers on a reexamination of the realm of spheres (Section 5) and the ensuing exploration of the associated geometry of Hopf fibrations (Section 6). Furthermore, we unravel the mesmerizing simplifications that the spherical symmetry contributes to explaining the Balmer lines, detailing the spectral line emissions of the hydrogen atom—a proto-quantum formalism dating back to 1885 (Section 7). The paper concludes with a succinct summary in Section 8.
For those seeking a more in-depth understanding, Appendix A and Appendix B provide additional details on group actions and the Lie algebra formalism.
2. Semi-Groups and Groups
In this section we recap main definitions concerning semi-groups, groups, and structures built from them. Usually these notions are supposed known but reviewing them lies in the self-contained spirit of this contribution.
2.1. Definitions
A semi-group is a set equipped with an operation that combines any two elements and to form a third element while being associative, i.e., .
A group is a semi-group having an identity element e, and inverse elements, .
A group or semi-group is Abelian if the operation is commutative: for all , e.g., translations in the line or to rotations on the circle or in the plane. Rotations in space are noncommutative.
Groups can be finite (e.g., permutations, point groups of symmetry of molecules), discrete (e.g., space group of symmetry of crystals), continuous (e.g., Euclidean displacements), Lie groups (infinitesimal transformations can be considered as well).
Continuous groups can be compact (parameters of transformation are bounded, e.g., rotations on the sphere) or non-compact, e.g., translations in the plane.
Two elements and of a group G are said to be conjugate if there exists such that . This is an equivalence relation whose equivalence classes are called conjugacy classes (one famous example is the Rubik cube where the essential property for winning is precisely the set of conjugate classes of one permutation group, see Figure 1 and [9] for explanation).

Figure 1.
Rubik cube.
2.2. Example: Chirality
Chirality is the simplest example of a group: , with , . P is like a mirror image. A figure is chiral if it cannot be mapped to its mirror image by rotations and translations alone. Examples are shown in Figure 2 and Figure 3.
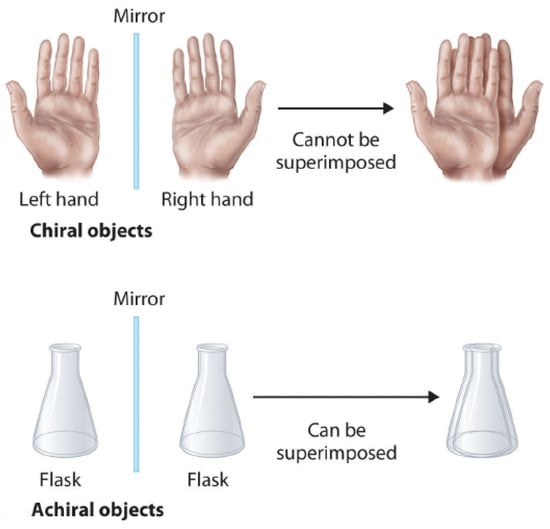
Figure 2.
From Licence CC BY-SA 4.0 DEED https://chem.libretexts.org/ (accessed on 6 January 2024).
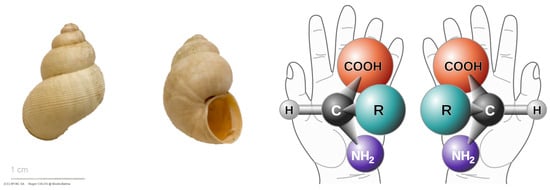
Figure 3.
Left: from Obs 7352-Doc 9412-Credits Roger CULOS-BY-NC-SA https://balma.biodiv.fr/spip.php?observation7352 (accessed on 6 January 2024); Right from [[File:Chirality with hands.svg|thumb|Chirality with hands]] https://commons.wikimedia.org/wiki/File:Chirality_with_hands.svg?uselang=en#Licensing (accessed on 6 January 2024).
A chiral object and its mirror image are said to be enantiomorphs.
An interesting question about mirrors is shown in Figure 4: why does a mirror reverse left to right, but not top to bottom?

Figure 4.
Why does a mirror flip the left and right orientation of Ossola, while leaving the top-to-bottom arrangement unaffected? Answer is found in [10].
Beyond space parity (usually noted P), notable similar instances are observed in the realm of particle physics. These include charge conjugation (C), where the charge of a particle is reversed (), time reversal (T), involving the reversal of time (), and the dichotomy between matter and antimatter. Furthermore, the interplay of these individual symmetries gives rise to intriguing combinations such as , , and , adding depth and complexity to our understanding of fundamental physical principles.
2.3. Building Groups from Subgroups
A subset H of a group G is a subgroup of G if it contains e and is stable versus group operations: and . The direct product of two groups and consists in gluing the two groups together, without interaction: is simply their Cartesian product, endowed with the group law:
The neutral element is . With the identifications , both and are invariant subgroups of (think of the plane as the product of two lines or of the torus as the product of two circles).
For the semi-direct product of two groups and , one supposes one is given a homomorphism from into the group of automorphisms of . Then, one defines the semi-direct product as the Cartesian product, endowed with the group law:
The neutral element is and the inverse of is (think of the affine group of the line, which combines dilation and translation).
2.4. Group Cosets
Let H be a subgroup of G. One says that mod H if there exists such that . Denoting the equivalence class of g mod H, the set of equivalence classes is denoted and called the left coset of G by H. The right coset is defined in a similar way as the set of equivalence classes .
2.5. Group Actions
Irreducibility linked to symmetry (and invariance) is the mathematical concept of a group, more precisely the group of transformations (see Appendix A for more details). Concretely, elements in a group G, like the group of Euclidean displacements in the plane (the semidirect product of rotations and translations), transform into themselves objects in a set X, like the set of triangles, in such a way that we can compose such transformations in an associative way and we can transform back too:
3. Numbers and Groups
In this section we implement the group material exposed above through the sequence of numbers, from the most elementary ones to some sophisticated objects like octonions and Cayley algebras.
3.1. Sets , ,
In preamble, one should remember that Arithmetic with (cardinal) Hindu–Arabic numerals is easy while it is inextricable with (ordinal) Roman numerals (e.g., Figure 5).

Figure 5.
Andry is acquiring proficiency in the Hindu–Arabic numeral system, encompassing the digits from 0 to 9. See: On the Calculation with Hindu Numerals by al-Kwharizmi (about 825 AD) and On the Use of Indian Numerals by Abu Yusuf Yaqub Ibn Ishdaq al-Kindi (830 AD). Eventually the Hindu–Arabic way of writing numbers and computations replaced Roman numerals [11].
The set of natural numbers (note that including 0 is now the common convention among set theorists and logicians, maybe not with artists’ assent, see Figure 6 and [12]) equipped with addition, is not a group (no inverse), just an Abelian semi-group. Equipped with multiplication, is an Abelian semi-group as well.

Figure 6.
OPAŁKA, 1965, série/ Détail, acrylic on canvas.
The set of rational integers , equipped with addition, is an Abelian group. Equipped with multiplication, it is a semi-group.
The set of rational integers modulo p, : , equipped with addition, is a finite Abelian group with p elements. Chirality corresponds to .
3.2. Example: Cubic Relations
Richard Kerner, in a comprehensive series of papers (refer to [3] for a detailed review), posited that cubic (or ternary) relations possess the ability to encapsulate diverse symmetries in relation to the permutation group or its cyclic subgroup .
Significantly, these insights find applications in the -graded generalization of Grassmann algebras, manifesting in their realization within the realm of generalized exterior differential forms. Moreover, they play an important role in the development of gauge theory founded upon this differential calculus and in the ternary generalization of Clifford algebras. These advancements not only unlock new perspectives in mathematical structures but also extend their reach to the realm of physics, providing a framework for describing families of quarks.
3.3. Set
The set of rational numbers is defined as the set of equivalence classes of pairs of integers with , . The equivalence class of is denoted .
The set , together with the addition and multiplication operations shown below, forms a field:
Actually, is the prototype of the concept of a field: a set in which addition, subtraction, multiplication, anddivision are defined and behave as the corresponding operations on rational numbers.
3.4. Is Not “Complete”
Let us equip the field with the metrical topology associated with the distance between two rationals x and y. This topology gives a sense to the notion of a Cauchy sequence of rationals: one says that is Cauchy if, for all , there exists such that, for all , one has
If is a convergent rational sequence (that is, ), then it is a Cauchy sequence. On the other hand not all Cauchy sequences of rationals are convergent in .
Our intuitive sense suggests that when a sequence of terms progressively approaches one another, they must be converging towards a specific value. Take, for instance, the sequence , an approximation for the positive solution to the algebraic equation , or the sequence , which approximates the non-algebraic (or transcendant) mythic length of the circumference of the unit circle. Both sequences adhere to the Cauchy criterion, signifying their terms draw near each other, yet they do not converge to a rational number.
This observation prompts the existence of certain “irrational” numbers, denoted as “” and “”, towards which these sequences converge. Consequently, to encompass these irrational values, as well as all other numbers that Cauchy sequences seem to approach, one extends the number system beyond rationals [13].
3.5. Unreal “Real” Numbers Complete Real Rationals!
It is this intuition which motivated Cauchy to use such sequences to define the real numbers: is a completion of . The real numbers are constructed as equivalence classes of Cauchy sequences [14]. Two Cauchy sequences and of rational numbers are equivalent if , i.e., if the sequence tends to 0. The real numbers are the equivalence classes of Cauchy sequences of rational numbers. That is, each such equivalence class is a real number. Through this construction, inherits the algebraic field structure of and is complete for the metric topology: all Cauchy sequences of real numbers are convergent in . In this sense one says that is the closure of : , i.e., contains all limit points of . However, there is a big difference: while is countable, i.e., there exists a one-to-one map , the field is uncountable.
3.6. Is Complete and “Algebraically Closed”
The algebraic equation has no solution in . So let us equip the set (Cartesian product) with the commutative addition and multiplication operations:
Both operations afford with a commutative field structure, and being the neutral elements for addition and multiplication, respectively. This is the field of complex numbers and is denoted by . One introduces the “imaginary” number , imaginary because it is the square root of [15,16,17]. Indeed, one checks that , and so is a solution of (like the real is a solution of ). The complex numbers also form the real vector space of dimension two, with as a standard basis. This justifies the notation .
Introducing the mirror symmetry with respect to the real axis, , one checks that . Equipped with the topology associated with the distance , is complete and, as a vector space, is isomorphic to the Euclidean plane.
Any algebraic equation , with complex coefficients, has n roots in , i.e., is algebraically closed (fundamental theorem of the algebra).
3.7. Complex Numbers Emerging from Tensor Product of Two Planes
There exists an interesting interpretation of the multiplication law (1) in terms of the tensor product of two planes. The tensor product stands as a cornerstone, arguably the most distinctive one, in the realm of quantum mechanics. In essence, the Cartesian product, traditionally employed to model two systems independently in classical physics, undergoes a transformative process known as quantization. This metamorphosis results in the emergence of the tensor product of two vector spaces, a fundamental framework indispensable for understanding the intricacies of quantum mechanical systems.
First, we remember that a vector space V over a field , e.g., or , is a set whose elements or vectors may be added together and multiplied (“scaled”) by elements (“scalars”) in . Two essential properties must be satisfied: the distributivity of scalar multiplication with respect to the vector addition and the distributivity of scalar multiplication with respect to field addition. Then, the tensor product of two vector spaces V and W (over the same field) is defined as the vector space over consisting of all bilinear forms from to . Note that while .
Hence, the tensor product of the plane with itself, with basis , is the four-dimensional vector space of bilinear forms
where . Any real matrix A can decompose as with
The matrices were introduced by Pauli [18]. Hence, we have for the matrix elements of :
Due to the algebraic relations
one can give the decomposition of the matrix the bicomplex form:
Due to , which means that the are square roots of , whilst , the expression
is a matrix representation of the complex number with the correspondences , , and . The multiplication law defined in (1) perfectly aligns with the matrix multiplication operation represented as . Now, any matrix of type (5) can be factorized as
This is the matrix form of the expression of the complex number in terms of its polar coordinates, , , mod .
The correspondence is not inherently absolute; an alternative choice could be . This ambiguity arises from the existence of two possible orientations when defining trigonometric functions: clockwise and anticlockwise. It is crucial to recognize that this feature should not be disregarded when transitioning from a formalism based on complex numbers to one expressed in terms of real numbers [19].
3.8. Two-Dimensional Lattices
3.8.1. General
Consider two complex numbers and such that is not real. They define the (“Bravais”) lattice in the plane with lattice basis (or primitive) and with fundamental parallelogram [or primitive (unit) cell] determined by . is a subgroup of for the addition (∼ translation). Two pairs and are equivalent if they generate the same lattice, i.e., if there exists , such that
The set of such matrices form the noncommutative modular group PSL (relevant for Weirstrass elliptic functions).
There are five possible Bravais lattices in two-dimensional space: monoclinic (arbitrary , ), tetragonal or (square ), hexagonal (), orthorhombic (rectangular , ), and orthorhombic centered (rectangular centered). They are shown in Figure 7.
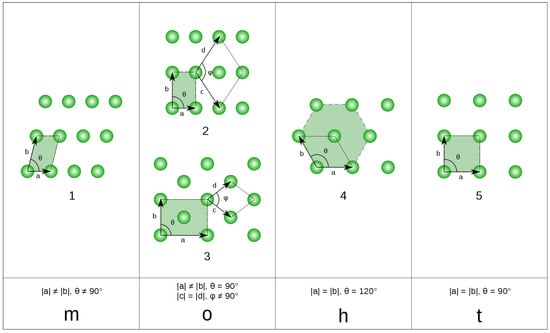
Figure 7.
Five 2D lattice types. From 2d Bravais Licence CC BY-SA 3.0 DEED https://en.m.wikipedia.org/wiki/File:2d-bravais.svg (accessed on 6 January 2024).
3.8.2. Graphene Example
A (two-dimensional) crystal is a periodic array of atoms. For the graphene (hexagonal lattice or honeycomb), Figure 8, the primitive translation vectors are alternatively defined as:
which means that .
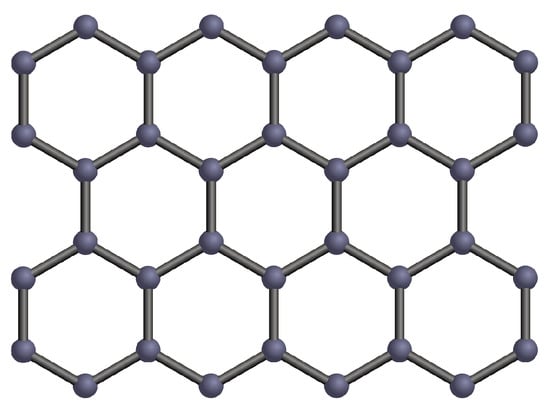
Figure 8.
An illustration of atomic organization of graphene. From Pixabay: Graphite https://pixabay.com/fr/vectors/graphène-graphite-benzène-chimie-161773/ (accessed on 6 January 2024).
4. Symmetry and Group(s)
4.1. Symmetry in Physics
D. Gross, in his enlightening 1995 Physics Today article [20] exploring Wigner’s legacy, aptly observed that
Einstein’s great advance in 1905 was to put symmetry first, to regard the symmetry principle as the primary feature of nature that constrains the allowable dynamical laws.
In contemporary physics, the principles of symmetry hold a paramount status as the most fundamental components of our description of nature. This prominence owes a significant debt to the influential contributions of the Princeton group, comprising notable figures such as Wigner, Bargmann, Weyl, Gödel, and von Neumann, from Princeton University and/or the Institute for Advanced Study (IAS). Their collective insights and groundbreaking work have played a pivotal role in elevating the significance of symmetry principles, making them a cornerstone in our understanding of the fundamental laws governing the physical universe.
In this context, it is essential to pay tribute to Emmy Noether, as highlighted in [21]. Albert Einstein hailed Noether as the most “significant” and “creative” female mathematician in history. She formulated a theorem [22] that, with magisterial concision, harmonized two fundamental concepts in physics: symmetry in nature and the universal laws of conservation. Noether’s theorem, now considered as crucial as Einstein’s theory of relativity, forms the bedrock for much of today’s cutting-edge research in physics, including recent breakthroughs such as the observation of the Higgs boson. Despite her pivotal contributions, Noether herself remains largely unknown, not only to the general public but also to a large part of the scientific community.
The foundation of our comprehension regarding the existence of elementary particles is rooted in the relativity principle. This principle posits that physical laws remain invariant under fundamental transformations of inertial frames, specifically translation (implying homogeneity in space–time), rotation (indicating isotropy in space–time), and boosts. Together, these transformations constitute a relativity or kinematic group, known as the Galileo or Poincaré group. Notably, both groups exhibit a structure that can be described as a semi-direct product of subgroups. In addition to these two well-known groups, there are other relativity groups identified and classified by Bacry and Lévy-Leblond in [23]. This group theoretical framework has laid the foundation for quantum field theory, enabling a profound understanding of the nature and existence of elementary particles within the realm of physics [24]. Note that the term “invariant”, strictly denoting the constancy of an observable in a physical system under a particular transformation, is used here in a broader sense of “covariance”. Precisely, “covariance” implies the absence of any alteration in the form of physical laws under a given transformation.
One should add the importance of
- Discrete translational and rotational symmetries in classifying molecules, crystals, and quasicrystals;
- Continuous rotational symmetries (together with parity and time reversal) in explaining and classifying atomic spectra;
- Unitary symmetries for describing and classifying nuclear spectra;
- Unitary symmetries for describing strong and weak interactions (gauge fields) and successfully predicting the existence of new elementary particles.
In his 1963 Nobel lecture quoted by D. Gross, Wigner pointed out that progress in physics was partly based on the ability to separate the analysis of a physical phenomenon into two parts:
- initial conditions that are arbitrary, complicated, unpredictable, as forming the “phase space” of a physical system in a wide sense, and laws of nature that summarize the regularities which are independent of the initial conditions.
- Then, Wigner argued that symmetry or invariance principles provide a structure and coherence to the laws of nature: they summarize the regularities of the laws that are independent of the specific dynamics. Without regularities in the laws of nature we would be unable to discover the laws themselves.
One should also mention what Pierre Curie noticed in 1894 [25] (Neuman–Minnigerode–Curie Principle):
- When certain causes produce certain effects, the elements of symmetry of the causes must be found in the effects produced.
- When certain effects reveal a certain asymmetry, this asymmetry must be found in the causes which gave rise to it.
Note that the reciprocal of these two assertions is not true. More precisely, the characteristic symmetry of a phenomenon is that symmetry which is best compatible with the existence of the phenomenon. A phenomenon can exist in surroundings which possess its characteristic symmetry or at least one subgroup of its characteristic symmetry. In other words, certain symmetry elements can exist together with certain phenomena but they are not necessary. But it is necessary that certain symmetry elements do not exist (Neuman–Minnigerode–Curie Principle).
4.2. Lie Groups and Lie Algebras
Building upon the foundational principles of symmetries and natural laws, as eloquently discussed by Levy-Leblond [26], we delve deeper into one of their unescapable mathematical frameworks: the theory of Lie groups and algebras [27].
To a Lie group G corresponds its Lie algebra , where the notation exp takes its usual sense when we deal with group of matrices (see Appendix B for more mathematical details). Simple or semisimple Lie groups (Lie algebras), like (pseudo-)rotation groups or unitary groups or symplectic groups, are ubiquitous in Physics, see Table 1 for the nomenclature.

Table 1.
Nomenclature for the most current Lie groups and algebras. The symbol M is for the algebra of matrices with coefficients in etc. Note that and that Sp is frequently written as Sp. : Manifold M with metric g, : vector fields on M, : Lie derivative, : Symplectic manifold M with symplectic 2-form .
Following previous works by Killing [28,29,30,31,32,33], simple Lie algebras have been classified by Cartan [34] through their one-to-one correspondence to possible (irreducible reduced) root systems in . See Table 1 for the nomenclature for the most current Lie groups and algebras, and Appendix B.2 and Appendix B.3 for details concerning root systems. There are four classes of classical (irreducible reduced) root systems in :
- associated with unitary groups or their complexified or the real form .
- associated with orthogonal (rotation) groups or their pseudo-rotation counterparts .
- associated with symplectic groups .
- associated with orthogonal (rotation) groups or their pseudo-rotation counterparts .
Moreover, there are five exceptional cases: , , , , and .
4.3. Physics and Low-Dimensional Root Systems
There exist isomorphisms between low-dimensional root systems (see Appendix B). Borrowing its terminology to atomic spectroscopy one can enunciate that the lowest levels in the Cartan classification are occupied by the most familiar or well-known symmetries of our physics discipline:
- (i)
- , (, ): space isotropy, spherical rotator, geometric optical devices, q-bits, Lorentz invariance, infinite well, isospin, kinematic groups of 1 + 1 de Sitter and anti-de Sitter space–times, …
- (ii)
- (, : orbital degeneracy of the Coulomb potential or Kepler problem [35], two-dimensional square infinite well (quantum dot), …
- (iii)
- (): spatial harmonic oscillator, standard model color, q-trits, …
- (iv)
- (, ): kinematic groups of 3+1 de Sitter [36] and anti-de Sitter [37] space–times, dynamical symmetry of the H atom discrete or continuous spectrum [35], …
- (v)
- (, , ): gauge symmetries, conformal group of 3 + 1 de Sitter, anti-de Sitter and Minkowski space–times, respectively, and their roles in the interpretation of the dark universe (e.g., see [38], and references therein), dynamical symmetry of the H atom discrete and continuous spectrum, AdS/DS-CFT, …
5. Playing with Spheres
We now explore the world of unit spheres in light of group theory.
5.1. The Circle and Its Complexified Version
The unit circle is defined in the complex plane as . It is a compact multiplicative commutative group, denoted . One should think of the importance of this group in mathematics (e.g., Fourier series and integral) and in physics (e.g., gauge invariance in electrodynamics).
The complexified unit circle is also a group. It is the non-compact multiplicative commutative group
An example is found with the motion of a particle on the unit circle: the corresponding phase space, i.e., the set of pairs (angular position, angular momentum) is the infinite cylinder
whose matrix form (7) is obtained through the maps for the first factor and for the second factor.
We could as well consider the free motion on the two-dimensional de Sitter space–time [36]. The latter has the topology . It may be visualized as the one-sheet hyperboloid .
The phase space for such a motion is also a one-sheet hyperboloid with the same cylinder topology. In this case both the configuration space and the phase space have SO0 as the invariance group.
5.2. The Sphere through Its Multifaceted Aspects
Our familiar sphere is “poor”: no intrinsic group structure, save the fact that it includes mythological structures, like the five Platonic solids (see next subsection). Then, let us consider the next one in the sequence: the sphere . It may be identified with the compact multiplicative noncommutative group corresponding to . Think of the importance of this group in mathematics (e.g., harmonic analysis in space) and in physics (angular momentum, spin, q-bit, …).
5.2.1. Sphere and Group SU
The relation of to SU is given by:
5.2.2. Sphere and Rotations in
Let us explain the relation between and the proper rotations in space . Any proper rotation in space is determined by a unit vector defining the rotation axis and a rotation angle about in the direct sense, as is shown in Figure 9.
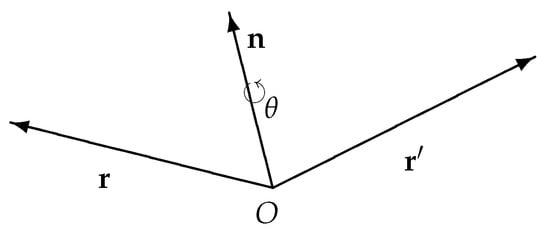
Figure 9.
Proper rotation of vector to by angle about unit vector in space .
The action of such a rotation, , on a vector is given by:
The correspondence between the element rotations and the matrix form of is understood as follows:
5.3. Sphere and Quaternions (Hamilton, 1843)
Let us equip the set with the commutative addition and noncommutative multiplication operations:
Both operations afford with a noncommutative field structure, and being the neutral elements for addition and multiplication, respectively. This is the field of quaternions [39,40] (see also [41] and references therein) and is denoted by . One identifies with the complex u and one introduces the “quaternionic imaginary” . One checks that and the fundamental commutation rule
Hence, we have the bicomplex notation for quaternions:
With the notations and , one has as well and , with . Quaternions form the real vector space of dimension 4, with as a standard basis. Quaternions with a null scalar component, i.e., , are said to be pure vector quaternions. It results that one can decompose a quaternion in two different forms:
With the bicomplex notation, one easily understands the origin of the multiplication law given in (9). With the scalar–vector notations, the quaternionic multiplication reads as
Introducing the mirror symmetry with respect to the 0th axis, , one checks that , (involutive), , and the inverse of is given by .
5.4. Quaternions and Space Rotations
Expressed in “polar” coordinates , , one obtains the matrix realization of quaternions:
Hence, the correspondence (8) between elements and rotations in space is now understood in terms of quaternions:
5.5. Coquaternions (Cockle, 1849) versus Quaternions
It is interesting to compare the matrix realization of quaternions with the decomposition (3) of the (Lie) algebra composed of real matrices. Forgetting this matrix realization and considering the matrix basis as pure numbers
obeying the same algebraic relations as those given in (2), one obtains the noncommutative ring of numbers , , , named coquaternions [42,43] or split-quaternions. Remember that rings are algebraic structures that generalize fields in the sense that multiplicative inverses need not exist. With this scalar–vector form, the multiplication law for coquaternions reads as
If instead we start from the bicomplex form (4) and adopt the one-to-one correspondence matrix ↔ coquaternion
then the multiplication law reads
a formula to be compared with (9).
Ring is equipped with the isotropic quadratic form
where is the conjugate of q. Each coquaternion q with has inverse . One checks that .
The multiplicative group of coquaternions with form the unit pseudo-sphere in :
The topology of is that of the Cartesian product . This is inferred from the parametrization with :
Like the matrix realization of is SU, the matrix realization of is the group SL. The symmetry group of the quadratic form (15) on is O.
5.6. Complex Quaternions
The ring of complex quaternions is the tensor product . It is just obtained from by extending real scalars to complex ones in (11):
Note the biquaternion form of a complex quaternion: (the correct writing should be ), which corresponds to the isomorphism . The matrix representation of is analogous to (13):
This establishes the ring isomorphism . For more in-depth information, refer to [37] where these objects are efficiently utilized to describe the two-fold covering Sp of the anti-de Sitter group SO0.
5.7. The Complexified Sphere
The complexified sphere is also a group. It is the (universal) covering of the Lorentz group . Let us consider the motion of a particle on . The phase space is the cotangent bundle
This phase space can be identified with the complex sphere through the following parametrization of the latter:
We could as well consider the free motion on the 3 + 1-dimensional de Sitter space–time. The latter may be viewed as a one-sheeted hyperboloid embedded in a five-dimensional Minkowski space with metric :
For the past few years it has been becoming a realistic model for our space–time because of the observed nonzero value of the cosmological constant , a model accompanied by concepts like “dark energy” or “quintessence”. The phase space for the motion of a test particle on the de Sitter space–time also has the topology or equivalently the complexified . In this case both configuration space and phase space have as the invariance group. More details are found in the volume [36].
5.8. The Sphere , Its Icosians and Its Icosian Ring
The group has a finite subgroup denoted here by with 120 elements, named icosians by Hamilton. There exists an icosian game invented by Hamilton [44,45]. It is a kind of Eulerian path through the 20 vertices of the dodecahedron, the dual polyhedron of the icosahedron (see Figure 10, and the nice illustration in [46]): a path such that every vertex is visited a single time, no edge is visited twice, and the ending point is the same as the starting point. Winning strategies use the icosian group .
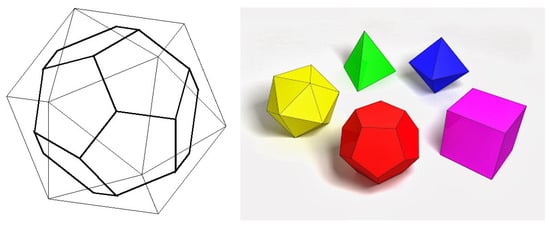
Figure 10.
Dodecahedron and its dual, the icosahedron (left). With its twenty triangular faces, twelve vertices and thirty edges, the latter is one of the five Platonic solids (right). From Don Steward: Platonic solids and duals https://donsteward.blogspot.com/2013/10/platonic-solids-and-duals.html (accessed on 2 February 2024). Among the Platonic solids (Theaetetus of Athens, 417–369 BC; Plato, 428/427–348/347 BC; Euclid, fl. c. 300 BC; Johannes Kepler, 1571–1630), either the dodecahedron or the icosahedron may be seen as the best approximation to the sphere. Remember that a Platonic solid is a convex polyhedron with vertices in a sphere of radius r. The faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex. All edges are congruent, as are its vertices and angles. See the celebrated Coxeter treatise [47] to know more about these objects.
One has the isomorphism , where Y is the symmetry group (60 proper rotations) of the icosahedron (or of its dual, the dodecahedron).
Let us consider, together with the quaternionic unity 1, three unit-norm quaternions describing through (14) 72° rotations around three distinct five-fold axes of the icosahedron,
Here, is the golden mean, with , both being algebraic integers, solutions of the algebraic equation with integer coefficients
The -span of is the icosian ring [48] which fills densely . One shows that
where is the extension ring of the golden mean.
5.9. The Root System and Quasicrystals
Let us now consider the root system . It is made of 240 vectors in . The corresponding root lattice is the -span of . Because of the crystallographic properties of , we have the following:
where the s are the basis roots of the corresponding Dynkin diagram shown in Figure A2.
Subsequently, by selecting a particular four-dimensional plane within possessing a distinct “golden mean” orientation and executing the orthogonal projection of the root lattice onto this hyperplane, the result is the formation of the icosian ring .
Similar manipulations on the root lattice projected onto , on the root lattice projected onto the plane , and on the root lattice projected onto the real line , accompanied by “cuts” based on the choice of appropriate “windows”, produce standard models for three-, two-, and one-dimensional quasicrystals (e.g., icosahedral quasicrystals, Penrose tilings, Fibonacci chain …), as is shown in Figure 11 [49].
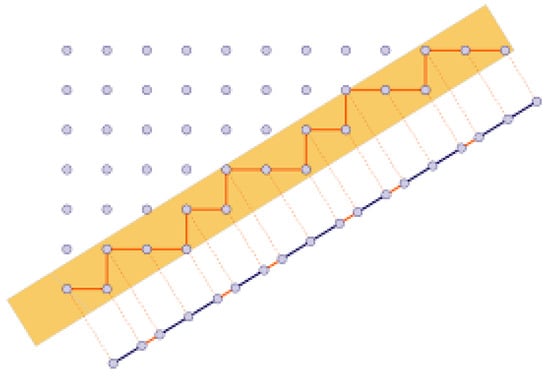
Figure 11.
The cut and project trick is a method to obtain a quasiperiodic set in from a lattice in (from Cut&Project Fibonacci CC BY-NC-SA 2.0 Deed https://tilings.math.uni-bielefeld.de/substitution/fibonacci// (accessed on 6 January 2024).
In Figure 12 is shown an example of an observed quasicrystalline surface.

Figure 12.
Quasicrystalline five-fold surface of Al70 Pd21 Mn9, from [50].
5.10. Algebraic Modeling of Quasicrystals
The identified self-similarity factors, denoted by , within quasicrystals exhibit a distinctive mathematical nature known as quadratic Pisot–Vijayaraghavan (PV) numbers. In essence, these numbers correspond to roots greater than 1 of specific quadratic polynomials. These polynomials possess a leading coefficient of 1 and consist of integer coefficients. Notably, the other root of these polynomials is characterized by an absolute value less than 1.
In the case presented above, the factor is the golden mean . The other ones are
Each value of serves as the defining parameter for a discrete set on the number line, denoted as or the set of “beta-integers”, as introduced in [51] (see also [52] and references therein). This set is specifically designed to function analogously to integers within the context of quasicrystalline investigations. A visual representation of this concept is illustrated in Figure 13, depicting the first tau-integers in proximity to the origin.

Figure 13.
First elements of (tau-integers) around the origin and associated tiling.
Beta-lattices are designed to serve as direct substitutes for traditional lattices within the unique framework of quasicrystals. Much like lattices are built upon sets of integers, beta-lattices find their structural basis in beta-integers. This deliberate choice aligns with the goal of seamlessly adapting mathematical structures to the intricate properties of quasicrystals. A typical beta-lattice is defined as:
with a base of . Examples are shown in Figure 14 and Figure 15.

Figure 14.
-lattice in .

Figure 15.
The mathematical five-fold quasicrystal in .
5.11. Sphere and Octonions (Graves, 1843, Cayley, 1845)
Like , the algebra of octonions [53,54] is built by providing the Cartesian product with the commutative addition and the noncommutative and non-associative product:
Let us introduce the eight octonionic basis numbers: (unity) and
with the commutation rules
We then obtain the biquaternion notation for octonions:
In octonionic calculations we should be aware of the non-associativity of the product, e.g., whilst .
The octonionic conjugate of the octonion x is defined as
This operation allows defining the Euclidean norm of and its inverse if .
Conjugation is involutive: and one checks that .
Like the bicomplex notation (10)–(12) for quaternions, we also have the quadricomplex notation for octonions:
The Hurwitz theorem establishes that the real numbers , complex numbers , quaternions , and octonions stand as the exclusive normed division algebras over the real numbers, up to isomorphism. Normed in the sense that the product of any two elements satisfies the norm property: . Moreover, these four algebras represent the sole examples of alternative, finite-dimensional division algebras over the real numbers.
A general rotation in , i.e., an element among the 28 elements of SO, can be written through successive right multiplications:
For a recent review on the role of octonions in Nuclear Physics, see [55].
6. Higher Spheres and Hopf Maps and Fibrations
What about ? There is nothing really special from a strictly group point of view when we deal with higher-dimensional spheres. Naturally, many interesting topological features exist, like the Hopf fibrations [56,57].
6.1. Hopf Fibrations
These are the following relations involving spheres, :
where “↪” stands for embedding and p is the Hopf map. The first one is displayed in Figure 16.

Figure 16.
Hopf fibration (from Niles Johnson CC BY 4.0 https://en.wikipedia.org/wiki/Hopf_fibration#/media/File:Hopf_Fibration.png (accessed on 6 February 2024)). The described fiber bundle structure, succinctly represented as , intricately intertwines the components of the fiber space within the overarching structure of the total space . The projection, denoted as p and referred to as Hopf’s map, serves as the intermediary, mapping the elements of onto the base space . In this visual representation, each fiber of projects to a circle in three-dimensional space, with one such circle extending to infinity, forming what is termed a “circle through infinity” or effectively a line. The resulting arrangement fills space with a captivating array of tori (products of two circles), each of which is the stereographic projection of the inverse image of a latitude circle on . The accompanying image on the right, depicting linked keyrings on the right, serves as an illustrative example of one of these tori. Points on and their corresponding fibers are color-matched, providing a visual insight into the intricate and captivating structure induced by the Hopf fibration.
The Hopf construction, in its broader application, yields circle bundles in the form of over complex projective space. This construction is essentially a restriction of the topological line bundle over to the unit sphere in .
Note the elementary example where one considers embedded in and factoring out by unit real multiplication. One then obtains . This results in a fiber bundle with the circle as the fiber.
Extending these constructions, one can view within quaternionic n-space () and factor out by unit quaternion multiplication () to obtain . Notably, a bundle with fiber emerges from this construction, connecting quaternionic and real projective spaces.
Similarly, leveraging octonions leads to a bundle with fiber .
These constructions are often referred to as Hopf bundles, encompassing the realms of real, quaternionic, and octonionic Hopf bundles. Importantly, Adams’ theorem asserts that these bundles represent the exclusive instances of fiber bundles with spheres as the total space, base space, and fiber.
Hopf fibration surfaces show up in the description of quantum entanglement [58,59]. In particle physics they underlie the mathematics of the Dirac monopole. It also appears in general relativity, for instance, in the Robinson congruence (see for instance [60]).
6.2. Group Interpretation of the First Hopf Map:
Let us consider the element of which brings the north pole of to the direction :
This gives the quadratic relations which exemplify the projection p (Hopf’s map) of onto the base space :
One easily checks that the Hopf inverse of a point is a circle and that the Hopf inverse of a circle is a torus .
6.3. Group Interpretation of the Second HOPF Map:
We here consider the special group isomorphism proper to (see Figure A1):
It is understood through the action of the group G on specific -quaternionic matrices
Just consider the group element , , which brings the “north pole” of , , to the point . We have , i.e., . This gives the quadratic relations:
The Hopf inverse of a point is the sphere and the Hopf inverse of a sphere is .
6.4. Group Interpretation of the Third Hopf Map:
The octonionic Hopf fibration finds its elegant description through the lens of the automorphism group G2 of the normed algebra of octonions. Actually, one can grasp its essence by considering the group Spin (where Spin serves as the two-fold covering of SO), as explained in [61].
7. Kepler–Coulomb Problem and Spheres
Concluding our exploration of the world of spheres, it is essential to acknowledge the pivotal role played by and , and their complexified versions, in understanding the symmetries of a particle’s motion subjected to the Kepler or Coulomb potential. Alongside the harmonic oscillator, it stands as one of the most emblematic examples of integrable systems within the domain of Galilean classical or quantum mechanics. This symmetry elucidates, at the quantum level, the empirical laws discovered by Balmer in 1885 [62] for describing the spectral line emissions of the hydrogen atom. The literature on this topic is extensive (see, for instance, the review [35]), and its content can attain a high level of mathematical sophistication. To provide some insight, we will first examine in detail the one-dimensional case before sketching the main concepts of the realistic three-dimensional model. It is worth noting that providing a comprehensive account of the symmetries inherent in the Kepler–Coulomb problems, both classically and quantum mechanically, would necessitate delving into a much broader scope of material.
7.1. One-Dimensional Kepler–Coulomb Problem
Consider the energy of a particle of mass m trapped in a well determined on the positive line by the attractive Kepler–Coulomb potential:
and for . Its energy is given by
Regularizing the Kepler problem in the case of negative energy consists in considering the alternative equation:
where . Let us see how the Balmer laws [62] come to light from the symmetry . One considers the three observables defined on the upper half-plane viewed as the phase space :
Their Poisson brackets obey the commutation relations of the Lie algebra of :
After quantization of these classical observables, say , Poisson brackets become commutators, quantum counterparts become (essentially) self-adjoint operators acting in some Hilbert space of quantum states, and a specific unitary irreducible representation of is involved, precisely, that one for which the generator has nonzero positive integers multiples of as spectral values. This is due to the fact the inverse operator is compact. Remember that an operator A on a infinite-dimensional Hilbert space is said to be compact if it can be written in the form where and are orthonormal sets (not necessarily complete) and the s form a sequence of positive numbers with limit zero (they can accumulate only at zero). Since the classical equation becomes , the spectral condition leads directly to the Balmer-like quantization of the energy:
7.2. Phase Space of the Regularized 1D Kepler–Coulomb Problem: The Complexified Circle with Zero Radius
Let us show that the phase space of the regularized 1D Kepler problem is the complexified circle with zero radius.
Following the Fock method [63,64] for displaying the symmetry of the H-atom, let us introduce the circle variable
(inverse stereographic projection transforming the compactified momentum real line into the unit circle). By imposing that this change of variable be part of a canonical transformation of the phase space, the conjugate variable to reads:
One easily checks the two constraints:
Therefore, the pair parametrizes the complex circle in with null radius:
This is a geometric model for the phase space of the one-dimensional regularized Kepler problem, which can be identified to (cotangent bundle on with the zero-section deleted, named Moser manifold or Kepler manifold).
7.3. Phase Space of the Three-Dimensional Regularized Kepler–Coulomb Problem
The above material is easily generalizable to three dimensions. Indeed, the phase space of the three-dimensional regularized Kepler problem is the complexification of with radius 0.
Following Fock again in dealing with the more realistic three-dimensional Kepler–Coulomb problem, let us introduce the variable
(inverse stereographic projection transforming the 3D-compactified momentum space into a 3-sphere).
By requiring that this change of variable be part of a canonical transformation of the phase space, the conjugate variable to together with parametrizes the complexification of in with a null radius. This is the phase space of the three-dimensional regularized Kepler problem, which can be identified with (cotangent bundle on with the zero-section deleted, Moser manifold or Kepler manifold, as named by Souriau [65]).
The three-dimensional aspect of this structure explains the accidental degeneracy of the discrete spectrum of the hydrogen atom with its SO symmetry.
8. Conclusions
This contribution is an invitation to embark on an exploration of the realm governed by numbers, symmetries, and intricate symmetry groups, and, as an appealing illustration, to delve into the profound significance encapsulated within the fundamental aspects of the circle and higher-dimensional spheres. Its aim is to share our appreciation for their value in shaping our mathematical comprehension of the natural world and establishing the foundational principles that underpin the laws of physics.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The author expresses gratitude both to the Krakow Interdisciplinary Doctoral School under the PROM Project PPI/PRO/2019/1/00016 of the Polish National Agency for Academic Exchange, 9–20 January 2023, and to the Programa de Pós-Graduação which includes both the Master’s and Doctorate programs in Physics, at the Centro Brasileiro de Pesquisas Físicas, Rio de Janeiro, for the invitation to deliver the 2023 course titled Symmetries in Physics in 5 lessons + complements. This article draws inspiration from the aforementioned course and the author acknowledges the valuable opportunity provided by both invitations. The author is grateful to Danièle Rousselier for providing the opportunity to explore the literary masterpiece crafted by Minh Tran Huy [8].
Conflicts of Interest
The author declares no conflicts of interest.
Abbreviation
The following abbreviation is used in this manuscript:
| UIR | Unitary irreducible representation |
Appendix A. Group Actions
A transformation of a set S is a one-to-one mapping of S onto itself. A group G is realized as a transformation group of a set S if, for each , there exists an associated transformation of S, where for any and in G and , the property holds. The set S is then referred to as a G-space, and a transformation group is deemed transitive on S if, for any and in S, there exists a such that . In such a scenario, the set S is termed a homogeneous G-space.
A (linear) representation of a group G is a continuous function that takes values in the group of nonsingular continuous linear transformations of a vector space . This function satisfies the functional equation and , where e is the identity element of G and is the identity operator in . Additionally, it follows that , meaning that is a homomorphism of G into the group of nonsingular continuous linear transformations of .
A representation is deemed unitary if the linear operators are unitary concerning the inner product on . In other words, holds for all vectors and in . Furthermore, a representation is irreducible if there is no non-trivial subspace such that, for all vectors , is in for all . In simpler terms, there exists no non-trivial subspace of that remains invariant under the operators .
Appendix B. Lie Algebra Material
Appendix B.1. General
Consider a complex Lie algebra , defined as a complex vector space equipped with an antisymmetric bracket satisfying the Jacobi identity:
For any , the adjoint representation is given by , providing a linear map ad: , where represents the endomorphisms of . This is known as the adjoint representation of .
If the dimension of is finite (dim ), one can define a symmetric bilinear form for as follows:
Here, B is termed the Killing form of .
Alternatively, one can choose a basis in , where dim . In terms of this basis, the commutation relations are expressed as:
where are the structure constants. It is then evident that defines a metric on . This metric is known as the Cartan–Killing metric.
Appendix B.2. Roots and Cartan Classification
The Lie algebra is classified as simple if it lacks any non-trivial ideal. In other words, there is no additive subgroup of that absorbs the left multiplication by elements of , i.e., . On the other hand, if contains an Abelian ideal, it is referred to as semisimple. A semisimple Lie algebra can be decomposed into a direct sum of simple Lie algebras. Importantly, is semisimple if and only if the Killing form is nondegenerate, as per Cartan’s criterion.
Let be a semisimple Lie algebra. Within , a Cartan subalgebra is chosen, defined as a maximal nilpotent subalgebra. Notably, this subalgebra is maximal Abelian and unique up to conjugation. The dimension ℓ of is referred to as the rank of . A root of with respect to is a linear form on , such that there exists a nonzero element X in satisfying for all .
Then, it is possible to find, as demonstrated by Cartan and Chevalley, a basis for with the following distinctive properties: the set forms a basis for the Cartan subalgebra . Each generator is associated with a nonzero root . Furthermore, these generators can be organized in such a way that the commutation relations, given by Equation (A3), may be expressed in a specific form. The precise details of this form would depend on the specific properties of the chosen basis:
where if is not a root.
The set of roots of is denoted by . Notably, the nonzero roots exhibit a specific pairing, , and no other nonzero multiple of a root is itself a root. As a consequence, the set of nonzero roots can be divided into two subsets: , comprising positive roots, and its corresponding counterpart of negative roots, denoted . The set is encapsulated within a simplex (a convex pyramid) in , where the edges are defined by the so-called simple positive roots. These are positive roots that cannot be expressed as the sum of two other positive roots. This characterization also applies to .
The examination of root systems provides the foundation for the Cartan classification of simple Lie algebras. This classification encompasses four infinite series, namely , and five exceptional algebras: .
Appendix B.3. Dynkin Diagrams: General
The roots of a complex Lie algebra collectively form a lattice of rank n within the dual space of a Cartan subalgebra , where n signifies the Lie algebra rank of . Consequently, the root lattice can be viewed as a lattice in . Each vertex, or node, in the Dynkin diagram [66,67] corresponds to a Lie algebra simple root, which is a generator of the root lattice. For any pair of nodes and in the Dynkin diagram, an edge is drawn if the simple roots associated with them are not perpendicular. The nature of the edge varies: a single undirected edge is drawn if the angle between them is , a directed double edge if the angle is , and a directed triple edge is drawn if the angle is . It is noteworthy that there are no other possible angles between Lie algebra simple roots. In the case of directed edges, double and triple edges point toward the shorter vector (indicated by a black circle).
Appendix B.4. From Top to Bottom, Dynkin Diagrams for An, Bn, Cn, and Dn
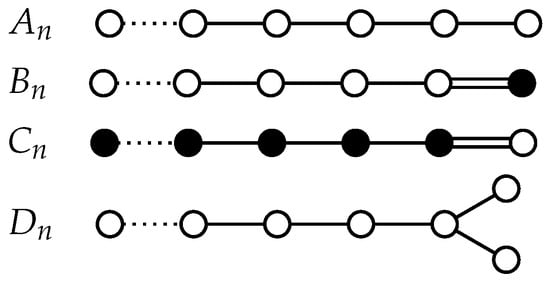
Figure A1.
Dynkin diagrams , , , and .
Appendix B.5. Dynkin Diagrams G2, F4, E6, E7, and E8
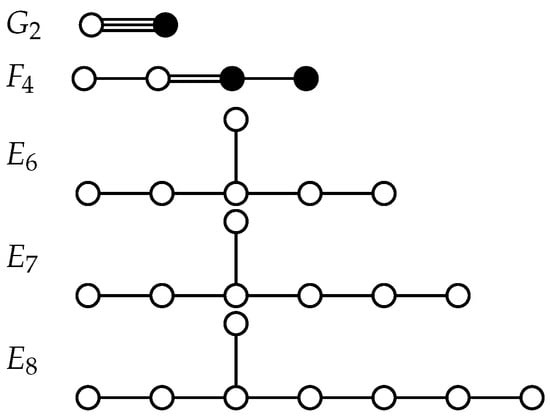
Figure A2.
From top to bottom: Dynkin diagrams for , , , , and .
Appendix B.6. Examples: Roots A1 × A1, A2, B2
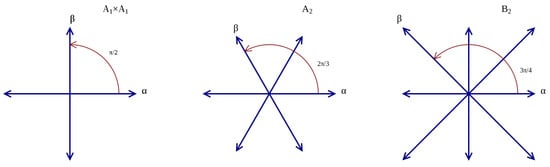
Figure A3.
rank-2 root systems , , (from Licence CC BY-SA 3.0 DEED http://en.wikipedia.org/wiki/Root_system (accessed on 6 January 2024)).
Appendix B.7. Examples: Roots C2, D2, G2
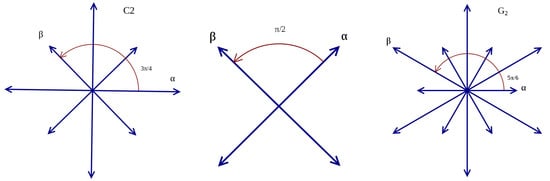
Figure A4.
rank-2 root systems , , (from Licence CC BY-SA 3.0 DEED http://en.wikipedia.org/wiki/Root_system (accessed on 6 January 2024)).
References
- Kerner, R. Generalization of the Kaluza-Klein theory for an arbitrary non-abelian gauge group. Ann. Inst. Henri Poincaré 1968, 9, 141–150. [Google Scholar]
- Kerner, R.; Phillips, J.C. Quantitative principles of silicate glass chemistry. Solid State Com. 2000, 117, 47–51. [Google Scholar] [CrossRef]
- Kerner, R. The cubic chessboard. Class. Quantum Grav. 1997, 14, A203. [Google Scholar] [CrossRef]
- Dubois-Violette, M.; Kerner, R.; Madore, J. Noncommutative differential geometry of matrix algebras. J. Math. Phys. 1990, 31, 316–322. [Google Scholar] [CrossRef]
- Kerner, R. Our Celestial Clockwork from Ancient Origins to Modern Astronomy of the Solar System; World Scientific: Singapore, 2021. [Google Scholar]
- Gazeau, J.-P. From classical to quantum models: The regularising rôle of integrals, symmetry and probabilities. Found. Phys. 2018, 48, 1648–1667. [Google Scholar] [CrossRef]
- Gazeau, J.-P. Symmetries in Physics: A journey in (high) spheres. In Proceedings of the Mario Novello’s 70th Anniversary Symposium, Rio de Janeiro, Brazil, 15–17 August 2012; Pinto Neto, N., Perez Bergliaffa, S.E., Eds.; Editora Livraria da Fisica: Sao Paulo, Brazil, 2012; pp. 133–149. [Google Scholar]
- Huy, M.T. Un Enfant Sans Histoire; Actes Sud: Arles, France, 2022. [Google Scholar]
- Chen, J. Group Theory and the Rubik’s Cube. Available online: https://people.math.harvard.edu/~jjchen/docs/Group%20Theory%20and%20the%20Rubik%27s%20Cube.pdf (accessed on 6 January 2024).
- Taylor, R. Ask Fuzzy: Why Does a Mirror Reverse Left to Right, But Not Top to Bottom? Available online: https://www.canberratimes.com.au/story/7661679/why-does-a-mirror-reverse-left-to-right-but-not-top-to-bottom/ (accessed on 6 January 2024).
- Rooney, A. The Story of Mathematics: From Creating the Pyramids to Exploring Infinity; Arcturus Publishing Limited: London, UK, 2009. [Google Scholar]
- Chévrier, J. OPAŁKA 1965/1—∞, Comme un Memento Mori à l’ère du Digital. Available online: https://www.echosciences-grenoble.fr/articles/opalka-1965-1-comme-un-memento-mori-a-l-ere-du-digital (accessed on 6 February 2024).
- Kemp, T. Cauchy’s Construction of R. Available online: https://mathweb.ucsd.edu/~bseward/140a_fall22/Cauchy_construction_of_R.pdf (accessed on 6 January 2024).
- Rudin, W. Principles of Mathematical Analysis, 3rd ed.; International Series in Pure and Applied Mathematics; McGraw-Hill Book Co.: New York, NY, USA; Aukland, New Zealand; Düsseldorf, Germany, 1976. [Google Scholar]
- Descartes, R. Discours de la Méthode; Jan Maire: Leiden, The Netherlands, 1637. [Google Scholar]
- Argand, J.R. Essai sur une Manière de Représenter des Quantités Imaginaires Dans les Constructions Géométriques, Chez Mme Vve Blanc, Paris. 1806, 2nd ed.; Gauthier Villars, Paris, 1874; Imaginary Quantities: Their Geometrical Interpretation, Translated from the French by Prof. Hardy, A.S.; D. Van Nostrand Publisher: New York, NY, USA, 1881. [Google Scholar]
- Nahin, P. An Imaginary Tale: The Story of the Square Root of −1; Princeton University Press: Princeton, NY, USA, 1998. [Google Scholar]
- Pauli, W. Zur Quantenmechanik des magnetischen Elektrons. Zeit. Phys. 1927, 43, 601–623. [Google Scholar] [CrossRef]
- Renou, M.-O.; Trillo, D.; Weilenmann, M.; Le, T.P.; Tavakoli, A.; Gisin, N.; Acín, A.; Navascués, M. Quantum theory based on real numbers can be experimentally falsified. Nature 2021, 600, 625–629. [Google Scholar] [CrossRef] [PubMed]
- Gross, D.J. Symmetry in Physics: Wigner’s Legacy. Phys. Today 1995, 12, 46–50. [Google Scholar] [CrossRef]
- Angier, N. Emmy Noether, the Most Significant Mathematician You’ve Never Heard of. Available online: http://www.nytimes.com/2012/03/27/science/emmy-noether-the-most-significant-mathematician-youve-never-heard-of.html (accessed on 6 February 2024).
- Noether, E. Invariante Variationsprobleme. Nachrichten von der Ges. der Wiss. zu Gött. Math.-Phys. Kl. 1918, 1918, 235–257. [Google Scholar]
- Bacry, H.; Lévy-Leblond, J.-M. Possible Kinematics. J. Math. Phys. 1968, 9, 1605. [Google Scholar] [CrossRef]
- Streater, R.F.; Wightman, A.S. PCT, Spin and Statistics, and All That; Princeton Landmarks in Mathematics and Physics; PUP: Manila, Philippines, 2001. [Google Scholar]
- Curie, P. Sur la symétrie dans les phénomènes physiques, symétrie d’un champ électrique et d’un champ magnétique. J. Phys. Theor. Appl. 1894, 3, 393–415. [Google Scholar] [CrossRef]
- Lévy-Leblond, J.-M. The Pedagogical Role and Epistemological Significance of Group Theory in Quantum Mechanics. Riv. Nuovo Cimento 1974, 4, 99–143. [Google Scholar] [CrossRef]
- Lie, S. Theorie der Transformationsgruppen I. Math. Ann. 1880, 16, 441–528, Translated in English by M. Ackermann, with mathematical comments by R. Hermann, Math. Sci. Press, Brookline, Mass., 1976. [Google Scholar] [CrossRef]
- Killing, W. Die Zusammensetzung der stetigen/endlichen Transformationsgruppen. Math. Ann. 1888, 31, 252–290. [Google Scholar] [CrossRef]
- Killing, W. Die Zusammensetzung der stetigen/endlichen Transformationsgruppen. Math. Ann. 1889, 33, 1–48. [Google Scholar] [CrossRef]
- Killing, W. Die Zusammensetzung der stetigen/endlichen Transformationsgruppen. Math. Ann. 1889, 34, 57–122. [Google Scholar] [CrossRef]
- Killing, W. Die Zusammensetzung der stetigen/endlichen Transformationsgruppen. Math. Ann. 1890, 35, 423–432. [Google Scholar] [CrossRef]
- Killing, W. Die Zusammensetzung der stetigen/endlichen Transformationsgruppen. Math. Ann. 1890, 36, 161–189. [Google Scholar] [CrossRef]
- Killing, W. Bestimmung der grössten Untergruppen von endlichen Transformationsgruppen. Math. Ann. 1890, 36, 239–254. [Google Scholar] [CrossRef]
- Cartan, E. Structure des Groupes de Transformation Finis et Continus; Thèse à La Faculté des Sciences de Paris, Nony: Paris, France, 1894. [Google Scholar]
- Maclay, G.J. Dynamical Symmetries of the H Atom, One of the Most Important Tools of Modern Physics: SO(4) to SO(4, 2), Background, Theory, and Use in Calculating Radiative Shifts. Symmetry 2020, 12, 1323. [Google Scholar] [CrossRef]
- Enayati, M.; Gazeau, J.-P.; Pejhan, H.; Wang, A. The de Sitter (dS) Group and Its Representations, An Introduction to Elementary Systems and Modeling the Dark Energy Universe; Synthesis Lectures on Mathematics & Statistics (SLMS); Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Enayati, M.; Gazeau, J.-P.; del Olmo, M.A.; Pejhan, H. Anti-de Sitterian “massive” elementary systems and their Minkowskian and Newtonian limits. arXiv 2023, arXiv:2307.06690v1. [Google Scholar]
- Cohen-Tannoudji, G.; Gazeau, J.-P. Dark matter as a QCD effect in an anti de Sitter geometry: Cosmogonic implications of de Sitter, anti de Sitter and Poincaré symmetries. SciPost Phys. Proc. 2023, 14, 004. [Google Scholar] [CrossRef]
- Hamilton, W.R. On quaternions, or on a new system of imaginaries in algebra. Philos. Mag. 1844, 25, 489–495. [Google Scholar]
- Girard, P.R. The quaternion group and modern physics. Eur. J. Phys. 1984, 5, 25–32. [Google Scholar] [CrossRef]
- Girard, P.R.; Pujol, R.; Clarysse, P.; Delachartre, P. Hyperquaternions and physics. SciPost Phys. Proc. 2023, 14, 030. [Google Scholar] [CrossRef]
- Cockle, J. On Systems of Algebra involving more than one Imaginary. Philos. Mag. 1849, 35, 434–435. [Google Scholar]
- Brody, D.C.; Graefe, E.-M. On complexified mechanics and coquaternions. J. Phys. A Math. Gen. 2011, 44, 072001. [Google Scholar] [CrossRef]
- Weisstein, E.W. Icosian Game. From MathWorld—A Wolfram Web Resource. Available online: https://mathworld.wolfram.com/IcosianGame.html (accessed on 6 January 2024).
- Lucas, E. Récréations Mathématiques, 2nd ed.; Librairie Scientifique et Technique Albert Blanchard: Paris, France, 1992. [Google Scholar]
- Encyclopedia Britannica. Available online: https://www.britannica.com/science/Platonic-solid (accessed on 6 January 2024).
- Coxeter, H.S.M. Regular Polytopes, 3rd ed.; Dover Publications, Inc.: New York, NY, USA, 1973. [Google Scholar]
- Moody, R.V.; Patera, J. Quasicrystals and icosians. J. Phys. A Math. Gen. 1993, 26, 2829–2853. [Google Scholar] [CrossRef]
- Barache, D.; Champagne, B.; Gazeau, J.-P. Pisot-Cyclotomic Quasilattices and Their Symmetry Semi-Groups; Fields Institute Monograph, Series; Patera, J., Ed.; American Mathematical Society: Ann Arbor, MI, USA, 1998; pp. 15–66. [Google Scholar]
- Papadopolos, Z.; Kasner, G.; Ledieu, J.; Cox, E.J.; Richardson, N.V.; Chen, Q.; Diehl, R.D.; Lograsso, T.A.; Ross, A.R.; McGrath, R. Bulk termination of the quasicrystalline fivefold surface of Al70Pd21Mn9. Phys. Rev. B 2002, 66, 184207–184220. [Google Scholar] [CrossRef]
- Gazeau, J.P. Pisot-Cyclotomic Integers for Quasilattices; The Mathematics of Long-Range Aperiodic Order (NATO advances Science Institutes, Series C: Mathematical and Physical Sciences 489); Kluwer Academic Publishers: Dordrecht, The Netherlands, 1997; pp. 175–198. [Google Scholar]
- Burdík, Č.; Frougny, C.; Gazeau, J.-P.; Krejcar, R. Beta-integers as natural counting systems for quasicrystals. J. Phys. Math. Gen. 1998, 31, 6449–6472. [Google Scholar] [CrossRef]
- Cayley, A. On Jacobi’s elliptic functions, in reply to the Rev. B. Brownwin; and on quaternions. Philos. Mag. 1845, 26, 208–211. [Google Scholar]
- Baez, J.C. The Octonions. Bull. Amer. Math. Soc. 2002, 39, 145–205. [Google Scholar] [CrossRef]
- Burdík, Č.; Catto, S.; Gürcan, Y.; Khalfan, A.; Nicolescu, B. Characterization of New Algebras Resembling Colour Algebras based on Split-Octonion units in the Classification of Hadronic Symmetries and Supersymmetries. J. Phys. Conf. Ser. 2023, 2667, 012004. [Google Scholar] [CrossRef]
- Hopf, H. Über die Abbildungen der dreidimensionalen Sphäre auf die Kugelfläche. Math. Ann. 1931, 104, 637–665. [Google Scholar] [CrossRef]
- Lyons, D.W. An Elementary Introduction to the Hopf Fibration. Math. Mag. 2003, 76, 87–98. [Google Scholar] [CrossRef]
- Mosseri, R.; Dandoloff, R. Geometry of entangled states, Bloch spheres and Hopf fibrations. J. Phys. A Math. Gen. 2001, 34, 10243–10253. [Google Scholar] [CrossRef]
- Bengtsson, I.; Brännlund, J.; Życzkowski, K. CPn, or, Entanglement Illustrated. Int. J. Mod. Phys. A 2002, 17, 4675–4695. [Google Scholar] [CrossRef]
- Dalhuisen, J.W. The Robinson Congruence in Electrodynamics and General Relativity. Ph.D. Thesis, University Leiden, Leiden, The Netherlands, 2014. Available online: https://inspirehep.net/files/9e2c1a0bbe25a2e9970a1bde1bcccf23 (accessed on 6 January 2024).
- Ornea, L.; Parton, M.; Piccinni, P.; Vuletescu, V. Spin(9) geometry of the octonionic Hopf fibration. Transform. Groups 2013, 18, 845–864. [Google Scholar] [CrossRef]
- Balmer, J.J. Notiz über die Spectrallinien des Wasserstoffs [Note on the spectral lines of hydrogen]. Ann. Der Phys. Und Chem. 3rd Ser. 1885, 25, 80–87. [Google Scholar] [CrossRef]
- Fock, V. Zur Theorie des Wasserstoffatoms. Z. Für Phys. A Hadron. Nucl. 1935, 98, 145–154. [Google Scholar] [CrossRef]
- Onofri, E. Dynamical quantization of the Kepler manifold. J. Math. Phys. 1976, 17, 401–409. [Google Scholar] [CrossRef]
- Souriau, J.M. Sur la variété de Kepler. Symp. Math. 1974, 14, 343–360. [Google Scholar]
- Dynkin, E.B. The structure of semi-simple algebras. Uspekhi Mat Nauk N.S. 1947, 2, 59–127. (In Russian) [Google Scholar]
- Baez, J. This Week’s Finds in Mathematical Physics (Week 230). Available online: https://math.ucr.edu/home/baez/week230.html (accessed on 6 January 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).