First-Order Event Plane Correlated Directed and Triangular Flow from Fixed-Target Energies at RHIC-STAR

Abstract

We report the measurement of first-order event plane-correlated directed flow $\left(v_1\right)$ and triangular flow ($v_3$) for identified hadrons (${\pi }^{\pm }$, $K^{\pm }$, and p), net particle (net-K, net-p), and light nuclei (d and t) in Au + Au collisions at $\sqrt{s_{\mathrm{NN}}}$ = 3.2, 3.5, and 3.9 GeV in the fixed-target mode from the second phase of the beam energy scan (BES-II) program at RHIC-STAR. The $v_1$ slopes at mid-rapidity for identified hadrons and net particles except ${\pi }^{+}$ are found to be positive, implying the effect of dominant repulsive baryonic interactions. The slope of $v_1$ for net-kaon undergoes a sign change from negative to positive at a lower collision energy compared to net-proton. An approximate atomic mass number scaling is observed in the measured $v_1$ slopes of light nuclei at mid-rapidity, which favors the nucleon coalescence mechanism for the production of light nuclei. The $v_3$ slope for all particles decreases in magnitude with increasing collision energy, suggesting a notable integrated impact of the mean-field, baryon stopping, and collision geometry at lower collision energies.

1. Introduction

The primary objective of ultra-relativistic heavy-ion collisions at the Relativistic Heavy Ion Collider (RHIC) and the Large Hadron Collider (LHC) is to create and characterize a novel state of matter with partonic degrees of freedom known as the Quark–Gluon Plasma (QGP). This state of strongly interacting matter is hypothesized to have been present during the initial microseconds following the Big Bang, and gaining an understanding of its properties holds the potential to offer insights into the evolution of the universe [1,2]. The lattice Quantum Chromodynamics (QCD) predicts a crossover region between the hadron gas and QGP at higher temperature (T) and low baryon chemical potential (${\mu }_B$) [3]. At lower temperatures and higher ${\mu }_B$, QCD-based models suggest a first-order phase transition concluding at a conjectured QCD critical point [4]. Numerous experimental observables measured at RHIC and LHC have presented compelling evidence of QGP formation for matter near ${\mu }_B=0$. However, experimental confirmation of the existence of a critical point and a first-order phase transition at higher ${\mu }_B$ is still pending.

Numerous signatures of QGP formation and associated characteristics of the medium have been proposed. This paper briefly delves into one of the suggested signatures, namely anisotropic flow. The patterns of azimuthal anisotropy in particle production are commonly referred to as flow. The azimuthal anisotropy in particle production stands out as one of the most distinct experimental signature of collective flow in heavy-ion collisions. It can be obtained by studying the Fourier expansion of the azimuthal angle $\left(\varphi \right)$ distribution of produced particles with respect to the event plane angle $\left({\mathsf{\Psi }}_n\right)$.

The particle azimuthal angle distribution is written in the form of a Fourier series [4],

$$E\frac{{\mathrm{d}}^{3}N}{\mathrm{d}{p}^3}=\frac{{\mathrm{d}}^{2}N}{2\pi p_T\mathrm{d}{p}_T\mathrm{d}y}\left\{1+\sum _{n\ge 1}2v_{n}cos\left[n\left(\varphi -{\mathsf{\Psi }}_n\right)\right]\right\},$$

(1)

where $p_T$, y, $\varphi$, and ${\mathsf{\Psi }}_n$ are particle transverse momentum, rapidity, azimuthal angle of the particle and the $n^{th}$ order event plane angle, respectively. The various (order n) coefficients in this expansion are defined as

$$v_n=\langle cos\left[n(\varphi -{\mathsf{\Psi }}_n)\right]\rangle .$$

(2)

The angular brackets in the definition denote an average over many particles and events [4]. The sine terms in the distribution become zero due to the reflection symmetry concerning the reaction plane.

Flow anisotropy parameters $\left(v_n\right)$ offer an insight into collective hydrodynamic expansion and transport properties of the produced medium at higher collision energies, while they are sensitive to the compressibility of the nuclear matter and nuclear EOS at lower collision energies. The first three Fourier expansion coefficients $v_1$ (directed flow), $v_2$ (elliptic flow) and $v_3$ (triangular flow) are sensitive probes for studying the properties of the matter created in high-energy nuclear collisions.

At higher energies (nucleon–nucleon center-of-mass energy $\sqrt{s_{NN}}\gtrsim$ 27 GeV), where the transit time of colliding nuclei $2R/\gamma \beta$ (where R is the radius of the nucleus, $\gamma$ is the Lorentz factor, and $\beta$ is the velocity of the nuclei) is smaller than the typical production time of particles [5], flow harmonics are predominantly influenced by the collective expansion of the initial partonic density distribution [6]. Conversely, at lower energies, the shadowing effect caused by passing spectator nucleons becomes significant. For $\sqrt{s_{NN}}\lesssim$ 4 GeV, nuclear mean-field effects contribute to the observed azimuthal anisotropies [7]. Numerous studies indicate that flow coefficients are notably sensitive to the incompressibility of nuclear matter $\left(\kappa \right)$ in the high baryon density region [8]. Comparing experimental data with results from theoretical transport models can provide constraints on $\kappa$, offering valuable insights into nuclear EOS.

The directed flow ($v_1$), sensitive to early collision dynamics, is proposed as a signature of first-order phase transition based on hydrodynamic calculations. These calculations, whose EOS incorporates a first-order phase transition from hadronic matter to QGP, predict a non-monotonic variation of the slope of the directed flow of baryons (and net-baryons) around midrapidity as a function of beam energy [9].

The traditional $v_3$, third-order flow coefficient, typically results from fluctuations in shape of the initial condition and is not correlated to the reaction plane. In contrast to this, initial observations were made by HADES, followed by the STAR collaboration, in Au + Au collisions at $\sqrt{s_{\mathrm{NN}}}$ = 2.4 GeV and 3 GeV, respectively. A noticeable triangular flow, correlated with the first-order event plane (${\mathsf{\Psi }}_1$), was observed [10].

$v_3$ is also observed to be sensitive to the EOS and can serve as a new tool to explore the time dependence of the pressure during heavy-ion collision [10]. The evolution of $v_3$ is influenced by two crucial factors: the first involves the appropriate geometry determined by stopping, the passing time of spectators, and the expansion of the fireball; the second entails a potential within the responsive medium that propels the collective motion of particles.

2. Star Fixed-Target Program

The fixed target (FXT) setup was implemented at the Solenoidal Tracker at RHIC (STAR) to explore the region of high ${\mu }_B$ on the QCD phase diagram. These data were collected during the second phase of the Beam Energy Scan program (BES-II) (2019–2020) after incorporating various detector upgrades.

2.1. Experimental Setup

The STAR FXT comprises a 0.25 mm thick gold foil (equivalent to a 1% nuclear interaction probability) mounted on a half collar with two aluminum support rods. Positioned at the west edge of the TPC, the target is longitudinally 200 cm away from the nominal interaction point at the center of the TPC. Placed at the bottom of the beam pipe, the top edge of the gold foil is situated 2 cm below the center of the beam pipe. This configuration is crucial to prevent unintended collisions between the beam and the target during collider mode operation. In the fixed-target mode, the accelerator technicians lowered the beam by 1.8 cm until the trigger rate reached 2 kHz, which is the limit of the Data Acquisition (DAQ) system.

During fixed-target mode operation, the accelerator utilizes only one cycling beam. In this setup, the beam is filled with only 12 bunches, with each bunch containing 7 × ${10}^9$ ions. This limitation on the number of bunches serves to separate out-of-time pileup by a sufficiently large distance and also restricts the DAQ rate. The rationale behind limiting the number of bunches is to avoid instances where two collisions occur too close together temporally. In such cases, the vertices may appear too close together longitudinally in the TPC and might be reconstructed as a single vertex with a multiplicity equal to the sum of the two independent collision multiplicities. To prevent these out-of-time pileup vertices, reduction in the number of bunches ensures spatial separation.

2.2. Fixed-Target Conventions

In contrast to collider mode collisions, in FXT collisions in the STAR coordinate system, the target is situated at the edge of TPC, and midrapidity is not zero. To convert the measured rapidity (y) in the coordinate system to the rapidity in the center of mass frame ($y_{cms}$), it is necessary to boost the measured rapidity by beam rapidity. The beam rapidity $\left(y_b\right)$ for a given center of mass energy is calculated with the following equation:

$$y_b={cosh}^{-1}\left[\frac{\sqrt{s_{\mathrm{NN}}}}{2m_p}\right],$$

(3)

where $\sqrt{s_{\mathrm{NN}}}$ is center of mass energy (e.g., 3.2 GeV) and $m_p$ is proton mass (0.938 GeV). In STAR convention, the beam-going direction is the positive direction (the target is located in the negative rapidity direction for 3.2 GeV at $y_{\mathrm{b}}$ = −1.127). To match the STAR conventions, when calculating rapidity in the center of the mass frame and shifting by midrapidity, we also need to flip the sign of rapidity.

$$y_{cms}=-(y_{lab}-y_b).$$

(4)

3. Dataset and Event Selection Cuts

In this paper, we present the results of first-order event plane $\left({\mathsf{\Psi }}_1\right)$-correlated $v_1$ and $v_3$ for identified hadrons (${\pi }^{\pm }$, $K^{\pm }$, and p), net particle (net-K, net-p), and light nuclei (d and t) in Au+Au collisions at $\sqrt{s_{NN}}$ = 3.2, 3.5, and 3.9 GeV using FXT data from the STAR experiment.

In the FXT mode, we apply a vertex cut along the z-direction ($v_z$) within [198, 202] cm. For the x and y directions, we set the $V_r$ value ($\sqrt{V_x^2+V_y^2}$) less than 2 cm centered around (0, −2).

4. Analysis Details

4.1. Track Quality Cuts

To ensure the quality of primary tracks, tracks with transverse momentum $p_T$ < 0.2 GeV/c are excluded. Additionally, we mandate the utilization of a minimum of 15 fit points and 52% of the total possible fit points in the track fitting process. The selection criterion involves choosing dE/dx hit points ≥ 10. Furthermore, the distance of the closest approach (DCA) is set to <3 cm.

4.2. Particle Identification

The identification of charged particles in STAR is performed by the combination of Time Projection Chamber (TPC) and Time-of-Flight (TOF) detectors. For low-momentum particles, TPC is used, whereas for particles with intermediate or high momenta ($p_T>$ 1 GeV/c), TOF is used. TPC uses the ionization energy loss (dE/dx) of the charged particles passing through it for particle identification. Using dE/dx information, the z variable is defined,

$$z=ln\left(\frac{\langle dE/dx\rangle }{{\langle dE/dx\rangle }_X^B}\right),$$

(5)

where ${\langle dE/dX\rangle }_X^B$ is the expected energy loss based on the Bichsel function and X is the particle type [11]. The raw yield from the TOF is obtained using the variable mass square ($m^2$) given by

$$m^2=p^2\left(\frac{c^2{T}^2}{L^2}-1\right),$$

(6)

where p, T, L, and c are the momentum, time of travel by the particle, path length and speed of light, respectively. The left panel of Figure 1 shows the average dE/dx of measured charged particles plotted as a function of “rigidity” (i.e., momentum/charge) of the particles. The curves represent the Bichsel expectation values. The right panel of Figure 1 shows the inverse of particle velocity in units of the speed of light, $1/\beta$, as a function of rigidity. The expected values of $1/\beta$ for charged particles are shown as curves.

In this analysis, for the identification of pion, kaon, and proton, we require TPC $n\sigma$ (z/R; R: TPC resolution) and TOF $m^2$ cuts which are listed in

Table 1. Particle identification cuts.

pion	$|n{\sigma }_{\pi }| <$ 3 and $-0.1<m^2<0.15$ (${(GeV/c^2)}^2$ )
kaon	$|n{\sigma }_K| <$ 3 and $0.16<m^2<0.36$ (${(GeV/c^2)}^2$)
proton	$|n{\sigma }_p| <$ 2 and $-0.6<m^2<1.2$ (${(GeV/c^2)}^2$)
deuteron	momentum-dependent z cut and $3.15<m^2<3.88$ (${(GeV/c^2)}^2$)
triton	momentum-dependent z cut and $7.01<m^2<8.75$ (${(GeV/c^2)}^2$)

. In addition to the $m^2$ cut, a momentum-dependent z cut is implemented for light nuclei identification.

4.3. Event Plane Reconstruction

Event plane angle can be estimated from particle azimuthal distribution on an event-by-event basis. In our calculations, we used first-order event plane angle ${\mathsf{\Psi }}_1$, which is measured using Event Plane Detector (EPD). EPD is designed to measure the pattern of forward-going charged particles emitted in a high-energy collision between heavy nuclei. In order to calculate the first-order event plane angle, first, we constructed the Q vector from the particle’s azimuthal angle.

$$\overrightarrow{Q}=(Q_x,Q_y)=\left(\sum _i{w}_{i}cos\left({\varphi }_i\right),\sum _i{w}_{i}sin\left({\varphi }_i\right)\right).$$

(7)

The first-order event plane angle ${\psi }_1$ is defined as

$${\psi }_1={tan}^{-1}(Q_y/Q_x),$$

(8)

where the sum extends over all detected hits i, ${\varphi }_i$ is the azimuthal angle in the laboratory frame, and $w_i$ is the weight for the $i^{th}$ hits. Here, we use nMip as weight, which is the calibrated ADC value [4]. In order to mitigate acceptance correlations arising from the imperfect detector, it is essential to render the event plane angle distribution isotropic or flat. Consequently, a procedure for flattening the event plane angle distribution becomes necessary. In this analysis, we implemented re-centering and shift corrections to extract flat event plane angle distribution [4].

In the re-centering correction, the Q-vector averaged over multiple events is subtracted from the Q-vector of each individual event. Subsequently, event plane angle is calculated. However, performing only the re-centering correction is insufficient. After the implementation of re-centering, a shift correction is additionally applied to ensure that event plane angle distribution becomes flat. In shift correction, one fits the non-flat distribution of ${\psi }_n$ averaged over many events with a Fourier expansion and calculates the shifts for each event ${\psi }_n$ necessary to force a flat distribution on average. The re-centering and shift correction are all performed run-by-run and centrality-by-centrality in this analysis.

4.4. Event Plane Resolution

The finite number of detected particles in detectors produces a limited resolution in the measured event plane angle. So, the observed flow coefficients must be corrected up to what they would be relative to the real reaction plane. This is achieved by dividing these coefficients by event plane resolution, estimated from the correlation of the planes of independent subevents,

$$v_n=\frac{v_n^{obs}}{R_n}=\frac{v_n^{obs}}{\langle cos\left[n({\psi }_n-{\mathsf{\Psi }}_R)\right]\rangle },$$

(9)

where $R_n$ is resolution, $v_n$ is the $n^{th}$ harmonic azimuthal anisotropy parameter, and ${\psi }_n$ is the $n^{th}$ harmonic order event plane, ${\mathsf{\Psi }}_r$ is the reaction plane angle. Angle brackets denote the average over all particles in all events [4].

In the fixed target mode, the final state particle’s acceptance is not symmetric around midrapidity. Therefore, the commonly used two-sub event method, employed in the collider BES-I analysis, cannot be used to calculate resolution. This method necessitates each sub-event to have similar multiplicity and resolution. Consequently, in this analysis, we opt for the three-sub event method to calculate resolution. Figure 2 shows the calculated first-order event plane resolution $R_{11}$ and the third-order event plane resolution $R_{13}$ estimated from the first-order event plane for $v_3$ calculation as functions of collision centrality.

5. Systematic Uncertainties

The systematic uncertainties associated with the measured flow harmonics stem from the charged track selection method, particle identification, and event plane resolution. These uncertainties are evaluated point by point on $v_1$ and $v_3$ as a function of y for each identified hadron and light nuclei. The systematic uncertainties arising from track selection are assessed by varying selection requirements. Those linked to particle misidentification are determined by varying z and $m^2$ cuts. A common systematic uncertainty arising from event plane resolution is assessed by employing combinations of different $\eta$ sub-events. In subsequent figures, the shaded boxes represent the total systematic uncertainty for each data point.

6. Results and Discussion

6.1. Directed Flow $\left(V_1\right)$

The rapidity (y), centrality and collision energy dependence of $v_1$ for identified hadrons, net particle, and light nuclei are measured at $\sqrt{s_{\mathrm{NN}}}$ = 3.2, 3.5, and 3.9 GeV.

Figure 3 illustrates the the centrality dependence of ${\pi }^{+}$ for $\sqrt{s_{NN}}$ = 3.2 GeV. $v_1$ changes the sign from negative to positive, moving from most central to peripheral collisions, implying the effect of dominant repulsive baryonic interactions and spectator shadowing.

The energy dependence of proton $v_1$ involves an interplay between the directed flow of protons associated with baryon stopping and particle–antiparticle pair production at mid-rapidity. A means to distinguish between the two mechanisms would thus be to look at net particle $v_1$. The net particle represents the excess yield of a particle species over its antiparticle. The net particle’s $v_1$ is defined as

$$v_{1,net}=\frac{v_{1,p}-r{v}_{1,\overline{p}}}{1-r},$$

(10)

where $v_{1,p}$, $v_{1,\overline{p}}$ correspond to $v_1$ of particle and anti-particle, and r represents the ratio of anti-particles to particles [9].

In relativistic heavy-ion collisions, the production of light nuclei can occur via two mechanisms. The first mechanism involves the direct production of nucleus–antinucleus pairs in elementary nucleon–nucleon (NN) or parton–parton interactions. Due to their small binding energies, the directly produced nuclei or antinuclei are likely to undergo dissociation in the medium before escaping. The second and presumably dominant mechanism for the production of nuclei and antinuclei is through the final state coalescence of produced nucleons and antinucleons or participant nucleons [12,13]. In this process, nucleons and antinucleons combine to form light nuclear and antinuclear clusters during the final stages of kinetic freeze-out. The probability of formation is proportional to the product of the phase space densities of its constituent nucleons [14,15]. Therefore, the production of light nuclei yields information about the size of the emitting system and its space-time evolution. Due to the longer passing time of the colliding ions in the few-GeV regime, the interference between the expanding central fireball and spectator remnants becomes more significant than at higher energies.

Figure 4 shows the y dependence of identified hadrons (left panel), net particles (middle panel), and light nuclei (right panel) for 10–40% centrality. The magnitude of $v_1$ increases with increasing rapidity for all particles, and mass ordering is also observed in the magnitude of $v_1$.

The $p_T$-integrated $v_1\left(y\right)$ slope at mid-rapidity, $d{v}_1{/dy|}_{y=0}$, is obtained by fitting data $v_1\left(y\right)$ with a third-order polynomial. Figure 5 shows the collision energy dependence of $d{v}_1{/dy|}_{y=0}$ for identified particles (left panel), net particle (middle panel), and light nuclei (right panel) in mid-central (10–40%) collisions. The extracted slope parameters, $d{v}_1{/dy|}_{y=0}$, are scaled by A for light nuclei to compare with protons. The magnitude of the slope decreases with increasing collision energy for all particles, including net particles and light nuclei.

At low energies, the transit time ($\tau$) is comparable to the formation time of particles. Consequently, the spectators are not sufficiently distant from the collision volume, and the medium does not have the freedom to expand freely. This results in interactions between baryon-dominated spectator particles and the produced particles. Among the produced particles, pions, being some of the lightest types, are particularly affected. The flow for ${\pi }^{+}$ is obstructed by the spectator particles, leading to a negative value for its $v_1$ slope. In contrast, ${\pi }^{-}$, influenced by Coulomb interactions from the baryons (protons), acquires a positive $v_1$ slope value.

The slope of $v_1$ for net-kaon undergoes a sign change from negative to positive at a lower collision energy range ($\sqrt{s_{\mathrm{NN}}}$ = 3.9–7.7 GeV) compared to that of net-proton ($\sqrt{s_{\mathrm{NN}}}$ = 11.5–19.6 GeV).

Light nuclei $v_1$ slope exhibits an approximate mass number (A) scaling, consistent with the nucleon coalescence mechanism for the production of light nuclei at low collision energies.

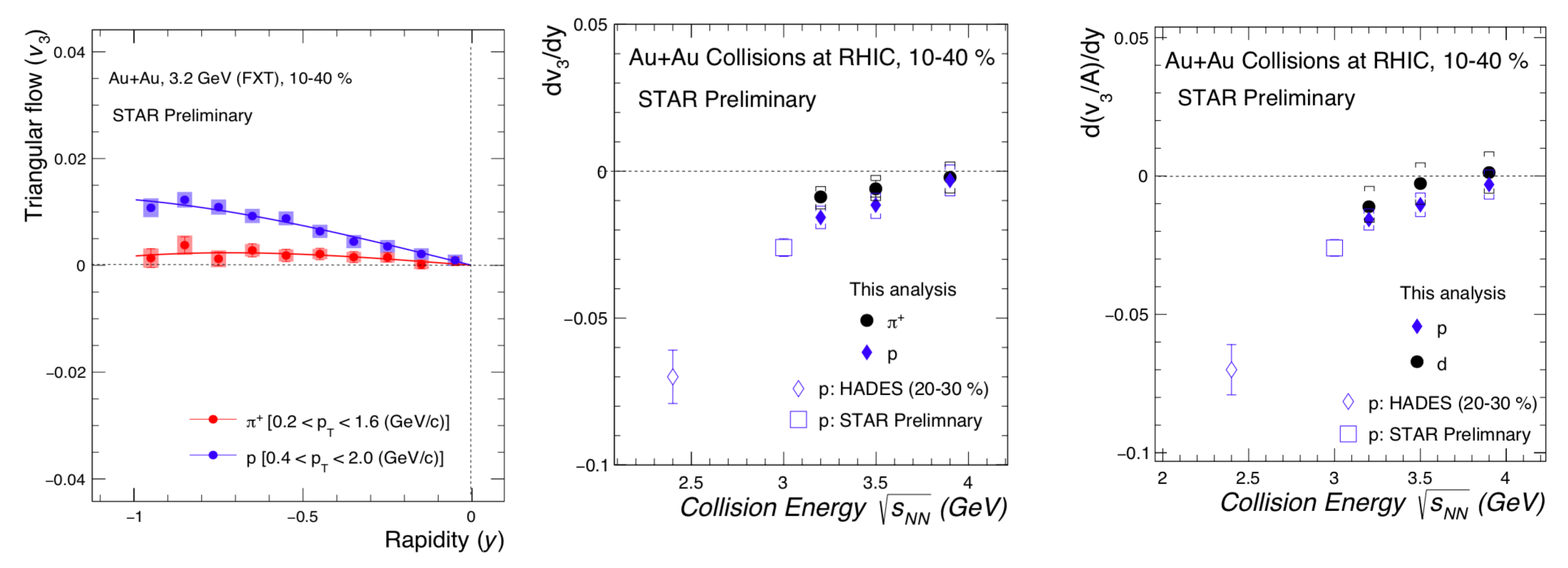
6.2. Triangular Flow $\left(V_3\right)$

The y and collision energy dependence of $v_3$ for identified hadrons and light nuclei are measured at $\sqrt{s_{\mathrm{NN}}}$ = 3.2, 3.5, and 3.9 GeV. The left panel of Figure 6 shows the rapidity dependence of $v_3$ for the identified hadrons. The magnitude of $v_3$ increases with increasing rapidity. The distribution is fitted with a polynomial of order three to extract the slope parameter.

The middle panel of Figure 6 shows the slope of $v_3$, $d{v}_3{/dy|}_{y=0}$, for identified hadrons as a function of collision energy. The magnitude of $d{v}_3{/dy|}_{y=0}$ decreases with increasing collision energy. It may indicates that the combined effect of the mean-field, baryon stopping, and collision geometry is considerably significant at low collision energies [16].

The right panel of Figure 6 shows the extracted slope parameters, $d{v}_3{/dy|}_{y=0}$, scaled by mass number (A) for light nuclei. The magnitude of the slope decreases with increasing collision energy. The light nuclei $v_3$ slope also exhibits an approximate mass number (A) scaling within systematic uncertainties, consistent with the nucleon coalescence mechanism for light nuclei production.

7. Conclusions

In summary, the rapidity, centrality, and collision energy dependence of directed flow $\left(v_1\right)$ of identified hadrons, net particle, and light nuclei in Au + Au collisions at $\sqrt{s_{NN}}$ = 3.2, 3.5, and 3.9 GeV is reported. The magnitude of $v_1$ increases with increasing rapidity for all particles. The extracted $v_1$ slope of all the particles decreases in magnitude with increasing collision energy. A positive $v_1$ slope at mid-rapidity for identified hadrons and net particles, excluding ${\pi }^{+}$, suggests prevalent repulsive baryonic interactions and spectator shadowing. As collision energy decreases, a non-monotonic trend is observed in the slope of both net-kaon and net-proton. The $v_1$ slope for net-kaon experiences transition from negative to positive at a collision energy lower than that observed for net-proton. The light nuclei $v_1$ slope exhibits an approximate mass number scaling consistent with the nucleon coalescence mechanism for the production of light nuclei.

The magnitude of the slope of $v_3$ decreases with increasing collision energy, indicating a substantial collective impact of the mean-field, baryon stopping, and collision geometry at lower collision energies. Similar to the $v_1$ slope of light nuclei, the $v_3$ slope of light nuclei also displays an approximate scaling with a mass number (A) within systematic uncertainties. This trend supports the nucleon coalescence mechanism as a favorable explanation for the production of light nuclei.