Abstract
This review devoted to the centenary of Alexander Friedmann’s prediction of the Universe expansion presents the results obtained by him in 1922 and 1924 and an overview of their further developments. Special attention is paid to the role of mathematics, which enabled Friedmann to perform a radical departure from the conventional practice of considering our universe as a static system. The effect of particle creation in the expanding universe is discussed concurrently with the earlier investigated phenomenon of pair creation from a vacuum by an external electric field. The numbers of scalar and spinor particles created at different stages of the Universe’s evolution are presented, and the possible role of the effect of the creation of particles in the formation of relativistic plasma and cold dark matter after the inflationary period is noted. It is stressed that by introducing the concept of the expanding universe, Friedmann made a contribution towards the understanding of the world around us that is compatible with those made by Ptolemy, Copernicus, and Newton in previous epochs.
1. Introduction
A hundred years ago, young mathematician Alexander Friedmann made an unexpected prediction that our universe expands with time. This prediction was in complete contradiction with all the previous scientific concepts of the Universe developed over the past millennia. One could mention the Ptolemy system, which was geocentric, and the Copernicus, Kepler, and Galilei system, which was heliocentric. Based on the laws of mechanics and gravitation discovered by him, Newton supposed [1] that our universe has an infinitely large volume, contains infinitely many stars and exists in time forever. As a theologian, Newton believed that the Universe was created by God. This means that not only all material bodies but also space and time are created in one creation act. The question of whether the existence of the Universe in time is finite or infinite must be solved by physics. All the mentioned pictures of the world are static in the sense that they do not change with time. And even Albert Einstein, after the creation of his general theory of relativity [2], especially modified its equations by introducing the cosmological constant in order to obtain the static model of the Universe [3] in agreement with the concepts of all previous epochs.
Like Einstein, Friedmann described the Universe as a whole on a basis of the general theory of relativity. In doing so, however, he restricted himself to the minimum number of additional assumptions. Specifically, following Newton and Einstein, he assumed that the 3-space of the Universe is homogeneous and isotropic, i.e., there are no preferential points and preferential directions. Otherwise, Friedmann acted as a mathematician by solving equations of the fundamental general theory of relativity and looking for the results obtained with no prejudice caused by some physical considerations like the desired static character of any model of the Universe. This method of attack helped him to make an outstanding prediction that our universe expands with time, which was very soon confirmed by astronomical observations and became the cornerstone of modern cosmology.
In this brief review, we discuss the scientific results of Alexander Friedmann contained in his famous papers [4,5] by placing more emphasis on the outstanding role of mathematics in their obtainment. According to Friedmann’s prediction, our universe started its evolution from a point (the so-called cosmological singularity), where it was characterized by the infinitely large values of the scalar curvature and energy density. A universe with a 3-space of negative or zero curvature, expands infinitely long, whereas a universe with a 3-space of positive curvature expands to some maximum size and then contracts down to a singular state.
Next, the outstanding phenomenon described by a unification of the general theory of relativity and quantum field theory is considered. This is the effect of particle–antiparticle pair creation from a vacuum, which occurs due to the Universe’s expansion, as was understood for the first time by Erwin Scrödinger [6]. The effect of particle creation makes it possible to trace a mathematical analogy between the well-understood case of a nonstationary electric field and the expanding space–time of the Friedmann Universe. Main approaches to the definition of the concept of particles in the Friedmann cosmological models and the calculation results for a creation rate are presented. The role of the effect of particle creation at different stages of the Universe’s evolution, including the epoch of inflation, is discussed.
This review is organized as follows. In Section 2, the Friedmann prediction of the Universe’s expansion is considered with an emphasis on several facts from his biography and mathematical educational background. Section 3 is devoted to the effect of particle–antiparticle pair creation in the nonstationary electric field. Section 4 contains the primary information relative to the effect of particle creation in the Friedmann Universe. The crucial role of the effect of particle creation in the transition period between the inflationary and the radiation-dominated stages of the Universe’s evolution is elucidated in Section 5. A discussion of the fundamental importance of Friedmann’s prediction for modern cosmology is presented in Section 6, and we will finish with the conclusions in Section 7.
The system of units is one in which is used, where c is the speed of light and ℏ is the reduced Planck constant.
2. Role of Mathematics in Friedmann’s Prediction of the Universe’s Expansion
It was difficult to imagine that Alexander Friedmann, who was born on 6 June 1888 to an artistic family (his father was a ballet artist and composer and his mother was a pianist [7,8]) would become the outstanding mathematician and physicist who would radically change our picture of the world. However, his exceptional abilities in mathematics became apparent very early. In 1905, while still a schoolboy, Alexander Friedmann, together with his schoolmate Yakov Tamarkin, obtained new interesting results in the field of Bernoulli numbers. In the next year, it was David Hilbert who recommended their paper for publication in the prestigious mathematical journal Mathematische Annalen [9].
After his graduation from high school, Friedmann became a student of the Department of Mathematics at Saint Petersburg University, where he gained in-depth knowledge in different areas of mathematics and physics. His successes were always evaluated as “excellent”. Because of this, after his graduation from the university in 1910, Friedmann remained at the same department in preparation for the position of Professor, under the supervision of the famous mathematician and academician Vladimir Steklov. During the next few years, he published many papers containing the solutions of several complicated problems of mathematical physics. Starting from 1913, Friedmann took an interest in the mathematical problems of dynamical meteorology, aerodynamics, and hydrodynamics, in which he obtained a lot of fundamental results which are well known to all experts in these fields and maintain their importance to the present day.
In 1920, Friedmann had close contacts with several professors of Petrograd (as St. Petersburg was called at that time) University who had just begun delivering lectures in the recently developed quantum physics and general theory of relativity. He took a great interest in the latter and embarked upon giving lectures on tensor calculus at the university as an introduction to the general theory of relativity. Friedmann was inspired by the idea that the Universe around us takes the form of Riemannian space–time, in which all bodies move freely along geodesic lines. This idea was radically different from Newton’s concept of the gravitational force which acts between all material bodies through an empty space.
In 1922, Friedmann applied the formalism of the general theory of relativity to the theoretical description of the Universe as a whole. As mentioned in Section 1, he restricted himself to the minimum physical assumptions by presuming that the 3-space of the Universe is homogeneous and isotropic. In this regard, Friedmann followed Einstein [3] and de Sitter [10].
Mathematically, the requirement of the homogeneity and isotropy of the 3-space is expressed in the following distance (interval) between two infinitesimally close space–time points and :
where t is the time variable, and the spatial coordinates , and are connected with the standard Cartesian coordinates by the relations
The quantity in Equation (1) has the dimension of length. It represents the radius of the curvature of space. As to the function , it is defined as
where is the sign of the curvature of the 3-space ( corresponds to the flat 3-space). Depending on the value of in Equation (3), the interval (1) relates to the closed space of the finite volume and positive curvature, to the open space of an infinite volume and negative curvature, or to the quasi-Euclidean space of an infinite volume and zero curvature.
Working as a mathematician, Friedmann solved the following Einstein equations:
where is the Ricci tensor describing the curvature of space–time, is the scalar curvature, is the cosmological constant, G is the gravitational constant, is the stress–energy tensor of matter in the Universe, and is the metrical tensor, the components of which for are defined in Equation (1) for the case of a homogeneous and isotropic space. In this space, the stress–energy tensor is diagonal, and its components are the energy density, , and pressure, , of matter. It is important to note that and R can be calculated for any given . Note that the stress–energy tensor is also often called the energy–momentum tensor.
Substituting the metrical tensor defined in Equation (1) in Equation (4), one obtains two Friedmann equations for the unknown scale factor and the energy density :
One should remember that the pressure P is connected with the energy density by the equation of state.
Note that, initially, Einstein introduced his Equation (4) with [2]. The cosmological term was introduced by him later [3], specifically for obtaining the static model of the Universe.
Friedmann considered dust-like matter with the equation of state (in our system of units, , where is the density of matter). The closed universe was considered by Friedmann in Ref. [4], published in 1922, and the open universe —in Ref. [5], published in 1924.
For instance, if and , Equation (5) for dust-like matter is simplified to
It is easy to check by the direct substitution that the solution of this system of equations can be represented in the following parametric form:
where is the constant expressed via the total mass of matter in the closed universe M as .
If one considers , Equation (7) reduces to
i.e., according to Friedmann, the evolution of the Universe starts from a point-like state , where the density of matter .
The Universe expands with time until the maximum size is reached at , and then contracts to a point . For or 0, the expansion of the Universe also starts from a point (called the cosmological singularity), where the density of matter is infinitely large, but in this case the expansion goes on infinitely. Similar results were later obtained for the radiation-dominated Universe, where matter has the equation of state (see Ref. [11] for details). This equation of state describes the hot Universe at the early stages of its evolution.
Thus, if , all the solutions of Equation (5) are nonstationary and describe the expanding (or contracting in the case ) Universe. According to Friedmann, the static cosmological solution of Einstein equations is possible only for the closed universe () with the cosmological constant satisfying the following conditions:
Under these conditions, Equation (5) reduces to
which means that . This is the static model of the Universe obtained by Einstein [3]. Friedmann did not discuss whether the Einstein model is stable relative to some disturbance which occurs at a definite time. This problem was investigated later after an experimental confirmation of the Universe’s expansion (see Ref. [12] for a summary of the obtained results). A more detailed consideration of the cosmological models with nonzero can be found in Ref. [13].
We only mention the famous solution of Equation (5) obtained by de Sitter [10] for the empty universe with but with a nonzero cosmological constant . In this case, Equation (5) takes the following form:
In the most simple, quasi-Euclidean case (), the de Sitter solution of Equation (11) is
The closed () and open () de Sitter solutions of Equation (11) are, respectively,
The scale factors in Equations (12) and (13) are the exponentially increasing with time functions which leave the scalar curvature constant, . The de Sitter solution found important applications in the theoretical description of the very early stages of the Universe’s evolution near the cosmological singularity (see Section 5).
Although Friedmann’s papers [4,5] were published in the leading journal of that time, his remarkable results did not gain widespread recognition for a long period of time. Just after the publication of Friedmann’s paper [4], Albert Einstein claimed [14] that the solutions found by Friedmann did not satisfy Equation (4) of the general theory of relativity. It was, however, Einstein who made a mistake in his note [14]. After receiving a letter explaining this from Friedmann, Einstein was obliged to recognize this fact in another published note [15].
From the experimental viewpoint, the expansion of the Universe predicted by Friedmann should manifest itself as the moving of all remote galaxies away from the Earth. This would lead to the redshift of the light emitted by them in accordance to the Doppler law. In fact, the redshift of the light from the Andromeda Nebula was registered by Slipher [16] as early as in 1913, i.e., before the Friedmann prediction.
In a systematic way, the experimental law connecting the redshift in the spectra of observable galaxies with the expansion of the Universe was found by Georges Lemaître in 1927 [17] and Edwin Hubble in 1929 [18] after they identified nebulas with remote galaxies [19]. Lemaître’s paper contains a rederivation of the main properties of the expanding universe from Einstein’s equations with no citation of the papers [4,5] by Friedmann, who passed away untimely of typhus on 16 September 1925 at the age of 37. Hubble’s paper [18] does not cite Alexander Friedmann’s papers either. Later on, the properties of homogeneous isotropic metrics were studied by H.P. Robertson [20] and A.G. Walker [21], whose papers also do not cite the Friedmann results.
In the meantime, after the elaboration of the theory of a hot universe by George Gamov [22], the prediction of the relic radiation [23] and its discovery by Arno Penzias and Robert Wilson [24], it became evident that the Friedmann solution describing the expanding Universe formed the foundation of modern cosmology and radically changed our picture of the world. Starting from the 1960s, Friedmann’s name as a pioneer of the theory of the Universe’s expansion became more and more popular. Friedmann’s background as a mathematician played a crucial role in his discovery, which was based on Einstein’s equations of the general theory of relativity alone with no unnecessary assumptions caused by either tradition or physical intuition. This is one more example of what was characterized by E.P. Wigner as “The unreasonable effectiveness of mathematics in the natural sciences” [25].
Though being a mathematician, Friedmann considered his prediction of the Universe’s expansion very seriously and expected that it would receive experimental confirmation. In his book “The World as Space and Time”, written for the general reader and published in 1923 [26], Alexander Friedmann not only explained the main concepts of Einstein’s general theory of relativity, but also discussed his own model of the expanding Universe, which starts its evolution from a point. The front cover of this book is presented in Figure 1. According to Friedmann’s estimation contained in Ref. [26], the interval between the Universe’s creation and the present day is of about tens of billions of years. This estimation is in qualitative agreement with modern measurements, which result in 13.7 billion years for the Universe’s age. Thus, Friedmann predicted the most dramatic phenomenon of nature, which completely changed our picture of the world.

Figure 1.
The front cover of the book [26]. Translation: Modern culture. A. Friedmann. The World as Space and Time. Academia, Petersburg, 1923.
3. Quantum Creation of Particle–Antiparticle Pairs in a Nonstationary Electric Field
As was mentioned in Section 1, the Universe’s expansion results in the effect of particle creation from the vacuum state of quantized fields. This is the quantum effect, which is described by the quantum field theory in curved space–time. It is most important at the very early stages of the Universe’s evolution near the cosmological singularity, where the Universe should be considered as a quantum object.
The quantum field theory and the general theory of relativity are very dissimilar theories. The former deals with the quantum fields defined on a flat Minkowski space–time, whereas the latter treats the gravitational field as a classical curved space–time. The quantum theory of gravitation is not yet available in spite of numerous attempts to develop it undertaken by many authors during half a century. It is possible, however, to consider the quantized matter fields defined not on a Minkowski background, but on a curved space–time of the expanding Universe. This theory has been well elaborated on since the beginning of the 1980s (see, for instance, the monographs [27,28,29,30,31]).
Some basic concepts of quantum field theory in curved space–time, including the concept of a particle, are, however, much more complicated and, unlike the standard quantum field theory, are not defined uniquely. Because of this, before considering the effect of particle creation in the Friedmann Universe, we discuss in this section the creation of particle–antiparticle pairs from a vacuum by the nonstationary space homogeneous electric field. Quantum electrodynamics allows us to describe this phenomenon in a rather transparent way [32,33,34,35]. At the same time, although, conceptually, the nonstationary electric field and the expanding space–time of the Universe are quite different, mathematically, the description of the effect of particle creation in both cases turns out to be very similar. Thus, the formalism briefly presented in this section will provide rather useful guidance in the next section.
The spatially homogeneous nonstationary electric field directed along the axis can be described by the following vector potential:
which leads to the following field strength:
It is assumed that the field is switched off at , i.e.,
Let us consider first the complex scalar field of mass m interacting with the electric field (15). A complete orthonormal set of solutions to the Klein–Fock–Gordon equation is as follows:
In the case of a vector potential, (14) takes the following form:
where is the momentum, the functions obey the following equation:
and the following notations are used:
Equation (19) is the equation of oscillator with a variable frequency [34,35]. The positive- and negative-frequency solutions of this equation are defined by the following asymptotic behavior:
An operator of the complex scalar field is
where is the annihilation operator for particles and is the creation operator for antiparticles defined at when the scalar field is free. The vacuum state at is defined as
where is the annihilation operator for antiparticles (the creation operator for particles is notated as ).
The Hamiltonian of the complex scalar field is defined by [36]
Substituting Equation (22) in Equation (24) and performing the integration with respect to x and to one of the momenta using (18), one obtains
where
Using Equation (21), Equation (27) leads to
As a result, at the Hamiltonian (24) takes the following diagonal form:
as it should be for the Hamiltonian of free fields.
At any t, in the presence of a nonstationary electric field, the Hamiltonian (25) can be diagonalized by means of the canonical Bogoliubov transformations, which preserve the commutation relations for the creation–annihilation operators:
where
Note that an addition of the creation operators to the annihilation ones in Equation (29) due to the action of a nonstationary external field is equivalent to the fact that the negative-frequency solution of the wave equation defined at becomes the linear combination of the negative- and positive-frequency solutions defined at a later time t.
In doing so, the operators and can be considered the creation and annihilation operators of quasiparticles defined at the moment t. The quasiparticle vacuum is defined by
It is easily seen that
so that the creation and annihilation operators of quasiparticles at coincide with the creation and annihilation operators , and the quasiparticle vacuum = defined in Equation (23).
Now, one can find the number of scalar quasiparticles with the momentum p and antiparticles with the momentum created from the vacuum state :
These quasiparticle pairs were created by the electric field during the time interval from to t in the space of an infinitely large volume V. Taking into account that
for the total number of scalar quasiparticle pairs with any momentum created in the unit space volume, one obtains
In the asymptotic limit , the electric field is switched off and in this "out" region the quasiparticles described by the operators , become the real free particles. Thus, the total number of real boson pairs created by the electric field during the time of its existence is
Similar results have been obtained for the fields and particles with nonzero spin. By omitting the technical details, here, we present only several facts concerning the case of spinor particles. Thus, after the separation of variables in the Dirac equation written for the spinor field interacting with the space homogeneous nonstationary electric field (14) and (15), it reduces to the oscillator equation with the following complex frequency [34,35]:
where is presented in Equation (19) and the positive- and negative-frequency solutions are defined by the following asymptotic behaviors:
The Hamiltonian of the spinor field interacting with the electric field (14) is given by
where the index corresponds to two possible spin projections on the axis and the coefficients E and F are defined as
Similar to the case of a scalar field, the Hamiltonian (41) becomes diagonal in the asymptotic limit :
At any t, the Hamiltonian (41) can be diagonalized by the canonical Bogoliubov transformation, preserving the anticommutation relations between the creation and annihilation operators of spinor particles:
where
If the coefficients of the Bogoliubov transformation (44) are equal to
the Hamiltonian (41) takes the diagonal form at any t in terms of the creation and annihilation operators of quasiparticles [34]:
Similar to Equation (33), the vacuum state of the quasiparticles is defined as
The number of spinor quasiparticles with momentum p and spin projection r (and respective antiquasiparticles) created from the ground state during the time interval from to t is given by
This number does not depend on the spin state r.
The total number of fermion quasiparticle pairs created in the unit space volume during the time interval from to t is obtained from Equation (49) with the help of Equation (36):
Thus, the total number of real fermion pairs created in the unit volume by the electric field is
The most simple exactly solvable example allowing an exact calculation of the numbers of created pairs (38) and (51) is the electric field of the following form [32,34]:
This field is switched off in the asymptotic regimes (see Figure 2).
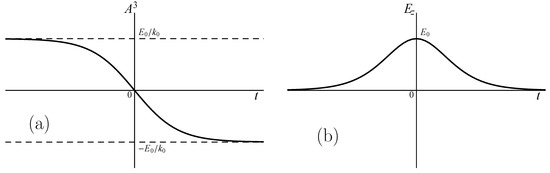
Figure 2.
(a) The component of the vector potential and (b) the strength of the space homogeneous nonstationary electric field (52), which is switched off in the asymptotic regimes , are shown as the functions of time.
In the limiting case , Equation (52) describes the space homogeneous constant electric field. Thus, Equations (38) and (51) allow for the rederivation of the famous Schwinger results for the pair creation from vacuum by a strong constant field derived by him [37,38] using another formalism.
For the inflationary cosmology (see Section 5, the effect of the exponential growth of the number of scalar particles created with some values of momentum by the periodic in time external field is of much importance. This effect was independently discovered in Ref. [39] for the sinusoidally depending on time and in Ref. [40] for the electric field of arbitrary form with a period T:
during the interval . Outside this interval, the electric field was assumed to be equal to zero, so that .
It was shown that the number of pairs of scalar particles created by the periodic field with some momenta p belonging to the instability zones of the oscillator equation during the time is the exponentially increasing function of the number of field periods n [40]:
Here, and are the solutions of the oscillator Equation (19) satisfying the following initial conditions:
and , .
From Equation (54), it can be seen that the number of created pairs increases with the number of field periods n as .
The effect of particle creation from a vacuum by an electric field is not observed yet because it becomes sizable for the fields of the order of , which are too large ( V/cm for electrons). With the discovery of graphene, in which the fermion quasiparticles are massless or very light, the possibility of observing the creation of these quasiparticles in much weaker fields was proposed [41,42,43,44,45,46]. This is some kind of a condensed matter analogy to Schwinger’s particle creation from a vacuum in quantum electrodynamics.
The above brief discussion allows one to conclude that in quantum field theory and, specifically, in quantum electrodynamics, a description of the effect of particle creation from a vacuum by an external field is based on the S-matrix picture. The concept of real particles is defined in the “in” and “out” regions where the external electric field is switched off. It is common knowledge that in the absence of external fields the theory is invariant relative to the transformations from the Poincaré group, the Casimir operators of which classify particles by the values of their mass and spin [36]. Thus, in curved space–time, which does not become flat in the asymptotic regions, one could expect difficulties with the definition of the concept of particles. In the next section, it is shown that in the case of the expanding Universe, these difficulties can be solved in close analogy to the concept of quasiparticles in the presence of a nonstationary electric field.
4. The Effect of Particle Creation in the Friedmann Universe
As discussed in Section 2, the Friedmann models of the Universe are described by the interval (19). By solving the Einstein equations (4) for the metrical tensor defined in Equation (1), one obtains the scale factors of the closed, open, and quasi-Euclidean models. The matter fields (scalar and spinor, for instance) should be considered in the background of curved space–time defined in Equation (1).
The general covariant generalization of the Klein–Fock–Gordon equation (17) with the electric field is given by
where is the covariant derivative and is the so-called coupling coefficient. The most simple case is referred to as the minimal coupling. In the case , considered in Refs. [47,48], Equation (56) becomes invariant under the conformal transformations when . This is called the conformal coupling.
As was first noticed by Schrödinger [6], the positive-frequency solution of Equation (56) with in the space–time with metric (1) defined at some moment becomes the linear combination of the negative- and positive-frequency solutions of the same equation defined at a later moment t. Schrödinger interpreted this fact as a creation of matter merely by the expansion of the Universe.
In more detail, the theory of particle creation in the expanding Universe was considered by Parker [49,50] (see also the review in [51]). This consideration was restricted to the quasi-Euclidean model with a flat 3-space (). The space–time of this model, as well as of the other Friedmann models, is not asymptotically flat. Therefore, as discussed in the end of Section 3, the standard concept of particles used in quantum field theory is not applicable.
To solve this problem, Parker elaborated the concept of the so-called adiabatic particles. For this purpose, the solution of Equation (56) was searched in the form of WKB-like approximation including some unknown function, which was next determined from the demand that the number of created particles and of its derivatives of several first orders would take the minimum values. The creation rate of scalar particles defined in this way in the present epoch of the Universe’s evolution was calculated and found to be negligibly small. A similar approach was applied to the effect of creation of spinor particles in the expanding Universe with [52]. A simple model was proposed where the scalar particles described by the field equation with minimal coupling are created near the cosmological singularity with a black-body spectrum [53].
The separation of variables in Equation (56) for the quasi-Euclidean, closed and open models of the Universe [ in Equations (1) and (3)] was made in the form
where the dimensionless time variable is connected with the proper synchronous time t by , is the dimensionless momentum quantum number connected with the magnitude of the physical momentum by , is the collective index, and the explicit expressions for the functions in terms of the associated Legendre polynomials and spherical harmonics in spaces with were found in Refs. [54,55,56].
The substitution of Equation (57) into Equations (1) and (17) results in the following equation for the functions :
where
For the dimensionless momentum varies from 0 to ∞, and for , it holds .
It is seen that Equation (58) describes the oscillator with a variable frequency like it was for a scalar field interacting with the nonstationary electric field [compare with Equation (19)]. In this case, the role of the electric field is played by the time-dependent scale factor of the Universe. Equation (58) takes the most simple form for the scalar field with conformal coupling , which is physically the most natural generalization of the Klein–Fock–Gordon equation in curved space–time [47,48]. The point is that the massless particles are not characterized by the parameter with a dimension of length and, thus, the corresponding field equation must be invariant with respect to the conformal transformations. Because of this, we consider Equations (56) and (58) with . As a result, the function satisfies the following equation:
where
An important difference in the scale factor of the expanding Universe from the vector potential of an external field is that does not become constant at any , which means that the space–time of the Universe does not become static. In this situation, the corpuscular interpretation of the field can be performed at some moment by imposing the initial conditions on the solutions of Equation (60):
and defining the positive- and negative-frequency solutions of Equation (56) as
Similar to the case of the nonstationary electric field, the functions lose the meaning of the negative- and positive-frequency solutions at a later moment .
The field operator of the complex scalar field is defined similarly to Equation (22):
where the measure on the set of quantum numbers is different for different values of :
Then, the vacuum state at the moment is defined as
From the above, it becomes clear that it is not possible to introduce the universal concept of particles in the expanding space–time of the Friedmann Universe. It is possible, however, to define the quasiparticles depending on time like it was done in Section 3 for the case of a nonstationary electric field using the method of the diagonalization of the Hamiltonian of a quantized field. Such an approach was suggested in Refs. [57,58] as an alternative to the adiabatic particles introduced in Refs. [49,50,51].
It is important, however, that the stress–energy tensor and respective Hamiltonian of the quantized scalar field satisfying Equation (56) with should be obtained by the variation in the action not with respect to the field , but with respect to the metrical tensor . This is the so-called metrical stress–energy tensor [59]. As a result, the metrical Hamiltonian of the scalar field in the space–time of the expanding Universe takes the following form:
After a substitution of Equation (64) in Equation (67), using the properties of functions (62), one obtains [60,61]
where and the coefficients and are expressed via the solutions of Equation (60) as
From Equation (70), it is seen that in fact depends on and does not depend on l and m, whereas depends also on m. The quantity represents the adiabatic invariant of the oscillator (60) and (61). From Equation (62), it follows that
i.e., the Hamiltonian (68) takes the diagonal form at the initial moment :
in perfect analogy to Equation (28) obtained for the case of an electric field.
Similar to the case of a nonstationary electric field, at any moment, the Hamiltonian (68) can be diagonalized by the canonical Bogoliubov transformations:
For this purpose, the coefficients and should be chosen as
Substituting Equation (73) with the coefficients (73) in Equation (68), one finds that the Hamiltonian of the scalar in the Friedmann Universe takes the following diagonal form:
at any moment .
The annihilation operators for quasiparticles and antiquasiparticles give the possibility to define the time-dependent vacuum state by the following equation:
which is similar to Equation (33) in the case of a nonstationary electric field. It is evident that
Next, one can define the number of quasiparticle pairs created from the vacuum state during the time interval from to in the unit space volume:
where
For the calculation of the number of created scalar particles, it is reasonable to put and impose on the scale factor the requirement of smoothness at the initial moment . This requirement does not contradict to the fact that at the point , there was the cosmological singularity where the invariants of the curvature tensor become infinitely large.
The typical scale factors used in the Friedmann cosmological models have the form ; see, for instance, Equation (8), where for dust-like matter . In the vicinity of the cosmological singularity, matter is in the radiation-dominated state . In this case, .
The calculations show that in the epoch the number of quasiparticle pairs (78) created in the unit volume does not depend on the value of q [60,62]:
An independence of the result (79) on time means that the decrease in the quasiparticle density due to the Universe’s expansion is compensated for by the creation of new quasiparticles.
In the epoch , for the radiation-dominated equation of state , one obtains [62]
It was shown [62] that, for , the similar result
holds for any q satisfying the inequalities .
The corresponding results have been obtained also for the energy density of created pairs (see Refs. [60,62] and the review [61]).
The creation of spinor particles in the space–time of the expanding Universe can be considered in perfect analogy with the scalar case, although the mathematical formalism becomes more involved. Thus, the general covariant generalization of the Dirac equation takes the form
where is the covariant derivative of a bispinor in the Riemannian space–time and is the 4-vector relative to the general coordinate transformations, which is expressed via the standard Dirac -matrices and the tetrad as
An important characteristic feature of Equation (82) is that in the limiting case , it becomes invariant under the conformal transformations with no additional modifications.
The separation of the variables in Equation (82) for the space–time (1) was performed in Refs. [55,63]. This results in the oscillator equation for the time-dependent functions :
where is defined in Equation (61). It is seen that although, physically, the space–time of the expanding Universe has little in common with the nonstationary electric field considered in Section 3, mathematically, Equation (84) is similar to Equation (39). In doing so, the mass of a spinor field in Equation (84) plays the same role as the electric charge in Equation (39), whereas the scale factor of the Universe a is akin to the vector potential .
The positive- and negative-frequency solutions of Equation (84) at the moment are defined by the following initial conditions [61]:
It holds also that
Now, the operator of the spinor field can be written in the form
where the collective index J includes four quantum numbers . In the case it holds that , , for one has , , and in both cases, , .
The vacuum state at the moment is defned by Equation (66). Substituting Equation (87) in the Hamiltonian of the spinor field
one obtains it in the same form as in Equation (24), but with the coefficients and expressed via the solutions of Equation (84):
These coefficients satisfy the initial conditions (70). As a consequence, at the moment , the Hamiltonian takes the diagonal form. At any moment, the Hamiltonian of the spinor field can be diagonalized by the Bogoliubov transformations:
which preserve the anticommutation relations for the creation and annihilation operators.
The Hamiltonian takes the diagonal form (74) at any moment if the Bogoliubov coefficients are defined as
The number of spinor quasiparticle pairs created in the unit space volume is given by [63]
where , and
It is notable that that the geometric nature of the spinor field reveals itself by the presence of in the measure of integration (93).
By using Equations (90), (91), and (93), one can calculate the number of spinor quasiparticles created at different epochs of the Universe’s evolution for the scale factors of power type . Thus, for , in the case , it holds [64] that
From the comparison of Equations (79) and (94), it is seen that . The additional terms which appear for are much smaller than (94).
For the epoch , the density of the created spinor quasiparticles is expressed as [61]
where for the radiation-dominated matter , the coefficient is equal to .
As is seen from the above, in the nonstationary curved space–time, the concept of particle loses its unique meaning. The effect of particle creation takes place with any concept of a particle but, for instance, the number of created adiabatic particles may differ from the number of quasiparticles defined by the method of the diagonalization of the Hamiltonian by means of the Bogoliubov transformations. The covariant quantity describing the quantum effects in the nonstationary space–time of cosmological models is the renormalized vacuum expectation value of the stress–energy tensor of quantized fields. This quantity includes the contributions of both the particle creation and vacuum polarization (see the monographs [27,28,29,30,31] for the obtained results).
5. The Role of Particle Creation in the Transition from Inflationary to Radiation-Dominated Epochs and Further Developments
As discussed in Section 2 and Section 4, at the radiation-dominated stage of its evolution the Friedmann Universe is described by the power-type scale factor . This result is obtained by solving the classical Einstein equations, and it does not take into account the quantum effects. However, the extension of the radiation-dominated scale factor down to the Planck time s creates serious problems. One of them is the following. Calculations show that, at the Planck time, the size of the Universe was cm, i.e., it was by almost 30 orders of magnitude larger than the Planck length cm traveled by light during .
From this it follows that if the radiation scale factor were valid down to , at the Universe would comprise of about causally disconnected domains. No evidence, however, was found regarding differences in the temperature of relic radiation received from different directions in the sky. Thus, the initial expansion of the Universe happened much faster than it is predicted by the power-type law. This inconsistency was called the horizon problem.
As noted in the end of Section 4, the covariant description of the vacuum quantum effects in curved space–time is provided by the renormalized vacuum expectation value of the stress–energy tensor of quantized matter fields. In Refs. [65,66] published in the beginning of 1980, this quantity was considered a single source of curved space–time of the Universe. For this purpose, the self-consistent Einstein equations with no cosmological term,
have been solved and the de Sitter solutions were obtained. For instance, for a stress–energy tensor of massless scalar field in the closed Friedmann model, the solution of Equation (96) is
i.e., for , the Universe’s expansion goes on exponentially fast. The comparison of Equation (97) with Equation (13) shows that the vacuum stress–energy tensor of the quantized scalar field plays the same role as the cosmological term in Einstein’s equations (4) with . In Ref. [66], it was shown that under the impact of the creation of scalarons and their subsequent decay into standard particles the exponentially fast de Sitter expansion of the Universe passes into the power-type expansion of the radiation-dominated stage of its evolution.
In 1981, another approach to the understanding of the exponentially fast expansion of the Universe near the cosmological singularity was suggested, which was called inflation [67]. This approach introduces the minimally coupled classical scalar field called the inflaton field with the following Lagrangian:
The corresponding Klein–Fock–Gordon equation in the space–time with metric (1) is
In the simplest case of the quasi-Euclidean model , the second equality in Equation (5) with is
where the space–time is determined by the energy density of the inflaton field:
According to Ref. [68], at the inflationary stage, the second term on the left-hand side of Equation (99) is much larger than the first one and the term in Equation (101) is much larger than . As a result, the scale factor found from Equations (100) and (101) takes the following quasi exponential form:
In subsequent years, many papers were published devoted to different versions of the inflationary cosmology (see, e.g., Refs. [69,70,71,72] and the monographs [73,74]).
The model of inflation has inspired a renewed interest in the effect of particle creation in the nonstationary external fields and in the space–time of the expanding Universe. The point is that at the end of the inflationary stage of the Universe’s evolution, the energy density becomes very low and the inflaton field oscillates near the minimum of its potential [in Equation (98), the simplest potential is chosen]. The standard elementary particles were created during this period, which was called the process of reheating after inflation [73,75].
The theory of the process of reheating is based on the effect of the exponential growth of the number of particle–antiparticle pairs created from vacuum by the time-periodic field with some momenta belonging to the instability zones of the Klein–Fock–Gordon equation (see Section 3). In this case, the role of a periodic electric field is played by the oscillating inflaton field [76,77]. The theory of reheating after inflation has been elaborated on by many authors (see, e.g., Refs. [78,79,80,81,82,83,84,85,86,87]). The main features of this theory are summarized in Ref. [68].
Over the last 25 years, the effect of particle creation in the expanding Universe continued to attract the considerable attention of experts in quantum field theory and cosmology. Here, we mention only several papers devoted to this subject. Thus, in Ref. [88], the effect of the creation of light particles called moduli during and after inflation was investigated not only numerically but also analytically. It was shown that the dominant contribution to the particle creation is given by the long-wavelength fluctuations of light scalar fields generated during inflation.
In Ref. [89], the complex WKB approximation technique was used to study the thermal particle creation in both the black holes and in the space–time of the expanding Universe. According to the results obtained, the temperature of the particle spectrum is determined by the slope of the scale factor of the cosmological model.
The effect of particle creation in the anisotropic expanding Universe (see the pioneer Ref. [90]) was further considered in Ref. [91] using the formalism of squeezed vacuum states for a minimally coupled scalar field. The semiclassical Einstein equations of the form of Equation (96), but in the anisotropic case, were discussed. Note that Ref. [90] presented the powerful regularization method for the vacuum stress–energy tensor and derived the dynamical equations for the nonstationary Bogoliubov coefficients, which were actively used in both anisotropic and isotropic spaces.
In Ref. [92], the above Equations (81) and (95) were used to describe the creation of superheavy scalar and spinor particles, the decay of which could explain the baryon number of the Universe and the nature of cold dark matter. Note that previously the creation of superheavy particles as the constituents of dark matter in various models of inflation was analyzed in Ref. [93]. It was hypothesized that the decay products of the superheavy constituents of cold dark matter are observed as the cosmic rays of ultra-high energy [92].
The method of the diagonalization of the Hamiltonian of a quantized massless scalar field with minimal coupling was used in Ref. [94] to calculate the particle creation rate in the expanding Universe of the quasi-Euclidean type. It was assumed that the background matter is described by the equation of state of a perfect fluid, which may violate the strong energy condition . According to the results obtained, the particle creation rate decreases with time if the strong energy condition is satisfied and increases otherwise.
The creation of dark matter particles, which interact only gravitationally, in the expanding Universe of the quasi-Euclidean type was investigated in Ref. [95]. In the suggested model, the real scalar field with an arbitrary coupling , the quanta of which can be considered the candidates for dark matter particles, enters into the Lagrangian density along with the inflaton field, but does not interact with it. By calculating the particle creation rate from the adiabatic vacuum [28] during the transition period from inflation to reheating, it was shown that heavy scalar particles of this kind can be effectively produced if their mass is of the order of or less than the mass of an inflaton field.
The method of Hamiltonian diagonalization discussed in Section 3 and Section 4 was also applied in Ref. [96] to describe the creation of superheavy particles conformally coupled to gravity in the model of quintessential inflation [97]. It was argued [96] that the subsequent decay of these particles leads to the formation of relativistic plasma and eventually results in the universally accepted picture of the hot universe.
Similar to the creation of particles in a nonstationary electric field, which has a condensed matter analogy with quasiparticles in graphene, there are the condensed matter analogies to the particle creation in cosmology. Recently, it was found [98] that the expanding Universe resembles the ultracold quantum fluid of light, where a spatial coordinate plays the role of time. According to the authors, they observed the acoustic peaks in the power spectrum, which is in quantitative agreement with theoretical predictions. The observed spectrum was compared with that of the cosmic microwave background power spectrum. Another possibility for the simulation of the process of particle creation in the expanding Universe in the laboratory by means of ultra-cold atoms in Raman optical lattices was considered in Ref. [99].
Some more recent publications devoted to the effect of particle creation in the expanding Universe are reflected on in the review [100].
6. Discussion
Herein, we have considered the prediction of the Universe’s expansion made by Alexander Friedmann a century ago that holds the greatest importance and interest today. Particular attention has been given to the way in which this discovery was made. According to the adduced arguments, it is not an accident that such a breakthrough result was obtained by a mathematician. Several outstanding physicists, including the great Einstein, worked on the same subject, but they were tied by some additional considerations of a methodological character implying the static character of our Universe.
Quite to the contrary, Friedmann restricted himself only to the necessary minimum assumptions, such as the homogeneity and isotropy of space, and searched for the formal mathematical consequences following from the fundamental Einstein equations with no prejudice. In doing so, Friedmann discovered that typical cosmological solutions of Einstein equations describe the expanding Universe. This example shows that the mathematical formalisms of fundamental physical theories, such as the general theory of relativity, may, in some sense, be more clever than their creators and again raises the question raised by Wigner about the unreasonable effectiveness of mathematics in natural sciences [25].
The importance of Friedmann’s prediction of the Universe’s expansion is difficult to overestimate. After a comprehensive experimental confirmation, the concept of the expanding Universe laid the groundwork for the modern picture of the world. As substantiated in Ref. [101], this fact gives grounds to include the name of Friedmann along with the names of Ptolemy, Copernicus, and Newton, who created the scientific pictures of the Universe accepted in previous epochs.
The expansion of the Universe leads to many outstanding consequences and one of them, foreshadowed by Erwin Schrödinger, is the creation of particle–antiparticle pairs from the vacuum of quantized fields. According to a comparison performed in Section 3 and Section 4, the effect of the creation of particles in the expanding Universe is mathematically analogous to that in the nonstationary electric field in spite of quite different physical situations in both cases.
The main results obtained in the literature on the creation of particles in the expanding Universe by the method of Hamiltonian diagonalization and other methods show that this effect played an important role at the very early stages of its evolution and, especially, during the transition period between the inflationary and radiation-dominated epochs. According to the results obtained, the effect of pair creation could also contribute to the formation of dark matter.
7. Conclusions
To conclude, in this brief review, devoted to the one hundredth anniversary of Alexander Friedmann’s prediction of the Universe’s expansion, we have considered several facts of his biography which were helpful for making this outstanding discovery. The results published by Friedmann in 1922 [4] and 1924 [5] were presented above with emphasis on the role of mathematics in their obtainment. Some historical facts, including the dispute with Albert Einstein, and further developments of the Friedmann cosmology, are elucidated.
The Universe’s expansion leads to the quantum creation from a vacuum of particle–antiparticle pairs. This effect was discussed above in close connection with a more familiar effect of pair creation by the nonstationary electric field. The comparison studies of these two effects by the method of Hamiltonian diagonalization was performed and both the similarities and distinctions between them were analyzed. Several results for the numbers of scalar and spinor pairs created at different stages of the Universe’s evolution are presented. Special attention was paid to the inflationary stage of the Universe’s evolution and to the transition period to the epoch of the radiation-dominated Universe, where the effect of particle creation was of primary importance for the formation of relativistic plasma and cold dark matter.
By and large, the prediction of the Universe’s expansion made by Alexander Friedmann laid the foundation for the development of modern cosmology during the last century and offered possibilities for the description of vacuum quantum effects in a nonstationary space–time by the formalism of quantum field theory in the presence of external fields.
Funding
This work was partially funded by the Ministry of Science and Higher Education of the Russian Federation (“The World-Class Research Center: Advanced Digital Technologies”, contract No. 075-15-2022-311 dated 20 April 2022). It was also partially carried out in accordance with the Strategic Academic Leadership Program “Priority 2030” of the Kazan Federal University.
Data Availability Statement
All references to the used data are contained in the text.
Acknowledgments
The author is grateful to G. L. Klimchitskaya for helpful discussions.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Newton, I. The Mathematical Principles of Natural Philosophy; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Einstein, A. Zur allgemeinen Relativitätstheorie. Sitzungsber. Königlich Preuss. Akad. Wiss. (Berlin) 1915, 44, 778–786, Translated: On the general theory of relativity. In The Collected Papers of Albert Einstein. Volume 6: The Berlin Years: Writings, 1914–1917 (English Translation Supplement); Klein, M.J., Kox, A.J., Schulman, R., Eds.; Princeton University Press: Princeton, NJ, USA, 1997; pp. 98–106. [Google Scholar]
- Einstein, A. Kosmologische Betrachtungen zur allgemeinen Relativitätstheorie. Sitzungsber. Königlich Preuss. Akad. Wiss. (Berlin) 1917, 6, 142–152, Translated: Cosmological considerations in the general theory of relativity. In The Collected Papers of Albert Einstein. Volume 6: The Berlin Years: Writings, 1914-1917 (English Translation Supplement); Klein, M.J., Kox, A.J., Schulman, R., Eds.; Princeton University Press: Princeton, NJ, USA, 1997; pp. 421–432. [Google Scholar]
- Friedmann, A.A. Über die Krümmung des Raumes. Z. Phys. 1922, 10, 377–386. [Google Scholar] [CrossRef]
- Friedmann, A.A. Über die Möglichkeit einer Welt mit konstanter negativer Krümmung des Raumes. Z. Phys. 1924, 21, 326–332. [Google Scholar] [CrossRef]
- Schrödinger, E. The proper vibrations of the expanding universe. Physica 1939, 6, 899–912. [Google Scholar] [CrossRef]
- Frenkel’, V.Y. Aleksandr Aleksandrovich Fridman (Friedmann): A biographical essay. Uspekhi Fiz. Nauk 1988, 155, 481–516, Translated: Sov. Phys. Usp. 1988, 31, 645–665. [Google Scholar] [CrossRef]
- Tropp, E.A.; Frenkel, V.Y.; Chernin, A.D. Alexander A. Friedmann: The Man Who Made the Universe Expand; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Tamarkine, J.; Friedmann, A.A. Sur les congruences du second degré et les nombres de Bernoulli. Math. Ann. 1906, 62, 409–412. [Google Scholar] [CrossRef][Green Version]
- de Sitter, W. On Einstein’s theory of gravitation and its astronomical consequences. First paper. Mon. Not. R. Astron. Soc. 1916, 76, 699–728. [Google Scholar] [CrossRef]
- Landau, E.M.; Lifshitz, E.M. The Classical Theory of Fields; Pergamon: Oxford, UK, 1971. [Google Scholar]
- Bonnor, W.B. The instability of the Einstein universe. Mon. Not. R. Astron. Soc. 1955, 115, 310–322. [Google Scholar] [CrossRef][Green Version]
- Zeldovich, Y.B.; Novikov, I.D. The Structure and Evolution of the Universe; University of Chicago Press: Chicago, IL, USA, 1983. [Google Scholar]
- Einstein, A. Bemerkung zu der Arbeit von A. Friedmann “Über die Krümmung des Raumes”. Z. Phys. 1922, 11, 326, Translated: Comment on A. Friedman’s paper: “On the curvature of space”. In The Collected Papers of Albert Einstein. Volume 13: The Berlin Years: & Correspondence, January 1922–March 1923 (English Translation Supplement); Kormos Buchwald, D.; Illy, J.; Rosenkranz, Z.; Sauer T., Eds.; Princeton University Press: Princeton, NJ, USA, 2013; pp. 271–272. [Google Scholar] [CrossRef]
- Einstein, A. Notiz zu der Arbeit von A. Friedmann “Über die Krümmung des Raumes”. Z. Phys. 1923, 16, 228, Translated: Note to the paper by A. Friedmann “On the curvature of space”. In The Collected Papers of Albert Einstein. Volume 14: The Berlin Years: & Correspondence, April 1923–May 1925 (English Translation Supplement); Kormos Buchwald, D.; Illy, J.; Rosenkranz, Z.; Sauer T., Eds.; Princeton University Press: Princeton, NJ, USA, 2015; p. 47. [Google Scholar] [CrossRef]
- Slipher, V.M. The radial velocity of the Andromeda Nebula. Lowell Observat. Bull. 1913, 2, 56–57. [Google Scholar]
- Lemaître, G. Un univers homogène de masse constante et de rayon croissant, rendant compte de la vitesse radiale des nébuleuses extra-galactiques. Ann. Soc. Sci. Brux. A 1927, 47, 49–59. [Google Scholar]
- Hubble, E. A relation between distance and radial velocity among extra-galactic nebulae. Proc. Nat. Acad. Sci. USA 1929, 15, 168–173. [Google Scholar] [CrossRef]
- Hubble, E.P. A spiral nebula as a stellar system, Messier 31. Astrophys. J. 1929, 69, 103–158. [Google Scholar] [CrossRef]
- Robertson, H.P. Kinematics and world structure. Astrophys. J. 1935, 82, 284–301. [Google Scholar] [CrossRef]
- Walker, A.G. On Milne’s theory of world-structure. Proc. Lond. Math. Soc. 1937, 42, 90–127. [Google Scholar] [CrossRef]
- Gamow, G. Expanding universe and the origin of elements. Phys. Rev. 1946, 70, 572–573. [Google Scholar] [CrossRef]
- Alpher, R.A.; Herman, R.C. Evolution of the Universe. Nature 1948, 162, 774–775. [Google Scholar] [CrossRef]
- Penzias, A.A.; Wilson, R.W. A Measurement of Excess Antenna Temperature at 4080 Mc/s. Astrophys. J. Lett. 1965, 142, 419–421. [Google Scholar] [CrossRef]
- Wigner, E.P. The unreasonable effectiveness of mathematics in the natural sciences. Comm. Pure Appl. Math. 1960, 13, 1–14. [Google Scholar] [CrossRef]
- Friedmann, A.A. Mir kak Prostranstvo i Vremya; Academia: Petersburg, Russia, 1923; Translated The World as Space and Time; Minkowski Institute Press: Montreal, QC, Canada, 2014. [Google Scholar]
- Grib, A.A.; Mamayev, S.G.; Mostepanenko, V.M. Kvantovye Effekty v Intensivnykh Vneshnikh Polyakh; Atomizdat: Moscow, Russia, 1980; Translated: Vacuum Quantum Effects in Strong Fields; Friedmann Laboratory Publishing: St. Petersburg, Russia, 1994. [Google Scholar]
- Birrell, N.D.; Davies, P.C.D. Quantum Fields in Curved Space; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Fulling, S.A. Aspects of Quantum Field Theory in Curved Space-Time; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Mukhanov, V.; Winitzki, S. Introduction to Quantum Effects in Gravity; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Parker, L.; Toms, D. Quantum Field Theory in Curved Spacetime: Quantized Fields and Gravity; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Nikishov, A.I. Barrier scattering in field theory removal of Klein paradox. Nucl. Phys. B 1970, 21, 346–358. [Google Scholar] [CrossRef]
- Brezin, E.; Itzykson, C. Pair production in vacuum by an alternating field. Phys. Rev. D 1970, 2, 1191–1198. [Google Scholar] [CrossRef]
- Grib, V.M.; Mostepanenko, V.M.; Frolov, V.M. Particle creation from vacuum by a homogeneous electric field in the canonical formalism. Teor. Matem. Fiz. 1972, 13, 377–390, Translated: Theor. Math. Phys. 1972, 13, 1207–1217. [Google Scholar] [CrossRef]
- Popov, V.S. Pair production in a variable and homogeneous electric field as an oscillator problem. Zh. Eksp. Teor. Fiz. 1972, 62, 1248–1262, Translated: Sov. Phys. JETP 1972, 35, 659–666. [Google Scholar]
- Schweber, S.S. Introduction to Relativistic Quantum Field Theory; Dover Publications: New York, NY, USA, 2005. [Google Scholar]
- Schwinger, J. On gauge invariance and vacuum polarization. Phys. Rev. 1951, 82, 664–679. [Google Scholar] [CrossRef]
- Schwinger, J. The theory of quantized fields. V. Phys. Rev. 1954, 93, 615–626. [Google Scholar] [CrossRef]
- Narozhnyi, N.B.; Nikishov, A.I. Pair production by a periodic electric field. Zh. Eksp. Teor. Fiz. 1973, 65, 862–874, Translated: Sov. Phys. JETP 1974, 38, 427–432. [Google Scholar]
- Mostepanenko, V.M.; Frolov, V.M. Production of particles from vacuum by a uniform electric-field with periodic time-dependence. Yad. Fiz. 1974, 19, 885–896, Translated: Sov. J. Nucl. Phys. 1974, 19 451–456. [Google Scholar]
- Allor, D.; Cohen, T.D.; McGady, D.A. Schwinger mechanism and graphene. Phys. Rev. D 2008, 78, 096009. [Google Scholar] [CrossRef]
- Beneventano, C.G.; Giacconi, P.; Santangelo, E.M.; Soldati, R. Planar QED at finite temperature and density: Hall conductivity, Berry’s phases and minimal conductivity of graphene. J. Phys. A 2009, 42, 275401. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Creation of quasiparticles in graphene by a time-dependent electric field. Phys. Rev. D 2013, 87, 125011. [Google Scholar] [CrossRef]
- Akal, I.; Egger, R.; Müller, C.; Villarba-Chávez, S. Low-dimensional approach to pair production in an oscillating electric field: Application to bandgap graphene layers. Phys. Rev. D 2016, 93, 116006. [Google Scholar] [CrossRef]
- Akal, I.; Egger, R.; Müller, C.; Villarba-Chávez, S. Simulating dynamically assisted production of Dirac pairs in gapped graphene monolayers. Phys. Rev. D 2019, 99, 016025. [Google Scholar] [CrossRef]
- Golub, A.; Egger, R.; Müller, C.; Villarba-Chávez, S. Dimensionality-Driven Photoproduction of Massive Dirac Pairs near Threshold in Gapped Graphene Monolayers. Phys. Rev. Lett. 2020, 124, 110403. [Google Scholar] [CrossRef]
- Gürsey, F. Reformulation of general relativity in accordance with Mach’s principle. Ann. Phys. 1963, 24, 211–242. [Google Scholar] [CrossRef]
- Penrose, R. Conformal treatment of infinity. In Relativity, Groups, and Topology; DeWitt, B.S., Ed.; Gordon and Breach: New York, NY, USA, 1964. [Google Scholar]
- Parker, L. Particle Creation in Expanding Universes. Phys. Rev. Lett. 1968, 21, 562–564. [Google Scholar] [CrossRef]
- Parker, L. Quantized fields and particle creation in expanding universes. I. Phys. Rev. 1969, 183, 1057–1068. [Google Scholar] [CrossRef]
- Parker, L. Particle creation and particle number in an expanding universe. J. Phys. A Math. Theor. 2012, 45, 374023. [Google Scholar] [CrossRef]
- Parker, L. Quantized fields and particle creation in expanding universes. II. Phys. Rev. D 1971, 3, 346–356. [Google Scholar] [CrossRef]
- Parker, L. Thermal radiation produced by the expansion of the universe. Nature 1976, 261, 20–23. [Google Scholar] [CrossRef]
- Grib, A.A.; Levitskii, B.A.; Mostepanenko, V.M. Particle creation from vacuum by a nonstationary gravitational field in the canonical formalism. Teor. Matem. Fiz. 1974, 19, 59–75, Translated: Theor. Math. Phys. 1974, 19, 349–361. [Google Scholar] [CrossRef]
- Levitskii, B.A.; Mostepanenko, V.M.; Frolov, V.M. The properties of basis functions of expansions invariant relative to the group O(4). Dokl. USSR 1975, 220, 61–64, Translated: Sov. Phys. Dokl. 1975, 20, 29–30. [Google Scholar]
- Parker, L.; Fulling, S.A. Adiabatic regularization of the energy-momentum tensor of a quantized field in homogeneous spaces. Phys. Rev. D 1974, 9, 341–354. [Google Scholar] [CrossRef]
- Grib, A.A.; Mamayev, S.G. On field theory in Friedmann space. Yad. Fiz. 1969, 10, 1276–1281, Translated: Sov. J. Nucl. Phys. 1970, 10, 722–725. [Google Scholar]
- Grib, A.A.; Mamayev, S.G. Creation of matter in Friedmann model of the Universe. Yad. Fiz. 1971, 14, 800–805, Translated: Sov. J. Nucl. Phys. 1972, 14 450–452. [Google Scholar]
- Chernikov, N.A.; Tagirov, E.A. Quantum theory of scalar field in de Sitter space-time. Ann. Inst. H. Poincaré Phys. Théor. 1968, 9, 109–141. [Google Scholar]
- Grib, A.A.; Mamayev, S.G.; Mostepanenko, V.M. Particle creation from vacuum in homogeneous isotropic models of the Universe. Gen. Relat. Gravit. 1976, 7, 535–547. [Google Scholar] [CrossRef]
- Grib, A.A.; Mamayev, S.G.; Mostepanenko, V.M. Vacuum stress-energy tensor and particle creation in isotropic cosmological models. Fortschr. Der Phys. 1980, 28, 173–199. [Google Scholar] [CrossRef]
- Mamayev, S.G.; Mostepanenko, V.M.; Starobinskii, A.A. Particle creation from the vacuum near a homogeneous isotropic singularity. Zh. Eksp. Teor. Fiz. 1976, 70, 1577–1591, Translated: Sov. Phys. JETP 1976, 43, 823–830. [Google Scholar]
- Mamayev, S.G.; Mostepanenko, V.M.; Frolov, V.M. Production of fermion pairs by a nonstationary gravitational field. Yad. Fiz. 1976, 23, 1118–1127, Translated: Sov. J. Nucl. Phys. 1976, 23, 592–597. [Google Scholar]
- Mamayev, S.G.; Mostepanenko, V.M. Regularization of the fermion stress-energy tensor in isotropic models of the Universe. Phys. Lett. A 1978, 67, 165–168. [Google Scholar] [CrossRef]
- Mamayev, S.G.; Mostepanenko, V.M. Isotropic cosmological models determined by the vacuum quantum effects. Zh. Eksp. Teor. Fiz. 1980, 78, 20–27, Translated: Sov. Phys. JETP 1980, 51, 9–13. [Google Scholar]
- Starobinsky, A.A. A new type of isotropic cosmological models without singularity. Phys. Lett. A 1980, 91, 99–102. [Google Scholar] [CrossRef]
- Guth, A.H. Inflationary universe: A possible solution to the horizon and flatness problems. Phys. Rev. D 1981, 23, 347–356. [Google Scholar] [CrossRef]
- Kofman, L.; Linde, A.D.; Starobinsky, A.A. Towards the theory of reheating after inflation. Phys. Rev. D 1997, 56, 3258–3295. [Google Scholar] [CrossRef]
- Linde, A.D. A new inflationary universe scenario: A possible solution of the horizon, flatness, homogeneity, isotropy and primordial monopole problems. Phys. Lett. B 1982, 108, 389–393. [Google Scholar] [CrossRef]
- Guth, A.H.; Weinberg, E.J. Could the universe have recovered from a slow first-order phase transition? Nucl. Phys. B 1983, 212, 321–364. [Google Scholar] [CrossRef]
- Albrecht, A.; Steinhardt, P.J. Cosmology for Grand Unified Theories with Radiatively Induced Symmetry Breaking. Phys. Rev. Lett. 1982, 48, 1220–1223. [Google Scholar] [CrossRef]
- Linde, A.D. Chaotic inflation. Phys. Lett. B 1983, 129, 177–181. [Google Scholar] [CrossRef]
- Linde, A.D. Particle Physics and Inflationary Cosmology; Harwood: Chur, Switzerland, 1990. [Google Scholar]
- Guth, A.H. The Inflationary Universe: The Quest for a New Theory of Cosmic Origins; Basic Books: New York, NY, USA, 1997. [Google Scholar]
- Kofman, L.; Linde, A.; Starobinsky, A.A. Reheating after Inflation. Phys. Rev. Lett. 1994, 73, 3195–3198. [Google Scholar] [CrossRef]
- Dolgov, A.D.; Kirilova, D.P. On particle creation by a time-dependent scalar field. Yad. Fiz. 1990, 51, 273–282, Translated: Sov. J. Nucl. Phys. 1990, 51 172–177. [Google Scholar]
- Traschen, J.H.; Brandenberger, R.H. Particle production during out-of-equilibrium phase transitions. Phys. Rev. D 1990, 42, 2491–2504. [Google Scholar] [CrossRef] [PubMed]
- Boyanovsky, D.; de Vega, H.J.; Holman, R.; Lee, D.-S.; Singh, A. Dissipation via particle production in scalar field theories. Phys. Rev. D 1995, 51, 4419–4444. [Google Scholar] [CrossRef] [PubMed]
- Kaiser, D.I. Post-inflation reheating in an expanding universe. Phys. Rev. D 1996, 53, 1776–1783. [Google Scholar] [CrossRef] [PubMed]
- Fujisaki, H.; Kumekawa, K.; Yamaguchi, M.; Yoshimura, M. Particle production and dissipative cosmic field. Phys. Rev. D 1996, 53, 6805–6812. [Google Scholar] [CrossRef] [PubMed]
- Kasuya, S.; Kawasaki, M. Restriction to parametric resonant decay after inflation. Phys. Lett. B 1996, 388, 686–691. [Google Scholar] [CrossRef][Green Version]
- Son, D.T. Reheating and thermalization in a simple scalar model. Phys. Rev. D 1996, 54, 3745–3761. [Google Scholar] [CrossRef] [PubMed]
- Riotto, A.; Tkachev, I.I. Non-equilibrium symmetry restoration beyond one loop. Phys. Lett. B 1996, 385, 57–62. [Google Scholar] [CrossRef]
- Allahverdi, R.; Campbell, B.A. Cosmological reheating and self-interacting final state bosons. Phys. Lett. B 1997, 395, 169–177. [Google Scholar] [CrossRef]
- Prokopec, T.; Roos, T.G. Lattice study of classical inflaton decay. Phys. Rev. D 1997, 55, 3768–3775. [Google Scholar] [CrossRef]
- Khlebnikov, S.; Tkachev, I. Relic gravitational waves produced after preheating. Phys. Rev. D 1997, 56, 653–660. [Google Scholar] [CrossRef]
- Moss, I.G.; Graham, C. Particle production and reheating of the inflationary universe. Phys. Rev. D 2008, 78, 123526. [Google Scholar] [CrossRef]
- Felder, G.; Kofman, L.; Linde, A. Gravitational particle production and the moduli problem. JHEP 2000, 2000, 027. [Google Scholar] [CrossRef][Green Version]
- Biswas, S.; Shaw, A.; Misra, P. Particle production in expanding spacetime. Gen. Relat. Gravit. 2002, 34, 665–678. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B.; Starobinsky, A.A. Particle production and vacuum polarization in an anisotropic gravitational field. Zh. Eksp. Teor. Fiz. 1971, 61, 2161–2175, Translated: Sov. Phys. JETP 1972, 34, 1159–1166. [Google Scholar]
- Suresh, P.K. Particle creation in anisotropically expanding Universe. Int. J. Theor. Phys. 2005, 44, 645–654. [Google Scholar] [CrossRef][Green Version]
- Grib, A.A.; Pavlov, Y.V. Dark matter in the early Universe and the creation of visible particles. Gravit. Cosmol. 2005, 11, 119–122. [Google Scholar]
- Chung, D.J.H.; Crotty, P.; Kolb, E.W.; Riotto, A. Gravitational production of superheavy dark matter. Phys. Rev. D 2001, 64, 043503. [Google Scholar] [CrossRef]
- Batista, A.B.; Fabris, J.C.; Houndjo, S.J.M. Particle production in an expanding universe dominated by dark energy fluid. Gravit. Cosmol. 2008, 14, 140–146. [Google Scholar] [CrossRef]
- Ema, Y.; Nakayama, K.; Tanga, Y. Production of purely gravitational dark matter. JHEP 2018, 2018, 135. [Google Scholar] [CrossRef]
- de Haro, J.; Pan, S.; Aresté Saló, L. Understanding gravitational particle production in quintessential inflation. J. Cosmol. Astropart. Phys. 2019, 2019, 056. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Vilenkin, A. Quintessential inflation. Phys. Rev. D 1999, 59, 063505. [Google Scholar] [CrossRef]
- Steinhauer, J.; Abuzarli, M.; Aladjidi, T.; Bienaimé, T.; Piekarski, C.; Liu, W.; Giacobino, E.; Bramati, A.; Glorieux, Q. Analogue cosmological particle creation in an ultracold quantum fluid of light. Nat. Commun. 2022, 13, 2890. [Google Scholar] [CrossRef]
- Fulgado-Claudio, C.; Sánchez Velázquez, J.M.; Bermudez, A. Fermion production at the boundary of an expanding universe: A cold-atom gravitational analogue. Quantum 2023, 7, 1042. [Google Scholar] [CrossRef]
- Ford, L.H. Cosmological particle production: A review. Rep. Progr. Phys. 2021, 84, 116901. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Centenary of Alexander Friedmann’s prediction of the Universe expansion and the quantum vacuum. Physics 2022, 4, 981–994. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).