Abstract
In the framework of the analogous Hawking effect, we significantly improve our previous analysis of the master equation that encompasses very relevant physical systems, like Bose–Einstein condensates (BECs), dielectric media, and water. In particular, we are able to provide two significant improvements to the analysis. As our main result, we provide a complete set of connection formulas for both the subluminal and superluminal cases without resorting to suitable boundary conditions, first introduced by Corley, but simply on the grounds of a rigorous mathematical setting. Moreover, we provide an extension to the four-dimensional case, showing explicitly that, apart from obvious changes, adding transverse dimensions does not substantially modify the Hawking temperature in the dispersive case. Furthermore, an important class of exact solutions of the so-called reduced equation that governs the behavior of non-dispersive modes is also provided.
1. Introduction
We again consider analytical calculations for the analog Hawking effect by developing and deepening our analysis in [1,2,3]. In the dispersive case, one can find several papers dedicated to analytical calculations (see, e.g., the following (non-exhaustive) list of papers: [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27]), albeit not within a unified general theoretical framework. There are also several papers describing experiments for the analogous Hawking effect [28,29,30,31,32,33,34,35,36,37,38].
In [1,2,3], we took into account a fourth-order ordinary differential equation that allowed us to treat the analogous Hawking effect in condensed matter systems (Bose–Einstein condensates (BECs), dielectric media, and water) in a systematic way, as far as weak dispersion effects are considered. The weak dispersion parameter appears in the aforementioned master equation as the expansion parameter for the physical problem at hand. Strong dispersion effects, which, for example, may occur in some experimental settings, like those involving fiber optics (see, e.g., [36]), cannot be discussed in the same framework and are still beyond the possibility of a full analytical calculation. Moreover, the proposed models, from the theoretical point of view, are 2D, in the sense that two spatial dimensions are suppressed. The latter simplification is, in some sense, natural, as providing robust theoretical models for a non-trivial physical situation is simpler in 2D.
In the present analysis, still in the framework of weak dispersive effects, we are able to provide, in a rigorous way, a complete set of connection formulas on purely mathematical grounds, thus complementing and completing, on the mathematical side, our analysis in [1,2,3]. In particular, we show that in place of the connection formulas originally introduced by Corley [5] using the so-called Corley’s diagrams (see, e.g., [1,2]) and then further developed in [11] for a specific and elementary toy model (the so-called Corley model), one can provide a set of rigorously obtained connection formulas that are at the root of the dispersive Hawking effect and are substantially associated with the behavior of the solutions near the turning point. This represents a fundamental contribution to the existing literature, as the analysis for the near-turning-point region we discussed in [1,2] is universal, i.e., holds for any physical model quoted above, being the same in form as the near-horizon equation governing the physical process near the turning point.
We will refer to the following papers from the mathematical literature: Ref. [39] for the subluminal case and [40,41] for the superluminal one. We will show rigorously that, as a consequence of the aforementioned connection formulas and due to the structure of the Stokes matrices that allow us to transition from a basis for modes inside the black hole region to a basis for modes in the exterior region, there is a mode (which corresponds to the trivial, constant solution of (5)) that decouples from the other three in the near-horizon region and then remains decoupled in a 2D framework, at least in the leading order in the weak dispersion parameter characterizing each model, and a blackbody spectrum is ensured both for the Hawking particle and for the Hawking partner. One can also obtain exact solutions for the near-turning-point equation, which can be expressed in terms of the generalized hypergeometric functions .
Then, we will also provide insights into the contribution of transverse dimensions, albeit in very simple but significant geometrical situations. We will show that transverse dimensions do not affect the main picture of the 2D case and leave the temperature of the Hawking effect unaltered. Still, of course, the possibility of obtaining and then detecting particles traveling with a non-vanishing transverse wavenumber is gained, and this can shed light on realistic experimental situations (occurring, e.g., by using laser pulses in dielectric media).
A further important contribution appearing in this paper is the calculation, for specific but physically meaningful velocity profiles, of exact solutions of the reduced equation governing non-dispersive modes in the WKB approximation. This is also an important improvement to our general approach, as, even in the WKB approximation, at the leading order in the weak dispersion parameter , one would be forced to find exact solutions of the reduced equation to provide solutions for non-dispersive modes, to be considered together with the leading-order WKB solutions that can be obtained for the dispersive modes. This improvement is important, as it provides us with a further neat improvement for analytical calculations of physical amplitudes for the Hawking phenomenon.
2. The Master Equation: An Orr–Sommerfeld-Type Fourth-Order Equation
As discussed in [1,2,3], three significant cases of wave equations in dispersive analog gravity can be studied using the following master equation:
where the upper sign occurs in the case of subluminal dispersion and the lower one in the case of superluminal dispersion. The latter case is considered in Nishimoto’s works (see, e.g., [40,41,42] and references therein). This fourth-order equation can be obtained by suitably manipulating the equations of motion in the Corley model in the case of dielectric media [1] and also in the case of a BEC and water [2], providing a unified framework for a systematic study of the analogous Hawking effect in weakly dispersive media and allowing a thermal spectrum to be found in all the cases at hand in the same limit, as expected.
A basic assumption of the present method is the analyticity of the coefficients in the following sense:
where is the parameter expressing the presence of weak dispersive effects. Solutions of
define the turning points (TPs) of the equation, as usual (cf., e.g., [41]), and one obtains the so-called reduced equation as :
In [41], it is assumed that the reduced equation displays a Fuchsian singularity at the TP (nothing actually prevents the general equation in itself from admitting regular behavior).
It can be shown [41] that near the TP , the original equation is replaced by the fourth-order differential equation
where, as discussed in [1], represents the (rescaled [1]) wavefunction in the so-called near-horizon approximation to then be matched in the so-called linear region, with WKB solutions that hold far from the turning point. We refer to [1] for further details. In (5), the upper sign is for the subluminal case, and the lower one is for the superluminal case, and
and
As we discussed in [1,2], Equation (5) is universal in form and is at the root of the analogous Hawking effect in dispersive media, as far as they are governed by the above Orr–Sommerfeld-like equation. In the following, without loss of generality, we limit ourselves to the case of a single TP (monotonic profile for the velocity field or the refractive index in the dielectric case), identified with .
3. Exact Solutions of the Near-Horizon Equation (5) and Connection Formulas
The problem concerning Equation (5) consists of not only finding solutions to the equation itself but also describing complete bases of solutions in different regions of the complex space and relating these bases (connection formulas). We point out that there exists a further connection problem, represented by the matching of solutions in the so-called linear region around the turning point, where both the near-horizon solutions and the WKB solutions are defined. This second problem (sometimes called the central connection problem [41]) can be solved very simply in the case where suitable bases of solutions in the near-horizon equation are assumed (see [41] and, for specific applications, [1,2]). The former problem (sometimes called the lateral connection problem [41]) is more difficult and is associated with the presence of the Stokes phenomenon, which does not allow us to find diagonal connection matrices. We will comment further on the Stokes phenomenon in the following.
Solutions to Equation (5) are found, e.g., by adopting the method of the Laplace transform, as discussed in [41] for the superluminal case, by means of Laplace integrals:
with a suitable choice of paths in the complex t-plane. It must be stressed that such solutions are regular at the TP and admit a series expansion there (see [40]). Of course, there is also a constant solution, which appears to be a Dirac delta in the space of the Laplace transform. This further solution is fundamental to obtaining a complete basis for the scattering problem, also in the region near the TP (i.e., near the horizon) [1]. Solutions of Equation (5) will be indexed by NH (near-horizon solutions, from a physical point of view).
3.1. The Subluminal Case
To be more specific, we first explore the subluminal case, i.e., the case where the plus sign appears both in (5) and in (8). We point out that it is possible to find exact solutions of Equation (5). For example, we can find the general solutions using Mathematica, and the result is
The generalized hypergeometric functions are analytic functions everywhere. They correspond, e.g., to the Airy functions one deals with in standard nonrelativistic quantum mechanics in a neighborhood of turning points, where the semiclassical WKB solutions fail. Even if they are analytic, their asymptotic expansion involves functions that are not analytic, and the Stokes phenomenon emerges. Furthermore, the main problem with these solutions is the fact that they are not in a simple relation with the physical modes involved in the problem in the following sense. As we recalled in the previous discussion, one has to match, in the linear region, WKB solutions and near-horizon solutions (9). This matching requires considering asymptotic expansion as (i.e., at the turning point) with asymptotic expansions of (9) as . The point is that, even if the asymptotic expansion of is known, they represent quite cumbersome linear combinations of the physical modes, so it is not so easy to use exact solutions in this sense. Still, the analysis by Langer in [39] allows us to find a basis of solutions and connection formulas. We prefer to adopt another strategy, mimicking the analysis in [40,41] for the superluminal case. We limit ourselves to notice that, with respect to the bases described in [40], the bases described below are obtained simply by a rotation , so we have the replacement . These bases are also confirmed by the analysis in [39]. We have the following representations for the non-constant subluminal solutions:
where the relevant paths for the bases are indicated in Figure 1, Figure 2 and Figure 3 below.
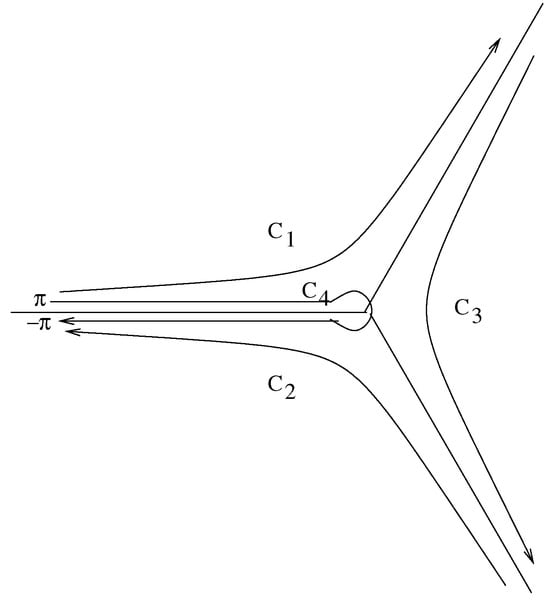
Figure 1.
Paths labeled with in the t-plane, , for the basis . There is a branch cut for .
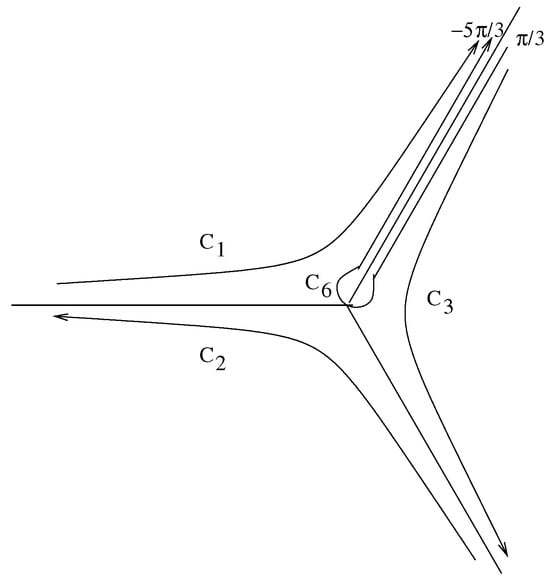
Figure 2.
Paths labeled with in the t-plane, , for the basis . There is a branch cut for .
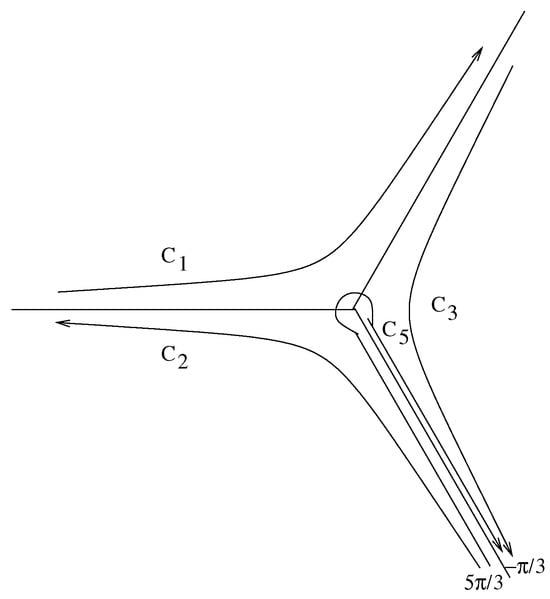
Figure 3.
Paths labeled with in the t-plane, , for the basis . There is a branch cut for .
The first basis, say B1, which is relative to the sector , is .
The second basis, say B2, which is relative to the sector , is .
The third basis, say B3, which is relative to the sector , is .
From a physical point of view, we adopt, substantially as in [1,2] for the subluminal Corley model and for the dielectric case with a single resonance frequency and water (both are subluminal), the basis to represent the near-horizon expressions for the physical modes (Hawking particle , positive-norm dispersive mode , negative-norm dispersive mode , and 1 for the disconnected regular entering mode), participating in the scattering process in the external region , and the basis to represent the Hawking partner (solution ), the exponentially decaying mode (), the exponentially growing mode (, for a comparison see, e.g., [11]), and the regular disconnected mode, represented by 1. Notice that the basis B2 could also be used to describe physical states in the black hole interior.
The present choice of bases in the different sectors has the following advantages. First of all, from the Cauchy formula, for B1, we have
as is evident from Figure 1. Furthermore, by defining, as in [40],
we find the following relations:
which represent the substantial advantage of using such choices. Let us also introduce the following notation:
for . Given (11), we can see that, for B2,
holds true, and for B3, the corresponding relation is
We can provide the following connection formulas:
where the matrices connect the bases above and, in the following, will be explicitly written at the leading order in the series in . It is not difficult to see that, in considering the relation between B1 and B2,
hold true, so
Analogously, as far as the relation between B3 and B1 is concerned, one finds
and then
As to the relation between B2 and B3, we obtain
and then
3.2. The Superluminal Case
In the superluminal case, which, from a physical point of view, is very relevant because the dispersion relation of a BEC is superluminal, both in (5) and in (8), a minus sign appears. Also, in this case, we can find the general solutions:
We do not delve into a discussion, as considerations analogous to those in the previous subsection hold true.
We refer instead to the framework in which generalized Airy solutions are introduced by means of the Laplace transform, as discussed in the previous subsection. For a complete analysis, readers can refer to [40,41]. We present, in a single figure, as in [41], the full set of six non-constant solutions, again expressed in terms of generalized Airy functions:
along the paths indicated in Figure 4.
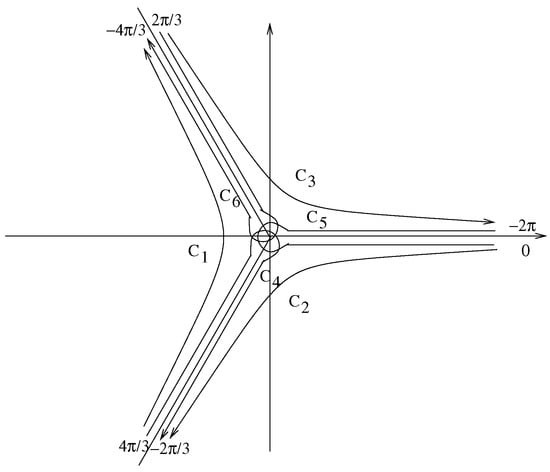
Figure 4.
Paths labeled with in the t-plane, . There are branch cuts for , , and .
To construct the three bases
one can simply select the corresponding paths in Figure 4, with just one branch cut (i.e., the branch cut involved in the definition of the specific function , , in the basis at hand), and construct figures analogous to Figure 1, Figure 2 and Figure 3. As in [40], the connection formulas are
where, for the matrices , we have for , with the same as in (24), (27), and (30).
4. Application to the Corley Model
We choose to work in the framework of the simplest possible model, both for brevity and for a more direct comparison with the most quoted literature [5,11]. We note that, even if it allows both a subluminal and a superluminal setting, it allows only a constant sound velocity c, and, moreover, it represents a strong simplification of the picture described in the previous analysis, as the coefficients do not actually depend on in this case. We limit ourselves to the subluminal case, and the superluminal one is sketched in Appendix C. We start with the following action:
which was deduced in [5,43]. The model is associated with a conserved inner product (see [5]) and with current conservation. By separating variables as in [5], , one obtains the fourth-order ordinary differential equation
where is the velocity field, stands for its first derivative with respect to x, and c is the constant sound velocity. We assume, as a significant physical scale, as in [5,43], the scale associated with nonlinearity, which is to be related to the presence of dispersion in the model itself, and, to allow a better comparison with the literature, we point out that, in [5], one has
(this is slightly different from the choice in [1], but substantially equivalent results are inferred). As is evident, the model is just 2D. In the limit , one obtains the so-called reduced equation,
In agreement with [5], we assume and a monotonic velocity profile, where is asymptotically constant, as in [1,2]. A real turning point occurs for
and the so-called linear region is the interval where the following approximation holds:
where
For a complete and exhaustive calculation of both the WKB solutions and the near-horizon solutions, we refer to [1]. We simply display the main results obtained in [1] in Section 4.1 and Section 4.2.
4.1. WKB Solutions
The following solutions
where (46) is the dispersive (non-normalized) positive-norm mode, and (47) is the dispersive (non-normalized) negative-norm mode. The seemingly weird numbering is useful for matching in the linear region (cf. Figure 1), where
These expansions also hold true for : let us assume ; then, in the linear region, one finds
where d indicates the decaying mode and g the growing mode (cf. [11]). We do not need to give a general WKB expansion for these modes, as they do not enter the asymptotic expansion of the S-matrix (as the decaying mode vanishes and the growing one must be set to zero).
Two further solutions can be obtained from the reduced equation, and, in order to maintain the same order of approximation in our WKB expansion, one would need exact solutions to avoid the introduction of a further expansion parameter. Nevertheless, near the regular singular point , which represents the real turning point, i.e., the horizon, we can provide the following series expansions:
where represents the Hawking mode, and represents a further short wavenumber mode, which, eventually, simply plays the role of a disconnected spectator mode, at least as far as the leading-order process is concerned. It is useful to provide approximate solutions to the reduced equation even for large x (in the external region with respect to the black hole). It is easy to show that for large x in the above sense, we have const, and then . As a consequence, e.g., under the conditions of theorem 1.9.1 in [44], we obtain, as ,
For , the reduced equation provides us with two further solutions:
with the asymptotic behavior
with . These solutions correspond to left-moving modes in the superluminal region, and they are the only propagating modes in that region. We notice that the mode is a negative-norm mode and that the regular mode is analogous to on the negative real axis.
As useful interpolating formulas inherited by [5] (WKB-like, but they cannot be rigorously obtained by using the -expansion as in the above framework), we could also use
which still display the correct behavior both in the linear region and in the asymptotic one.
In the appendix, we also provide exact solutions of the reduced equation for very specific velocity profiles.
4.2. Solutions Near the Turning Point
Let us introduce
and point out that, in our case, we obtain
In order to find physically relevant solutions of (5), we adopt the strategy utilized in [1]. We refer to Figure 1, and we choose to directly construct the relevant physical states by exploiting the method of the steepest descents [45,46,47] for approximating, as , the solutions occurring in B1. We need to consider, of course, the solutions (10), which, by setting , can be rewritten as
where
and
where and are the same as in Figure 1. We notice that the constant solution indicated as 1, as in [40,41], is the same on both sides of the linear region. The following analysis involves just the non-trivial solutions of (5) in the asymptotic portions of the linear region, i.e., as , as this is the behavior we need to know for matching with WKB solutions. This is by no means different from what is implemented in standard quantum mechanics near a TP.
For , the solutions and can be found through the steepest descents passing through the saddle points , respectively:
As to the cut contribution for , i.e., , it represents the Hawking mode. As shown in [1], the branch cut lies along the steepest descent, and this allows us to find [1]
For , we must refer to the basis B3 and to Figure 3. The decaying mode passing through the saddle point is
The mode corresponds to the growing mode:
And one may also simply consider the contribution (70) by choosing a suitable analytical continuation for . It turns out that, by choosing the branch where , the further solution one obtains,
is such that it corresponds to the Hawking partner (an antiparticle state, i.e., a state with a negative norm).
4.3. Matching: Complete Solutions
A careful comparison with the WKB expansion displayed in the previous section provides us with the connection formulas (cf. the so-called central connections in [41]). We have to match, in a single solution, the WKB part and the near-horizon part of the modes introduced above in such a way as to obtain basis functions that are defined in the whole domain (cf. also [1]). Let us use and to denote the parts to be joined for the i-mode in a specific sector of the complex plane, with indexes that match those in B1, B2, or B3, according to the sector one chooses, and with x taking complex values.
In the matching region, which, in our case, will be considered to be the linear region, where the two approximations coexist, we have
and also
with the same functional dependence and with known constants . We remark that, in a rigorous approach, one should also take into account the dependence on the parameter of both expansions. We limit ourselves to the leading order. For details, see [41]. Let us consider the region . As we must connect and in the linear region, where there exists a coexistence region for both the solutions, we find
i.e., matching in the linear region requires
As can be seen, the aforementioned matching is diagonal (in [41], this is indicated as the central connection problem) in the sense that the WKB and NH expansions of each single i-esime mode are connected. We notice that, for the complete solution, which is indicated as , in the aforementioned sector of the complex plane, we must obtain
where identifies part of the linear region where both expansions coexist, represents the neighborhood of the TP where the near-horizon approximation holds, and indicates the region where the WKB approximation holds. As a consequence, either or equivalently identifies the complete solution . is the most interesting for scattering problems, where has to be taken into account.
Analogously, for , we will find
with an obvious notation (where the replacements and are made to distinguish between outer and inner constants), which takes into account that we have different bases for the black hole region and for the exterior one so that such matching will involve solutions on both sides of the horizon (TP).
Herein, we deepen and develop our results obtained in [1,2,3] by taking into account rigorously, from a mathematical point of view, what happens in the scattering process associated with the analog (weakly dispersive) Hawking effect. We consider, in the near-horizon region and then in the matching with WKB solutions, the basis B1 for representing physical states for and the basis B3 for representing states for (notice that, in line with principles, one could also choose the basis B2 for the states at ). The horizon corresponds to in our assumed setting. Formally, let us define as the sets of indices associated with the bases in the near-horizon region. We choose the index 0 for the constant solution, and then, for example, we have .
The first obvious observation is that, as mode (72) explodes at , when one considers the generic states that can be constructed with the basis B3,
where is a constant, one must set . As the lateral connection formulas are not diagonal, this does not imply that for , the element , which corresponds to a negative-norm state, disappears. Indeed, the Stokes phenomenon (cf. [41]) arises so that the different bases in the different regions of the complex plane are related through non-diagonal matrices. This happens because, although exact solutions of (5) are analytical everywhere, their asymptotic expansions as (which are needed because of the matching in the linear region with the WKB solutions) are not analytical and, in particular, at infinity an irregular singularity appears for the WKB solutions. The finding of Stokes lines, for a higher-order linear ordinary differential equation, represents a highly non-trivial problem, as pointed out in [48], and often requires numerical calculations (see also [49]). Their presence, in our case, is implicit in the non-triviality of the connection matrices and the non-diagonality of the matrices connecting the bases of states for and . Following the mathematical literature, we will refer to the aforementioned matrices as Stokes matrices.
For the Stokes matrices connecting asymptotic states, we have the following situation, for which we adopt a general notation, to be specified in the next discussion. Let indicate the specific basis one is referring to. Let be the central connection coefficient for the basis (we mean , discussed in the previous section), indexed by , and be the analogous coefficient for the basis indexed by , and let represent the (lateral) connection matrix associated with the transition from to (we mean , discussed in the previous section). Then, we have
where the coefficients are a priori arbitrary coefficients for constructing a generic state, and the Stokes connection matrix has the elements
i.e., (see also the discussion in [41]).
Herein, we start by discussing Stokes matrices for our specific case of interest. As , i.e., in the black hole region, there are two non-dispersive WKB solutions of the reduced equation, representing the Hawking partner and the spectator mode, which are the only propagating ones, with central connections in the linear region, with and with the constant solution 1, respectively. The other two dispersive WKB solutions represent the decaying mode, connected with in the linear region, and the growing mode, connected with . In the opposite region, as , i.e., in the external region, all four solutions propagate. There are, as can be seen, two dispersive and two non-dispersive WKB solutions, to be connected in the linear region with . Let us introduce , i.e., the set without the index of the diverging mode (the growing mode).
As discussed in detail in [1] and inherited by the analysis in [5], in the situations involved with the analog Hawking effect for , the propagating modes behave as plane waves:
where defines (known) constants emerging in the asymptotic expansion of WKB solutions such that
For a direct comparison with the coefficients appearing in [5], one has . As to the situation for , we have, analogously,
where the constants are known and emerge in the asymptotic expansion of the WKB solutions. Then, for the generic state for , we obtain (cf. (81))
As a consequence, we have, for ,
and, as ,
where the lateral connection matrix enters in a fundamental way. By comparison with (82), we infer, in our case,
We refer, for a more general discussion, involving n-th-order ordinary differential equations and their WKB solutions, to [48], specifically Section 7 therein.
As to the scattering amplitudes, it is interesting to introduce
where denotes the normalizations of the propagating modes in the asymptotic region, as in [5,11] (see [1] and references therein). In particular, we have
where is the group velocity of the mode. We note that, as to normalizations, the above formula also holds for the propagating modes for (i.e., in the black hole region), i.e., one can, e.g., define as well. We note that the decaying mode is not normalizable, but this is irrelevant. See the discussion in the following subsection.
The coefficients are given by
For , we find analogously
These quantities are very relevant, as, in the calculation of the ratio of currents whose conserved flux is measured at infinity, one has, for example,
if both the currents are relative to the external region, with an obvious change if currents in the black hole region are involved. See also the following subsection.
4.4. S-Matrix Revisited: A Further Labeling of States, Stokes Matrices Elements, and Particle Creation
Let us adopt the following physical notation for states: in the external region , we set, for the indices, the following correspondence: , , , , where P and N represent the dispersive modes with positive and negative norms, respectively, and H and V are the modes that correspond to solutions of the reduced equation, representing Hawking particles and regular modes, respectively. For , the correspondence is , for the propagating modes, where is the regular mode propagating toward , and is associated with the Hawking partner; furthermore, we consider for the decaying mode. It is simpler to write the connection matrix by referring to physical modes instead of using the basis elements described in the previous section, as it makes the process associated with the elements of the Stokes matrix more explicit in a trivial way. A subtlety could occur, as some modes, particularly the decaying mode, do not admit normalization; still, this does not represent a problem at all. As is seen, in regard to the growing mode, its amplitude must be set to zero.
The transition from (87) to (85) involves the following non-vanishing elements of the Stokes matrix (90):
These matrix elements tell us how the various solutions, and thus how the physical modes, are related to each other. As in a Feynman diagram, we consider that there is a so-called mode conversion ([43]) only in the case of non-zero non-diagonal matrix elements.
All the constants appearing in (99), (100), and (101) are known, and, explicitly, in particular, we have
It is important to stress that the modes and V correspond to particle states (positive norm), and there is no association between them and negative particle states, so no possible involvement in the process of particle creation from the vacuum is foreseeable. Moreover, the corresponding solutions are regular and analytic at the TP, in contrast to every other solution at hand. The only physically sensible choice is to connect these solutions to each other at , and this amounts to setting , as in a standard scattering in nonrelativistic quantum mechanics. is simply V inside the horizon, at least as far as the leading order in is considered in the basis construction, as previously discussed. Furthermore, it is correct to consider, in the same order, the modes V and as giving rise to a sort of disconnected line of a disconnected Feynman diagram. A corroboration of this picture is found in Appendix B.1, where we have explicit solutions to the reduced equation for a specific but physically meaningful monotonic transcritical velocity profile, and we can see that the regular solution is analytic and describes both V and asymptotically. As to the disconnected mode V, one has
where represents the flux of L-modes at , with , and where (107) holds true at least at the leading order in .
From (11), one obtains the following current conservation:
where no contribution from the decaying mode arises, being as , of course.1 Then, by considering (99), (100), and (101), we obtain
where
Explicitly, we find
The ingoing modes moving from ∞ toward the horizon (TP), namely, P and N, at initial times correspond to the only mode H going to ∞ at final times (again, at infinity, the decaying mode cannot contribute, as above):
where the various amplitudes are obtained as follows: the ratio giving the particle-creation rate is
and
It is very important to notice that, if is the vacuum state, then for the number of Hawking particles (created at frequency ), as a consequence of (115), one obtains
Thermality, as is well known, is associated with the ratio
where
is the inverse of the expected Hawking temperature. This ratio and (109) imply a blackbody spectrum,
that, at least at the leading order in , is purely Planckian, because no contribution of the disconnected mode V is present. We notice that this result can also be obtained from a direct calculation of , as it is easy to verify.
Finally, let us discuss the state associated with the Hawking partner. Let us recall that we have the set . Then, we obtain (see (57) but also compare (70) with (73)). Furthermore,
As a consequence, we have
where we have used (115) for and . Notice that the term proportional to cannot contribute to the vacuum expectation value of , so we do not need to make the factor explicit. We find
i.e., the same rate of production from the vacuum for as for H, as is expected if one is the antiparticle of the other one. Also, in this case, the latest result is a pure consequence of the rigorous mathematical setting adopted, and no particular effort to find a suitable Corley’s diagram must be made.
One might wonder which results could be obtained if, instead of the basis B3 for describing the near-horizon physical states in the black hole region, one were to use the basis B2. The following (obvious) changes occur in the construction of the scattering matrix:
with
where the following holds:
As a consequence, it is easy to see that, as far as the decaying mode is concerned, which is represented by in the linear region, the standard calculation of the Hawking particle production occurs, exactly as above. Instead, for the Hawking partner, the lateral connection formula
leads to
and then the same result as in the above discussion is obtained.
In concluding this section, we stress that the present analysis also holds not only for dielectric media and water, which are subluminal, but also for BECs (superluminal case), as discussed in [1,2,3], and we considered the subluminal Corley model just for simplicity. For completeness, in Appendix C, we sketch the basic calculations for the superluminal Corley model as well, which is just the one most directly related to a BEC (see [2] for calculations for BECs in the present framework).
5. The 4D Extension of the Corley Model
We take into account the simplest possible model, i.e., the Corley model, and limit our considerations to the subluminal case, which is considered in [5,11,17]. In contrast to, e.g., BEC and water waves [2], it does not allow a variable speed of sound velocity . Furthermore, it cannot be related to the dielectric model, which is discussed in the following section. It represents the reference model for analytical studies of the dispersive analog Hawking effect, and thus, it is a useful benchmark for the discussion of a 4D extension and also for the search for exact solutions of the reduced equation. A possible extension consists of both extending the model to transverse directions and considering the following extension of the action. In particular, we add transverse coordinates , both in the kinetic term and in the dispersive one, in the simplified hypothesis that the velocity field still depends only on x. This is necessary in order to allow variable separation and analytic studies of the model itself. The present restriction, which is admittedly strong, is not necessary in the Hopfield model that we discuss in the following section.
The extension we propose is the following:
where . With the separation ansatz , we obtain the modified equation of motion
where we have enhanced the spatial dependence of . We further adopt the variable separation ansatz:
Let us define and assume that , i.e., that transverse momenta are not big with respect to the scale ϵ (they are not order as the wavenumbers associated with the dispersive modes). Then, we obtain
and then, in terms of the Orr–Sommerfeld-type equation we discussed in the previous section, we obtain the following coefficients:
With respect to the original model, the only corrections we obtain concern an correction of and an correction of , and, as a consequence, we can again corroborate the general picture, in the sense that we confirm, once again, the need to use a more general and less model-dependent approach than the one discussed in [11].
As to the near-turning-point approximation, at the leading order, nothing changes, as it involves only the leading-order coefficient , which remains trivially unaltered.
Also, the leading-order WKB approximation for the above-separated equation is only affected by the shift , and, again, nothing substantial changes, as the leading-order WKB wavefunctions remain unaltered.
There is an important change in the classification of the modes; indeed, one finds that the new quantum number appears, and then we have to replace the modes and D with a one-parameter family of the modes , , , , , , and . The scattering is, in this situation, by no means as simple as in the 2D setting because of the presence of the transverse contributions, albeit in the most simple choice to allow a trivial separation of variables.
As to thermality, again, it is straightforward to show that the temperature is unaffected and is universal, as expected (cf. the discussion in [51] about the contributions beyond the s-waves; herein, we could say that we consider contributions beyond the case ).
It is also remarkable that the possible presence of massive modes [11,52] in a 4D framework, but even in the 2D case, does not modify the black hole temperature and can also be treated in the present framework. Indeed, a mass contribution in the action functional corresponds to the term , which is a non-derivative term. As a consequence, by imposing (cf. [11]), it may only contribute a further additive term to above. Under this assumption, no modification to the temperature occurs (still, modifications to the dispersion relation arise). We refer again to the discussion in [51].
6. The 4D Extension of the Hopfield Model and the Analogous Hawking Effect
The electromagnetic Lagrangian for the full Hopfield model is quite involved and has been discussed, using different theoretical tools, in [21]. A simplified model is then a better choice. Our model, introduced in [18], is related to the two-dimensional reduction of the Hopfield model adopted in [53] and is such that the electromagnetic field and the polarization field are simulated by a pair of scalar fields, and , respectively, in the so-called –model. We also provided a new approach, in a perturbative framework, for the subcritical case in [26] and even exact solutions for a specific monotonic profile for the refractive index in [27], with a full description of connection formulas. Despite its simplification, it is still set up in such a way that we obtain exactly the same dispersion relation, and, moreover, we can simulate the same coupling as in the full case. Its Lagrangian is
where plays the role of the dielectric susceptibility, is the usual four-velocity vector of the dielectric, is the proper frequency of the medium, and g is the coupling constant between the fields. The latter constant is henceforth set equal to one, as its original motivation (see [18]) can be relaxed without problems in a more advanced discussion (cf. also [1]).
We adopt a phenomenological model where we can leave room for a spacetime dependence of the microscopic parameters in such a way that is a constant. In particular, our parameter for a perturbative expansion is
which corresponds to the parameter appearing in the Orr–Sommerfeld-like equation (master equation). The equations of motion are
We can separate the above system, obtaining equations involving only one of the fields . As in [1], we focus on the electromagnetic field , obtaining
As we wish to discuss the 4D setting, we assume that the velocity of the perturbation is along the x-axis. The latter assumption is quite natural, as the velocity in the model is assumed to be spatially homogeneous and constant. We, again, designate as the transverse spatial directions . As a consequence, in the above formula (145), the only explicit dependence on the transverse directions appears in the terms involving the operator □. One may observe that, in the Fourier space, the transverse directions are associated with the contribution to the wavenumber and are constants in a separation-of-variables process, which is allowed in our settings, and that this contribution affects only the coefficient of the master equation, at the leading order. This has a very interesting consequence: the near-horizon equation is totally unaffected by the presence of transverse contributions, as the coefficient does not participate in its construction at the leading order. Also, the temperature remains unaffected, but satisfies a different dispersion relation due to the presence of transverse modes. This finding, which is a natural consequence of our general approach, is, of course, in perfect agreement with statements in [21,51].
7. Conclusions
Our main result concerns the analytical calculations of the various interesting rates of particle production for the analog Hawking effect. We have first deduced suitable bases of solutions in the near-horizon region in different sectors of the complex plane and then calculated the relative connection matrices, both in the subluminal case and the superluminal one, in agreement with the analysis in [39,40,41]. Then, for simplicity, we have applied our general analysis, which can also be applied to BECs, dielectrics, and water (cf. [1,2]), to the most well-known theoretical model, the so-called Corley model [5,11], and we have shown how to deduce physical amplitudes without introducing hypotheses ad hoc, like the Corley’s boundary condition appearing in [5], but just on rigorous mathematical grounds. See also [11], where a refinement of Corley’s analysis is found, but not a complete and rigorous analysis of the connection formulas. The subtle point is that the main features of the analog Hawking effect are associated with the Stokes phenomenon, i.e., the appearance of non-trivial Stokes matrices. The Stokes phenomenon, on rigorous mathematical grounds, was discussed before in the context of the dispersive Hawking effect only in [27] for dielectrics, using the Hopfield model and thanks to exact solutions associated with a specific but physically very relevant choice of the refractive index profile. A general setting, albeit for weak dispersive effects, as discussed in [1,2,3], was still lacking.
In our view, our analysis in the present paper represents a strong corroboration, in terms of analytical calculations, of the analog Hawking effect in the framework of weak dispersive effects and completes the analysis in previous papers [1,2,3].
Then, we have taken into account the problem of extending, at least in a preliminary way, our framework to 4D cases, albeit allowing for the separation of variables. We have shown that the expression of the Hawking temperature remains unaltered, as it happens in the standard Hawking effect (see [51]). As a final (but still relevant) contribution, we provide, in Appendix B, exact solutions for the so-called reduced equation that governs the behavior of the short-wavelength modes in the WKB approximation (non-dispersive modes).
Future investigations should involve a more detailed analysis of the 4D case, as well as a better comprehension of the subcritical case, which, from the point of view of analytical calculations, remains a challenging problem (see [22,26]).
There are further possible lines of investigation. The first one concerns the explicit evaluation of the contributions arising from higher-order terms in the expansion parameter . In particular, as discussed in previous works (see, e.g., [1,2] and see also [54]), there is, for small but non-zero , a maximum value of the frequency beyond which the Hawking process is not allowed, and, moreover, its thermal appearance at low frequencies must be corrected. This may happen either when considering a model where transverse dimensions (and/or massive modes) are also allowed because of the possible arising of a non-trivial gray-body factor, or as a consequence of higher-order contributions. Going beyond the leading order in epsilon is possible but is non-trivial (we refer to the papers quoted by Nishimoto, in particular, [40]) and requires further analytical studies, which we intend to develop in the future.
A further line of investigation might be represented by the Unruh effect [55], which is, as is well known, a phenomenon with strong similarities to the Hawking effect. A very important issue from the experimental point of view consists of measuring the effect itself in analog condensed matter systems. See, for example, [56,57,58,59] and references therein. BECs coupled with lasers are, e.g., involved in this picture [56]. As far as a fourth-order equation of the Orr–Sommerfeld kind can be obtained, as is standard in BECs (see, e.g., [2,60]), the present framework could help in performing analytical calculations. We reserve the analysis of this problem for future investigations.
Author Contributions
F.B. planned and developed the preliminary draft of the paper; S.L.C. and S.T. carefully verified the calculations and participated in them and in the final draft of the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Corley’s Boundary Condition
For completeness and a better comparison with previous calculations, we sketch how thermality is usually recovered and the Hawking effect calculated in the external region (see [5] as the seminal paper and [1] and references therein). The starting point is the so-called Corley’s boundary condition, which amounts to the following diagram for modes in the linear region.
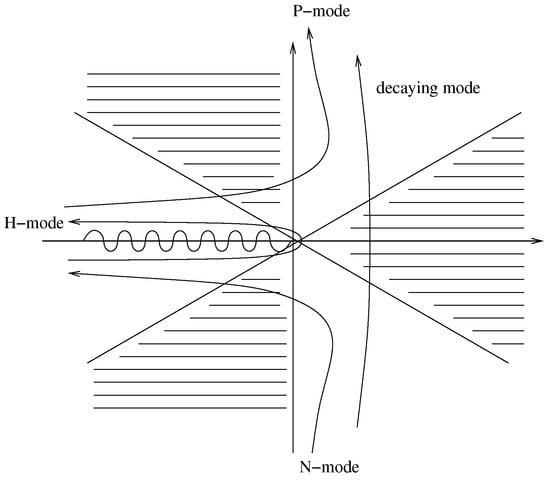
Figure A1.
The paths used in the subluminal case in Corley’s work [5]. Given the universality of (5), this diagram holds true for all the subluminal cases that can be rewritten in terms of the Orr–Sommerfeld-like equation discussed in [1]. The paths for the dispersive modes, called P-mode and N-mode in the text, are indicated, as well as those for the Hawking mode (H-mode) and for the decaying mode. The last mode is the one in the black hole region .
To be more explicit, Corley’s boundary condition amounts to a shortcut for finding connection formulas, and in particular, it resembles Figure 1, where, instead of considering at the same z, one considers and at , and at is identified with the decaying mode.
As discussed in [1,5], in the external region,
holds true. Also,
holds true, and thermality is found, but on less rigorous grounds and with a less clear role for the mode V, which still was found not to modify the blackbody spectrum at the leading order in [1] (and which is often neglected, at least in the linear region, as in [5,11]). A complete calculation, as we have shown in Section 4.4, reveals that V does not participate in (A1), and .
Appendix B. The Exact Solution of the Reduced Equation
As discussed in [1], non-dispersive modes, which are modes at low wavenumbers, satisfy the reduced Equation (4) in the WKB approximation. This is a second-order ordinary differential equation, which cannot be solved in the general case. Note that, corresponding to the leading-order equation governing non-dispersive modes in the WKB approximation in the parameter , one cannot approach its solutions using the WKB approximation itself (unless a further scale is taken into account in the problem, but there is no physical indication for such a new scale). As a consequence, consistency would require calculating exact solutions of the reduced equation to maintain a well-behaved WKB approximation. Of course, WKB works very well for the non-degenerate dispersive modes (the ones with non-zero wavenumbers from the eikonal equation) but is still problematic for degenerate non-dispersive modes (both with zero wavenumbers). Knowledge of the solutions of the reduced equation is necessary to implement S-matrix calculations. What is true is that it remains possible to provide solutions asymptotically at (see [1]) and also near the turning point in the transcritical case (as near , a Fuchsian singularity appears). In the following, at least for the case of the Corley model, and for a physically meaningful profile, we can provide exact solutions. Notice that, as the same reduced equation is shared by the subluminal and superluminal cases (cf. Appendix C), the following solutions hold for both cases.
We consider two specific velocity profiles, one for the transcritical case and the other for the subcritical one.
Appendix B.1. Transcritical Case
In order to allow for supersonic velocities and then for the presence of a real turning point , we choose the following velocity profile:
where L is a length scale. Then, we can obtain the following two solutions:
where corresponds to the Hawking mode for , presents a logarithmic branch point at , and represents, by analytic continuation, the Hawking partner for . It may be noted that, by taking into account the due inner product for the model, the Hawking mode in the exterior region has a positive norm, whereas the same mode obtained by the analytical continuation in the black hole region of the Hawking mode acquires a negative mode (antiparticle state). This changing of the norm is a special feature of the transcritical case; for the subcritical one, there is a substantially unaltered characterization for the states at the left and right of the dielectric perturbation, in the specific sense that no change in the signs of norms happens.
As to , it corresponds to an analytical solution defined everywhere and represents the (spectator) mode V for and its part for .
Appendix B.2. Subcritical Case
We choose the following velocity profile:
so that the velocity is such that . In this case, we have no real turning point; still, it may be interesting to also provide solutions for this situation. Then, we can obtain the following two solutions:
where corresponds to the (would-be) Hawking mode, and to the regular (spectator) mode.
Appendix C. The Corley Model in the Superluminal Case
The superluminal case of the Corley model was discussed both in the original paper [5] and in [11]. In both cases, connection formulas are presented, but not on rigorous mathematical grounds. Here, we report all basic calculations.
We also consider herein the model studied analytically in [5], with specific reference to the superluminal case (the subluminal one is considered in [1]). We notice that the superluminal Corley model amounts to replacing in the subluminal one. As a consequence, we have the following fourth-order ordinary differential equation:
where, again, is the velocity field and remains its first derivative with respect to x. The reduced equation is the same as (42), and the TP is again a solution of . The linear region is defined in the same way as in the subluminal case.
Appendix C.1. WKB Approximation
We set
For the leading order, we obtain
whose solutions are (multiplicity two, non-dispersive modes that are solutions of the reduced equation) and, in the black hole region , two purely imaginary solutions corresponding to dispersive propagating modes:
As is evident, again, the superluminal nature of the dispersion relation emerges because the aforementioned solutions correspond to modes that propagate on the black hole side of the horizon (turning point). In the exterior region , we find real dispersive solutions , corresponding to the growing mode (plus sign) and the decaying mode (minus sign).
By taking into account the so-called transport equation, as in [1], we obtain the solutions corresponding to the high-wavenumber mode solutions appearing in [5,11]:
It is fundamental to notice that, in the linear region, we have
where we stress the change of sign in the exponential factor, as we must match these solutions with that of the near-horizon approximation.
As to non-dispersive modes, the solutions and that we found in Section 4.1 also hold in this case and have the same properties (as they solve the same reduced equation).
We point out that the positive-norm states are , and the negative-norm ones are .
Appendix C.2. Near-Horizon Approximation
Near the TP, again, Equation (5) holds with the minus sign, with given by (63), and for z, relation (62) holds true. The bases we are interested in are the ones described in detail in [41], and in particular, we limit our attention to , representing states in the black hole region , and to , representing states for (exterior region). In particular, we are interested in appealing to the lateral connection formula , where
We refer to [41] for the asymptotic expansions of the functions in the different sectors of the complex plane. We just limit ourselves to providing the asymptotic expressions on the real axis, both in the black hole region and in the exterior one. For , we obtain the same expression as in (73) for , which corresponds to the Hawking partner (a state with the negative norm). Dispersive modes are to be associated with
Notice that must be connected with the positive-norm state , and must be connected with the negative-norm state . For , we have that is the same as in (70), whereas
correspond to the decaying and growing modes, respectively.
Appendix C.3. Stokes Matrix and Physical Processes
We adopt the following physical notation for states: in the external region , we set for the indices the following correspondence: , , , and , where D and G represent the decaying and growing modes, respectively, and H and V are the modes that correspond to solutions of the reduced equation, representing the Hawking particles propagating toward and the regular mode V propagating toward the horizon , respectively. For , the correspondence is , for the propagating non-dispersive modes, where is the regular mode and is associated with the Hawking partner, both propagating toward ; furthermore, we consider for the dispersive antiparticle mode and for the dispersive mode with the positive norm, both propagating toward the horizon . Also, in the present case, it is simpler to write the connection matrix by referring to physical modes.
In what follows, we adopt the convention of using and to indicate the coefficients relative to the mode L in the initial basis and using and to represent the coefficients relative to the mode S in the final basis. The transition from the external basis to the inner one corresponds to the following non-vanishing elements of the associated Stokes matrix (we omit the ones involving the growing mode G, as its coefficient in the initial basis has to be set to zero):
For V and , the same considerations as in Section 4.4 hold true. From (A23)–(A25), we find, from current conservation,
where, explicitly,
Furthermore, we have
so that
and
as expected.
From (A20), (A21), and the associated current conservation (cf. Section 4.4), we can write
where we also use (A31). We find
and, again, thermality is recovered.
In conclusion, we have shown, even in the superluminal case, the performance of the proposed method.
Note
| 1 | It would appear puzzling that the Hawking process is so strictly related to an evanescent state like the decaying one, like a sort of evanescent Cheshire Cat. The mathematical ratio behind this fact is that there must be a tail beyond the horizon of the modes and N propagating in the exterior region, and this tail is represented by the decaying mode. This would be mostly evident if, in a still more correct approach, one would use wave packets (see, e.g., [43]). In such a case, the modes and N, which would involve integrals over positive , could not be confined to the half-space with (cf. also [50], where this argument was suggested in the case of the standard Hawking effect.) |
References
- Belgiorno, F.; Cacciatori, S.L.; Viganò, A. Analog Hawking effect: A master equation. Phys. Rev. D 2020, 102, 105003. [Google Scholar] [CrossRef]
- Belgiorno, F.; Cacciatori, S.L.; Farahat, A.; Viganò, A. Analog Hawking effect: BEC and surface waves. Phys. Rev. D 2020, 102, 105004. [Google Scholar] [CrossRef]
- Belgiorno, F.; Cacciatori, S.L. Analogous Hawking Effect: S-Matrix and Thermofield Dynamics. Universe 2022, 8, 105. [Google Scholar] [CrossRef]
- Brout, R.; Massar, S.; Parentani, R.; Spindel, P. Hawking radiation without trans-Planckian frequencies. Phys. Rev. D 1995, 52, 4559. [Google Scholar] [CrossRef] [PubMed]
- Corley, S. Computing the spectrum of black hole radiation in the presence of high frequency dispersion: An analytical approach. Phys. Rev. D 1998, 57, 6280. [Google Scholar] [CrossRef]
- Himemoto, Y.; Tanaka, T. A generalization of the model of Hawking radiation with modified high frequency dispersion relation. Phys. Rev. D 2000, 61, 064004. [Google Scholar] [CrossRef]
- Saida, H.; Sakagami, M. Black hole radiation with high frequency dispersion. Phys. Rev. D 2000, 61, 084023. [Google Scholar] [CrossRef]
- Schutzhold, R.; Unruh, W.G. On the origin of the particles in black hole evaporation. Phys. Rev. D 2008, 78, 041504. [Google Scholar] [CrossRef]
- Unruh, W.G.; Schützhold, R. Universality of the Hawking effect. Phys. Rev. D 2005, 71, 024028. [Google Scholar] [CrossRef]
- Balbinot, R.; Fabbri, A.; Fagnocchi, S.; Parentani, R. Hawking radiation from acoustic black holes, short distance and back-reaction effects. Riv. Nuovo Cim. 2005, 28, 1. [Google Scholar]
- Coutant, A.; Parentani, R.; Finazzi, S. Black hole radiation with short distance dispersion, an analytical S-matrix approach. Phys. Rev. D 2012, 85, 024021. [Google Scholar] [CrossRef]
- Leonhardt, U.; Robertson, S. Analytical theory of Hawking radiation in dispersive media. New J. Phys. 2012, 14, 053003. [Google Scholar] [CrossRef]
- Coutant, A.; Fabbri, A.; Parentani, R.; Balbinot, R.; Anderson, P. Hawking radiation of massive modes and undulations. Phys. Rev. D 2012, 86, 064022. [Google Scholar] [CrossRef]
- Coutant, A.; Parentani, R. Undulations from amplified low frequency surface waves. Phys. Fluids 2014, 26, 044106. [Google Scholar] [CrossRef]
- Schutzhold, R.; Unruh, W.G. Hawking radiation with dispersion versus breakdown of WKB. Phys. Rev. D 2013, 88, 124009. [Google Scholar] [CrossRef]
- Petev, M.; Westerberg, N.; Moss, D.; Rubino, E.; Rimoldi, C.; Cacciatori, S.L.; Belgiorno, F.; Faccio, D. Blackbody emission from light interacting with an effective moving dispersive medium. Phys. Rev. Lett. 2013, 111, 043902. [Google Scholar] [CrossRef]
- Coutant, A.; Parentani, R. Hawking radiation with dispersion: The broadened horizon paradigm. Phys. Rev. D 2014, 90, 121501. [Google Scholar] [CrossRef]
- Belgiorno, F.; Cacciatori, S.L.; Piazza, F.D. Hawking effect in dielectric media and the Hopfield model. Phys. Rev. D 2015, 91, 124063. [Google Scholar] [CrossRef]
- Linder, M.F.; Schutzhold, R.; Unruh, W.G. Derivation of Hawking radiation in dispersive dielectric media. Phys. Rev. D 2016, 93, 104010. [Google Scholar] [CrossRef]
- Philbin, T.G. An exact solution for the Hawking effect in a dispersive fluid. Phys. Rev. D 2016, 94, 064053. [Google Scholar] [CrossRef]
- Belgiorno, F.; Cacciatori, S.L.; Piazza, F.D.; Doronzo, M. Hopfield-Kerr model and analogue black hole radiation in dielectrics. Phys. Rev. D 2017, 96, 096024. [Google Scholar] [CrossRef]
- Coutant, A.; Weinfurtner, S. The imprint of the analogue Hawking effect in subcritical flows. Phys. Rev. D 2016, 94, 064026. [Google Scholar] [CrossRef]
- Coutant, A.; Weinfurtner, S. Low-frequency analogue Hawking radiation: The Korteweg—De Vries mode. Phys. Rev. D 2018, 97, 025005. [Google Scholar] [CrossRef]
- Coutant, A.; Weinfurtner, S. Low frequency analogue Hawking radiation: The Bogoliubov-de Gennes model. Phys. Rev. D 2018, 97, 025006. [Google Scholar] [CrossRef]
- Jacquet, M.J.; König, F. Analytical description of quantum emission in optical analogs to gravity. Phys. Rev. A 2020, 102, 013725. [Google Scholar] [CrossRef]
- Trevisan, S.; Belgiorno, F.; Cacciatori, S.L. Perturbative approach to analog Hawking radiation in dielectric media in subcritical regime. Phys. Rev. D 2023, 108, 025001. [Google Scholar] [CrossRef]
- Trevisan, S.; Belgiorno, F.; Cacciatori, S.L. Exact solutions for analog Hawking effect in dielectric media. Phys. Rev. D 2024, 110, 085009. [Google Scholar] [CrossRef]
- Rousseaux, G.; Mathis, C.; Maissa, P.; Philbin, T.G.; Leonhardt, U. Observation of negative phase velocity waves in a water tank: A classical analogue to the Hawking effect? New J. Phys. 2008, 10, 053015. [Google Scholar] [CrossRef]
- Belgiorno, F.; Cacciatori, S.L.; Clerici, M.; Gorini, V.; Ortenzi, G.; Rizzi, L.; Rubino, E.; Sala, V.G.; Faccio, D. Hawking radiation from ultrashort laser pulse filaments. Phys. Rev. Lett. 2010, 105, 203901. [Google Scholar] [CrossRef]
- Weinfurtner, S.; Tedford, E.W.; Penrice, M.C.J.; Unruh, W.G.; Lawrence, G.A. Measurement of stimulated Hawking emission in an analogue system. Phys. Rev. Lett. 2011, 106, 021302. [Google Scholar] [CrossRef]
- Chaline, J.; Jannes, G.; Maissa, P.; Rousseaux, G. Some aspects of dispersive horizons: Lessons from surface waves. Lect. Notes Phys. 2013, 870, 145. [Google Scholar]
- Weinfurtner, S.; Tedford, E.W.; Penrice, M.C.J.; Unruh, W.G.; Lawrence, G.A. Classical aspects of Hawking radiation verified in analogue gravity experiment. Lect. Notes Phys. 2013, 870, 167. [Google Scholar]
- Steinhauer, J. Observation of self-amplifying Hawking radiation in an analog black hole laser. Nat. Phys. 2014, 10, 864. [Google Scholar] [CrossRef]
- Euvé, L.-P.; Michel, F.; Parentani, R.; Philbin, T.G.; Rousseaux, G. Observation of noise correlated by the Hawking effect in a water tank. Phys. Rev. Lett. 2016, 117, 121301. [Google Scholar] [CrossRef]
- de Nova, J.R.M.; Golubkov, K.; Kolobov, V.I.; Steinhauer, J. Observation of thermal Hawking radiation and its temperature in an analogue black hole. Nature 2019, 569, 688. [Google Scholar] [CrossRef]
- Drori, J.; Rosenberg, Y.; Bermudez, D.; Silberberg, Y.; Leonhardt, U. Observation of Stimulated Hawking Radiation in an Optical Analogue. Phys. Rev. Lett. 2019, 122, 010404. [Google Scholar] [CrossRef] [PubMed]
- Euvè, L.P.; Robertson, S.; James, N.; Fabbri, A.; Rousseaux, G. Scattering of co-current surface waves on an analogue black hole. Phys. Rev. Lett. 2020, 124, 141101. [Google Scholar] [CrossRef]
- Fourdrinoy, J.; Robertson, S.; James, N.; Fabbri, A.; Rousseaux, G. Correlations on weakly time-dependent transcritical white-hole flows. Phys. Rev. D 2022, 105, 085022. [Google Scholar] [CrossRef]
- Langer, R.E. The solutions of the differential equation v‴ + λ2zv′ + 3μλ2v = 0. Duke Math. J. 1955, 22, 525. [Google Scholar] [CrossRef]
- Nishimoto, T. Global solutions of certain fourth order differential equations. Kŏdai Math. Sem. Rep. 1976, 27, 128. [Google Scholar] [CrossRef]
- Nishimoto, T. On the Orr-Sommerfeld type equations, II Connection formulas. Kŏdai Math. Sem. Rep. 1978, 29, 233. [Google Scholar] [CrossRef]
- Nishimoto, T. On the Orr-Sommerfeld type equations, I; W.K.B. approximation. Kŏdai Math. Sem. Rep. 1972, 24, 281. [Google Scholar] [CrossRef]
- Corley, S.; Jacobson, T. Hawking spectrum and high frequency dispersion. Phys. Rev. D 1996, 54, 1568. [Google Scholar] [CrossRef]
- Eastham, M.S.P. The Asymptotic Solution of Linear Differential Systems: Application of the Levinson Theorem; London Mathematical Society Monographs New Series; Clarendon Press: Oxford, UK, 1989; Volume 4. [Google Scholar]
- Olver, F.W.I. Asymptotics and Special Functions; CRC Press: New York, NY, USA, 1997. [Google Scholar]
- Wong, R. Asymptotic Approximation of Integrals; Academic Press: New York, NY, USA, 1989. [Google Scholar]
- Miller, P.D. Applied Asymptotic Analysis; Graduate Studies in Mathematics; American Mathematical Society: Providence, RI, USA, 2006; Volume 75. [Google Scholar]
- Berk, H.L.; Nevins, W.M.; Roberts, K.V. New Stokes’ line in WKB theory. J. Math. Phys. 1982, 23, 988. [Google Scholar] [CrossRef]
- Nakano, M.; Namiki, M.; Nishimoto, T. On the WKB method for certain third order ordinary differential equations. Kodai Math. J. 1991, 14, 432. [Google Scholar] [CrossRef]
- Damour, T. Klein paradox and vacuum polarization. In Proceedings of the First Marcel Grossmann Meeting on General Relativity, Trieste, Italy, 7–12 July 1975; Ruffini, R., Ed.; North Holland Publishing Company: New York, NY, USA, 1977; p. 459. [Google Scholar]
- Visser, M. Essential and inessential features of Hawking radiation. Int. J. Mod. Phys. D 2003, 12, 649. [Google Scholar] [CrossRef]
- Jannes, G.; Maissa, P.; Philbin, T.G.; Rousseaux, G. Hawking radiation and the boomerang behaviour of massive modes near a horizon. Phys. Rev. D 2011, 83, 104028. [Google Scholar] [CrossRef]
- Finazzi, S.; Carusotto, I. Spontaneous quantum emission from analog white holes in a nonlinear optical medium. Phys. Rev. A 2014, 89, 053807. [Google Scholar] [CrossRef]
- Macher, J.; Parentani, R. Black/white hole radiation from dispersive theories. Phys. Rev. D 2009, 79, 124008. [Google Scholar] [CrossRef]
- Unruh, W.G. Notes on black hole evaporation. Phys. Rev. D 1976, 14, 870. [Google Scholar] [CrossRef]
- Gooding, C.; Biermann, S.; Erne, S.; Louko, J.; Unruh, W.G.; Schmiedmayer, J.; Weinfurtner, S. Interferometric Unruh detectors for Bose-Einstein condensates. Phys. Rev. Lett. 2020, 125, 213603. [Google Scholar] [CrossRef] [PubMed]
- Biermann, S.; Erne, S.; Gooding, C.; Louko, J.; Schmiedmayer, J.; Unruh, W.G.; Weinfurtner, S. Unruh and analogue Unruh temperatures for circular motion in 3+1 and 2+1 dimensions. Phys. Rev. D 2020, 102, 085006. [Google Scholar] [CrossRef]
- Bunney, C.R.D.; Parry, L.; Perche, T.R.; Louko, J. Ambient temperature versus ambient acceleration in the circular motion Unruh effect. Phys. Rev. D 2024, 109, 065001. [Google Scholar] [CrossRef]
- Unruh, W.G. Black Holes, Acceleration Temperature and Low Temperature Analog Experiments. J. Low Temp. Phys. 2022, 208, 196–209. [Google Scholar] [CrossRef]
- Macher, J.; Parentani, R. Black-hole radiation in Bose-Einstein condensates. Phys. Rev. A 2009, 80, 043601. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).