Photometry and Models of Seven Main-Belt Asteroids
Abstract
1. Introduction
2. Observational Data
2.1. Instruments and Sites
- The CNEOST is a Schmidt telescope system featuring a 1.2 m primary mirror complemented by a 1.04 m corrector. It operates with a focal ratio of and is equipped with an STA1600LN CCD detector (Semiconductor Technology Associates, Inc., San Clemente, CA, USA), which delivers a resolution of 10,000 × 10,000 pixels, resulting in an FOV of .
- The Yaoan High Precision Telescope (YAHPT) is a 0.8 m telescope located at Yaoan Station in China. It has a focal length of 8 m and is fitted with a 2048 × 2048 PI camera. This configuration provides an FOV of with a pixel scale of . For this telescope, CCD images were captured using the Bessel V filter from July to October 2022, followed by observations with the Rc filter in November 2022.
- A 0.7 m Maksutov system mirror telescope utilized at Abastumani Observatory [11] possesses a focal length of 2.46 m and is equipped with a PL4240 CCD (Finger Lakes Instrumentation, Lima, NY, USA), yielding an FOV of . Photometric observations with this telescope were conducted using the Bessel V filter.
- A 0.8 m telescope at Cerro Tololo Inter-American Observatory3 is outfitted with an FLI ML16803 camera (Finger Lakes Instrumentation, Lima, NY, USA) with a resolution of 4096 × 4096 pixels, providing an FOV of . Photometric observations from this telescope employed binning on the detector alongside the use of the Lum filter.
- A 0.4 m telescope stationed at Ali Observation Station in China features a focal length of 1.52 m and is equipped with a 4088 × 3066 FLI Microline ML50100 (Finger Lakes Instrumentation, Lima, NY, USA). This setup affords an FOV of , with photometric observations conducted using binning on the detector and the Bessel R filter.
2.2. Data Reduction
2.3. Published Data
3. Data Analysis
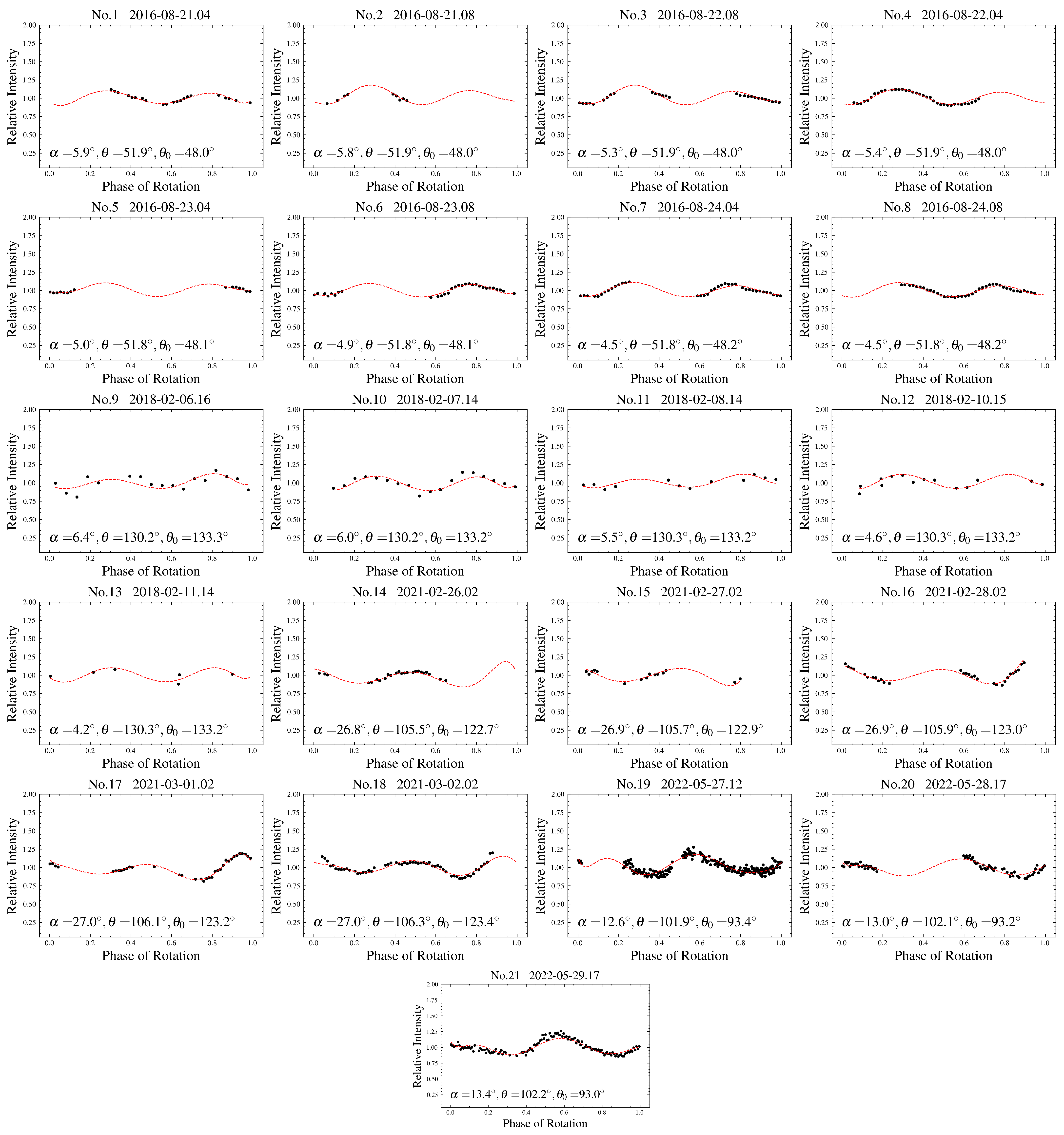
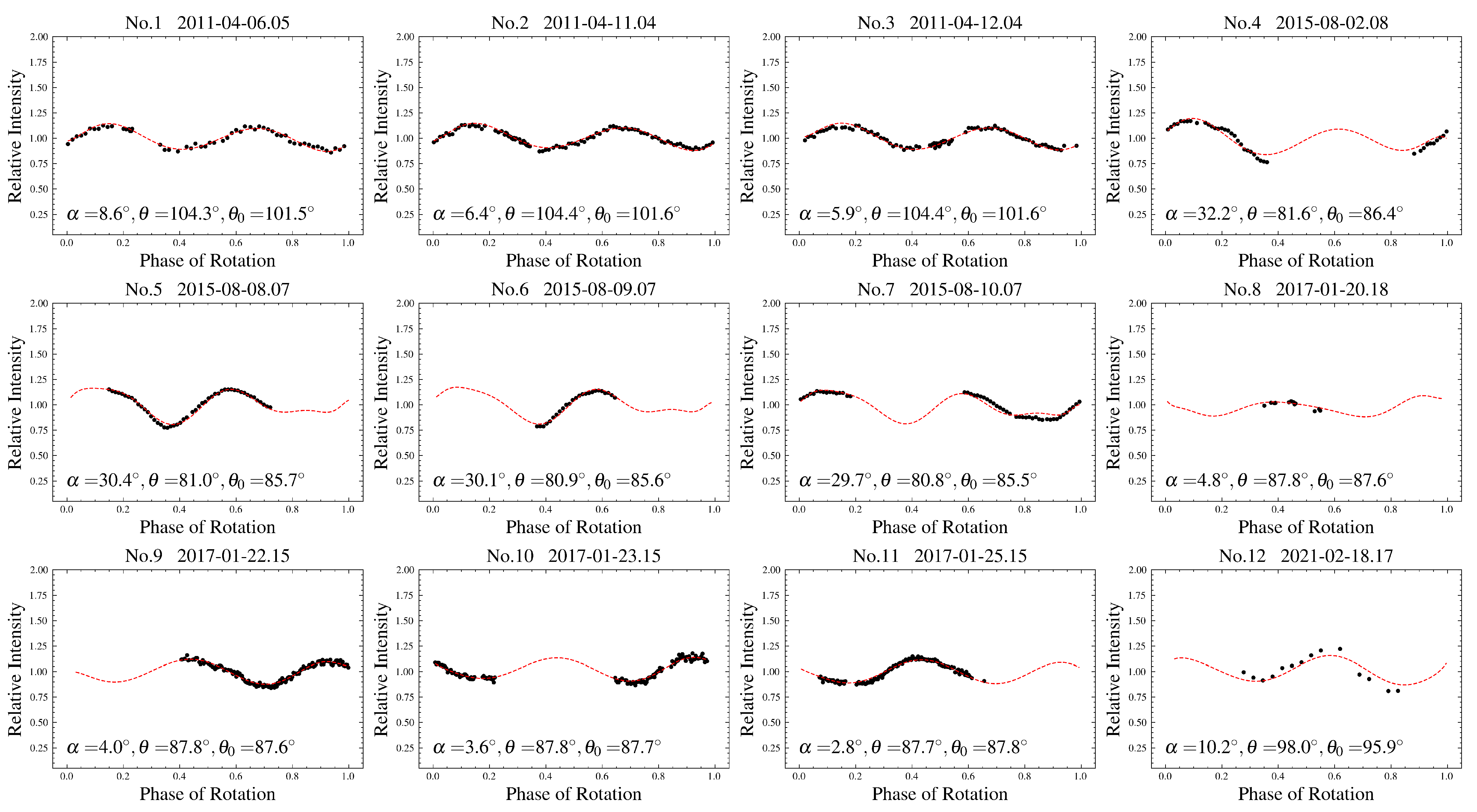
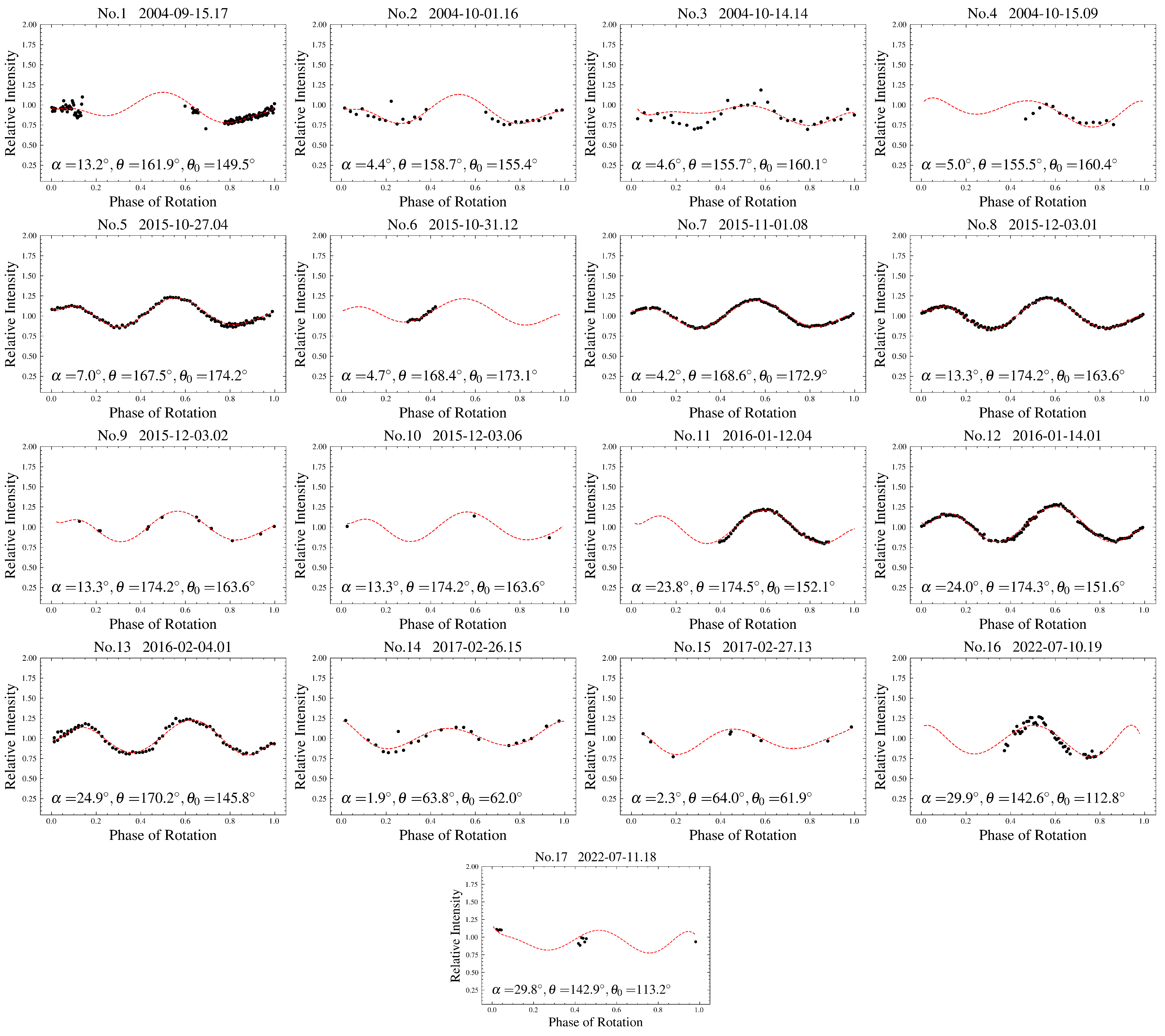
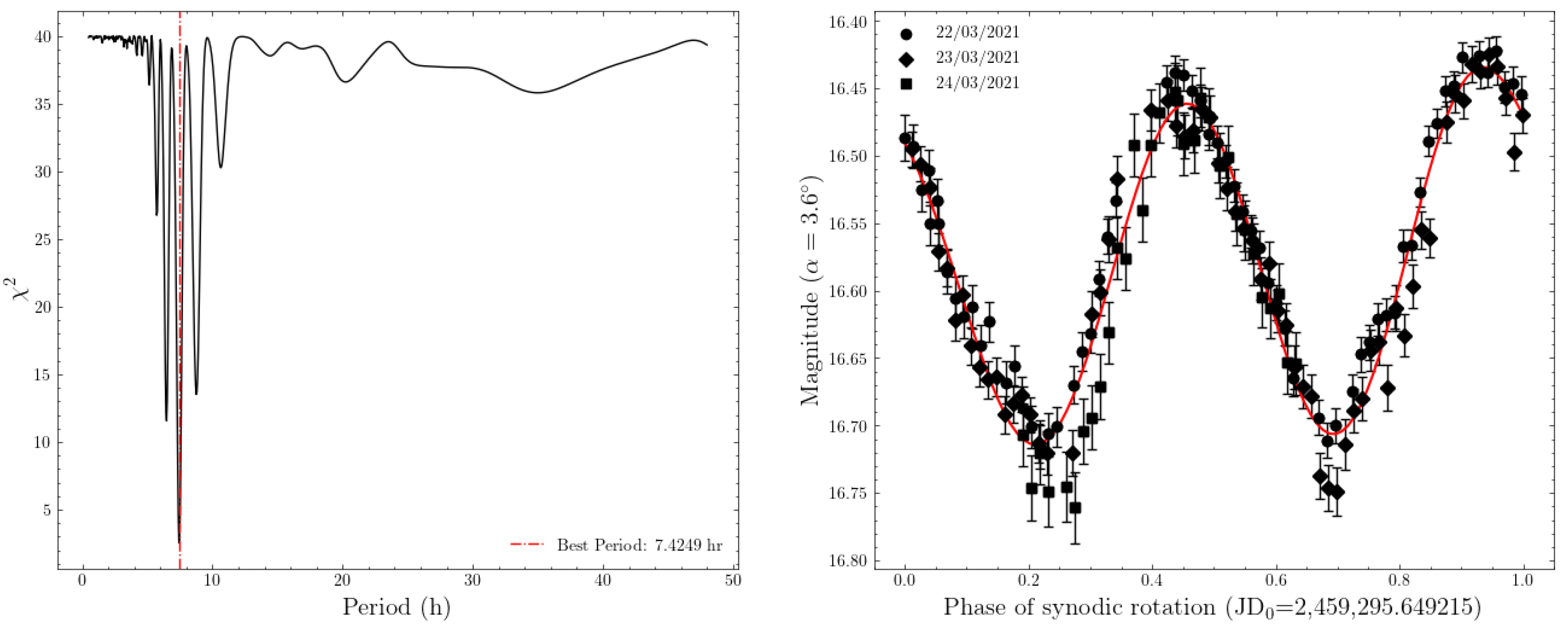
3.1. Rotation Period Analysis
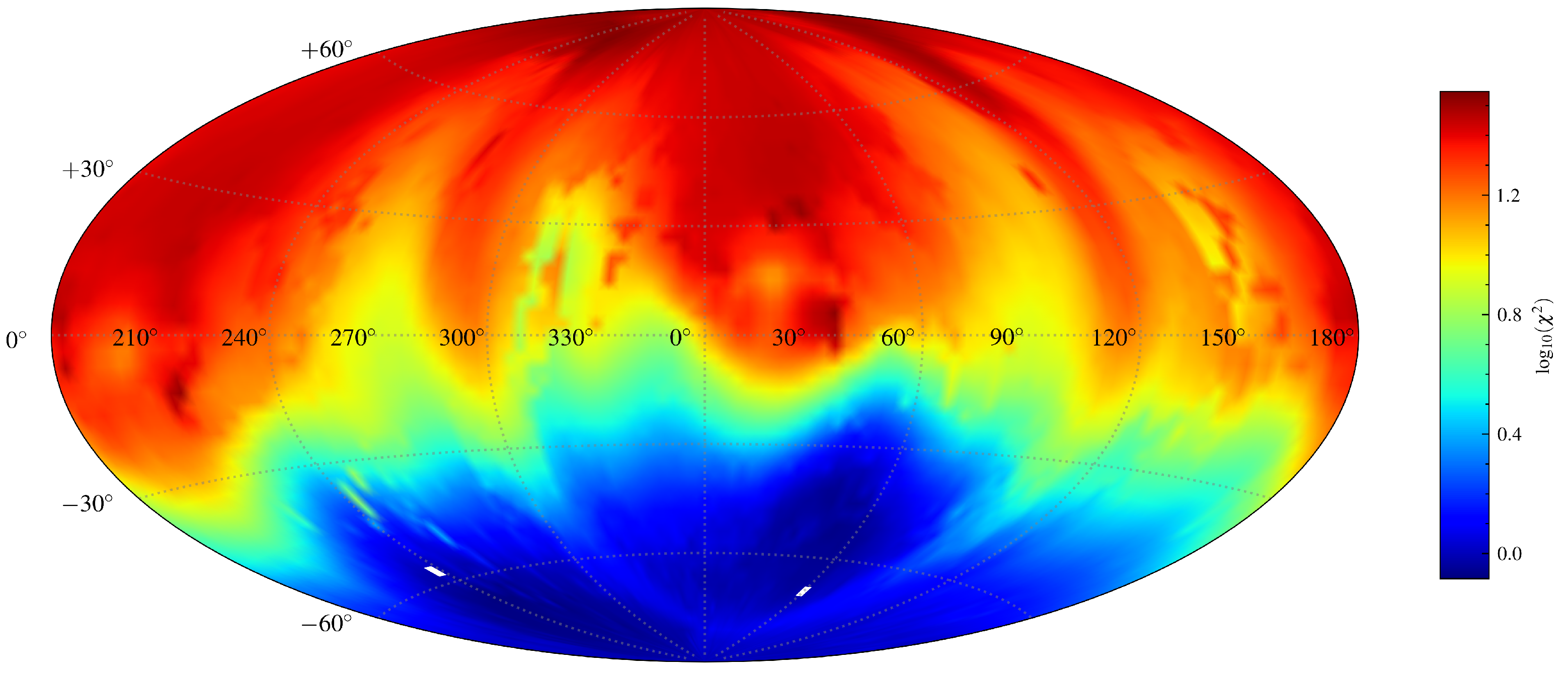
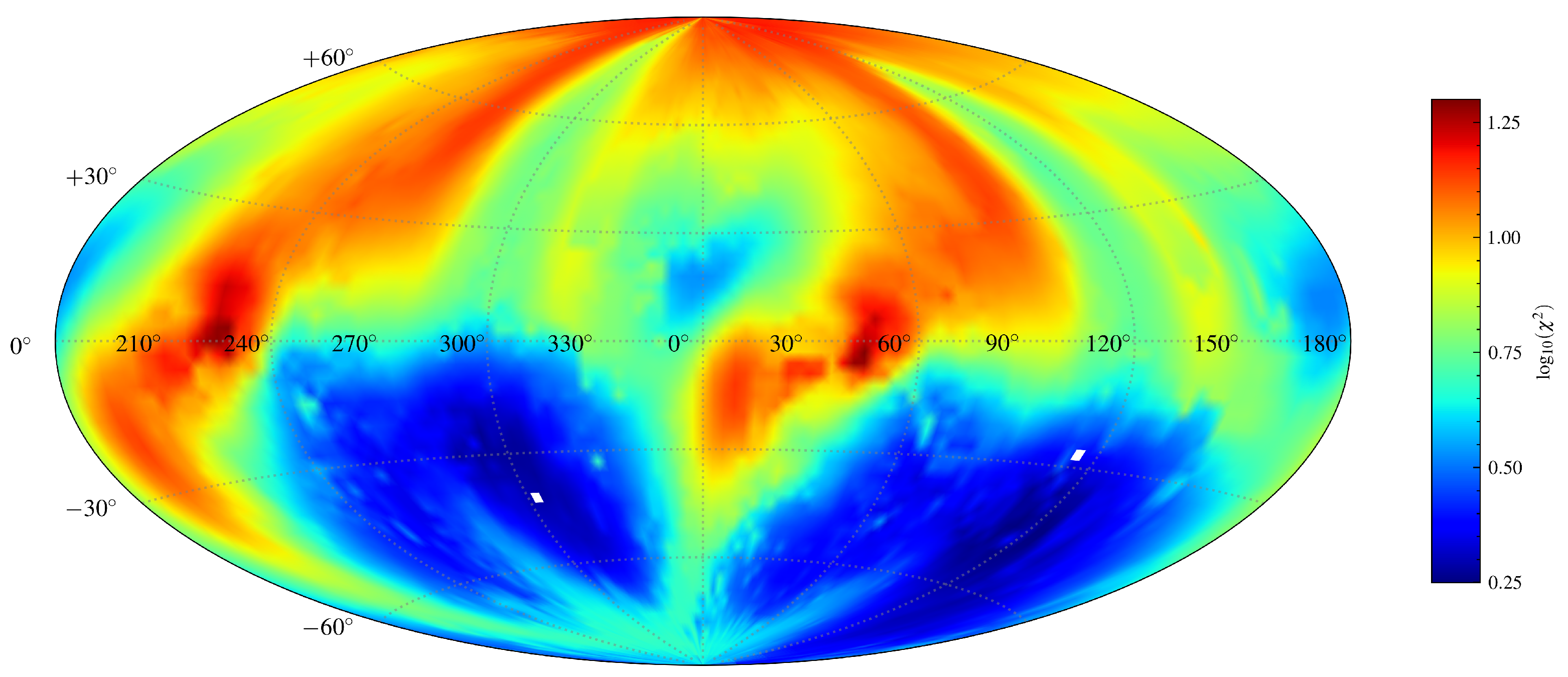
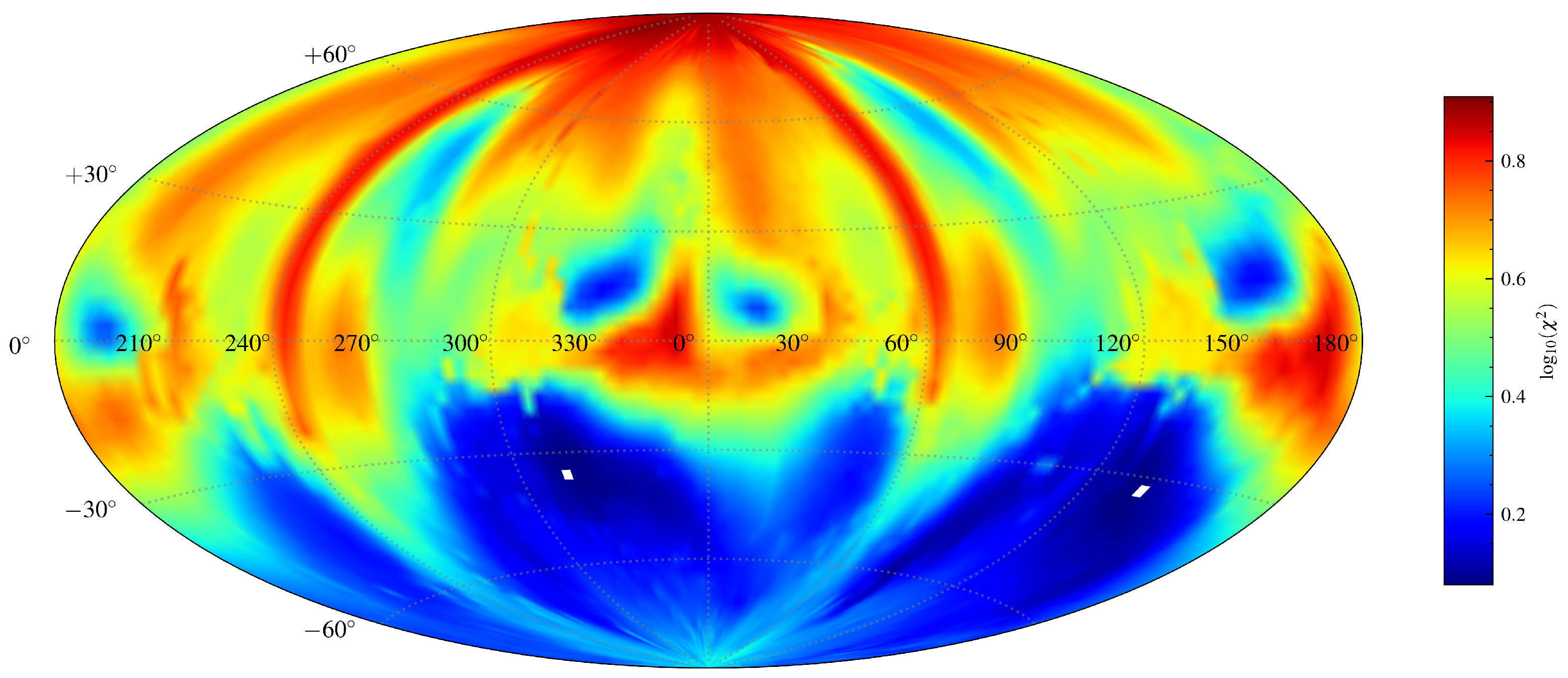
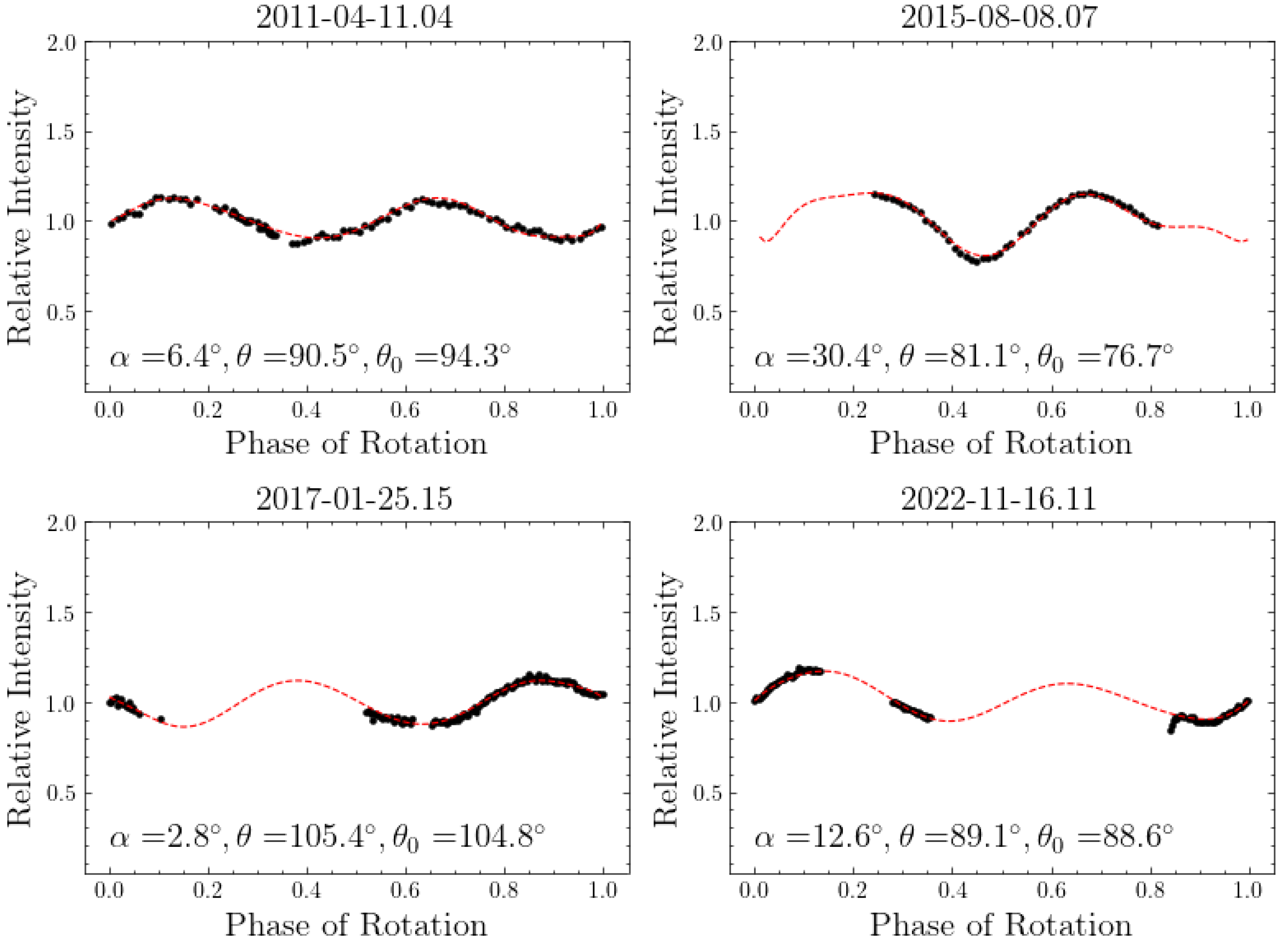
3.2. Shape and Spin Reconstruction with Light Curve Inversion
4. Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CNESOT | China Near-Earth Object Survey Telescope |
| NEAs | Near-Earth Asteroids |
| MBAs | Main Belt Asteroids |
| FOV | Field of View |
| MPC | Minor Planet Center |
| CCD | Charge-Coupled Device |
| PSF | Point Spread Function |
| MPBu | Minor Planet Bulletin |
| ALCDEF | Asteroid Light Curve Data Exchange Format |
| JPL | Jet Propulsion Laboratory |
| LCDB | Light Curve Database |
| IRAF | Image Reduction and Analysis Facility |
| DAMIT | Database of Asteroid Models from Inversion Techniques |
| YORP | Yarkovsky–O’Keefe–Radzievskii–Paddack |
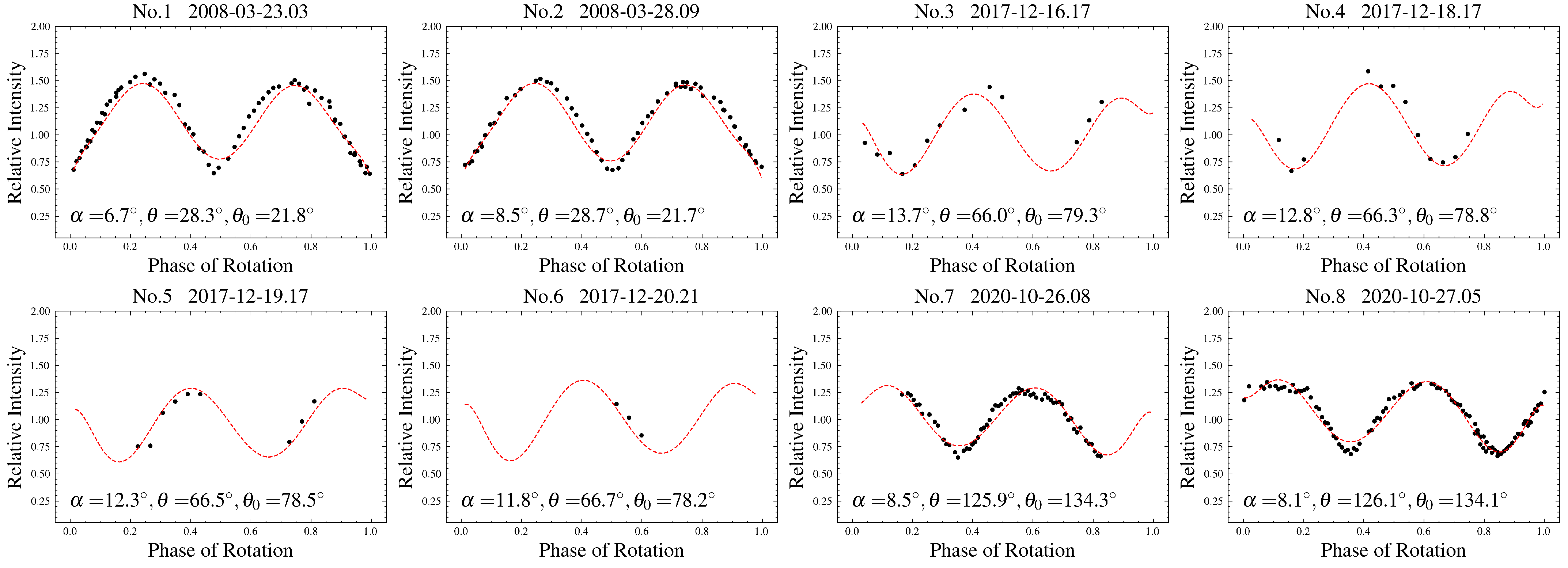
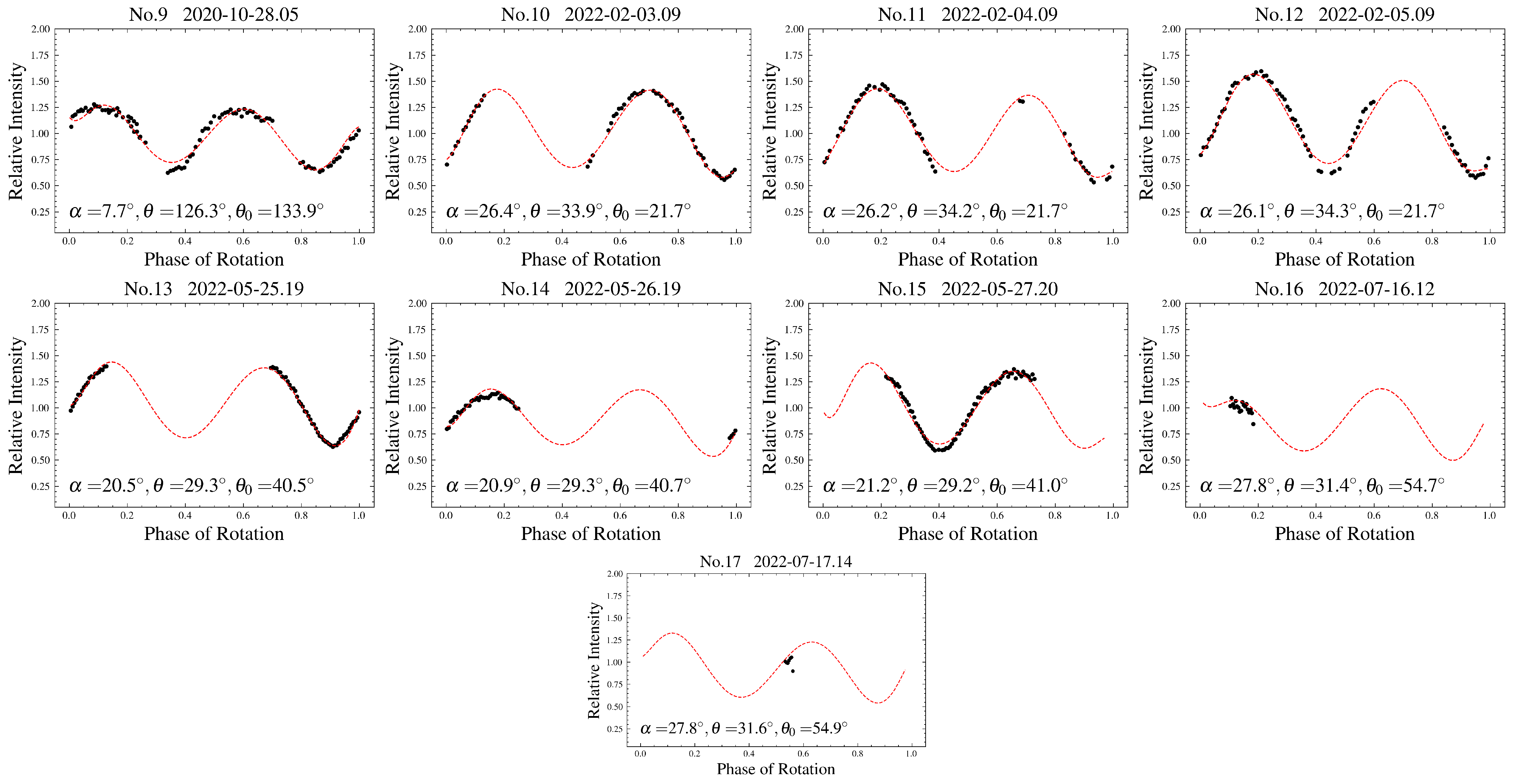
Appendix A. Observational Circumstances of the Light Curves of the Seven MBAs
| ID | UT Date | r | Amplitude | Total | Observing | Ref. | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| [dd-mm-yyyy] | [AU] | [AU] | [°] | [°] | [°] | [mag] | [h] | Facility | ||
| 1 | 21-08-2016 | 1.210 | 2.207 | 5.9 | 339.7 | 6.2 | 0.22 | 3.4 | 0.35-m f/11 SCT | |
| 2 | 21-08-2016 | 1.209 | 2.207 | 5.8 | 339.6 | 6.2 | 0.14 | 2.0 | 0.35-m f/11 SCT | |
| 3 | 22-08-2016 | 1.207 | 2.206 | 5.3 | 339.4 | 6.2 | 0.18 | 3.4 | 0.35-m f/11 SCT | |
| 4 | 22-08-2016 | 1.207 | 2.207 | 5.4 | 339.4 | 6.2 | 0.23 | 3.1 | 0.35-m f/11 SCT | |
| 5 | 23-08-2016 | 1.204 | 2.206 | 5.0 | 339.2 | 6.3 | 0.09 | 1.3 | 0.35-m f/11 SCT | |
| 6 | 23-08-2016 | 1.204 | 2.206 | 4.9 | 339.1 | 6.3 | 0.20 | 2.8 | 0.35-m f/11 SCT | |
| 7 | 24-08-2016 | 1.202 | 2.205 | 4.5 | 338.9 | 6.3 | 0.21 | 3.3 | 0.35-m f/11 SCT | |
| 8 | 24-08-2016 | 1.202 | 2.205 | 4.5 | 338.9 | 6.3 | 0.20 | 3.3 | 0.35-m f/11 SCT | |
| 9 | 06-02-2018 | 1.327 | 2.293 | 6.4 | 151.7 | −5.8 | 0.40 | 4.3 | CNEOST | |
| 10 | 07-02-2018 | 1.325 | 2.294 | 6.0 | 151.4 | −5.8 | 0.36 | 6.1 | CNEOST | |
| 11 | 08-02-2018 | 1.323 | 2.295 | 5.5 | 151.2 | −5.8 | 0.22 | 3.7 | CNEOST | |
| 12 | 10-02-2018 | 1.320 | 2.297 | 4.6 | 150.6 | −5.8 | 0.28 | 5.6 | CNEOST | |
| 13 | 11-02-2018 | 1.319 | 2.298 | 4.2 | 150.4 | −5.9 | 0.22 | 5.1 | CNEOST | |
| 14 | 26-02-2021 | 1.777 | 2.167 | 26.8 | 76.6 | −2.5 | 0.18 | 3.1 | 0.40-m F/10 SCT | |
| 15 | 27-02-2021 | 1.790 | 2.167 | 26.9 | 76.9 | −2.5 | 0.21 | 3.3 | 0.40-m F/10 SCT | |
| 16 | 28-02-2021 | 1.802 | 2.168 | 26.9 | 77.1 | −2.5 | 0.33 | 3.3 | 0.40-m F/10 SCT | |
| 17 | 01-03-2021 | 1.815 | 2.169 | 27.0 | 77.4 | −2.5 | 0.42 | 3.7 | 0.40-m F/10 SCT | |
| 18 | 02-03-2021 | 1.827 | 2.170 | 27.0 | 77.7 | −2.5 | 0.38 | 4.2 | 0.40-m F/10 SCT | |
| 19 | 27-05-2022 | 1.545 | 2.463 | 12.6 | 214.1 | −1.9 | 0.42 | 5.7 | 0.80-m f/10 | |
| 20 | 28-05-2022 | 1.552 | 2.463 | 13.0 | 213.9 | −1.9 | 0.34 | 2.9 | 0.7-m Maksutov system | |
| 21 | 29-05-2022 | 1.559 | 2.463 | 13.4 | 213.8 | −1.9 | 0.42 | 4.9 | 0.7-m Maksutov system |
| ID | UT Date | r | Amplitude | Total | Observing | Ref. | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| [dd-mm-yyyy] | [AU] | [AU] | [°] | [°] | [°] | [mag] | [h] | Facility | ||
| 1 | 06-04-2011 | 1.393 | 2.356 | 8.6 | 215.9 | 5.9 | 0.29 | 6.7 | VARGBTEL | |
| 2 | 11-04-2011 | 1.358 | 2.340 | 6.4 | 214.7 | 6.1 | 0.29 | 7.2 | VARGBTEL | |
| 3 | 12-04-2011 | 1.352 | 2.337 | 5.9 | 214.5 | 6.1 | 0.26 | 7.1 | VARGBTEL | |
| 4 | 02-08-2015 | 0.917 | 1.666 | 32.2 | 10.6 | −1.8 | 0.46 | 3.6 | 0.40-m f/10 SCT | |
| 5 | 08-08-2015 | 0.884 | 1.673 | 30.4 | 11.8 | −2.2 | 0.43 | 4.3 | 0.40-m f/10 SCT | |
| 6 | 09-08-2015 | 0.878 | 1.674 | 30.1 | 12.0 | −2.3 | 0.40 | 2.1 | 0.40-m f/10 SCT | |
| 7 | 10-08-2015 | 0.873 | 1.675 | 29.7 | 12.1 | −2.4 | 0.31 | 4.4 | 0.40-m f/10 SCT | |
| 8 | 20-01-2017 | 1.940 | 2.904 | 4.8 | 135.0 | −1.4 | 0.11 | 1.5 | CNEOST | |
| 9 | 22-01-2017 | 1.935 | 2.905 | 4.0 | 134.5 | −1.4 | 0.35 | 4.4 | CNEOST | |
| 10 | 23-01-2017 | 1.932 | 2.905 | 3.6 | 134.2 | −1.3 | 0.33 | 4.3 | CNEOST | |
| 11 | 25-01-2017 | 1.928 | 2.906 | 2.8 | 133.7 | −1.3 | 0.30 | 4.3 | CNEOST | |
| 12 | 18-02-2021 | 1.875 | 2.777 | 10.2 | 179.7 | 2.5 | 0.45 | 4.1 | CNEOST | |
| 13 | 19-02-2021 | 1.866 | 2.775 | 9.8 | 179.5 | 2.5 | 0.32 | 2.3 | CNEOST | |
| 14 | 20-02-2021 | 1.858 | 2.773 | 9.4 | 179.3 | 2.5 | 0.48 | 3.6 | CNEOST | |
| 15 | 22-03-2021 | 1.734 | 2.721 | 3.7 | 172.0 | 3.2 | 0.29 | 7.8 | MI-500 | |
| 16 | 23-03-2021 | 1.734 | 2.719 | 4.1 | 171.8 | 3.2 | 0.32 | 7.2 | MI-500 | |
| 17 | 24-03-2021 | 1.735 | 2.717 | 4.6 | 171.5 | 3.2 | 0.31 | 7.8 | MI-500 | |
| 18 | 29-04-2021 | 1.326 | 2.330 | 2.8 | 212.8 | −0.1 | 0.6 | 1.7 | 0.4-m f/3.8 | |
| 19 | 12-07-2022 | 1.399 | 1.686 | 37.0 | 23.1 | −1.8 | 0.96 | 2.4 | 0.80-m f/10 | |
| 20 | 13-07-2022 | 1.392 | 1.687 | 37.0 | 23.6 | −1.8 | 0.42 | 1.4 | 0.80-m f/10 | |
| 21 | 14-07-2022 | 1.385 | 1.689 | 37.0 | 24.1 | −1.9 | 0.12 | 0.8 | 0.80-m f/10 | |
| 22 | 16-11-2022 | 1.082 | 2.017 | 12.6 | 28.3 | −7.0 | 0.32 | 3.8 | 0.80-m f/10 |

| ID | UT Date | r | Amplitude | Total | Observing | Ref. | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| [dd-mm-yyyy] | [AU] | [AU] | [°] | [°] | [°] | [mag] | [h] | Facility | ||
| 1 | 15-09-2004 | 1.033 | 1.983 | 13.2 | 19.7 | 4.1 | 0.08 | 1.9 | 1.05-m | * |
| 2 | 01-10-2004 | 1.008 | 2.003 | 4.4 | 16.4 | 4.4 | 0.11 | 2.6 | 0.36-m | |
| 3 | 14-10-2004 | 1.031 | 2.021 | 4.6 | 13.3 | 4.4 | 0.16 | 3.9 | 0.3-m | |
| 4 | 15-10-2004 | 1.033 | 2.022 | 5.0 | 13.1 | 4.4 | 0.06 | 1.4 | 0.3-m | |
| 5 | 27-10-2015 | 1.165 | 2.140 | 7.0 | 48.0 | 4.0 | 0.41 | 4.3 | VARGBTEL | |
| 6 | 31-10-2015 | 1.164 | 2.148 | 4.7 | 47.0 | 4.0 | 0.20 | 0.4 | VARGBTEL | |
| 7 | 01-11-2015 | 1.165 | 2.150 | 4.2 | 46.7 | 4.0 | 0.38 | 3.4 | VARGBTEL | |
| 8 | 03-12-2015 | 1.310 | 2.214 | 13.3 | 39.7 | 3.4 | 0.43 | 8.1 | VARGBTEL | |
| 9 | 03-12-2015 | 1.310 | 2.214 | 13.3 | 39.7 | 3.4 | 0.32 | 7.7 | VARGBTEL | |
| 10 | 03-12-2015 | 1.310 | 2.214 | 13.3 | 39.6 | 3.4 | 0.29 | 3.8 | VARGBTEL | |
| 11 | 12-01-2016 | 1.771 | 2.296 | 23.8 | 40.7 | 2.3 | 0.46 | 1.7 | VARGBTEL | |
| 12 | 14-01-2016 | 1.798 | 2.300 | 24.0 | 41.1 | 2.3 | 0.49 | 4.3 | VARGBTEL | |
| 13 | 04-02-2016 | 2.099 | 2.343 | 24.9 | 46.0 | 1.8 | 0.47 | 4.0 | VARGBTEL | |
| 14 | 26-02-2017 | 1.791 | 2.779 | 1.9 | 153.2 | −2.2 | 0.43 | 4.5 | CNEOST | |
| 15 | 27-02-2017 | 1.792 | 2.779 | 2.3 | 152.9 | −2.2 | 0.42 | 5.0 | CNEOST | |
| 16 | 10-07-2022 | 1.350 | 1.931 | 29.9 | 359.7 | 1.8 | 0.56 | 1.5 | 0.80-m f/10 | |
| 17 | 11-07-2022 | 1.340 | 1.931 | 29.8 | 359.9 | 1.8 | 0.25 | 1.7 | 0.80-m f/10 |

| ID | UT Date | r | Amplitude | Total | Observing | Ref. | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| [dd-mm-yyyy] | [AU] | [AU] | [°] | [°] | [°] | [mag] | [h] | Facility | ||
| 1 | 30-08-2006 | 1.282 | 2.280 | 5.2 | 327.9 | 7.4 | 0.13 | 3.1 | 0.81-m f/7.9 | |
| 2 | 30-08-2006 | 1.283 | 2.280 | 5.3 | 327.8 | 7.4 | 0.10 | 2.3 | 0.81-m f/7.9 | |
| 3 | 31-08-2006 | 1.285 | 2.280 | 5.7 | 327.6 | 7.4 | 0.04 | 0.9 | 0.81-m f/7.9 | |
| 4 | 31-08-2006 | 1.285 | 2.280 | 5.7 | 327.6 | 7.4 | 0.13 | 3.0 | 0.81-m f/7.9 | |
| 5 | 01-09-2006 | 1.285 | 2.280 | 5.8 | 327.6 | 7.4 | 0.05 | 1.1 | 0.81-m f/7.9 | |
| 6 | 03-09-2006 | 1.293 | 2.280 | 7.0 | 327.0 | 7.5 | 0.05 | 1.3 | 0.81-m f/7.9 | |
| 7 | 03-09-2006 | 1.293 | 2.280 | 7.0 | 327.0 | 7.5 | 0.13 | 3.1 | 0.81-m f/7.9 | |
| 8 | 04-09-2006 | 1.294 | 2.280 | 7.1 | 327.0 | 7.5 | 0.06 | 1.4 | 0.81-m f/7.9 | |
| 9 | 16-03-2009 | 1.866 | 2.831 | 6.0 | 190.8 | −9.2 | 0.09 | 2.1 | 1.00-m | |
| 10 | 25-03-2009 | 1.837 | 2.825 | 3.6 | 188.8 | −9.4 | 0.13 | 3.2 | 0.50-m f/8.4 | |
| 11 | 27-03-2009 | 1.834 | 2.823 | 3.4 | 188.3 | −9.5 | 0.17 | 4.0 | 0.50-m f/8.4 | |
| 12 | 06-02-2016 | 2.196 | 2.658 | 20.8 | 64.0 | 3.4 | 0.45 | 2.1 | CNEOST | |
| 13 | 07-02-2016 | 2.210 | 2.659 | 20.9 | 64.1 | 3.3 | 0.47 | 2.6 | CNEOST | |
| 14 | 08-02-2016 | 2.224 | 2.660 | 21.0 | 64.3 | 3.3 | 0.44 | 3.5 | CNEOST | |
| 15 | 09-02-2016 | 2.238 | 2.661 | 21.0 | 64.4 | 3.2 | 0.48 | 3.3 | CNEOST | |
| 16 | 11-02-2017 | 1.954 | 2.884 | 8.0 | 166.2 | −6.9 | 0.30 | 0.9 | 1.60-m f/3.22 | |
| 17 | 13-05-2022 | 1.579 | 2.560 | 6.9 | 248.0 | −7.7 | 0.55 | 2.8 | 0.80-m f/7 | |
| 18 | 21-05-2022 | 1.548 | 2.550 | 4.0 | 246.3 | −7.6 | 0.39 | 1.4 | 0.80-m f/7 |
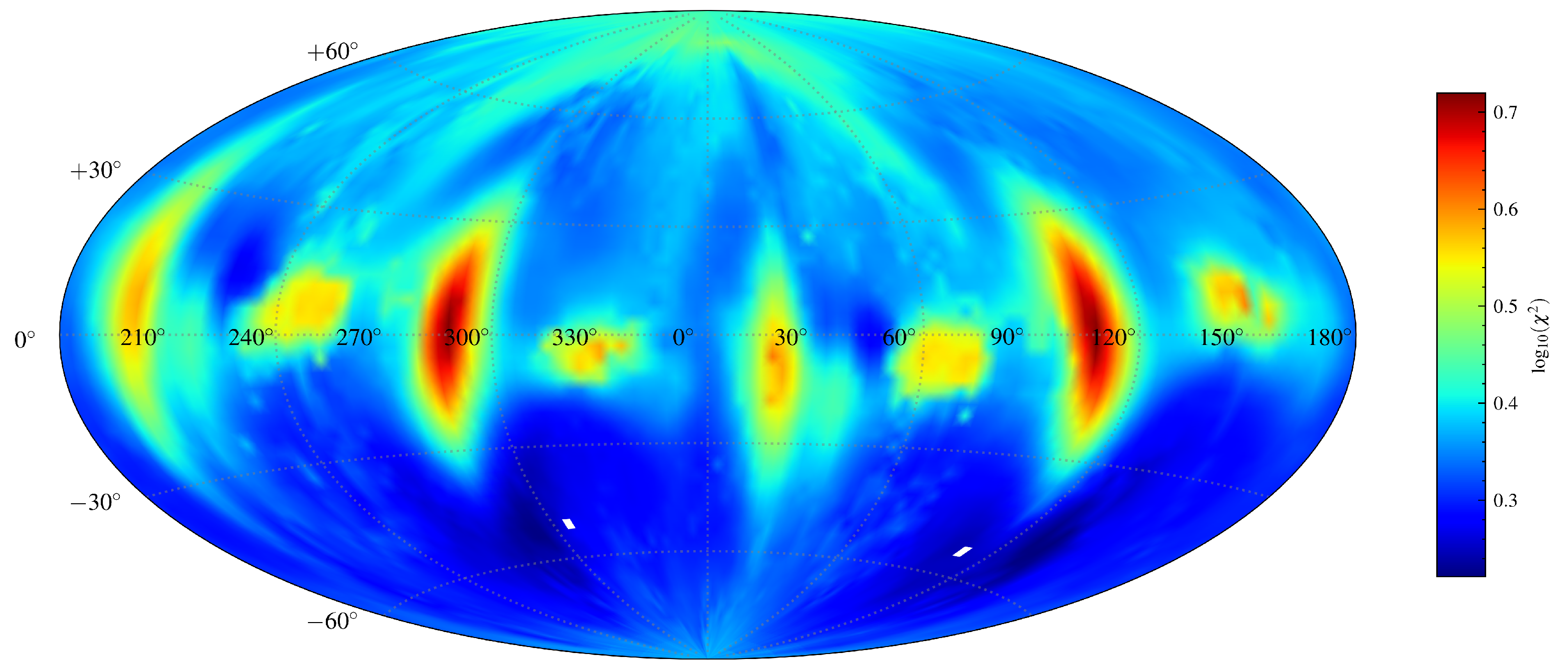
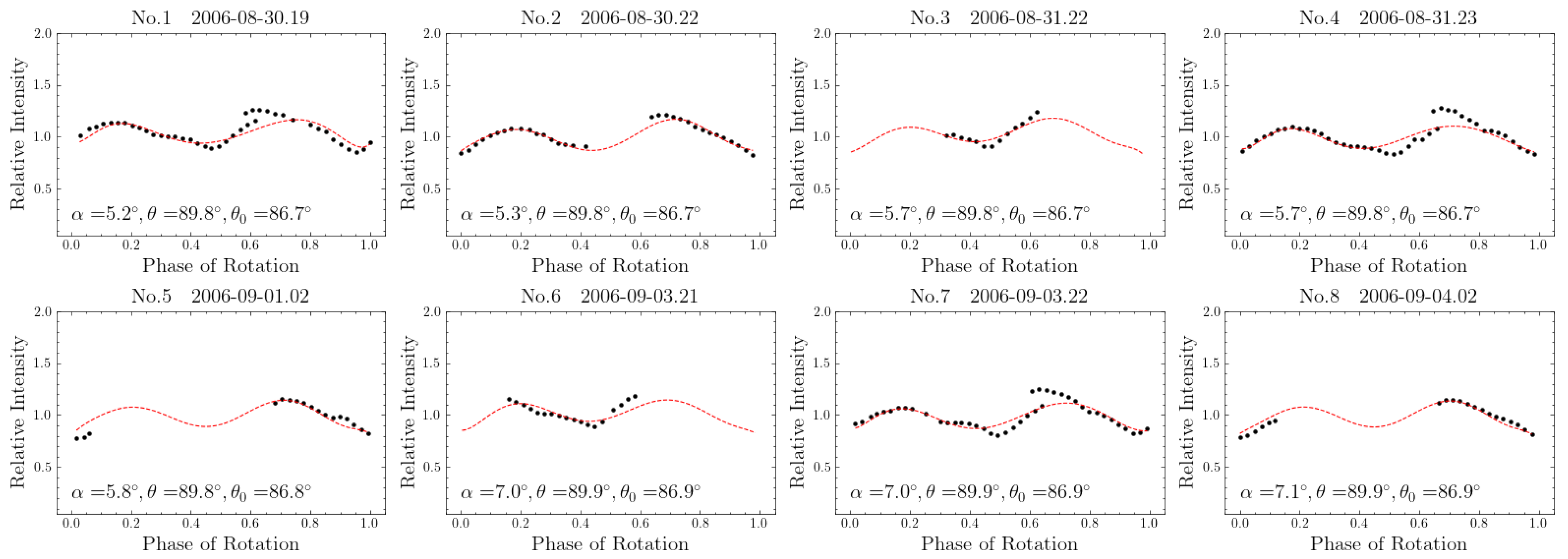
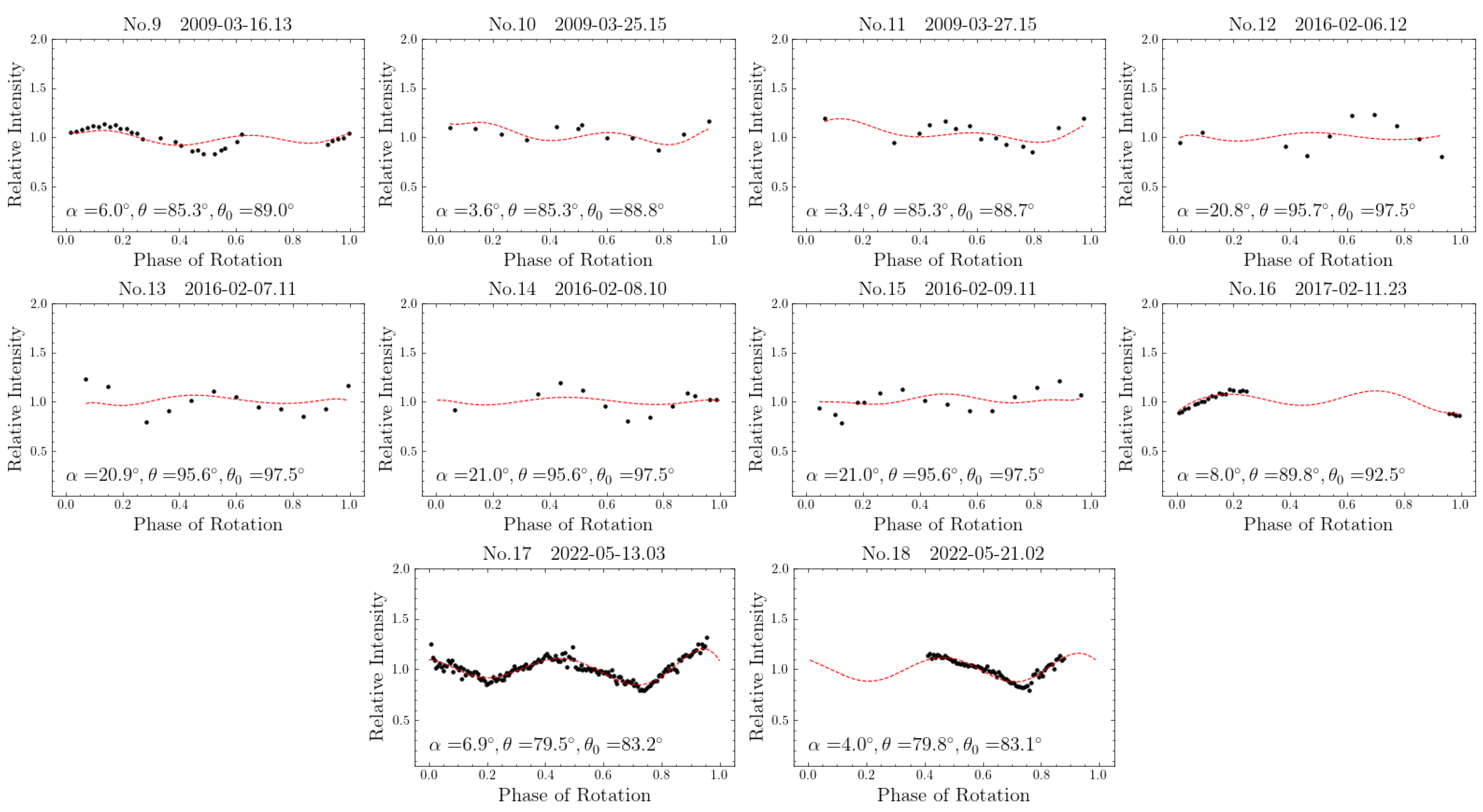
| ID | UT Date | r | Amplitude | Total | Observing | Ref. | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| [dd-mm-yyyy] | [AU] | [AU] | [°] | [°] | [°] | [mag] | [h] | Facility | ||
| 1 | 03-04-2008 | 1.028 | 2.022 | 4.4 | 199.5 | 7.1 | 0.15 | 4.2 | 0.25-m f/5.2 SCT | |
| 2 | 04-04-2008 | 1.028 | 2.023 | 4.1 | 199.2 | 7.1 | 0.16 | 6.5 | VARGBTEL | |
| 3 | 05-04-2008 | 1.027 | 2.023 | 3.8 | 199.0 | 7.0 | 0.16 | 4.9 | 0.25-m f/5.2 SCT | |
| 4 | 14-06-2015 | 1.310 | 2.242 | 13.5 | 293.3 | −7.4 | 0.14 | 3.9 | 0.35-m f/5.9 SCT | |
| 5 | 19-06-2015 | 1.288 | 2.247 | 11.3 | 292.4 | −7.8 | 0.15 | 2.6 | 0.35-m f/5.9 SCT | |
| 6 | 20-06-2015 | 1.284 | 2.248 | 10.9 | 292.2 | −7.8 | 0.20 | 2.9 | 0.35-m f/5.9 SCT | |
| 7 | 22-06-2015 | 1.276 | 2.250 | 9.9 | 291.7 | −8.0 | 0.20 | 3.2 | 0.35-m f/5.9 SCT | |
| 8 | 26-06-2015 | 1.265 | 2.253 | 8.1 | 290.8 | −8.2 | 0.19 | 7.2 | 0.35-m f/5.9 SCT | |
| 9 | 27-06-2015 | 1.263 | 2.254 | 7.6 | 290.6 | −8.2 | 0.20 | 8.6 | 0.35-m f/5.9 SCT | |
| 10 | 24-11-2016 | 1.247 | 2.234 | 1.0 | 61.4 | 1.6 | 0.16 | 3.8 | 0.5/0.7-m SCT | |
| 11 | 25-11-2016 | 1.247 | 2.233 | 1.4 | 61.1 | 1.6 | 0.16 | 3.9 | 0.5/0.7-m SCT | |
| 12 | 07-12-2016 | 1.264 | 2.222 | 7.9 | 58.0 | 2.2 | 0.17 | 4.5 | CNEOST | |
| 13 | 08-12-2016 | 1.267 | 2.221 | 8.4 | 57.7 | 2.3 | 0.20 | 6.5 | CNEOST | |
| 14 | 09-12-2016 | 1.270 | 2.220 | 8.9 | 57.5 | 2.3 | 0.17 | 2.0 | CNEOST | |
| 15 | 09-10-2019 | 1.365 | 2.341 | 6.8 | 30.9 | −5.0 | 0.20 | 7.6 | 0.40m F/10 SCT | |
| 16 | 10-10-2019 | 1.361 | 2.340 | 6.3 | 30.6 | −5.0 | 0.25 | 7.6 | 0.40m F/10 SCT | |
| 17 | 11-10-2019 | 1.358 | 2.340 | 5.8 | 30.4 | −5.0 | 0.20 | 3.8 | 0.40m F/10 SCT | |
| 18 | 16-10-2019 | 1.346 | 2.337 | 3.5 | 29.1 | −4.8 | 0.20 | 6.9 | 0.40m F/10 SCT | |
| 19 | 18-10-2019 | 1.343 | 2.336 | 2.7 | 28.5 | −4.7 | 0.21 | 7.8 | 0.40m F/10 SCT | |
| 20 | 19-10-2019 | 1.341 | 2.335 | 2.3 | 28.3 | −4.7 | 0.19 | 7.3 | 0.40m F/10 SCT | |
| 21 | 20-10-2019 | 1.341 | 2.334 | 2.1 | 28.0 | −4.6 | 0.23 | 7.6 | 0.40m F/10 SCT | |
| 22 | 21-10-2019 | 1.340 | 2.334 | 2.0 | 27.7 | −4.6 | 0.18 | 7.5 | 0.40m F/10 SCT | |
| 23 | 23-10-2019 | 1.340 | 2.333 | 2.1 | 27.2 | −4.5 | 0.19 | 2.9 | 0.40m F/10 SCT | |
| 24 | 24-10-2019 | 1.340 | 2.332 | 2.4 | 26.9 | −4.5 | 0.15 | 3.6 | 0.40m F/10 SCT | |
| 25 | 24-10-2019 | 1.340 | 2.332 | 2.4 | 26.9 | −4.5 | 0.19 | 4.0 | 0.40m F/10 SCT | |
| 26 | 25-10-2019 | 1.340 | 2.331 | 2.7 | 26.6 | −4.4 | 0.15 | 1.4 | 0.40m F/10 SCT | |
| 27 | 26-10-2019 | 1.341 | 2.331 | 3.1 | 26.4 | −4.4 | 0.16 | 2.9 | 0.40m F/10 SCT | |
| 28 | 27-10-2019 | 1.342 | 2.330 | 3.6 | 26.1 | −4.3 | 0.21 | 7.6 | 0.40m F/10 SCT | |
| 29 | 29-10-2019 | 1.345 | 2.329 | 4.5 | 25.5 | −4.2 | 0.21 | 7.2 | 0.40m F/10 SCT | |
| 30 | 30-10-2019 | 1.347 | 2.328 | 5.0 | 25.3 | −4.2 | 0.18 | 7.6 | 0.40m F/10 SCT | |
| 31 | 31-10-2019 | 1.349 | 2.327 | 5.5 | 25.0 | −4.1 | 0.20 | 6.6 | 0.40m F/10 SCT | |
| 32 | 01-11-2019 | 1.352 | 2.327 | 6.0 | 24.7 | −4.1 | 0.25 | 6.9 | 0.40m F/10 SCT | |
| 33 | 06-07-2022 | 1.933 | 2.373 | 24.7 | 1.6 | −7.2 | 0.21 | 2.2 | 0.80-m f/10 | |
| 34 | 30-09-2022 | 1.399 | 2.376 | 6.8 | 353.0 | −8.3 | 0.19 | 0.7 | 0.80-m f/10 | |
| 35 | 11-11-2022 | 1.716 | 2.366 | 21.4 | 348.4 | −5.7 | 0.26 | 1.9 | 0.80-m f/10 | |
| 36 | 11-11-2022 | 1.717 | 2.366 | 21.4 | 348.4 | −5.7 | 0.33 | 2.3 | 0.80-m f/10 |

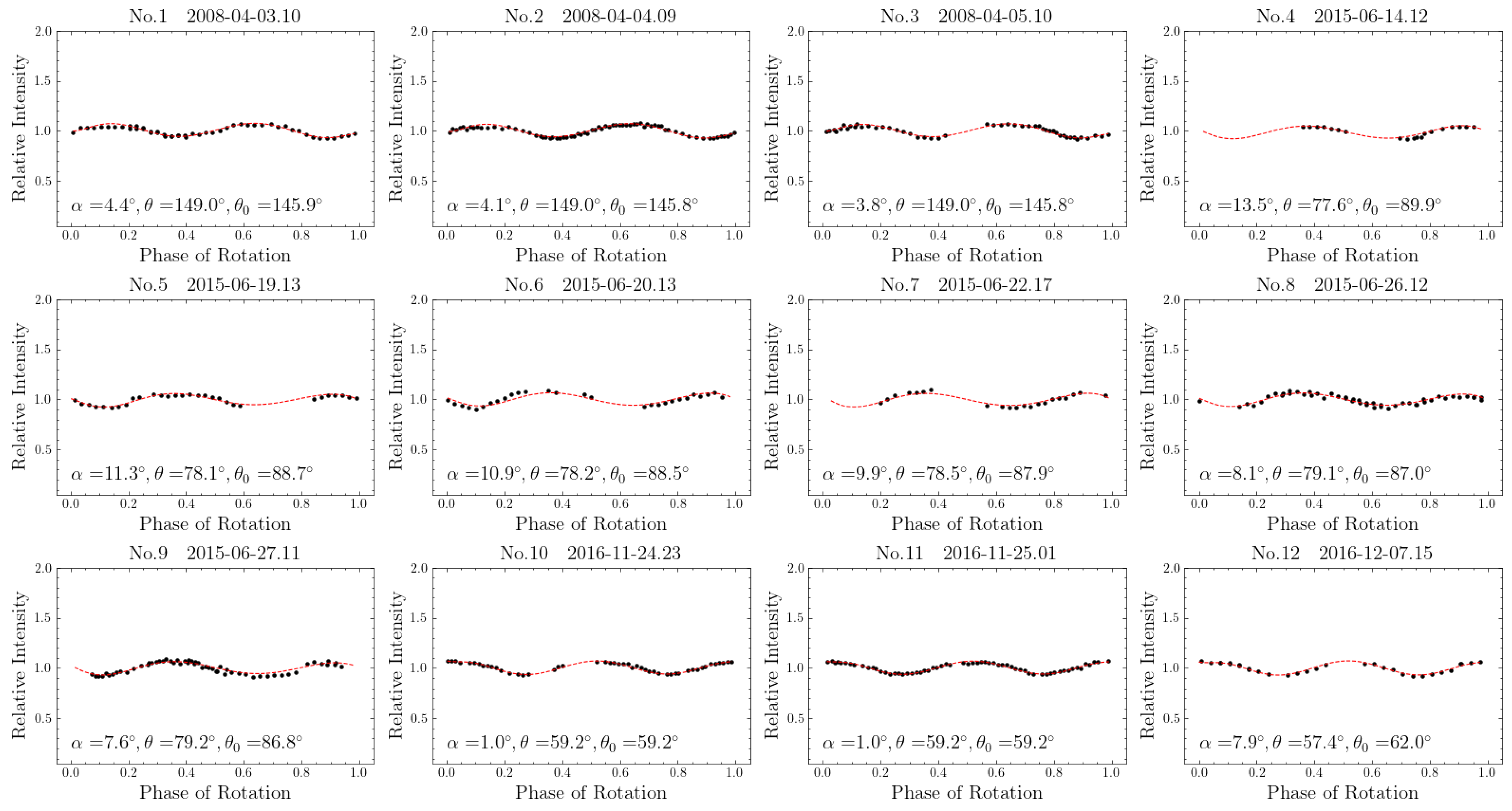
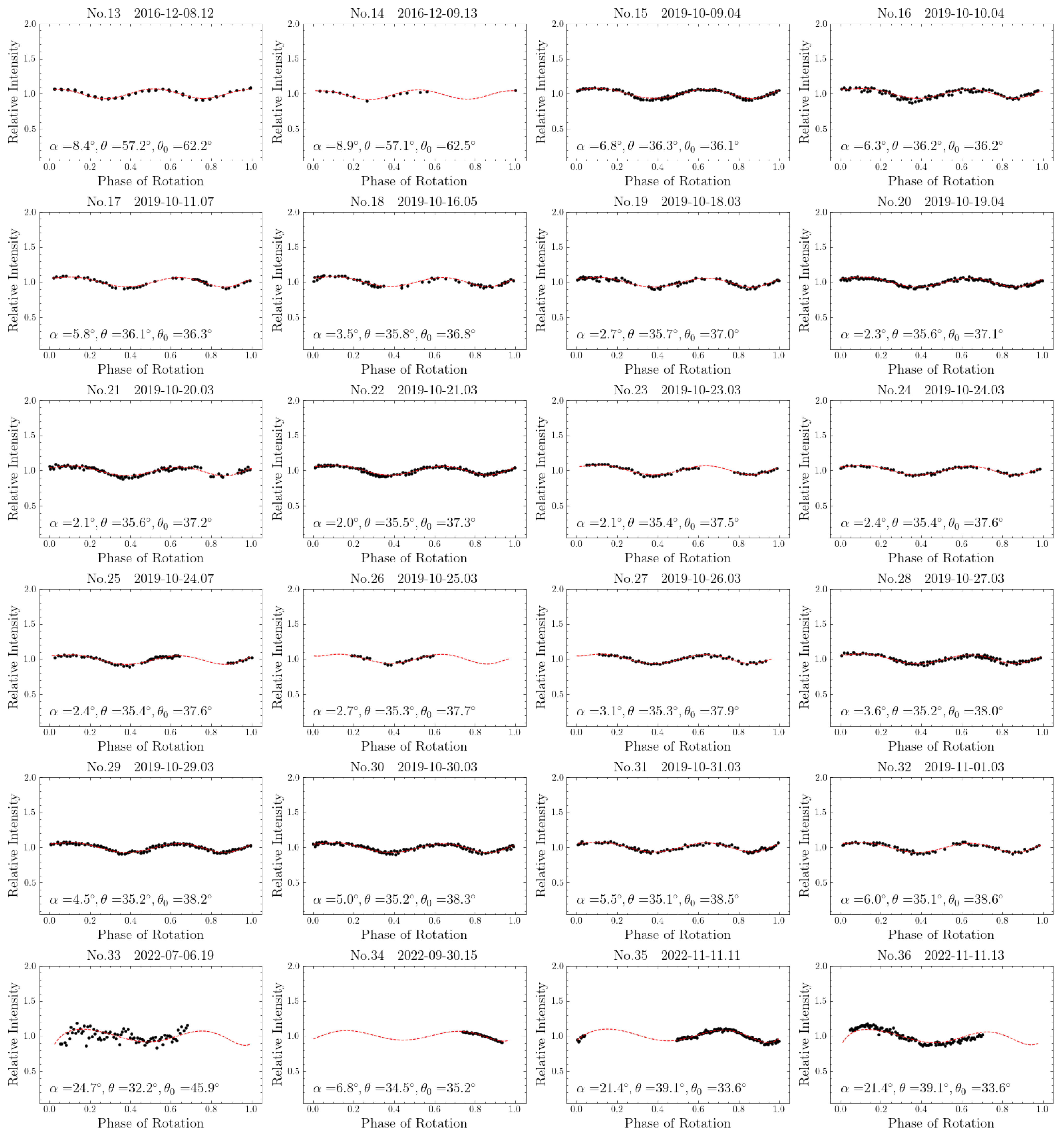
| ID | UT Date | r | Amplitude | Total | Observing | Ref. | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| [dd-mm-yyyy] | [AU] | [AU] | [°] | [°] | [°] | [mag] | [h] | Facility | ||
| 1 | 23-03-2008 | 1.149 | 2.129 | 6.7 | 176.2 | 12.8 | 0.25 | 6.1 | 0.3-m f/11.5 | |
| 2 | 28-03-2008 | 1.158 | 2.129 | 8.4 | 175.0 | 12.9 | 0.26 | 6.2 | 0.3-m f/11.5 | |
| 3 | 16-12-2017 | 1.360 | 2.251 | 13.7 | 117.5 | -0.9 | 0.88 | 4.5 | CNEOST | |
| 4 | 18-12-2017 | 1.346 | 2.250 | 12.8 | 117.2 | -0.8 | 0.94 | 4.5 | CNEOST | |
| 5 | 19-12-2017 | 1.338 | 2.249 | 12.3 | 117.0 | -0.7 | 0.54 | 4.0 | CNEOST | |
| 6 | 20-12-2017 | 1.331 | 2.248 | 11.8 | 116.9 | -0.7 | 0.31 | 0.5 | CNEOST | |
| 7 | 26-10-2020 | 1.455 | 2.410 | 8.5 | 51.1 | -10.9 | 0.74 | 7.3 | 0.40-m F/10 SCT | |
| 8 | 27-10-2020 | 1.452 | 2.410 | 8.1 | 50.9 | -10.9 | 0.77 | 7.1 | 0.40-m F/10 SCT | |
| 9 | 28-10-2020 | 1.448 | 2.409 | 7.7 | 50.6 | -10.9 | 0.78 | 7.0 | 0.40-m F/10 SCT | |
| 10 | 03-02-2022 | 1.621 | 2.126 | 26.4 | 207.4 | 9.1 | 1.01 | 3.7 | 0.40-m F/10 SCT | |
| 11 | 04-02-2022 | 1.610 | 2.126 | 26.2 | 207.6 | 9.2 | 1.10 | 4.0 | 0.40-m F/10 SCT | |
| 12 | 05-02-2022 | 1.599 | 2.126 | 26.1 | 207.8 | 9.3 | 1.10 | 4.3 | 0.40-m F/10 SCT | |
| 13 | 25-05-2022 | 1.337 | 2.150 | 20.5 | 197.1 | 11.1 | 0.87 | 2.5 | 0.7-m Maksutov system | |
| 14 | 26-05-2022 | 1.345 | 2.150 | 20.9 | 197.1 | 11.0 | 0.52 | 1.6 | 0.7-m Maksutov system | |
| 15 | 27-05-2022 | 1.354 | 2.151 | 21.2 | 197.1 | 10.9 | 0.91 | 2.9 | 0.7-m Maksutov system | |
| 16 | 16-07-2022 | 1.884 | 2.178 | 27.8 | 206.1 | 6.8 | 0.28 | 0.5 | 0.80-m f/10 | |
| 17 | 17-07-2022 | 1.897 | 2.178 | 27.8 | 206.4 | 6.8 | 0.17 | 0.2 | 0.80-m f/10 |
| ID | UT Date | r | Amplitude | Total | Observing | Ref. | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| [dd-mm-yyyy] | [AU] | [AU] | [°] | [°] | [°] | [mag] | [h] | Facility | ||
| 1 | 02-11-2015 | 1.557 | 2.535 | 4.9 | 51.8 | 2.3 | 0.49 | 8.0 | VARGBTEL | |
| 2 | 20-11-2015 | 1.537 | 2.515 | 4.1 | 47.4 | 3.1 | 0.50 | 8.5 | VARGBTEL | |
| 3 | 22-11-2015 | 1.540 | 2.513 | 5.0 | 46.9 | 3.1 | 0.48 | 5.5 | VARGBTEL | |
| 4 | 02-12-2015 | 1.575 | 2.501 | 9.8 | 44.6 | 3.5 | 0.58 | 4.8 | CNEOST | |
| 5 | 03-12-2015 | 1.580 | 2.500 | 10.2 | 44.4 | 3.5 | 0.48 | 5.8 | CNEOST | |
| 6 | 05-02-2016 | 2.198 | 2.427 | 24.0 | 46.6 | 4.3 | 0.51 | 2.3 | VARGBTEL | |
| 7 | 12-02-2016 | 2.282 | 2.419 | 24.0 | 48.4 | 4.3 | 0.68 | 3.8 | VARGBTEL | |
| 8 | 25-02-2016 | 2.433 | 2.404 | 23.6 | 52.2 | 4.3 | 0.77 | 3.4 | VARGBTEL | |
| 9 | 07-05-2021 | 1.352 | 2.338 | 6.9 | 211.0 | −0.6 | 0.80 | 6.4 | 0.4-m f/3.8 | |
| 10 | 10-05-2021 | 1.365 | 2.341 | 8.3 | 210.4 | −0.7 | 0.53 | 6.3 | 0.4-m f/3.8 | |
| 11 | 12-05-2021 | 1.375 | 2.343 | 9.3 | 210.0 | −0.8 | 0.55 | 5.4 | 0.4-m f/3.8 | |
| 12 | 02-06-2021 | 1.533 | 2.366 | 17.5 | 207.6 | −1.8 | 0.78 | 3.5 | 0.4-m f/3.8 | |
| 13 | 03-06-2021 | 1.542 | 2.367 | 17.8 | 207.5 | −1.8 | 0.51 | 1.8 | 0.4-m f/3.8 | |
| 14 | 08-08-2022 | 1.753 | 2.734 | 6.6 | 331.2 | −9.8 | 0.54 | 4.9 | 0.80-m f/10 | |
| 15 | 01-10-2022 | 1.960 | 2.739 | 15.6 | 321.1 | −7.9 | 0.45 | 1.0 | 0.80-m f/10 |

| 1 | https://astro.troja.mff.cuni.cz/projects/damit/ (accessed on 21 July 2024). |
| 2 | http://157.0.0.68:32280/alc/ (accessed on 5 October 2024). |
| 3 | https://noirlab.edu/science/programs/ctio/telescopes/tenants (accessed on 5 October 2024). |
| 4 | https://mpbulletin.org/ (accessed on 5 October 2024). |
| 5 | https://alcdef.org/ (accessed on 5 October 2024). |
| 6 | https://ssd.jpl.nasa.gov/horizons/ (accessed on 5 October 2024). |
| 7 | https://astro.troja.mff.cuni.cz/projects/damit/pages/documentation#anchor_light_curves (accessed on 5 October 2024). |
| 8 | https://minorplanet.info/php/lcdb.php (accessed on 5 October 2024). |
References
- Davis, D.R.; Weidenschilling, S.J.; Farinella, P.; Paolicchi, P.; Binzel, R.P. Asteroid collisional history: Effects on sizes and spins. In Asteroids II; Binzel, R.P., Gehrels, T., Matthews, M.S., Eds.; University of Arizona Press: Tucson, AZ, USA, 1989; pp. 805–826. [Google Scholar]
- Rossi, A.; Marzari, F.; Scheeres, D.J.; Jacobson, S. Effects of YORP-Induced Rotational Fission on the Asteroid Size Distribution at the Small Size End. In Proceedings of the 43rd Annual Lunar and Planetary Science Conference, The Woodlands, TX, USA, 19–23 March 2012; p. 2095. [Google Scholar]
- Scheeres, D.J.; Fahnestock, E.G.; Ostro, S.J.; Margot, J.L.; Benner, L.A.M.; Broschart, S.B.; Bellerose, J.; Giorgini, J.D.; Nolan, M.C.; Magri, C.; et al. Dynamical Configuration of Binary Near-Earth Asteroid (66391) 1999 KW4. Science 2006, 314, 1280–1283. [Google Scholar] [CrossRef] [PubMed]
- Nolan, M.C.; Magri, C.; Howell, E.S.; Benner, L.A.M.; Giorgini, J.D.; Hergenrother, C.W.; Hudson, R.S.; Lauretta, D.S.; Margot, J.L.; Ostro, S.J.; et al. Shape model and surface properties of the OSIRIS-REx target Asteroid (101955) Bennu from radar and lightcurve observations. Icarus 2013, 226, 629–640. [Google Scholar] [CrossRef]
- Li, X.; Scheeres, D.J. The shape and surface environment of 2016 HO3. Icarus 2021, 357, 114249. [Google Scholar] [CrossRef]
- Ďurech, J.; Sidorin, V.; Kaasalainen, M. DAMIT: A database of asteroid models. Astron. Astrophys. 2010, 513, A46. [Google Scholar] [CrossRef]
- Kaasalainen, M.; Torppa, J. Optimization Methods for Asteroid Lightcurve Inversion: I. Shape Determination. Icarus 2001, 153, 24–36. [Google Scholar] [CrossRef]
- Kaasalainen, M.; Torppa, J.; Muinonen, K. Optimization Methods for Asteroid Lightcurve Inversion: II. The Complete Inverse Problem. Icarus 2001, 153, 37–51. [Google Scholar] [CrossRef]
- Kaasalainen, M.; Ďurech, J. Asteroid models from generalised projections: Essential facts for asteroid modellers and geometric inverse problem solvers. arXiv 2020, arXiv:2005.09947. [Google Scholar]
- Zhaori, G.T.; Zhao, H.B.; Liu, W.; Li, B. Correction of Off-axis Aberration of the China Near Earth Object Survey Telescope with 10k CCD. Acta Astron. Sin. 2019, 60, 52. [Google Scholar]
- Molotov, I.; Agapov, V.; Kouprianov, V.; Titenko, V.; Rumyantsev, V.; Biryukov, V.; Borisov, G.; Burtsev, Y.; Khutorovsky, Z.; Kornienko, G.; et al. ISON Worldwide Scientific Optical Network. In Proceedings of the Fifth European Conference on Space Debris, Darmstadt, Germany, 30 March–2 April 2009; Lacoste, H., Ed.; ESA Special Publication: Noordwijk, The Netherlands, 2009; Volume 672, p. 7. [Google Scholar]
- Tody, D. The IRAF Data Reduction and Analysis System. In Proceedings of the Instrumentation in Astronomy VI, Tucson, AZ, USA, 1–2 March 1986; Crawford, D.L., Ed.; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series. SPIE: St. Bellingham, WA, USA, 1986; Volume 627, p. 733. [Google Scholar] [CrossRef]
- Tody, D. IRAF in the Nineties. In Astronomical Data Analysis Software and Systems II; Hanisch, R.J., Brissenden, R.J.V., Barnes, J., Eds.; Astronomical Society of the Pacific Conference Series; Astronomical Society of the Pacific: San Francisco, CA, USA, 1993; Volume 52, p. 173. [Google Scholar]
- Gaia Collaboration; Vallenari, A.; Brown, A.G.A.; Prusti, T.; de Bruijne, J.H.J.; Arenou, F.; Babusiaux, C.; Biermann, M.; Creevey, O.L.; Ducourant, C.; et al. Gaia Data Release 3. Summary of the content and survey properties. Astron. Astrophys. 2023, 674, A1. [Google Scholar] [CrossRef]
- Zacharias, N.; Finch, C.T.; Girard, T.M.; Henden, A.; Bartlett, J.L.; Monet, D.G.; Zacharias, M.I. The Fourth US Naval Observatory CCD Astrograph Catalog (UCAC4). Astron. J. 2013, 145, 44. [Google Scholar] [CrossRef]
- Howell, S.B. Handbook of CCD Astronomy; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Demleitner, M.; Accomazzi, A.; Eichhorn, G.; Grant, C.S.; Kurtz, M.J.; Murray, S.S. ADS’s Dexter Data Extraction Applet. In Proceedings of the Astronomical Data Analysis Software and Systems X, Boston, MA, USA, 12–15 November 2000; Harnden, F.R.J., Primini, F.A., Payne, H.E., Eds.; Astronomical Society of the Pacific Conference Series. Astronomical Society of the Pacific: San Francisco, CA, USA, 2001; Volume 238, p. 321. [Google Scholar]
- Apostolovska, G.; Kostov, A.; Donchev, Z.; Ovcharov, E. Lightcurve of 1563 Noel at Low Phase Angle. Minor Planet Bull. 2017, 44, 143. [Google Scholar]
- Brinsfield, J.W. Asteroid Lightcurve Analysis at the via Capote Observatory: First Quarter 2008. Minor Planet Bull. 2008, 35, 119–122. [Google Scholar]
- Carbognani, A. Lightcurve and Rotational Period of Asteroids 1456 Saldanha, 2294 Andronikov, and 2006 NM. Minor Planet Bull. 2007, 34, 4–5. [Google Scholar]
- Carbo, L.; Green, D.; Kragh, K.; Krotz, J.; Meiers, A.; Patino, B.; Pligge, Z.; Shaffer, N.; Ditteon, R. Asteroid Lightcurve Analysis at the Oakley Southern Sky Observatory: 2008 October thru 2009 March. Minor Planet Bull. 2009, 36, 152–157. [Google Scholar]
- Harris, A.W.; Young, J.W.; Bowell, E.; Martin, L.J.; Millis, R.L.; Poutanen, M.; Scaltriti, e.a. Photoelectric observations of asteroids 3, 24, 60, 261, and 863. Icarus 1989, 77, 171–186. [Google Scholar] [CrossRef]
- Warner, B.D.; Harris, A.W.; Pravec, P.; Durech, J.; Benner, L.A.M. Lightcurve Photometry Opportunities: July–September 2008. Minor Planet Bull. 2008, 35, 139–141. [Google Scholar]
- Warner, B.D.; Harris, A.W.; Pravec, P. The asteroid lightcurve database. Icarus 2009, 202, 134–146. [Google Scholar] [CrossRef]
- Ďurech, J.; Hanuš, J. Reconstruction of asteroid spin states from Gaia DR3 photometry. Astron. Astrophys. 2023, 675, A24. [Google Scholar] [CrossRef]
- Fowler, J.W.; Chillemi, J.R. IRAS Minor Planet Survey; Phillips Laboratory Technical Report No. PL-TR-92-2049; Phillips Laboratory, Directorate of Geophysics, Air Force Materiel Command: Hanscom Air Force Base, MA, USA, 1992. [Google Scholar]
- Muinonen, K.; Penttilä, A.; Cellino, A.; Belskaya, I.N.; Delbò, M.; Levasseur-Regourd, A.C.; Tedesco, E.F. Asteroid photometric and polarimetric phase curves: Joint linear-exponential modeling. Meteorit. Planet. Sci. 2009, 44, 1937–1946. [Google Scholar] [CrossRef]
- Magnusson, P.; Dahlgren, M.; Barucci, M.A.; Jorda, L.; Binzel, R.P.; Slivan, S.M.; Blanco, C.; Riccioli, D.; Buratti, B.J.; Colas, F.; et al. Photometric Observations and Modeling of Asteroid 1620 Geographos. Icarus 1996, 123, 227–244. [Google Scholar] [CrossRef]
- Lu, X.; Zhao, H.; You, Z. Cellinoid Shape Model for Asteroids. Earth Moon Planets 2014, 112, 73–87. [Google Scholar] [CrossRef]
- Kaasalainen, M.; Lamberg, L. Inverse problems of generalized projection operators. Inverse Probl. 2006, 22, 749–769. [Google Scholar] [CrossRef]
- Stephens, R.D. Asteroids Observed from CS3: 2016–September. Minor Planet Bull. 2017, 44, 49–52. [Google Scholar] [PubMed]
- Skiff, B.A.; McLelland, K.P.; Sanborn, J.J.; Pravec, P.; Koehn, B.W. Lowell Observatory Near-Earth Asteroid Photometric Survey (NEAPS): Paper 3. Minor Planet Bull. 2019, 46, 238–265. [Google Scholar]
- Stephens, R.D. Asteroids Observed from CS3: 2015 July–September. Minor Planet Bulletin 2016, 43, 52–56. [Google Scholar]
- Stephens, R.D.; Coley, D.R.; Warner, B.D. Main-belt Asteroids Observed from CS3: 2021 January to March. Minor Planet Bull. 2021, 48, 246–267. [Google Scholar]
- Hasegawa, S.; Miyasaka, S.; Mito, H.; Sarugaku, Y.; Ozawa, T.; Kuroda, D.; Nishihara, S.; Harada, A.; Yoshida, M.; Yanagisawa, K.; et al. Lightcurve survey of V-type asteroids in the inner asteroid belt. Publ. Astron. Soc. Jpn. 2014, 66, 54. [Google Scholar] [CrossRef]
- Oszkiewicz, D.A.; Skiff, B.A.; Moskovitz, N.; Kankiewicz, P.; Marciniak, A.; Licandro, J.; Galiazzo, M.A.; Zeilinger, W.W. Non-Vestoid candidate asteroids in the inner main belt. Astron. Astrophys. 2017, 599, A107. [Google Scholar] [CrossRef]
- Polishook, D. Lightcurves and Spin Periods from the Wise Observatory: 2008 August–2009 March. Minor Planet Bull. 2009, 36, 104–107. [Google Scholar]
- Erasmus, N.; McNeill, A.; Mommert, M.; Trilling, D.E.; Sickafoose, A.A.; van Gend, C. Taxonomy and Light-curve Data of 1000 Serendipitously Observed Main-belt Asteroids. Astrophys. J. Suppl. Ser. 2018, 237, 19. [Google Scholar] [CrossRef]
- Oey, J. Lightcurve Analysis of Asteroids from Leura and Kingsgrove Observatories in the First Half of 2008. Minor Planet Bull. 2009, 36, 4–6. [Google Scholar]
- Stephens, R.D.; Warner, B.D. Main-Belt Asteroids Observed from CS3: 2019 October to December. Minor Planet Bull. 2020, 47, 125–133. [Google Scholar]
- Stephens, R.D.; Warner, B.D. Main-belt Asteroids Observed from CS3: 2020 October to December. Minor Planet Bull. 2021, 48, 150–158. [Google Scholar]








| Asteroid Name | Date | Filters | Observers | Observatory | MPC Code * | |
|---|---|---|---|---|---|---|
| (2233) Kuznetsov | 06–11/02/2018 | 5 | Bessel I | CNEOST Team | Xuyi, China | D29 |
| 27/05/2022 | 1 | Rc | Jian Chen; Jun Tian | Yaoan, China | O49 | |
| 28–29/05/2022 | 2 | Bessel V | Leonid Elenin | Abastumani, Georgian | 119 | |
| (2253) Espinette | 20/01/2017–19/02/2021 | 7 | Bessel R | CNEOST Team | Xuyi, China | D29 |
| 29/04/2022 | 1 | Bessel R | CNEOST Team | Ali, China | N56 | |
| 12/07/2022–16/11/2022 | 4 | Rc | Jian Chen; Jun Tian | Yaoan, China | O49 | |
| (2294) Andronikov | 06–09/02/2016 | 4 | Bessel R | CNEOST Team | Xuyi, China | D29 |
| 13–21/05/2022 | 2 | Lum | Leonid Elenin | Cerro Tolollo, Chile | 807 | |
| (4796) Lewis | 26–27/02/2017 | 2 | Bessel R | CNEOST Team | Xuyi, China | D29 |
| 10–11/07/2022 | 2 | Rc | Jian Chen; Jun Tian | Yaoan, China | O49 | |
| (1563) Noel | 07–09/12/2016 | 3 | Bessel R | CNEOST Team | Xuyi, China | D29 |
| 30/09/2022–11/11/2022 | 4 | Rc | Jian Chen; Jun Tian | Yaoan, China | O49 | |
| (2912) Lapalma | 16–20/12/2017 | 4 | Bessel R | CNEOST Team | Xuyi, China | D29 |
| 25–27/05/2022 | 3 | Bessel V | Leonid Elenin | Abastumani, Georgian | 119 | |
| 17/07/2022 | 2 | Rc | Jian Chen; Jun Tian | Yaoan, China | O49 | |
| (5150) Fellini | 02–04/12/2015 | 2 | Bessel R | CNEOST Team | Xuyi, China | D29 |
| 03/06/2021–07/05/2021 | 5 | Bessel R | CNEOST Team | Ali, China | N56 | |
| 01/10/2022–08/08/2022 | 2 | Rc | Jian Chen; Jun Tian | Yaoan, China | O49 |
| Asteroid | * | H | Albedo | ||
|---|---|---|---|---|---|
| [km] | [mag] | [h] | [h] | ||
| (2113) Ehrdni | 6.81 | 3.2 | 0.2 | 13.2 | 5.035 |
| (2640) Hallstrom | 7.16 | 3.09 | 0.2 | 22.9 | 11.17 |
| (4334) Foo | 11.3 | 3.24 | 0.07 | 7.42 | 11.04 |
| (7147) Feijth | 2.84 | 5.22 | 0.179 | 5.318 | 8.505 |
| (11202) Teddunham | 7.58 | 3.08 | 0.18 | 7.414 | 15.505 |
| (12659) Schlegel | 2.59 | 5.42 | 0.179 | 9.7 | 5.6975 |
| (13014) Hasslacher | 11.95 | 3.4 | 0.054 | 7.62 | 11.8075 |
| (16115) 1999 XH25 | 12.48 | 3.28 | 0.0553 | 14.68 | 11.095 |
| (17953) 1999 JB20 | 10.32 | 3.66 | 0.057 | 37.279 | 4.885 |
| (38663) 2000 OK49 | 2.8 | 5.13 | 0.2 | 5.51 | 6.115 |
| (42535) 1995 VN9 | 1.77 | 6.12 | 0.2 | 2.37 | 6.1375 |
| (43321) 2000 JR52 | 2.85 | 5.09 | 0.2 | 4.75 | 3.7575 |
| (44576) 1999 GJ10 | 5.83 | 4.9 | 0.057 | 0.48 | 5.5425 |
| (55002) 2001 QF19 | 4.11 | 4.61 | 0.15 | 4.56 | 5.0625 |
| (60381) 2000 AX180 | 15.62 | 2.76 | 0.057 | 28.96 | 5.885 |
| (82333) 2001 LF7 | 5.59 | 4.99 | 0.057 | 2.303 | 19.3225 |
| (85338) 1995 SX37 | 2.06 | 5.8 | 0.2 | 1.1 | 3.5825 |
| (90050) 2002 VQ23 | 2.85 | 5.84 | 0.1 | 17.3 | 5.6375 |
| (103541) 2000 BU18 | 4.48 | 5.47 | 0.057 | 7.11 | 6.035 |
| (282631) 2005 SV1 | 2.76 | 5.63 | 0.13 | 16.8 | 6.41 |
| Asteroid | Axial Ratio | Obliquity * | |||
|---|---|---|---|---|---|
| [h] | [deg], [deg] | [deg] | [km] | ||
| (2233) Kuznetsov | a/c = 1.4, b/c = 1.2 | 154.6 | 6.70 | ||
| 152.4 | |||||
| (2294) Andronikov | a/c = 2.0, b/c = 1.4 | 55.1 | 15.1 | ||
| 50.5 | |||||
| (2253) Espinette | a/c = 1.2, b/c = 1.0 | 123.9 | 6.23 | ||
| 125.0 | |||||
| (4796) Lewis | a/c = 1.9, b/c = 1.1 | 56.6 | 4.20 | ||
| 61.5 | |||||
| (1563) Noel | a/c = 2.5, b/c = 2.2 | 149.3 | 7.24 | ||
| 152.7 | |||||
| (2912) Lapalma | a/c = 2.0, b/c = 1.0 | 151.2 | 6.52 | ||
| 151.9 | |||||
| (5150) Fellini | a/c = 2.2, b/c = 1.0 | 131.3 | 5.40 | ||
| 134.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, J.; Zhao, H.; Li, B.; Zhang, Y.; Chen, J.; Elenin, L.; Lu, X. Photometry and Models of Seven Main-Belt Asteroids. Universe 2024, 10, 395. https://doi.org/10.3390/universe10100395
Tian J, Zhao H, Li B, Zhang Y, Chen J, Elenin L, Lu X. Photometry and Models of Seven Main-Belt Asteroids. Universe. 2024; 10(10):395. https://doi.org/10.3390/universe10100395
Chicago/Turabian StyleTian, Jun, Haibin Zhao, Bin Li, Yongxiong Zhang, Jian Chen, Leonid Elenin, and Xiaoping Lu. 2024. "Photometry and Models of Seven Main-Belt Asteroids" Universe 10, no. 10: 395. https://doi.org/10.3390/universe10100395
APA StyleTian, J., Zhao, H., Li, B., Zhang, Y., Chen, J., Elenin, L., & Lu, X. (2024). Photometry and Models of Seven Main-Belt Asteroids. Universe, 10(10), 395. https://doi.org/10.3390/universe10100395








