Improved Small Molecule Identification through Learning Combinations of Kernel Regression Models
Abstract
1. Introduction
2. Materials and Methods
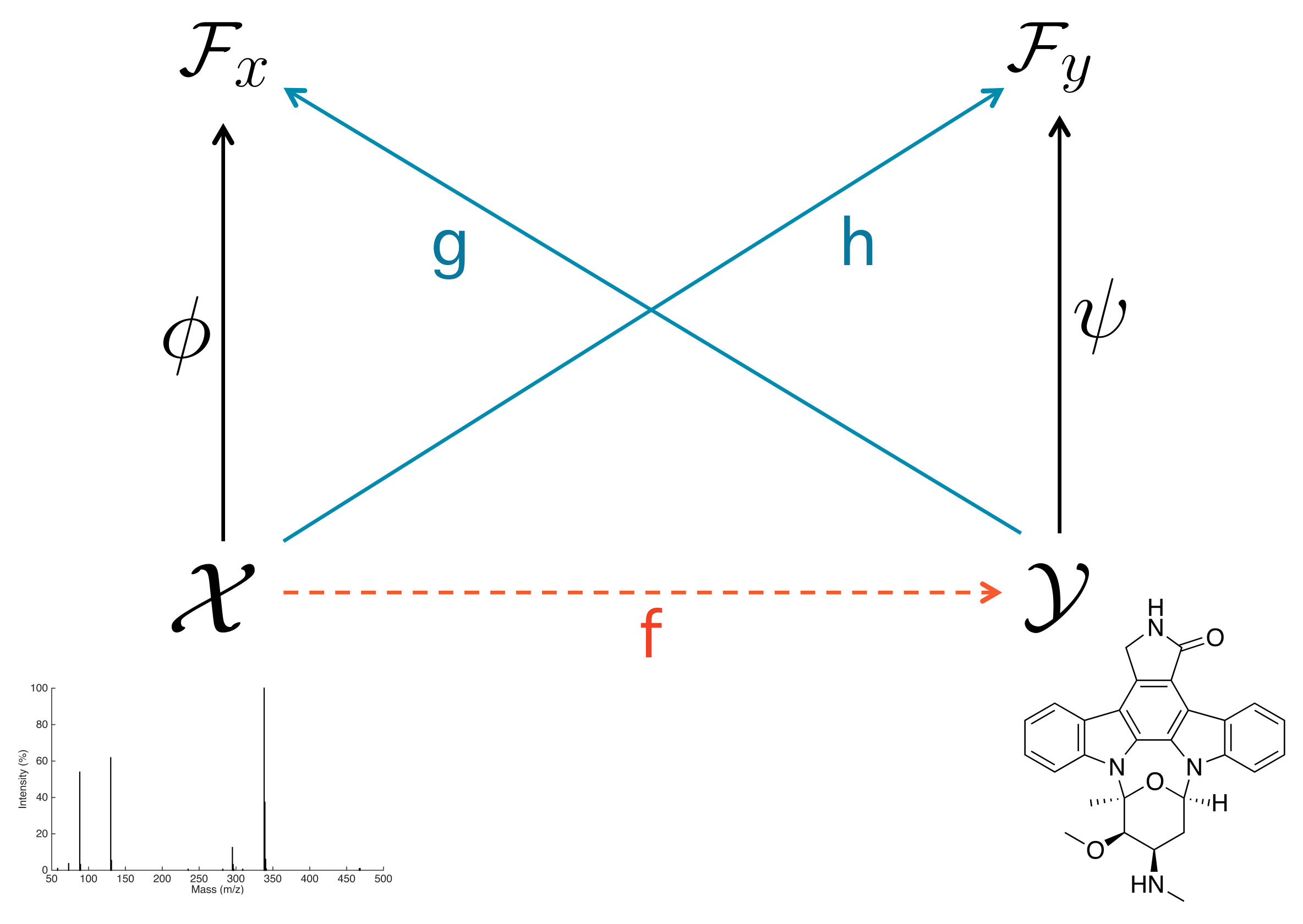
2.1. Input–Output Kernel Regression
2.2. IOKRreverse: Mapping Kernel Representations of Molecules to Kernel Representation of MS/MS Spectra
2.3. Combining Multiple Models to Maximize Top-1 Accuracy
| Algorithm 1:Mini-batch subgradient descent for the score aggregation. |
 |
2.4. Kernels
2.4.1. Input Kernels
2.4.2. Output Kernels
3. Results
3.1. Experimental Protocol
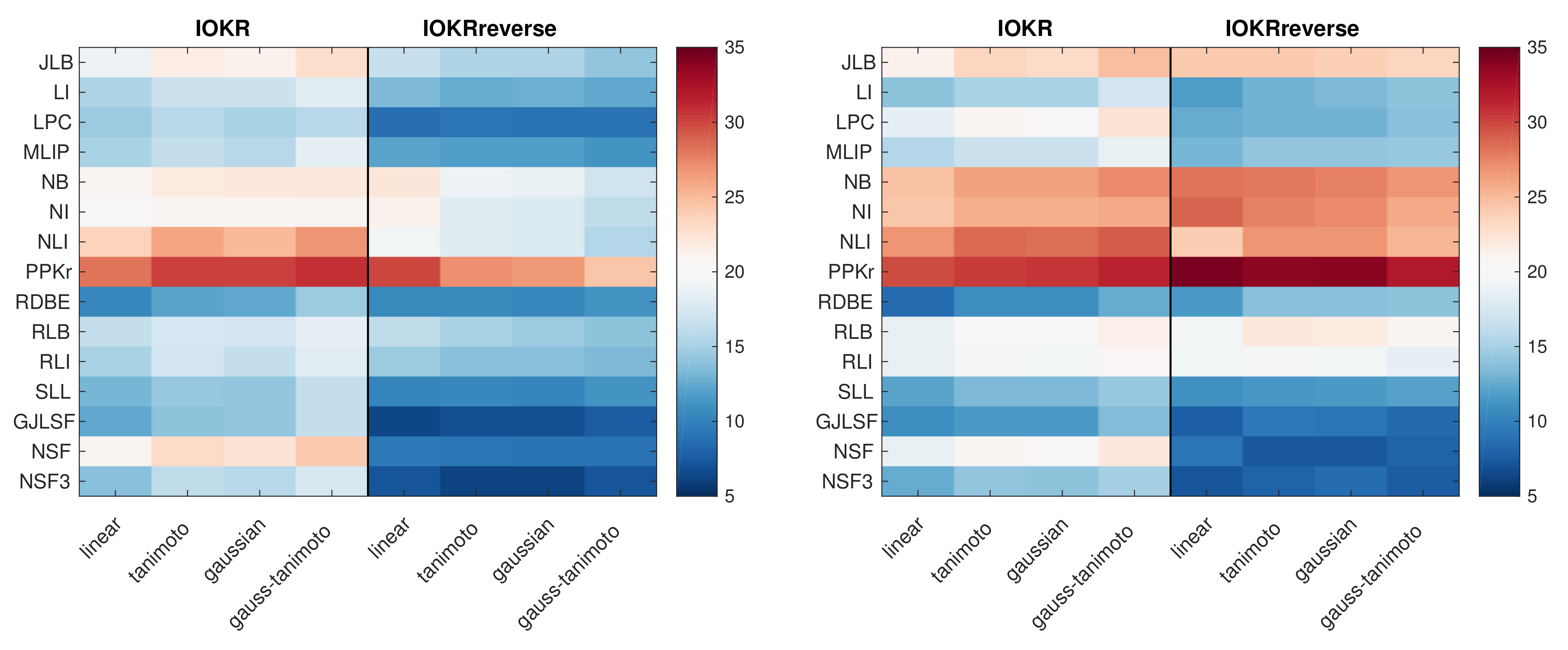
3.2. Results Obtained with IOKR and IOKRreverse Using Different Kernels
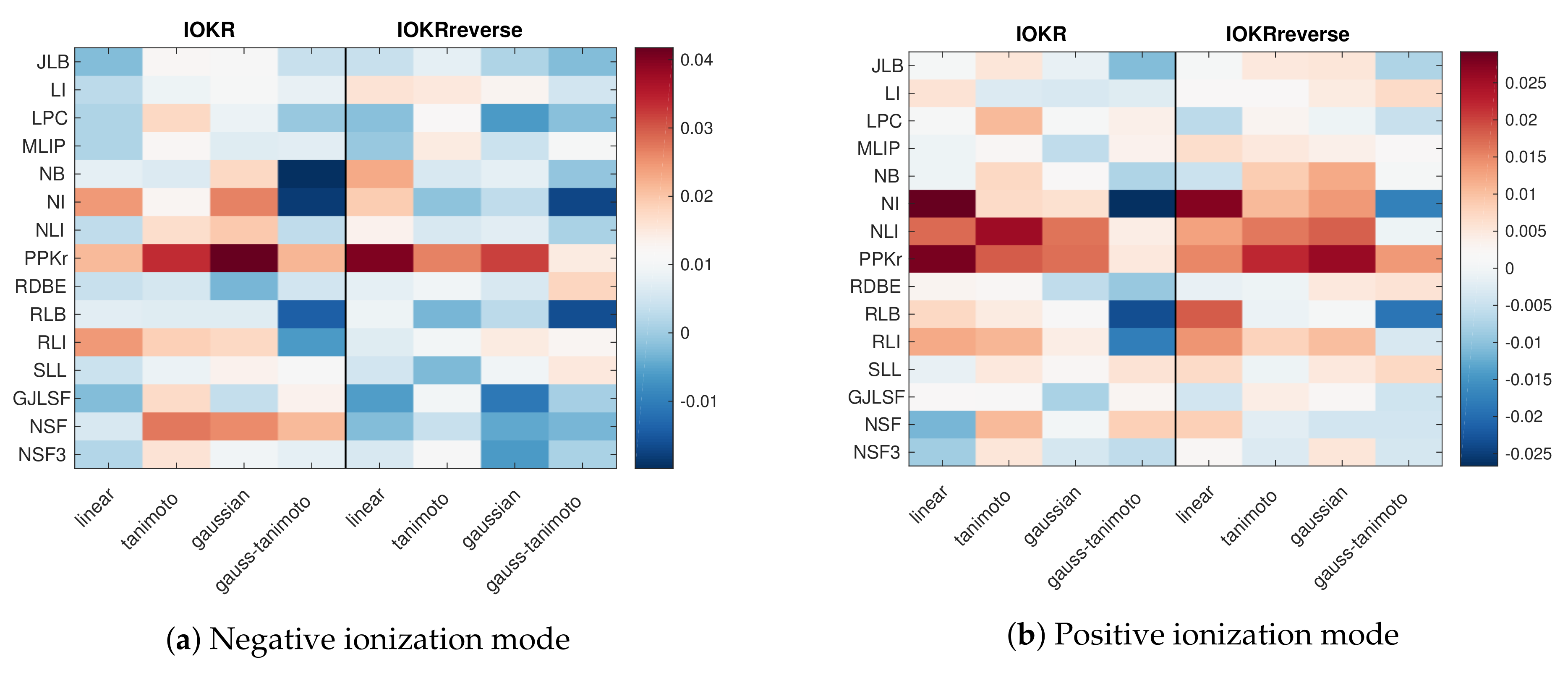
3.3. Weights Learned by the Aggregation Model
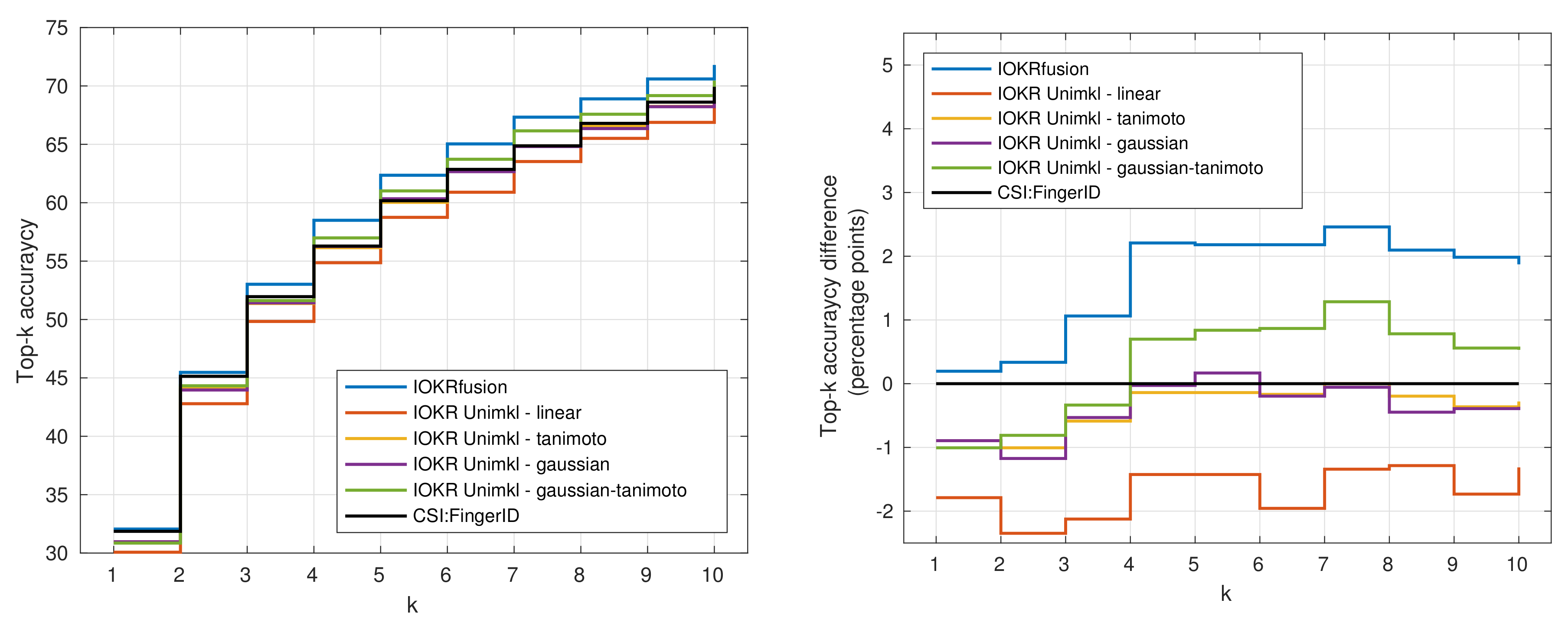
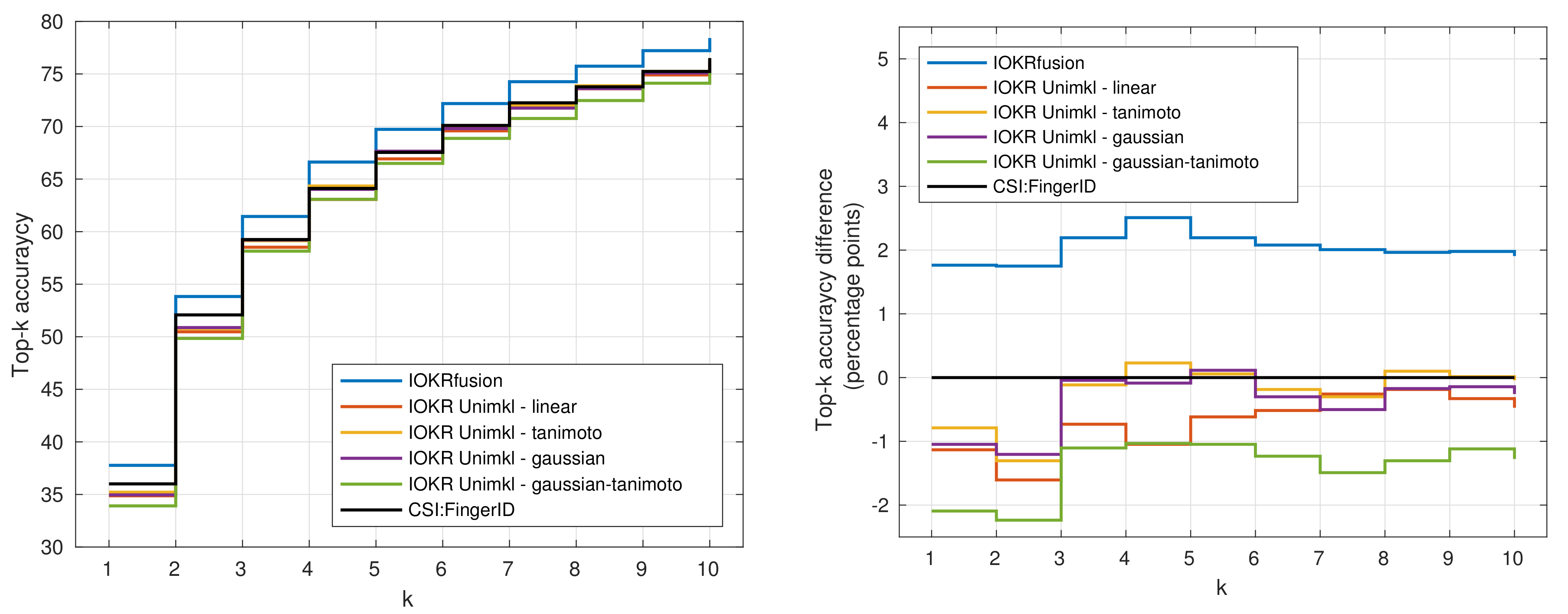
3.4. Results for Combined Models
3.5. Running Times
4. Discussion
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, M.; Carver, J.J.; Phelan, V.V.; Sanchez, L.M.; Garg, N.; Peng, Y.; Nguyen, D.D.; Watrous, J.; Kapono, C.A.; Luzzatto-Knaan, T.; et al. Sharing and community curation of mass spectrometry data with Global Natural Products Social Molecular Networking. Nat. Biotechnol. 2016, 34, 828–837. [Google Scholar] [CrossRef] [PubMed]
- Horai, H.; Arita, M.; Kanaya, S.; Nihei, Y.; Ikeda, T.; Suwa, K.; Ojima, Y.; Tanaka, K.; Tanaka, S.; Aoshima, K.; et al. MassBank: A public repository for sharing mass spectral data for life sciences. J. Mass Spectrom. 2010, 45, 703–714. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, D.H.; Nguyen, C.H.; Mamitsuka, H. Recent advances and prospects of computational methods for metabolite identification: A review with emphasis on machine learning approaches. Briefings Bioinform. 2018. [Google Scholar] [CrossRef] [PubMed]
- Heinonen, M.; Shen, H.; Zamboni, N.; Rousu, J. Metabolite identification and molecular fingerprint prediction through machine learning. Bioinformatics 2012, 28, 2333–2341. [Google Scholar] [CrossRef] [PubMed]
- Shen, H.; Zamboni, N.; Heinonen, M.; Rousu, J. Metabolite identification through machine learning—Tackling CASMI challenge using fingerID. Metabolites 2013, 3, 484–505. [Google Scholar] [CrossRef] [PubMed]
- Djoumbou-Feunang, Y.; Pon, A.; Karu, N.; Zheng, J.; Li, C.; Arndt, D.; Gautam, M.; Allen, F.; Wishart, D.S. CFM-ID 3.0: Significantly Improved ESI-MS/MS Prediction and Compound Identification. Metabolites 2019, 9, 72. [Google Scholar] [CrossRef] [PubMed]
- Allen, F.; Pon, A.; Wilson, M.; Greiner, R.; Wishart, D. CFM-ID: A web server for annotation, spectrum prediction and metabolite identification from tandem mass spectra. Nucleic Acids Res. 2014, 42, W94–W99. [Google Scholar] [CrossRef] [PubMed]
- Dührkop, K.; Shen, H.; Meusel, M.; Rousu, J.; Böcker, S. Searching molecular structure databases with tandem mass spectra using CSI:FingerID. Proc. Natl. Acad. Sci. USA 2015, 112, 12580–12585. [Google Scholar] [CrossRef] [PubMed]
- Brouard, C.; Shen, H.; Dührkop, K.; d’Alché-Buc, F.; Böcker, S.; Rousu, J. Fast metabolite identification with Input Output Kernel Regression. Bioinformatics 2016, 32, i28–i36. [Google Scholar] [CrossRef]
- Brouard, C.; Bach, E.; Böcker, S.; Rousu, J. Magnitude-preserving ranking for structured outputs. In Proceedings of the Asian Conference on Machine Learning, Seoul, Korea, 15–17 November 2017; pp. 407–422. [Google Scholar]
- Laponogov, I.; Sadawi, N.; Galea, D.; Mirnezami, R.; Veselkov, K.A. ChemDistiller: an engine for metabolite annotation in mass spectrometry. Bioinformatics 2018, 34, 2096–2102. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Nguyen, C.H.; Mamitsuka, H. SIMPLE: Sparse Interaction Model over Peaks of moLEcules for fast, interpretable metabolite identification from tandem mass spectra. Bioinformatics 2018, 34, i323–i332. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, D.H.; Nguyen, C.H.; Mamitsuka, H. ADAPTIVE: leArning DAta-dePendenT, concIse molecular VEctors for fast, accurate metabolite identification from tandem mass spectra. Bioinformatics 2019, 35, i164–i172. [Google Scholar] [CrossRef]
- Dührkop, K.; Fleischauer, M.; Ludwig, M.; Aksenov, A.A.; Melnik, A.V.; Meusel, M.; Dorrestein, P.C.; Rousu, J.; Böcker, S. SIRIUS 4: A rapid tool for turning tandem mass spectra into metabolite structure information. Nat. Methods 2019, 16, 299–302. [Google Scholar] [CrossRef] [PubMed]
- CSI:FingerID Passed 10 Million Compound Queries. Available online: https://bio.informatik.uni-jena.de/2019/01/csifingerid-passed-10-million-compound-queries/ (accessed on 26 January 2019).
- Schymanski, E.L.; Ruttkies, C.; Krauss, M.; Brouard, C.; Kind, T.; Dührkop, K.; Allen, F.; Vaniya, A.; Verdegem, D.; Böcker, S.; et al. Critical assessment of small molecule identification 2016: Automated methods. J. Cheminform. 2017, 9, 22. [Google Scholar] [CrossRef] [PubMed]
- Webpage of CASMI 2017 contest. Available online: http://casmi-contest.org/2017/index.shtml (accessed on 31 July 2019).
- Wolf, S.; Schmidt, S.; Müller-Hannemann, M.; Neumann, S. In silico fragmentation for computer assisted identification of metabolite mass spectra. BMC Bioinform. 2010, 11, 148. [Google Scholar] [CrossRef] [PubMed]
- Ruttkies, C.; Schymanski, E.L.; Wolf, S.; Hollender, J.; Neumann, S. MetFrag relaunched: incorporating strategies beyond in silico fragmentation. J. Cheminform. 2016, 8, 3. [Google Scholar] [CrossRef] [PubMed]
- Shen, H.; Dührkop, K.; Böcker, S.; Rousu, J. Metabolite identification through multiple kernel learning on fragmentation trees. Bioinfomatics 2014, 30, i157–i164. [Google Scholar] [CrossRef] [PubMed]
- Bakir, G.H.; Hofmann, T.; Schölkopf, B.; Smola, A.J.; Taskar, B.; Vishwanathan, S.V.N. Predicting Structured Data (Neural Information Processing); The MIT Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Brouard, C.; Szafranski, M.; d’Alché-Buc, F. Input Output Kernel Regression: supervised and semi-supervised structured output prediction with operator-valued kernels. J. Mach. Learn. Res. 2016, 17, 1–48. [Google Scholar]
- Cortes, C.; Mohri, M.; Rostamizadeh, A. Algorithms for Learning Kernels Based on Centered Alignment. J. Mach. Learn. Res. 2012, 13, 795–828. [Google Scholar]
- Hazan, T.; Keshet, J.; McAllester, D.A. Direct loss minimization for structured prediction. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 6–11 December 2010; pp. 1594–1602. [Google Scholar]
- Bolton, E.; Wang, Y.; Thiessen, P.; Bryant, S. Chapter 12—PubChem: Integrated platform of small molecules and biological activities. Annu. Rep. Comput. Chem. 2008, 4, 217–241. [Google Scholar]
- Radovanovic, M.; Nanopoulos, A.; Ivanovic, M. Hubs in Space: Popular Nearest Neighbors in High-Dimensional Data. J. Mach. Learn. Res. 2010, 11, 2487–2531. [Google Scholar]
- Shigeto, Y.; Suzuki, I.; Hara, K.; Shimbo, M.; Matsumoto, Y. Ridge regression, hubness, and zero-shot learning. In Machine Learning and Knowledge Discovery in Databases; Springer: Berlin, Germany, 2015; pp. 135–151. [Google Scholar]
- Larochelle, H.; Erhan, D.; Bengio, Y. Zero-data Learning of New Tasks. In Proceedings of the Twenty-Third AAAI Conference on Artificial Intelligence, AAAI 2008, Chicago, IL, USA, 13–17 July 2008; pp. 646–651. [Google Scholar]
- Xian, Y.; Schiele, B.; Akata, Z. Zero-Shot Learning—The Good, the Bad and the Ugly. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2017), Honolulu, HI, USA, 21–26 July 2017; pp. 3077–3086. [Google Scholar]
- Baltrušaitis, T.; Ahuja, C.; Morency, L.P. Multimodal machine learning: A survey and taxonomy. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 41, 423–443. [Google Scholar] [CrossRef]
- Tsochantaridis, I.; Joachims, T.; Hofmann, T.; Altun, Y. Large margin methods for structured and interdependent output variables. J. Mach. Learn. Res. 2005, 6, 1453–1484. [Google Scholar]
- Böcker, S.; Rasche, F. Towards de novo identification of metabolites by analyzing tandem mass spectra. Bioinfomatics 2008, 24, i49–i55. [Google Scholar] [CrossRef]
- Böcker, S.; Dührkop, K. Fragmentation trees reloaded. J. Cheminform. 2016, 8, 5. [Google Scholar] [CrossRef]
- Dührkop, K. Computational Methods for Small Molecule Identification. Ph.D. Thesis, Friedrich-Schiller-Universität Jena, Jena, Germany, 2018. [Google Scholar]
- Ralaivola, L.; Swamidass, S.; Saigo, H.; Baldi, P. Graph kernels for chemical informatics. Neural Netw. 2005, 18, 1093–1110. [Google Scholar] [CrossRef]
- Willighagen, E.L.; Mayfield, J.W.; Alvarsson, J.; Berg, A.; Carlsson, L.; Jeliazkova, N.; Kuhn, S.; Pluskal, T.; Rojas-Chertó, M.; Spjuth, O.; et al. The Chemistry Development Kit (CDK) v2.0: atom typing, depiction, molecular formulas, and substructure searching. J. Cheminform. 2017, 9, 33. [Google Scholar] [CrossRef]
- Klekota, J.; Roth, F. Chemical substructures that enrich for biological activity. Bioinformatics 2008, 24, 2518–2525. [Google Scholar] [CrossRef]
- Rogers, D.; Hahn, M. Extended-Connectivity Fingerprints. J. Chem. Inf. Model. 2010, 50, 742–754. [Google Scholar] [CrossRef]
| Name | Description | |
|---|---|---|
| LI | Loss intensity | counts the number of common losses weighted by the intensity |
| RLB | Root loss binary | counts the number of common losses from the root to some node |
| RLI | Root loss intensity | weighted variant of RLB that uses the intensity of terminal nodes |
| JLB | Joined loss binary | counts the number of common joined losses |
| LPC | Loss pair counter | counts the number of two consecutive losses within the tree |
| MLIP | Maximum loss in path | counts the maximum frequencies of each molecular formula in any path |
| NB | Node binary | counts the number of nodes with the same molecular formula |
| NI | Node intensity | weighted variant of NB that uses the intensity of nodes |
| NLI | Node loss interaction | counts common paths and weights them by comparing the molecular formula of their terminal fragments |
| SLL | Substructure in losses and leafs | counts for different molecular formula in how many paths they are conserved (part of all nodes) or cleaved off intact (part of a loss) |
| NSF | Node subformula | considers a set of molecular formula and counts how often each of them occurs as subset of nodes in both trees |
| NSF3 | takes the value of NSF to the power of three | |
| GJLSF | Generalized joined loss subformula | counts how often each molecular formula from occurs as subset of joined losses in both fragmentation graphs |
| RDBE | Ring double-bond equivalent | compares the distribution of ring double-bond equivalent values between two trees |
| PPKr | Recalibrated probability product kernel | computes the probability product kernel on preprocessed spectra |
| Method | Negative Mode | Positive Mode | ||||
|---|---|---|---|---|---|---|
| Top-1 | Top-5 | Top-10 | Top-1 | Top-5 | Top-10 | |
| CSI:FingerID | 31.9 | 60.2 | 69.9 | 36.0 | 67.5 | 76.5 |
| IOKR Unimkl - Linear | 30.1 | 58.8 | 68.6 | 34.9 | 66.9 | 76.0 |
| IOKR Unimkl - Tanimoto | 31.0 | 60.0 | 69.7 | 35.2 | 67.6 | 76.5 |
| IOKR Unimkl - Gaussian | 31.0 | 60.3 | 69.6 | 35.0 | 67.7 | 76.3 |
| IOKR Unimkl - Gaussian Tanimoto | 30.9 | 61.0 | 70.5 | 33.9 | 66.5 | 75.2 |
| IOKRfusion - only IOKR scores | 28.4 | 57.0 | 67.2 | 33.5 | 64.4 | 73.4 |
| IOKRfusion - only IOKRreverse scores | 30.1 | 60.4 | 71.4 | 37.6 | 69.2 | 77.9 |
| IOKRfusion - all scores | 32.1 | 62.4 | 71.8 | 37.8 | 69.7 | 78.4 |
| Method | Training Time | Test Time |
|---|---|---|
| IOKR - linear | 0.85 s | 1 min 15 s |
| IOKR - tanimoto | 3.9 s | 7 min 40 s |
| IOKR - gaussian | 7.2 s | 8 min 38 s |
| IOKR - gaussian-tanimoto | 7.6 s | 8 min 44 s |
| IOKRreverse - linear | 3.9 s | 28 min 20 s |
| IOKRreverse - tanimoto | 4.1 s | 33 min 57 s |
| IOKRreverse - gaussian | 7.4 s | 34 min 49 s |
| IOKRreverse - gaussian-tanimoto | 7.5 s | 35 min 4 s |
| IOKR Unimkl - linear | 4.3 s | 1 min 10 s |
| IOKR Unimkl - tanimoto | 8.7 s | 7 min 52 s |
| IOKR Unimkl - gaussian | 11.7 s | 8 min 28 s |
| IOKR Unimkl - gaussian-tanimoto | 11.9 s | 8 min 42 s |
| IOKRfusion | 3 min 3 s | 0.1 s |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brouard, C.; Bassé, A.; d’Alché-Buc, F.; Rousu, J. Improved Small Molecule Identification through Learning Combinations of Kernel Regression Models. Metabolites 2019, 9, 160. https://doi.org/10.3390/metabo9080160
Brouard C, Bassé A, d’Alché-Buc F, Rousu J. Improved Small Molecule Identification through Learning Combinations of Kernel Regression Models. Metabolites. 2019; 9(8):160. https://doi.org/10.3390/metabo9080160
Chicago/Turabian StyleBrouard, Céline, Antoine Bassé, Florence d’Alché-Buc, and Juho Rousu. 2019. "Improved Small Molecule Identification through Learning Combinations of Kernel Regression Models" Metabolites 9, no. 8: 160. https://doi.org/10.3390/metabo9080160
APA StyleBrouard, C., Bassé, A., d’Alché-Buc, F., & Rousu, J. (2019). Improved Small Molecule Identification through Learning Combinations of Kernel Regression Models. Metabolites, 9(8), 160. https://doi.org/10.3390/metabo9080160





