Statistical Workflow for Feature Selection in Human Metabolomics Data
Abstract
1. Introduction
2. Analytical Challenges
3. Statistical Methods for Analyzing Metabolomics Data
4. Metabolomics Statistical Analysis Workflow
4.1. Study Design
4.2. Data Management
4.3. Optional Simulation Analyses
4.4. Cross-Sectional or Prospective Analyses (i.e., Outcomes Analyses)
4.5. Real-Life Application of Multiple Statistical Methods
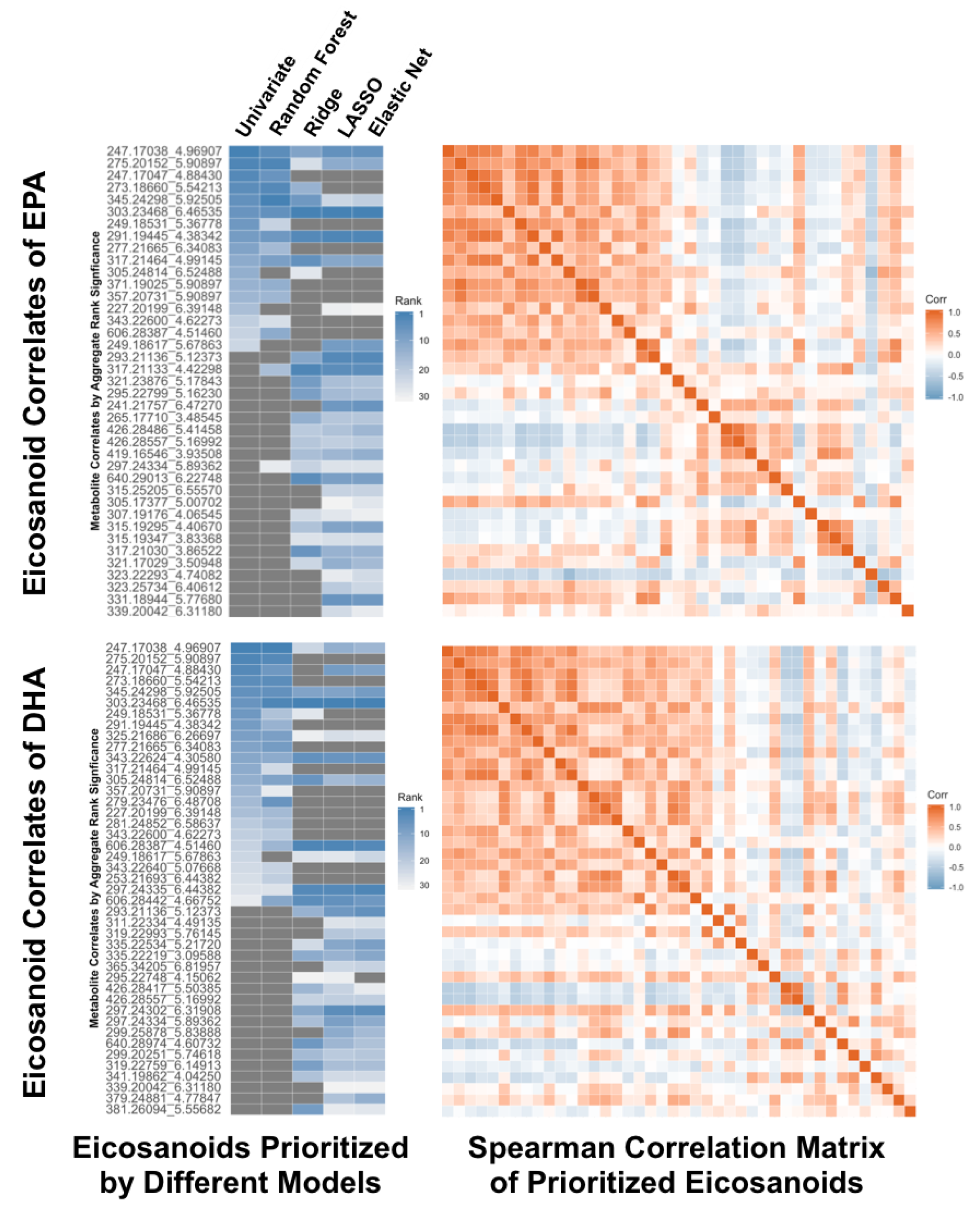
4.6. Prioritization of Results for Follow-Up Investigations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Benjamini, Y.; Hochberg, Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. R. Stat. Soc. Ser. B 1995, 57, 289–300. [Google Scholar] [CrossRef]
- Wishart, D.; Arndt, D.; Pon, A.; Sajed, T.; Guo, A.C.; Djoumbou, Y.; Knox, C.; Wilson, M.; Liang, Y.; Grant, J. T3 DB: The toxic exposome database. Nucleic Acids Res. 2014, 43, D928–D934. [Google Scholar] [CrossRef] [PubMed]
- Mayers, J.R.; Wu, C.; Clish, C.B.; Kraft, P.; Torrence, M.E.; Fiske, B.P.; Yuan, C.; Bao, Y.; Townsend, M.K.; Tworoger, S.S. Elevation of circulating branched-chain amino acids is an early event in human pancreatic adenocarcinoma development. Nat. Med. 2014, 20, 1193–1198. [Google Scholar] [CrossRef] [PubMed]
- Hinton, D.J.; Vázquez, M.S.; Geske, J.R.; Hitschfeld, M.J.; Ho, A.M.; Karpyak, V.M.; Biernacka, J.M.; Choi, D.-S. Metabolomics biomarkers to predict acamprosate treatment response in alcohol-dependent subjects. Sci. Rep. 2017, 7, 2496. [Google Scholar] [CrossRef] [PubMed]
- Lewis, G.D.; Asnani, A.; Gerszten, R.E. Application of metabolomics to cardiovascular biomarker and pathway discovery. J. Am. Coll. Cardiol. 2008, 52, 117–123. [Google Scholar] [CrossRef] [PubMed]
- Ganna, A.; Salihovic, S.; Sundström, J.; Broeckling, C.D.; Hedman, Å.K.; Magnusson, P.K.; Pedersen, N.L.; Larsson, A.; Siegbahn, A.; Zilmer, M. Large-scale metabolomic profiling identifies novel biomarkers for incident coronary heart disease. PLoS Genet. 2014, 10, e1004801. [Google Scholar] [CrossRef] [PubMed]
- Shah, S.H.; Bain, J.R.; Muehlbauer, M.J.; Stevens, R.D.; Crosslin, D.R.; Haynes, C.; Dungan, J.; Newby, L.K.; Hauser, E.R.; Ginsburg, G.S. Association of a peripheral blood metabolic profile with coronary artery disease and risk of subsequent cardiovascular events. Circ. Cardiovasc. Genet. 2010, 3, 207–214. [Google Scholar] [CrossRef]
- Würtz, P.; Havulinna, A.S.; Soininen, P.; Tynkkynen, T.; Prieto-Merino, D.; Tillin, T.; Ghorbani, A.; Artati, A.; Wang, Q.; Tiainen, M. Metabolite profiling and cardiovascular event risk: A prospective study of 3 population-based cohorts. Circulation 2015, 131, 774–785. [Google Scholar] [CrossRef]
- Wei, R.; Wang, J.; Su, M.; Jia, E.; Chen, S.; Chen, T.; Ni, Y. Missing value imputation approach for mass spectrometry-based metabolomics data. Sci. Rep. 2018, 8, 663. [Google Scholar] [CrossRef]
- Armitage, E.G.; Godzien, J.; Alonso-Herranz, V.; López-Gonzálvez, Á.; Barbas, C. Missing value imputation strategies for metabolomics data. Electrophoresis 2015, 36, 3050–3060. [Google Scholar] [CrossRef]
- Gromski, P.; Xu, Y.; Kotze, H.; Correa, E.; Ellis, D.; Armitage, E.; Turner, M.; Goodacre, R. Influence of missing values substitutes on multivariate analysis of metabolomics data. Metabolites 2014, 4, 433–452. [Google Scholar] [CrossRef] [PubMed]
- Little, R.J.; Rubin, D.B. Statistical Analysis with Missing Data, 2nd ed.; Wiley: Hoboken, NJ, USA, 2019; Volume 793. [Google Scholar]
- Lazar, C. imputeLCMD: A Collection of Methods for Left-Censored Missing Data Imputation; R Package. Available online: https://rdrr.io/cran/imputeLCMD/ (accessed on 12 July 2019).
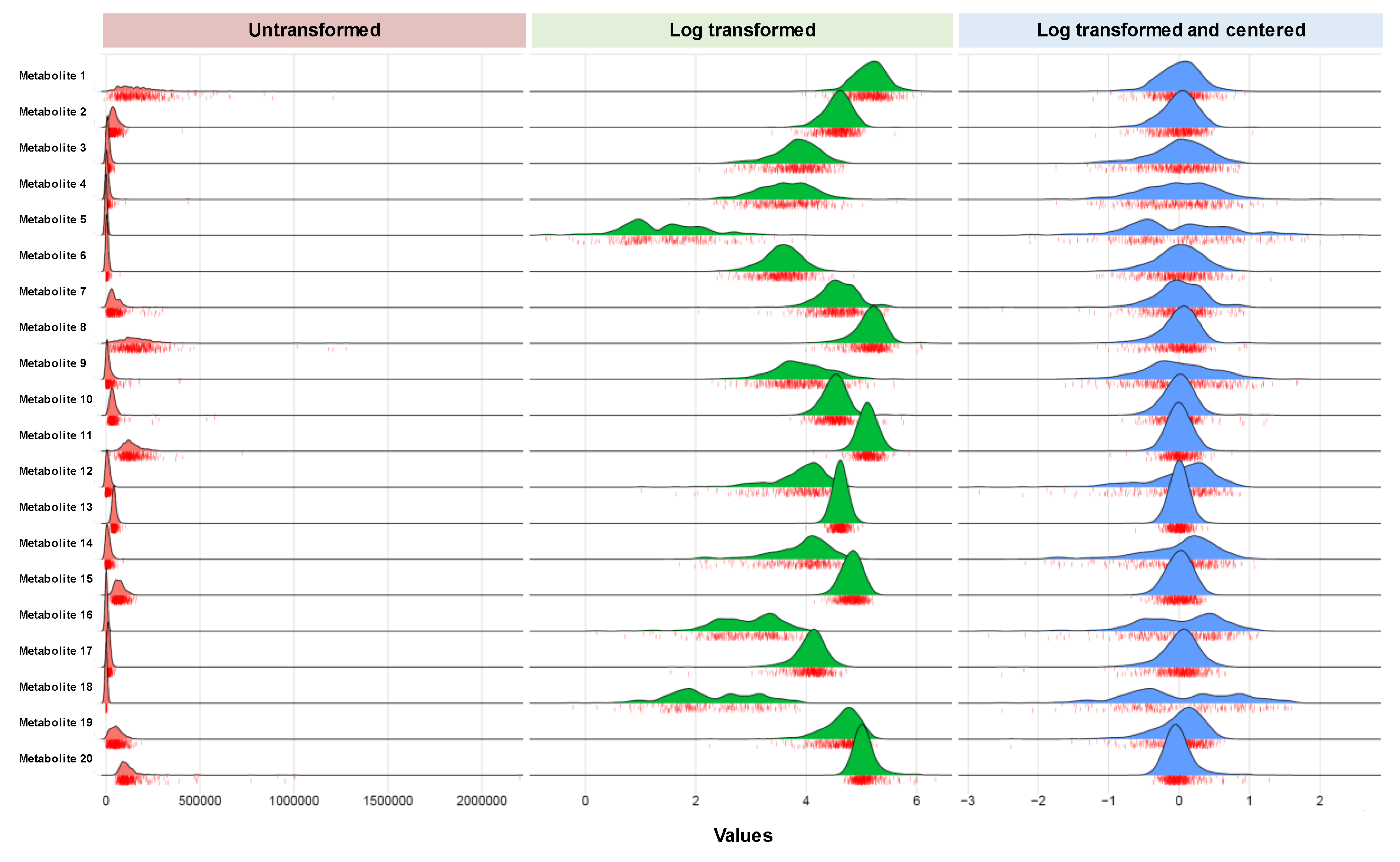
- van den Berg, R.A.; Hoefsloot, H.C.; Westerhuis, J.A.; Smilde, A.K.; van der Werf, M.J. Centering, scaling, and transformations: Improving the biological information content of metabolomics data. BMC Genom. 2006, 7, 142. [Google Scholar] [CrossRef] [PubMed]
- Jolliffe, I.T. Principal Component Analysis; Springer: New York, NY, USA, 1986; pp. 115–128. [Google Scholar]
- Pan, W. A comparative review of statistical methods for discovering differentially expressed genes in replicated microarray experiments. Bioinformatics 2002, 18, 546–554. [Google Scholar] [CrossRef] [PubMed]
- Ogutu, J.O.; Schulz-Streeck, T.; Piepho, H.-P. Genomic selection using regularized linear regression models: Ridge regression, lasso, elastic net and their extensions. BMC Proc. 2012, 6, S10. [Google Scholar] [CrossRef] [PubMed]
- Waldmann, P.; Mészáros, G.; Gredler, B.; Fuerst, C.; Sölkner, J. Evaluation of the lasso and the elastic net in genome-wide association studies. Front. Genet. 2013, 4, 270. [Google Scholar] [CrossRef] [PubMed]
- Acharjee, A.; Finkers, R.; Visser, R.G.; Maliepaard, C. Comparison of regularized regression methods for omics data. Metabolomics 2013, 3, 126. [Google Scholar] [CrossRef]
- Scholtens, D.M.; Bain, J.R.; Reisetter, A.C.; Muehlbauer, M.J.; Nodzenski, M.; Stevens, R.D.; Ilkayeva, O.; Lowe, L.P.; Metzger, B.E.; Newgard, C.B. Metabolic networks and metabolites underlie associations between maternal glucose during pregnancy and newborn size at birth. Diabetes 2016, 65, 2039–2050. [Google Scholar] [CrossRef] [PubMed]
- Worley, B.; Powers, R. Multivariate analysis in metabolomics. Curr. Metab. 2013, 1, 92–107. [Google Scholar]
- Yi, L.-Z.; He, J.; Liang, Y.-Z.; Yuan, D.-L.; Chau, F.-T. Plasma fatty acid metabolic profiling and biomarkers of type 2 diabetes mellitus based on GC/MS and PLS-LDA. FEBS Lett. 2006, 580, 6837–6845. [Google Scholar] [CrossRef]
- Ramadan, Z.; Jacobs, D.; Grigorov, M.; Kochhar, S. Metabolic profiling using principal component analysis, discriminant partial least squares, and genetic algorithms. Talanta 2006, 68, 1683–1691. [Google Scholar] [CrossRef]
- Yuan, K.; Kong, H.; Guan, Y.; Yang, J.; Xu, G. A GC-based metabonomics investigation of type 2 diabetes by organic acids metabolic profile. J. Chromatogr. B 2007, 850, 236–240. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.; Aronov, P.; Zakharkin, S.O.; Anderson, D.; Perroud, B.; Thompson, I.M.; Weiss, R.H. Urine metabolomics analysis for kidney cancer detection and biomarker discovery. Mol. Cell. Proteom. 2009, 8, 558–570. [Google Scholar] [CrossRef] [PubMed]
- Mayr, M.; Yusuf, S.; Weir, G.; Chung, Y.-L.; Mayr, U.; Yin, X.; Ladroue, C.; Madhu, B.; Roberts, N.; De Souza, A. Combined metabolomic and proteomic analysis of human atrial fibrillation. J. Am. Coll. Cardiol. 2008, 51, 585–594. [Google Scholar] [CrossRef] [PubMed]
- Kaiser, H.F. The varimax criterion for analytic rotation in factor analysis. Psychometrika 1958, 23, 187–200. [Google Scholar] [CrossRef]
- Wikoff, W.R.; Anfora, A.T.; Liu, J.; Schultz, P.G.; Lesley, S.A.; Peters, E.C.; Siuzdak, G. Metabolomics analysis reveals large effects of gut microflora on mammalian blood metabolites. Proc. Natl. Acad. Sci. USA 2009, 106, 3698–3703. [Google Scholar] [CrossRef] [PubMed]
- Cubbon, S.; Antonio, C.; Wilson, J.; Thomas-Oates, J. Metabolomic applications of HILIC-LC-MS. Mass Spectrom. Rev. 2010, 29, 671–684. [Google Scholar] [CrossRef] [PubMed]
- Wold, S.; Ruhe, A.; Wold, H.; Dunn, W.J., III. The collinearity problem in linear regression. The partial least squares (PLS) approach to generalized inverses. SIAM J. Sci. Stat. Comput. 1984, 5, 735–743. [Google Scholar] [CrossRef]
- Barker, M.; Rayens, W. Partial least squares for discrimination. J. Chemom. A J. Chemom. Soc. 2003, 17, 166–173. [Google Scholar] [CrossRef]
- Gromski, P.S.; Muhamadali, H.; Ellis, D.I.; Xu, Y.; Correa, E.; Turner, M.L.; Goodacre, R. A tutorial review: Metabolomics and partial least squares-discriminant analysis—A marriage of convenience or a shotgun wedding. Anal. Chim. Acta 2015, 879, 10–23. [Google Scholar] [CrossRef]
- Szymańska, E.; Saccenti, E.; Smilde, A.K.; Westerhuis, J.A. Double-check: validation of diagnostic statistics for PLS-DA models in metabolomics studies. Metabolomics 2012, 8, 3–16. [Google Scholar] [CrossRef]
- Jiang, M.; Wang, C.; Zhang, Y.; Feng, Y.; Wang, Y.; Zhu, Y. Sparse Partial-least-squares Discriminant Analysis for Different Geographical Origins of Salvia miltiorrhiza by 1 H-NMR-based Metabolomics. Phytochem. Anal. 2014, 25, 50–58. [Google Scholar] [CrossRef] [PubMed]
- Kind, T.; Tolstikov, V.; Fiehn, O.; Weiss, R.H. A comprehensive urinary metabolomic approach for identifying kidney cancer. Anal. Biochem. 2007, 363, 185–195. [Google Scholar] [CrossRef]
- Roy, P.P.; Roy, K. On some aspects of variable selection for partial least squares regression models. QSAR Comb. Sci. 2008, 27, 302–313. [Google Scholar] [CrossRef]
- Mehmood, T.; Martens, H.; Sæbø, S.; Warringer, J.; Snipen, L. A Partial Least Squares based algorithm for parsimonious variable selection. Algorithms Mol. Biol. 2011, 6, 27. [Google Scholar] [CrossRef]
- Chun, H.; Keleş, S. Expression quantitative trait loci mapping with multivariate sparse partial least squares regression. Genetics 2009, 182, 79–90. [Google Scholar] [CrossRef] [PubMed]
- Chun, H.; Keleş, S. Sparse partial least squares regression for simultaneous dimension reduction and variable selection. J. R. Stat. Soc. Ser. B Stat. Methodol. 2010, 72, 3–25. [Google Scholar] [CrossRef]
- Lê Cao, K.-A.; Boitard, S.; Besse, P. Sparse PLS discriminant analysis: Biologically relevant feature selection and graphical displays for multiclass problems. BMC Bioinform. 2011, 12, 253. [Google Scholar] [CrossRef]
- Lê Cao, K.-A.; Rossouw, D.; Robert-Granié, C.; Besse, P. A sparse PLS for variable selection when integrating omics data. Stat. Appl. Genet. Mol. Biol. 2008, 7, 1544–6115. [Google Scholar] [CrossRef]
- Bickel, P.J.; Levina, E. Some theory for Fisher’s linear discriminant function, naive Bayes’, and some alternatives when there are many more variables than observations. Bernoulli 2004, 10, 989–1010. [Google Scholar] [CrossRef]
- Cai, T.; Liu, W. A direct estimation approach to sparse linear discriminant analysis. J. Am. Stat. Assoc. 2011, 106, 1566–1577. [Google Scholar] [CrossRef]
- Clemmensen, L.; Hastie, T.; Witten, D.; Ersbøll, B. Sparse discriminant analysis. Technometrics 2011, 53, 406–413. [Google Scholar] [CrossRef]
- Mai, Q.; Zou, H.; Yuan, M. A direct approach to sparse discriminant analysis in ultra-high dimensions. Biometrika 2012, 99, 29–42. [Google Scholar] [CrossRef]
- Witten, D.M.; Tibshirani, R. Penalized classification using Fisher’s linear discriminant. J. R. Stat. Soc. Ser. B Stat. Methodol. 2011, 73, 753–772. [Google Scholar] [CrossRef] [PubMed]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Huang, J.; Ma, S.; Zhang, C.-H. Adaptive Lasso for sparse high-dimensional regression models. Stat. Sin. 2008, 18, 1603–1618. [Google Scholar]
- Chan, A.W.; Mercier, P.; Schiller, D.; Bailey, R.; Robbins, S.; Eurich, D.T.; Sawyer, M.B.; Broadhurst, D. 1 H-NMR urinary metabolomic profiling for diagnosis of gastric cancer. Br. J. Cancer 2016, 114, 59–62. [Google Scholar] [CrossRef] [PubMed]
- Ng, D.; Salim, A.; Liu, Y.; Zou, L.; Xu, F.; Huang, S.; Leong, H.; Ong, C. A metabolomic study of low estimated GFR in non-proteinuric type 2 diabetes mellitus. Diabetologia 2012, 55, 499–508. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, T.; Cao, Y.; Zhang, Y.; Liu, J.; Bao, Y.; Wang, C.; Jia, W.; Zhao, A. Random forest in clinical metabolomics for phenotypic discrimination and biomarker selection. Evid.-Based Complement. Altern. Med. 2013, 2013, 298183. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- H2O.ai. H2O Version 3.10.0.8; GitHub. Available online: https://github.com/h2oai/h2o-3 (accessed on 12 July 2019).
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Deng, L.; Yu, D. Deep learning: Methods and applications. Found. Trends® Signal. Process. 2014, 7, 197–387. [Google Scholar] [CrossRef]
- Brunius, C.; Shi, L.; Landberg, R. Large-scale untargeted LC-MS metabolomics data correction using between-batch feature alignment and cluster-based within-batch signal intensity drift correction. Metabolomics 2016, 12, 173. [Google Scholar] [CrossRef] [PubMed]
- Rusilowicz, M.; Dickinson, M.; Charlton, A.; O’Keefe, S.; Wilson, J. A batch correction method for liquid chromatography–mass spectrometry data that does not depend on quality control samples. Metabolomics 2016, 12, 56. [Google Scholar] [CrossRef] [PubMed]
- Wehrens, R.; Hageman, J.A.; van Eeuwijk, F.; Kooke, R.; Flood, P.J.; Wijnker, E.; Keurentjes, J.J.; Lommen, A.; van Eekelen, H.D.; Hall, R.D. Improved batch correction in untargeted MS-based metabolomics. Metabolomics 2016, 12, 88. [Google Scholar] [CrossRef] [PubMed]
- Reisetter, A.C.; Muehlbauer, M.J.; Bain, J.R.; Nodzenski, M.; Stevens, R.D.; Ilkayeva, O.; Metzger, B.E.; Newgard, C.B.; Lowe, W.L.; Scholtens, D.M. Mixture model normalization for non-targeted gas chromatography/mass spectrometry metabolomics data. BMC Bioinform. 2017, 18, 84. [Google Scholar] [CrossRef]
- Xia, J.; Wishart, D.S. Using MetaboAnalyst 3.0 for comprehensive metabolomics data analysis. Curr. Protoc. Bioinform. 2016, 55. [Google Scholar] [CrossRef]
- Kannel, W.B.; Feinleib, M.; McNamara, P.M.; Garrison, R.J.; Castelli, W.P. An investigation of coronary heart disease in families. The Framingham offspring study. Am. J. Epidemiol. 1979, 110, 281–290. [Google Scholar] [CrossRef]
- Watrous, J.D.; Niiranen, T.J.; Lagerborg, K.A.; Henglin, M.; Xu, Y.J.; Rong, J.; Sharma, S.; Vasan, R.S.; Larson, M.G.; Armando, A.; et al. Directed Non-targeted Mass Spectrometry and Chemical Networking for Discovery of Eicosanoids and Related Oxylipins. Cell Chem. Biol. 2019, 26, 433–442. [Google Scholar] [CrossRef]
- Innes, J.K.; Calder, P.C. The Differential Effects of Eicosapentaenoic Acid and Docosahexaenoic Acid on Cardiometabolic Risk Factors: A Systematic Review. Int. J. Mol. Sci. 2018, 19, 532. [Google Scholar] [CrossRef] [PubMed]
| Consideration | Notes and Examples |
|---|---|
| Missingness | Patterns of missing values tend to be non-random and are even sometimes predictable. For example, missing values may often but not always be more frequent for metabolites that are intrinsically low in abundance when measured from a given tissue type. |
| Missingness may be due to biological and/or technical reasons. | |
| Data distributions | Many but not all metabolites tend to demonstrate right-skewed distributions in most types of human studies (e.g., healthy controls or disease-specific referral samples). |
| Certain metabolites will display a substantial proportion of zero values that may be considered true zero values based on biology (an issue to be considered along with but distinguished from missingness). | |
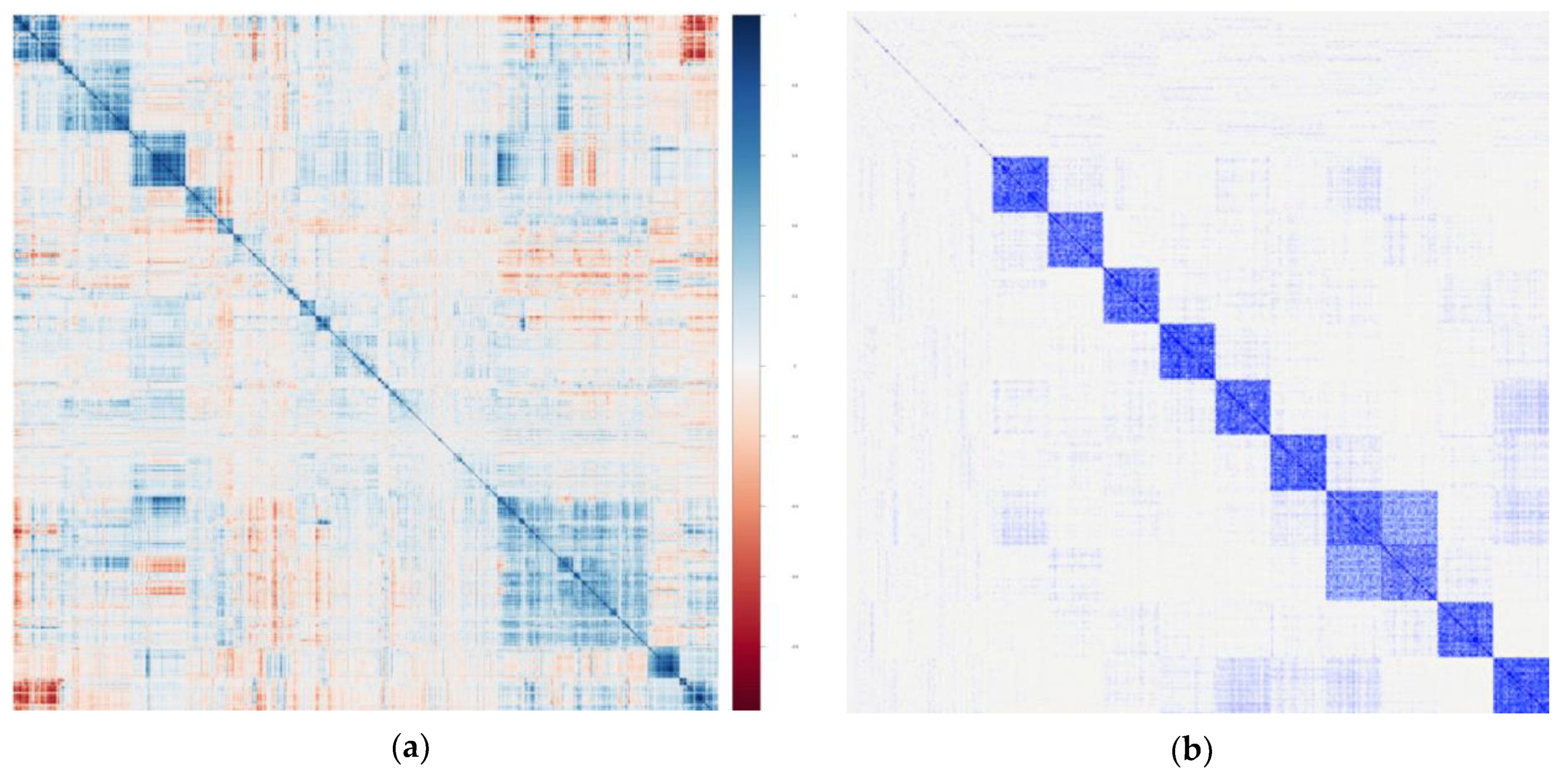
| Intercorrelations | Intercorrelations between metabolites may well reflect clustering of small molecules by known or (mostly) unknown biological pathways. |
| Intercorrelations will vary widely depending on a given exposure or background, chronic disease status, and other yet unidentified factors. | |
| Intercorrelations will also vary depending on the underlying mass spectrometry (MS) method used to create a given dataset (i.e., nontargeted vs. targeted, and the specific technical methods used). | |
| Time-dependence | Whereas a portion of the human metabolome changes dynamically in response to acute perturbation or stress, many other metabolites display variation only over several days to weeks in response to subacute perturbations; other portions of the metabolome may yet exhibit relatively little change over time, except in response to major chronic exposures. |
| Confounding factors | Metabolite values will vary in response to factors that are measurable as well as factors that are not easily measurable for a given study, such as acute and chronic dietary patterns, microbiota, and environmental exposures. |
| Method | Univariate or Multivariate | Handling Binary Outcome | Handling Continuous Outcome | p Value for Significant Metabolites | Metabolite Selection | Advantages | Disadvantages |
|---|---|---|---|---|---|---|---|
| Multiple tests (e.g., univariate linear regression) with Bonferroni correction | Univariate | Yes | Yes | Yes | Yes | Simple, easy to use and interpret results | Very conservative and does not account for intercorrelation |
| Multiple tests with false discovery rate (FDR) | Univariate | Yes | Yes | Yes | Yes | Simple, easy to use, less conservative than Bonferroni correction | Does not account for intercorrelation among features |
| Principal component analysis (PCA) | Multivariate | Yes | Yes | No | No | Effective for variable reduction | No intrinsic clarity on how to select or rank variables |
| Sparse partial least squares (SPLS) | Multivariate | No | Yes | No | Yes | Can quickly find a subset of variables that predicts the outcome well | Multiple tuning parameters are needed to be chosen via cross validation |
| Linear discriminant analysis (LDA) | Multivariate | Yes | No | No | Yes | Simple and works for categorical outcomes | Can not handle large numbers of features |
| Least absolute shrinkage and selection operator (LASSO) | Multivariate | Yes | Yes | No | Yes | Can quickly find a subset of variables that predicts the outcome well | May not perform well for metabolite selection when the features are highly correlated |
| Random forests and other machine learning approaches | Multivariate | Yes | Yes | No | No | Can find complex relationships between variables | If data is truly linear, this will be less efficient |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antonelli, J.; Claggett, B.L.; Henglin, M.; Kim, A.; Ovsak, G.; Kim, N.; Deng, K.; Rao, K.; Tyagi, O.; Watrous, J.D.; et al. Statistical Workflow for Feature Selection in Human Metabolomics Data. Metabolites 2019, 9, 143. https://doi.org/10.3390/metabo9070143
Antonelli J, Claggett BL, Henglin M, Kim A, Ovsak G, Kim N, Deng K, Rao K, Tyagi O, Watrous JD, et al. Statistical Workflow for Feature Selection in Human Metabolomics Data. Metabolites. 2019; 9(7):143. https://doi.org/10.3390/metabo9070143
Chicago/Turabian StyleAntonelli, Joseph, Brian L. Claggett, Mir Henglin, Andy Kim, Gavin Ovsak, Nicole Kim, Katherine Deng, Kevin Rao, Octavia Tyagi, Jeramie D. Watrous, and et al. 2019. "Statistical Workflow for Feature Selection in Human Metabolomics Data" Metabolites 9, no. 7: 143. https://doi.org/10.3390/metabo9070143
APA StyleAntonelli, J., Claggett, B. L., Henglin, M., Kim, A., Ovsak, G., Kim, N., Deng, K., Rao, K., Tyagi, O., Watrous, J. D., Lagerborg, K. A., Hushcha, P. V., Demler, O. V., Mora, S., Niiranen, T. J., Pereira, A. C., Jain, M., & Cheng, S. (2019). Statistical Workflow for Feature Selection in Human Metabolomics Data. Metabolites, 9(7), 143. https://doi.org/10.3390/metabo9070143






