Genetic Optimization Algorithm for Metabolic Engineering Revisited
Abstract
1. Introduction
2. Materials and Methods
2.1. A Basic Genetic Algorithm for Metabolic Engineering
- A genetic representation of solutions. Here, we employ a binary coding.
- Populations of individuals as evolutionary communities.
- A fitness function for evaluating the goodness of individuals.
- Operators, which generate a new population from an existing one and which can be controlled by parameters that shape the fitness-related or random transformation behavior.
2.1.1. Population of Binary Individuals
2.1.2. The Fitness Function
2.1.3. Selection, Mating, and Crossover
2.1.4. Mutation and Elitism
2.1.5. Parallelism
2.2. Adaptive Probabilities of Mutation
2.3. Additional Features
2.3.1. Gene Deletion Targets
2.3.2. Multi-Objective Optimization
2.3.3. Minimization of Perturbations
2.3.4. Non-Native Network Edge Insertions
2.4. Analysis of the Evolution of Populations
A Measure of Population Diversity: The Hamming Distance
2.5. Metabolic Model Preprocessing
2.6. General Conduct for the Application of the Genetic Algorithm
3. Results
3.1. GA Parameter Sensitivity Analysis
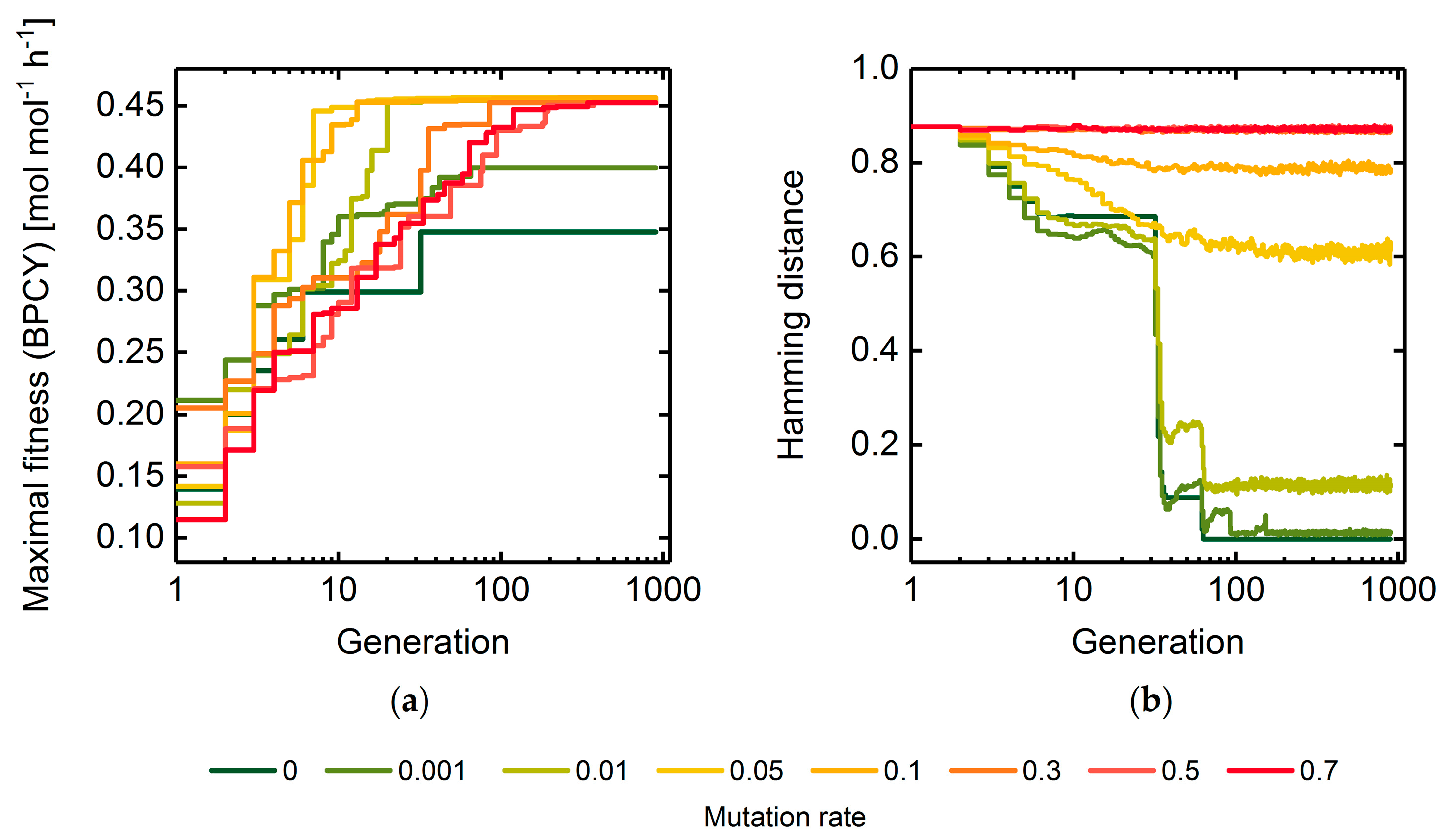
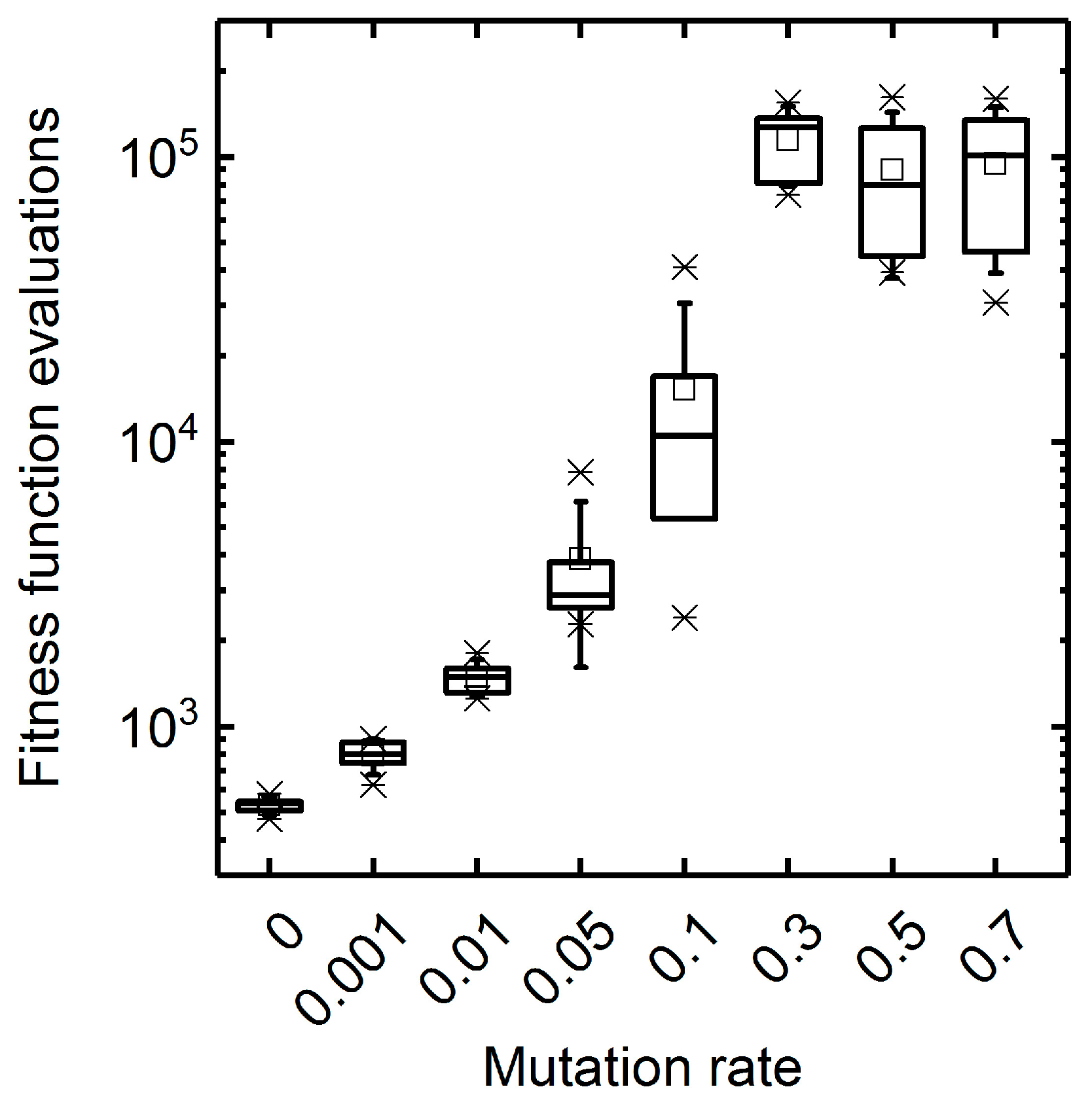
3.1.1. Mutation Rate
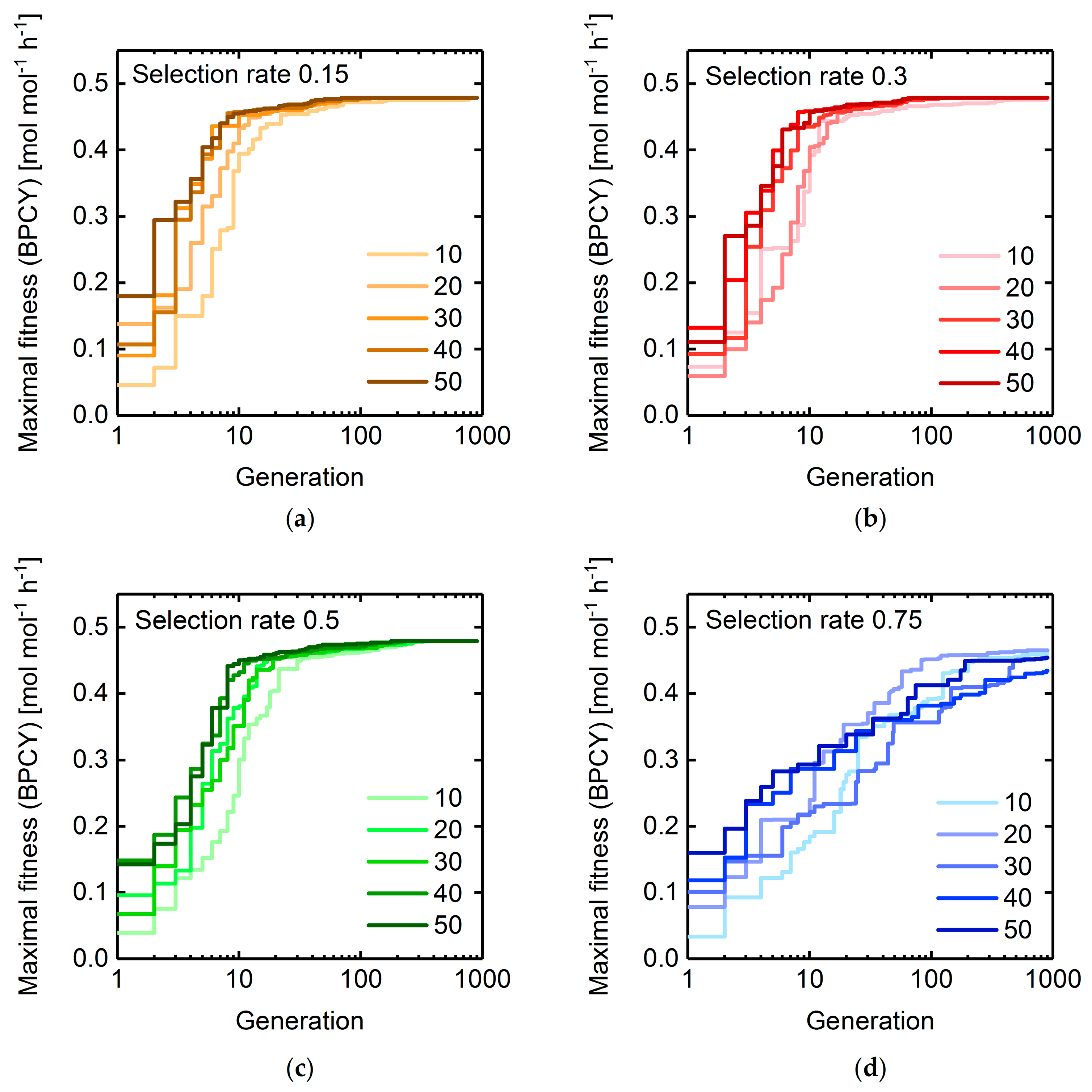
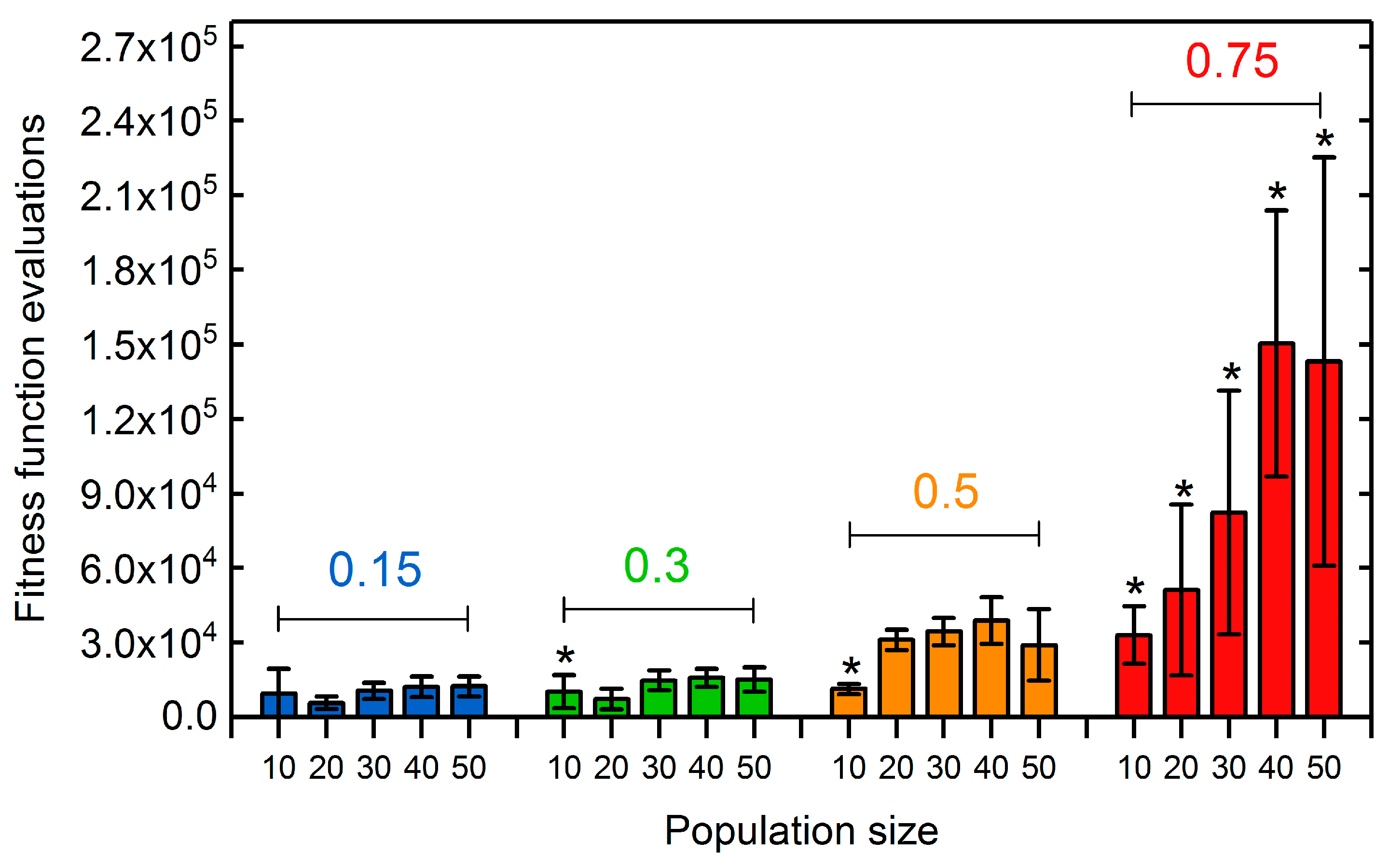
3.1.2. Selection Rate and Population Size
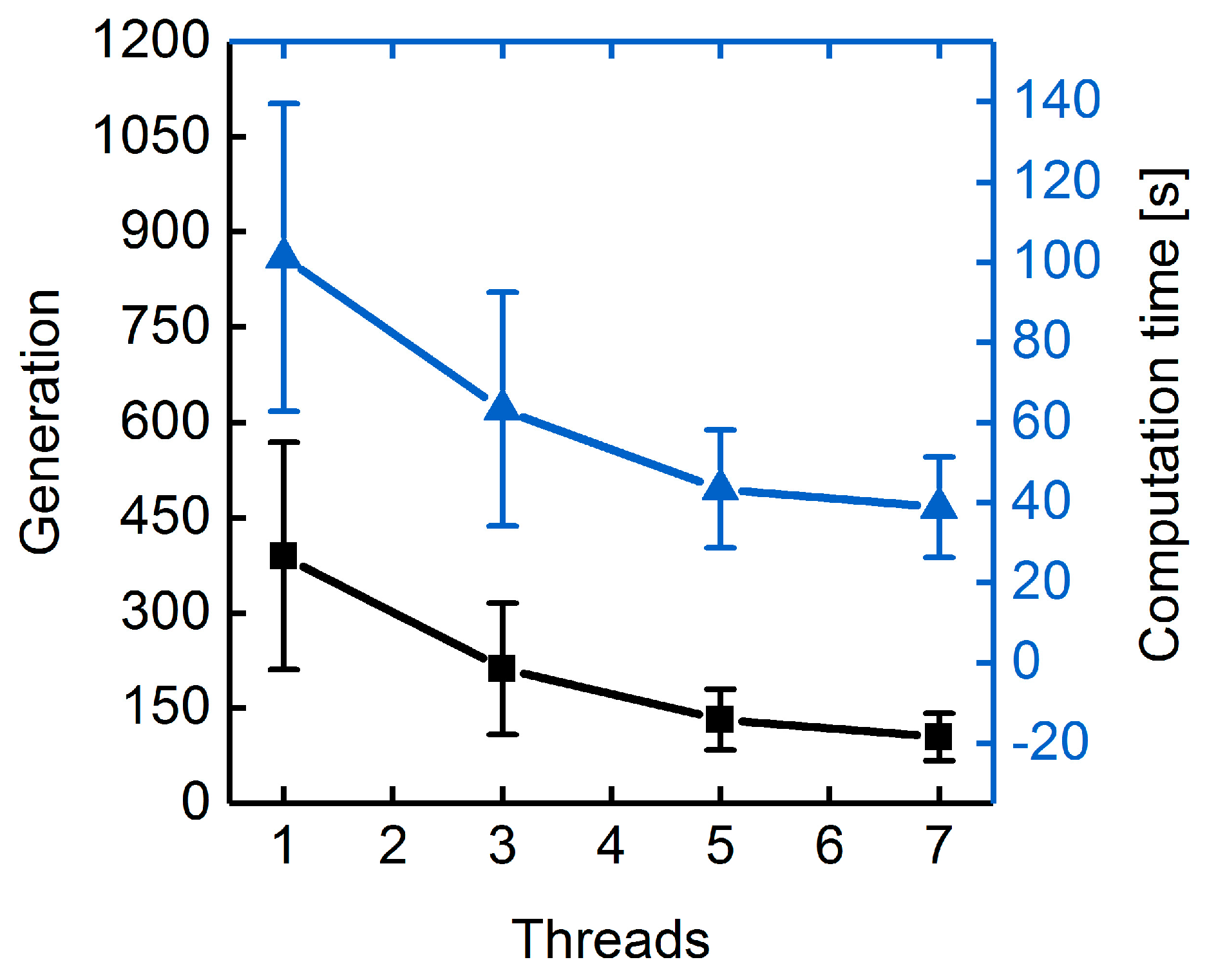
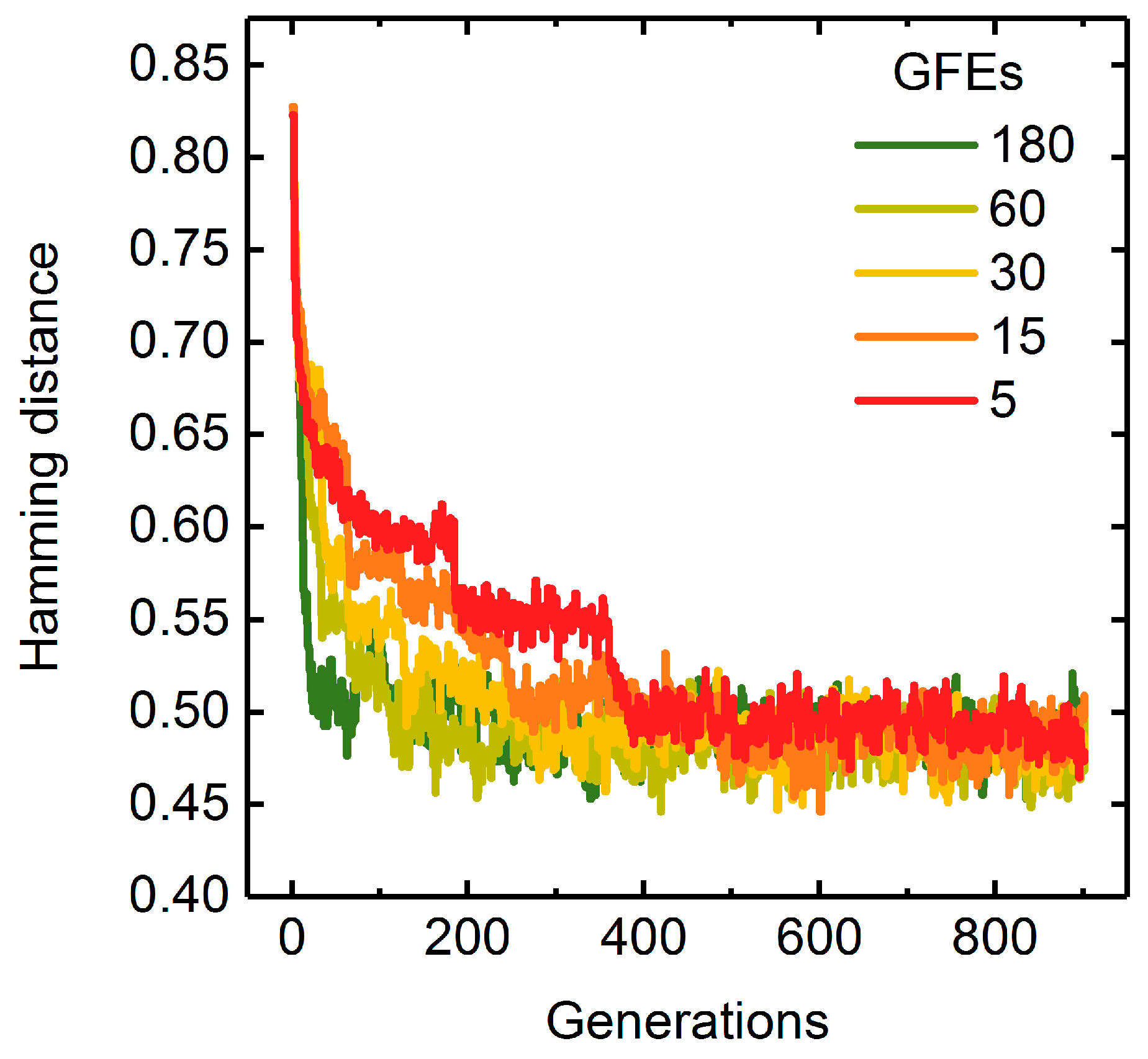
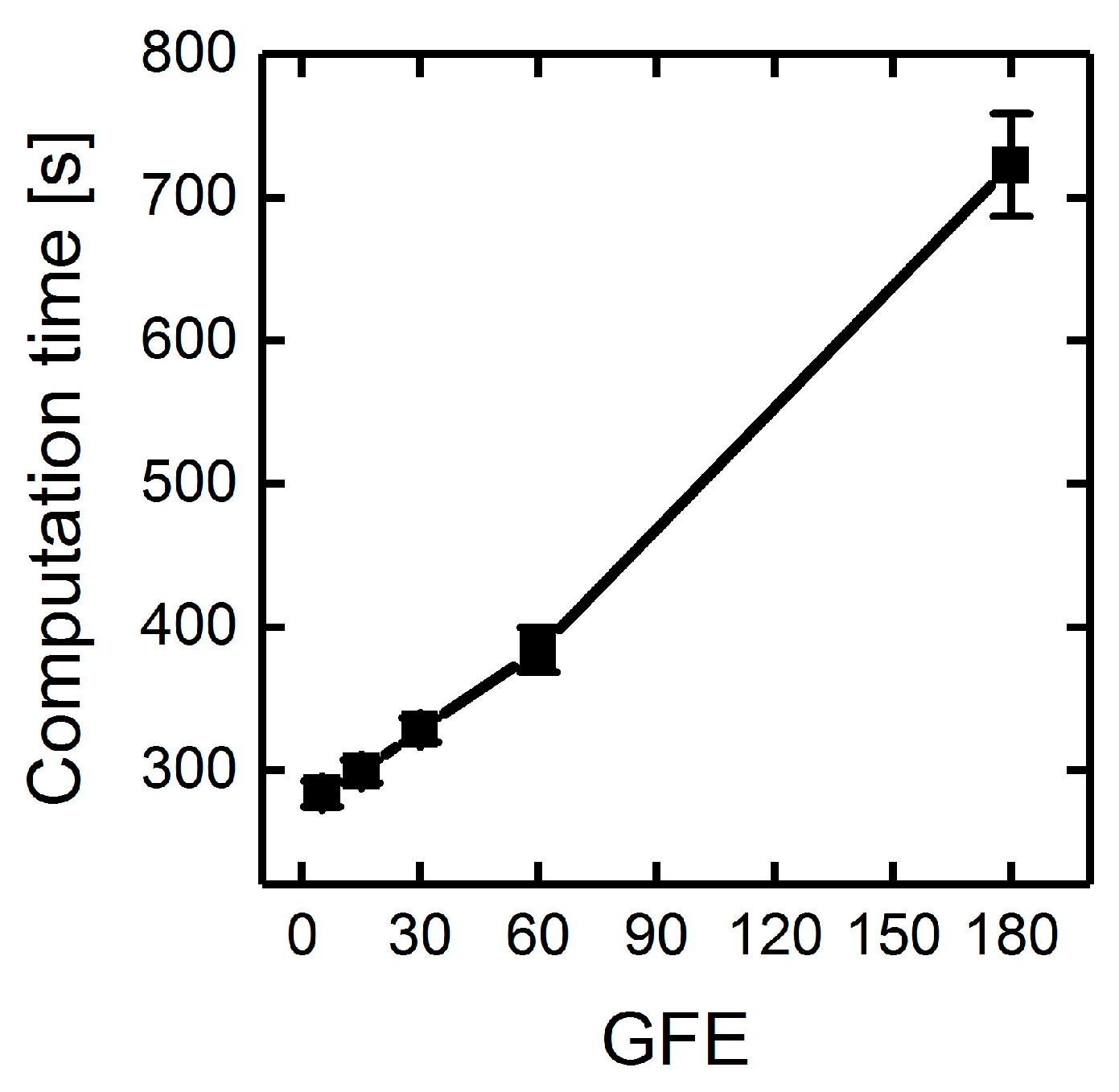
3.1.3. Parallelization: Numbers of Generations, Gene-Flow Events, and Threads
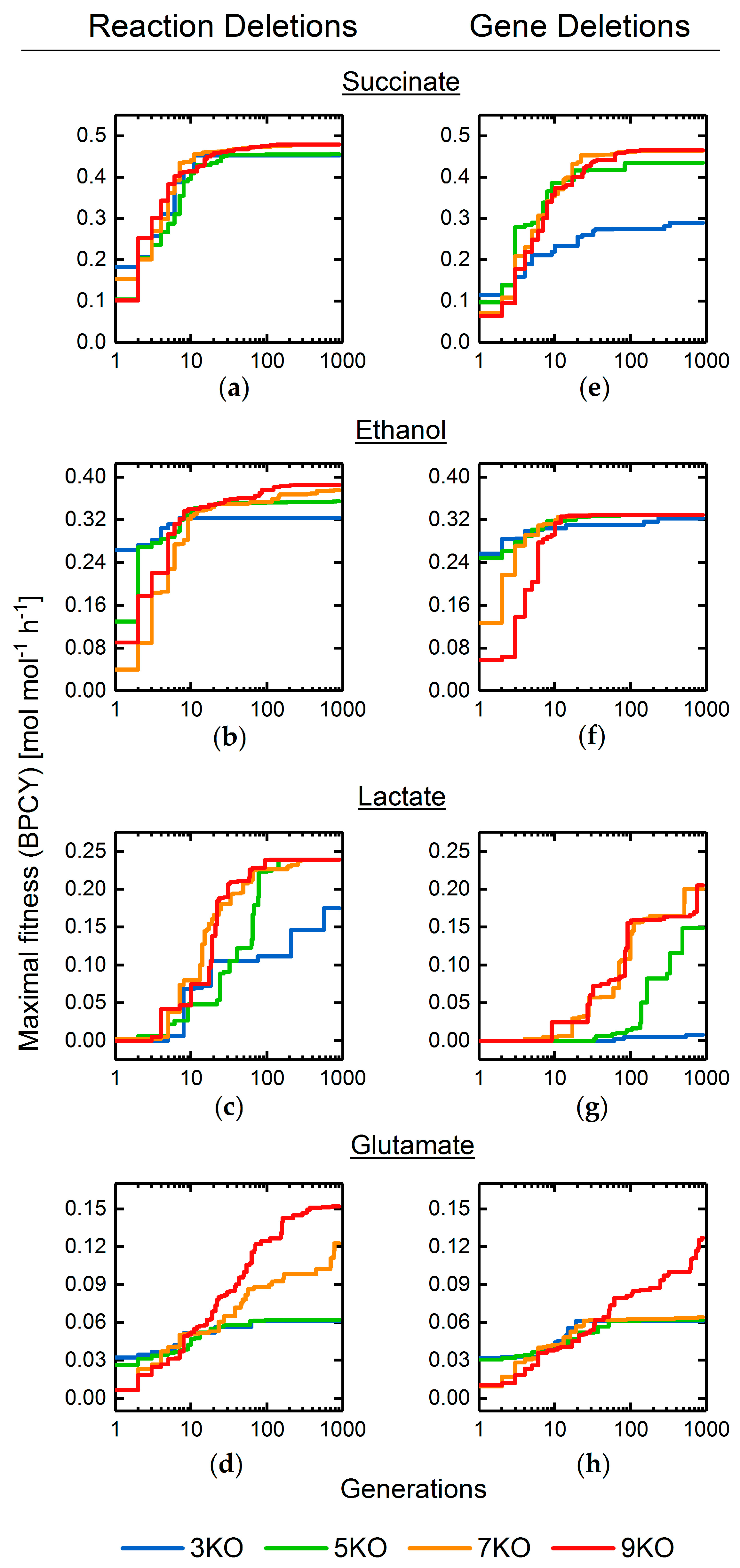
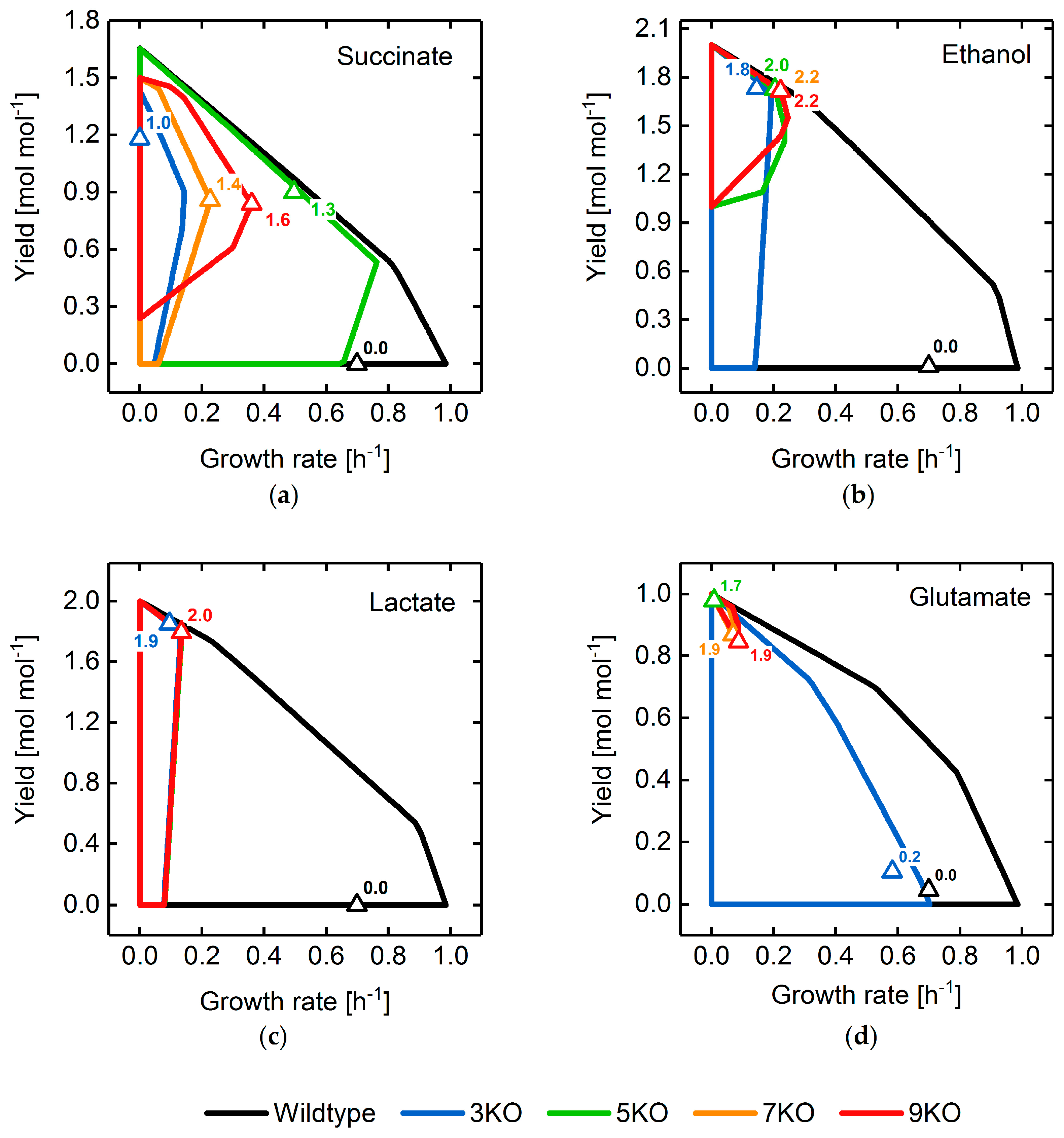
3.2. Target Product Varieties and Minimal Intervention Set Sizes
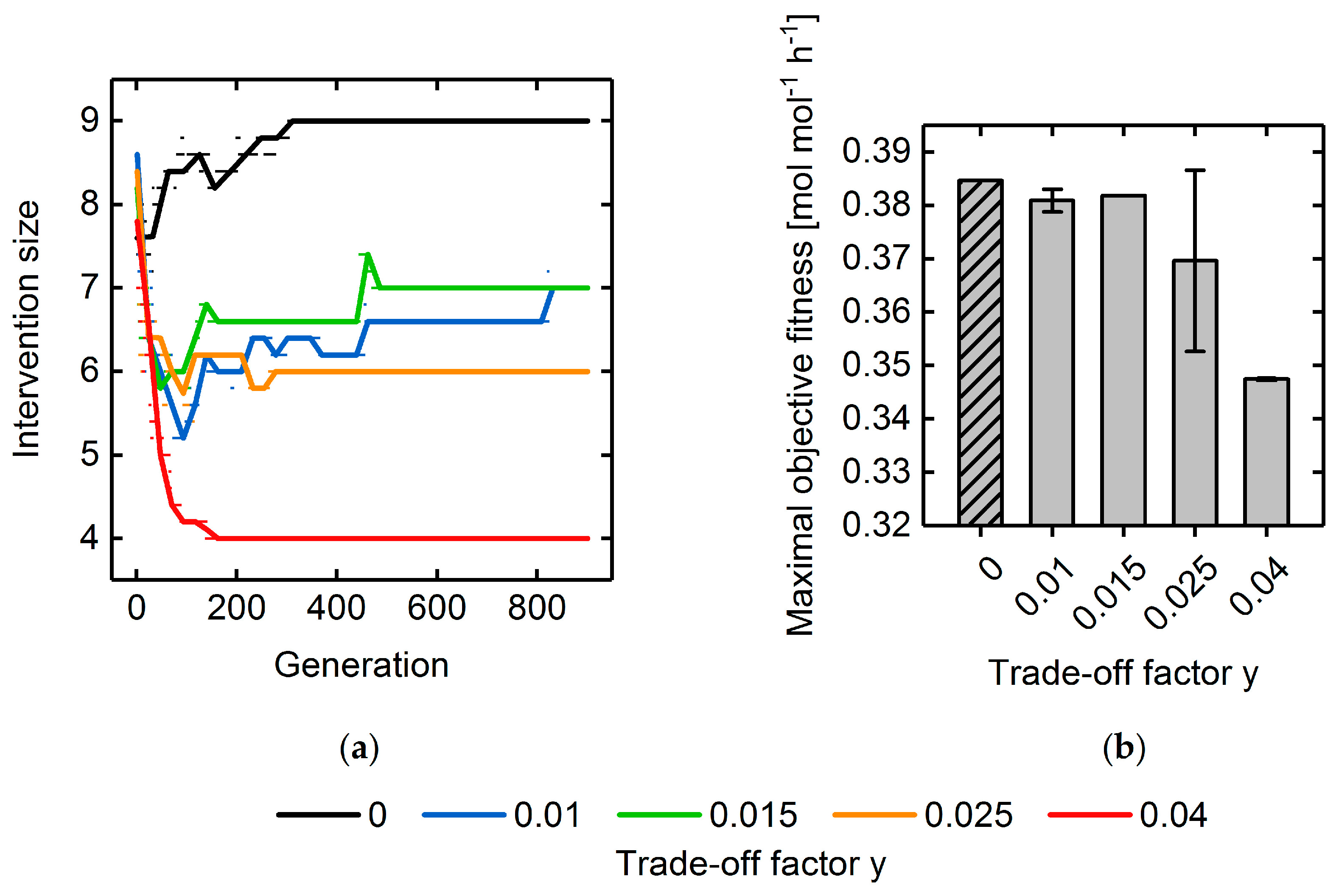
3.3. Multi-Objective Fitness Function Optimization
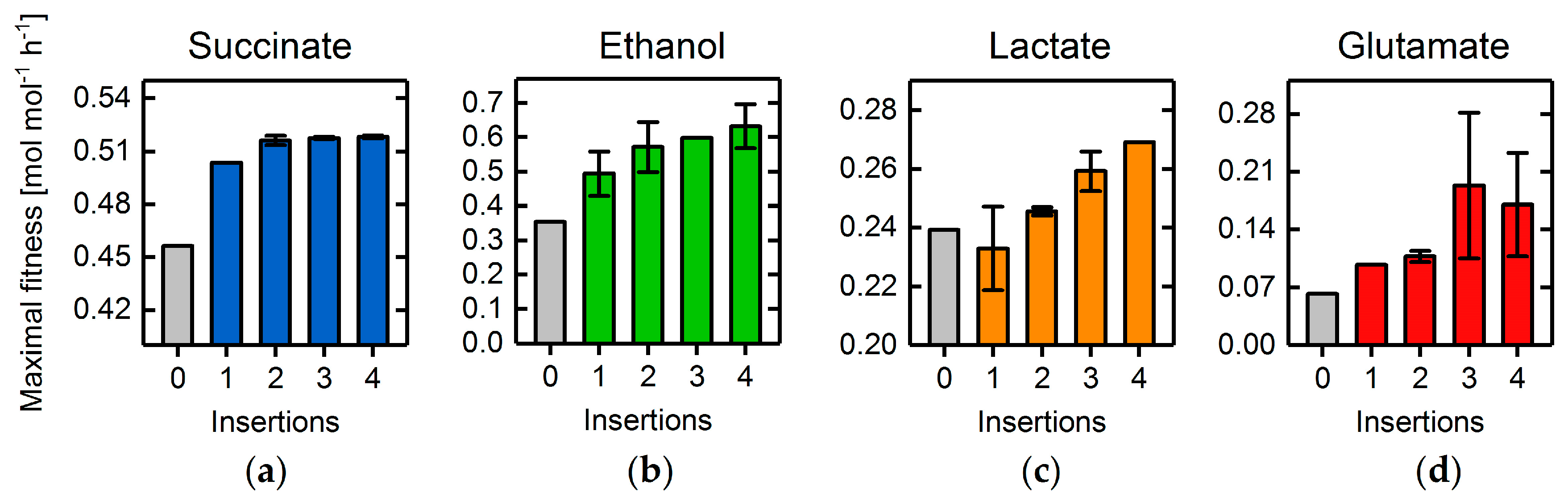
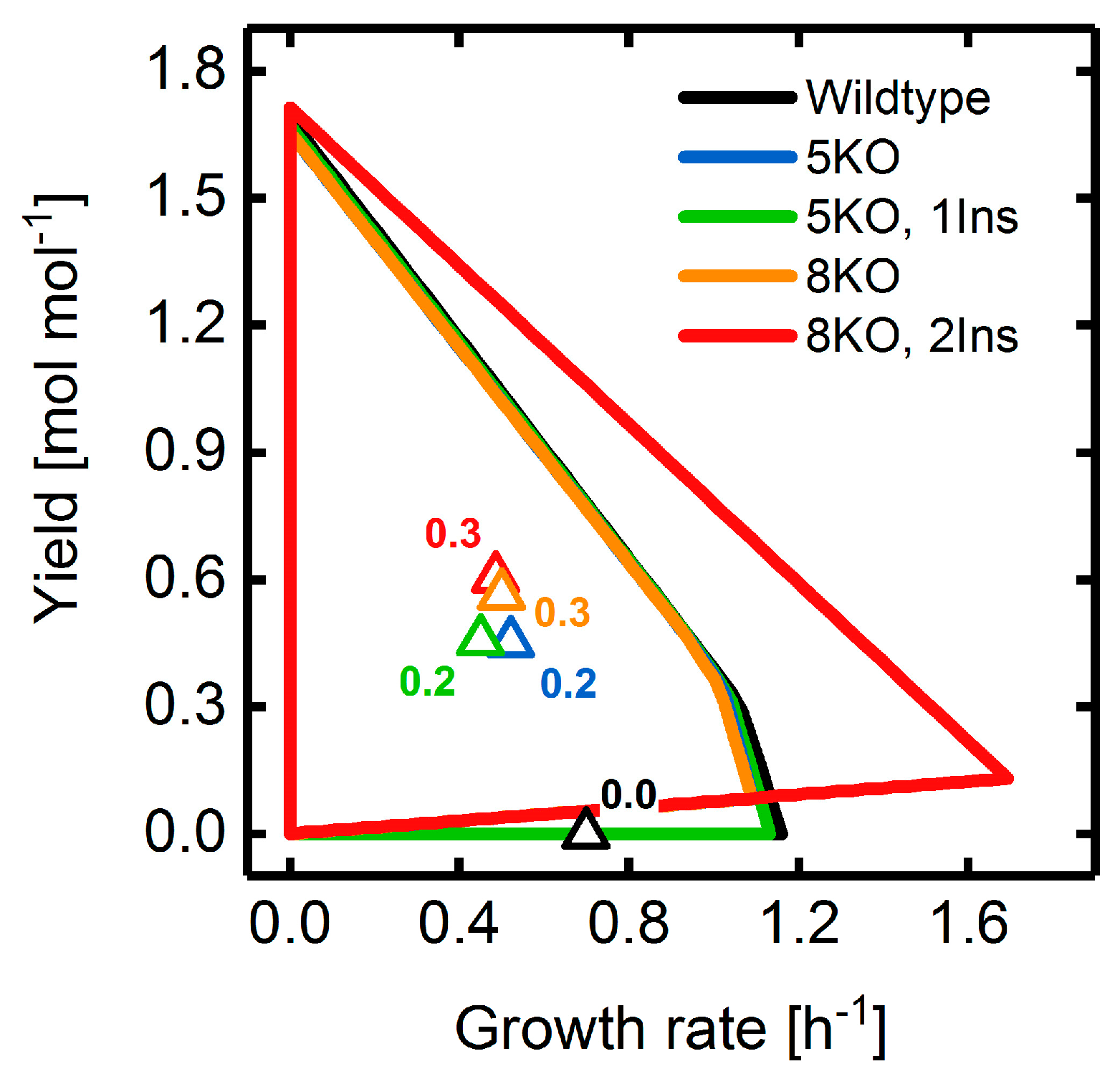
3.4. Heterologous Reaction Insertion
3.5. Increasing the Complexity and Predictive Power of Employing Genome-Scale Models
4. Discussion
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Symbol | Explanation |
| B | A bit in the binary representation of an individual |
| Intervention size-scaled fitness | |
| Objective fitness | |
| Fitness of the best discarded individual | |
| Specific growth rate | |
| Number of bits per individual | |
| Number of interventions per individual | |
| Number of subsequent generations | |
| Number of subsequent gene flow events | |
| Population size | |
| Number of possible pairs of individuals | |
| Number of selected individuals | |
| Number of target reactions | |
| Mutation rate | |
| Production rate | |
| Substrate uptake rate | |
| Selection rate | |
| Trade-off factor |
References
- Stephanopoulos, G.; Aristidou, A.A.; Nielsen, J. Metabolic Engineering: Principles and Methodologies; Elsevier: Amsterdam, The Netherlands, 1998; ISBN 0126662606. [Google Scholar]
- Woolston, B.M.; Edgar, S.; Stephanopoulos, G. Metabolic engineering: Past and future. Annu. Rev. Chem. Biomol. Eng. 2013, 4, 259–288. [Google Scholar] [CrossRef] [PubMed]
- Varma, A.; Palsson, B.O. Stoichiometric flux balance models quantitatively predict growth and metabolic by-product secretion in wild-type Escherichia coli W3110. Appl. Environ. Microbiol. 1994, 60, 3724–3731. [Google Scholar] [PubMed]
- Schuster, S.; Fell, D.A.; Schuster, S.; Dandekar, T.; Fell, D.A. Detection of elementary flux modes in pathway analysis and metabolic engineering. Trends Biotechnol. 1999, 17, 53–60. [Google Scholar] [CrossRef]
- Mahadevan, R.; Schilling, C.H. The effects of alternate optimal solutions in constraint-based genome-scale metabolic models. Metab. Eng. 2003, 5, 264–276. [Google Scholar] [CrossRef] [PubMed]
- Maia, P.; Rocha, M.; Rocha, I. In silico constraint-based strain optimization methods: The quest for optimal cell factories. Microbiol. Mol. Biol. Rev. 2016, 80, 45–67. [Google Scholar] [CrossRef] [PubMed]
- Burgard, A.P.; Pharkya, P.; Maranas, C.D. OptKnock: A bilevel programming framework for identifying gene knockout strategies for microbial strain optimization. Biotechnol. Bioeng. 2003, 84, 647–657. [Google Scholar] [CrossRef] [PubMed]
- Pharkya, P.; Burgard, A.P.; Maranas, C.D. OptStrain: A computational framework for redesign of microbial production systems. Genome Res. 2004, 2367–2376. [Google Scholar] [CrossRef] [PubMed]
- Tepper, N.; Shlomi, T. Predicting metabolic engineering knockout strategies for chemical production: Accounting for competing pathways. Bioinformatics 2009, 26, 536–543. [Google Scholar] [CrossRef] [PubMed]
- Von Kamp, A.; Klamt, S. Enumeration of smallest intervention strategies in genome-scale metabolic networks. PLoS Comput. Biol. 2014, 10. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Reed, J.L.; Maravelias, C.T. Large-scale bi-level strain design approaches and mixed-integer programming solution techniques. PLoS ONE 2011, 6. [Google Scholar] [CrossRef] [PubMed]
- Trinh, C.T.; Unrean, P.; Srienc, F. Minimal Escherichia coli cell for the most efficient production of ethanol from hexoses and pentoses. Appl. Environ. Microbiol. 2008, 74, 3634–3643. [Google Scholar] [CrossRef] [PubMed]
- Harder, B.J.; Bettenbrock, K.; Klamt, S. Model-based metabolic engineering enables high yield itaconic acid production by Escherichia coli. Metab. Eng. 2016, 38, 29–37. [Google Scholar] [CrossRef] [PubMed]
- Ng, C.Y.; Jung, M.; Lee, J.; Oh, M.-K. Production of 2,3-butanediol in Saccharomyces cerevisiae by in silico aided metabolic engineering. Microb. Cell Fact. 2012, 11, 68. [Google Scholar] [CrossRef] [PubMed]
- Yim, H.; Haselbeck, R.; Niu, W.; Pujol-Baxley, C.; Burgard, A.; Boldt, J.; Khandurina, J.; Trawick, J.D.; Osterhout, R.E.; Stephen, R.; et al. Metabolic engineering of Escherichia coli for direct production of 1,4-butanediol. Nat. Chem. Biol. 2011, 7, 445–452. [Google Scholar] [CrossRef] [PubMed]
- Balagurunathan, B.; Kumar, V.; Crystal, J.; Ying, J. In silico design of anaerobic growth-coupled product formation in Escherichia coli: Experimental validation using a simple polyol, glycerol. Bioprocess Biosyst. Eng. 2017, 40, 361–372. [Google Scholar] [CrossRef] [PubMed]
- Sean, L. Essentials of Metaheuristics; Lulu: Morrisville, NC, USA, 2013; ISBN 978-1-300-54962-8. [Google Scholar]
- Grefenstette, J.J. Optimization of control parameters for genetic algorithms. IEEE Trans. Syst. Man Cybern. 1986, 16, 122–128. [Google Scholar] [CrossRef]
- Patil, K.R.; Rocha, I.; Forster, J.; Nielsen, J. Evolutionary programming as a platform for in silico metabolic engineering. BMC Bioinform. 2005, 6, 308. [Google Scholar] [CrossRef]
- Nair, G.; Jungreuthmayer, C.; Hanscho, M.; Zanghellini, J. Designing minimal microbial strains of desired functionality using a genetic algorithm. Algorithms Mol. Biol. 2015, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Rocha, I.; Maia, P.; Evangelista, P.; Vilaça, P.; Soares, S.; Pinto, J.P.; Nielsen, J.; Patil, K.R.; Ferreira, E.C.; Rocha, M. OptFlux: An open-source software platform for in silico metabolic engineering. BMC Syst. Biol. 2010, 4, 45. [Google Scholar] [CrossRef] [PubMed]
- Segrè, D.; Vitkup, D.; Church, G.M. Analysis of optimality in natural and perturbed metabolic networks. Proc. Natl. Acad. Sci. USA 2002, 99, 15112–15117. [Google Scholar] [CrossRef] [PubMed]
- Feist, A.M.; Zielinski, D.C.; Orth, J.D.; Schellenberger, J.; Herrgard, M.J.; Palsson, B.O. Model-driven evaluation of the production potential for growth-coupled products of Escherichia coli. Metab. Eng. 2010, 12, 173–186. [Google Scholar] [CrossRef] [PubMed]
- Shabestary, K.; Hudson, E.P. Computational metabolic engineering strategies for growth-coupled biofuel production by Synechocystis. Metab. Eng. Commun. 2016, 3, 216–226. [Google Scholar] [CrossRef] [PubMed]
- Rocha, M.; Maia, P.; Mendes, R.; Pinto, J.P.; Ferreira, E.C.; Nielsen, J.; Patil, K.R.; Rocha, I. Natural computation meta-heuristics for the in silico optimization of microbial strains. BMC Bioinform. 2008, 9, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Otero, J.M.; Cimini, D.; Patil, K.R.; Poulsen, S.G.; Olsson, L.; Nielsen, J. Industrial systems biology of Saccharomyces cerevisiae enables novel succinic acid cell factory. PLoS ONE 2013, 8, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Brochado, A.R.; Matos, C.; Møller, B.L.; Hansen, J.; Mortensen, U.H.; Patil, K.R. Improved vanillin production in baker’s yeast through in silico design. Microb. Cell Fact. 2010, 9, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Asadollahi, M.A.; Maury, J.; Patil, K.R.; Schalk, M.; Clark, A.; Nielsen, J. Enhancing sesquiterpene production in Saccharomyces cerevisiae through in silico driven metabolic engineering. Metab. Eng. 2009, 11, 328–334. [Google Scholar] [CrossRef] [PubMed]
- Brochado, A.R.; Patil, K.R. Overexpression of O-methyltransferase leads to improved vanillin production in baker’s yeast only when complemented with model-guided network engineering. Biotechnol. Bioeng. 2013, 110, 656–659. [Google Scholar] [CrossRef] [PubMed]
- Mutturi, S.V.R. FOCuS: A metaheuristic algorithm for computing knockouts from genome-scale models for strain optimization. Mol. Biosyst. 2017, 13, 1355–1363. [Google Scholar] [CrossRef] [PubMed]
- Nair, G.; Jungreuthmayer, C.; Zanghellini, J. Optimal knockout strategies in genome-scale metabolic networks using particle swarm optimization. BMC Bioinform. 2017, 18, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Lun, D.S.; Rockwell, G.; Guido, N.J.; Baym, M.; Kelner, J.A.; Berger, B.; Galagan, J.E.; Church, G.M. Large-scale identification of genetic design strategies using local search. Mol. Syst. Biol. 2009, 5, 296. [Google Scholar] [CrossRef] [PubMed]
- Chong, S.K.; Mohamad, M.S.; Mohamed Salleh, A.H.; Choon, Y.W.; Chong, C.K.; Deris, S. A hybrid of ant colony optimization and minimization of metabolic adjustment to improve the production of succinic acid in Escherichia coli. Comput. Biol. Med. 2014, 49, 74–82. [Google Scholar] [CrossRef] [PubMed]
- Pandey, H.M.; Chaudhary, A.; Mehrotra, D. A comparative review of approaches to prevent premature convergence in GA. Appl. Soft Comput. J. 2014, 24, 1047–1077. [Google Scholar] [CrossRef]
- Lerman, J.A.; Hyduke, D.R.; Latif, H.; Portnoy, V.A.; Lewis, N.E.; Orth, J.D.; Schrimpe-Rutledge, A.C.; Smith, R.D.; Adkins, J.N.; Zengler, K.; et al. In silico method for modelling metabolism and gene product expression at genome scale. Nat. Commun. 2012, 3, 929. [Google Scholar] [CrossRef] [PubMed]
- Srinivas, M.; Patnaik, L.M. Adaptive probabilities of crossover and mutation in genetic algorithms. IEEE Trans. Syst. Man Cybern. 1994, 24, 656–667. [Google Scholar] [CrossRef]
- Haupt, R.L.; Haupt, S.E. Practical Genetic Algorithms, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2004; ISBN 0471455652. [Google Scholar]
- Brochado, A.R.; Andrejev, S.; Maranas, C.D.; Patil, K.R. Impact of stoichiometry representation on simulation of genotype-phenotype relationships in metabolic networks. PLoS Comput. Biol. 2012, 8. [Google Scholar] [CrossRef] [PubMed]
- Ishii, N.; Nakahigashi, K.; Baba, T.; Robert, M.; Soga, T.; Kanai, A.; Hirasawa, T.; Naba, M.; Hirai, K.; Hoque, A.; et al. Multiple high-throughput analyses monitor the response of E. coli to perturbations. Science 2007, 316, 593–597. [Google Scholar] [CrossRef] [PubMed]
- Moretti, S.; Martin, O.; Van Du Tran, T.; Bridge, A.; Morgat, A.; Pagni, M. MetaNetX/MNXref—Reconciliation of metabolites and biochemical reactions to bring together genome-scale metabolic networks. Nucleic Acids Res. 2016, 44, D523–D526. [Google Scholar] [CrossRef] [PubMed]
- Alter, T.B.; Blank, L.M.; Ebert, B.E. Determination of growth-coupling strategies and their underlying principles. bioRxiv 2018. [Google Scholar] [CrossRef]
- Schellenberger, J.; Park, J.O.; Conrad, T.M.; Palsson, B.T. BiGG: A Biochemical Genetic and Genomic knowledgebase of large scale metabolic reconstructions. BMC Bioinform. 2010, 11. [Google Scholar] [CrossRef] [PubMed]
- Flamholz, A.; Noor, E.; Bar-Even, A.; Milo, R. EQuilibrator—The biochemical thermodynamics calculator. Nucleic Acids Res. 2012, 40, 770–775. [Google Scholar] [CrossRef] [PubMed]
- Kanehisa, M.; Furumichi, M.; Tanabe, M.; Sato, Y.; Morishima, K. KEGG: New perspectives on genomes, pathways, diseases and drugs. Nucleic Acids Res. 2017, 45, D353–D361. [Google Scholar] [CrossRef] [PubMed]
- Louis, S.J.; Rawlins, G.J.E. Predicting convergence time for genetic algorithms. Found. Genet. Algorithms 1993, 2, 141–161. [Google Scholar]
- Orth, J.D.; Fleming, R.M.T.; Palsson, B.Ø. Reconstruction and use of microbial metabolic networks: The core Escherichia coli metabolic model as an educational guide. EcoSal 2010. [Google Scholar] [CrossRef] [PubMed]
- Orth, J.D.; Conrad, T.M.; Na, J.; Lerman, J.A.; Nam, H.; Feist, A.M.; Palsson, B.O. A comprehensive genome-scale reconstruction of Escherichia coli metabolism—2011. Mol. Syst. Biol. 2011, 7, 535. [Google Scholar] [CrossRef] [PubMed]
- Mori, M.; Hwa, T.; Martin, O.C.; De Martino, A.; Marinari, E. Constrained allocation flux balance analysis. PLoS Comput. Biol. 2016, 12. [Google Scholar] [CrossRef] [PubMed]
- Sánchez, B.J.; Zhang, C.; Nilsson, A.; Lahtvee, P.; Kerkhoven, E.J.; Nielsen, J. Improving the phenotype predictions of a yeast genome-scale metabolic model by incorporating enzymatic constraints. Mol. Syst. Biol. 2017, 13, 935. [Google Scholar] [CrossRef] [PubMed]
- Valderrama-Gomez, M.A.; Kreitmayer, D.; Wolf, S.; Marin-Sanguino, A.; Kremling, A. Application of theoretical methods to increase succinate production in engineered strains. Bioprocess Biosyst. Eng. 2017, 40, 479–497. [Google Scholar] [CrossRef] [PubMed]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alter, T.B.; Blank, L.M.; Ebert, B.E. Genetic Optimization Algorithm for Metabolic Engineering Revisited. Metabolites 2018, 8, 33. https://doi.org/10.3390/metabo8020033
Alter TB, Blank LM, Ebert BE. Genetic Optimization Algorithm for Metabolic Engineering Revisited. Metabolites. 2018; 8(2):33. https://doi.org/10.3390/metabo8020033
Chicago/Turabian StyleAlter, Tobias B., Lars M. Blank, and Birgitta E. Ebert. 2018. "Genetic Optimization Algorithm for Metabolic Engineering Revisited" Metabolites 8, no. 2: 33. https://doi.org/10.3390/metabo8020033
APA StyleAlter, T. B., Blank, L. M., & Ebert, B. E. (2018). Genetic Optimization Algorithm for Metabolic Engineering Revisited. Metabolites, 8(2), 33. https://doi.org/10.3390/metabo8020033





