1. Introduction
One of the main research areas in metabolomics is to study the metabolic response to one or a few factors of interest in a given biological system. Design of experiment (DOE) [
1] has been widely employed to determine such cause-and-effect relationships. There are many statistical tests to analyse these data generated by different types of DOEs in univariate analyses. However, how to incorporate the DOE information into multivariate modelling is comparatively less well explored. There are several multivariate models proposed in the literature in recent years which can make use of a priori knowledge of DOEs, most notably multilevel simultaneous component analysis (MSCA) [
2], analysis of variance (ANOVA)-principal component analysis (ANOVA-PCA) [
3], and ANOVA-simultaneous component analysis (ASCA) [
4]. These methods share a common methodology, which is to decompose the independent data matrix
X (i.e., the observed data generated by the instruments) to a series of sub-matrices according to the experimental design and perform principal component analysis (PCA) on the decomposed sub-matrices to study the effect of each factor separately. In addition, multi-block models, such as multi-block principal component analysis (MB-PCA) [
5], have also been successfully employed to analyse such datasets by repartitioning
X into blocks according to the experimental design, and then performing MB-PCA on the repartitioned multi-block data [
6,
7]. In addition, multiple supervised models, mostly based on well-known partial least squares (PLS) [
1,
8] have also been proposed in the literature using a similar methodology, such as priority PLS [
9], ANOVA-PLS [
10], ANOVA-target projection (ANOVA-TP) [
11], and multi-block orthogonal PLS [
12]. All of these methods have, to date, focused on processing the
X matrix: where
X is either re-partitioned into blocks according to the experimental design (multi-block approaches) or decomposed into a series of sub-matrices (ANOVA approaches). However, designing the response matrix
Y according to the information in the DOE and to build a supervised model to fit the designed
Y may also be an efficient method to analyse the data generated by the DOE. In fact, this type of method has already been reported previously, albeit in a rather ad hoc manner [
13]. In our present study we aim to investigate such a methodology within the framework of structural modelling and propose a workflow for general use.
Historically, the design of output Y is usually categorised into two types: regression and classification. If the coded output is a series of continuous numbers (e.g., different concentrations of a specific metabolite, time points, temperatures, and so on), these numbers can be directly used as Y and the corresponding model is called a regression model (e.g., PLS-R). By contrast, if the target is a number of different groups (classes), such as different types of bacteria or different diseases, then Y is normally coded as a binary matrix in which one column represents one distinct group while each row is the target vector of a sample. A sample of a specific class has its element in the corresponding column coded as “1” and all other elements coded as “0”. The regression models are most suitable for modelling a series of continuous or at least ordinal (e.g., ranks) numbers, while classifications are most suitable for discriminating a set of categories “in parallel”; i.e., there is no particular spatial relationship between these categories.
However, there are cases when neither regression nor classification would be able to present the information in a DOE well. For example, if one conducted an experiment in which two different extraction methods (denoted as E1 and E2) were applied to extract metabolites from three different bacterial cells (denoted as B1, B2, and B3); where the objective was to investigate the differences in metabolic profiles of the three different types of cells and also to compare the extraction efficiency of the two extraction methods. To achieve this objective, a two factor full-factorial experimental design would typically be employed and six different combinations of the two factors need to be examined. This could be considered as a multi-class classification problem having six distinct classes, one for a specific combination of E and B. However, strictly speaking, in this particular case the six classes were probably not truly all “in parallel” because there were pairs of classes, which shared a common factor (e.g., E1B1 vs. E1B2). Therefore, it is reasonable to assume that the E1B1 class should be closer to E1B2 than E2B3. Such a spatial relationship, as a part of the prior knowledge of the experimental design, would be ignored by binary coding.
It has been recognised that not all problems can be explained well in real numbers (regression) or discrete coding (classification) schemes and, sometimes, more general, structured outputs are needed to cope with these data, which cannot be formulated as simple regression or binary classification problems [
14]. The key difference between classical regression/classification modelling and structured output modelling is that instead of using a simple error function (e.g., absolute difference between the predicted and known output for regression, correct or wrong (0/1) in predicting a class membership in classification) to evaluate how closely a predicted output matched the expected (target) output, structured output modelling evaluates such qualities using a set of errors. This error set enumerates all possible scenarios, which could happen in the prediction and ensure that there is a sensible gradient between these errors which can reflect the structured nature of the output [
14]. Using the same example given above, suppose there is a properly-trained model and one tests it with a group of blind test samples, if an E1B1-labelled sample had been predicted as E2B1 and another E1B1 sample had been predicted as E2B2, then the former prediction should have a lower error than the latter; i.e., the sensible error gradient between the three possible outcomes would be: a correct prediction in both E and B < one wrong prediction in either E or B < wrong predictions in both E and B. A sensible error set for this particular example could be defined as {0,1,2} and each prediction would have an error of one of those numbers in the set. The design of a structured output and the corresponding error set is largely problem-based and it has to be performed based on the available a priori knowledge, then one would need a modelling technique to build a model to establish the relationship between the structural coded output and the observed data and minimise the error derived from the designed error set. Many machine learning models have been extended to model structured data, such as structured support vector machines (S-SVM) [
15], deep learning neural networks [
16], etc. Compared to those machine learning approaches, PLS has a much larger following in the metabolomics community [
17] and almost all major statistical software packages provide easy-to-use PLS routines. As structured output coding only involves designing a more sensible targeted output
Y and the (usually human) interpretations on the predicted outputs afterwards, this can be easily adapted by any software package which supports PLS.
In this study, we explored such a possibility of using a structured output, designed according to the DOE, for PLS modelling and compared the results with classic binary coding. Two recently published real metabolomics datasets were employed which used two different DOEs with different complexity and characteristics.
One dataset (denoted as
riboswitch in this paper), was obtained from an experiment to investigate the metabolic effects of producing enhanced green fluorescent protein (eGFP) as a recombinant protein in
Escherichia coli (
E. coli) cells [
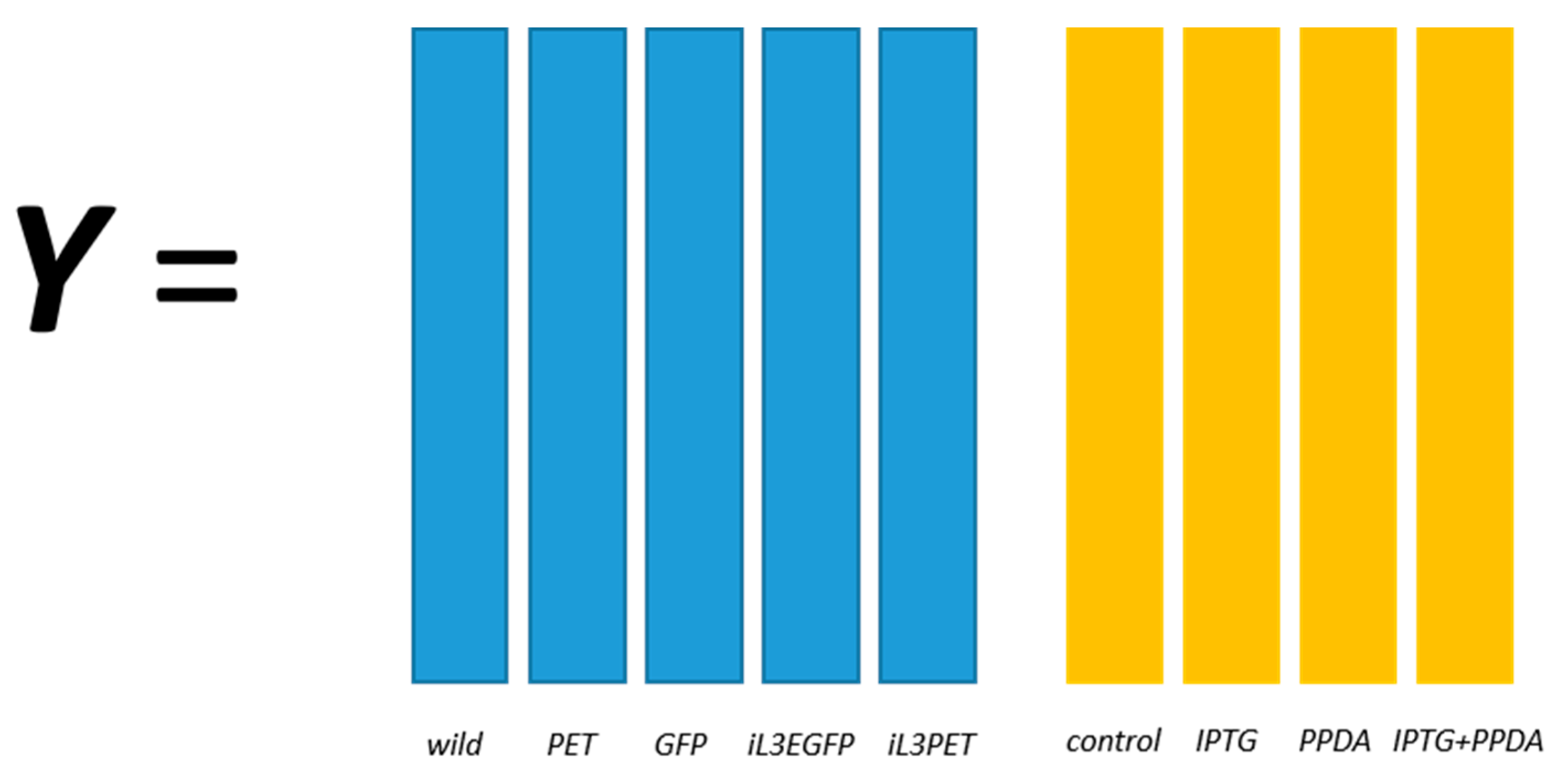
18]. A two-factor, full-factorial experimental design was employed and the metabolic profiles of five different
E. coli strains, namely BL21(DE3) (wild-type), BL21(DE3) pET-empty (PET), BL21(DE3) pET-eGFP (EGFP), BL21(IL3) pET-empty (iL3PET), BL21(IL3) pETeGFP (iL3EGFP), under four different inducer conditions (control,
lac inducer Isopropyl β-
d-1-thiogalactopyranoside (IPTG), pyimido[4,5-
d] pyrimidine-2,4-diamine (PPDA), and IPTG + PPDA) were measured by Fourier transform infrared (FT-IR) spectroscopy and gas chromatography-mass spectrometry (GC-MS) on cell extracts (the details of this experiment and a more detailed description of the strains can be found in [
19]). Since the FT-IR and GC-MS data showed very similar results, only the GC-MS results were reported in this paper. The data will be uploaded and available at MetaboLights.
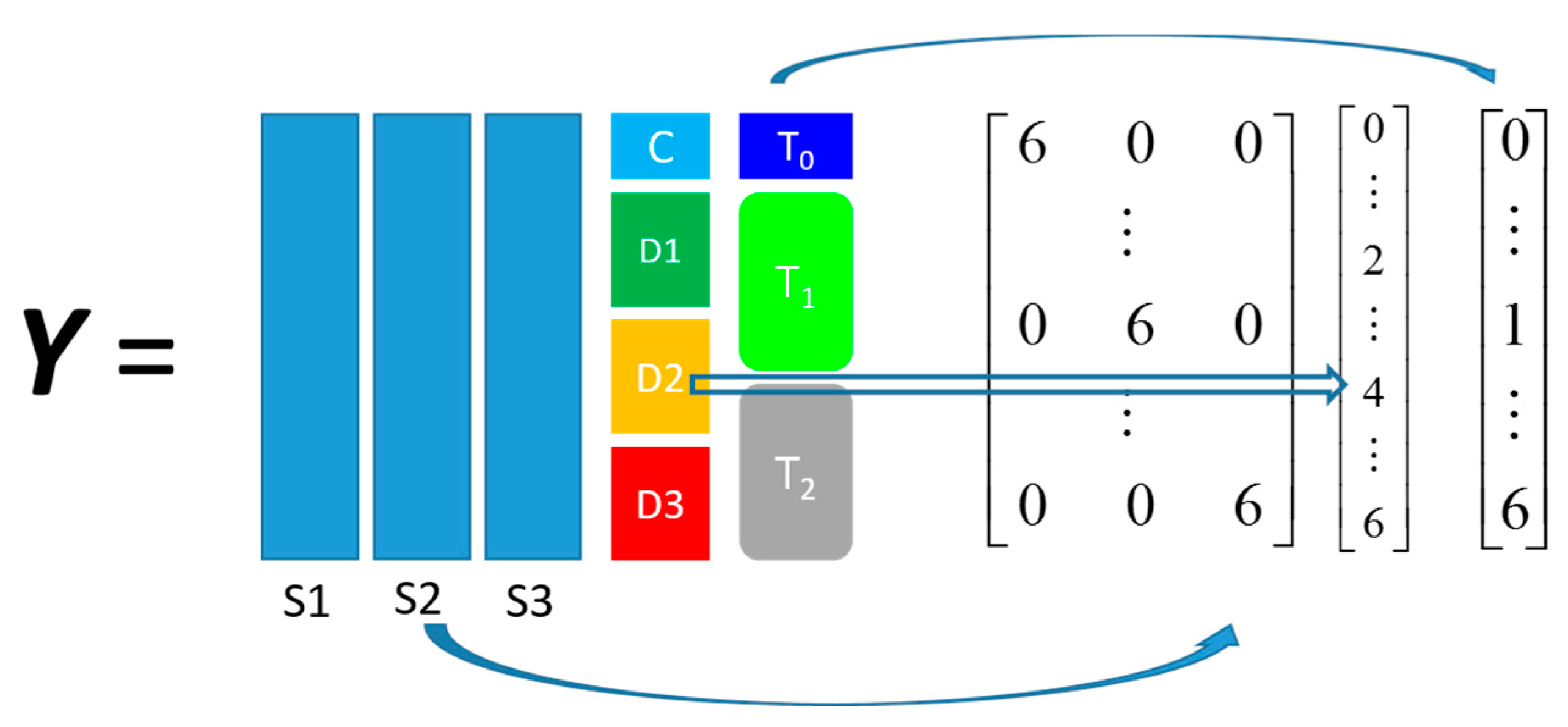
The other dataset, denoted as
propranolol, was the results of an experiment investigating the role of efflux pumps in stress tolerance
Pseudomonas putida exposed to toxic hydrocarbons. In this experiment three different strains of
P. putida (denoted as DOT-T1E, DOT-T1E-PS28, and DOT-T1E-18) were exposed to four different dosages of propranolol (control, 0.2, 0.4, and 0.6 mg/mL), and three time points were monitored over a period of one hour (start (0), 10, and 60 min after exposure to the drug). At each time point, a sample of cells were collected, extracted, and analysed by GC-MS. The details can be found in [
20] and these data are available at MetaboLights under study identifier MTBLS320 [
21]. In our previous publications, we employed a series of different MB-PCA models to examine the effect of each factor separately while, in this study, we designed structured outputs to capture the essence of the experimental designs, and used PLS to model these structured outputs so that the effect of the factors of interest can be analysed simultaneously using a single model.