Metabolism at Evolutionary Optimal States
Abstract
:1. Environments, Natural Selection and Fitness
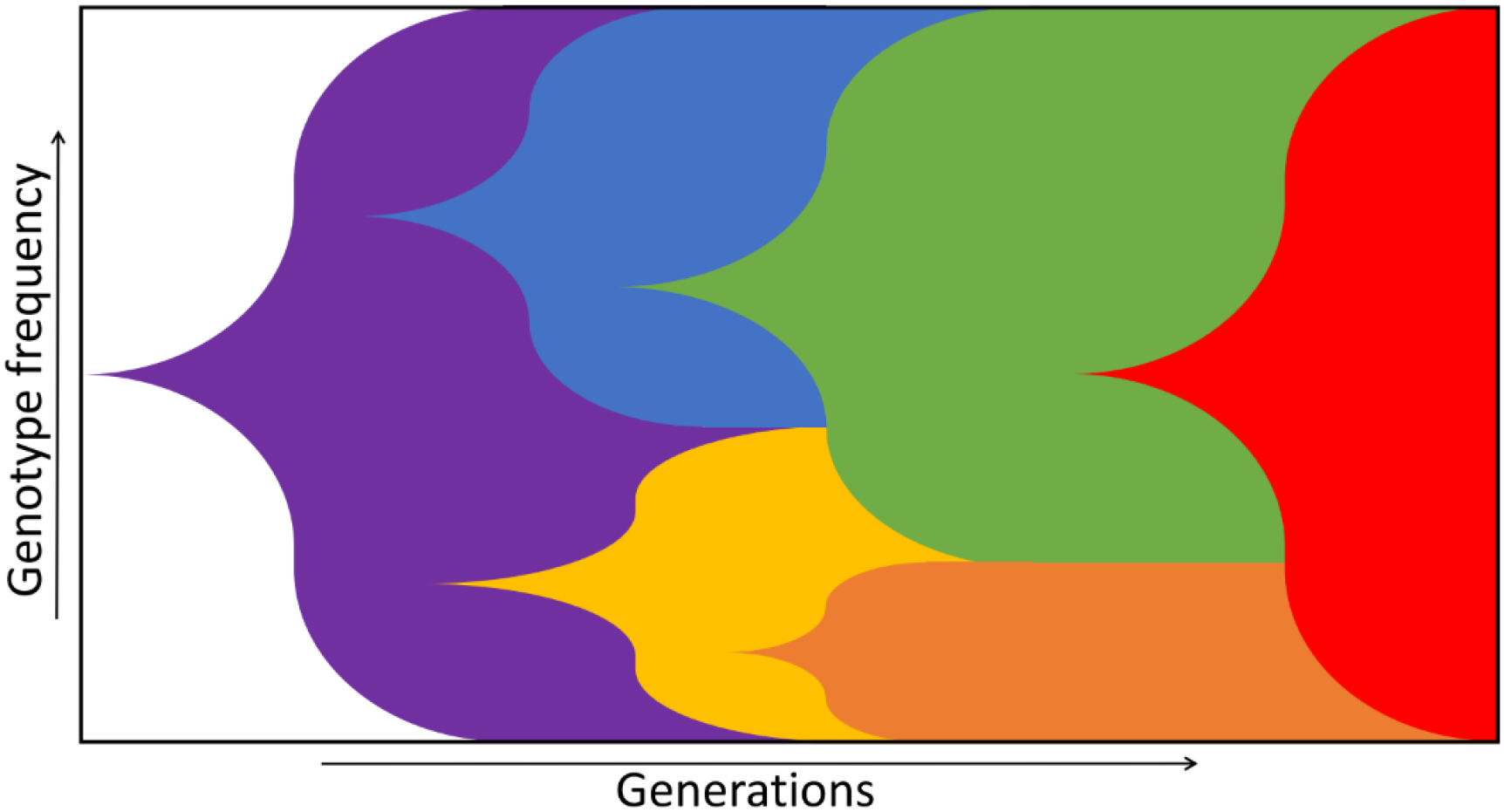
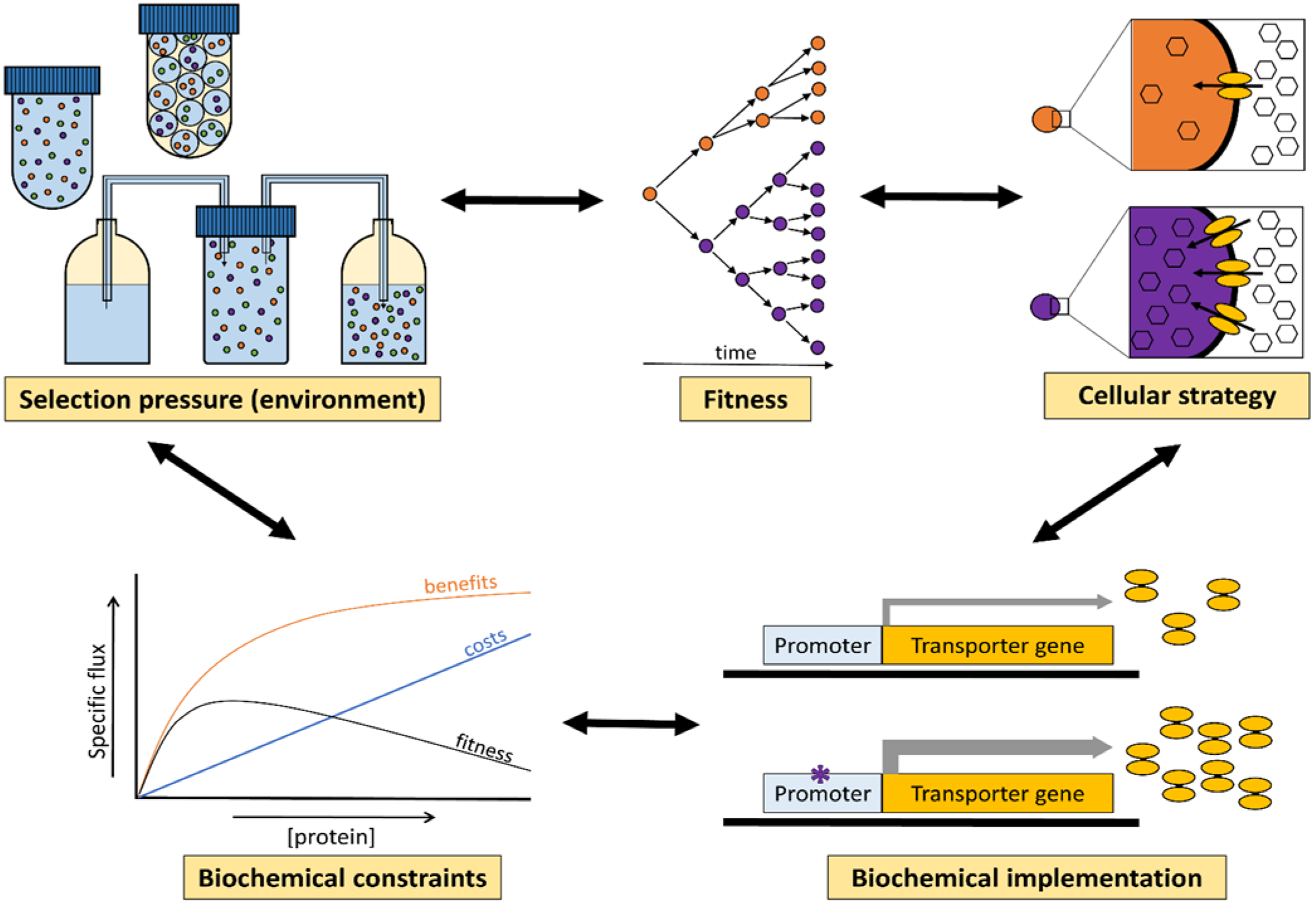
2. Fitness Landscapes
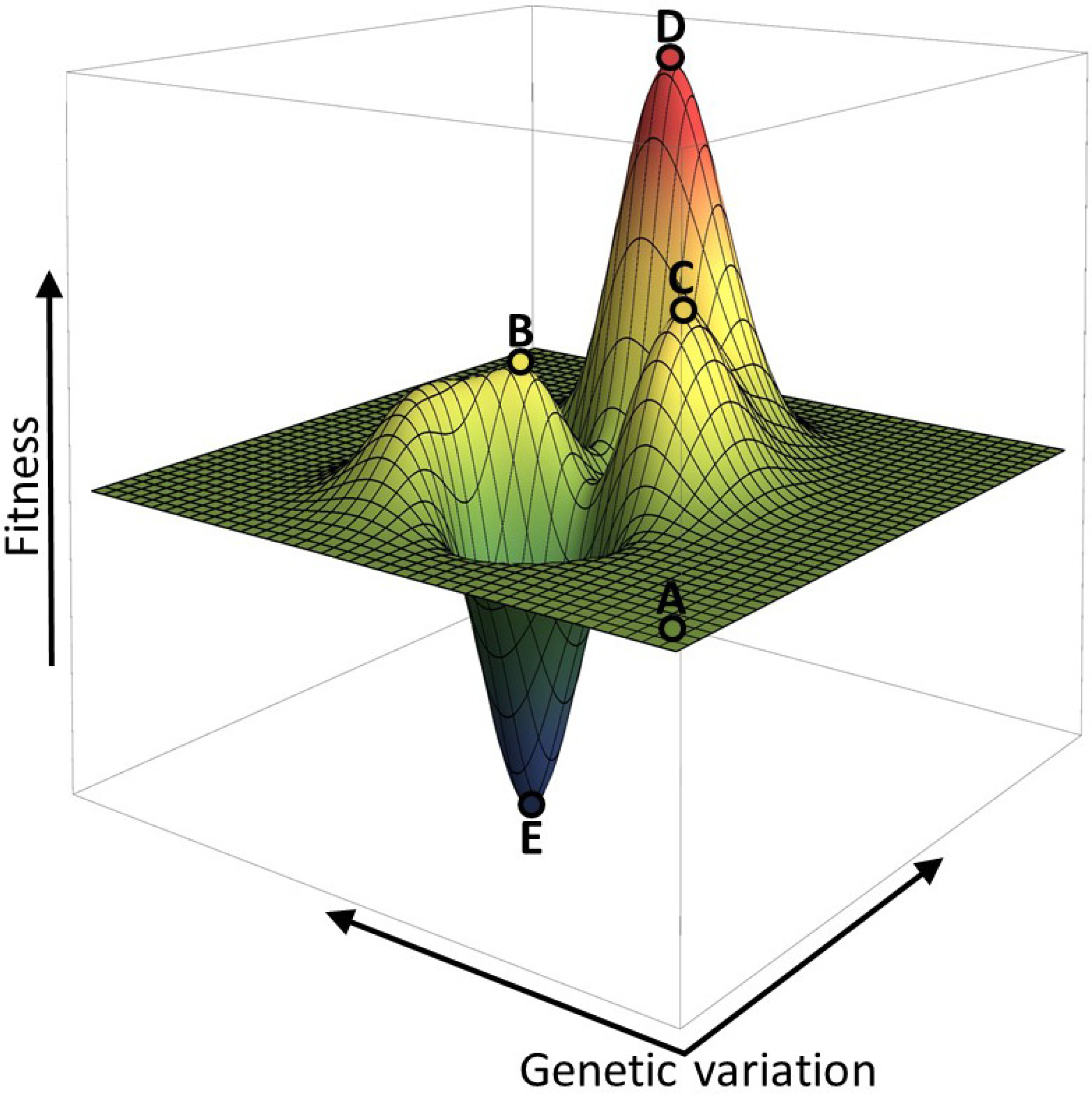
3. Selection Pressures Imposed by the Environment
3.1. Experimental Culturing Methods
| Batch | Emulsion [29] | Chemostat | |
|---|---|---|---|
| Fitness measure | Growth rate (μ) | Number of cells (N) | Substrate concentration [S] at dilution rate (D) = μ |
| Evolutionary objective | Maximize μ | Maximize N | Minimize [S] at D = μ |
| Possible strategies | High μmax | (a) High metabolic yield (b) Small cells | (a) Low KM (b) High μmax |
| Examples | Fermentation in yeast; overflow metabolism in E. coli | Mixed acid fermentation in L. lactis | Metabolic switches |
| Trade-offs | Low yield | Low μmax | (a) Low μmax (b) Low yield |
| Method for prediction of optimality | EFM + enzyme kinetics | FBA | EFM + enzyme kinetics |
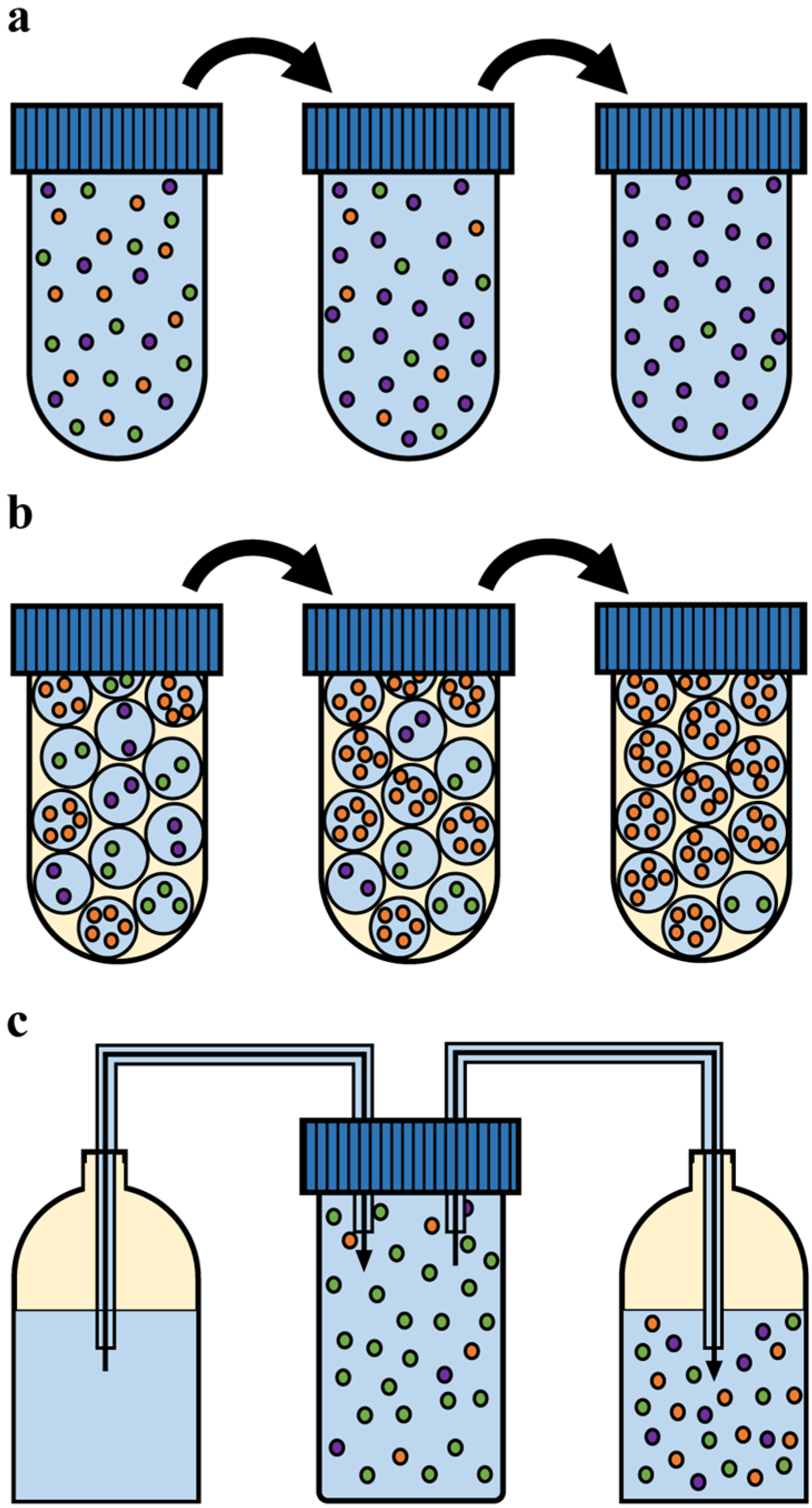
3.1.1. Batch Cultivation
3.1.2. Emulsion Cultivation
3.1.3. Chemostat Cultivation
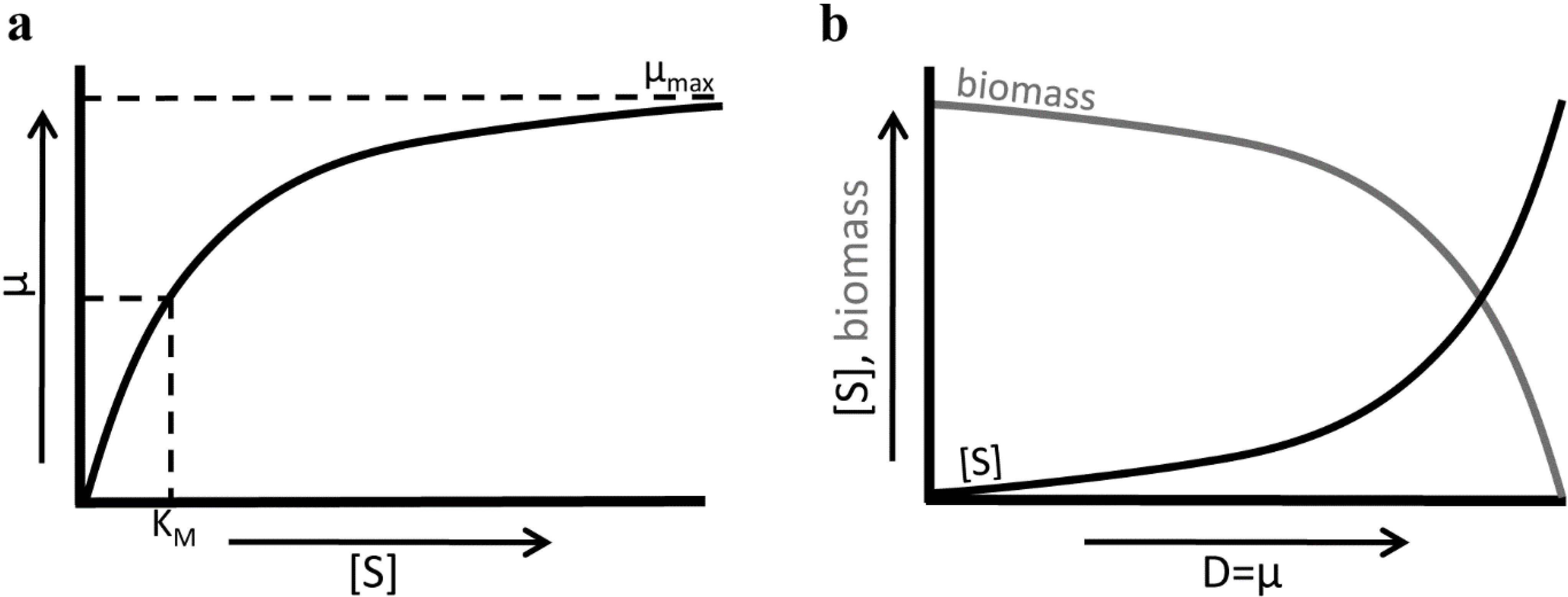
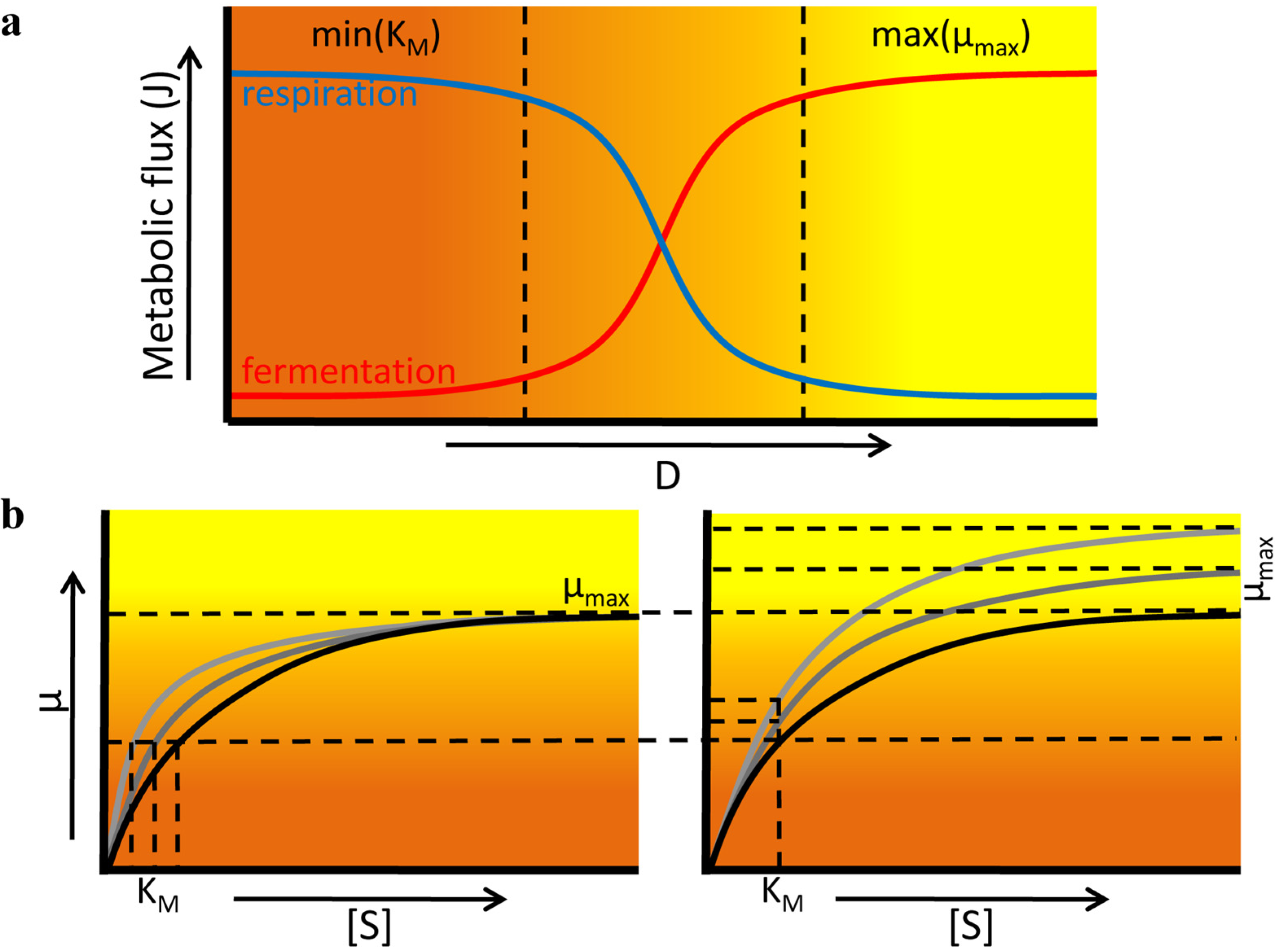
3.2. Fitness Effects of Changing Environments
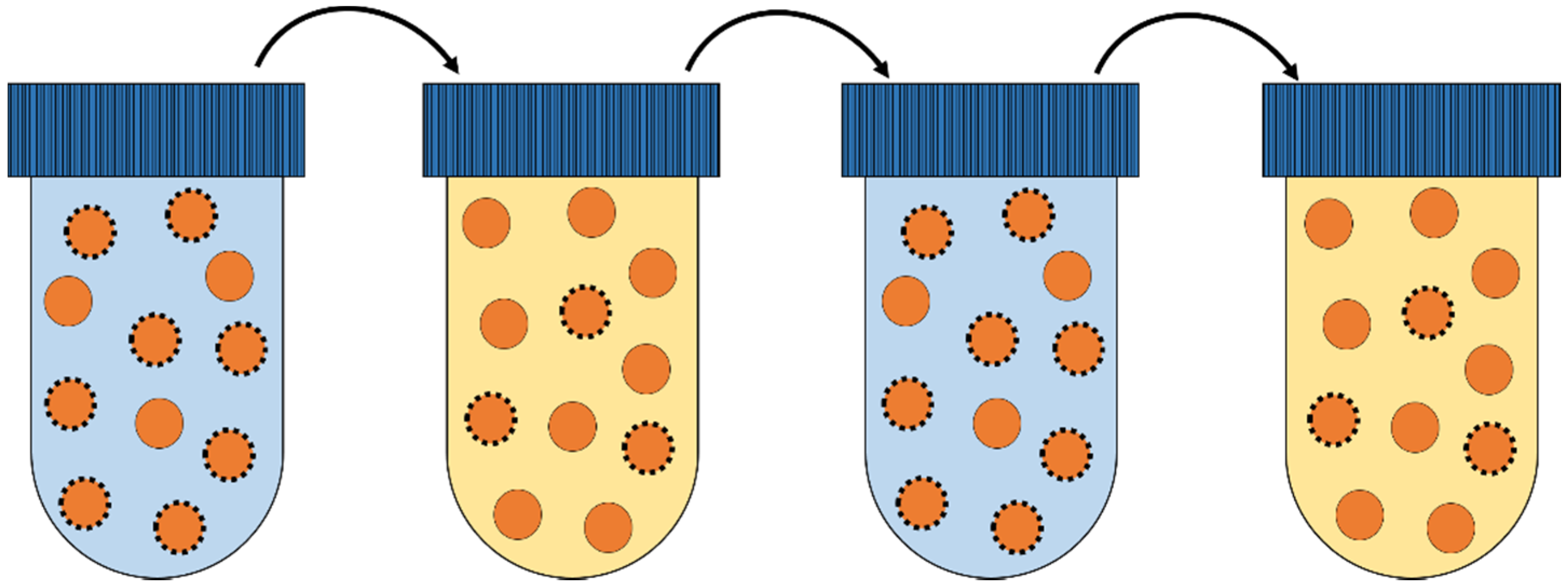
3.3. Environmental Stress Conditions
4. Physical, Biochemical, and Cellular Constraints on Evolutionary Optimisation of Metabolism
4.1. Thermodynamics of Biochemistry Limits Cellular Processes
4.2. Relation between Enzyme Benefits, Enzyme Costs and Cellular Fitness
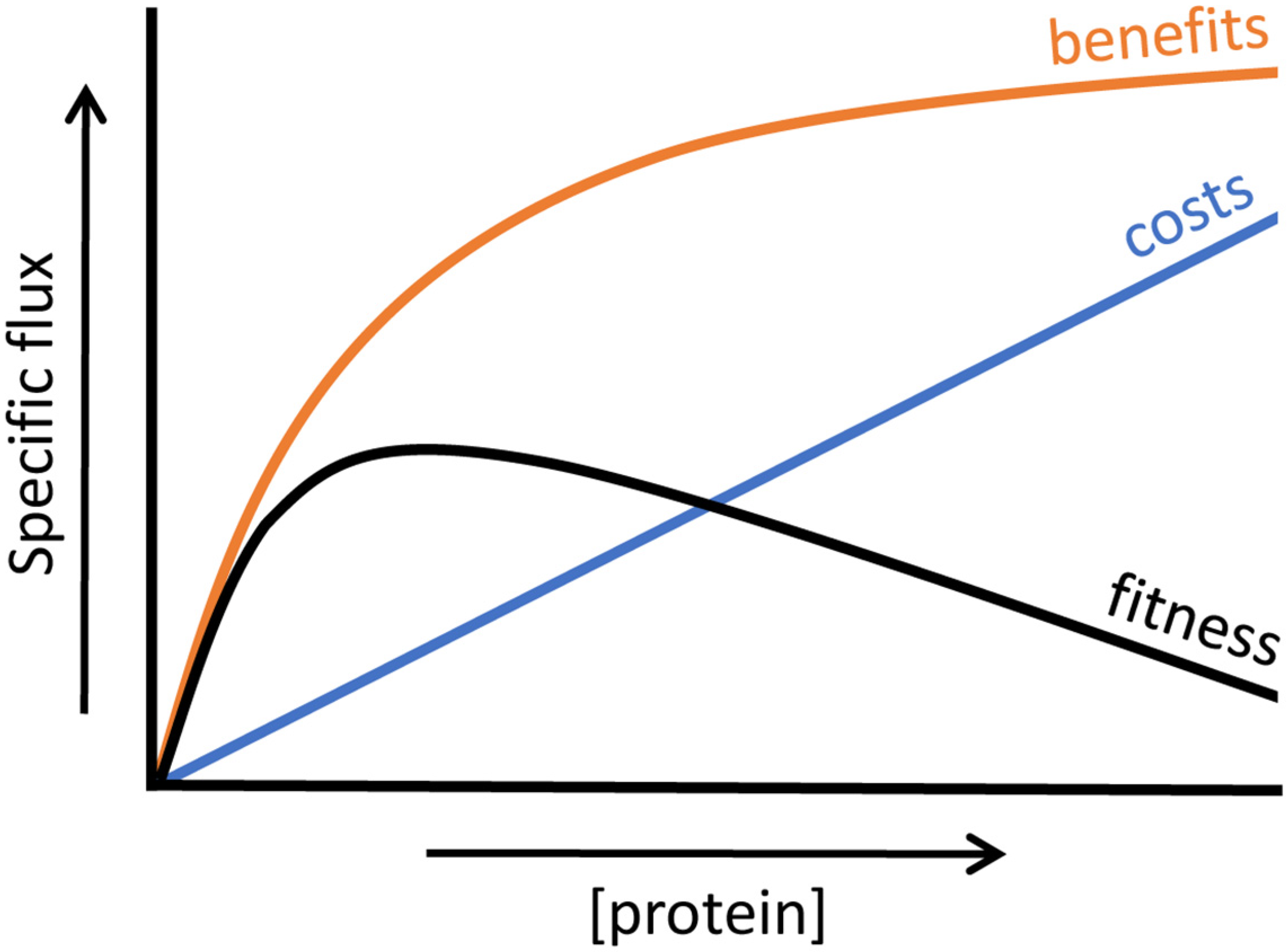
4.3. Trade-Offs in Metabolic Evolution
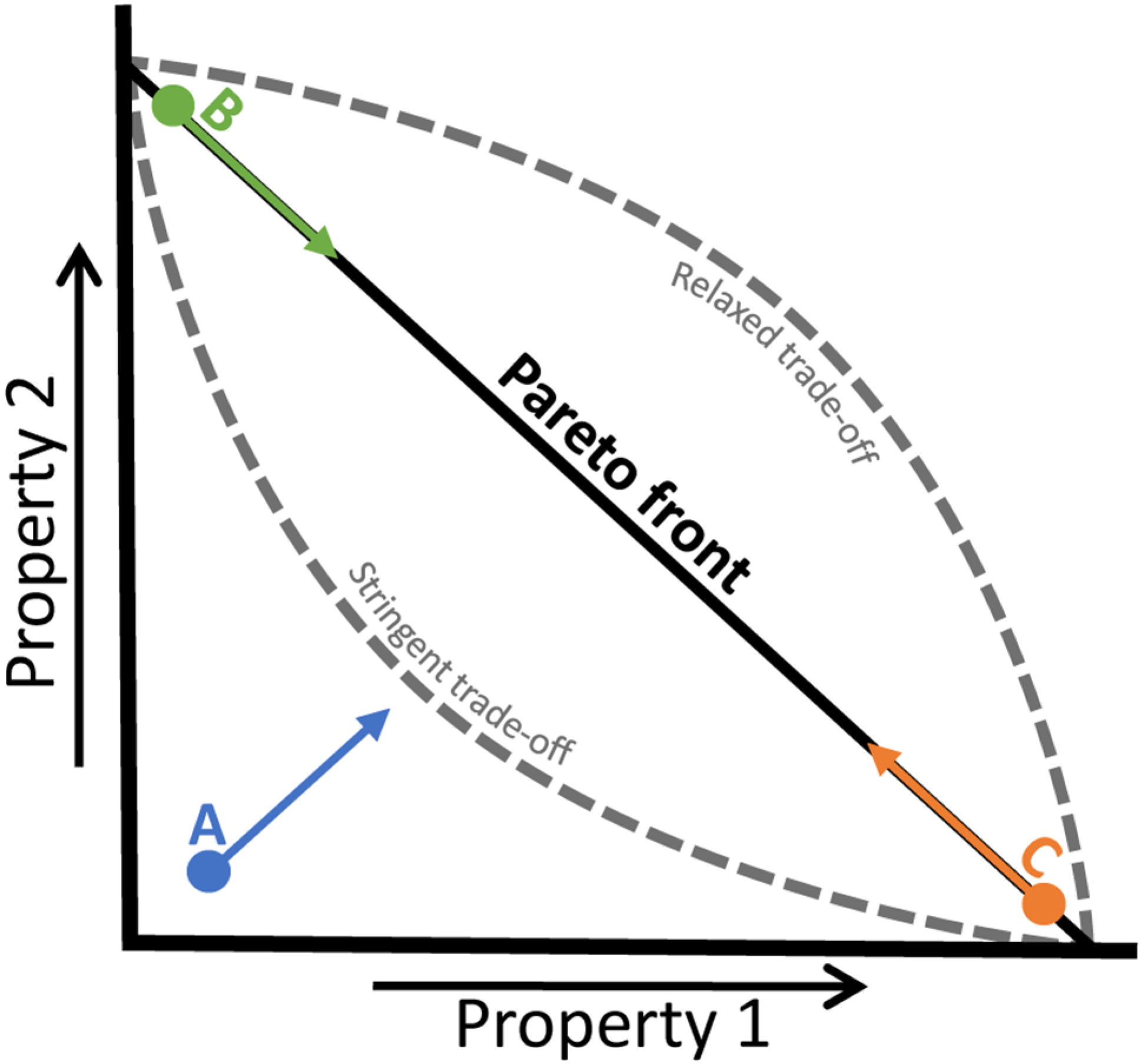
5. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Barrick, J.E.; Lenski, R.E. Genome dynamics during experimental evolution. Nat. Rev. Genet. 2013, 14, 827–839. [Google Scholar] [CrossRef] [PubMed]
- Klumpp, S.; Hwa, T. Bacterial growth: Global effects on gene expression, growth feedback and proteome partition. Curr. Opin. Biotechnol. 2014, 28, 96–102. [Google Scholar] [CrossRef] [PubMed]
- Klumpp, S.; Zhang, Z.; Hwa, T. Growth rate-dependent global effects on gene expression in bacteria. Cell 2009, 139, 1366–1375. [Google Scholar] [CrossRef] [PubMed]
- Scott, M.; Gunderson, C.W.; Mateescu, E.M.; Zhang, Z.; Hwa, T. Interdependence of cell growth and gene expression: Origins and consequences. Science 2010, 330, 1099–1102. [Google Scholar] [CrossRef] [PubMed]
- Dekel, E.; Alon, U. Optimality and evolutionary tuning of the expression level of a protein. Nature 2005, 436, 588–592. [Google Scholar] [CrossRef] [PubMed]
- Berkhout, J.; Bruggeman, F.J.; Teusink, B. Optimality Principles in the Regulation of Metabolic Networks. Metabolites 2012, 2, 529–552. [Google Scholar] [CrossRef] [PubMed]
- Wright, S. The roles of mutation, inbreeding, crossbreeding and selection in evolution. Proc. Int. Congr. Genet. 1932, 1, 356–366. [Google Scholar]
- Romero, P.A.; Arnold, F.H. Exploring protein fitness landscapes by directed evolution. Nat. Rev. Mol. Cell Biol. 2009, 10, 866–876. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.M. Natural selection and the concept of a protein space. Nature 1970, 225, 563–564. [Google Scholar] [CrossRef] [PubMed]
- Näsvall, J.; Sun, L.; Roth, J.R.; Andersson, D.I. Real-time evolution of new genes by innovation, amplification, and divergence. Science 2012, 338, 384–387. [Google Scholar] [CrossRef] [PubMed]
- Alberts, B.; Johnson, A.; Lewis, J.; Raff, M.; Roberts, K.; Walter, P. Molecular Biology of the Cell, 5th ed.; Garland Science: New York, NY, USA, 2008; pp. 304–316. [Google Scholar]
- Ochman, H.; Lawrence, J.G.; Groisman, E.A. Lateral gene transfer and the nature of bacterial innovation. Nature 2000, 405, 299–304. [Google Scholar] [CrossRef] [PubMed]
- Poelwijk, F.J.; Kiviet, D.J.; Weinreich, D.M.; Tans, S.J. Empirical fitness landscapes reveal accessible evolutionary paths. Nature 2007, 445, 383–386. [Google Scholar] [CrossRef] [PubMed]
- Nagel, A.C.; Joyce, P.; Wichman, H.A.; Miller, C.R. Stickbreaking: A novel fitness landscape model that harbors epistasis and is consistent with commonly observed patterns of adaptive evolution. Genetics 2012, 190, 655–667. [Google Scholar] [CrossRef] [PubMed]
- Elena, S.F.; Lenski, R.E. Evolution experiments with microorganisms: The dynamics and genetic bases of adaptation. Nat. Rev. Genet. 2003, 4, 457–469. [Google Scholar] [CrossRef] [PubMed]
- Kussell, E. Evolution in microbes. Annu. Rev. Biophys. 2013, 42, 493–514. [Google Scholar] [CrossRef] [PubMed]
- Chou, H.-H.; Chiu, H.-C.; Delaney, N.F.; Segrè, D.; Marx, C.J. Diminishing returns epistasis among beneficial mutations decelerates adaptation. Science 2011, 332, 1190–1192. [Google Scholar] [CrossRef] [PubMed]
- De Vos, M.G.J.; Poelwijk, F.J.; Battich, N.; Ndika, J.D.T.; Tans, S.J. Environmental dependence of genetic constraint. PLoS Genet. 2013, 9, e1003580. [Google Scholar] [CrossRef] [PubMed]
- Koonin, E.V.; Wolf, Y.I. Constraints and plasticity in genome and molecular-phenome evolution. Nat. Rev. Genet. 2010, 11, 487–498. [Google Scholar] [CrossRef] [PubMed]
- Wagner, A. Robustness and evolvability: A paradox resolved. Proc. Biol. Sci. 2008, 275, 91–100. [Google Scholar] [CrossRef] [PubMed]
- Wielgoss, S.; Barrick, J.E.; Tenaillon, O.; Wiser, M.J.; Dittmar, W.J.; Cruveiller, S.; Chane-Woon-Ming, B.; Médigue, C.; Lenski, R.E.; Schneider, D. Mutation rate dynamics in a bacterial population reflect tension between adaptation and genetic load. Proc. Natl. Acad. Sci. USA 2013, 110, 222–227. [Google Scholar] [CrossRef] [PubMed]
- Wiser, M.J.; Ribeck, N.; Lenski, R.E. Long-term dynamics of adaptation in asexual populations. Science 2013, 342, 1364–1367. [Google Scholar] [CrossRef] [PubMed]
- McDonald, M.J.; Hsieh, Y.-Y.; Yu, Y.-H.; Chang, S.-L.; Leu, J.-Y. The evolution of low mutation rates in experimental mutator populations of Saccharomyces cerevisiae. Curr. Biol. 2012, 22, 1235–1240. [Google Scholar] [CrossRef] [PubMed]
- Weinreich, D.M.; Delaney, N.F.; Depristo, M.A.; Hartl, D.L. Darwinian evolution can follow only very few mutational paths to fitter proteins. Science 2006, 312, 111–114. [Google Scholar] [CrossRef] [PubMed]
- Couñago, R.; Chen, S.; Shamoo, Y. In vivo molecular evolution reveals biophysical origins of organismal fitness. Mol. Cell 2006, 22, 441–449. [Google Scholar] [CrossRef] [PubMed]
- Peña, M.I.; Davlieva, M.; Bennett, M.R.; Olson, J.S.; Shamoo, Y. Evolutionary fates within a microbial population highlight an essential role for protein folding during natural selection. Mol. Syst. Biol. 2010, 6, 387. [Google Scholar] [CrossRef] [PubMed]
- Lobkovsky, A.E.; Koonin, E.V. Replaying the tape of life: Quantification of the predictability of evolution. Front. Genet. 2012, 3, 246. [Google Scholar] [CrossRef] [PubMed]
- Carneiro, M.; Hartl, D.L. Colloquium papers: Adaptive landscapes and protein evolution. Proc. Natl. Acad. Sci. USA 2010, 107, 1747–1751. [Google Scholar] [CrossRef] [PubMed]
- Bachmann, H.; Fischlechner, M.; Rabbers, I.; Barfa, N.; Branco dos Santos, F.; Molenaar, D.; Teusink, B. Availability of public goods shapes the evolution of competing metabolic strategies. Proc. Natl. Acad. Sci. USA 2013, 110, 14302–14307. [Google Scholar] [CrossRef] [PubMed]
- Bryson, V.; Szybalski, W. Microbial Selection. Science 1952, 116, 45–51. [Google Scholar] [CrossRef] [PubMed]
- Bull, A.T. The renaissance of continuous culture in the post-genomics age. J. Ind. Microbiol. Biotechnol. 2010, 37, 993–1021. [Google Scholar] [CrossRef] [PubMed]
- Ibarra, R.U.; Edwards, J.S.; Palsson, B.O. Escherichia coli K-12 undergoes adaptive evolution to achieve in silico predicted optimal growth. Nature 2002, 420, 186–189. [Google Scholar] [CrossRef] [PubMed]
- Jasmin, J.-N.; Dillon, M.M.; Zeyl, C. The yield of experimental yeast populations declines during selection. Proc. Biol. Sci. 2012, 279, 4382–4388. [Google Scholar] [CrossRef] [PubMed]
- Zeyl, C.; Vanderford, T.; Carter, M. An evolutionary advantage of haploidy in large yeast populations. Science 2003, 299, 555–558. [Google Scholar] [CrossRef] [PubMed]
- Wortel, M.T.; Peters, H.; Hulshof, J.; Teusink, B.; Bruggeman, F.J. Metabolic states with maximal specific rate carry flux through an elementary flux mode. FEBS J. 2014, 281, 1547–1555. [Google Scholar] [CrossRef] [PubMed]
- Müller, S.; Regensburger, G.; Steuer, R. Enzyme allocation problems in kinetic metabolic networks: Optimal solutions are elementary flux modes. J. Theor. Biol. 2014, 347, 182–190. [Google Scholar] [CrossRef] [PubMed]
- Schuster, S.; Fell, D.A.; Dandekar, T. A general definition of metabolic pathways useful for systematic organization and analysis of complex metabolic networks. Nat. Biotechnol. 2000, 18, 326–332. [Google Scholar] [CrossRef] [PubMed]
- Dragosits, M.; Mattanovich, D. Adaptive laboratory evolution—Principles and applications for biotechnology. Microb. Cell Factories 2013, 12, 64. [Google Scholar] [CrossRef] [PubMed]
- Schuster, S.; Pfeiffer, T.; Fell, D.A. Is maximization of molar yield in metabolic networks favoured by evolution? J. Theor. Biol. 2008, 252, 497–504. [Google Scholar] [CrossRef] [PubMed]
- Teusink, B.; Wiersma, A.; Molenaar, D.; Francke, C.; de Vos, W.M.; Siezen, R.J.; Smid, E.J. Analysis of growth of Lactobacillus plantarum WCFS1 on a complex medium using a genome-scale metabolic model. J. Biol. Chem. 2006, 281, 40041–40048. [Google Scholar] [CrossRef] [PubMed]
- MacLean, R.C. The tragedy of the commons in microbial populations: Insights from theoretical, comparative and experimental studies. Heredity (Edinb). 2008, 100, 233–239. [Google Scholar] [CrossRef] [PubMed]
- Molenaar, D.; van Berlo, R.; de Ridder, D.; Teusink, B. Shifts in growth strategies reflect tradeoffs in cellular economics. Mol. Syst. Biol. 2009, 5, 323. [Google Scholar] [CrossRef] [PubMed]
- Postma, E.; Verduyn, C.; Scheffers, W.A.; Van Dijken, J.P. Enzymic analysis of the crabtree effect in glucose-limited chemostat cultures of Saccharomyces cerevisiae. Appl. Environ. Microbiol. 1989, 55, 468–477. [Google Scholar] [PubMed]
- Lipson, D.A.; Monson, R.K.; Schmidt, S.K.; Weintraub, M.N. The trade-off between growth rate and yield in microbial communities and the consequences for under-snow soil respiration in a high elevation coniferous forest. Biogeochemistry 2008, 95, 23–35. [Google Scholar] [CrossRef]
- Pfeiffer, T.; Schuster, S.; Bonhoeffer, S. Cooperation and competition in the evolution of ATP-producing pathways. Science 2001, 292, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Jansen, M.L.A.; Diderich, J.A.; Mashego, M.; Hassane, A.; de Winde, J.H.; Daran-Lapujade, P.; Pronk, J.T. Prolonged selection in aerobic, glucose-limited chemostat cultures of Saccharomyces cerevisiae causes a partial loss of glycolytic capacity. Microbiology 2005, 151, 1657–1669. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Mashego, M.R.; Proell, A.M.; Vinke, J.L.; Ras, C.; van Dam, J.; van Winden, W.A.; van Gulik, W.M.; Heijnen, J.J. In vivo kinetics of primary metabolism in Saccharomyces cerevisiae studied through prolonged chemostat cultivation. Metab. Eng. 2006, 8, 160–171. [Google Scholar] [CrossRef] [PubMed]
- Tsen, S.D.; Lai, S.C.; Pang, C.P.; Lee, J.I.; Wilson, T.H. Chemostat selection of an Escherichia coli mutant containing permease with enhanced lactose affinity. Biochem. Biophys. Res. Commun. 1996, 224, 351–357. [Google Scholar] [CrossRef] [PubMed]
- Dykhuizen, D.E.; Dean, A.M.; Hartl, D.L. Metabolic flux and fitness. Genetics 1987, 115, 25–31. [Google Scholar] [PubMed]
- Jørgensen, T.R.; vanKuyk, P.A.; Poulsen, B.R.; Ruijter, G.J.G.; Visser, J.; Iversen, J.J.L. Glucose uptake and growth of glucose-limited chemostat cultures of Aspergillus niger and a disruptant lacking MstA, a high-affinity glucose transporter. Microbiology 2007, 153, 1963–1973. [Google Scholar] [CrossRef] [PubMed]
- Wick, L.M.; Weilenmann, H.; Egli, T. The apparent clock-like evolution of Escherichia coli in glucose-limited chemostats is reproducible at large but not at small population sizes and can be explained with Monod kinetics. Microbiology 2002, 148, 2889–2902. [Google Scholar] [PubMed]
- Van Hoek, P.; Van Dijken, J.P.; Pronk, J.T. Effect of specific growth rate on fermentative capacity of baker’s yeast. Appl. Environ. Microbiol. 1998, 64, 4226–4233. [Google Scholar] [PubMed]
- Beardmore, R.E.; Gudelj, I.; Lipson, D.A.; Hurst, L.D. Metabolic trade-offs and the maintenance of the fittest and the flattest. Nature 2011, 472, 342–346. [Google Scholar] [CrossRef] [PubMed]
- Gudelj, I.; Beardmore, R.E.; Arkin, S.S.; MacLean, R.C. Constraints on microbial metabolism drive evolutionary diversification in homogeneous environments. J. Evol. Biol. 2007, 20, 1882–1889. [Google Scholar] [CrossRef] [PubMed]
- Maharjan, R.P.; Seeto, S.; Ferenci, T. Divergence and redundancy of transport and metabolic rate-yield strategies in a single Escherichia coli population. J. Bacteriol. 2007, 189, 2350–2358. [Google Scholar] [CrossRef] [PubMed]
- Novak, M.; Pfeiffer, T.; Lenski, R.E.; Sauer, U.; Bonhoeffer, S. Experimental tests for an evolutionary trade-off between growth rate and yield in E. coli. Am. Nat. 2006, 168, 242–251. [Google Scholar] [CrossRef] [PubMed]
- Weusthuis, R.A.; Pronk, J.T.; van den Broek, P.J.; van Dijken, J.P. Chemostat cultivation as a tool for studies on sugar transport in yeasts. Microbiol. Rev. 1994, 58, 616–630. [Google Scholar] [PubMed]
- Poelwijk, F.J.; de Vos, M.G.J.; Tans, S.J. Tradeoffs and optimality in the evolution of gene regulation. Cell 2011, 146, 462–470. [Google Scholar] [CrossRef] [PubMed]
- Saxer, G.; Krepps, M.D.; Merkley, E.D.; Ansong, C.; Deatherage Kaiser, B.L.; Valovska, M.-T.; Ristic, N.; Yeh, P.T.; Prakash, V.P.; Leiser, O.P.; et al. Mutations in Global Regulators Lead to Metabolic Selection during Adaptation to Complex Environments. PLoS Genet. 2014, 10, e1004872. [Google Scholar] [CrossRef] [PubMed]
- Notley-McRobb, L.; Seeto, S.; Ferenci, T. The influence of cellular physiology on the initiation of mutational pathways in Escherichia coli populations. Proc. Biol. Sci. 2003, 270, 843–848. [Google Scholar] [CrossRef] [PubMed]
- Blank, D.; Wolf, L.; Ackermann, M.; Silander, O.K. The predictability of molecular evolution during functional innovation. Proc. Natl. Acad. Sci. USA 2014, 111, 3044–3049. [Google Scholar] [CrossRef] [PubMed]
- Maharjan, R.; Seeto, S.; Notley-McRobb, L.; Ferenci, T. Clonal adaptive radiation in a constant environment. Science 2006, 313, 514–517. [Google Scholar] [CrossRef] [PubMed]
- Philippe, N.; Crozat, E.; Lenski, R.E.; Schneider, D. Evolution of global regulatory networks during a long-term experiment with Escherichia coli. Bioessays 2007, 29, 846–860. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, K. Metabolic Regulation of a Bacterial Cell System with Emphasis on Escherichia coli Metabolism. ISRN Biochem. 2013, 2013. [Google Scholar] [CrossRef] [PubMed]
- Puentes-Téllez, P.E.; Kovács, Á.T.; Kuipers, O.P.; van Elsas, J.D. Comparative genomics and transcriptomics analysis of experimentally evolved Escherichia coli MC1000 in complex environments. Environ. Microbiol. 2014, 16, 856–870. [Google Scholar] [CrossRef] [PubMed]
- Zaslaver, A.; Mayo, A.E.; Rosenberg, R.; Bashkin, P.; Sberro, H.; Tsalyuk, M.; Surette, M.G.; Alon, U. Just-in-time transcription program in metabolic pathways. Nat. Genet. 2004, 36, 486–491. [Google Scholar] [CrossRef] [PubMed]
- New, A.M.; Cerulus, B.; Govers, S.K.; Perez-Samper, G.; Zhu, B.; Boogmans, S.; Xavier, J.B.; Verstrepen, K.J. Different levels of catabolite repression optimize growth in stable and variable environments. PLoS Biol. 2014, 12, e1001764. [Google Scholar] [CrossRef] [PubMed]
- Acar, M.; Mettetal, J.T.; van Oudenaarden, A. Stochastic switching as a survival strategy in fluctuating environments. Nat. Genet. 2008, 40, 471–475. [Google Scholar] [CrossRef] [PubMed]
- Gaál, B.; Pitchford, J.W.; Wood, A.J. Exact results for the evolution of stochastic switching in variable asymmetric environments. Genetics 2010, 184, 1113–1119. [Google Scholar] [CrossRef] [PubMed]
- Liberman, U.; Van Cleve, J.; Feldman, M.W. On the evolution of mutation in changing environments: Recombination and phenotypic switching. Genetics 2011, 187, 837–851. [Google Scholar] [CrossRef] [PubMed]
- Poole, K. Bacterial stress responses as determinants of antimicrobial resistance. J. Antimicrob. Chemother. 2012, 67, 2069–2089. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, K. Regulation Systems of Bacteria such as Escherichia coli in Response to Nutrient Limitation and Environmental Stresses. Metabolites 2013, 4, 1–35. [Google Scholar] [CrossRef] [PubMed]
- Dragosits, M.; Mozhayskiy, V.; Quinones-Soto, S.; Park, J.; Tagkopoulos, I. Evolutionary potential, cross-stress behavior and the genetic basis of acquired stress resistance in Escherichia coli. Mol. Syst. Biol. 2013, 9, 643. [Google Scholar] [CrossRef] [PubMed]
- Landini, P.; Egli, T.; Wolf, J.; Lacour, S. sigmaS, a major player in the response to environmental stresses in Escherichia coli: Role, regulation and mechanisms of promoter recognition. Environ. Microbiol. Rep. 2014, 6, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Toprak, E.; Veres, A.; Michel, J.-B.; Chait, R.; Hartl, D.L.; Kishony, R. Evolutionary paths to antibiotic resistance under dynamically sustained drug selection. Nat. Genet. 2012, 44, 101–105. [Google Scholar] [CrossRef] [PubMed]
- Huovinen, P. Trimethoprim resistance. Antimicrob. Agents Chemother. 1987, 31, 1451–1456. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.R.; Calvo, J.M. Nucleotide sequence of dihydrofolate reductase genes from trimethoprim-resistant mutants of Escherichia coli. Evidence that dihydrofolate reductase interacts with another essential gene product. Mol. Gen. Genet. 1982, 187, 72–78. [Google Scholar] [CrossRef] [PubMed]
- Flensburg, J.; Sköld, O. Massive overproduction of dihydrofolate reductase in bacteria as a response to the use of trimethoprim. Eur. J. Biochem. 1987, 162, 473–476. [Google Scholar] [CrossRef] [PubMed]
- Hagiwara, D.; Yamashino, T.; Mizuno, T. A Genome-wide view of the Escherichia coli BasS-BasR two-component system implicated in iron-responses. Biosci. Biotechnol. Biochem. 2004, 68, 1758–1767. [Google Scholar] [CrossRef] [PubMed]
- Reyes, L.H.; Almario, M.P.; Winkler, J.; Orozco, M.M.; Kao, K.C. Visualizing evolution in real time to determine the molecular mechanisms of n-butanol tolerance in Escherichia coli. Metab. Eng. 2012, 14, 579–590. [Google Scholar] [CrossRef] [PubMed]
- Smith, W.M.; Pham, T.H.; Lei, L.; Dou, J.; Soomro, A.H.; Beatson, S.A.; Dykes, G.A.; Turner, M.S. Heat resistance and salt hypersensitivity in Lactococcus lactis due to spontaneous mutation of llmg_1816 (gdpP) induced by high-temperature growth. Appl. Environ. Microbiol. 2012, 78, 7753–7759. [Google Scholar] [CrossRef] [PubMed]
- Marians, K.J. Understanding how the replisome works. Nat. Struct. Mol. Biol. 2008, 15, 125–127. [Google Scholar] [CrossRef] [PubMed]
- Milo, R.; Jorgensen, P.; Moran, U.; Weber, G.; Springer, M. BioNumbers—The database of key numbers in molecular and cell biology. Nucleic Acids Res. 2010, 38, D750–D753. [Google Scholar] [CrossRef] [PubMed]
- Reshes, G.; Vanounou, S.; Fishov, I.; Feingold, M. Timing the start of division in E. coli: A single-cell study. Phys. Biol. 2008, 5, 046001. [Google Scholar] [CrossRef] [PubMed]
- Bremer, H.; Dennis, P. Modulation of chemical composition and other parameters of the cell by growth rate. In Escherichia coli and Salmonella: Cellular and Molecular Biology; Neidhardt, F.C., Ed.; ASM Press: Washington, Washington DC, USA, 1996; Volume 2, pp. 1553–1569. [Google Scholar]
- Atkinson, M.R.; Savageau, M.A.; Myers, J.T.; Ninfa, A.J. Development of Genetic Circuitry Exhibiting Toggle Switch or Oscillatory Behavior in Escherichia coli. Cell 2003, 113, 597–607. [Google Scholar] [CrossRef]
- Dill, K.A.; Ghosh, K.; Schmit, J.D. Physical limits of cells and proteomes. Proc. Natl. Acad. Sci. USA 2011, 108, 17876–17882. [Google Scholar] [CrossRef] [PubMed]
- Klumpp, S.; Scott, M.; Pedersen, S.; Hwa, T. Molecular crowding limits translation and cell growth. Proc. Natl. Acad. Sci. USA 2013, 110, 16754–16759. [Google Scholar] [CrossRef] [PubMed]
- Koch, A. The Mechanical Aspects of Cell. In Bacterial Growth and Form; Kluwer Academic Publishers: Dordrecht (the Netherlands), 2001; Volume 2, pp. 191–214. [Google Scholar]
- Koch, A.L. What size should a bacterium be? A question of scale. Annu. Rev. Microbiol. 1996, 50, 317–348. [Google Scholar] [CrossRef] [PubMed]
- Fick, A. On liquid diffusion. J. Membr. Sci. 1995, 100, 33–38. [Google Scholar] [CrossRef]
- Labbe, R.G.; Huang, T.H. Generation Times and Modeling of Enterotoxin-Positive and Enterotoxin-Negative Strains of Clostridium perfringens in Laboratory Media and Ground Beef. J. Food Prot. 1995, 12, 1303–1306. [Google Scholar]
- Eagon, R.G. Pseudomonas natriegens, a marine bacterium with a generation time of less than 10 min. J. Bacteriol. 1962, 83, 736–737. [Google Scholar] [PubMed]
- Maida, I.; Bosi, E.; Perrin, E.; Papaleo, M.C.; Orlandini, V.; Fondi, M.; Fani, R.; Wiegel, J.; Bianconi, G.; Canganella, F. Draft Genome Sequence of the Fast-Growing Bacterium Vibrio natriegens Strain DSMZ 759. Genome Announc. 2013. [Google Scholar] [CrossRef] [PubMed]
- Engle, M.; Li, Y.; Rainey, F.; DeBlois, S.; Mai, V.; Reichert, A.; Mayer, F.; Messner, P.; Wiegel, J. Thermobrachium celere gen. nov., sp. nov., a rapidly growing thermophilic, alkalitolerant, and proteolytic obligate anaerobe. Int. J. Syst. Bacteriol. 1996, 46, 1025–1033. [Google Scholar] [CrossRef] [PubMed]
- Burgess, S.A.; Lindsay, D.; Flint, S.H. Thermophilic bacilli and their importance in dairy processing. Int. J. Food Microbiol. 2010, 144, 215–225. [Google Scholar] [CrossRef] [PubMed]
- Berkhout, J.; Bosdriesz, E.; Nikerel, E.; Molenaar, D.; de Ridder, D.; Teusink, B.; Bruggeman, F.J. How biochemical constraints of cellular growth shape evolutionary adaptations in metabolism. Genetics 2013, 194, 505–512. [Google Scholar] [CrossRef] [PubMed]
- Dong, H.; Nilsson, L.; Kurland, C.G. Gratuitous overexpression of genes in Escherichia coli leads to growth inhibition and ribosome destruction. J. Bacteriol. 1995, 177, 1497–1504. [Google Scholar] [PubMed]
- Stoebel, D.M.; Dean, A.M.; Dykhuizen, D.E. The cost of expression of Escherichia coli lac operon proteins is in the process, not in the products. Genetics 2008, 178, 1653–1660. [Google Scholar] [CrossRef] [PubMed]
- Vind, J.; Sørensen, M.A.; Rasmussen, M.D.; Pedersen, S. Synthesis of proteins in Escherichia coli is limited by the concentration of free ribosomes. Expression from reporter genes does not always reflect functional mRNA levels. J. Mol. Biol. 1993, 231, 678–688. [Google Scholar] [CrossRef] [PubMed]
- Bachmann, H.; Starrenburg, M.J.C.; Molenaar, D.; Kleerebezem, M.; van Hylckama Vlieg, J.E.T. Microbial domestication signatures of Lactococcus lactis can be reproduced by experimental evolution. Genome Res. 2012, 22, 115–124. [Google Scholar] [CrossRef] [PubMed]
- Gore, J.; Youk, H.; van Oudenaarden, A. Snowdrift game dynamics and facultative cheating in yeast. Nature 2009, 459, 253–256. [Google Scholar] [CrossRef] [PubMed]
- Bachmann, H.; Molenaar, D.; Kleerebezem, M.; van Hylckama Vlieg, J.E.T. High local substrate availability stabilizes a cooperative trait. ISME J. 2011, 5, 929–932. [Google Scholar] [CrossRef] [PubMed]
- Buckling, A.; Harrison, F.; Vos, M.; Brockhurst, M.A.; Gardner, A.; West, S.A.; Griffin, A. Siderophore-mediated cooperation and virulence in Pseudomonas aeruginosa. FEMS Microbiol. Ecol. 2007, 62, 135–141. [Google Scholar] [CrossRef] [PubMed]
- Fasan, R.; Meharenna, Y.T.; Snow, C.D.; Poulos, T.L.; Arnold, F.H. Evolutionary history of a specialized p450 propane monooxygenase. J. Mol. Biol. 2008, 383, 1069–1080. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Minasov, G.; Shoichet, B.K. Evolution of an antibiotic resistance enzyme constrained by stability and activity trade-offs. J. Mol. Biol. 2002, 320, 85–95. [Google Scholar] [CrossRef]
- Meyer, J.R.; Agrawal, A.A.; Quick, R.T.; Dobias, D.T.; Schneider, D.; Lenski, R.E. Parallel changes in host resistance to viral infection during 45,000 generations of relaxed selection. Evolution 2010, 64, 3024–3034. [Google Scholar] [CrossRef] [PubMed]
- Pfeiffer, T.; Bonhoeffer, S. Evolutionary Consequences of Tradeoffs between Yield and Rate of ATP Production. Z. Phys. Chem. 2002, 216, 51–63. [Google Scholar] [CrossRef]
- Waddell, T.G.; Repovic, P.; Meléndez-Hevia, E.; Heinrich, R.; Montero, F. Optimization of glycolysis: New discussions. Biochem. Educ. 1999, 27, 12–13. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rabbers, I.; Van Heerden, J.H.; Nordholt, N.; Bachmann, H.; Teusink, B.; Bruggeman, F.J. Metabolism at Evolutionary Optimal States. Metabolites 2015, 5, 311-343. https://doi.org/10.3390/metabo5020311
Rabbers I, Van Heerden JH, Nordholt N, Bachmann H, Teusink B, Bruggeman FJ. Metabolism at Evolutionary Optimal States. Metabolites. 2015; 5(2):311-343. https://doi.org/10.3390/metabo5020311
Chicago/Turabian StyleRabbers, Iraes, Johan H. Van Heerden, Niclas Nordholt, Herwig Bachmann, Bas Teusink, and Frank J. Bruggeman. 2015. "Metabolism at Evolutionary Optimal States" Metabolites 5, no. 2: 311-343. https://doi.org/10.3390/metabo5020311
APA StyleRabbers, I., Van Heerden, J. H., Nordholt, N., Bachmann, H., Teusink, B., & Bruggeman, F. J. (2015). Metabolism at Evolutionary Optimal States. Metabolites, 5(2), 311-343. https://doi.org/10.3390/metabo5020311





