Mathematical Modelling of Metabolic Regulation in Aging
Abstract
:1. Introduction
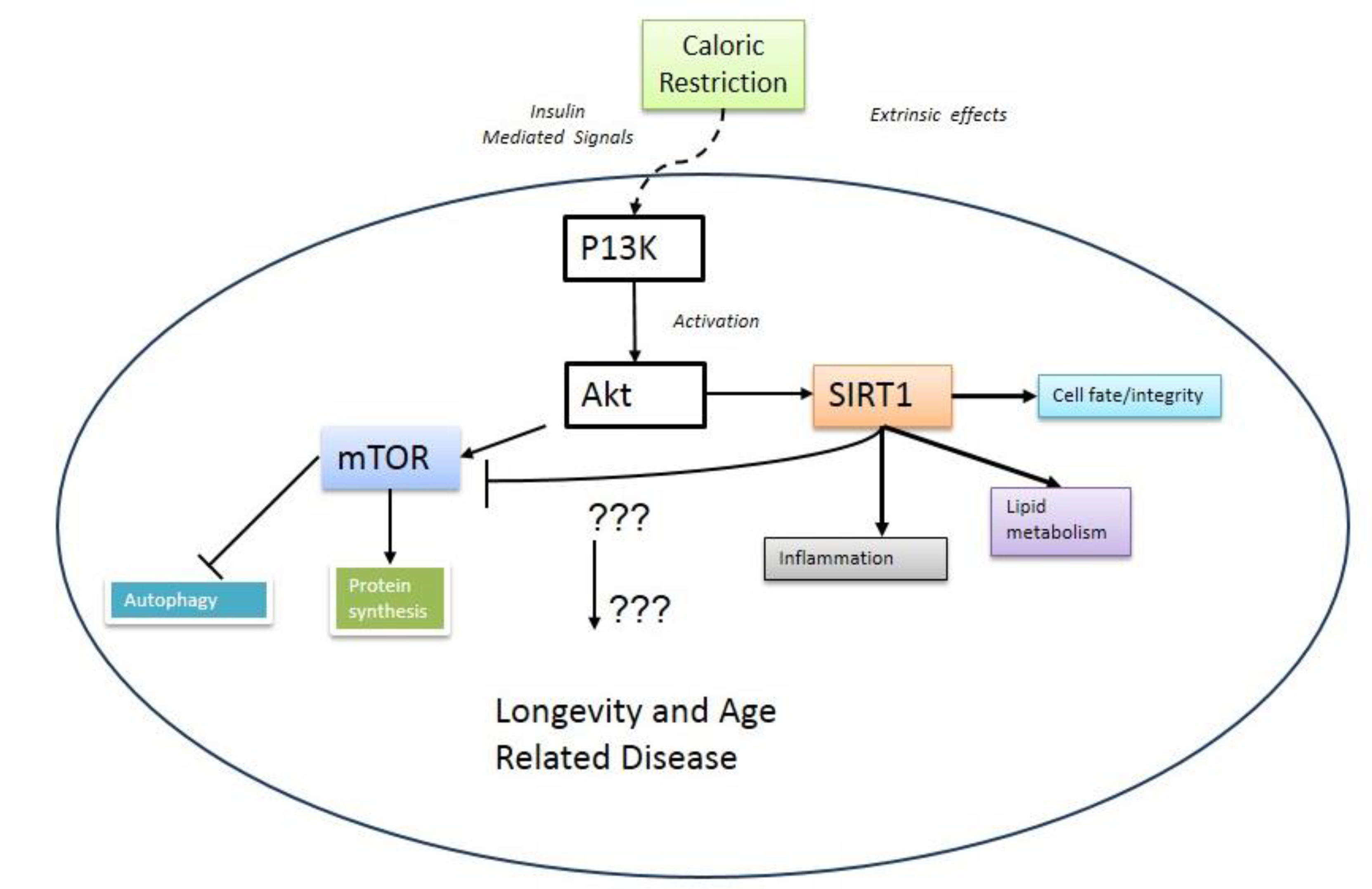
2. mTOR and Aging
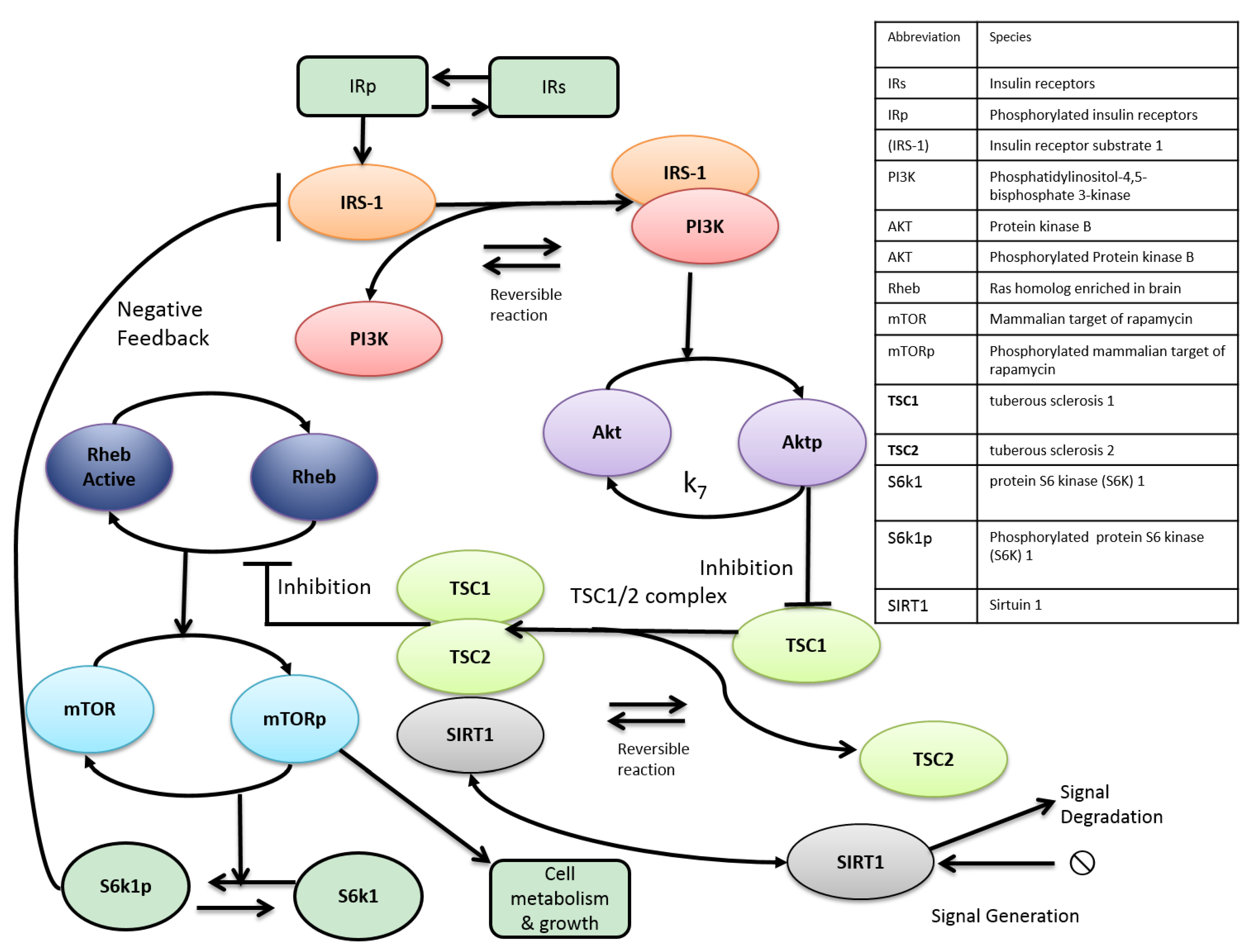
3. Metabolic Crosstalk between mTOR and SIRT1
4. Therapeutic Avenues for Treating Age-Related Disease?
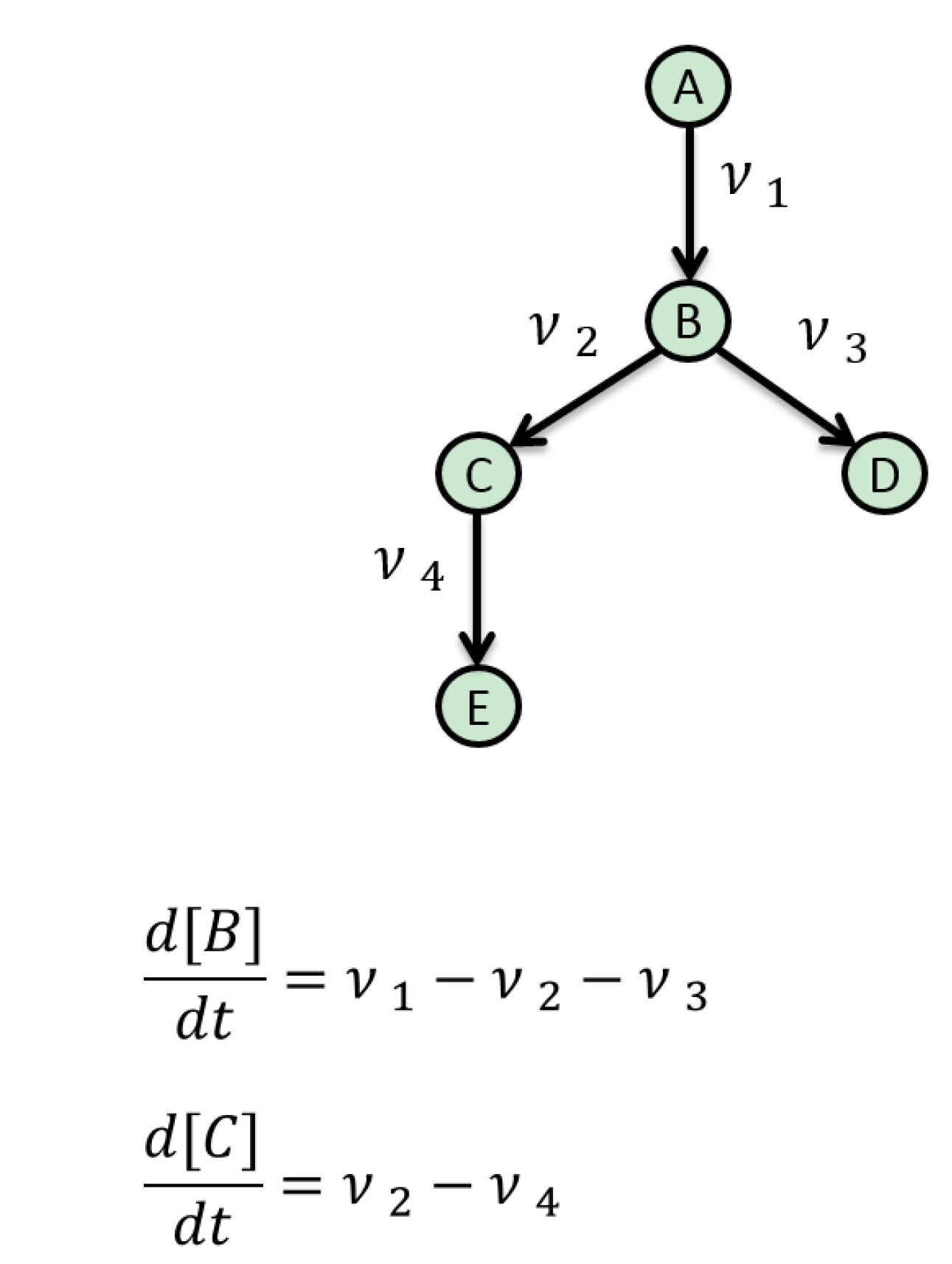
5. Mathematical Approaches to Modelling of Biological Pathways
6. Resources for Model Assembly
7. Current Limitations and Future Developments
8. Conclusions
Author Contributions
Conflicts of Interest
References
- Kirkwood, T.B.; Austad, S.N. Why do we age? Nature 2000, 408, 233–238. [Google Scholar] [CrossRef] [PubMed]
- Hayflick, L.; Moorhead, P.S. The serial cultivation of human diploid cell strains. Exp. Cell Res. 1961, 25, 585–621. [Google Scholar] [CrossRef] [PubMed]
- Van Deursen, J.M. The role of senescent cells in ageing. Nature 2014, 509, 439–446. [Google Scholar] [CrossRef] [PubMed]
- Harley, C.B.; Futcher, A.B.; Greider, C.W. Telomeres shorten during ageing of human fibroblasts. Nature 1990, 345, 458–460. [Google Scholar] [CrossRef] [PubMed]
- Kuilman, T.; Michaloglou, C.; Mooi, W.J.; Peeper, D.S. The essence of senescence. Genes Dev. 2010, 24, 2463–2479. [Google Scholar] [CrossRef] [PubMed]
- Harman, D. Aging: A theory based on free radical and radiation chemistry. J. Gerontol. 1956, 11, 298–300. [Google Scholar] [CrossRef] [PubMed]
- Finkel, T.; Holbrook, N.J. Oxidants, oxidative stress and the biology of ageing. Nature 2000, 408, 239–247. [Google Scholar] [CrossRef] [PubMed]
- Harman, D. The biologic clock: The mitochondria? J. Am. Geriatr. Soc. 1972, 20, 145–147. [Google Scholar] [PubMed]
- Liochev, S.I. Reactive oxygen species and the free radical theory of aging. Free Radic. Biol. Med. 2013, 60, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Von Zglinicki, T.; Saretzki, G.; Docke, W.; Lotze, C. Mild hyperoxia shortens telomeres and inhibits proliferation of fibroblasts: A model for senescence? Exp. Cell Res. 1995, 220, 186–193. [Google Scholar] [CrossRef] [PubMed]
- Passos, J.F.; Nelson, G.; Wang, C.; Richter, T.; Simillion, C.; Proctor, C.J.; Miwa, S.; Olijslagers, S.; Hallinan, J.; Wipat, A.; et al. Feedback between p21 and reactive oxygen production is necessary for cell senescence. Mol. Syst. Biol. 2010. [Google Scholar] [CrossRef]
- Sedelnikova, O.A.; Horikawa, I.; Zimonjic, D.B.; Popescu, N.C.; Bonner, W.M.; Barrett, J.C. Senescing human cells and ageing mice accumulate DNA lesions with unrepairable double-strand breaks. Nat. Cell Biol 2004, 6, 168–170. [Google Scholar] [CrossRef] [PubMed]
- Reinhardt, H.C.; Schumacher, B. The p53 network: Cellular and systemic DNA damage responses in aging and cancer. Trends Genet. 2012, 28, 128–136. [Google Scholar] [CrossRef] [PubMed]
- Cuervo, A.M.; Wong, E. Chaperone-mediated autophagy: Roles in disease and aging. Cell Res. 2014, 24, 92–104. [Google Scholar] [CrossRef] [PubMed]
- Cencioni, C.; Spallotta, F.; Martelli, F.; Valente, S.; Mai, A.; Zeiher, A.M.; Gaetano, C. Oxidative stress and epigenetic regulation in ageing and age-related diseases. Int. J. Mol. Sci. 2013, 14, 17643–17663. [Google Scholar] [CrossRef] [PubMed]
- Hou, L.; Huang, J.; Green, C.D.; Boyd-Kirkup, J.; Zhang, W.; Yu, X.; Gong, W.; Zhou, B.; Han, J.D. Systems biology in aging: Linking the old and the young. Curr. Genomics 2012, 13, 558–565. [Google Scholar] [CrossRef] [PubMed]
- Cevenini, E.; Bellavista, E.; Tieri, P.; Castellani, G.; Lescai, F.; Francesconi, M.; Mishto, M.; Santoro, A.; Valensin, S.; Salvioli, S.; et al. Systems biology and longevity: An emerging approach to identify innovative anti-aging targets and strategies. Curr. Pharm. Des. 2010, 16, 802–813. [Google Scholar] [CrossRef] [PubMed]
- Mc Auley, M.T.; Mooney, K.M. Lipid metabolism and hormonal interactions: Impact on cardiovascular disease and healthy aging. Expert Rev. Endocrinol. Metab. 2014, 9, 357–367. [Google Scholar] [CrossRef]
- Ideker, T.; Galitski, T.; Hood, L. A new approach to decoding life: Systems biology. Annu. Rev. Genomics Hum. Genet. 2001, 2, 343–372. [Google Scholar] [CrossRef] [PubMed]
- Schneider, M.V. Defining systems biology: A brief overview of the term and field. Methods Mol. Biol. 2013, 1021, 1–11. [Google Scholar] [PubMed]
- Mc Auley, M.T.; Choi, H.; Mooney, K.; Paul, E.; Miller, V.M. Systems biology and synthetic biology: A new epoch for toxicology research. Adv. Toxicol. 2015, 2015. Article ID 575403. [Google Scholar] [CrossRef]
- Mc Auley, M.; Jones, J.; Wilkinson, D.; Kirkwood, T. Modelling lipid metabolism to improve healthy ageing. BMC Bioinform. 2005. [Google Scholar] [CrossRef]
- Choi, H.; Mc Auley, M.T.; Lawrence, D.A. Prenatal exposures and exposomics of asthma. AIMS Environ. Sci. 2015, 2, 87–109. [Google Scholar] [CrossRef]
- Mc Auley, M.T.; Kenny, R.A.; Kirkwood, T.B.; Wilkinson, D.J.; Jones, J.J.; Miller, V.M. A mathematical model of aging-related and cortisol induced hippocampal dysfunction. BMC Neurosci. 2009. [Google Scholar] [CrossRef]
- Mc Auley, M.T.; Wilkinson, D.J.; Jones, J.J.; Kirkwood, T.B. A whole-body mathematical model of cholesterol metabolism and its age-associated dysregulation. BMC Syst. Biol. 2012. [Google Scholar] [CrossRef]
- Mc Auley, M.T.; Mooney, K.M. Computational systems biology for aging reserach. In Aging and Health—A Systems Biology Perspective; Yashin, A., Jazwinski, S., Eds.; Karger: Basel, Switzerland, 2014; Volume 40, pp. 35–48. [Google Scholar]
- Mc Auley, M.T.; Mooney, K.M. Computationally modeling lipid metabolism and aging: A mini-review. Comput. Struct. Biotechnol. J. 2015, 13, 38–46. [Google Scholar] [CrossRef] [PubMed]
- Craig, T.; Smelick, C.; Tacutu, R.; Wuttke, D.; Wood, S.H.; Stanley, H.; Janssens, G.; Savitskaya, E.; Moskalev, A.; Arking, R.; et al. The digital ageing atlas: Integrating the diversity of age-related changes into a unified resource. Nucleic Acids Res. 2014, 43, 873–878. [Google Scholar]
- Johnson, S.C.; Rabinovitch, P.S.; Kaeberlein, M. mTOR is a key modulator of ageing and age-related disease. Nature 2013, 493, 338–345. [Google Scholar] [CrossRef] [PubMed]
- Nakagawa, T.; Guarente, L. Sirtuins at a glance. J. Cell Sci 2011, 124, 833–838. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, H.S.; McBurney, M.; Robbins, P.D. SIRT1 negatively regulates the mammalian target of rapamycin. PLoS One 2010, 5, e9199. [Google Scholar] [CrossRef] [PubMed]
- Heilbronn, L.K.; Ravussin, E. Calorie restriction and aging: Review of the literature and implications for studies in humans. Am. J. Clin. Nutr. 2003, 78, 361–369. [Google Scholar] [PubMed]
- Taormina, G.; Mirisola, M.G. Calorie restriction in mammals and simple model organisms. Biomed. Res. Int. 2014. [Google Scholar] [CrossRef]
- Guarente, L. Calorie restriction and sirtuins revisited. Genes Dev. 2013, 27, 2072–2085. [Google Scholar] [CrossRef] [PubMed]
- Barzilai, N.; Huffman, D.M.; Muzumdar, R.H.; Bartke, A. The critical role of metabolic pathways in aging. Diabetes 2012, 61, 1315–1322. [Google Scholar] [CrossRef] [PubMed]
- De Magalhaes, J.P.; Wuttke, D.; Wood, S.H.; Plank, M.; Vora, C. Genome-environment interactions that modulate aging: Powerful targets for drug discovery. Pharmacol. Rev. 2012, 64, 88–101. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Kim, S.G.; Blenis, J. Rapamycin: One drug, many effects. Cell Metab. 2014, 19, 373–379. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.H.; Min, K.J. Caloric restriction and its mimetics. BMB Rep. 2013, 46, 181–187. [Google Scholar] [CrossRef] [PubMed]
- Shimobayashi, M.; Hall, M.N. Making new contacts: The mTOR network in metabolism and signalling crosstalk. Nat. Rev. Mol. Cell Biol. 2014, 15, 155–162. [Google Scholar] [CrossRef] [PubMed]
- Albert, V.; Hall, M.N. mTOR signaling in cellular and organismal energetics. Curr. Opin. Cell Biol. 2014, 33C, 55–66. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.G.; Buel, G.R.; Blenis, J. Nutrient regulation of the mTOR complex 1 signaling pathway. Mol. Cells 2013, 35, 463–473. [Google Scholar] [CrossRef] [PubMed]
- Sengupta, S.; Peterson, T.R.; Sabatini, D.M. Regulation of the mTOR complex 1 pathway by nutrients, growth factors, and stress. Mol. Cell 2010, 40, 310–322. [Google Scholar] [CrossRef] [PubMed]
- Zoncu, R.; Efeyan, A.; Sabatini, D.M. mTOR: From growth signal integration to cancer, diabetes and ageing. Nat. Rev. Mol. Cell Biol. 2011, 12, 21–35. [Google Scholar] [CrossRef] [PubMed]
- Tsang, C.K.; Qi, H.; Liu, L.F.; Zheng, X.F. Targeting mammalian target of rapamycin (mTOR) for health and diseases. Drug Discov. Today 2007, 12, 112–124. [Google Scholar] [CrossRef] [PubMed]
- Bononi, A.; Agnoletto, C.; de Marchi, E.; Marchi, S.; Patergnani, S.; Bonora, M.; Giorgi, C.; Missiroli, S.; Poletti, F.; Rimessi, A.; et al. Protein kinases and phosphatases in the control of cell fate. Enzym. Res. 2011, 2011. Article ID 329098. [Google Scholar] [CrossRef]
- De Magalhaes, J.P. How ageing processes influence cancer. Nat. Rev. Cancer 2013, 13, 357–365. [Google Scholar] [CrossRef] [PubMed]
- Spilman, P.; Podlutskaya, N.; Hart, M.J.; Debnath, J.; Gorostiza, O.; Bredesen, D.; Richardson, A.; Strong, R.; Galvan, V. Inhibition of mTOR by rapamycin abolishes cognitive deficits and reduces amyloid-beta levels in a mouse model of alzheimer’s disease. PLoS ONE 2010, 5, e9979. [Google Scholar] [CrossRef] [PubMed]
- Caccamo, A.; Majumder, S.; Richardson, A.; Strong, R.; Oddo, S. Molecular interplay between mammalian target of rapamycin (mTOR), amyloid-beta, and tau: Effects on cognitive impairments. J. Biol. Chem. 2010, 285, 13107–13120. [Google Scholar] [CrossRef] [PubMed]
- Lin, A.L.; Zheng, W.; Halloran, J.J.; Burbank, R.R.; Hussong, S.A.; Hart, M.J.; Javors, M.; Shih, Y.Y.; Muir, E.; Solano Fonseca, R.; et al. Chronic rapamycin restores brain vascular integrity and function through no synthase activation and improves memory in symptomatic mice modeling alzheimer’s disease. J. Cereb. Blood Flow Metab. 2013, 33, 1412–1421. [Google Scholar] [CrossRef] [PubMed]
- Yuan, T.L.; Cantley, L.C. Pi3k pathway alterations in cancer: Variations on a theme. Oncogene 2008, 27, 5497–5510. [Google Scholar] [CrossRef] [PubMed]
- Inoki, K.; Corradetti, M.N.; Guan, K.L. Dysregulation of the tsc-mTOR pathway in human disease. Nature Genet. 2005, 37, 19–24. [Google Scholar] [CrossRef] [PubMed]
- Matsuoka, T.; Yashiro, M. The role of pi3k/akt/mTOR signaling in gastric carcinoma. Cancers 2014, 6, 1441–1463. [Google Scholar] [CrossRef] [PubMed]
- Karar, J.; Maity, A. Pi3k/akt/mTOR pathway in angiogenesis. Front. Mol. Neurosci. 2011. [Google Scholar] [CrossRef]
- Law, B.K. Rapamycin: An anti-cancer immunosuppressant? Crit. Rev. Oncol. Hematol. 2005, 56, 47–60. [Google Scholar] [CrossRef] [PubMed]
- Gibbons, J.J.; Abraham, R.T.; Yu, K. Mammalian target of rapamycin: Discovery of rapamycin reveals a signaling pathway important for normal and cancer cell growth. Semin. Oncol. 2009, 36 (Suppl. 3), S3–S17. [Google Scholar] [CrossRef] [PubMed]
- O’Donnell, A.; Faivre, S.; Burris, H.A., 3rd; Rea, D.; Papadimitrakopoulou, V.; Shand, N.; Lane, H.A.; Hazell, K.; Zoellner, U.; Kovarik, J.M.; et al. Phase i pharmacokinetic and pharmacodynamic study of the oral mammalian target of rapamycin inhibitor everolimus in patients with advanced solid tumors. J. Clin. Oncol. 2008, 26, 1588–1595. [Google Scholar] [CrossRef] [PubMed]
- Baselga, J.; Campone, M.; Piccart, M.; Burris, H.A., 3rd; Rugo, H.S.; Sahmoud, T.; Noguchi, S.; Gnant, M.; Pritchard, K.I.; Lebrun, F.; et al. Everolimus in postmenopausal hormone-receptor-positive advanced breast cancer. N. Engl. J. Med. 2012, 366, 520–529. [Google Scholar] [CrossRef] [PubMed]
- Awada, A.; Cardoso, F.; Fontaine, C.; Dirix, L.; de Greve, J.; Sotiriou, C.; Steinseifer, J.; Wouters, C.; Tanaka, C.; Zoellner, U.; et al. The oral mTOR inhibitor rad001 (everolimus) in combination with letrozole in patients with advanced breast cancer: Results of a phase i study with pharmacokinetics. Eur. J. Cancer 2008, 44, 84–91. [Google Scholar] [CrossRef] [PubMed]
- Guba, M.; von Breitenbuch, P.; Steinbauer, M.; Koehl, G.; Flegel, S.; Hornung, M.; Bruns, C.J.; Zuelke, C.; Farkas, S.; Anthuber, M.; et al. Rapamycin inhibits primary and metastatic tumor growth by antiangiogenesis: Involvement of vascular endothelial growth factor. Nat. Med. 2002, 8, 128–135. [Google Scholar] [CrossRef] [PubMed]
- Harrison, D.E.; Strong, R.; Sharp, Z.D.; Nelson, J.F.; Astle, C.M.; Flurkey, K.; Nadon, N.L.; Wilkinson, J.E.; Frenkel, K.; Carter, C.S.; et al. Rapamycin fed late in life extends lifespan in genetically heterogeneous mice. Nature 2009, 460, 392–395. [Google Scholar] [PubMed]
- Neff, F.; Flores-Dominguez, D.; Ryan, D.P.; Horsch, M.; Schroder, S.; Adler, T.; Afonso, L.C.; Aguilar-Pimentel, J.A.; Becker, L.; Garrett, L.; et al. Rapamycin extends murine lifespan but has limited effects on aging. J. Clin. Investig. 2013, 123, 3272–3291. [Google Scholar] [CrossRef] [PubMed]
- Kapahi, P.; Zid, B.M.; Harper, T.; Koslover, D.; Sapin, V.; Benzer, S. Regulation of lifespan in drosophila by modulation of genes in the tor signaling pathway. Curr. Biol. 2004, 14, 885–890. [Google Scholar] [CrossRef] [PubMed]
- Kaeberlein, M.; Powers, R.W., 3rd; Steffen, K.K.; Westman, E.A.; Hu, D.; Dang, N.; Kerr, E.O.; Kirkland, K.T.; Fields, S.; Kennedy, B.K.; et al. Regulation of yeast replicative life span by tor and sch9 in response to nutrients. Science 2005, 310, 1193–1196. [Google Scholar] [CrossRef] [PubMed]
- Zid, B.M.; Rogers, A.N.; Katewa, S.D.; Vargas, M.A.; Kolipinski, M.C.; Lu, T.A.; Benzer, S.; Kapahi, P. 4e-bp extends lifespan upon dietary restriction by enhancing mitochondrial activity in drosophila. Cell 2009, 139, 149–160. [Google Scholar] [CrossRef] [PubMed]
- Schieke, S.M.; Phillips, D.; McCoy, J.P., Jr.; Aponte, A.M.; Shen, R.F.; Balaban, R.S.; Finkel, T. The mammalian target of rapamycin (mTOR) pathway regulates mitochondrial oxygen consumption and oxidative capacity. J. Biol. Chem. 2006, 281, 27643–27652. [Google Scholar] [CrossRef] [PubMed]
- Cunningham, J.T.; Rodgers, J.T.; Arlow, D.H.; Vazquez, F.; Mootha, V.K.; Puigserver, P. mTOR controls mitochondrial oxidative function through a yy1-pgc-1alpha transcriptional complex. Nature 2007, 450, 736–740. [Google Scholar] [CrossRef] [PubMed]
- Guarente, L. Sirtuins in aging and disease. Cold Spring Harb. Symp. Quant. Biol. 2007, 72, 483–488. [Google Scholar] [CrossRef] [PubMed]
- Houtkooper, R.H.; Pirinen, E.; Auwerx, J. Sirtuins as regulators of metabolism and healthspan. Nat. Rev. Mol. Cell Biol 2012, 13, 225–238. [Google Scholar] [CrossRef] [PubMed]
- Gorenne, I.; Kumar, S.; Gray, K.; Figg, N.; Yu, H.; Mercer, J.; Bennett, M. Vascular smooth muscle cell sirtuin 1 protects against DNA damage and inhibits atherosclerosis. Circulation 2013, 127, 386–396. [Google Scholar] [CrossRef] [PubMed]
- Wei, D.; Tao, R.; Zhang, Y.; White, M.F.; Dong, X.C. Feedback regulation of hepatic gluconeogenesis through modulation of shp/nr0b2 gene expression by SIRT1 and foxo1. Am. J. Physiol. Endocrinol. Metab. 2011, 300, E312–E320. [Google Scholar] [CrossRef] [PubMed]
- Satoh, A.; Stein, L.; Imai, S. The role of mammalian sirtuins in the regulation of metabolism, aging, and longevity. Handb. Exp. Pharmacol. 2011, 206, 125–162. [Google Scholar] [PubMed]
- Planavila, A.; Iglesias, R.; Giralt, M.; Villarroya, F. SIRT1 acts in association with pparalpha to protect the heart from hypertrophy, metabolic dysregulation, and inflammation. Cardiovasc. Res. 2011, 90, 276–284. [Google Scholar] [CrossRef] [PubMed]
- Hong, S.; Zhao, B.; Lombard, D.B.; Fingar, D.C.; Inoki, K. Cross-talk between sirtuin and mammalian target of rapamycin complex 1 (mtorc1) signaling in the regulation of s6 kinase 1 (s6k1) phosphorylation. J. Biol. Chem. 2014, 289, 13132–13141. [Google Scholar] [CrossRef] [PubMed]
- Guo, W.; Qian, L.; Zhang, J.; Zhang, W.; Morrison, A.; Hayes, P.; Wilson, S.; Chen, T.; Zhao, J. SIRT1 overexpression in neurons promotes neurite outgrowth and cell survival through inhibition of the mTOR signaling. J. Neurosci. Res. 2011, 89, 1723–1736. [Google Scholar] [CrossRef] [PubMed]
- Bodine, S.C.; Stitt, T.N.; Gonzalez, M.; Kline, W.O.; Stover, G.L.; Bauerlein, R.; Zlotchenko, E.; Scrimgeour, A.; Lawrence, J.C.; Glass, D.J.; et al. Akt/mTOR pathway is a crucial regulator of skeletal muscle hypertrophy and can prevent muscle atrophy in vivo. Nat. Cell Biol. 2001, 3, 1014–1019. [Google Scholar] [CrossRef] [PubMed]
- Bartke, A.; Sun, L.Y.; Longo, V. Somatotropic signaling: Trade-offs between growth, reproductive development, and longevity. Physiol. Rev. 2013, 93, 571–598. [Google Scholar] [CrossRef] [PubMed]
- Bassel-Duby, R.; Olson, E.N. Signaling pathways in skeletal muscle remodeling. Annu. Rev. Biochem. 2006, 75, 19–37. [Google Scholar] [CrossRef] [PubMed]
- Wilkinson, J.E.; Burmeister, L.; Brooks, S.V.; Chan, C.C.; Friedline, S.; Harrison, D.E.; Hejtmancik, J.F.; Nadon, N.; Strong, R.; Wood, L.K.; et al. Rapamycin slows aging in mice. Aging Cell 2012, 11, 675–682. [Google Scholar] [CrossRef] [PubMed]
- Powers, R.W., 3rd; Kaeberlein, M.; Caldwell, S.D.; Kennedy, B.K.; Fields, S. Extension of chronological life span in yeast by decreased tor pathway signaling. Genes Dev. 2006, 20, 174–184. [Google Scholar] [CrossRef] [PubMed]
- Miller, R.A.; Harrison, D.E.; Astle, C.M.; Baur, J.A.; Boyd, A.R.; de Cabo, R.; Fernandez, E.; Flurkey, K.; Javors, M.A.; Nelson, J.F.; et al. Rapamycin, but not resveratrol or simvastatin, extends life span of genetically heterogeneous mice. J. Gerontol. A Biol. Sci. Med. Sci. 2011, 66, 191–201. [Google Scholar] [CrossRef] [PubMed]
- Pearson, K.J.; Baur, J.A.; Lewis, K.N.; Peshkin, L.; Price, N.L.; Labinskyy, N.; Swindell, W.R.; Kamara, D.; Minor, R.K.; Perez, E.; et al. Resveratrol delays age-related deterioration and mimics transcriptional aspects of dietary restriction without extending life span. Cell Metab. 2008, 8, 157–168. [Google Scholar] [CrossRef] [PubMed]
- Cottart, C.H.; Nivet-Antoine, V.; Beaudeux, J.L. Review of recent data on the metabolism, biological effects, and toxicity of resveratrol in humans. Mol. Nutr. Food Res. 2014, 58, 7–21. [Google Scholar] [CrossRef] [PubMed]
- Demidenko, Z.N.; Blagosklonny, M.V. At concentrations that inhibit mtor, resveratrol suppresses cellular senescence. Cell Cycle 2009, 8, 1901–1904. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Wilk, S.A.; Wang, A.; Zhou, L.; Wang, R.H.; Ogawa, W.; Deng, C.; Dong, L.Q.; Liu, F. Resveratrol inhibits mTOR signaling by promoting the interaction between mTOR and deptor. J. Biol. Chem. 2010, 285, 36387–36394. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhang, Y.; Tang, L.; Zhang, N.; Fan, D. Protective effects of resveratrol through the up-regulation of SIRT1expression in the mutant hsod1-g93a-bearing motor neuron-like cell culture model of amyotrophic lateral sclerosis. Neurosci. Lett. 2011, 503, 250–255. [Google Scholar] [CrossRef] [PubMed]
- Orth, J.D.; Thiele, I.; Palsson, B.O. What is flux balance analysis? Nat. Biotechnol. 2010, 28, 245–248. [Google Scholar] [CrossRef] [PubMed]
- Coquin, L.; Feala, J.D.; McCulloch, A.D.; Paternostro, G. Metabolomic and flux-balance analysis of age-related decline of hypoxia tolerance in drosophila muscle tissue. Mol. Syst. Biol. 2008, 4, 233. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.M.; Gianchandani, E.P.; Eddy, J.A.; Papin, J.A. Dynamic analysis of integrated signaling, metabolic, and regulatory networks. PLoS Comput. Biol. 2008, 4, e1000086. [Google Scholar] [CrossRef] [PubMed]
- Covert, M.W.; Schilling, C.H.; Palsson, B. Regulation of gene expression in flux balance models of metabolism. J. Theor. Biol. 2001, 213, 73–88. [Google Scholar] [CrossRef] [PubMed]
- Ramakrishna, R.; Edwards, J.S.; McCulloch, A.; Palsson, B.O. Flux-balance analysis of mitochondrial energy metabolism: Consequences of systemic stoichiometric constraints. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2001, 280, R695–R704. [Google Scholar]
- Nogiec, C.; Burkart, A.; Dreyfuss, J.; Lerin, C.; Kasifm, S.; Patti, M. Metabolic modeling of muscle metabolism identifies key reactions linked to insulin resistance phenotypes. Mol. Metab. 2015, 4, 151–163. [Google Scholar] [CrossRef]
- Yizhak, K.; Gabay, O.; Cohen, H.; Ruppin, E. Model-based identification of drug targets that revert disrupted metabolism and its application to ageing. Nat. Commun. 2013. [Google Scholar] [CrossRef]
- Kauffman, K.J.; Prakash, P.; Edwards, J.S. Advances in flux balance analysis. Curr. Opin. Biotechnol. 2003, 14, 491–496. [Google Scholar] [CrossRef]
- Kowald, A.; Hamann, A.; Zintel, S.; Ullrich, S.; Klipp, E.; Osiewacz, H.D. A systems biological analysis links ros metabolism to mitochondrial protein quality control. Mech. Ageing Dev. 2012, 133, 331–337. [Google Scholar] [CrossRef] [PubMed]
- Proctor, C.J.; Macdonald, C.; Milner, J.M.; Rowan, A.D.; Cawston, T.E. A computer simulation approach to assessing therapeutic intervention points for the prevention of cytokine-induced cartilage breakdown. Arthritis Rheumatol. 2014, 66, 979–989. [Google Scholar] [CrossRef] [PubMed]
- Wilkinson, D.J. Stochastic modelling for quantitative description of heterogeneous biological systems. Nat. Rev. Genet. 2009, 10, 122–133. [Google Scholar] [CrossRef] [PubMed]
- Gibson, M.A.; Bruck, J. Efficient exact stochastic simulation of chemical systems with many species and many channels. J. Phys. Chem. 2000, A104, 1876–1889. [Google Scholar] [CrossRef]
- Gillespie, D. A general method for numerically simulating stochastic time evolution of coupled chemical-reactions. J. Comput. Phys. 1976, 22, 403–434. [Google Scholar] [CrossRef]
- Gillespie, D.T. Approximate accelerated stochastic simulation of chemically reacting systems. J. Chem. Phys. 2001, 115, 1716–1733. [Google Scholar] [CrossRef]
- Mettetal, J.T.; Muzzey, D.; Pedraza, J.M.; Ozbudak, E.M.; van Oudenaarden, A.; et al. Predicting stochastic gene expression dynamics in single cells. Proc. Natl. Acad. Sci. USA 2006, 103, 7304–7309. [Google Scholar] [CrossRef] [PubMed]
- Kaern, M.; Elston, T.C.; Blake, W.J.; Collins, J.J. Stochasticity in gene expression: From theories to phenotypes. Nat. Rev. Genet. 2005, 6, 451–464. [Google Scholar] [CrossRef] [PubMed]
- Proctor, C.J.; Pienaar, I.S.; Elson, J.L.; Kirkwood, T.B. Aggregation, impaired degradation and immunization targeting of amyloid-beta dimers in alzheimer’s disease: A stochastic modelling approach. Mol. Neurodegener. 2012. [Google Scholar] [CrossRef]
- Lawless, C.; Jurk, D.; Gillespie, C.S.; Shanley, D.; Saretzki, G.; von Zglinicki, T.; Passos, J.F. A stochastic step model of replicative senescence explains ros production rate in ageing cell populations. PLoS One 2012, 7, e32117. [Google Scholar] [CrossRef] [PubMed]
- Grasman, J.; Salomons, H.M.; Verhulst, S. Stochastic modeling of length-dependent telomere shortening in corvus monedula. J. Theor. Biol. 2011, 282, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Proctor, C.J.; Lorimer, I.A. Modelling the role of the hsp70/hsp90 system in the maintenance of protein homeostasis. PLoS ONE 2011, 6, e22038. [Google Scholar] [CrossRef] [PubMed]
- Pahle, J. Biochemical simulations: Stochastic, approximate stochastic and hybrid approaches. Brief. Bioinform. 2009, 10, 53–64. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Donizelli, M.; Rodriguez, N.; Dharuri, H.; Endler, L.; Chelliah, V.; Li, L.; He, E.; Henry, A.; Stefan, M.I.; et al. Biomodels database: An enhanced, curated and annotated resource for published quantitative kinetic models. BMC Syst. Biol. 2010. [Google Scholar] [CrossRef]
- Hucka, M.; Finney, A.; Bornstein, B.J.; Keating, S.M.; Shapiro, B.E.; Matthews, J.; Kovitz, B.L.; Schilstra, M.J.; Funahashi, A.; Doyle, J.C.; et al. Evolving a lingua franca and associated software infrastructure for computational systems biology: The systems biology markup language (sbml) project. Syst. Biol. 2004, 1, 41–53. [Google Scholar] [CrossRef]
- Le Novere, N.; Hucka, M.; Mi, H.; Moodie, S.; Schreiber, F.; Sorokin, A.; Demir, E.; Wegner, K.; Aladjem, M.I.; Wimalaratne, S.M.; et al. The systems biology graphical notation. Nat. Biotechnol. 2009, 27, 735–741. [Google Scholar] [CrossRef] [PubMed]
- Scheer, M.; Grote, A.; Chang, A.; Schomburg, I.; Munaretto, C.; Rother, M.; Sohngen, C.; Stelzer, M.; Thiele, J.; Schomburg, D.; et al. Brenda, the enzyme information system in 2011. Nucleic Acids Res. 2011, 39, D670–D676. [Google Scholar] [CrossRef] [PubMed]
- Wittig, U.; Kania, R.; Golebiewski, M.; Rey, M.; Shi, L.; Jong, L.; Algaa, E.; Weidemann, A.; Sauer-Danzwith, H.; Mir, S.; et al. Sabio-rk—Database for biochemical reaction kinetics. Nucleic Acids Res. 2012, 40, D790–D796. [Google Scholar] [CrossRef] [PubMed]
- Milo, R.; Jorgensen, P.; Moran, U.; Weber, G.; Springer, M. Bionumbers—The database of key numbers in molecular and cell biology. Nucleic Acids Res. 2010, 38, D750–D753. [Google Scholar] [CrossRef] [PubMed]
- Mc Auley, M.T.; Proctor, C.J.; Corfe, B.M.; Cuskelly, C.J.; Mooney, K.M. Nutrition research and the impact of computational systems biology. J. Comput. Sci. Syst. Biol. 2013, 6, 271–285. [Google Scholar] [CrossRef]
- Wilkinson, S.J.; Benson, N.; Kell, D.B. Proximate parameter tuning for biochemical networks with uncertain kinetic parameters. Mol. Biosyst. 2008, 4, 74–97. [Google Scholar] [CrossRef] [PubMed]
- Jia, G.; Stephanopoulos, G.; Gunawan, R. Ensemble kinetic modeling of metabolic networks from dynamic metabolic profiles. Metabolites 2012, 2, 891–912. [Google Scholar] [CrossRef] [PubMed]
- Kriete, A.; Bosl, W.J.; Booker, G. Rule-based cell systems model of aging using feedback loop motifs mediated by stress responses. PLoS Comput. Biol. 2010, 6, e1000820. [Google Scholar] [CrossRef] [PubMed]
- Floettmann, M.; Uhlendorf, J.; Scharp, T.; Klipp, E.; Spiesser, T.W. Sensa: Web-based sensitivity analysis of sbml models. Bioinformatics 2014, 30, 2830–2831. [Google Scholar] [CrossRef] [PubMed]
- Dokoumetzidis, A.; Aarons, L. Proper lumping in systems biology models. IET Syst. Biol. 2009, 3, 40–51. [Google Scholar] [CrossRef] [PubMed]
- Rao, S.; van der Schaft, A.; van Eunen, K.; Bakker, B.M.; Jayawardhana, B. A model reduction method for biochemical reaction networks. BMC Syst. Biol. 2014. [Google Scholar] [CrossRef]
- Stockton, D.J.; Schilstra, M.; Khalil, R.; McAuley, M. Biological control processes and their application to manufacturing planning. In Advances in manufacturing technology-XXI: proceedings of the 5th international conference on manufacturing research(ICMR2007), 11th–13th September 2007; 2007; pp. 259–264. [Google Scholar]
- Matsuoka, Y.; Funahashi, A.; Ghosh, S.; Kitano, H. Modeling and simulation using celldesigner. Methods Mol. Biol. 2014, 1164, 121–145. [Google Scholar] [PubMed]
- Hoops, S.; Sahle, S.; Gauges, R.; Lee, C.; Pahle, J.; Simus, N.; Singhal, M.; Xu, L.; Mendes, P.; Kummer, U.; et al. Copasi—A complex pathway simulator. Bioinformatics 2006, 22, 3067–3074. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Wu, M.; Du, J.; Liu, D.; Chan, C. Systematic modeling for the insulin signaling network mediated by irs(1) and irs(2). J. Theor. Biol. 2014, 355, 40–52. [Google Scholar] [CrossRef] [PubMed]
- Magnuson, B.; Ekim, B.; Fingar, D.C. Regulation and function of ribosomal protein s6 kinase (s6k) within mTOR signalling networks. Biochem. J. 2012, 441, 1–21. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mc Auley, M.T.; Mooney, K.M.; Angell, P.J.; Wilkinson, S.J. Mathematical Modelling of Metabolic Regulation in Aging. Metabolites 2015, 5, 232-251. https://doi.org/10.3390/metabo5020232
Mc Auley MT, Mooney KM, Angell PJ, Wilkinson SJ. Mathematical Modelling of Metabolic Regulation in Aging. Metabolites. 2015; 5(2):232-251. https://doi.org/10.3390/metabo5020232
Chicago/Turabian StyleMc Auley, Mark T., Kathleen M. Mooney, Peter J. Angell, and Stephen J. Wilkinson. 2015. "Mathematical Modelling of Metabolic Regulation in Aging" Metabolites 5, no. 2: 232-251. https://doi.org/10.3390/metabo5020232
APA StyleMc Auley, M. T., Mooney, K. M., Angell, P. J., & Wilkinson, S. J. (2015). Mathematical Modelling of Metabolic Regulation in Aging. Metabolites, 5(2), 232-251. https://doi.org/10.3390/metabo5020232





