Minimal Cut Sets and the Use of Failure Modes in Metabolic Networks
Abstract
:1. Introduction
2. Defining Minimal Cut Sets
“We call a set of reactions a cut set (with respect to a defined objective reaction) if after the removal of these reactions from the network no feasible balanced flux distribution involves the objective reaction”; and “A cut set C (related to a defined objective reaction) is a minimal cut set (MCS) if no proper subset of C is a cut set.”
2.1. The Initial Concept of MCSs
2.2. Example Network to Illustrate MCSs
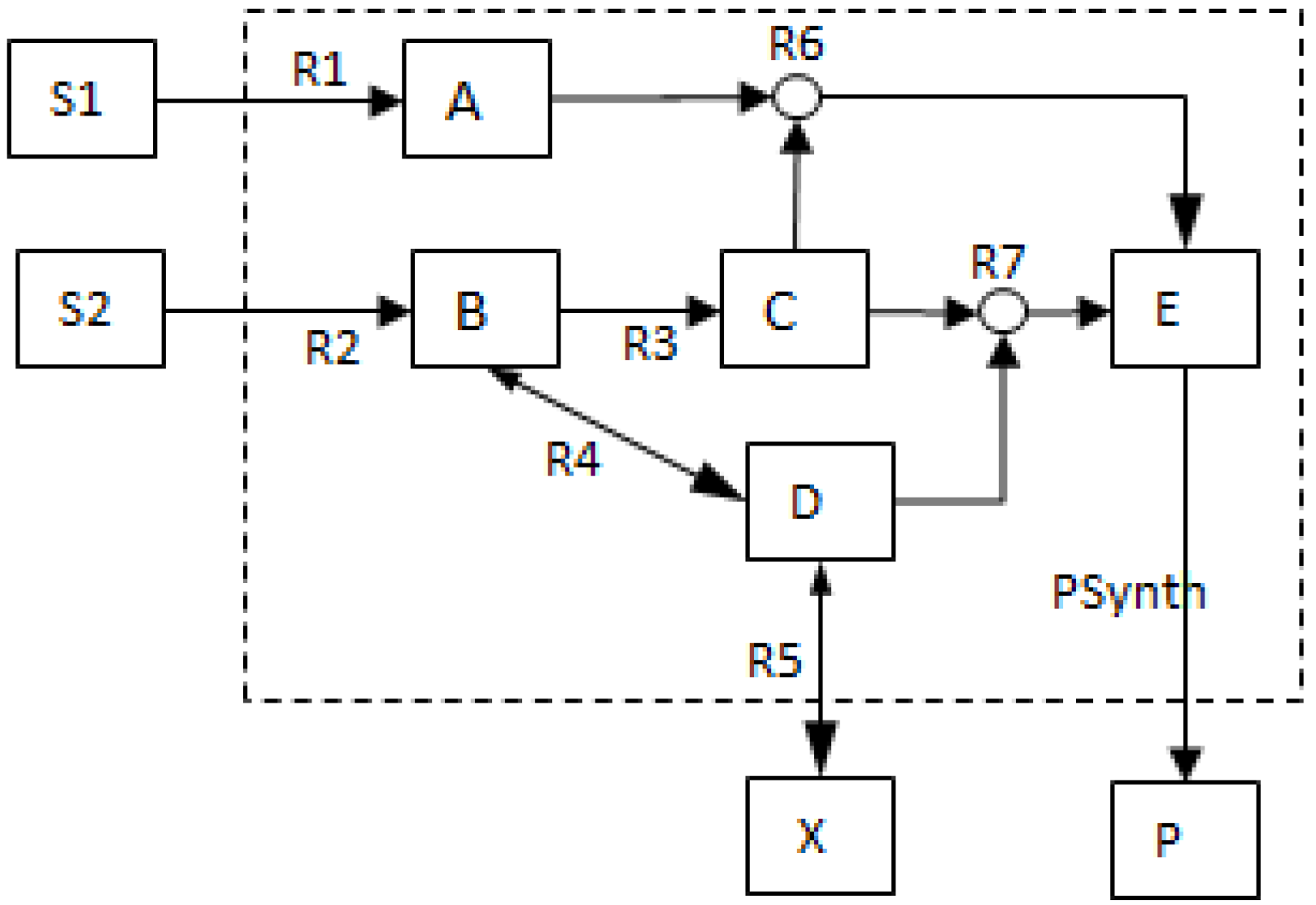
- The network consists of five internal metabolites and eight reactions, of which R4 and R5 are reversible;
- Reactions crossing the system boundaries are coming from/leading to buffered/buffer metabolites.
2.3. Other Definitions
2.3.1. Fault Trees
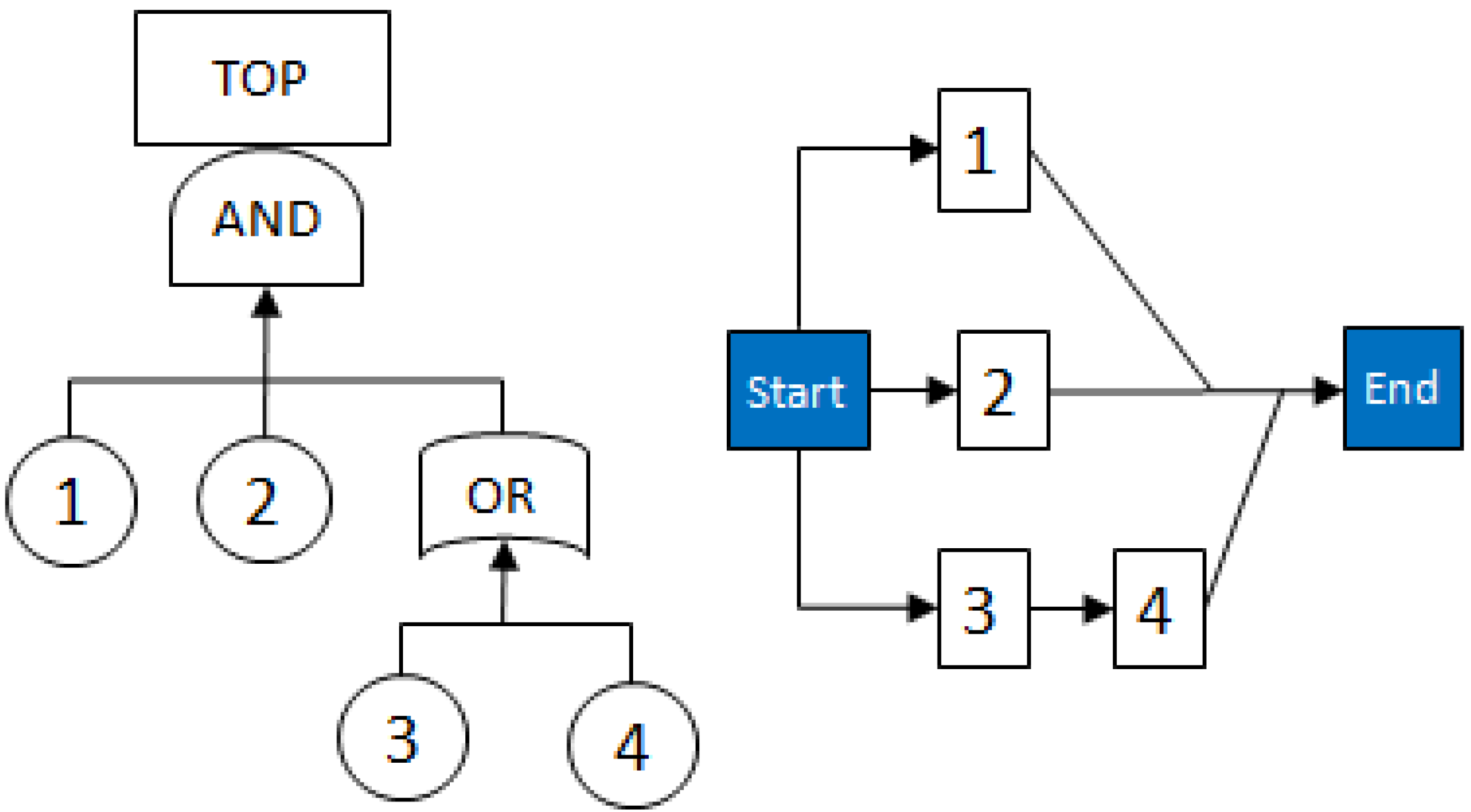
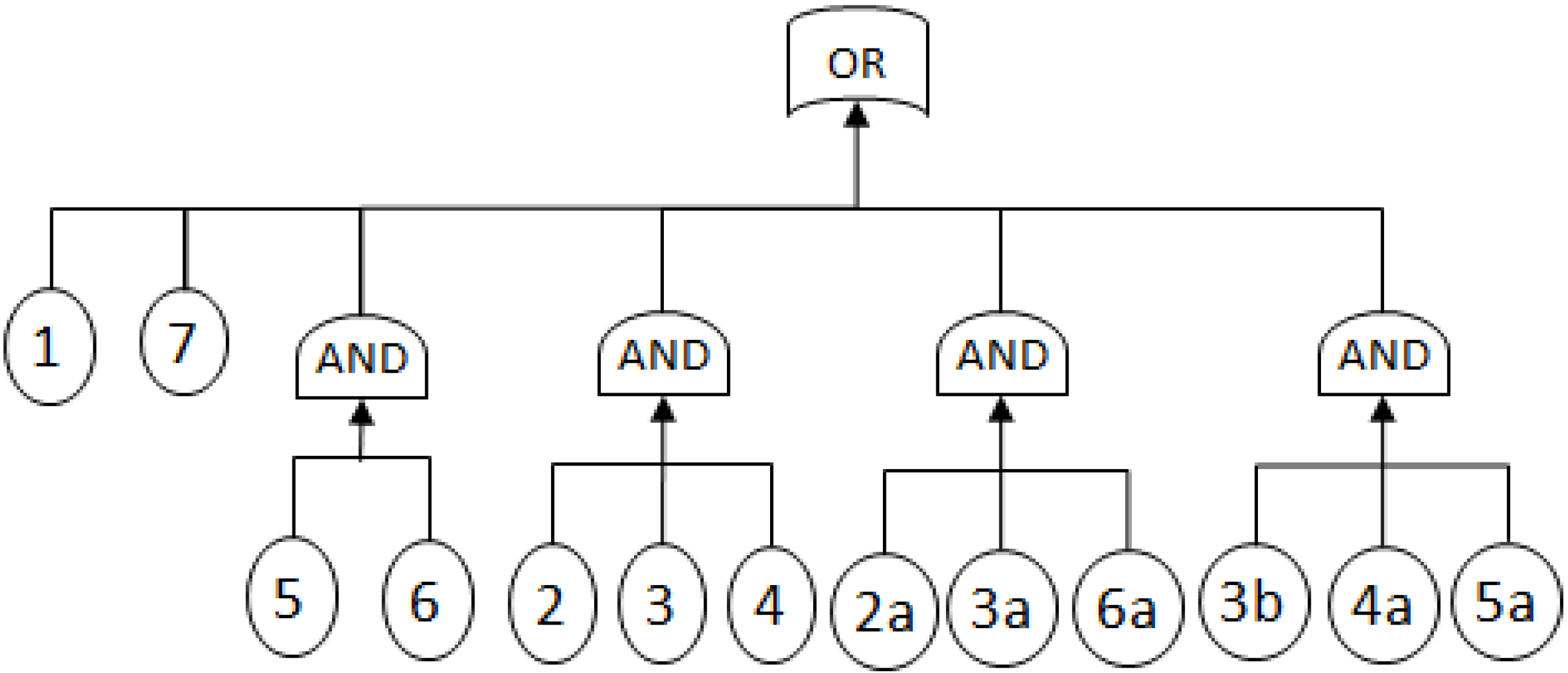
- MCSs obtained from the RBD are: {1}, {7}, {5,6}, {2,3,4}, {2,3,6} and {3,4,5};
- The Fault Tree is constructed by connecting the MCSs using the OR gate. Within each set that contains multiple blocks, the multiple blocks are connected with an AND gate. The equivalent Fault Tree is shown in Figure 5 below:
2.3.2. Graph Theory
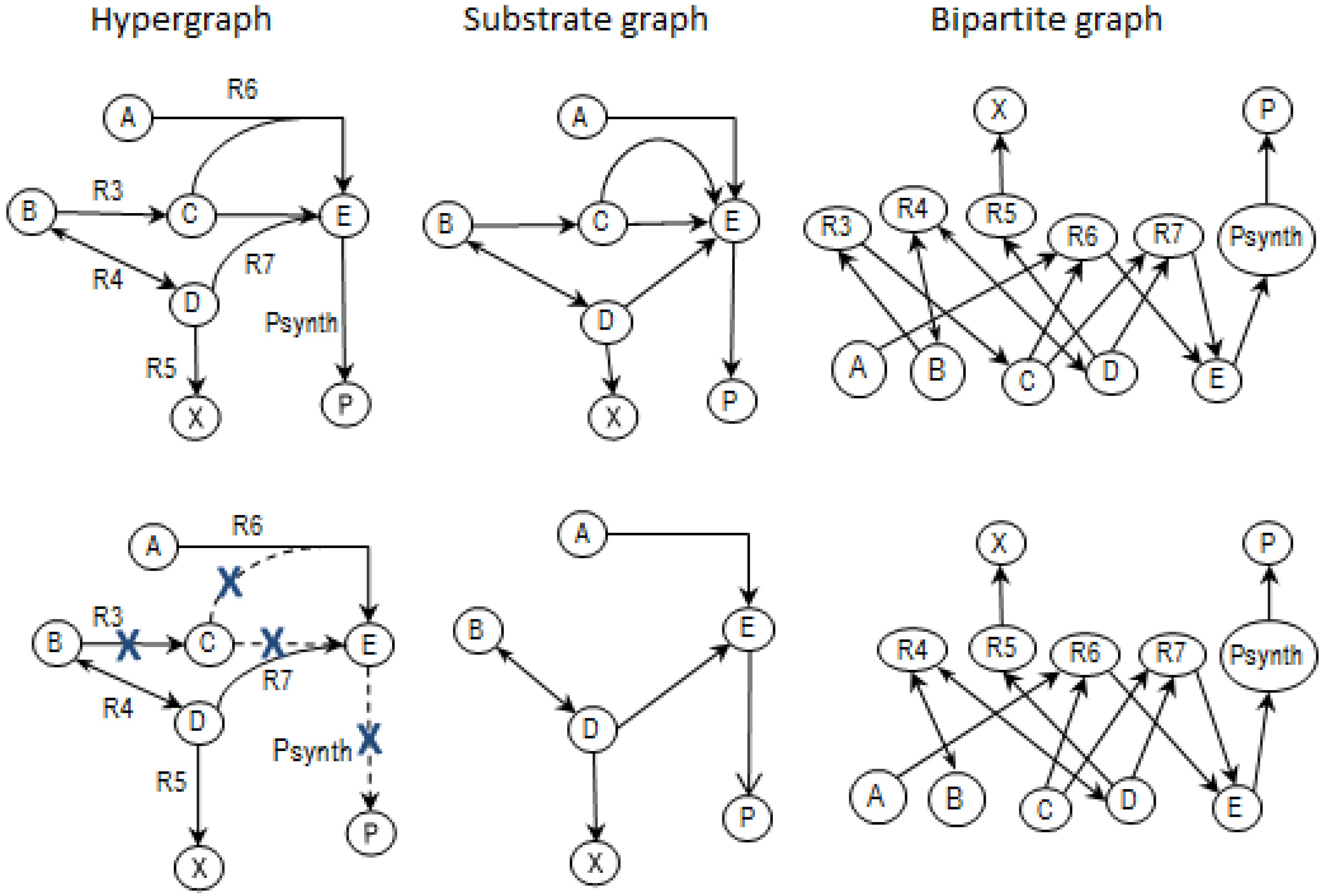
2.4. Determining MCSs
- (1)
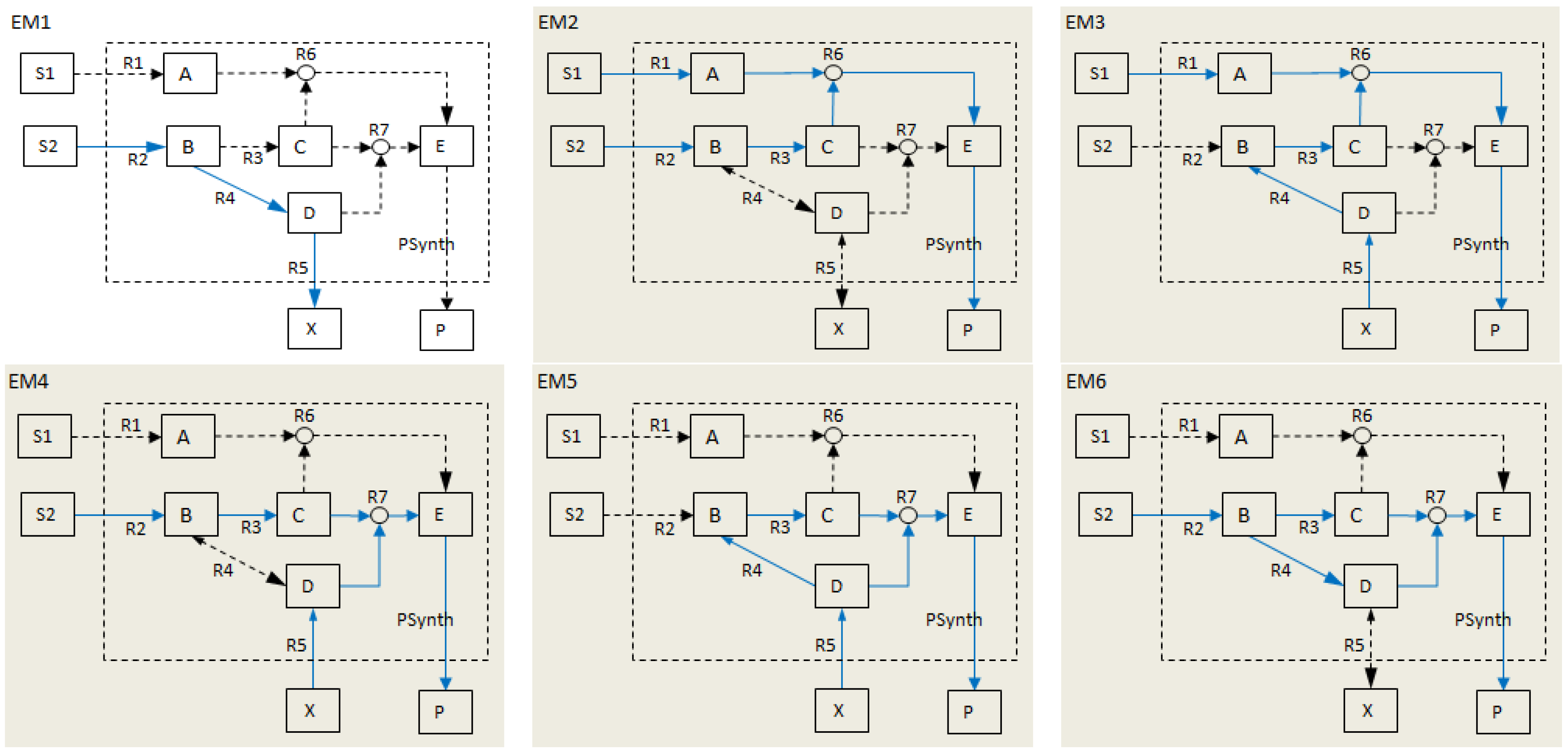
- Calculate EMs [3] in NetEx and identify those that start from a buffered metabolite and lead to the formation of metabolite E or the objective reaction PSynth. Since EMs are non-decomposable, removing one of the reactions from these EM will prevent the system from producing E and subsequently achieving the PSynth.There are six EMs in total, of which five lead to the formation of metabolite X and the objective reaction.
- (2)
- Determine how to prevent PSynth from taking place, i.e. stop the five EMs that involve PSynth from being functional. This can be done in various ways e.g. inactivating one or more reactions in the EMs by deleting genes of certain enzymes or other manipulations that inhibit the enzymes. Different numbers and combination of reactions can be removed to eliminate PSynth.
- any feasible steady-state flux distribution in a given network, expressed by a vector of the net reaction rates, r, can be represented by a non-negative linear combination of elementary modes as illustrated in Equation 1 (adapted from [11]):
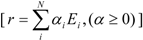
- the removal of reactions from the network results in a new set of EMs constituted by those EMs from the original network that do not involve the deleted reactions [24].
- the set of target modes (Et), i.e., all EMs (et,j) involving the objective reaction, t
- the set of non-target modes (Ent), i.e., EMs not involving the objective reaction, nt

2.5. Generalized Concept of MCSs
2.6. Further Refined Concept of MCSs
2.7. Comparing MCS Concepts
2.7.1. Same Properties
- there will always be a trivial MCS- the objective reaction itself;
- some reactions such as the biomass synthesis, are actually pseudo-reactions that are not related to a single gene or enzyme and thus cannot be repressed by inhibitions such as gene deletions;
- the definition of the MCSs: each MCS provides a minimal (irreducible) set of deletions or EMs from the set of target modes, that will achieve the elimination of the objective reaction.
2.7.2. Different Properties
- A deletion task T is a set of constraints that characterize the stationary flux patterns (reactions) r to be repressed while D, derived from T, characterizes the target modes (EMs) to be targeted by MCSs. As such, D (for the target modes) and T (for the flux vectors r) are, in most cases such as in the earlier MCS concept, identical.
- In the generalized MCS concept, however, the deletion task D can either differ from T or T must be transformed into several Di that lead to sub-tasks. So, instead of only dealing with a simple deletion task T where all non-trivial flux distributions for an objective reaction are blocked, other more complicated deletion tasks and intervention goals are possible.
- The generalized MCS concept offers a wider range of capacity to assess, manipulate and design biochemical networks. MCSs are no longer restricted to the removal of reactions as shown in Figure 2 but can also contain network nodes such that more general deletion problems can be tackled. The MCSs that involve the removal of other network parameters besides reactions are shown in the lower two tables (1b and 1c) of Table 1 below.
| Elementary modes EM2-EM6 (grey) involve the objective reaction PSynth. | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R1 | R2 | R3 | R4 | R5 | R6 | R7 | PSynth | A | B | C | D | E | |
| EM1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| EM2 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 |
| EM3 | 1 | 0 | 1 | −1 | −1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| EM4 | 0 | 1 | 1 | 0 | −1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| EM5 | 0 | 0 | 1 | −1 | −2 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| EM6 | 0 | 2 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| MCSs of NetEx for the objective reaction PSynth | |||||||||||||
| 1a) Initial concept: MCSs removing reactions only | |||||||||||||
| MCS0 | 1 | ||||||||||||
| MCS1 | 1 | ||||||||||||
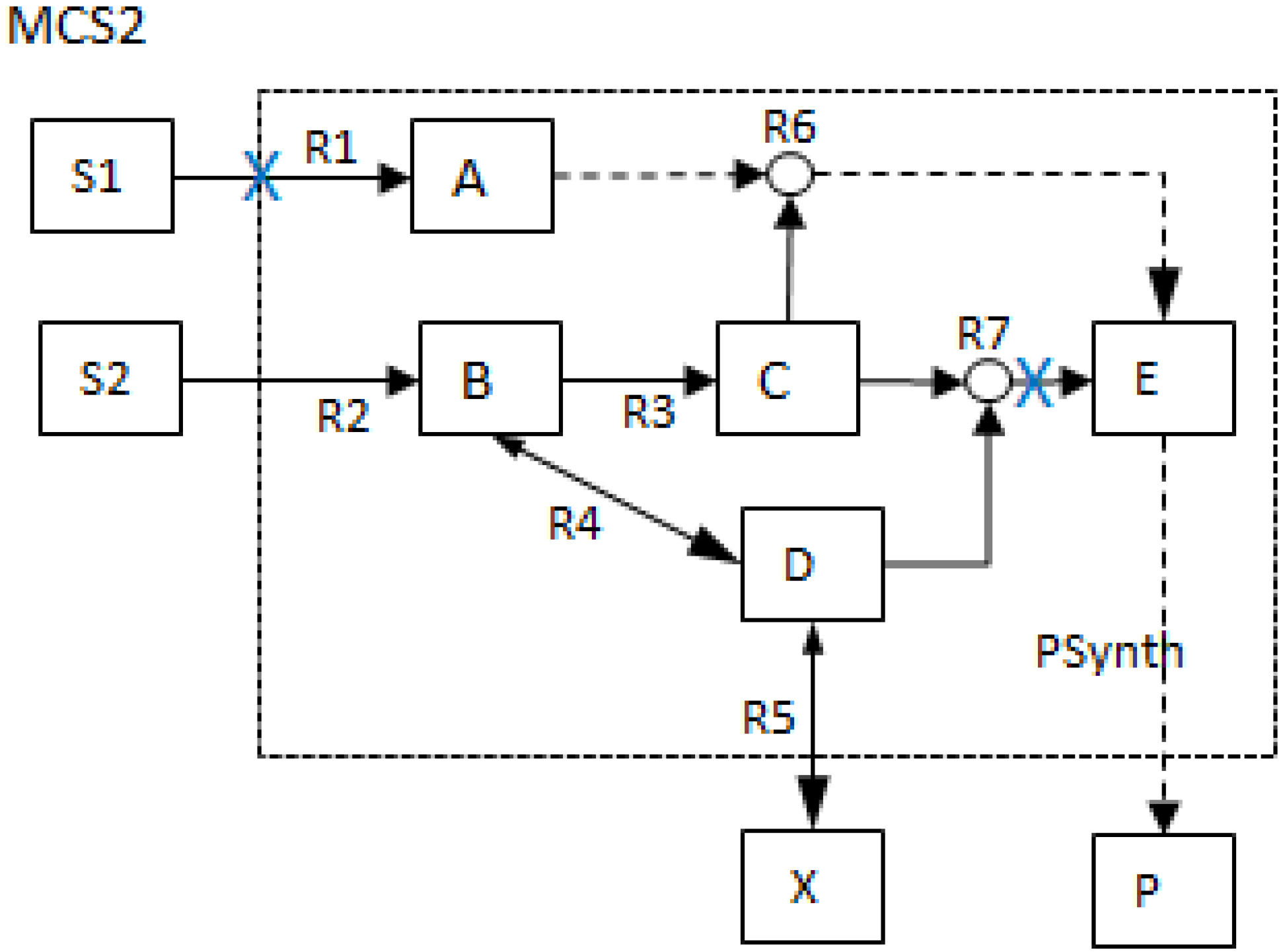
| MCS2 | 1 | 1 | |||||||||||
| MCS3 | 1 | 1 | |||||||||||
| MCS4 | 1 | 1 | |||||||||||
| MCS5 | 1 | 1 | |||||||||||
| MCS6 | 1 | 1 | 1 | ||||||||||
| MCS7 | 1 | 1 | 1 | ||||||||||
| 1b) Generalized concept: Minimal cut sets removing metabolites only | |||||||||||||
| MCS8 | 1 | ||||||||||||
| MCS9 | 1 | ||||||||||||
| MCS10 | 1 | ||||||||||||
| MCS11 | 1 | 1 | |||||||||||
| 1c) Generalized concept: Minimal cut sets removing reactions and metabolites | |||||||||||||
| MCS12 | 1 | 1 | |||||||||||
| MCS13 | 1 | 1 | 1 | ||||||||||
| MCS14 | 1 | 1 | |||||||||||
| MCS15 | 1 | 1 | |||||||||||
| MCS16 | 1 | 1 | |||||||||||
| Intervention Problems | Target modes T | Desired modes D1 | n1 | MCSs | |
|---|---|---|---|---|---|
| I1) | No synthesis of undesired product P | EM2, EM3, EM4, EM5, EM6 | MCS0={ Psynth}, MCS1={R3}, MCS2={R1,R7}, MCS3={R6,R7}, MCS4= {R2, R4}, MCS5={R2,R5}, MCS6={R1,R4,R5}, MCS7={R4,R5,R6} | ||
| I2) | No synthesis of undesired product P and production of X with maximal yield possible | EM2, EM3, EM4, EM5, EM6 | EM1 | 1 | MCS0={ Psynth}, MCS1={R3}, MCS2={R1,R7}, MCS3={R6,R7}, |
3. Computational Complexity
3.1. Deterministic and Non-Deterministic Polynomial Complexity
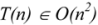
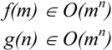
3.2. MCS Computational Methods
- i)
- The first method was presented by Imielinski and Belta [35] and considers obtaining cut sets from the computation of sub-EMs which are EMs of a submatrix of the stoichiometry matrix [36]; the submatrix in turn is formed by taking a subset of the rows of the stoichiometry matrix. In other words, the sub-EMs are flux configurations that place only a subset of species in the system at steady state. Because the sub-EMs naturally emerge from the intermediate steps of the tableau algorithm for EM computing [3], it means that the sub-EMs can be obtained from a network of any size, hence overcoming the problem where the metabolic network is too large and complex that it becomes NP-hard to find MCSs. A possible drawback is that there is no guarantee that all the cut sets will be found and their minimality is also not guaranteed so the cut sets would need to be checked for minimality and further reduced to MCSs where necessary. Development of this computational framework is described in detail in [35] as well as its application to a genome scale metabolic model of E.coli.
- ii)
- The second method is by Haus et al. [14] and involves modifying existing algorithms to develop more efficient methods for computing MCSs. Their first algorithm is a modification of Berge’s algorithm [37] and computes MCSs from EMs, thereby improving on the time and memory required for enumeration; the second algorithm is based on Fredman and Khachiyan [38] and directly computes MCSs from the stoichiometric matrix, with the hypergraph of EMs containing the blocked reactions being generated on the side.
- iii)
- The third method, contributed by Ballerstein et al. [29], also determines MCSs directly without knowing EMs. Their computational method is based on a duality framework for metabolic networks where the enumeration of MCSs in the original network is reduced to identifying the EMs in a dual network so both EMs and MCSs can be computed with the same algorithm. They also proposed a generalization of MCSs by allowing the combination of inhomogeneous constraints on reaction rates.
- iv)
- The fourth method includes an approximation algorithm for computing the minimum reaction cut and an improvement for enumerating MCSs, recently proposed by Acuña et al. [30]. These emerged from their systematic analysis of the complexity of the MCS concept and EMs, in which it was proved that finding a MCS, finding an EM containing a specified set of reactions, and counting EMs are all NP-hard problems.
4. Applications of MCSs
- i)
- If the cut occurred naturally, e.g., a reaction malfunctioning due to spontaneous mutation, the MCS would serve as an internal failure mode with respect to a certain functionality and could be applied to study structural fragility and robustness on a local and global scale.
- ii)
- If, on the other hand, the cut is a deliberate intervention e.g., gene deletion, enzyme inhibition or RNA interference, then the MCS would be seen as a target set that could, for example, be suitable for blocking metabolic functionalities, and thus have significant potential in metabolic engineering and drug discovery. These applications can be extended to enable the MCSs to be used for assessing/verifying, manipulating and designing biochemical networks.
4.1. Fragility Analysis
| R1 | R2 | R3 | R4 | R5 | R6 | R7 | Psynth | |
|---|---|---|---|---|---|---|---|---|
| Fi | 0.4 | 0.5 | 1 | 0.375 | 0.375 | 0.4 | 0.5 | 1 |
4.2. Network Verification
4.3. Observability of Reaction Rates in Metabolic Flux Analyses
| R1 | R2 | R3 | R4 | R5 | R6 | R7 | PSynth | |
|---|---|---|---|---|---|---|---|---|
| EM1 | 1 | 0 | 1 | -1 | -1 | 1 | 0 | 1 |
| EM2 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| EM3 | 1 | 0 | 0 | 0 | 1 | 1 | -1 | 0 |
| EM4 | 0 | 2 | 1 | 1 | 0 | 0 | 1 | 1 |
| EM5 | 0 | 1 | 1 | 0 | -1 | 0 | 1 | 1 |
| EM6 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| EM7 | 0 | 0 | 1 | -1 | -2 | 0 | 1 | 1 |
| EM8 | 1 | -1 | 0 | -1 | 0 | 1 | -1 | 0 |
| EM9 | 2 | 0 | 1 | -1 | 0 | 2 | -1 | 1 |
| R1 | R2 | R3 | R4 | R5 | R6 | R7 | PSynth | |
| MCS1 | 1 | |||||||
| MCS2 | 1 | |||||||
| MCS3 | 1 | 1 | ||||||
| MCS4 | 1 | 1 | ||||||
| MCS5 | 1 | 1 | ||||||
| MCS6 | 1 | 1 | 1 | |||||
| MCS7 | 1 | 1 | 1 | |||||
| MCS8 | 1 | 1 | 1 | |||||
| MCS9 | 1 | 1 | 1 | |||||
| MCS10 | 1 | 1 | 1 |
4.4. Pathway Energy Balance Constraints
4.5. Target Identification and Metabolic Interventions
5. Similar concepts
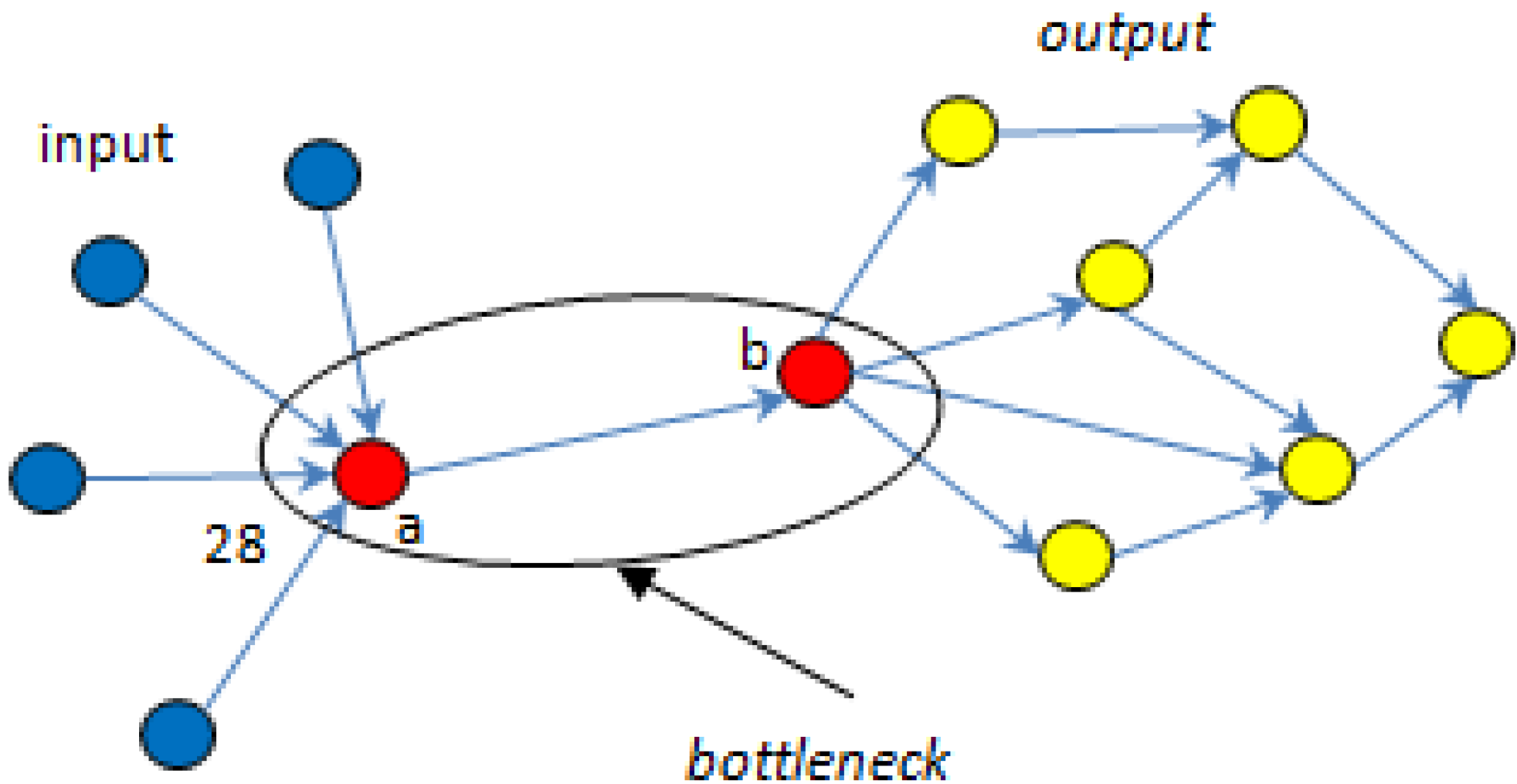
5.1. Bottlenecks
| ▪ MCSs | R1 | R2 | R3 | R4 | R5 | R6 | R7 | PSynth | Total |
|---|---|---|---|---|---|---|---|---|---|
| ▪ MCS1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 2 |
| ▪ MCS2 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 2 |
| ▪ MCS3 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 2 |
| ▪ MCS4 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 2 |
| ▪ MCS5 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 2 |
| ▪ MCS6 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 2 |
| ▪ MCS7 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 2 |
| ▪ MCS8 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 2 |
| ▪ MCS9 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 3 |
| ▪ MCS10 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 3 |
| ▪ MCS11 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 3 |
| ▪ MCS12 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 3 |
| ▪ MCS13 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 3 |
| ▪ MCS14 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 3 |
| ▪ MCS15 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 3 |
| ▪ MCS16 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 3 |
| ▪ Total | 4 | 6 | 3 | 7 | 7 | 4 | 6 | 3 | |
| ▪ Fj | 0.33 | 0.43 | 0.5 | 0.39 | 0.39 | 0.33 | 0.33 | 0.50 |
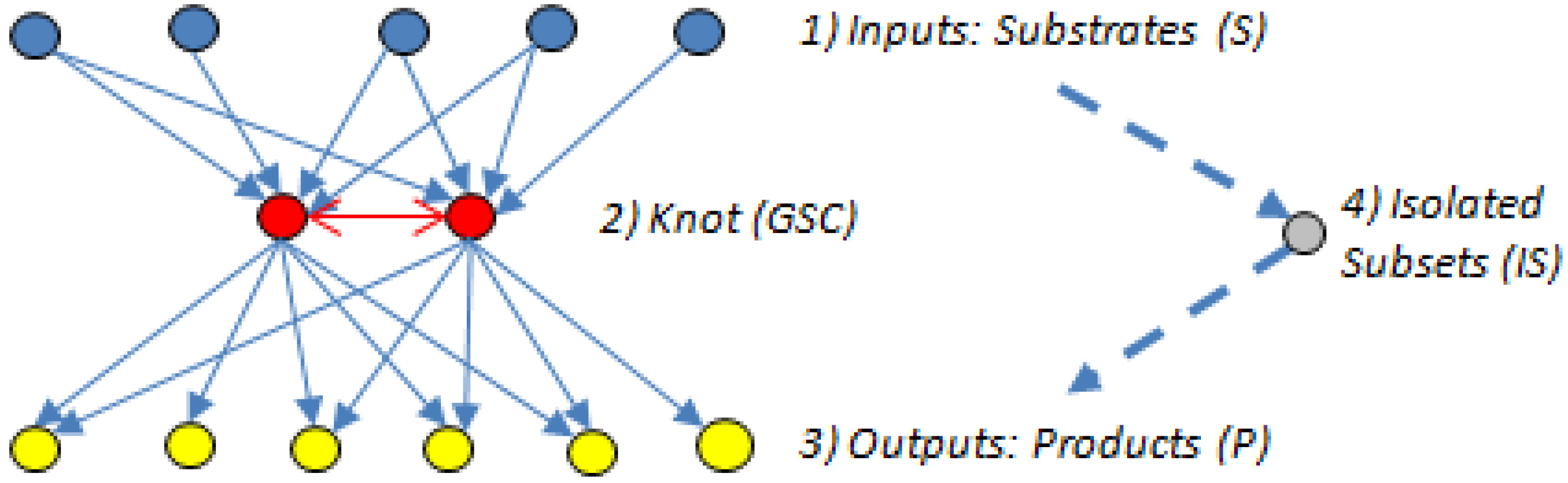
5.2. Bow-Ties
- (1)
- The input domain (substrate subset (S)), which contains substrates that can be converted reversibly to intermediates or directly to metabolites in the GSC, but those directly connected to the GSC cannot be produced from the GSC.
- (2)
- The knot or GSC, which is the metabolite converting hub [60], where protocols manage, organize and process inputs, and from where, in turn, the outputs get propagated. The GSC follows the graph theory definition [62] and contains metabolites that have routes (can be several) connecting them to each other; it is the most important subnet in the bow-tie structure.
- (3)
- The output domain (product subset (P)), which contains products from metabolites in the GSC and can also have intermediate metabolites but the products cannot be converted back into the GSC [7]. In other words, the reactions directly linking substrates to the GSC and the GSC to the products are irreversible.
- (4)
- The resulting metabolites that are not in the GSC, S or P subsets form an isolated subset (IS), the simplest structured of the four bow-tie components [7], which can include metabolites from the input domain S or the output domain P but those metabolites cannot reach the GSC or be reached from it.
- (1)
- All substrate reactions (S subnet) plus GSC reactions blocking any cyclic EMs that could take place without inputs from the substrate reactions. In this case, no product reactions (P subnet) need blocking;
- (2)
- All product reactions(P subnet) plus GSC reactions blocking the cyclic EMs- in this case no substrate (S subnet) need to be blocked;
- (3)
- All GSC reactions that connect the S to the P subnet. No substrate or product reactions need to be blocked;
- (4)
- A combination of S reactions plus GSC reactions reached from the unblocked S reactions. P reactions don’t need to be blocked;
- (5)
- A combination of P reactions plus GSC reactions that could reach the unblocked P reactions. S reactions don’t need blocking.
- From all MCS, eliminate any that involve reactions that are known to belong to S or P;
- Order the remainder by increasing size and/or decreasing mean fragility coefficient;
- Choose a cutoff value in this sequence, and allocate all reactions that belong to MCSs in the top section of the sequence to the GSC.
5.3. Weak Nutrient Sets
5.4. Flux Balance Analysis
6. Conclusions
Acknowledgments
Conflict of Interest
References
- Gagneur, J.; Klamt, S. Computation of elementary modes: A unifying framework and the new binary approach. BMC Bioinformatics 2004, 5. [Google Scholar]
- Schuster, S.; Dandekar, T.; Fell, D.A. Detection of elementary flux modes in biochemical networks: A promising tool for pathway analysis and metabolic engineering. Trends Biotechnol. 1999, 17, 53–60. [Google Scholar] [CrossRef]
- Schuster, S.; Fell, D.; Dandekar, T. A general definition of metabolic pathways useful for systematic organization and analysis of complex metabolic networks. Nat. Biotechnol. 2000, 18, 326–332. [Google Scholar] [CrossRef]
- Trinh, C.T.; Wlaschin, A.; Srienc, F. Elementary mode analysis: A useful metabolic pathway analysis tool for characterizing cellular metabolism. Appli. Microbiol. Biotechnol. 2009, 81, 813–826. [Google Scholar] [CrossRef]
- Fell, D.A.; Wagner, A. The small world of metabolism. Nat. Biotechnol. 2000, 18, 1121–1122. [Google Scholar] [CrossRef]
- Ma, H.; Zeng, A.-P. Reconstruction of metabolic networks from genome data and analysis of their global structure for various organisms. Bioinformatics 2003, 19, 270–277. [Google Scholar] [CrossRef]
- Ma, H.-W.; Zeng, A.-P. The connectivity structure, giant strong component and centrality of metabolic networks. Bioinformatics 2003, 19, 1423–1430. [Google Scholar] [CrossRef]
- Rockafellar, R. Convex Analysis; Princeton University Press: Princeton, NY, USA, 1970. [Google Scholar]
- Schilling, C.H.; Schuster, S.; Palsson, B.O.; Heinrich, R. Metabolic pathway analysis: Basic concepts and scientific applications in the post-genomic era. Biotechnol. Prog. 1999, 15, 296–303. [Google Scholar] [CrossRef]
- Papin, J.A. Comparison of network-based pathway analysis methods. Trends Biotechnol. 2004, 22, 400–405. [Google Scholar] [CrossRef]
- Klamt, S. Generalized concept of minimal cut sets in biochemical networks. Biosystems 2006, 83, 233–247. [Google Scholar] [CrossRef]
- Klamt, S.; Gilles, E. Minimal cut sets in biochemical reaction networks. Bioinformatics 2004, 20, 226–234. [Google Scholar] [CrossRef]
- Klamt, S.; Sae-Rodriguez, J.; Gilles, E.D. Structural and functional analysis of cellular networks with cellnetanalyzer. BMC Syst. Biol. 2007, 1. [Google Scholar]
- Haus, U.-U.; Klamt, S.; Stephen, T. Computing knock-out strategies in metabolic networks. J. Comput. Biol. 2008, 15, 259–268. [Google Scholar] [CrossRef]
- Hädicke, O.; Klamt, S. Computing complex metabolic intervention strategies using constrained minimal cut sets. Metab. Eng. 2011, 13, 204–213. [Google Scholar] [CrossRef]
- Clark, S.; Verwoerd, W. A systems approach to identifying correlated gene targets for the loss of colour pigmentation in plants. BMC Bioinformatics 2011, 12, 343. [Google Scholar] [CrossRef]
- Wilhelm, T.; Behre, J.; Schuster, S. Analysis of structural robustness of metabolic networks. Syst. Biol. 2004, 1, 114–120. [Google Scholar] [CrossRef]
- Fard, N.S. Determination of minimal cut sets of a complex fault tree. Comput. Ind. Eng. 1997, 33, 59–62. [Google Scholar] [CrossRef]
- Sinnamon, R.M.; Andrews, J.D. Improved accuracy in quantitative fault tree analysis. Qual. Reliab. Eng. Int. 1997, 13, 285–292. [Google Scholar] [CrossRef]
- Minimal cut sets. Available online: http://www.weibull.com/hotwire/issue63/relbasics63.htm, (accessed on 18 December 2011).
- Fault tree analysis. Available online: http://www.weibull.com/basics/fault-tree/index.htm, (accessed on 18 December 2011).
- Empowering the reliability professional. Available online: http://www.reliasoft.com/, (accessed on 18 December 2011),.
- Bollabas, B. Modern Graph Theory; Springer-Verlag: New York, NY, 1998. [Google Scholar]
- Schuster, S.; Hilgetag, C.; Woods, J.H.; Fell, D.A. Reaction routes in biochemical reaction systems: Algebraic properties, validated calculation procedure and example from nucleotide metabolism. J. Math. Biol. 2002, 45, 153–181. [Google Scholar] [CrossRef]
- Trinh, C.T.; Carlson, R.; Wlaschin, A.; Srienc, F. Design, construction and performance of the most efficient biomass producing e. Coli bacterium. Metab. Eng. 2006, 8, 628–638. [Google Scholar] [CrossRef]
- Unrean, P.; Trinh, C.T.; Srienc, F. Rational design and construction of an efficient e. Coli for production of diapolycopendioic acid. Metab. Eng. 2010, 12, 112–122. [Google Scholar] [CrossRef]
- Burgard, A.P.; Pharkya, P.; Maranas, C.D. Optknock: A bilevel programming framework for identifying gene knockout strategies for microbial strain optimization. Biotechnol. Bioeng. 2003, 84, 647–657. [Google Scholar] [CrossRef]
- Tepper, N.; Shlomi, T. Predicting metabolic engineering knockout strategies for chemical production: Accounting for competing pathways. Bioinformatics 2010, 26, 536–543. [Google Scholar] [CrossRef]
- Ballerstein, K.; von Kamp, A.; Klamt, S.; Haus, U.-U. Minimal cut sets in a metabolic network are elementary modes in a dual network. Bioinformatics 2012, 28, 381–387. [Google Scholar] [CrossRef]
- Acuña, V.; Chierichetti, F.; Lacroix, V.; Marchetti-Spaccamela, A.; Sagot, M.-F.; Stougie, L. Modes and cuts in metabolic networks: Complexity and algorithms. Biosystems 2009, 95, 51–60. [Google Scholar] [CrossRef]
- Acuña, V.; Marchetti-Spaccamela, A.; Sagot, M.-F.; Stougie, L. A note on the complexity of finding and enumerating elementary modes. Biosystems 2010, 99, 210–214. [Google Scholar] [CrossRef]
- Garey, M.R.; Johnson, D.S. Computers and Intractability. A Guide to the Theory of NP-Completeness; W. H. Freeman and Co.: San Francisco, CA, USA, 1979. [Google Scholar]
- Alsuwaiyel, M.H. Algorithms: Design Techniques and Analysis, 3rd ed; World Scientific Publishing Co., Pte., Ltd.: Singapore, 2003; Volume 7. [Google Scholar]
- Kozen, D.C. Theory of Computation; Springer: New York, NY, USA, 2006. [Google Scholar]
- Imielinski, M.; Belta, C. On the computation of minimal cut sets in genome scale metabolic networks. Amer. Contr. Conf. 2007, 1329–1334. [Google Scholar] [CrossRef]
- Famili, I.; Palsson, B.O. Systemic metabolic reactions are obtained by singular value decomposition of genome-scale stoichiometric matrices. J. Theor. Biol. 2003, 224, 87–96. [Google Scholar] [CrossRef]
- Berge, C. Hypergraphs. Combinatorics of Finite Sets; North-Holland Mathematical Library: Amsterdam, North-Holland, 1989; Volume 43. [Google Scholar]
- Fredman, M.L.; Khachiyan, L. On the complexity of dualization of monotone disjunctive normal forms. J. Algorithm 1996, 21, 618–628. [Google Scholar] [CrossRef]
- Csete, M.E.; Doyle, J.C. Reverse engineering of biological complexity. Science 2002, 295, 1664–1669. [Google Scholar] [CrossRef]
- Kitano, H. Biological robustness. Nat. Publ. Group 2004, 5. [Google Scholar]
- Papin, J.A.; Price, N.D.; Palsson, B.O. Extreme pathway lengths and reaction participation in genome-scale metabolic networks. Genome Res. 2002, 12, 1889–1900. [Google Scholar] [CrossRef]
- Stelling, J.; Klamt, S.; Bettenbrock, K.; Schuster, S.; Gilles, E.D. Metabolic network structure determines key aspects of functionality and regulation. Nature 2002, 420, 190–193. [Google Scholar] [CrossRef]
- Min, Y.; Jin, X.; Chen, M.; Pan, Z.; Ge, Y.; Chang, J. Pathway knockout and redundancy in metabolic networks. J. Theor. Biol. 2011, 270, 63–69. [Google Scholar] [CrossRef]
- Holzhütter, S.; Holzhütter, H.-G. Computational design of reduced metabolic networks. Chem. Bio. Chem. 2004, 5, 1401–1422. [Google Scholar]
- Papp, B.; Pal, C.; Hurst, L.D. Metabolic network analysis of the causes and evolution of enzyme dispensability in yeast. Nature 2004, 429, 661–664. [Google Scholar] [CrossRef]
- Edwards, J.S.; Palsson, B.O. Metabolic flux balance analysis and the in silico analysis of escherichia coli k-12 gene deletions. BMC Bioinformatics 2000, 1, 1–10. [Google Scholar] [CrossRef]
- Wiechert, W.; Möllney, M.; Petersen, S.; de Graaf, A.A. A universal framework for 13c metabolic flux analysis. Metab. Eng. 2001, 3, 265–283. [Google Scholar] [CrossRef]
- Klamt, S.; Schuster, S.; Gilles, E.D. Calculability analysis in underdetermined metabolic networks illustrated by a model of the central metabolism in purple nonsulfur bacteria. Biotechnol. Bioeng. 2002, 77, 734–751. [Google Scholar] [CrossRef]
- Edwards, J.S.; Covert, M.; Palsson, B. Metabolic modelling of microbes: The flux-balance approach. Environ. Microbiol. 2002, 4, 133–140. [Google Scholar] [CrossRef]
- Schwender, J. Metabolic flux analysis as a tool in metabolic engineering of plants. Curr. Opin. Biotechnol. 2008, 19, 131–137. [Google Scholar] [CrossRef]
- Nolan, R.P.; Fenley, A.P.; Lee, K. Identification of distributed metabolic objectives in the hypermetabolic liver by flux and energy balance analysis. Metab. Eng. 2006, 8, 30–45. [Google Scholar] [CrossRef]
- Schilling, C.H.; Edwards, J.S.; Letscher, D.; Palsson, B.O. Combining pathway analysis with flux balance analysis for the comprehensive study of metabolic systems. Biotechnol. Bioeng. 2000, 71, 286–306. [Google Scholar] [CrossRef]
- Cherkassky, B.; Goldberg, A.; Radzik, T. Shortest paths algorithms: Theory and experimental evaluation. Math. Program. 1996, 73, 129–174. [Google Scholar]
- Wu, X.; Qi, X. Genes encoding hub and bottleneck enzymes of the arabidopsis metabolic network preferentially retain homeologs through whole genome duplication. BMC Evol. Biol. 2010, 10. [Google Scholar]
- Yu, H.; Kim, P.M.; Sprecher, E.; Trifonov, V.; Gerstein, M. The importance of bottlenecks in protein networks: Correlation with gene essentiality and expression dynamics. PLoS Comput. Biol. 2007, 3, e59. [Google Scholar] [CrossRef]
- Homeolog-cogepedia. Available online: http://genomevolution.org/wiki/index.php/Homeolog, accessed on 10 September 2012.
- Bordel, S.; Nielsen, J. Identification of flux control in metabolic networks using non-equilibrium thermodynamics. Metab. Eng. 2010, 12, 369–377. [Google Scholar] [CrossRef]
- Ma, H.; Zhao, X.; Yuan, Y.; Zeng, A. Decomposition of metabolic network into functional modules based on the global connectivity structure of reaction graph. Bioinformatics 2004, 20, 1870–1876. [Google Scholar] [CrossRef]
- Csete, M.; Doyle, J. Bow ties, metabolism and disease. Trends Biotechnol. 2004, 22, 446–450. [Google Scholar] [CrossRef]
- Zhao, J.; Tao, L.; Yu, H.; Luo, J.-H.; Cao, Z.-W.; Li, Y.-X. Bow-tie topological features of metabolic networks and the functional significance. Chin. Sci. Bull. 2007, 52, 1036–1045. [Google Scholar] [CrossRef]
- Zhao, J.; Yu, H.; Luo, J.-H.; Cao, Z.-W.; Li, Y.-X. Hierarchical modularity of nested bow-ties in metabolic networks. BMC Bioinformatics 2006, 7, 386. [Google Scholar] [CrossRef]
- White, D.R.; Batagelj, V.; Mrvar, A. Anthropology—Analyzing large kinship and marriage networks with pgraph and pajek. Soc. Sci. Comput. Rev. 1999, 17, 245–274. [Google Scholar] [CrossRef]
- Imielinski, M.; Belta, C.; Rubin, H.; Halasz, A. Systematic analysis of conservation relations in escherichia coli genome-scale metabolic network reveals novel growth media. Biophys. J. 2006, 90, 2659–2672. [Google Scholar] [CrossRef]
- Kauffman, K.J.; Prakash, P.; Edwards, J.S. Advances in flux balance analysis. Curr. Opin. Biotechnol. 2003, 14, 491–496. [Google Scholar] [CrossRef]
- Lee, J.M.; Gianchandani, E.P.; Papin, J.A. Flux balance analysis in the era of metabolomics. Brief. Bioinform. 2006, 7, 140–150. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Clark, S.T.; Verwoerd, W.S. Minimal Cut Sets and the Use of Failure Modes in Metabolic Networks. Metabolites 2012, 2, 567-595. https://doi.org/10.3390/metabo2030567
Clark ST, Verwoerd WS. Minimal Cut Sets and the Use of Failure Modes in Metabolic Networks. Metabolites. 2012; 2(3):567-595. https://doi.org/10.3390/metabo2030567
Chicago/Turabian StyleClark, Sangaalofa T., and Wynand S. Verwoerd. 2012. "Minimal Cut Sets and the Use of Failure Modes in Metabolic Networks" Metabolites 2, no. 3: 567-595. https://doi.org/10.3390/metabo2030567
APA StyleClark, S. T., & Verwoerd, W. S. (2012). Minimal Cut Sets and the Use of Failure Modes in Metabolic Networks. Metabolites, 2(3), 567-595. https://doi.org/10.3390/metabo2030567




