Optimality Principles in the Regulation of Metabolic Networks
Abstract
:1. Introduction
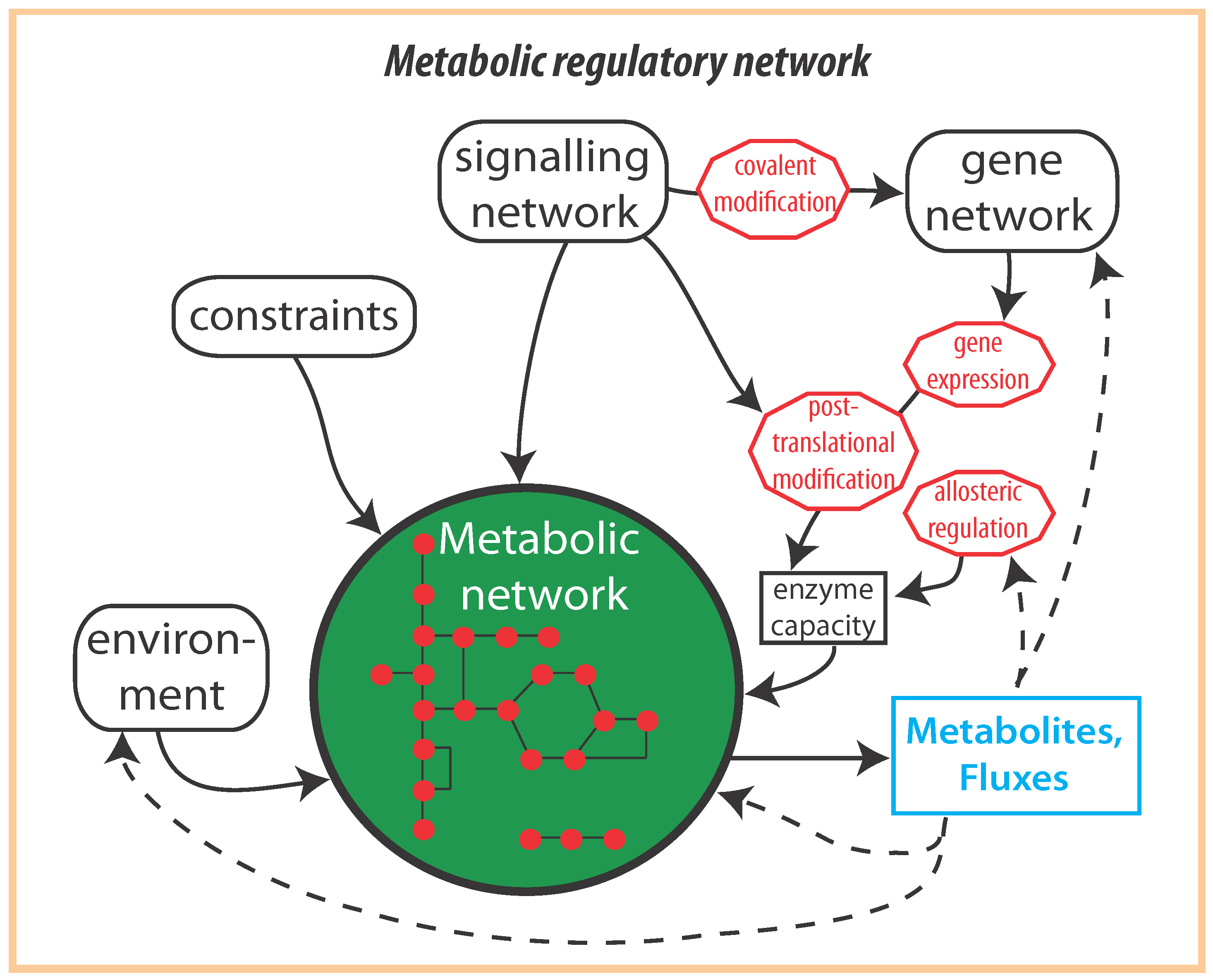
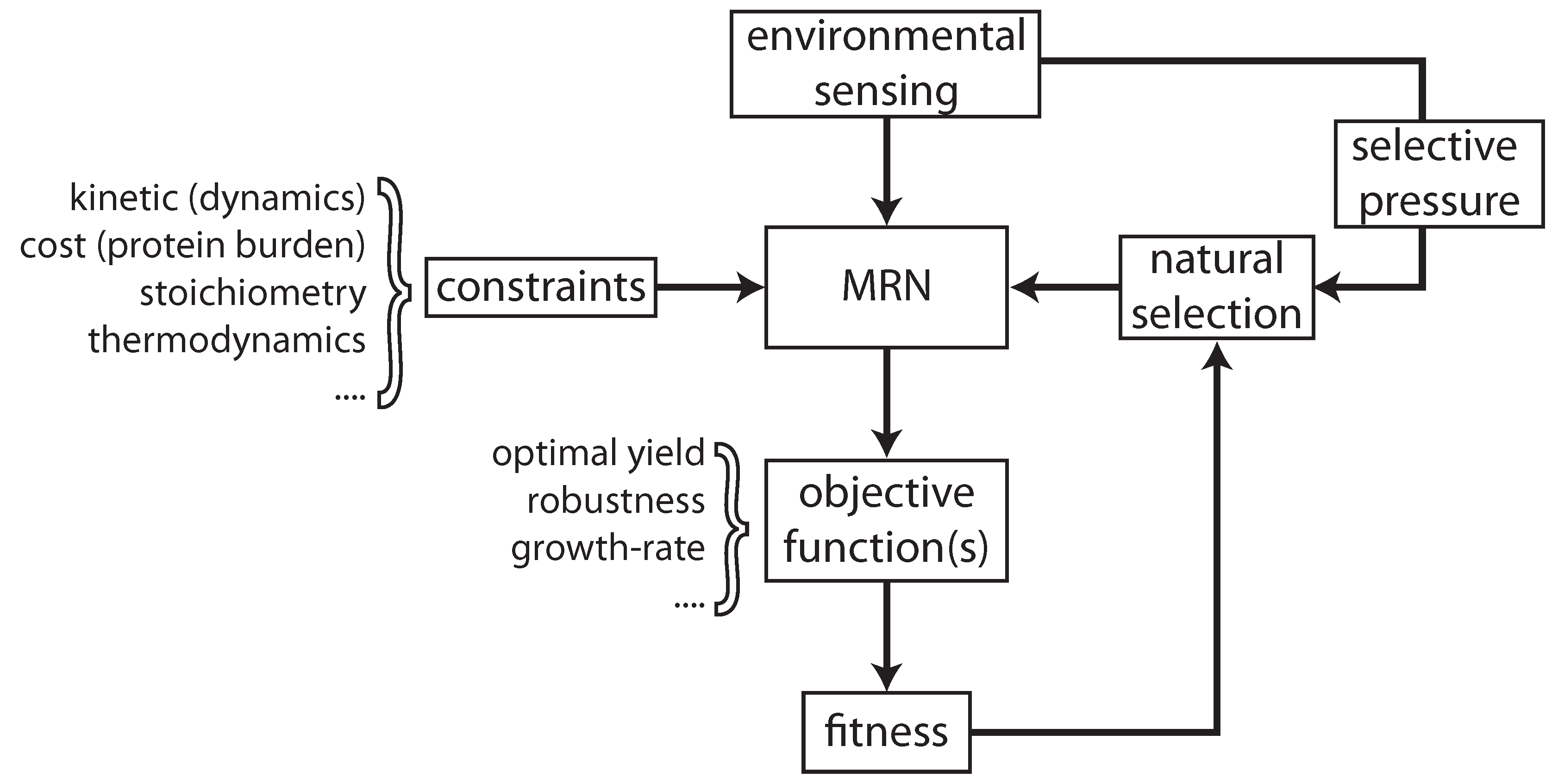
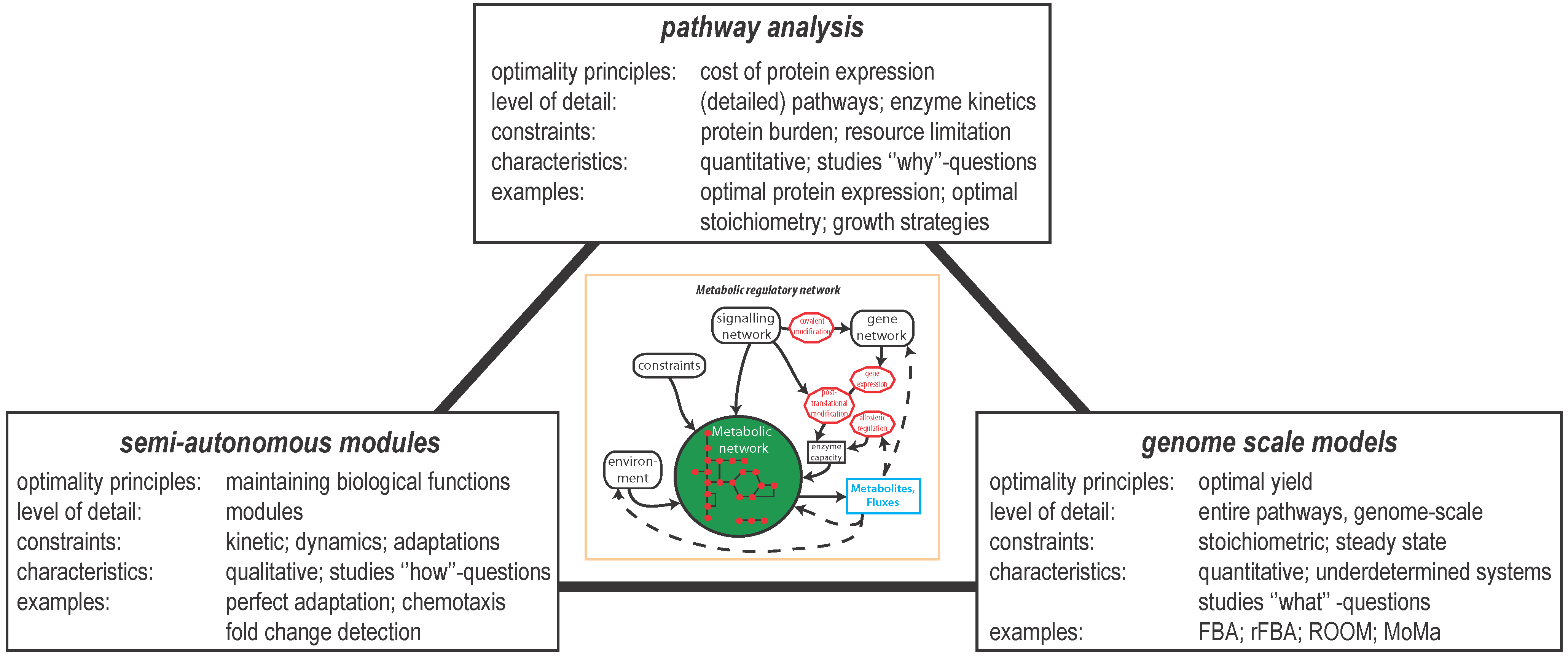
2. Optimal Control of Metabolic Reaction Networks for Semi-Autonomous Modules
2.1. Maintaining Biological Function in Dynamic Environments
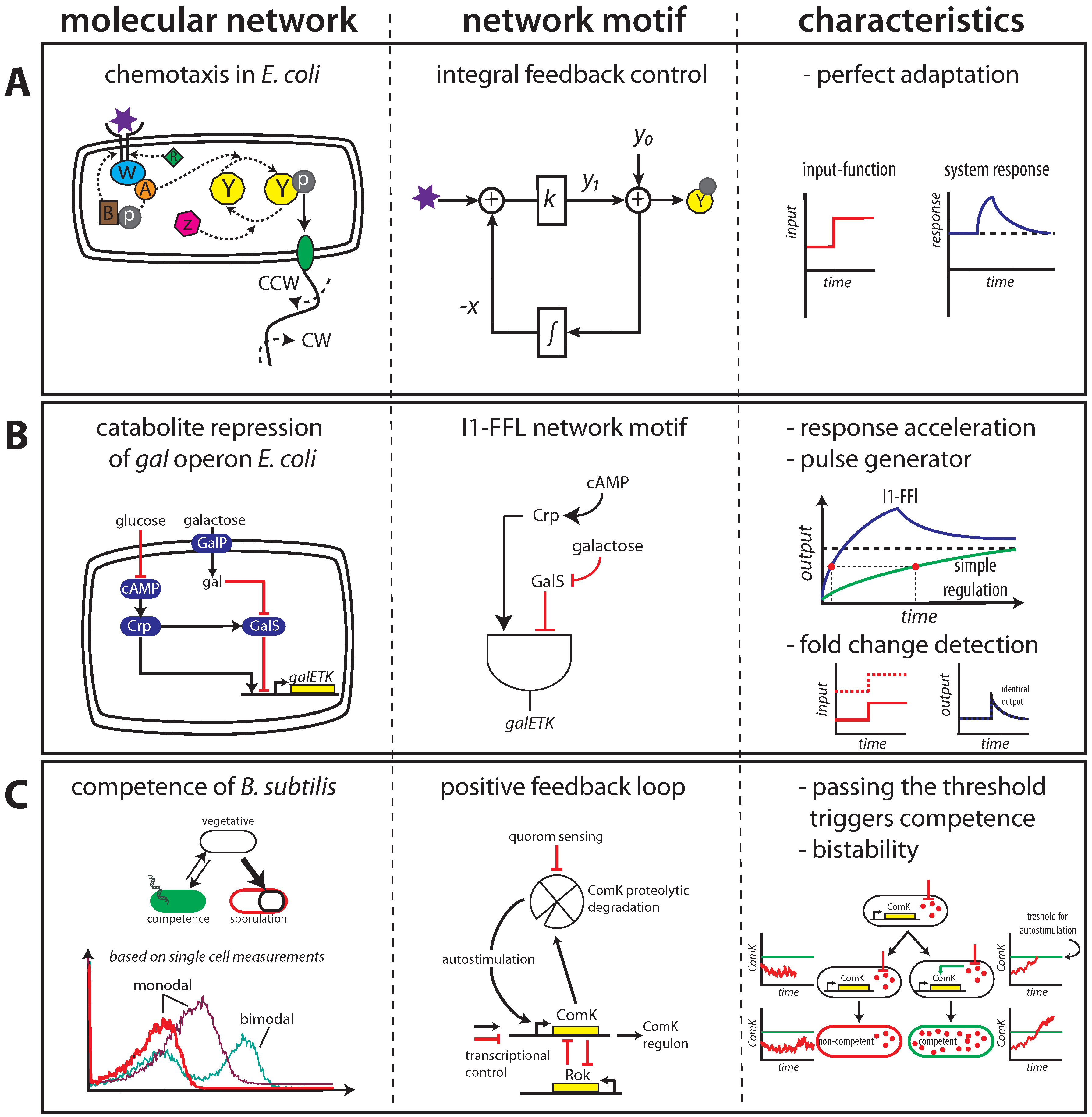
2.2. Managing and Profiting from Inevitable Molecular “Noise”
3. Global Pathway Analysis
3.1. Optimal Gene Expression in Un-branched Metabolic Pathways
3.2. Playing the Optimality Game
3.3. Growth Rate Optimisation Shapes Growth Strategies
3.4. Optimal Protein Expression Levels Maximise Growth Rate
3.5. Feasibility Analysis
4. Genome Scale Models
4.1. Flux Balance Analysis
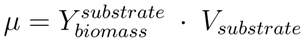
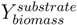 is the biomass yield with respect to the substrate (unit gram dry weight per mmol substrate, gDW mmol−1) and Vsubstrate is the specific uptake rate of the growth substrate (unit mmol h−1 gDW−1). With the uptake rate fixed as an environment-dependent capacity constraint, in order to find the highest µ, FBA just finds the flux distribution with the highest yield. Thus, it should be realised that the maximisation of growth rate is essentially done by finding a flux distribution that maximises
is the biomass yield with respect to the substrate (unit gram dry weight per mmol substrate, gDW mmol−1) and Vsubstrate is the specific uptake rate of the growth substrate (unit mmol h−1 gDW−1). With the uptake rate fixed as an environment-dependent capacity constraint, in order to find the highest µ, FBA just finds the flux distribution with the highest yield. Thus, it should be realised that the maximisation of growth rate is essentially done by finding a flux distribution that maximises 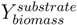 (see also [96]). Hence, FBA can rather accurately predict flux distributions for cases where high-yield strategies are favourable [97]; however predictions using FBA fail when organisms display strategies whereby substrate is “wasted” into byproducts, thereby lowering the biomass yield (high rate strategies). Indeed, E. coli [23] as well as the lactic acid bacterium Lactobacillus plantarum [96] achieve optimal in silico predicted growth when adapted on the poor substrate glycerol by serial dilution. However, on glucose, FBA predicted for L. plantarum, biomass yields, which were too high and incompatible with the observed lactate production [98]; similar discrepancies between model and experiment were observed for E. coli on glucose [23].
(see also [96]). Hence, FBA can rather accurately predict flux distributions for cases where high-yield strategies are favourable [97]; however predictions using FBA fail when organisms display strategies whereby substrate is “wasted” into byproducts, thereby lowering the biomass yield (high rate strategies). Indeed, E. coli [23] as well as the lactic acid bacterium Lactobacillus plantarum [96] achieve optimal in silico predicted growth when adapted on the poor substrate glycerol by serial dilution. However, on glucose, FBA predicted for L. plantarum, biomass yields, which were too high and incompatible with the observed lactate production [98]; similar discrepancies between model and experiment were observed for E. coli on glucose [23]. 4.2. Optimising the Predictive Power of FBA
5. Conclusion and Outlook
Acknowledgments
References
- Bruggeman, F.J.; Westerhoff, H.V. The nature of systems biology. Trends Mircobol. 2007, 15, 45–50. [Google Scholar] [CrossRef]
- Kitano, H. Systems biology: A brief overview. Science 2002, 295, 1662–1664. [Google Scholar] [CrossRef]
- Alon, U. An Introduction to Systems Biology: Design Principles of Biological Circuits; Chapman & Hall/CRC: Boca Raton, FL, USA, 2007. [Google Scholar]
- Sauer, U. Metabolic networks in motion: 13C-based flux analysis. Mol. Syst. Biol. 2006, 2, 62. [Google Scholar]
- Oberhardt, M.A.; Palsson, B.O.; Papin, J.A. Applications of genome-scale metabolic reconstructions. Mol. Syst. Biol. 2009, 5, 320. [Google Scholar]
- Heinemann, M.; Sauer, U. Systems biology of microbial metabolism. Curr. Opin. Microbiol. 2010, 13, 337–343. [Google Scholar]
- Rossell, S.; van der Weijden, C.C.; Lindenbergh, A.; van Tuijl, A.; Francke, C.; Bakker, B.M.; Westerhoff, H.V. Unraveling the complexity of flux regulation: a new method demonstrated for nutrient starvation in Saccharomyces cerevisiae. Proc. Natl. Acad. Sci. USA 2006, 103, 2166–2171. [Google Scholar]
- Thomas, C.E.; Ganji, G. Integration of genomic and metabonomic data in systems biology–are we ’there’ yet? Curr. Opin. Drug Discov. Devel. 2006, 9, 92–100. [Google Scholar]
- Bennett, M.R.; Pang, W.L.; Ostroff, N.A.; Baumgartner, B.L.; Nayak, S.; Tsimring, L.S.; Hasty, J. Metabolic gene regulation in a dynamically changing environment. Nature 2008, 454, 1119–1122. [Google Scholar]
- Kresnowati, M.T.A.P.; Van Winden, W.A.; Almering, M.J.H.; ten Pierick, A.; Ras, C.; Knijnenburg, T.A.; Daran-Lapujade, P.; Pronk, J.T.; Heijnen, J.J.; Daran, J.M. When transcriptome meets metabolome: fast cellular responses of yeast to sudden relief of glucose limitation. Mol. Syst. Biol. 2006, 2, 49. [Google Scholar]
- Hong, K.; Vongsangnak, W.; Vemuri, G.N.; Nielsen, J. Unravelling evolutionary strategies of yeast for improving galactose utilization through integrated systems level analysis. Proc. Natl. Acad. Sci. USA 2011, 108, 12179–12184. [Google Scholar]
- Cho, B.K.; Federowicz, S.; Park, Y.S.; Zengler, K.; Palsson, B.O. Deciphering the transcriptional regulatory logic of amino acid metabolism. Nat. Chem. Biol. 2012, 8, 65–71. [Google Scholar]
- Smith, J.M. Optimality theory in evolutionary biology. Nature 1990, 348, 27–33. [Google Scholar]
- Papp, B.; Teusink, B.; Notebaart, R.A. A critical view of metabolic network adaptations. HFSP J. 2009, 3, 24–35. [Google Scholar] [CrossRef]
- Gould, S.J.; Lewontin, R.C. The Spandrels of San Marco and the Panglossian Paradigm : A Critique of the Adaptationist Programme. Proc. R. Soc. Lond. B 1979, 205, 581–598. [Google Scholar] [CrossRef]
- Koch, A. The protein burden of lac operon products. J. Mol. Evol. 1983, 19, 455–462. [Google Scholar] [CrossRef]
- Snoep, J.; Yomano, L.P.; Westerhoff, H.V.; Ingram, L. Protein burden in Zymomonas mobilis: negative flux and growth control due to overproduction of glycolytic enzymes. Microbiology 1995, 141, 2329–2337. [Google Scholar] [CrossRef]
- Stoebel, D.M.; Dean, A.M.; Dykhuizen, D.E. The cost of expression of Escherichia coli lac operon proteins is in the process, not in the products. Genetics 2008, 178, 1653–1660. [Google Scholar] [CrossRef]
- Shachrai, I.; Zaslaver, A.; Alon, U.; Dekel, E. Cost of Unneeded Proteins in E. coli Is Reduced after Several Generations in Exponential Growth. Mol. Cell 2010, 38, 758–767. [Google Scholar] [CrossRef]
- Dekel, E.; Alon, U. Optimality and evolutionary tuning of the expression level of a protein. Nature 2005, 436, 588–592. [Google Scholar] [CrossRef]
- Eames, M.; Kortemme, T. Cost-Benefit Tradeoffs in Engineered lac Operons. Science 2012, 336, 911–915. [Google Scholar] [CrossRef]
- Dykhuizen, D.E.; Dean, A.M.; Hartl, D.L. Metabolic flux and fitness. Genetics 1987, 115, 25–31. [Google Scholar]
- Ibarra, R.U.; Edwards, J.S.; Palsson, B.O. Escherichia coli K-12 undergoes adaptive evolution to achieve in silico predicted optimal growth. Nature 2002, 420, 186–189. [Google Scholar]
- Cooper, T.F.; Rozen, D.E.; Lenski, R.E. Parallel changes in gene expression after 20,000 generations of evolution in Escherichiacoli. Proc. Natl. Acad. Sci. USA 2003, 100, 1072–1077. [Google Scholar]
- Macnab, R.M.; Koshland, D.E. The gradient-sensing mechanism in bacterial chemotaxis. Proc. Natl. Acad. Sci. USA 1972, 69, 2509–2512. [Google Scholar] [CrossRef]
- Yi, T.M.; Huang, Y.; Simon, M.I.; Doyle, J. Robust perfect adaptation in bacterial chemotaxis through integral feedback control. Proc. Natl. Acad. Sci. USA 2000, 97, 4649–4653. [Google Scholar] [CrossRef]
- Zaslaver, A.; Mayo, A.E.; Rosenberg, R.; Bashkin, P.; Sberro, H.; Tsalyuk, M.; Surette, M.G.; Alon, U. Just-in-time transcription program in metabolic pathways. Nat. Genet. 2004, 36, 486–491. [Google Scholar] [CrossRef]
- Kaltenbach, H.M.; Stelling, J. Modular Analysis of Biological Networks. In Advances in Experimental Medicine and Biology; Goryanin, I.I., Goryachev, A.B., Eds.; Springer: New York, NY, USA, 2012; Volume 736, pp. 3–17. [Google Scholar]
- Csete, M.E.; Doyle, J.C. Reverse engineering of biological complexity. Science 2002, 295, 1664–1669. [Google Scholar] [CrossRef]
- Hartwell, L.H.; Hopfield, J.J.; Leibler, S.; Murray, A.W. From molecular to modular cell biology. Nature 1999, 402, C47–C52. [Google Scholar]
- Alon, U. Network motifs: Theory and experimental approaches. Nat. Rev. Genet. 2007, 8, 450–461. [Google Scholar] [CrossRef]
- Kitano, H. Biological robustness. Nat. Rev. Genet. 2004, 5, 826–837. [Google Scholar] [CrossRef]
- Stelling, J.; Sauer, U.; Szallasi, Z.; Doyle, F.J.; Doyle, J. Robustness of cellular functions. Cell 2004, 118, 675–685. [Google Scholar] [CrossRef]
- Kitano, H. Towards a theory of biological robustness. Mol. Syst. Biol. 2007, 3, 137. [Google Scholar]
- Barkai, N.; Leibler, S. Robustness in simple biochemical networks. Nature 1997, 387, 913–917. [Google Scholar]
- Alon, U.; Surette, M.G.; Barkai, N.; Leibler, S. Robustness in bacterial chemotaxis. Nature 1999, 397, 168–171. [Google Scholar] [CrossRef]
- Lenski, R.E.; Barrick, J.E.; Ofria, C. Balancing robustness and evolvability. Plos Biol. 2006, 4, e428. [Google Scholar] [CrossRef]
- Larsen, S.H.; Reader, R.W.; Kort, E.N.; Tso, W.W.; Aler, J. Change in direction of flagellar rotation is the basis of the chemotactic response in Escherichia coli. Nature 1974, 249, 74–77. [Google Scholar]
- Berg, H.C.; Tedesco, P.M. Transient response to chemotactic stimuli in Escherichia coli. Proc. Natl. Acad. Sci. USA 1975, 72, 3235–3239. [Google Scholar] [CrossRef]
- Roberts, M.A.J.; Papachristodoulou, A.; Armitage, J.P. Adaptation and control circuits in bacterial chemotaxis. Biochem Soc T 2010, 38, 1265–1269. [Google Scholar] [CrossRef]
- Porter, S.L.; Wadhams, G.H.; Armitage, J.P. Signal processing in complex chemotaxis pathways. Nat. Rev. Microbiol. 2011, 9, 153–165. [Google Scholar] [CrossRef]
- Celani, A.; Shimizu, T.S.; Vergassola, M. Molecular and Functional Aspects of Bacterial Chemotaxis. J. Stat. Phys. 2011, 144, 219–240. [Google Scholar] [CrossRef]
- Lazova, M.D.; Ahmed, T.; Bellomo, D.; Stocker, R.; Shimizu, T.S. Response rescaling in bacterial chemotaxis. Proc. Natl. Acad. Sci. USA 2011, 108, 13870–13875. [Google Scholar] [CrossRef]
- Ma, W.; Trusina, A.; El-Samad, H.; Lim, W.A.; Tang, C. Defining network topologies that can achieve biochemical adaptation. Cell 2009, 138, 760–773. [Google Scholar] [CrossRef]
- Muzzey, D.; Gomez-Uribe, C.A.; Mettetal, J.T.; van Oudenaarden, A. A Systems-Level Analysis of Perfect Adaptation in Yeast Osmoregulation. Cell 2009, 138, 160–171. [Google Scholar] [CrossRef] [Green Version]
- Sourjik, V. Receptor clustering and signal processing in E. coli chemotaxis. Trends Microbiol. 2004, 12, 569–576. [Google Scholar] [CrossRef]
- Smits, W.K.; Kuipers, O.P.; Veening, J.W. Phenotypic variation in bacteria: the role of feedback regulation. Nat. Rev. Microbiol. 2006, 4, 259–271. [Google Scholar] [CrossRef]
- Avery, S.V. Cell individuality: the bistability of competence development. Trends Microbiol. 2005, 13, 457–459. [Google Scholar] [CrossRef]
- Goentoro, L.; Kirschner, M.W. Evidence that fold-change, and not absolute level, of beta-catenin dictates Wnt signaling. Mol. Cell 2009, 36, 872–884. [Google Scholar] [CrossRef]
- Cohen-Saidon, C.; Cohen, A.A.; Sigal, A.; Liron, Y.; Alon, U. Dynamics and variability of ERK2 response to EGF in individual living cells. Mol. Cell 2009, 36, 885–893. [Google Scholar] [CrossRef]
- Shoval, O.; Goentoro, L.; Hart, Y.; Mayo, A.; Sontag, E.; Alon, U. Fold-change detection and scalar symmetry of sensory input fields. Proc. Natl. Acad. Sci. USA 2010, 107, 15995–16000. [Google Scholar]
- Mangan, S.; Itzkovitz, S.; Zaslaver, A.; Alon, U. The incoherent feed-forward loop accelerates the response-time of the gal system of Escherichia coli. J. Mol. Biol. 2006, 356, 1073–1081. [Google Scholar] [CrossRef]
- Ozbudak, E.M.; Thattai, M.; Kurtser, I.; Grossman, A.D.; van Oudenaarden, A. Regulation of noise in the expression of a single gene. Nat. Genet. 2002, 31, 69–73. [Google Scholar] [CrossRef]
- Elowitz, M.B.; Levine, A.J.; Siggia, E.D.; Swain, P.S. Stochastic gene expression in a single cell. Science 2002, 297, 1183–1186. [Google Scholar] [CrossRef]
- Raj, A.; van Oudenaarden, A. Single-molecule approaches to stochastic gene expression. Annu. Rev. Biophys. 2009, 38, 255–270. [Google Scholar] [CrossRef]
- Xie, X.S.; Choi, P.J.; Li, G.W.; Lee, N.K.; Lia, G. Single-molecule approach to molecular biology in living bacterial cells. Annu. Rev. Biophys. 2008, 37, 417–444. [Google Scholar] [CrossRef]
- Davidson, C.J.; Surette, M.G. Individuality in bacteria. Ann. Rev. Genet. 2008, 42, 253–268. [Google Scholar] [CrossRef]
- Schwabe, A.; Dobrzyski, M.; Rybakova, K.; Verschure, P.; Bruggeman, F.J. Origins of stochastic intracellular processes and consequences for cell-to-cell variability and cellular survival strategies. Method Enzymol. 2011, 500, 597–625. [Google Scholar] [CrossRef]
- Veening, J.W.; Smits, W.K.; Kuipers, O.P. Bistability, epigenetics, and bet-hedging in bacteria. Annu. Rev. Microbiol. 2008, 62, 193–210. [Google Scholar]
- Tkačik, G.; Walczak, A.M. Information transmission in genetic regulatory networks: a review. J. Phys-Condens. Mat. 2011, 23, 153102. [Google Scholar] [CrossRef]
- Cheong, R.; Rhee, A.; Wang, C.J.; Nemenman, I.; Levchenko, A. Information transduction capacity of noisy biochemical signaling networks. Science 2011, 334, 354–358. [Google Scholar] [CrossRef]
- Heinrich, R.; Schuster, S.; Holzhütter, H.G. Mathematical analysis of enzymic reaction systems using optimization principles. Eur. J. Biochem. 1991, 201, 1–21. [Google Scholar] [CrossRef]
- Heinrich, R.; Hoffmann, E. Kinetic parameters of enzymatic reactions in states of maximal activity; an evolutionary approach. J. Theor. Biol. 1991, 151, 249–283. [Google Scholar] [CrossRef]
- Klipp, E.; Heinrich, R. Evolutionary optimization of enzyme kinetic parameters; effect of constraints. J. Theor. Biol. 1994, 171, 309–323. [Google Scholar] [CrossRef]
- Heinrich, R.; Klipp, E. Control analysis of unbranched enzymatic chains in states of maximal activity. J. Theor. Biol. 1996, 182, 243–252. [Google Scholar] [CrossRef]
- Liebermeister, W.; Klipp, E.; Schuster, S.; Heinrich, R. A theory of optimal differential gene expression. Bio. Systems 2004, 76, 261–278. [Google Scholar] [CrossRef]
- Heinrich, R.; Montero, F.; Klipp, E.; Waddel, T.; Melendez-Hevia, E. Theoretical approaches to the evolutionary optimization of glycolysis. Thermodynamic and kinetic constraints. Eur. J. Biochem. 1997, 201, 191–201. [Google Scholar]
- Bachmann, H.; Molenaar, D.; Kleerebezem, M.; van Hylckama Vlieg, J.E.T. High local substrate availability stabilizes a cooperative trait. The ISME journal 2011, 5, 929–932. [Google Scholar] [CrossRef]
- Gore, J.; Youk, H.; van Oudenaarden, A. Snowdrift game dynamics and facultative cheating in yeast. Nature 2009, 459, 253–256. [Google Scholar]
- Schuster, S.; Kreft, J.U.; Brenner, N.; Wessely, F.; Theissen, G.; Ruppin, E.; Schroeter, A. Cooperation and cheating in microbial exoenzyme production-theoretical analysis for biotechnological applications. Biotechnol. J. 2010, 5, 751–758. [Google Scholar] [CrossRef]
- Molenaar, D.; van Berlo, R.; de Ridder, D.; Teusink, B. Shifts in growth strategies reflect tradeoffs in cellular economics. Mol. Syst. Biol. 2009, 5, 323. [Google Scholar]
- Hartl, D.; Dykhuizen, D.; Dean, A.M. Limits of adaptation: the evolution of selective neutrality. Genetics 1985, 111, 655–674. [Google Scholar]
- Jensen, P.; Michelsen, O.; Westerhoff, H.V. Control analysis of the dependence of Escherichia coli physiology on the H (+)-ATPase. Proc. Natl. Acad. Sci. USA 1993, 90, 8068–8072. [Google Scholar] [CrossRef]
- Walsh, K.; Koshland, D.E. Characterization of rate-controlling steps in vivo by use of an adjustable expression vector. Proc. Natl. Acad. Sci. USA 1985, 82, 3577–3581. [Google Scholar] [CrossRef]
- Solem, C.; Koebmann, B.J.; Jensen, P.R. Glyceraldehyde-3-Phosphate Dehydrogenase Has No Control over Glycolytic Flux in Lactococcus lactis MG1363. J. Bacteriol. 2003, 185, 1564–1571. [Google Scholar] [CrossRef]
- Koebmann, B.; Solem, C.; Jensen, P. Control analysis of the importance of phosphoglycerate enolase for metabolic fluxes in Lactococcus lactis subsp. lactis IL1403. Syst. Biol. (Stevenage) 2006, 153, 346–349. [Google Scholar] [CrossRef]
- Koebmann, B.; Solem, C.; Jensen, P.R. Control analysis as a tool to understand the formation of the las operon in Lactococcus lactis. FEBS J. 2005, 272, 2292–2303. [Google Scholar] [CrossRef]
- Pelosi, L.; Kühn, L.; Guetta, D.; Garin, J.; Geiselmann, J.; Lenski, R.E.; Schneider, D. Parallel changes in global protein profiles during long-term experimental evolution in Escherichia coli. Genetics 2006, 173, 1851–1869. [Google Scholar] [CrossRef]
- Elena, S.F.; Lenski, R.E. Evolution experiments with microorganisms: the dynamics and genetic bases of adaptation. Nat. Rev. Genet. 2003, 4, 457–469. [Google Scholar]
- Kalisky, T.; Dekel, E.; Alon, U. Cost-benefit theory and optimal design of gene regulation functions. Phys. Biol. 2007, 4, 229–245. [Google Scholar] [CrossRef]
- Garcia Sanchez, R.; Hahn-Hägerdal, B.; Gorwa-Grauslund, M. PGM2 overexpression improves anaerobic galactose fermentation in Saccharomyces cerevisiae. MIicrob. Cell Fact. 2010, 9, 1–8. [Google Scholar] [CrossRef]
- Lee, K.S.; Hong, M.E.; Jung, S.C.; Ha, S.J.; Yu, B.J.; Koo, H.M.; Park, S.M.; Seo, J.H.; Kweon, D.H.; Park, J.C.; Jin, Y.S. Improved galactose fermentation of Saccharomyces cerevisiae through inverse metabolic engineering. Biotechnol. Bioeng. 2011, 108, 621–631. [Google Scholar] [CrossRef]
- Ihmels, J.; Levy, R.; Barkai, N. Principles of transcriptional control in the metabolic network of Saccharomyces cerevisiae. Nat. Biotechnol. 2004, 22, 86–92. [Google Scholar] [CrossRef]
- ter Kuile, B.H.; Westerhoff, H.V. Transcriptome meets metabolome: hierarchical and metabolic regulation of the glycolytic pathway. FEBS Lett. 2001, 500, 169–171. [Google Scholar] [CrossRef]
- Nikerel, E.; Berkhout, J.; Hu, F.; Teusink, B.; Reinders, M.J.T.; de Ridder, D. Understanding Regulation of Metabolism through Feasibility Analysis. Plos One 2012, 7, e39396. [Google Scholar]
- Wu, L.; Mashego, M.R.; Proell, A.M.; Vinke, J.L.; Ras, C.; van Dam, J.; Van Winden, W.A.; Van Gulik, W.M.; Heijnen, J.J. In vivo kinetics of primary metabolism in Saccharomyces cerevisiae studied through prolonged chemostat cultivation. Metab. Eng. 2006, 8, 160–171. [Google Scholar]
- Schuetz, R.; Zamboni, N.; Zampieri, M.; Heinemann, M.; Sauer, U. Multidimensional Optimality of Microbial Metabolism. Science 2012, 336, 601–604. [Google Scholar] [CrossRef]
- Smallbone, K.; Simeonidis, E.; Broomhead, D.S.; Kell, D.B. Something from nothing bridging the gap between constraint-based and kinetic modelling. FEBS J. 2007, 274, 5576–5585. [Google Scholar] [CrossRef]
- Smallbone, K.; Simeonidis, E.; Swainston, N.; Mendes, P. Towards a genome-scale kinetic model of cellular metabolism. BMC Syst. Biol. 2010, 4, 6. [Google Scholar] [CrossRef]
- Teusink, B.; Passarge, J.; Reijenga, C.A.; Esgalhado, E.; van der Weijden, C.C.; Schepper, M.; Walsh, M.C.; Bakker, B.M.; van Dam, K.; Westerhoff, H.V.; Snoep, J.L. Can yeast glycolysis be understood in terms of in vitro kinetics of the constituent enzymes? Testing biochemistry. Eur. J. Biochem. 2000, 267, 5313–5329. [Google Scholar]
- Goel, A.; Santos, F.; Vos, W.M.D.; Teusink, B.; Molenaar, D.; de Vos, W.M. Standardized Assay Medium To Measure Lactococcus lactis Enzyme Activities while Mimicking Intracellular Conditions. Appl. Environ. Microb. 2012, 78, 134–143. [Google Scholar] [CrossRef]
- van Eunen, K.; Kiewiet, J.A.L.; Westerhoff, H.V.; Bakker, B.M. Testing Biochemistry Revisited: How In Vivo Metabolism Can Be Understood from In Vitro Enzyme Kinetics. Plos Comput. Biol. 2012, 8, e1002483. [Google Scholar] [CrossRef]
- Olivier, B.G.; Snoep, J.L. Web-based kinetic modelling using JWS Online. Bioinformatics 2004, 20, 2143–2144. [Google Scholar] [CrossRef]
- Li, C.; Donizelli, M.; Rodriguez, N.; Dharuri, H.; Endler, L.; Chelliah, V.; Li, L.; He, E.; Henry, A.; Stefan, M.I.; Snoep, J.L.; Hucka, M.; Le Novère, N.; Laibe, C. BioModels Database: An enhanced, curated and annotated resource for published quantitative kinetic models. BMC Syst. Biol. 2010, 4, 92. [Google Scholar] [CrossRef]
- Feist, A.M.; Palsson, B.O. The biomass objective function. Curr. Opin. Microbiol. 2010, 13, 344–349. [Google Scholar] [CrossRef]
- Teusink, B.; Wiersma, A.; Jacobs, L.; Notebaart, R.A.; Smid, E.J. Understanding the adaptive growth strategy of Lactobacillus plantarum by in silico optimisation. Plos Comput. Biol. 2009, 5, e1000410. [Google Scholar] [CrossRef]
- Schuster, S.; Pfeiffer, T.; Fell, D.A. Is maximization of molar yield in metabolic networks favoured by evolution? J. Theor. Biol. 2008, 252, 497–504. [Google Scholar] [CrossRef]
- Teusink, B.; Wiersma, A.; Molenaar, D.; Francke, C.; de Vos, W.M.; Siezen, R.J.; Smid, E.J. Analysis of Growth of Lactobacillus plantarum WCFS1 on a Complex Medium Using a Genome-scale Metabolic Model. J. Biol. Chem. 2006, 281, 40041–40048. [Google Scholar]
- Teusink, B.; Smid, E.J. Modelling strategies for the industrial exploitation of lactic acid bacteria. Nat. Rev. Microbiol. 2006, 4, 46–56. [Google Scholar] [CrossRef]
- Mahadevan, R.; Schilling, C. The effects of alternate optimal solutions in constraint-based genome-scale metabolic models. Metab. Eng. 2003, 5, 264–276. [Google Scholar] [CrossRef]
- Kuepfer, L.; Sauer, U. Systematic evaluation of objective functions for predicting intracellular fluxes in Escherichia coli. Mol. Syst. Biol. 2007, 3, 119. [Google Scholar]
- Holzhütter, H.G. The principle of flux minimization and its application to estimate stationary fluxes in metabolic networks. Eur. J. Biochem. 2004, 271, 2905–2922. [Google Scholar] [CrossRef]
- Holzhütter, H.G. The generalized flux-minimization method and its application to metabolic networks affected by enzyme deficiencies. Bio. Systems 2006, 83, 98–107. [Google Scholar] [CrossRef]
- Shlomi, T.; Berkman, O.; Ruppin, E. Regulatory on/off minimization of metabolic flux changes after genetic perturbations. Proc. Natl. Acad. Sci. USA 2005, 102, 7695–7700. [Google Scholar] [CrossRef]
- Segre, D.; Vitkup, D.; Church, G.M.; Segrè, D. Analysis of optimality in natural and perturbed metabolic networks. Proc. Natl. Acad. Sci. USA 2002, 99, 15112–15117. [Google Scholar]
- Beg, Q.K.; Vazquez, A.; Ernst, J.; de Menezes, M.A.; Bar-Joseph, Z.; Barabási, A.L.; Oltvai, Z.N. Intracellular crowding defines the mode and sequence of substrate uptake by Escherichia coli and constrains its metabolic activity. Proc. Natl. Acad. Sci. USA 2007, 104, 12663–12668. [Google Scholar]
- van Hoek, M.; Merks, R. Redox balance is key to explaining full vs. partial switching to low-yield metabolism. BMC Syst. Biol. 2012, 6, 22. [Google Scholar] [CrossRef]
- Covert, M.W.; Schilling, C.H.; Palsson, B.O. Regulation of Gene Expression in Flux Balance Models of Metabolism. J. Theor. Biol. 2001, 213, 73–88. [Google Scholar] [CrossRef]
- Herrgard, M.J.; Covert, M.W.; Palsson, B.O. Reconciling Gene Expression Data With Known Genome-Scale Regulatory Network Structures. Genome Res. 2003, 13, 2423–2434. [Google Scholar] [CrossRef]
- Covert, M.W.; Knight, E.M.; Reed, J.L.; Herrgard, M.J.; Palsson, B.O. Integrating high-throughput and computational data elucidates bacterial networks. Nature 2004, 429, 92–96. [Google Scholar]
- Shlomi, T.; Eisenberg, Y.; Sharan, R.; Ruppin, E. A genome-scale computational study of the interplay between transcriptional regulation and metabolism. Mol. Syst. Biol. 2007, 3, 101. [Google Scholar]
- van Berlo, R.J.P.; de Ridder, D.; Daran, J.M.; Daran-Lapujade, P.A.S.; Teusink, B.; Reinders, M.J.T. Predicting Metabolic Fluxes Using Gene Expression Differences As Constraints. IEEE Acm T Comput. Bi 2011, 8, 206–216. [Google Scholar]
- Zhuang, K.; Vemuri, G.N.; Mahadevan, R. Economics of membrane occupancy and respiro-fermentation. Mol. Syst. Biol. 2011, 7, 500. [Google Scholar]
- Park, J.M.; Kim, T.Y.; Lee, S.Y. Prediction of metabolic fluxes by incorporating genomic context and flux-converging pattern analyses. Proc. Natl. Acad. Sci. USA 2010, 107, 14931–14936. [Google Scholar] [CrossRef]
- Covert, M.W.; Xiao, N.; Chen, T.J.; Karr, J.R. Integrating metabolic, transcriptional regulatory and signal transduction models in Escherichia coli. Bioinformatics 2008, 24, 2044–2050. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Berkhout, J.; Bruggeman, F.J.; Teusink, B. Optimality Principles in the Regulation of Metabolic Networks. Metabolites 2012, 2, 529-552. https://doi.org/10.3390/metabo2030529
Berkhout J, Bruggeman FJ, Teusink B. Optimality Principles in the Regulation of Metabolic Networks. Metabolites. 2012; 2(3):529-552. https://doi.org/10.3390/metabo2030529
Chicago/Turabian StyleBerkhout, Jan, Frank J. Bruggeman, and Bas Teusink. 2012. "Optimality Principles in the Regulation of Metabolic Networks" Metabolites 2, no. 3: 529-552. https://doi.org/10.3390/metabo2030529
APA StyleBerkhout, J., Bruggeman, F. J., & Teusink, B. (2012). Optimality Principles in the Regulation of Metabolic Networks. Metabolites, 2(3), 529-552. https://doi.org/10.3390/metabo2030529



