Adapting OptCouple to Identify Strategies with Increased Product Yields in Community Cohorts of E. coli
Abstract
:1. Introduction
2. Materials and Methods
2.1. Adapting OptCouple to Community GSMs
2.2. Adapting OptCouple to Maximise the Minimum Possible Product Yield in Community Strains
3. Results
3.1. Coupling 2,3-Butanediol to Community Growth
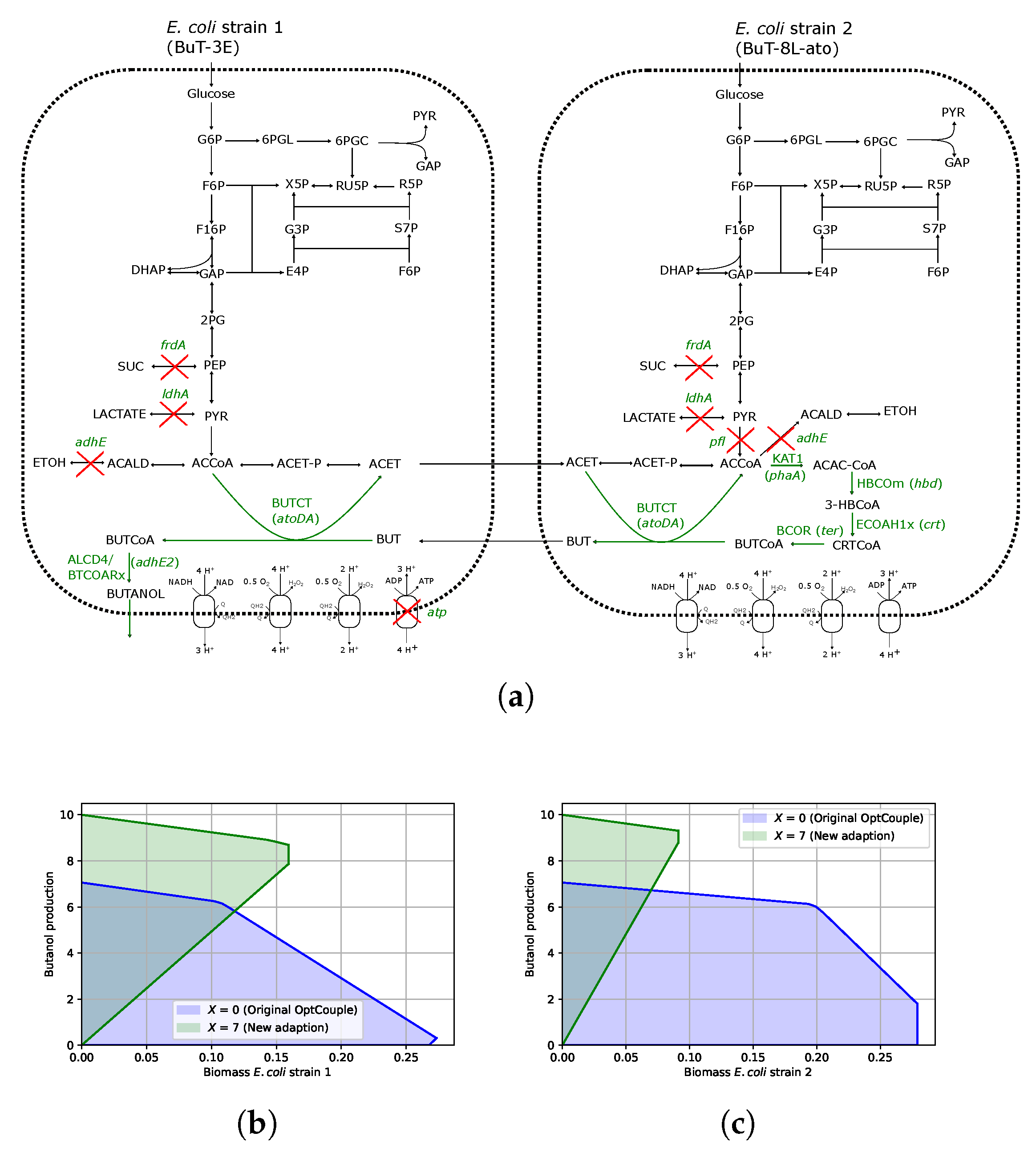
3.2. Coupling Butanol to Community Growth
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MILP | Mixed integer linear program |
| GSM | Genome-scale model |
References
- Matuszyńska, A.; Ebenhöh, O.; Zurbriggen, M.D.; Ducat, D.C.; Axmann, I.M. A new era of synthetic biology—Microbial community design. Synth. Biol. 2024, 9, ysae011. [Google Scholar] [CrossRef]
- Lloyd, C.J.; King, Z.A.; Sandberg, T.E.; Hefner, Y.; Olson, C.A.; Phaneuf, P.V.; O’Brien, E.J.; Sanders, J.G.; Salido, R.A.; Sanders, K.; et al. The genetic basis for adaptation of model-designed syntrophic co-cultures. PLoS Comput. Biol. 2019, 15, e1006213. [Google Scholar] [CrossRef]
- García-Jiménez, B.; Torres-Bacete, J.; Nogales, J. Metabolic modelling approaches for describing and engineering microbial communities. Comput. Struct. Biotechnol. J. 2021, 19, 226–246. [Google Scholar] [CrossRef] [PubMed]
- Jensen, K.; Broeken, V.; Hansen, A.S.L.; Sonnenschein, N.; Herrgård, M.J. OptCouple: Joint simulation of gene knockouts, insertions and medium modifications for prediction of growth-coupled strain designs. Metab. Eng. Commun. 2019, 8, e00087. [Google Scholar] [CrossRef]
- Ji, X.J.; Huang, H.; Zhu, J.G.; Ren, L.J.; Nie, Z.K.; Du, J.; Li, S. Engineering Klebsiella oxytoca for efficient 2,3-butanediol production through insertional inactivation of acetaldehyde dehydrogenase gene. Appl. Microbiol. Biotechnol. 2010, 85, 1751–1758. [Google Scholar] [CrossRef]
- Białkowska, A.M. Strategies for efficient and economical 2, 3-butanediol production: New trends in this field. World J. Microbiol. Biotechnol. 2016, 32, 200. [Google Scholar] [CrossRef]
- Keo-Oudone, C.; Phommachan, K.; Suliya, O.; Nurcholis, M.; Bounphanmy, S.; Kosaka, T.; Yamada, M. Highly efficient production of 2, 3-butanediol from xylose and glucose by newly isolated thermotolerant Cronobacter sakazakii. BMC Microbiol. 2022, 22, 164. [Google Scholar] [CrossRef] [PubMed]
- Gawal, P.M.; Subudhi, S. Advances and challenges in bio-based 2,3-BD downstream purification: A comprehensive review. Bioresour. Technol. Rep. 2023, 24, 101638. [Google Scholar] [CrossRef]
- Xu, Y.; Chu, H.; Gao, C.; Tao, F.; Zhou, Z.; Li, K.; Li, L.; Ma, C.; Xu, P. Systematic metabolic engineering of Escherichia coli for high-yield production of fuel bio-chemical 2,3-butanediol. Metab. Eng. 2014, 23, 22–33. [Google Scholar] [CrossRef] [PubMed]
- Orth, J.D.; Fleming, R.M.T.; Palsson, B. Reconstruction and Use of Microbial Metabolic Networks: The Core Escherichia coli Metabolic Model as an Educational Guide. EcoSal Plus 2010, 4, 1–47. [Google Scholar] [CrossRef] [PubMed]
- E. coli Core Model. 2016. Available online: http://bigg.ucsd.edu/models/e_coli_core (accessed on 1 April 2025).
- Tan, Z.; Chen, J.; Zhang, X. Systematic engineering of pentose phosphate pathway improves Escherichia coli succinate production. Biotechnol. Biofuels 2016, 9, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Saini, M.; Chen, M.H.; Chiang, C.J.; Chao, Y.P. Potential production platform of n-butanol in Escherichia coli. Metab. Eng. 2015, 27, 76–82. [Google Scholar] [CrossRef] [PubMed]

| Product | Knockouts | Cross-Feeding | Production Rate | Yield |
|---|---|---|---|---|
| 2,3-butanediol | ||||
| Butanol |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pearcy, N.; Twycross, J. Adapting OptCouple to Identify Strategies with Increased Product Yields in Community Cohorts of E. coli. Metabolites 2025, 15, 309. https://doi.org/10.3390/metabo15050309
Pearcy N, Twycross J. Adapting OptCouple to Identify Strategies with Increased Product Yields in Community Cohorts of E. coli. Metabolites. 2025; 15(5):309. https://doi.org/10.3390/metabo15050309
Chicago/Turabian StylePearcy, Nicole, and Jamie Twycross. 2025. "Adapting OptCouple to Identify Strategies with Increased Product Yields in Community Cohorts of E. coli" Metabolites 15, no. 5: 309. https://doi.org/10.3390/metabo15050309
APA StylePearcy, N., & Twycross, J. (2025). Adapting OptCouple to Identify Strategies with Increased Product Yields in Community Cohorts of E. coli. Metabolites, 15(5), 309. https://doi.org/10.3390/metabo15050309






