Robust Moiety Model Selection Using Mass Spectrometry Measured Isotopologues
Abstract
1. Introduction
2. Results
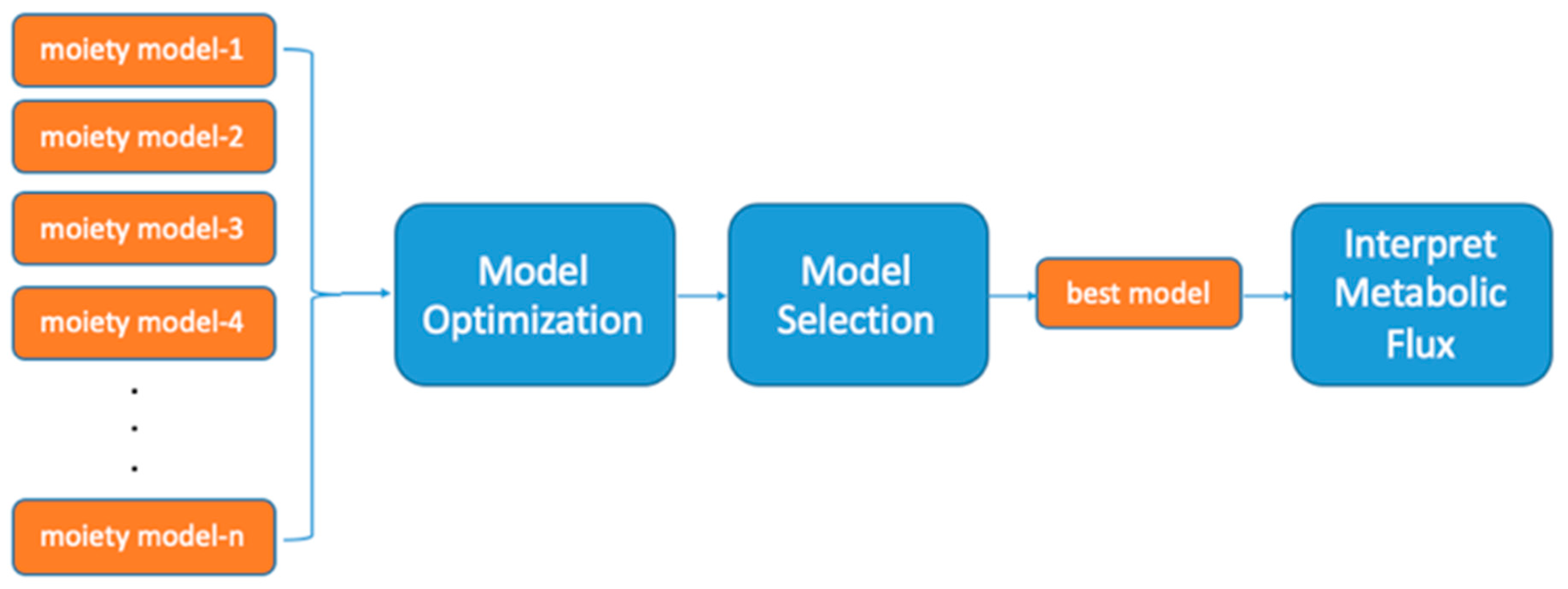
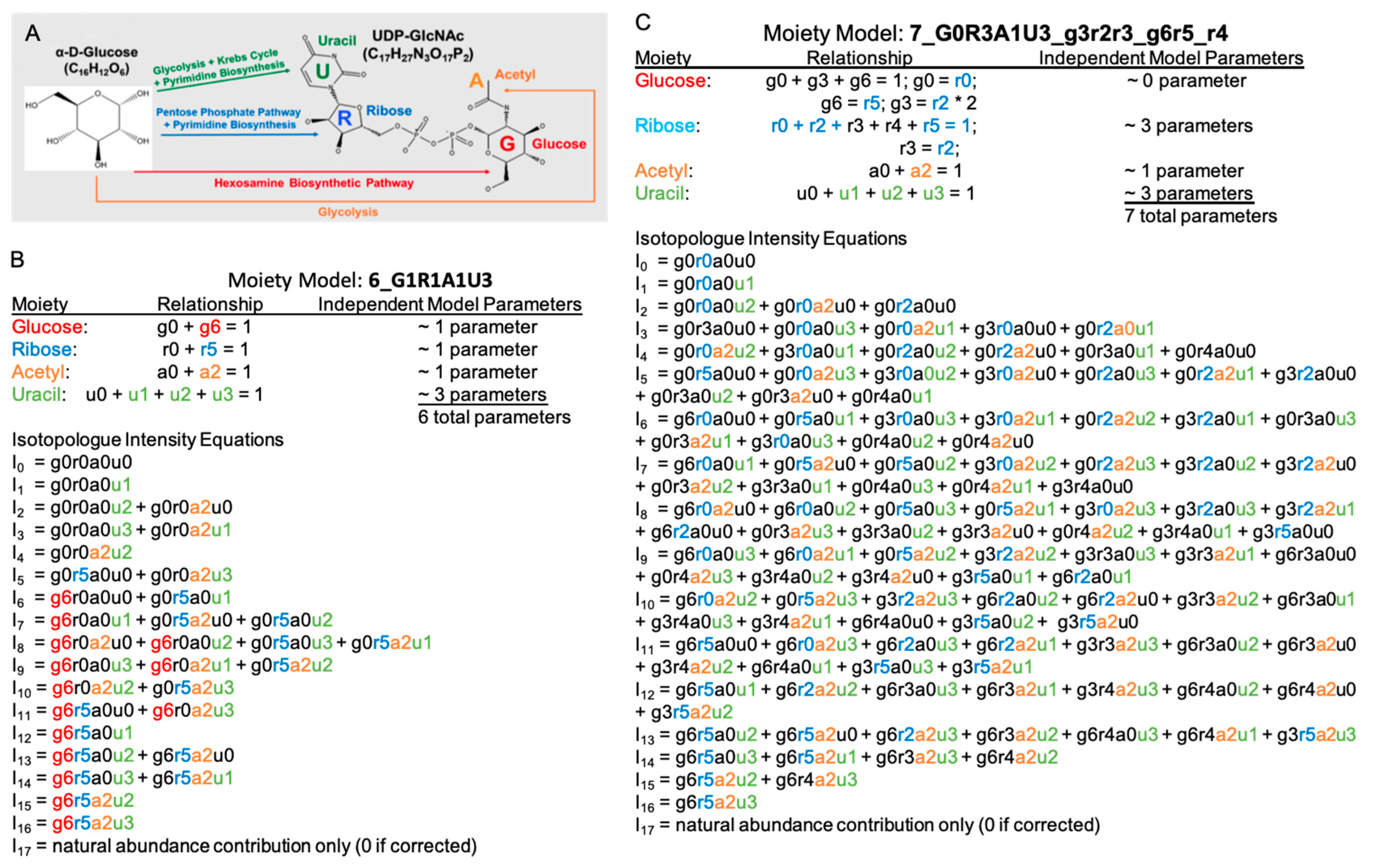
2.1. UDP-GlcNAc Moiety Model Construction
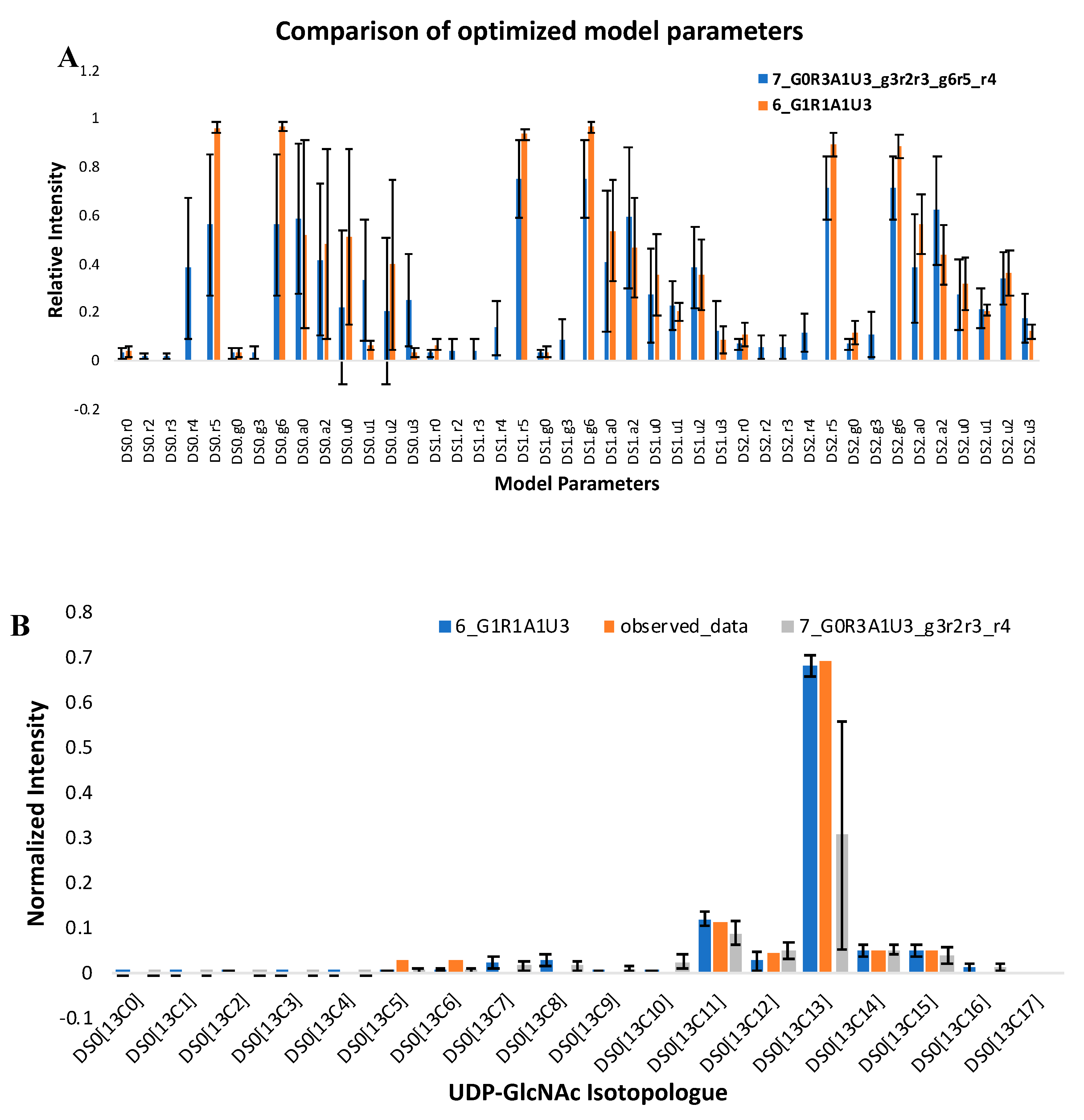
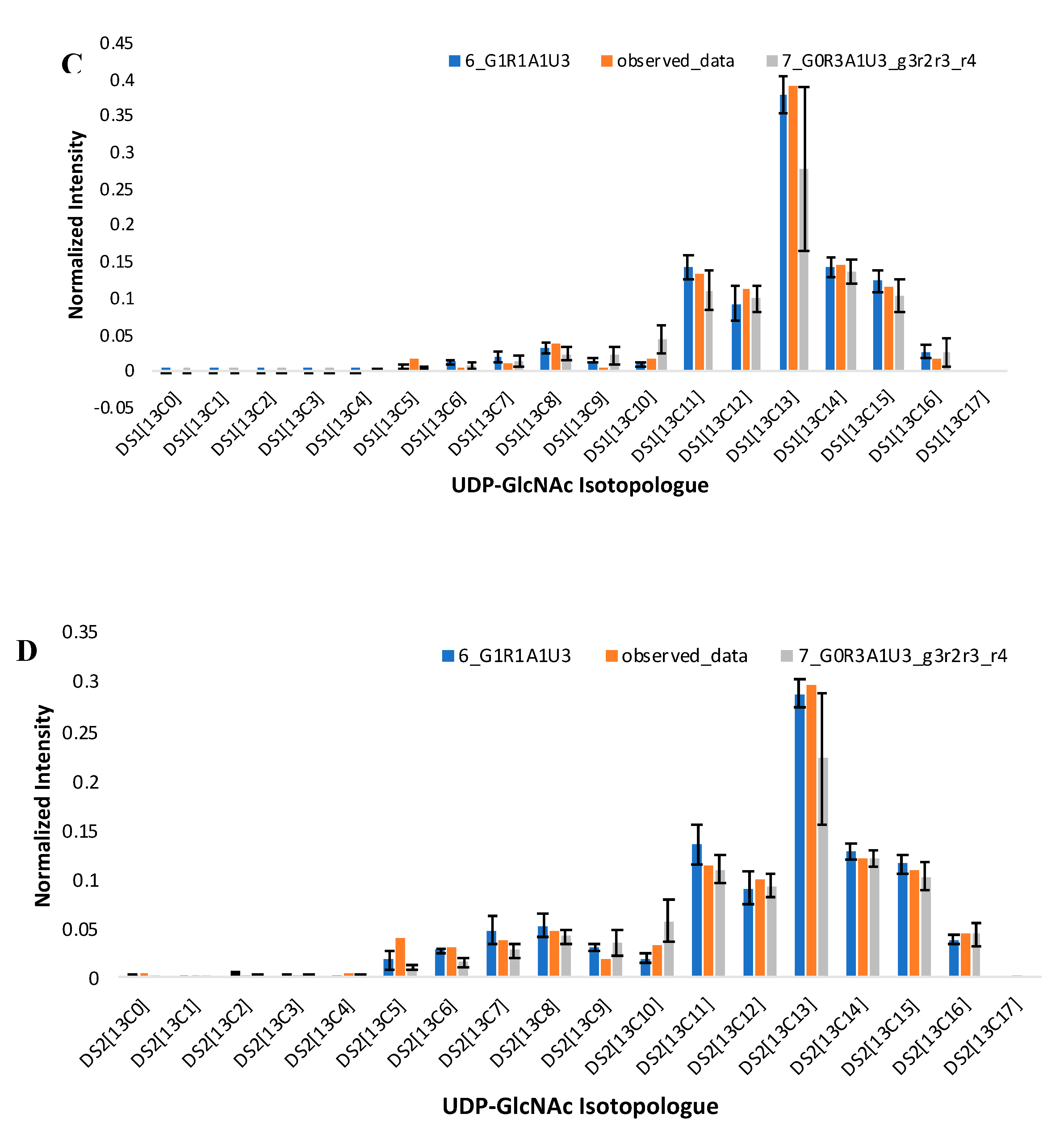
2.2. A Simple Comparison of Two Moiety Models
2.3. Effects of Optimization Method on Model Selection
2.4. Over-optimization Leads to Failure in Model Selection
2.5. Effects of Selection Criterion on Model Selection
2.6. Effects of Selection Criterion on Model Selection
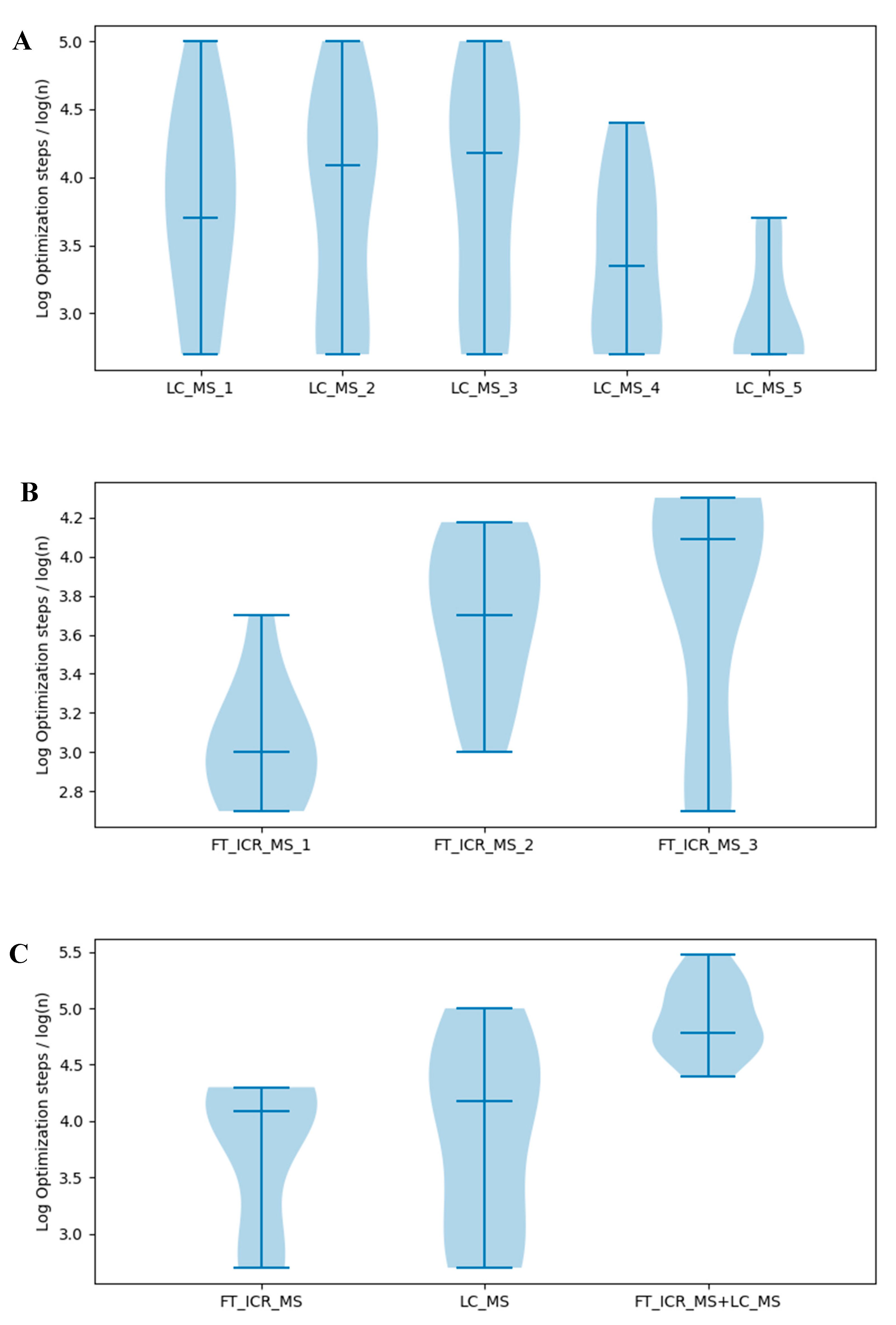
2.7. Effects of Information Quantity on Model Selection
3. Discussion
4. Materials and Methods
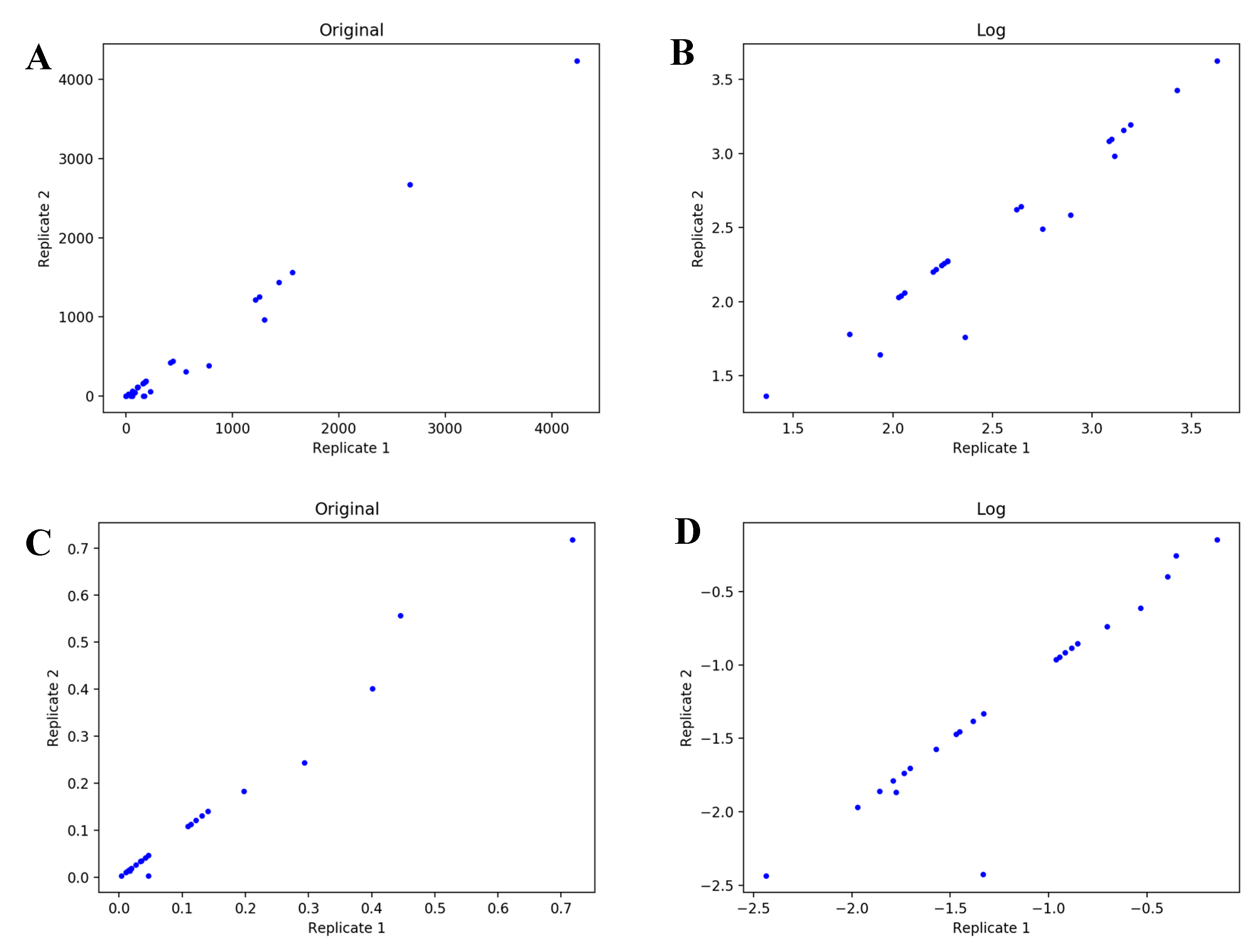
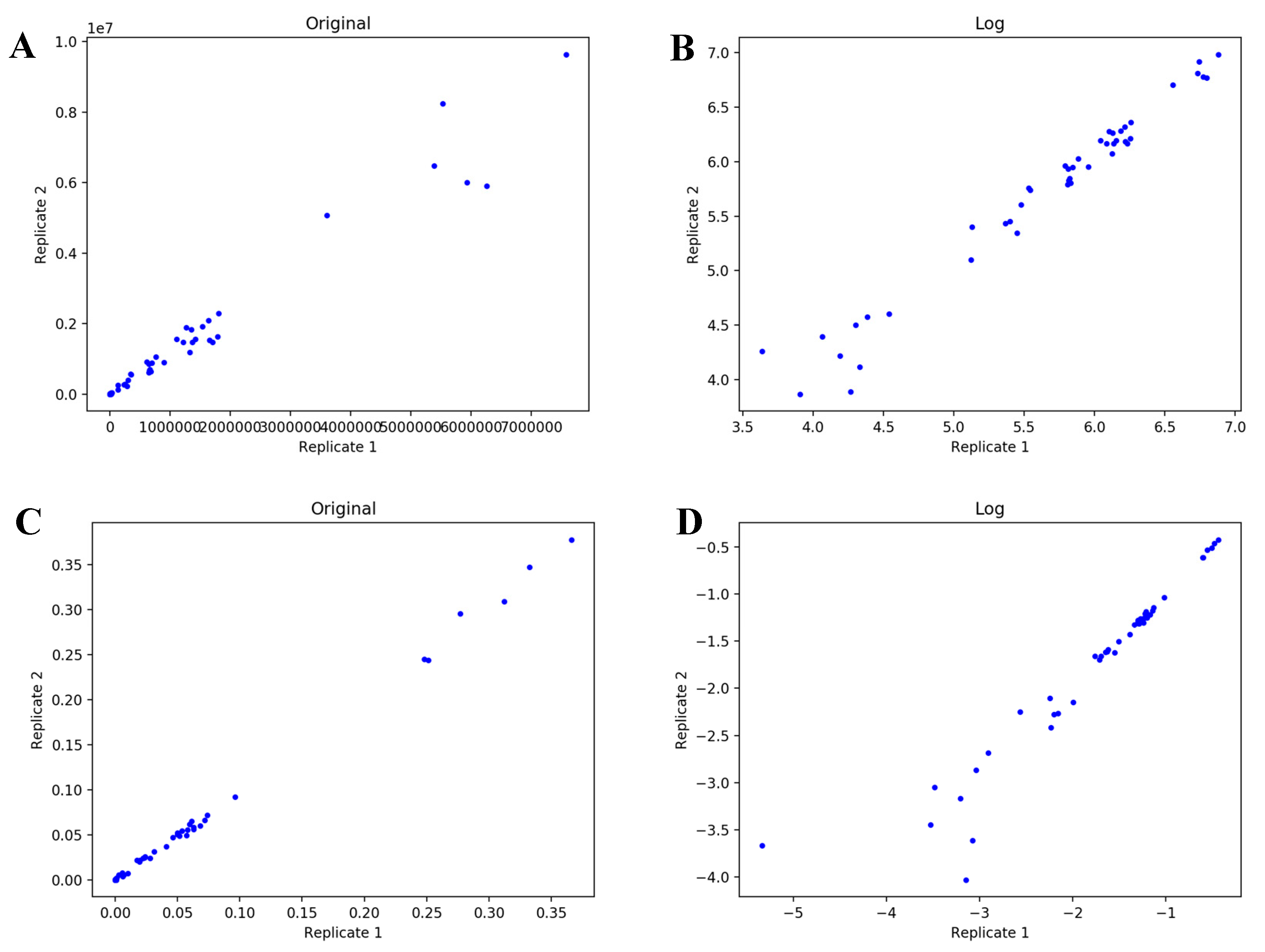
4.1. UDP-GlcNAc Time Course MS Isotopologue Datasets
4.2. Objective Functions
4.3. Optimization Methods
4.4. Model Selection Estimators
4.5. Computer Code and Software
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Data Availability
References
- Pavlova, N.N.; Thompson, C.B. Perspective The Emerging Hallmarks of Cancer Metabolism. Cell Metab. 2016, 23, 27–47. [Google Scholar] [CrossRef] [PubMed]
- Wishart, D.S. Applications of Metabolomics in Drug Discovery and Development. Drugs R D 2008, 9, 307–322. [Google Scholar] [CrossRef] [PubMed]
- DeBerardinis, R.J.; Thompson, C.B. Cellular Metabolism and Disease: What Do Metabolic Outliers Teach Us? Cell 2012, 148, 1132–1144. [Google Scholar] [CrossRef] [PubMed]
- Fan, T.W.-M.; Lorkiewicz, P.K.; Sellers, K.; Moseley, H.N.B.; Higashi, R.M.; Lane, A.N. Stable isotope-resolved metabolomics and applications for drug development. Pharmacol. Ther. 2012, 133, 366–391. [Google Scholar] [CrossRef] [PubMed]
- Young, J.D. INCA: A computational platform for isotopically non-stationary metabolic flux analysis. Bioinformatics 2014, 30, 1333–1335. [Google Scholar] [CrossRef] [PubMed]
- Sauer, U. Metabolic networks in motion: 13 C-based flux analysis. Mol. Syst. Biol. 2006, 2, 62. [Google Scholar] [CrossRef] [PubMed]
- Antoniewicz, M.R. Methods and advances in metabolic flux analysis: A mini-review. J. Ind. Microbiol. Biotechnol. 2015, 42, 317–325. [Google Scholar] [CrossRef] [PubMed]
- Antoniewicz, M.R.; Kelleher, J.K.; Stephanopoulos, G. Elementary metabolite units (EMU): A novel framework for modeling isotopic distributions. Metab. Eng. 2007, 9, 68–86. [Google Scholar] [CrossRef] [PubMed]
- Krumsiek, J.; Suhre, K.; Evans, A.M.; Mitchell, M.W.; Mohney, R.P.; Milburn, M.V.; Wägele, B.; Römisch-Margl, W.; Illig, T.; Adamski, J.; et al. Mining the Unknown: A Systems Approach to Metabolite Identification Combining Genetic and Metabolic Information. PLoS Genet. 2012, 8, e1003005. [Google Scholar] [CrossRef] [PubMed]
- Basu, S.; Duren, W.; Evans, C.R.; Burant, C.F.; Michailidis, G.; Karnovsky, A. Sparse network modeling and Metscape-based visualization methods for the analysis of large-scale metabolomics data. Bioinformatics 2017, 33, 1545–1553. [Google Scholar] [CrossRef] [PubMed]
- Wilken, S.E.; Swift, C.L.; Podolsky, I.A.; Lankiewicz, T.S.; Seppälä, S.; O’Malley, M.A. Linking ‘omics’ to function unlocks the biotech potential of non-model fungi. Curr. Opin. Syst. Biol. 2019, 14, 9–17. [Google Scholar] [CrossRef]
- Moseley, H.N.B. Error analysis and propagation in metabolomics data analysis. Comput. Struct. Biotechnol. J. 2013, 4, e201301006. [Google Scholar] [CrossRef] [PubMed]
- Jin, H.; Moseley, H.N.B. Moiety Modeling Framework for Deriving Moiety Abundances from Mass Spectrometry Measured Isotopologues. BMC Bioinform. 2019, 20, 524. [Google Scholar] [CrossRef] [PubMed]
- Moseley, H.N.; Lane, A.N.; Belshoff, A.C.; Higashi, R.M.; Fan, T.W. A novel deconvolution method for modeling UDP-N-acetyl-D-glucosamine biosynthetic pathways based on 13C mass isotopologue profiles under non-steady-state conditions. BMC Biol. 2011, 9, 37. [Google Scholar] [CrossRef] [PubMed]
- Verdegem, D.; Moseley, H.N.B.; Vermaelen, W.; Sanchez, A.A.; Ghesquière, B. MAIMS: A software tool for sensitive metabolic tracer analysis through the deconvolution of 13C mass isotopologue profiles of large composite metabolites. Metabolomics 2017, 13, 123. [Google Scholar] [CrossRef]
- Nash, S. Newton-Type Minimization via the Lanczos Method. SIAM J. Numer. Anal. 1984, 21, 770–788. [Google Scholar] [CrossRef]
- Boggs, P.T.; Tolle, J.W. Sequential Quadratic Programming. Acta Numer. 1995, 4, 1–51. [Google Scholar] [CrossRef]
- Zhu, C.; Byrd, R.H.; Lu, P.; Nocedal, J. Algorithm 778: L-BFGS-B: Fortran subroutines for large-scale bound-constrained optimization. ACM Trans. Math. Softw. 1997, 23, 550–560. [Google Scholar] [CrossRef]
- Akaike, H. Information Theory and an Extension of the Maximum Likelihood Principle. In Selected Papers of Hirotugu Akaike; Springer: New York, NY, USA, 1998; pp. 199–213. [Google Scholar] [CrossRef]
- Cavanaugh, J.E. Unifying the derivations for the Akaike and corrected Akaike information criteria. Stat. Probab. Lett. 1997, 33, 201–208. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
| Optimization Method | Loss Value | AICc | Selected Model |
|---|---|---|---|
| SAGA | 0.469 | −401.760 | Expert-derived model |
| SLSQP | 0.320 | −408.341 | 7_G2R1A1U3_g5 |
| L-BFGS-B | 0.763 | −342.164 | Expert-derived model |
| TNC | 0.870 | −327.344 | Expert-derived model |
| Optimization Method | Loss Value | AICc | Selected Model | Stop Criterion |
|---|---|---|---|---|
| SLSQP | 0.320 | −408.341 | 7_G2R1A1U3_g5 | ‘ftol’: 1e-06 |
| SLSQP | 0.514 | −393.934 | Expert-derived model | ‘ftol’: 1e-05 |
| Optimization Steps | Loss Value | AICc | Selected Model |
|---|---|---|---|
| 500 | 2.070 | −219.488 | Expert-derived model |
| 1000 | 1.754 | −235.728 | Expert-derived model |
| 2000 | 1.377 | −260.654 | Expert-derived model |
| 5000 | 0.941 | −305.651 | Expert-derived model |
| 10000 | 0.664 | −375.192 | Expert-derived model |
| 25000 | 0.469 | −401.760 | Expert-derived model |
| 50000 | 0.408 | −414.737 | Expert-derived model |
| 75000 | 0.328 | −418.228 | 7_G2R1A1U3_g5 |
| 100000 | 0.316 | −424.924 | 7_G1R2A1U3_r4 |
| Models | AICc | Rank | AIC | Rank | BIC | Rank |
|---|---|---|---|---|---|---|
| Expert-derived model | −401.7597 | 1 | −421.3026 | 1 | −385.5009 | 1 |
| 7_G1R1A2U3 | −384.3075 | 2 | −413.1825 | 2 | −371.4139 | 2 |
| 7_G2R1A1U3_g5 | −381.2868 | 3 | −410.1618 | 3 | −368.3932 | 3 |
| 7_G1R2A1U3_r3 | −379.2657 | 4 | −408.1407 | 4 | −366.3720 | 4 |
| 7_G1R2A1U3_r4 | −378.8969 | 5 | −407.7719 | 5 | −366.0033 | 5 |
| 7_G2R1A1U3_g4 | −375.9538 | 6 | −404.8288 | 6 | −363.0601 | 6 |
| 9_G2R2A2U3_r2r3_g5 | −254.4087 | 37 | −312.5625 | 36 | −258.8599 | 37 |
| 9_G2R2A2U3_r2r3_g3 | −248.2277 | 38 | −306.3815 | 38 | −252.6789 | 38 |
| 9_G2R2A2U3_r2r3_g2 | −242.9984 | 39 | −301.1522 | 39 | −247.4497 | 39 |
| 9_G2R2A2U3_r2r3_g1 | −242.4110 | 40 | −300.5648 | 40 | −246.8623 | 40 |
| 7_G0R3A1U3_g3r2r3_g6r5_r4 | −226.7271 | 41 | −255.6021 | 41 | −213.8334 | 41 |
| Optimization Steps | Loss Value | AICc | Selected Model |
|---|---|---|---|
| 500 | 1.045 | −293.540 | Expert-derived model |
| 1000 | 0.819 | −330.411 | Expert-derived model |
| 2000 | 0.651 | −361.038 | Expert-derived model |
| 5000 | 0.459 | −408.167 | Expert-derived model |
| 10000 | 0.392 | −422.516 | Expert-derived model |
| 15000 | 0.359 | −431.276 | Expert-derived model |
| 20000 | 0.290 | −434.468 | 7_G1R1A2U3 |
| 25000 | 0.285 | −436.909 | 7_G1R1A2U3 |
| Optimization Steps | Loss Value | AICc | Selected Model |
|---|---|---|---|
| 500 | 0.085 | −298.516 | Expert-derived model |
| 1000 | 0.047 | −330.096 | Expert-derived model |
| 2000 | 0.023 | −367.279 | Expert-derived model |
| 5000 | 0.011 | −404.509 | Expert-derived model |
| 10000 | 0.007 | −425.695 | Expert-derived model |
| 15000 | 0.005 | −429.869 | 7_G2R1A1U3_g5 |
| 20000 | 0.005 | −435.348 | 7_G1R2A1U3_r4 |
| Optimization Steps | Loss Value | Selected Model |
|---|---|---|
| 500 | −345.559 | Expert-derived model |
| 1000 | −371.852 | Expert-derived model |
| 2000 | −398.570 | Expert-derived model |
| 5000 | −436.582 | Expert-derived model |
| 10000 | −458.064 | 7_G1R1A2U3 |
| 15000 | −467.960 | 7_G2R1A1U3_g5 |
| Optimization Steps | Loss Value | AICc | Selected Model |
|---|---|---|---|
| 500 | 31.647 | −221.501 | Expert-derived model |
| 1000 | 29.628 | −223.363 | Expert-derived model |
| 2000 | 28.164 | −224.330 | Expert-derived model |
| 5000 | 27.096 | −225.911 | Expert-derived model |
| 10000 | 26.631 | −227.499 | Expert-derived model |
| 15000 | 26.469 | −227.690 | Expert-derived model |
| 20000 | 26.398 | −227.780 | Expert-derived model |
| 25000 | 26.271 | −228.178 | Expert-derived model |
| 50000 | 26.126 | −228.892 | Expert-derived model |
| 100000 | 25.949 | −228.926 | Expert-derived model |
| 150000 | 25.865 | −229.926 | Expert-derived model |
| 250000 | 25.777 | −230.232 | Expert-derived model |
| Objective Function | Equation |
|---|---|
| Absolute difference | Σ|In,obs – In,calc| |
| Absolute difference of logs | Σ|log(In,obs) – log(In,calc)| |
| Square difference | Σ(In,obs – In,calc)2 |
| Difference of AIC |
| Selection Criterion | Equation |
|---|---|
| Akaike Information Criterion (AIC) | |
| Sample size corrected AIC (AICc) | |
| Bayesian Information Criterion (BIC) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, H.; Moseley, H.N.B. Robust Moiety Model Selection Using Mass Spectrometry Measured Isotopologues. Metabolites 2020, 10, 118. https://doi.org/10.3390/metabo10030118
Jin H, Moseley HNB. Robust Moiety Model Selection Using Mass Spectrometry Measured Isotopologues. Metabolites. 2020; 10(3):118. https://doi.org/10.3390/metabo10030118
Chicago/Turabian StyleJin, Huan, and Hunter N.B. Moseley. 2020. "Robust Moiety Model Selection Using Mass Spectrometry Measured Isotopologues" Metabolites 10, no. 3: 118. https://doi.org/10.3390/metabo10030118
APA StyleJin, H., & Moseley, H. N. B. (2020). Robust Moiety Model Selection Using Mass Spectrometry Measured Isotopologues. Metabolites, 10(3), 118. https://doi.org/10.3390/metabo10030118






