Extraction and Integration of Genetic Networks from Short-Profile Omic Data Sets
Abstract
1. Introduction
2. Materials and Methods
2.1. Similarity Measures for Short Omic Profiles
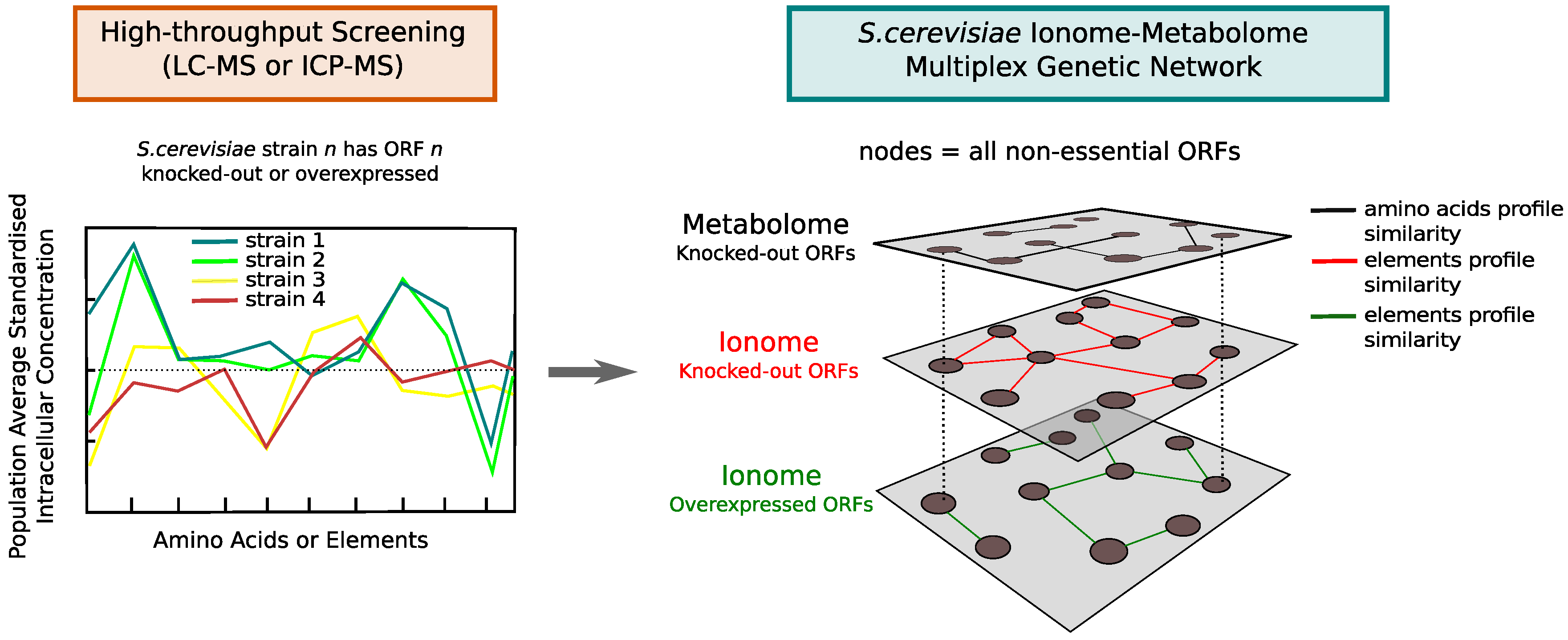
2.2. Omic Benchmark Data Sets
- (1)
- The yeast ionome knock-out (ko) data set contains population-average intracellular concentrations of 14 different elements (Ca, Cd, Co, Cu, Fe, K, Mg, Mn, Mo, Na, Ni, P, S, and Zn) quantified by means of inductively coupled plasma–mass spectrometry (ICP–MS) for a library of 4944 S. cerevisiae haploid mutant strains having a single non-essential open reading frame knocked out.This data set includes a total of 26,976 samples measured in 305 different plates. Most of the strains were measured in replicates of four (4207), 684 strains in replicates of eight, 48 strains in replicates of 12, and two strains in replicates of 16. Additionally, three control strains present in multiple trays were included in our analysis: YDL227C, 1620 replicates; YLR396C, 1224 replicates; YPR065W, 1224 replicates.
- (2)
- The yeast ionome overexpression (oe) data set contains population-average intracellular concentrations of 17 different elements (As, Ca, Cd, Cl, Co, Cu, Fe, K, Mg, Mn, Mo, Na, Ni, P, S, Se, and Zn) quantified by means of inductively coupled plasma–mass spectrometry (ICP–MS) for a library of 5718 S. cerevisiae haploid mutant strains having a single essential or non-essential open reading frame overexpressed. This data set includes a total of 24,060 samples measured in 310 different plates. Most of the strains were measured in replicates of four (5426), 287 strains in replicates of eight, and five strains in replicates of 12.
- (3)
- Yeast metabolome aa (amino acid profile of non-essential ORF knock-out mutants [7]).The yeast metabolome (aa) data set contains population-average intracellular concentrations of 19 different amino acids (A, D, E, F, G, H, I, K, L, M, N, P, Q, R, S, T, V, W, Y) quantified by means of liquid chromatography–mass spectrometry (LC–MS) for a library of 4475 S. cerevisiae haploid mutant strains having a single non-essential open reading frame knocked out. This data set includes a total of 4653 samples measured in 12 different batches. Most of the strains are associated with a single sample (4324), 128 strains have two replicates, 19 strains have three replicates, and four strains have four replicates.
2.3. Genetic Networks Inference
- Score computation: we compute all pairwise similarity scores between the N genes of a given data set with each similarity measure of interest.
- Score ranking: we rank in descending value order each set of scores computed with a different similarity measure.
- Relevance network extraction: we retain the top-n ranked scores in each set to define for each similarity measure a genetic association network of N nodes and n links; the links correspond to the n highest values in the score rank statistic.
2.4. Multiplex Integration of Genetic Networks
3. Results
- By increasing the relevance threshold n and considering more and more links in the inferred networks, tends to generate faster than and than a giant component whose node size is a finite fraction of the genome size N (yellow curves in top and middle panels, the number of connected components goes to one, and the size of the LC increases asymptotically to N), with a relatively (comparable to and ) low level of clustering of the nodes (bottom panels).
- On the other hand, tends to aggregate genes in few connected components or modules (purple curves, top panels) which grow in parallel with relatively comparable sizes (middle panels, the size of the LC is far below N), and are highly clustered (purple marks in bottom panels, high clustering coefficient).
3.1. Retrieval of Known Biological Information
- (1)
- Protein–Protein Interactions (PPI) from STRING [48] (v11, database scores only).
- (2)
- BIOGRID [49] (v3.4.158, genetic interactions only).
- (3)
- Protein Complex Consensus [50] (co-occurrence in protein complexes).
- (4)
- KEGG Biological Pathways [51] (Release 90.1, co-occurrence in metabolic pathways).
- (5)
- Yeast Net Gold Standard [52] (v3, Gene Ontology based gold-standard associations).
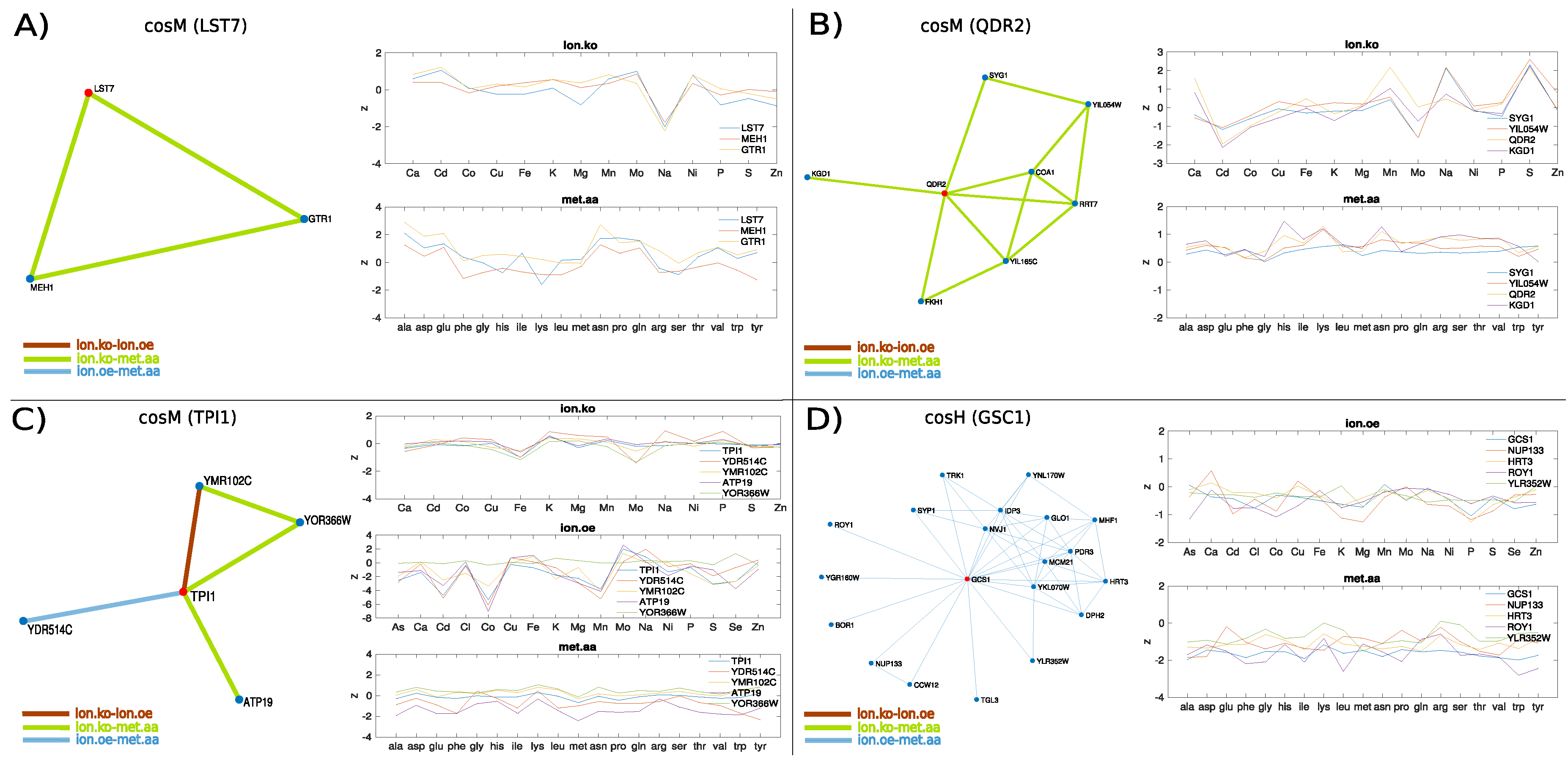
3.2. The Ionome–Metabolome Multiplex Genetic Network of the Yeast S. cerevisiae
4. Discussion
Author Contributions
Funding
Conflicts of Interest
Data and Codes Availability
Appendix A. Mahalanobis Vector Space
Appendix B. Data Processing Pipeline
| Outliers | Samples Removed | Mutants Removed | % Samples Removed | |
|---|---|---|---|---|
| Ionome (KO) | 211 | 166 | 0 | 0.62 |
| Ionome (OE) | 1218 | 271 | 1 | 1.13 |
| Metabolome (AA) | 136 | 48 | 44 | 1.03% |



Appendix C. Synthetic Data Sets
- Step (1): We constructed a square correlation matrix A with ones on the main diagonal and the elements of the upper triangular matrix sampled uniformly at random within a certain correlation interval (e.g., if we want high correlation level, within the interval [0.9,1]). The elements of the lower triangular matrix are imputed from the upper triangular matrix so to have A symmetric.
- Step (2): As the eigenvalues of A are required to be greater than zero, we computed S as the nearest positive definite to the correlation matrix A.
- Step (3): We derived the lower triangular L matrix of S via Cholesky decomposition so to have S = ′.



Appendix D. False Positive Rate of Genetic Associations
| PCC | cos | cosM | cosH | |
|---|---|---|---|---|
| 1 K Top Associations | p-value (max FPR) | |||
| Ionome KO | 0.000205983 | |||
| Ionome OE | 0 | |||
| Meatbolome AA | 0 | 0 | ||
| 10 K Top Associations | p-value (max FPR) | |||
| Ionome KO | 0.00028 | 0.000265 | 0.000729 | 0.000513 |
| Ionome OE | 0.00011 | 0.000115 | 0.000557 | 0.000006 |
| Metabolome AA | 0 | 0.000408 | 0 | |
| 100 K Top Associations | p-value (max FPR) | |||
| Ionome KO | 0.00408 | 0.00337 | 0.00756 | 0.00285 |
| Ionome OE | 0.00239 | 0.00142 | 0.00555 | 0.00071 |
| Metabolome AA | 0.00012 | 0.00795 | 0 |

References
- Warringer, J.; Ericson, E.; Fernandez, L.; Nerman, O.; Blomberg, A. High-resolution yeast phenomics resolves different physiological features in the saline response. Proc. Natl. Acad. Sci. USA 2003, 100, 15724–15729. [Google Scholar] [CrossRef] [PubMed]
- King, R.D.; Whelan, K.E.; Jones, F.M.; Reiser, P.G.; Bryant, C.H.; Muggleton, S.H.; Kell, D.B.; Oliver, S.G. Functional genomic hypothesis generation and experimentation by a robot scientist. Nature 2004, 427, 247. [Google Scholar] [CrossRef] [PubMed]
- Prelich, G. Gene overexpression: Uses, mechanisms, and interpretation. Genetics 2012, 190, 841–854. [Google Scholar] [CrossRef] [PubMed]
- Kemmeren, P.; Sameith, K.; van de Pasch, L.A.; Benschop, J.J.; Lenstra, T.L.; Margaritis, T.; O’Duibhir, E.; Apweiler, E.; van Wageningen, S.; Ko, C.W.; et al. Large-scale genetic perturbations reveal regulatory networks and an abundance of gene-specific repressors. Cell 2014, 157, 740–752. [Google Scholar] [CrossRef] [PubMed]
- Bino, R.J.; Hall, R.D.; Fiehn, O.; Kopka, J.; Saito, K.; Draper, J.; Nikolau, B.J.; Mendes, P.; Roessner-Tunali, U.; Beale, M.H.; et al. Potential of metabolomics as a functional genomics tool. Trends Plant Sci. 2004, 9, 418–425. [Google Scholar] [CrossRef] [PubMed]
- Peng, B.; Li, H.; Peng, X.X. Functional metabolomics: From biomarker discovery to metabolome reprogramming. Protein Cell 2015, 6, 628–637. [Google Scholar] [CrossRef] [PubMed]
- Mülleder, M.; Calvani, E.; Alam, M.T.; Wang, R.K.; Eckerstorfer, F.; Zelezniak, A.; Ralser, M. Functional metabolomics describes the yeast biosynthetic regulome. Cell 2016, 167, 553–565. [Google Scholar] [CrossRef] [PubMed]
- Salt, D.E.; Baxter, I.; Lahner, B. Ionomics and the study of the plant ionome. Annu. Rev. Plant Biol. 2008, 59, 709–733. [Google Scholar] [CrossRef]
- Baxter, I. Ionomics: The functional genomics of elements. Brief. Funct. Genom. 2010, 9, 149–156. [Google Scholar] [CrossRef]
- Nielsen, T.D.; Jensen, F.V. Bayesian Networks and Decision Graphs; Springer Science & Business Media: New York, NY, USA, 2009. [Google Scholar]
- Friedman, N.; Linial, M.; Nachman, I.; Pe’er, D. Using Bayesian networks to analyze expression data. J. Comput. Biol. 2000, 7, 601–620. [Google Scholar] [CrossRef] [PubMed]
- Schäfer, J.; Strimmer, K. A shrinkage approach to large-scale covariance matrix estimation and implications for functional genomics. Stat. Appl. Genet. Mol. Biol. 2005, 4. [Google Scholar] [CrossRef] [PubMed]
- Krumsiek, J.; Suhre, K.; Illig, T.; Adamski, J.; Theis, F.J. Gaussian graphical modeling reconstructs pathway reactions from high-throughput metabolomics data. BMC Syst. Biol. 2011, 5, 21. [Google Scholar] [CrossRef]
- Martínez, C.A.; Khare, K.; Rahman, S.; Elzo, M.A. Modeling correlated marker effects in genome-wide prediction via Gaussian concentration graph models. J. Theor. Biol. 2018, 437, 67–78. [Google Scholar] [CrossRef] [PubMed]
- Liang, S.; Fuhrman, S.; Somogyi, R. Reveal, a general reverse engineering algorithm for inference of genetic network architectures. In Proceedings of the Pacific Symposium on Biocomputing, Maui, HI, USA, 4–9 January 1998. [Google Scholar]
- Butte, A.J.; Kohane, I.S. Mutual information relevance networks: Functional genomic clustering using pairwise entropy measurements. In Biocomputing 2000; World Scientific: Singapore, 1999; pp. 418–429. [Google Scholar]
- Butte, A.J.; Tamayo, P.; Slonim, D.; Golub, T.R.; Kohane, I.S. Discovering functional relationships between RNA expression and chemotherapeutic susceptibility using relevance networks. Proc. Natl. Acad. Sci. USA 2000, 97, 12182–12186. [Google Scholar] [CrossRef] [PubMed]
- Werhli, A.V.; Grzegorczyk, M.; Husmeier, D. Comparative evaluation of reverse engineering gene regulatory networks with relevance networks, graphical Gaussian models and Bayesian networks. Bioinformatics 2006, 22, 2523–2531. [Google Scholar] [CrossRef]
- Newman, M. Networks; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Barabási, A.L. Network Science; Cambridge University Press: Oxford, UK, 2016. [Google Scholar]
- Latora, V.; Nicosia, V.; Russo, G. Complex Networks: Principles, Methods and Applications; Cambridge University Press: Oxford, UK, 2017. [Google Scholar]
- Bravais, A. Analyse Mathématique sur les Probabilités des Erreurs de Situation d’un Point; Impr. Royale: Paris, France, 1844. [Google Scholar]
- Pearson, K. VII. Note on regression and inheritance in the case of two parents. Proc. R. Soc. Lond. 1895, 58, 240–242. [Google Scholar]
- Havlicek, L.L.; Peterson, N.L. Robustness of the Pearson correlation against violations of assumptions. Percept. Mot. Skills 1976, 43, 1319–1334. [Google Scholar] [CrossRef]
- Van Eck, N.J.; Waltman, L. Appropriate similarity measures for author co-citation analysis. J. Am. Soc. Inf. Sci. Technol. 2008, 59, 1653–1661. [Google Scholar] [CrossRef]
- Egghe, L.; Leydesdorff, L. The relation between Pearson’s correlation coefficient r and Salton’s cosine measure. J. Am. Soc. Inf. Sci. Technol. 2009, 60, 1027–1036. [Google Scholar] [CrossRef]
- Hauke, J.; Kossowski, T. Comparison of values of Pearson’s and Spearman’s correlation coefficients on the same sets of data. Quaest. Geogr. 2011, 30, 87–93. [Google Scholar] [CrossRef]
- Chandra, M.P. On the generalised distance in statistics. Proceedings of the National Institute of Sciences of India 1936, 2, 49–55. [Google Scholar]
- Patil, S.A.; Deore, P.J. Principle Component Analysis (PCA) and Linear Discriminant Analysis (LDA) based Face Recognition. Int. J. Comput. Appl. 2014, 975, 8887. [Google Scholar]
- Jones, W.P.; Furnas, G.W. Pictures of relevance: A geometric analysis of similarity measures. J. Am. Soc. Inf. Sci. 1987, 38, 420–442. [Google Scholar] [CrossRef]
- iHUB. Available online: https://www.ionomicshub.org/home/PiiMS (accessed on 1 January 2019).
- Baxter, I.; Ouzzani, M.; Orcun, S.; Kennedy, B.; Jandhyala, S.S.; Salt, D.E. Purdue ionomics information management system. An integrated functional genomics platform. Plant Physiol. 2007, 143, 600–611. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Danku, J.M.; Gumaelius, L.; Baxter, I.; Salt, D.E. A high-throughput method for Saccharomyces cerevisiae (yeast) ionomics. J. Anal. At. Spectrom. 2009, 24, 103–107. [Google Scholar] [CrossRef]
- Yu, D.; Danku, J.M.; Baxter, I.; Kim, S.; Vatamaniuk, O.K.; Vitek, O.; Ouzzani, M.; Salt, D.E. High-resolution genome-wide scan of genes, gene-networks and cellular systems impacting the yeast ionome. BMC Genom. 2012, 13, 623. [Google Scholar] [CrossRef] [PubMed]
- Boccaletti, S.; Bianconi, G.; Criado, R.; Del Genio, C.I.; Gómez-Gardenes, J.; Romance, M.; Sendina-Nadal, I.; Wang, Z.; Zanin, M. The structure and dynamics of multilayer networks. Phys. Rep. 2014, 544, 1–122. [Google Scholar] [CrossRef]
- Kivelä, M.; Arenas, A.; Barthelemy, M.; Gleeson, J.P.; Moreno, Y.; Porter, M.A. Multilayer networks. J. Complex Netw. 2014, 2, 203–271. [Google Scholar] [CrossRef]
- Battiston, F.; Nicosia, V.; Latora, V. Structural measures for multiplex networks. Phys. Rev. E 2014, 89, 032804. [Google Scholar] [CrossRef]
- Menichetti, G.; Remondini, D.; Panzarasa, P.; Mondragón, R.J.; Bianconi, G. Weighted multiplex networks. PLoS ONE 2014, 9, e97857. [Google Scholar] [CrossRef] [PubMed]
- Bianconi, G. Statistical mechanics of multiplex networks: Entropy and overlap. Phys. Rev. E 2013, 87, 062806. [Google Scholar] [CrossRef] [PubMed]
- Iacovacci, J.; Rahmede, C.; Arenas, A.; Bianconi, G. Functional multiplex pagerank. EPL (Europhys. Lett.) 2016, 116, 28004. [Google Scholar] [CrossRef]
- Bollobás, B.; Béla, B. Random Graphs; Number 73; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Molloy, M.; Reed, B. A critical point for random graphs with a given degree sequence. Random Struct. Algorithms 1995, 6, 161–180. [Google Scholar] [CrossRef]
- Holland, P.W.; Leinhardt, S. Transitivity in structural models of small groups. Small Group Res. 1971, 2, 107–124. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ?small-world?networks. Nature 1998, 393, 440. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E. Modularity and community structure in networks. Proc. Natl. Acad. Sci. USA 2006, 103, 8577–8582. [Google Scholar] [CrossRef] [PubMed]
- Bianconi, G.; Darst, R.K.; Iacovacci, J.; Fortunato, S. Triadic closure as a basic generating mechanism of communities in complex networks. Phys. Rev. E 2014, 90, 042806. [Google Scholar] [CrossRef] [PubMed]
- Battiston, F.; Iacovacci, J.; Nicosia, V.; Bianconi, G.; Latora, V. Emergence of multiplex communities in collaboration networks. PLoS ONE 2016, 11, e0147451. [Google Scholar] [CrossRef]
- Szklarczyk, D.; Gable, A.L.; Lyon, D.; Junge, A.; Wyder, S.; Huerta-Cepas, J.; Simonovic, M.; Doncheva, N.T.; Morris, J.H.; Bork, P.; et al. STRING v11: Protein–protein association networks with increased coverage, supporting functional discovery in genome-wide experimental datasets. Nucleic Acids Res. 2018, 47, D607–D613. [Google Scholar] [CrossRef]
- Stark, C.; Breitkreutz, B.J.; Reguly, T.; Boucher, L.; Breitkreutz, A.; Tyers, M. BioGRID: A general repository for interaction datasets. Nucleic Acids Res. 2006, 34, D535–D539. [Google Scholar] [CrossRef]
- Benschop, J.J.; Brabers, N.; van Leenen, D.; Bakker, L.V.; van Deutekom, H.W.; van Berkum, N.L.; Apweiler, E.; Lijnzaad, P.; Holstege, F.C.; Kemmeren, P. A consensus of core protein complex compositions for Saccharomyces cerevisiae. Mol. Cell 2010, 38, 916–928. [Google Scholar] [CrossRef]
- Kanehisa, M.; Goto, S. KEGG: Kyoto encyclopedia of genes and genomes. Nucleic Acids Res. 2000, 28, 27–30. [Google Scholar] [CrossRef]
- Kim, H.; Shin, J.; Kim, E.; Kim, H.; Hwang, S.; Shim, J.E.; Lee, I. YeastNet v3: A public database of data-specific and integrated functional gene networks for Saccharomyces cerevisiae. Nucleic Acids Res. 2013, 42, D731–D736. [Google Scholar] [CrossRef] [PubMed]
- Cherry, J.M.; Adler, C.; Ball, C.; Chervitz, S.A.; Dwight, S.S.; Hester, E.T.; Jia, Y.; Juvik, G.; Roe, T.; Schroeder, M.; et al. SGD: Saccharomyces genome database. Nucleic Acids Res. 1998, 26, 73–79. [Google Scholar] [CrossRef] [PubMed]
- Eide, D.J.; Clark, S.; Nair, T.M.; Gehl, M.; Gribskov, M.; Guerinot, M.L.; Harper, J.F. Characterization of the yeast ionome: A genome-wide analysis of nutrient mineral and trace element homeostasis in Saccharomyces cerevisiae. Genome Biol. 2005, 6, R77. [Google Scholar] [CrossRef] [PubMed]
- Péli-Gulli, M.P.; Sardu, A.; Panchaud, N.; Raucci, S.; De Virgilio, C. Amino acids stimulate TORC1 through Lst4-Lst7, a GTPase-activating protein complex for the Rag family GTPase Gtr2. Cell Rep. 2015, 13, 1–7. [Google Scholar] [CrossRef]
- Tarassov, K.; Messier, V.; Landry, C.R.; Radinovic, S.; Molina, M.M.S.; Shames, I.; Malitskaya, Y.; Vogel, J.; Bussey, H.; Michnick, S.W. An in vivo map of the yeast protein interactome. Science 2008, 320, 1465–1470. [Google Scholar] [CrossRef] [PubMed]
- Zoncu, R.; Bar-Peled, L.; Efeyan, A.; Wang, S.; Sancak, Y.; Sabatini, D.M. mTORC1 senses lysosomal amino acids through an inside-out mechanism that requires the vacuolar H+-ATPase. Science 2011, 334, 678–683. [Google Scholar] [CrossRef]
- Wang, S.; Tsun, Z.Y.; Wolfson, R.L.; Shen, K.; Wyant, G.A.; Plovanich, M.E.; Yuan, E.D.; Jones, T.D.; Chantranupong, L.; Comb, W.; et al. Lysosomal amino acid transporter SLC38A9 signals arginine sufficiency to mTORC1. Science 2015, 347, 188–194. [Google Scholar] [CrossRef]
- Chen, E.Y.; Tan, C.M.; Kou, Y.; Duan, Q.; Wang, Z.; Meirelles, G.V.; Clark, N.R.; Ma’ayan, A. Enrichr: Interactive and collaborative HTML5 gene list enrichment analysis tool. BMC Bioinform. 2013, 14, 128. [Google Scholar] [CrossRef]
- Brengues, M.; Teixeira, D.; Parker, R. Movement of eukaryotic mRNAs between polysomes and cytoplasmic processing bodies. Science 2005, 310, 486–489. [Google Scholar] [CrossRef]
- Wang, C.; Schmich, F.; Srivatsa, S.; Weidner, J.; Beerenwinkel, N.; Spang, A. Context-dependent deposition and regulation of mRNAs in P-bodies. eLife 2018, 7, e29815. [Google Scholar] [CrossRef]
- Miller, J.E.; Zhang, L.; Jiang, H.; Li, Y.; Pugh, B.F.; Reese, J.C. Genome-wide mapping of decay factor–mrna interactions in yeast identifies nutrient-responsive transcripts as targets of the deadenylase ccr4. G3 Genes Genomes Genet. 2018, 8, 315–330. [Google Scholar] [CrossRef] [PubMed]
- Grüning, N.M.; Rinnerthaler, M.; Bluemlein, K.; Mülleder, M.; Wamelink, M.M.; Lehrach, H.; Jakobs, C.; Breitenbach, M.; Ralser, M. Pyruvate kinase triggers a metabolic feedback loop that controls redox metabolism in respiring cells. Cell Metab. 2011, 14, 415–427. [Google Scholar] [CrossRef] [PubMed]
- Khatri, I.; Akhtar, A.; Kaur, K.; Tomar, R.; Prasad, G.S.; Ramya, T.N.C.; Subramanian, S. Gleaning evolutionary insights from the genome sequence of a probiotic yeast Saccharomyces boulardii. Gut Pathog. 2013, 5, 30. [Google Scholar] [CrossRef]
- Ma, M.; Liu, L.Z. Quantitative transcription dynamic analysis reveals candidate genes and key regulators for ethanol tolerance in Saccharomyces cerevisiae. BMC Microbiol. 2010, 10, 169. [Google Scholar] [CrossRef]
- Hutchins, A.P.; Liu, S.; Diez, D.; Miranda-Saavedra, D. The repertoires of ubiquitinating and deubiquitinating enzymes in eukaryotic genomes. Mol. Biol. Evol. 2013, 30, 1172–1187. [Google Scholar] [CrossRef]
- Bigay, J.; Casella, J.F.; Drin, G.; Mesmin, B.; Antonny, B. ArfGAP1 responds to membrane curvature through the folding of a lipid packing sensor motif. EMBO J. 2005, 24, 2244–2253. [Google Scholar] [CrossRef]
- Doucet, C.M.; Talamas, J.A.; Hetzer, M.W. Cell cycle-dependent differences in nuclear pore complex assembly in metazoa. Cell 2010, 141, 1030–1041. [Google Scholar] [CrossRef] [PubMed]
- Galan, J.M.; Wiederkehr, A.; Seol, J.H.; Haguenauer-Tsapis, R.; Deshaies, R.J.; Riezman, H.; Peter, M. Skp1p and the F-box protein Rcy1p form a non-SCF complex involved in recycling of the SNARE Snc1p in yeast. Mol. Cell. Biol. 2001, 21, 3105–3117. [Google Scholar] [CrossRef] [PubMed]
- Hariri, H.; Rogers, S.; Ugrankar, R.; Liu, Y.L.; Feathers, J.R.; Henne, W.M. Lipid droplet biogenesis is spatially coordinated at ER–vacuole contacts under nutritional stress. EMBO Rep. 2018, 19, 57–72. [Google Scholar] [CrossRef]
- Ragni, E.; Piberger, H.; Neupert, C.; García-Cantalejo, J.; Popolo, L.; Arroyo, J.; Aebi, M.; Strahl, S. The genetic interaction network of CCW12, a Saccharomyces cerevisiae gene required for cell wall integrity during budding and formation of mating projections. BMC Genom. 2011, 12, 107. [Google Scholar] [CrossRef]
- Baudouin-Cornu, P.; Labarre, J. Regulation of the cadmium stress response through SCF-like ubiquitin ligases: Comparison between Saccharomyces cerevisiae, Schizosaccharomyces pombe and mammalian cells. Biochimie 2006, 88, 1673–1685. [Google Scholar] [CrossRef] [PubMed]
- Kitano, H. Systems biology: A brief overview. Science 2002, 295, 1662–1664. [Google Scholar] [CrossRef]
- Barabasi, A.L.; Oltvai, Z.N. Network biology: Understanding the cell’s functional organization. Nat. Rev. Genet. 2004, 5, 101. [Google Scholar] [CrossRef]
- Alon, U. An Introduction to Systems Biology: Design Principles of Biological Circuits; Chapman and Hall: London, UK; CRC: Boca Raton, FL, USA, 2006. [Google Scholar]
- Haas, R.; Zelezniak, A.; Iacovacci, J.; Kamrad, S.; Townsend, S.; Ralser, M. Designing and interpreting multi-omic experiments that may change our understanding of biology. Curr. Opin. Syst. Biol. 2017, 6, 37–45. [Google Scholar] [CrossRef] [PubMed]
- Maaten, L.V.d.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- McInnes, L.; Healy, J.; Melville, J. Umap: Uniform manifold approximation and projection for dimension reduction. arXiv 2018, arXiv:1802.03426. [Google Scholar]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. Kdd 1996, 96, 226–231. [Google Scholar]
- Ankerst, M.; Breunig, M.M.; Kriegel, H.P.; Sander, J. OPTICS: Ordering Points to Identify the Clustering Structure. In ACM Sigmod Record; ACM: New York, NY, USA, 1999; Volume 28, pp. 49–60. [Google Scholar]






| AAFS | ||
|---|---|---|
| Ionome (ko) | 2 | 0.003 |
| Ionome (oe) | 1.45 | 0.003 |
| Metabolome (aa) | 1.15 | 0.004 |
| Ionome (ko) | ||||||
|---|---|---|---|---|---|---|
| Top 1000 Scores | Top 10,000 Scores | Top 100,000 Scores | ||||
| Best Performance | Gain | Best Performance | Gain | Best Performance | Gain | |
| PPI | cosH | 18.1% | PCC | 7.7% | PCC | 2.9% |
| Protein Complexes | cosM | 100% | cosM | 12.5% | cosH | 2.1% |
| KEGG Pathways | cosH | 140.8% | cosH | 39.2% | cosH | 1% |
| BIOGRID | cosM | 50% | cosM | 3% | cosM | 5.9% |
| YeastNet GS | cos | 100% | cosH | 21.2% | PCC | 3.7% |
| Ionome (oe) | ||||||
| Top 1000 Scores | Top 10,000 Scores | Top 100,000 Scores | ||||
| Best Performance | Gain | Best Performance | Gain | Best Performance | Gain | |
| PPI | cosM | 60% | PCC | 16% | PCC | 2.9% |
| Protein Complexes | cosH | inf | cosM | 50% | cosH | 2.1% |
| KEGG Pathways | cosM | 7.7% | cosM | 3.5% | cosH | 1% |
| BIOGRID | cosH | 7.1% | cosM | 2.5% | cosM | 5.9% |
| YeastNet GS | cos | 14.3% | PCC | 2% | PCC | 3.7% |
| Metabolome (aa) | ||||||
| Top 1000 Scores | Top 10,000 Scores | Top 100,000 Scores | ||||
| Best Performance | Gain | Best Performance | Gain | Best Performance | Gain | |
| PPI | cosM | 146.7% | cosM | 91.1% | cosM | 41.8% |
| Protein Complexes | cosM | 200% | cosM | 80% | cosM | 35.1% |
| KEGG Pathways | cosM | 44% | cosM | 8.6% | cosM | 4.8% |
| BIOGRID | PCC | 0% | cos | 0.7% | cos | 1.7% |
| YeastNet GS | cosH | 16.7% | cos | 8% | cosH | 1.8% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iacovacci, J.; Peluso, A.; Ebbels, T.; Ralser, M.; Glen, R.C. Extraction and Integration of Genetic Networks from Short-Profile Omic Data Sets. Metabolites 2020, 10, 435. https://doi.org/10.3390/metabo10110435
Iacovacci J, Peluso A, Ebbels T, Ralser M, Glen RC. Extraction and Integration of Genetic Networks from Short-Profile Omic Data Sets. Metabolites. 2020; 10(11):435. https://doi.org/10.3390/metabo10110435
Chicago/Turabian StyleIacovacci, Jacopo, Alina Peluso, Timothy Ebbels, Markus Ralser, and Robert C. Glen. 2020. "Extraction and Integration of Genetic Networks from Short-Profile Omic Data Sets" Metabolites 10, no. 11: 435. https://doi.org/10.3390/metabo10110435
APA StyleIacovacci, J., Peluso, A., Ebbels, T., Ralser, M., & Glen, R. C. (2020). Extraction and Integration of Genetic Networks from Short-Profile Omic Data Sets. Metabolites, 10(11), 435. https://doi.org/10.3390/metabo10110435







