Association of Antibiotic Use with the Resistance Epidemiology of Pseudomonas aeruginosa in a Hospital Setting: A Four-Year Retrospective Time Series Analysis
by
, ,
Rania Kousovista
1
,
Christos Athanasiou
2,
Konstantinos Liaskonis
3,
Olga Ivopoulou
3 and
Vangelis Karalis
4,*
1
Department of Mathematics, University of Crete, Heraklion, 70013 Crete, Greece
2
Pharmacy Department, General Military Hospital of Athens, 11525 Athens, Greece
3
Department of Medical Biopathology, General Military Hospital of Athens, 11525 Athens, Greece
4
Department of Pharmacy, School of Health Sciences, National and Kapodistrian University of Athens, 15784 Athens, Greece
*
Author to whom correspondence should be addressed.
Sci. Pharm. 2021, 89(1), 13; https://doi.org/10.3390/scipharm89010013
Submission received: 14 December 2020
/
Revised: 6 February 2021
/
Accepted: 22 February 2021
/
Published: 5 March 2021
Abstract
Background: Even though, Pseudomonas aeruginosa is a common cause of hospital-acquired infections, treatment is challenging because of decreasing rates of susceptibility to many broad-spectrum antibiotics. Methods: Consumption data of eight broad spectrum antimicrobial agents and resistance rates of P. aeruginosa were collected for 48 consecutive months. Autoregressive integrated moving average (ARIMA) and transfer functions models were used to develop relationships between antibiotic use and resistance. Results: Positive correlations between P. aeruginosa resistance and uses of ciprofloxacin (p < 0.001), meropenem (p < 0.001), and cefepime (p = 0.005) were identified. Transfer function models showed the quantified effect of each of these antibiotics on resistance. Regarding levofloxacin, ceftazidime, piperacillin/tazobactam and imipenem, no significant relationships were found. For ceftazidime and levofloxacin, this was probably due to their low consumption, while for imipenem the reason can possibly be ascribed to the already high established P. aeruginosa resistance in the hospital. Conclusion: In the hospital setting, the effect of antimicrobial agents’ consumption on the susceptibility epidemiology of P. aeruginosa differs significantly for each one of them. In this study, the role of precedent use of meropenem, cefepime and ciprofloxacin was quantified in the development of P. aeruginosa resistance.
1. Introduction
Pseudomonas aeruginosa, a common cause of hospital-acquired infections, has become a challenge for clinicians worldwide because of its decreasing rates of susceptibility to broad spectrum antibiotics [1,2,3,4,5]. Twenty years ago, it was considered that anti-P. aeruginosa antibiotics, such as amikacin, piperacillin, cefoperazone, cefepime, meropenem and polymyxin B, had low-resistance potentials, but this is not the case today [6]. A number of novel antimicrobial agents, including antibiotic combinations with activity against resistant strains of P. aeruginosa have recently become available [7]. However, even resistance to these new antimicrobial agents has already been reported, both in vitro and in clinical case reports [8,9,10]. Inevitably, the only way to preserve susceptibility in both old and new antibiotics is the prudent use of them by applying the principles of antimicrobial stewardship. In this case, it is necessary to enhance our knowledge around the mechanisms that promote resistance, especially the impact of in-hospital antimicrobial use.
In 2002, Lepper et al., highlighted the demand for more information on the influence of a hospital’s antibiotic policy on the resistance epidemiology of P. aeruginosa [11]. Even though many studies have been published during these last two decades, this necessity is still unsatisfied. The variety of study designs and objectives makes the situation difficult. It is interesting, though, that Tóth et al., explored the phenomenon of the indirect association between the increase in consumption of one antimicrobial and the increased resistance to another [12]. There is also a lack of surveys on the direct association of antimicrobial consumption with the resistance rate to the targeted antimicrobials [13]. Moreover, the use of different methodologies is a perplexing factor, though it is now widely acknowledged that time series analysis is an appropriate tool to investigate the correlation of antimicrobial use and resistance rates [14,15]. Time series analysis not only takes into account the possible relationship between consecutive observations, but also assesses cross-correlation between two time series. An autoregressive integrated moving average (ARIMA) model is a practical technique of time series analysis as described by Box and Jenkins [16]. ARIMA models can describe the nature of a time series variable relying on its past values (autoregression) and the weighted average of past random shocks (moving average). To explore the relationship between two or more time series, an extension of the method, called a transfer function, can be applied [16]. In this context, univariate transfer function models have been used to determine the relationship between antimicrobial use and resistance rate [14,17,18].
In this retrospective study, monthly data of P. aeruginosa susceptibility to selected antimicrobials and antibiotic consumption for 48 consecutive months were collected from a tertiary care hospital. The aim of this analysis was to examine possible associations between antibiotic use and resistance rates. In order to achieve this task, ARIMA and transfer function models were developed.
2. Materials and Methods
2.1. Clinical Setting
From January 2014 until December 2017, an observational study was performed at the 401 General Military Hospital of Athens, Greece. The latter is a tertiary care hospital with medical and surgical wards as well as two Intensive Care Units (ICUs). The hospital scientific committee gave permission for this research. Due to the retrospective character of the study, and the fact that no personal information was required for this study, the need for an informed consent from the patients was waived by the ethics review board. With regard to the hospital restriction policy, all prescriptions for broad spectrum antibiotics need written approval by an infectious diseases specialist before administration. During the study period, no change in the restriction policy or other major change took place.
2.2. Antibiotic Consumption
Data on monthly antibiotic consumption of selected antimicrobials were exported from the hospital pharmacy database. Antibiotic consumption was expressed in term of Defined Daily Doses per 100 Patient Days (DDDs/100 PDs) according to the 2019 version of the ATC/DDD classification (World Health Organization Collaborating Centre for Drug Statistics Methodology, ATC/DDD index 2019, Oslo, Norway). DDD is the assumed average maintenance dose per day for a drug used for its main indication in adults.
The antimicrobial agents examined in this study, referred to carbapenems (meropenem and imipenem), cephalosporins (ceftazidime and cefepime), fluoroquinolones (ciprofloxacin and levofloxacin), a combination of penicillin/beta-lactamase inhibitor (piperacillin/tazobactam) and colistin.
2.3. Microbiological Data
Microbiological data and susceptibility test results were obtained from the general microbiology department of the hospital. Interpretation of the results was performed according to Clinical and Laboratory Standards Institute criteria. For the purposes of this study, all nonsusceptible isolates (resistant and intermediate) were considered as resistant. All clinical isolates of P. aeruginosa from every biological sample, from all wards and ICUs, were included in the analysis. Isolates, other than the first one, which were obtained from the same patient during the same admission, were excluded as duplicates. Microbiological data were expressed as the detection rate defined as the number of antibiotic-resistant isolates per month. For reasons of simplicity, from this point forward the term “resistance” refers to the detection rate of resistant to the targeted antibiotic P. aeruginosa isolates.
2.4. Data Analysis
All data were obtained at monthly intervals from the hospital databases. The study used anonymized confidential routinely collected data. Time series analysis was applied to provide methods that could account for autocorrelation. One practical method is the construction of ARIMA models as described by Box and Jenkins [16]. Initially, ARIMA models were developed for any time series of antimicrobial use and resistance. Stationarity was tested by using the Dickey-Fuller test. Autocorrelation and partial autocorrelation function plots (ACF and PACF, respectively) were employed to identify the order of an ARIMA model. Subsequently, the parameters of the identified model were estimated by maximum likelihood or unconditional least squares functions. Using Bartlett’s periodogram based test, an ARIMA model was accepted if residuals corresponded to a white noise process [19].
To explore and quantify the effect of antimicrobial use on resistance, transfer function models (TF) were constructed. In order to avoid multiple testing, an initial screening was used to find promising pairs for the development of TF models. Time series analyses of antibiotic use and resistance rates series were developed separately. Cross-correlation of “resistance” and “use” series was performed at lags of up to one year, and a backward selection option was applied to eliminate nonsignificant correlations. A candidate was deemed suitable for further testing if the correlation coefficient was statistically significant. Specifically, antimicrobial resistance was defined as the “output” series, whereas antimicrobial consumption was the “input” variable. An additive noise term, following a stationary autoregressive-moving average process, was integrated when existent. monthly time lags of antimicrobial consumption were applied to the antimicrobial resistance series. After applying the ARIMA filter of the input on the output series, the residual of both series was cross-correlated [20]. Candidate identification was attained as with simple cross-correlation. Selected candidates of antimicrobial consumption were integrated into the TF models. The Akaike Information Criterion (AIC) and the coefficient of determination (R2) were computed as diagnostic checks. Relying on the concept of Wiener-Granger causality, past or present values of the input series (antimicrobial consumption) were imported in the model if they were found to assist the prediction of the output series (antimicrobial resistance). This required the AIC and R2 of the TF model to be improved by at least 10% compared with the AIC and R2 of the output series ARIMA model. All statistical analyses were performed in R version 3.6.1 (the R project for statistical computing; http://www.r-project.org (accessed on 1 December 2020)).
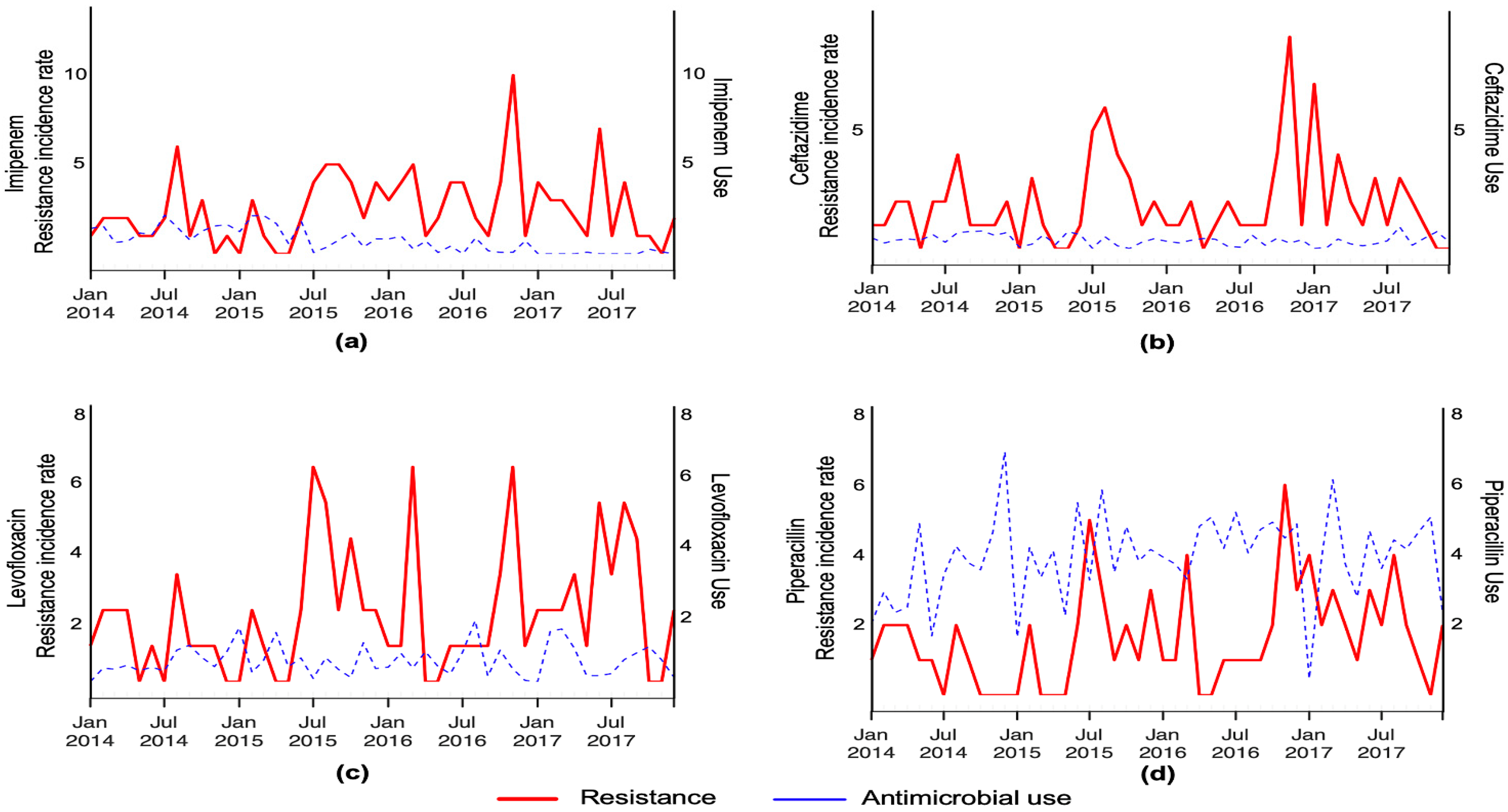
3. Results
Antibiotic susceptibility rates of P. aeruginosa are shown in Table 1. The highest resistance values were observed for levofloxacin and the lowest for colistin (36.4% and 6%, respectively). Table 2 lists the mean monthly consumption of antibiotics expressed as DDD/100 PD, as well as their association with antibiotic-resistant P. aeruginosa. Univariate analysis revealed that the use of meropenem, cefepime and ciprofloxacin was associated with high resistance. The monthly use of these three antipseudomonal drugs over the four-year period is depicted in Figure 1. Colistin consumption was not analyzed due to its small resistant rates.
ARIMA and transfer function models were built to estimate meropenem resistance among P. aeruginosa isolates (Table 3). Meropenem resistant P. aeruginosa and meropenem consumption series in a four-year period are shown in Figure 2A. Meropenem resistant P. aeruginosa series was stationary, while meropenem consumption became stationary after log transformation and differencing. ACF and PACF did not indicate any order for meropenem-resistant’s ARIMA model (Table 3A). In this stable model, the residuals corresponded to white noise. In addition, an ARIMA model was identified for a meropenem consumption series showing nice adjustment with three significant autoregressive terms of orders one, two and three months (p < 0.001) in ACF and PACF plots (Table 3B). The meropenem consumption univariate model verified that its residuals corresponded to white noise. Furthermore, a linear transfer function model was assessed in order to study how meropenem consumption influenced meropenem resistant P. aeruginosa. Cross-correlation between the two series’ residuals (i.e., consumption and resistance) showed significant relationships without lag time. After the diagnostic checks, it was found that meropenem use (p < 0.001) was the only factor affecting the meropenem resistant P. aeruginosa isolates (Table 3C).
The analysis concerning the association of cefepime consumption with cefepime resistant P. aeruginosa is shown in Table 4. Figure 2B shows the smoothed monthly hospital cefepime use and cefepime-resistant P. aeruginosa series. ARIMA models were built to assess the behavior of the two time-series. Both of them became stationary, in variance and mean, after log transformation and simple differentiation. ACF and PACF plots indicated one significant autoregressive order of one month for cefepime-resistant P. aeruginosa (p = 0.013), while the residuals corresponded to white noise (Table 4A). In addition, cefepime use series indicated good adjustment with two significant autoregressive terms of orders one and two months (p < 0.001) in ACF and PACF plots (Table 4B). Again, the residuals of the cefepime consumption series referred to white noise. The cross-correlation function of the residuals of both ARIMA models showed only one significant correlation with no time lag between the cefepime use and the resistance (p = 0.005) (Table 4C). The final transfer function model also contained one significant autoregressive term of one month in resistance (p = 0.004).
Finally, another transfer model was developed in this study to quantify the effect of ciprofloxacin use on ciprofloxacin resistance in P. aeruginosa isolates (Table 5). Ciprofloxacin resistance of P. aeruginosa and ciprofloxacin consumption series in a four-year period are shown in Figure 2C. ARIMA models were further built for the ciprofloxacin-resistant P. aeruginosa and the ciprofloxacin use series, after simple differentiation. Table 5A shows that ciprofloxacin-resistant P. aeruginosa had a one-month significant autoregressive term (p = 0.002). Moreover, the identified model of ciprofloxacin use series contained two significant autoregressive terms of orders one and three months (p < 0.001) (Table 5B). Both series’ residuals followed white noise, and their cross-correlation function showed only one significant correlation with lag of two months between the ciprofloxacin use series and resistance (p < 0.001). Examination of the ACF and PACF of the transfer function showed a good adjustment, with only one autoregressive term of one-month order (p = 0.001).
It is worth mentioning that ARIMA and transfer function models were also investigated for the remaining five antimicrobials, namely, imipenem, ceftazidime, levofloxacin, piperacillin and colistin. The monthly resistance detection rate of P. aeruginosa and hospital use for each of these antibiotics is depicted in Figure 3.
Colistin use and P. aeruginosa resistance (to colistin) were not analyzed due to their low values and resistant rates. For the antimicrobials shown in Figure 3 (i.e., imipenem, ceftazidime, levofloxacin and piperacillin) no statistically significant association (p > 0.05) was found between their use and resistance (Table 6).
4. Discussion
P. aeruginosa has developed resistance to all known antibiotics over the past few years that otherwise could be used as treatments [3,4]. As a consequence, Taconelli et al. (2018) prioritized a list for research and development of new antibiotics for antibiotic-resistant bacteria, concluding that one of the most critical and aggressive antibiotic resistant pathogens was carbapenem-resistant P. aeruginosa [5]. Thus, promoting prudent antimicrobial use has become an imperative need if susceptibility to antibiotics is to be preserved. However, attention should be paid since there is a fragile balance in every hospital setting. Thus, any change in prescribing policies and formulary restrictions may have implications that needed to be taken into account, since every decrease in a specific antibiotic class will almost inevitably promote an increase in the consumption of another class; a phenomenon that has been characterized as “squeezing the balloon”. The latter can have an impact on resistance incidence if it surpasses a critical point [12,15,21]. In this context, the findings of this study will be compared to the results from previous time series analyses.
In the case of Greece, hospital-acquired infections are a major problem due to the dramatic increase of resistance to Gram-negative bacteria [22]. Among these infections, multidrug resistance is observed for P. aeruginosa, which is associated with mortality and morbidity. A recent clinical study, which was performed in several wards of Greek hospitals, identified P. aeruginosa strains of ICU exhibiting high resistance to gentamycin, cefepime, fluoroquinolones and carbapenems [22]. These findings are in accordance with our results showing high resistance rates of the previous three antimicrobials. In addition, P. aeruginosa was sensitive to colistin treatment, as in our data (Table 1). Regarding carbapenems, both for meropenem and imipenem high resistance of Pseudomonas was observed. This is in line with the results of a study conducted in a Greek hospital, which reported that resistance to carbapenems is an endemic problem in P. aeruginosa infections [23]. The situation of multidrug resistant strains of P. aeruginosa is a health problem affecting southern Europe. In particular, not only multi drug-resistant, but also extremely drug-resistant isolates of P. aeruginosa were found to have high prevalence in Greece [24]. In this context, the application of time series analyses has become a useful tool towards studying resistance rates of several pathogens and their relationship with antibiotics. Only in the case of P. aeruginosa more than 20 analyses, either quasi-experimental or ecological observational studies, have been performed the last decade [13].
4.1. Carbapenems
This analysis did not identify any significant correlation between imipenem use and resistance, even though there are several studies that have demonstrated a strong temporal association between these two parameters [25,26,27,28]. A possible explanation for this difference is that imipenem resistance was very high in the analyzed hospital data, so that susceptibility rates had already reached a minimum, beyond which no change was to be expected. With regard to meropenem, the transfer function model built in this analysis (Table 3), revealed a positive correlation between use and resistance. This finding is in agreement with previous studies also documenting a strong correlation [25,29].
4.2. Cephalosporins
With regard to antipseudomonal cephalosporins, this study revealed a significant association between cefepime use and resistance. According to the final model, an increase of 1 DDD/100PD in cefepime consumption, would lead to a 0.48 increase in the monthly detection rate of cefepime resistant isolates (Table 4). This is in accordance with previous studies of Xu et al. and Erdeljic et al. [25,29]. Other studies utilizing different methodologies came to similar conclusions [30,31]. It can be assumed that cefepime use, even in low levels, has a significant impact on P. aeruginosa resistance. This analysis revealed no statistically significant association between ceftazidime use and resistance, but the recorded in-hospital use was very low (less than 0.5 DDD/100PD). On the contrary, a study from China [32] reported a positive association between ceftazidime use and resistance, but the total use of antipseudomonal cephalosporins in that study was high (up to 19.39 DDD/100 PD).
4.3. Fluoroquinolones
With regard to ciprofloxacin, our final model identified a positive association of consumption with resistance (Table 5), where an increase of ciprofloxacin use by 1 DDD/100 PD (i.e., a 21.5% raise (mean monthly use 4.65)), would lead to a symmetrical increase in resistance detection rate by 16% (mean monthly detection rate 2.83). No statistically significant correlation was observed between levofloxacin use and resistance, which can be attributed to the low levofloxacin use (0.58 DDD/100 PD). These findings, on ciprofloxacin, are in accordance with a previous time series analysis study and a number of studies with different methodological and statistical approaches [29,30,31,33]. A time series analysis conducted in a hospital in China during the years 2003–2011 revealed no correlation between the usage of fluoroquinolones and the prevalence of resistant P. aeruginosa [25]. However, the total consumption of fluoroquinolones (ciprofloxacin and levofloxacin) in the aforementioned study was low (1.6–2.5 DDD/100 PD). Thus, a postulation can be made that there is a threshold between 2 and 4.5 DDD/100 PD above which ciprofloxacin use in a certain setting induces the development of resistance in P. aeruginosa.
4.4. Piperacillin/Tazobactam
This analysis found no correlation between piperacillin/tazobactam use and resistance, though the consumption levels were not insignificant (3.94 DDD/100 PD), which is in line with two previous studies [25,29]. It can be considered that the use of piperacillin/tazobactam at least up to 4 DDD/100 PD does not promote resistance in P. aeruginosa.
4.5. Colistin
Colistin use in the hospital data under study was rather high, i.e., 3.56 DDD/100 PD. Nevertheless, detection rate of resistance to colistin was low (0.35 resistant isolates/month) and, therefore, a time series analysis could not be performed.
4.6. Limitations of the Study
One limitation of the study can be ascribed to the fact that the analysis of antibiotic consumption and resistance was based on aggregate hospital data and not at the individual patient level. The absence of full automatization in Greek hospitals led to the manual collection of many of the required data. Finally, cross-correlations among the antimicrobials, and their possible impact on each other’s resistance, was not performed. In other words, this study did not analyze meropenem consumption on cefepime resistance of P. aeruginosa.
5. Conclusions
The aim of this study was to identify possible relationships between P. aeruginosa resistance rates and the consumption of eight antimicrobial agents. Data collected from a tertiary hospital, in a four-year period, were utilized to perform time series analyses. ARIMA models were constructed for the resistance rate of P. aeruginosa, as well as the use of meropenem, cefepime and ciprofloxacin. In addition, aiming to explore and quantify the effect of antimicrobial use on resistance, statistically significant transfer function models were developed for these three antimicrobials. The latter allow identifying the extent and direction of the observed relationship between P. aeruginosa resistance and antimicrobial consumption. No association was found between P. aeruginosa resistance and the use of levofloxacin, imipenem, ceftazidime and piperacillin/tazobactam. For imipenem, the inability to associate consumption and resistance can possibly be attributed to the already observed high resistance rates in the hospital, implying that susceptibility of P. aeruginosa had already reached a minimum. In the cases of ceftazidime and levofloxacin, the low recorded consumption in the hospital, possibly hampered the development. Overall, the impact of meropenem, cefepime and ciprofloxacin consumption on the susceptibility epidemiology of P. aeruginosa, was quantified.
Author Contributions
Conceptualization, C.A. and V.K.; methodology, R.K. and V.K.; software, R.K.; validation, V.K. and C.A.; formal Analysis, R.K.; investigation, R.K.; resources, C.A., K.L. and O.I.; data curation, R.K.; writing—original draft preparation, R.K.; writing—review & editing, R.K., C.A. and V.K.; visualization, R.K.; supervision, V.K.; project administration, V.K.; funding acquisition, R.K. All authors have participated in the preparation of the manuscript and have read the manuscript and approve its submission to the Journal of Scientia Pharmaceutica. All authors have read and agreed to the published version of the manuscript.
Funding
R.K. was supported by the Hellenic Foundation for Research and Innovation (HFRI) under the HFRI PhD Fellowship grant (Fellowship Number: 261).
Institutional Review Board Statement
Ethical review and approval were waived for this study, due to the retrospective character of the study and the fact that no personal information was required for this study.
Informed Consent Statement
Patient consent was waived due to the retrospective character of the study and the fact that no personal information was required for this study.
Data Availability Statement
Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Baron, S.; Hadjadj, L.; Rolain, J.M.; Olaitan, A.O. Molecular mechanisms of polymyxin resistance: Knowns and unknowns. Int. J. Antimicrob. Agents 2016, 48, 583–591. [Google Scholar] [CrossRef] [PubMed]
- Paterson, D.L. The epidemiological profile of infections with multidrug-resistant Pseudomonas aeruginosa and Acinetobacter species. Clin. Infect. Dis. 2006, 43, S43–S48. [Google Scholar] [CrossRef]
- Magiorakos, A.P.; Srinivasan, A.; Carey, R.B.; Carmeli, Y.; Falagas, M.E.; Giske, C.G.; Harbarth, S.; Hindler, J.; Kahlmeter, G.; Paterson, D.L.; et al. Multidrug-resistant, extensively drug-resistant and pandrug-resistant bacteria: An international expert proposal for interim standard definitions for acquired resistance. Clin. Microbiol. Infect. 2012, 18, 268–281. [Google Scholar] [CrossRef]
- Bassetti, M.; Vena, A.; Croxatto, A.; Righi, E.; Guery, B. How to manage Pseudomonas aeruginosa infections. Drugs Context 2018, 7, 212527. [Google Scholar] [CrossRef] [PubMed]
- Tacconelli, E.; Carrara, E.; Savoldi, A.; Harbarth, S.; Mendelson, M.; Monnet, D.L.; Ouellette, M.; Pulcini, C.; Kahlmeter, G.; Kluytmans, J.; et al. Discovery, research, and development of new antibiotics: The WHO priority list of antibiotic-resistant bacteria and tuberculosis. Lancet Infect. Dis. 2018, 18, 318–327. [Google Scholar] [CrossRef]
- Cunha, B.A. Pseudomonas aeruginosa: Resistance and therapy. Semin. Respir. Infect. 2002, 17, 231–239. [Google Scholar] [CrossRef]
- Pontefract, B.A.; Ho, H.T.; Crain, A.; Kharel, M.K.; Nybo, S.E. Drugs for Gram-Negative Bugs from 2010–2019: A Decade in Review. Open Forum Inf. Dis. 2020, 7, ofaa276. [Google Scholar] [CrossRef] [PubMed]
- Skoglund, E.; Abodakpi, H.; Rios, R.; Diaz, L.; De La Cadena, E.; Dinh, A.Q.; Tran, T.T.; Ardila, J.; Miller, W.R.; Munita, J.; et al. In Vivo Resistance to Ceftolozane/Tazobactam in Pseudomonas aeruginosa Arising by AmpC- and Non-AmpC-Mediated Pathways. Case Rep. Infect. Dis. 2018, 23, 9095203. [Google Scholar] [CrossRef] [PubMed]
- Poirel, L.; Ortiz De La Rosa, J.M.; Kieffer, N.; Dubois, V.; Jayol, A.; Nordmann, P. Acquisition of Extended-Spectrum β-Lactamase GES-6 Leading to Resistance to Ceftolozane-Tazobactam Combination in Pseudomonas aeruginosa. Antimicrob. Agents Chemother. 2019, 63, e01809–e01818. [Google Scholar] [CrossRef] [PubMed]
- Fraile-Ribot, P.A.; Cabot, G.; Mulet, X.; Periañez, L.; Martín-Pena, M.L.; Juan, C.; Oliver, A.; Pérez, J.A. Mechanisms leading to in vivo ceftolozane/tazobactam resistance development during the treatment of infections caused by MDR Pseudomonas aeruginosa. J. Antimicrob. Chemother. 2018, 73, 658–663. [Google Scholar] [CrossRef]
- Lepper, P.M.; Grusa, E.; Reichl, H.; Högel, J.; Trautmann, M. Consumption of imipenem correlates with β-lactam resistance in Pseudomonas aeruginosa. Antimicrob. Agents Chemother. 2002, 46, 2920–2925. [Google Scholar] [CrossRef]
- Tóth, H.; Fésűs, A.; Kungler-Gorácz, O.; Balázs, B.; Majoros, L.; Szarka, K.; Kardos, G. Utilization of Vector Autoregressive and Linear Transfer Models to Follow Up the Antibiotic Resistance Spiral in Gram-negative Bacteria from Cephalosporin Consumption to Colistin Resistance. Clin. Infect. Dis. 2019, 69, 1410–1421. [Google Scholar] [CrossRef] [PubMed]
- Athanasiou, C.I.; Kopsini, A. Systematic review of the use of time series data in the study of antimicrobial consumption and Pseudomonas aeruginosa resistance. J. Glob. Antimicrob. Resist. 2018, 15, 69–73. [Google Scholar] [CrossRef] [PubMed]
- López-Lozano, J.M.; Monnet, D.L.; Yagüe, A.; Burgos, A.; Gonzalo, N.; Campillos, P.; Saez, M. Modelling and forecasting antimicrobial resistance and its dynamic relationship to antimicrobial use: A time series analysis. Int. J. Antimicrob. Agents 2000, 14, 21–31. [Google Scholar] [CrossRef]
- Lopez-Lozano, J.M.; Lawes, T.; Nebot, C.; Beyaert, A.; Bertrand, X.; Hocquet, D.; Gould, I.; Aldeyab, M.; Scott, M.; Conlon-Bingham, G.; et al. A nonlinear time-series analysis approach to identify thresholds in associations between population antibiotic use and rates of resistance. Nat. Microbiol. 2019, 4, 1160–1172. [Google Scholar] [CrossRef]
- Box, G.P.; Jenkins, G.M. Time Series Analysis: Forecasting and Control, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2015; pp. 21–192. [Google Scholar]
- Mahamat, A.; Lavigne, J.P.; Fabbro-Peray, P.; Kinowski, J.M.; Daures, J.P.; Sotto, A. Evolution of fluoroquinolone resistance among Escherichia coli urinary tract isolates from a French university hospital: Application of the dynamic regression model. Clin. Microbiol. Infect. 2005, 11, 301–306. [Google Scholar] [CrossRef]
- Willmann, M.; Marschal, M.; Hölzl, F.; Schröppel, K.; Autenrieth, I.B.; Peter, S. Time series analysis as a tool to predict the impact of antimicrobial restriction in antibiotic stewardship programs using the example of multidrug-resistant Pseudomonas aeruginosa. Antimicrob. Agents Chemother. 2013, 57, 1797–1803. [Google Scholar] [CrossRef][Green Version]
- Bartlett, M.S. Periodogram analysis and continuous spectra. Biometrika 1950, 37, 1–16. [Google Scholar] [CrossRef] [PubMed]
- McDowell, A. Transfer functions. Stata J. 2002, 2, 71–85. [Google Scholar] [CrossRef]
- Peterson, L.R. Squeezing the antibiotic balloon: The impact of antimicrobial classes on emerging resistance. Clin. Microbiol. Infect. 2005, 11, 4–16. [Google Scholar] [CrossRef]
- Feretzakis, G.; Loupelis, E.; Sakagianni, A.; Skarmoutsou, N.; Michelidou, S.; Velentza, A.; Martsoukou, M.; Valakis, K.; Petropoulou, S.; Koutalas, E. A 2-Year Single-Centre Audit on Antibiotic Resistance of Pseudomonas aeruginosa, Acinetobacter baumannii and Klebsiella pneumoniae Strains from an Intensive Care Unit and Other Wards in a General Public Hospital in Greece. Antibiotics 2019, 8, 62. [Google Scholar] [CrossRef]
- Karampatakis, T.; Antachopoulos, C.; Tsakris, A.; Roilides, E. Molecular epidemiology of carbapenem-resistant Pseudomonas aeruginosa in an endemic area: Comparison with global data. Eur. J. Clin. Microbiol. Infect. Dis. 2018, 37, 1211–1220. [Google Scholar] [CrossRef]
- Pérez, A.; Gato, E.; Pérez-Llarena, J.; Fernández-Cuenca, F.; Gude, M.J.; Oviaño, M.; Pachón, M.E.; Garnacho, J.; González, V.; Pascual, Á.; et al. High incidence of MDR and XDR Pseudomonas aeruginosa isolates obtained from patients with ventilator-associated pneumonia in Greece, Italy and Spain as part of the MagicBullet clinical trial. J. Antimicrob. Chemother. 2019, 74, 1244–1252. [Google Scholar] [CrossRef]
- Xu, L.; Sun, X.; Ma, X. Systematic review and meta-analysis of mortality of patients infected with carbapenem-resistant Klebsiella pneumoniae. Ann. Clin. Microbiol. Antimicrob. 2017, 16, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Sousa, D.; Castelo-Corral, L.; Gutiérrez-Urbón, J.M.; Molina, F.; López-Calviño, B.; Bou, G.; Llinares, P. Impact of ertapenem use on Pseudomonas aeruginosa and Acinetobacter baumannii imipenem susceptibility rates: Collateral damage or positive effect on hospital ecology? J. Antimicrob. Chemother. 2013, 68, 1917–1925. [Google Scholar] [CrossRef][Green Version]
- Carmeli, Y.; Lidji, S.K.; Shabtai, E.; Navon-Venezia, S.; Schwaber, M.J. The effects of group 1 versus group 2 carbapenems on imipenem-resistant Pseudomonas aeruginosa: An ecological study. Diagn. Microbiol. Infect. Dis. 2011, 70, 367–372. [Google Scholar] [CrossRef] [PubMed]
- Zou, Y.M.; Ma, Y.; Liu, J.H.; Shi, J.; Fan, T.; Shan, Y.Y.; Yao, H.P.; Dong, Y.L. Trends and correlation of antibacterial usage and bacterial resistance: Time series analysis for antibacterial stewardship in a Chinese teaching hospital (2009–2013). Eur. J. Clin. Microbiol. Infect. Dis. 2015, 34, 795–803. [Google Scholar] [CrossRef] [PubMed]
- Erdeljić, V.; Francetić, I.; Bošnjak, Z.; Budimir, A.; Kalenić, S.; Bielen, L.; Likić, R.; Makar-Aušperger, K. Distributed lags time series analysis versus linear correlation analysis (Pearson’s r) in identifying the relationship between antipseudomonal antibiotic consumption and the susceptibility of Pseudomonas aeruginosa isolates in a single Intensive Care Unit of a tertiary hospital. Int. J. Antimicrob. Agents. 2011, 37, 467–471. [Google Scholar] [PubMed]
- Yang, P.; Chen, Y.; Jiang, S.; Shen, P.; Lu, X.; Xiao, Y. Association between the rate of fluoroquinolones-resistant gram-negative bacteria and antibiotic consumption from China based on 145 tertiary hospitals data in 2014. BMC Infect. Dis. 2020, 20, 269. [Google Scholar] [CrossRef]
- Cook, P.P.; Gooch, M.; Rizzo, S. Reduction in fluoroquinolone use following introduction of ertapenem into a hospital formulary is associated with improvement in susceptibility of Pseudomonas aeruginosa to group 2 carbapenems: A 10-year study. Antimicrob. Agents Chemother. 2011, 55, 5597–5601. [Google Scholar] [CrossRef]
- Dou, Y.; Huan, J.; Guo, F.; Zhou, Z.; Shi, Y. Pseudomonas aeruginosa prevalence, antibiotic resistance and antimicrobial use in Chinese burn wards from 2007 to 2014. J. Int. Med. Res. 2017, 45, 1124–1137. [Google Scholar] [CrossRef]
- Kallel, H.; Mahjoubi, F.; Dammak, H.; Bahloul, M.; Hammami, A.; Bouaziz, M. Correlation between antibiotic use and changes in susceptibility patterns of Pseudomonas aeruginosa in a medical-surgical intensive care unit. Indian J. Crit. Care Med. Peer Rev. Indian J. Crit. Care Med. 2008, 12, 18–23. [Google Scholar] [CrossRef] [PubMed][Green Version]
Figure 1.
Use of meropenem, cefepime, and ciprofloxacin over a four-year study period. Usage is defined in defined daily doses per 100 patient days (DDD/100 PD).
Figure 1.
Use of meropenem, cefepime, and ciprofloxacin over a four-year study period. Usage is defined in defined daily doses per 100 patient days (DDD/100 PD).
Figure 2.
Smoothed monthly resistance detection rate of P. aeruginosa and hospital use of meropenem (a), cefepime (b), and ciprofloxacin (c).
Figure 2.
Smoothed monthly resistance detection rate of P. aeruginosa and hospital use of meropenem (a), cefepime (b), and ciprofloxacin (c).
Figure 3.
Smoothed monthly resistance detection rate of P. aeruginosa and hospital use of imipenem (a), ceftazidime (b), levofloxacin (c) and piperacillin (d).
Figure 3.
Smoothed monthly resistance detection rate of P. aeruginosa and hospital use of imipenem (a), ceftazidime (b), levofloxacin (c) and piperacillin (d).
Table 1.
Susceptibility data of P. aeruginosa isolates expressed as mean rate for the entire study period of the four years following the Clinical and Laboratory Standards Institute criteria.
Table 1.
Susceptibility data of P. aeruginosa isolates expressed as mean rate for the entire study period of the four years following the Clinical and Laboratory Standards Institute criteria.
| Antimicrobial Agent | S (%) | I (%) | R (%) |
|---|---|---|---|
| Imipenem | 63.4 | 2.5 | 34 |
| Meropenem | 66.4 | 5.5 | 28 |
| Ceftazidime | 63.2 | 10.5 | 26.1 |
| Cefepime | 60.9 | 12.5 | 26.5 |
| Ciprofloxacin | 62.3 | 7.4 | 30.1 |
| Levofloxacin | 52.4 | 11.2 | 36.4 |
| Piperacillin/tazobactam | 70.2 | 0 | 29.7 |
| Colistin | 93.1 | 0.8 | 6 |
S, susceptible; I, intermediate; R, resistant.
Table 2.
Antibiotic use expressed as the mean of monthly Defined Daily Doses per 100 patient-days (DDDs/100 PD) between January 2014 and December 2017 and the association in univariate time series analysis with its antibiotic-resistant Pseudomonas aeruginosa.
Table 2.
Antibiotic use expressed as the mean of monthly Defined Daily Doses per 100 patient-days (DDDs/100 PD) between January 2014 and December 2017 and the association in univariate time series analysis with its antibiotic-resistant Pseudomonas aeruginosa.
| Antimicrobial Agent/Class | DDDs/100 PD a | Delay b (In Months) | p-Value c |
|---|---|---|---|
| Carbapenems | |||
| Imipenem | 0.71 | 0 | 0.091 |
| Meropenem | 6.74 | 0 | <0.001 |
| Cephalosporins | |||
| Ceftazidime | 0.48 | 0 | 0.201 |
| Cefepime | 1.85 | 0 | 0.005 |
| Fluoroquinolones | |||
| Ciprofloxacin | 4.65 | 2 | <0.001 |
| Levofloxacin | 0.58 | 0 | 0.115 |
| Other | |||
| Piperacillin | 3.94 | 0 | 0.34 |
| Colistin | 3.56 | NA d | NA |
a Mean monthly use. b Delay (in months) between resistance observation and antibiotic use. c p-value for the association between antimicrobial use and P. aeruginosa resistance of the Autoregressive integrated moving average (ARIMA) model. d NA, not assessed due to limited data.
Table 3.
ARIMA models for meropenem-resistant P. aeruginosa (A) and meropenem use (B). Dynamic regression model for the association between meropenem-resistant P. aeruginosa and hospital meropenem use (C).
Table 3.
ARIMA models for meropenem-resistant P. aeruginosa (A) and meropenem use (B). Dynamic regression model for the association between meropenem-resistant P. aeruginosa and hospital meropenem use (C).
| Estimate | Model Parameter | Standard Error | p-Value |
|---|---|---|---|
| A. Resistance | |||
| Intercept | 1.25 | 0.244 | <0.001 |
| AIC | 80.82 | / | / |
| R2 | 0.587 | / | / |
| B. Meropenem use (in DDD/100 PD) | |||
| ar1 | −0.831 | 0.122 | <0.001 |
| ar2 | −0.637 | 0.144 | <0.001 |
| ar3 | −0.569 | 0.117 | <0.001 |
| AIC | 242.91 | / | / |
| R2 | 0.638 | / | / |
| C. Impact of meropenem use on resistance | |||
| mer0 | 0.175 | 0.029 | <0.001 |
| AIC | 77.09 | / | / |
| R2 | 0.183 | / | / |
AIC, the estimated Akaike Information Criterion value for the model; ARIMA, autoregression moving average model; ar1, autoregression term with lag of one month in the ARIMA model; ar2, autoregressive component with lag equal to two months of the ARIMA model; ar3, autoregressive component with lag equal to three months of the ARIMA model; DDD/100 PD, defined daily doses per 100 patient days; mer0, meropenem use with no lag time; R2, coefficient of determination of the model.
Table 4.
ARIMA models for cefepime-resistant P. aeruginosa (A) and cefepime use (B). Dynamic regression model for the association between cefepime-resistant P. aeruginosa and hospital cefepime use (C).
Table 4.
ARIMA models for cefepime-resistant P. aeruginosa (A) and cefepime use (B). Dynamic regression model for the association between cefepime-resistant P. aeruginosa and hospital cefepime use (C).
| Estimate | Model Parameter | Standard Error | p-Value |
|---|---|---|---|
| A. Resistance | |||
| ar1 | −0.453 | 0.18368 | 0.013 |
| AIC | 87.58 | / | / |
| R2 | 0.175 | / | / |
| B. Cefepime use (in DDD/100 PD) | |||
| ar1 | −0.463 | 0.137 | <0.001 |
| ar2 | −0.466 | 0.133 | <0.001 |
| AIC | 139.03 | / | / |
| R2 | 0.619 | / | / |
| C. Impact of cefepime use on resistance | |||
| ar1 | −0.506 | 0.176 | 0.004 |
| cef0 | 0.482 | 0.175 | 0.005 |
| AIC | 73.3 | / | / |
| R2 | 0.422 | / | / |
AIC, the estimated Akaike Information Criterion value for the model; ARIMA, autoregression moving average model; ar1, autoregression term with lag of one month in the ARIMA model; ar2, autoregressive component with lag equal to two months of the ARIMA model; DDD/100 PD, defined daily doses per 100 patient days; cef0, cefepime use with no lag time; R2, coefficient of determination of the model.
Table 5.
ARIMA models for ciprofloxacin-resistant P. aeruginosa (A) and ciprofloxacin use (B). Dynamic regression model for the association between ciprofloxacin-resistant P. aeruginosa and hospital ciprofloxacin use (C).
Table 5.
ARIMA models for ciprofloxacin-resistant P. aeruginosa (A) and ciprofloxacin use (B). Dynamic regression model for the association between ciprofloxacin-resistant P. aeruginosa and hospital ciprofloxacin use (C).
| Estimate | Model Parameter | Standard Error | p-Value |
|---|---|---|---|
| A. Resistance | |||
| ar1 | 0.502 | 0.167 | 0.002 |
| intercept | 2.556 | 0.727 | <0.001 |
| AIC | 106.74 | / | / |
| R2 | 0.267 | / | / |
| B. Ciprofloxacin use (in DDD/100 PD) | |||
| ar1 | −0.527 | 0.147 | 0.000 |
| ar3 | −0.299 | 0.152 | 0.004 |
| AIC | 77.76 | / | / |
| R2 | 0.550 | / | / |
| C. Impact of ciprofloxacin use on resistance | |||
| ar1 | 0.560 | 0.17137 | 0.001 |
| cip2 | 0.464 | 0.12727 | <0.001 |
| AIC | 93.62 | / | / |
| R2 | 0.404 | / | / |
AIC, the estimated Akaike Information Criterion value for the model; ARIMA, autoregression moving average model; ar1, autoregression term with lag of one month in the ARIMA model; ar3, autoregressive component with lag equal to three months of the ARIMA model; DDD/100 PD, defined daily doses per 100 patient days; cip2, ciprofloxacin use with lag time of two months; R2, coefficient of determination of the model.
Table 6.
Dynamic regression models for the resistance of P. aeruginosa to the additional antimicrobials explored in this study, taking into account their hospital use. The transfer models refer to imipenem (A), ceftazidime (B), levofloxacin (C) and piperacillin (D).
Table 6.
Dynamic regression models for the resistance of P. aeruginosa to the additional antimicrobials explored in this study, taking into account their hospital use. The transfer models refer to imipenem (A), ceftazidime (B), levofloxacin (C) and piperacillin (D).
| Estimate | Model Parameter | Standard Error | p-Value |
|---|---|---|---|
| A. Imipenem | |||
| Model | ARIMA (0,0,0) | / | / |
| Intercept | 3.166 | 0.435 | <0.001 |
| Imipenem use | −0.792 | 0.450 | 0.091 |
| AIC | 191.880 | / | / |
| R2 | 0.066 | / | / |
| B. Ceftazidime | |||
| Model | ARIMA (0,1,1) | / | / |
| Intercept | −1.000 | 0.083 | <0.001 |
| Ceftazidime use | −1.550 | 1.213 | 0.201 |
| AIC | 184.690 | / | / |
| R2 | 0.043 | / | / |
| C. Levofloxacin | |||
| Model | ARIMA (0,0,0) | / | / |
| Intercept | 2.510 | 0.463 | <0.001 |
| Levofloxacin use | −0.972 | 0.618 | 0.115 |
| AIC | 179.270 | / | / |
| R2 | 0.053 | / | / |
| D. Piperacillin | |||
| Model | ARIMA (1,0,0) | / | / |
| Intercept | 0.305 | 0.152 | 0.0448 |
| Piperacillin use | 0.368 | 0.072 | 0.34 |
| AIC | 155.290 | / | / |
| R2 | 0.079 | / | / |
AIC, the estimated Akaike Information Criterion value for the model; DDD/100 PD, defined daily doses per 100 patient days; R2, the coefficient of determination of the model; ARIMA (a,b,c), ARIMA model with “a” autoregressive terms, “b” nonseasonal differences, and “c” lagged forecast errors.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
MDPI and ACS Style
Kousovista, R.; Athanasiou, C.; Liaskonis, K.; Ivopoulou, O.; Karalis, V. Association of Antibiotic Use with the Resistance Epidemiology of Pseudomonas aeruginosa in a Hospital Setting: A Four-Year Retrospective Time Series Analysis. Sci. Pharm. 2021, 89, 13. https://doi.org/10.3390/scipharm89010013
AMA Style
Kousovista R, Athanasiou C, Liaskonis K, Ivopoulou O, Karalis V. Association of Antibiotic Use with the Resistance Epidemiology of Pseudomonas aeruginosa in a Hospital Setting: A Four-Year Retrospective Time Series Analysis. Scientia Pharmaceutica. 2021; 89(1):13. https://doi.org/10.3390/scipharm89010013
Chicago/Turabian StyleKousovista, Rania, Christos Athanasiou, Konstantinos Liaskonis, Olga Ivopoulou, and Vangelis Karalis. 2021. "Association of Antibiotic Use with the Resistance Epidemiology of Pseudomonas aeruginosa in a Hospital Setting: A Four-Year Retrospective Time Series Analysis" Scientia Pharmaceutica 89, no. 1: 13. https://doi.org/10.3390/scipharm89010013
APA StyleKousovista, R., Athanasiou, C., Liaskonis, K., Ivopoulou, O., & Karalis, V. (2021). Association of Antibiotic Use with the Resistance Epidemiology of Pseudomonas aeruginosa in a Hospital Setting: A Four-Year Retrospective Time Series Analysis. Scientia Pharmaceutica, 89(1), 13. https://doi.org/10.3390/scipharm89010013
