Stability Analysis of Company Co-Mention Network and Market Graph Over Time Using Graph Similarity Measures
Abstract
:1. Introduction
- One of the possibilities in discovering connections between companies is to use correlations between the returns of companies’ assets. In accordance with the efficient market hypothesis, it is assumed that stock prices of companies and their mutual behavior reflect all publicly available information about companies. Thus, economic and financial connections between companies may be reflected by the correlation of the log returns of company assets [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32].
- Also, in various applications it can be useful to build graphs of industrial or spatial affiliation of companies [40].
- by building the so-called market graphs in which nodes represent financial assets (e.g., stocks) and the edges between nodes stand for the correlation between the corresponding assets.
- based on companies’ co-mention in the news flow. The company co-mention network is constructed as follows: two companies are connected by an edge if a news item mentioning both companies has been published in a certain period of time.
- Does the market graph remain stable over time? How significantly do the market graphs constructed for two consecutive 6-month windows differ? How did the crisis of 2008 change the stability of the market graph? Were the changes of the market graph during the crisis minor or noticeable?
- Does the company co-mention network remain stable over time? How significantly do the company co-mention networks constructed for two consecutive windows differ? How did the crisis of 2008 change the stability of the company co-mention network? Were the changes of the company co-mention network during the crisis small or huge?
- What of the two networks was more stable over time: the market graph or the company co-mention network?
- How do the market graph and the company co-mention network constructed for the same time window differ?
- the Hamming distance (h) between graphs;
- a network similarity measure d proposed in [46] that quantifies how the set of central nodes (their ranking) has changed in a network;
- D-measure which is proposed in [47] and proved to be discriminative and computationally efficient to distinguish and quantify graph dissimilarities and which can identify and quantify topological differences between graphs;
- graph diffusion distance () [48] based on measuring the average similarity of heat diffusion on each graph.
2. Data Transformation for Network Representation
2.1. Market Network Construction
2.2. Network Representation of News Analytics Data
- we assemble all economic, business-related and financial news published over six years (2005–2010);
- we accomplish the process of data cleansing;
- we chose companies cited in news reports during this time;
- we divide the 6-year period into overlapping semiannual intervals. Each subsequent interval is obtained by shifting the previous one 1 month ahead. The result is 67 intervals of the same 6-month size (approximately 125 trading days).
- we calculate the number of co-mentions (link weight) for every two companies cited together at least in one piece of news over each time interval. In case the companies are not co-mentioned in the given interval, the link weight is 0.
- we used these weighted calculations of the collective companies’ mentions to obtain symmetric co-mention matrices for each interval;
- we explore the evolution of the co-mention matrices over the time, and the results of this study are being visualized and interpreted.
2.3. Methodology
- We construct the market graphs based on the correlations between assets for a 6-month window, moving the sliding window by one month ahead to construct the following subsequent graph.
- We construct the company co-mention network (for the same companies that form the market graph), adding an edge between two companies, if a news item mentioning both these companies was published during a 6-month window, shifting the sliding window by one month forward to construct the subsequent network.
2.3.1. Dynamics Analysis Based on the Assessment of the Neighboring Graphs Similarity
- to find the periods in which the greatest changes occurred during the transition from one time interval to another;
- to find periods of stability in which there were no changes between adjacent graphs in terms of measures and ;
- to understand which characteristics of graphs have changed more: those that are evaluated by or those that are related to the measure .
2.3.2. Multidimensional Scaling Analysis Approach
3. Graph Similarity Measurement
3.1. The Hamming Distance: Similarity of Local Structure
3.2. d-Measure: Node Similarity Measure Based on Interval Orders
3.3. D-Measure
3.4. Graph Diffusion Distance
3.5. Combined Similarity Metric
3.6. QAP Procedure
- the dependence between the adjacency matrix of the market graph constructed in a given period and matrices constructed for other periods;
- the dependence between the adjacency matrix of the company co-mention network constructed in a given period and matrices constructed for other periods;
- the dependence between the adjacency matrix of the market graph constructed in a given period and the adjacency matrix of the company co-mention network constructed for the same period.
4. Data
4.1. Financial Data
4.2. News Analytics Data
5. Empirical Result
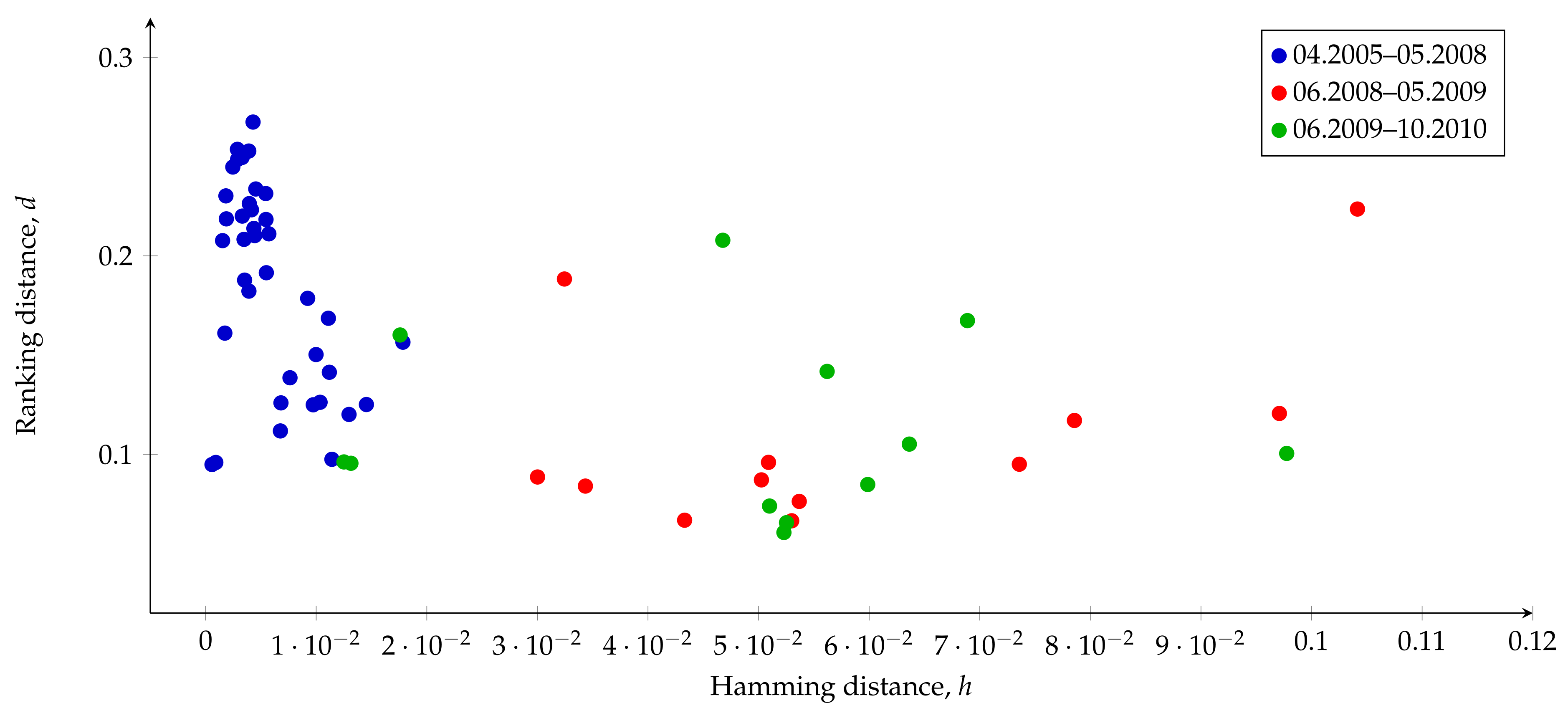
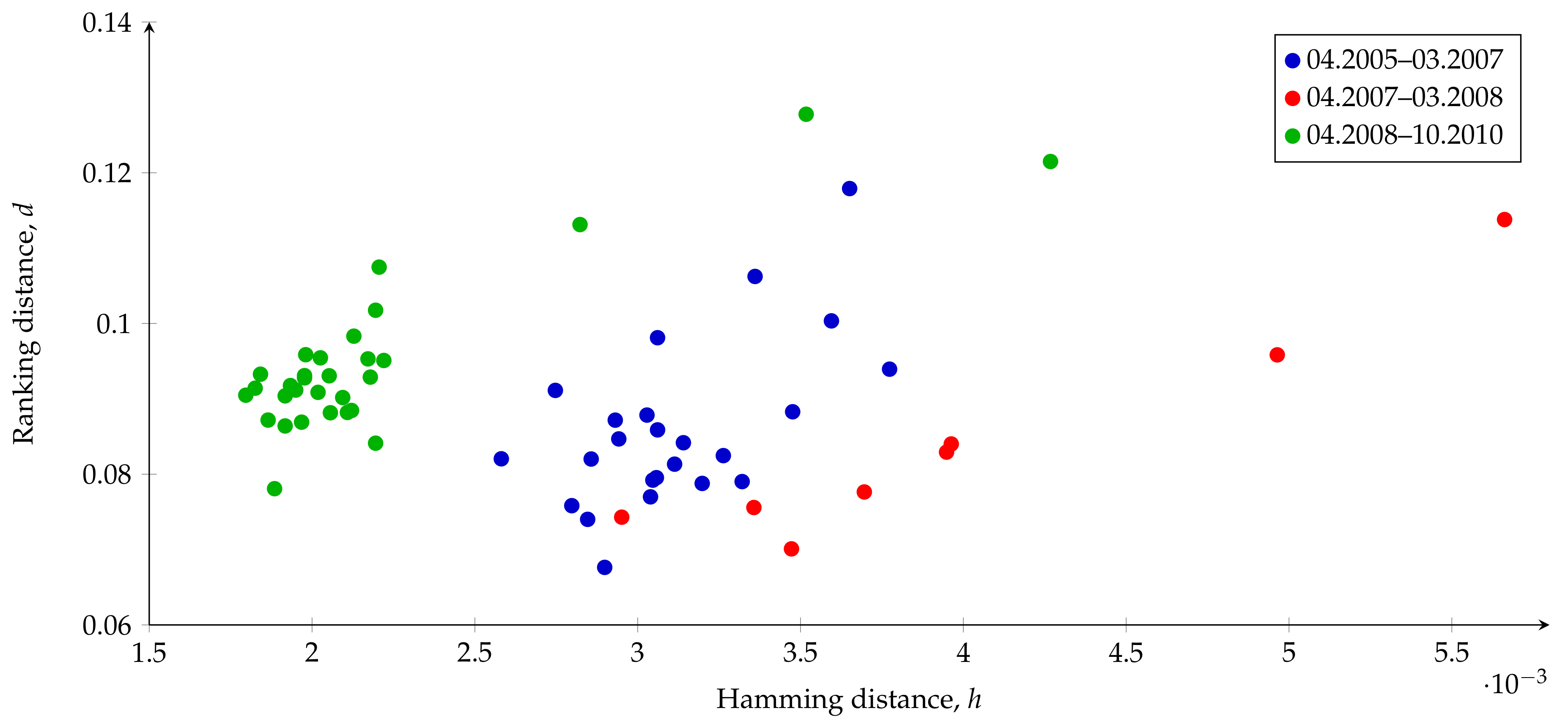
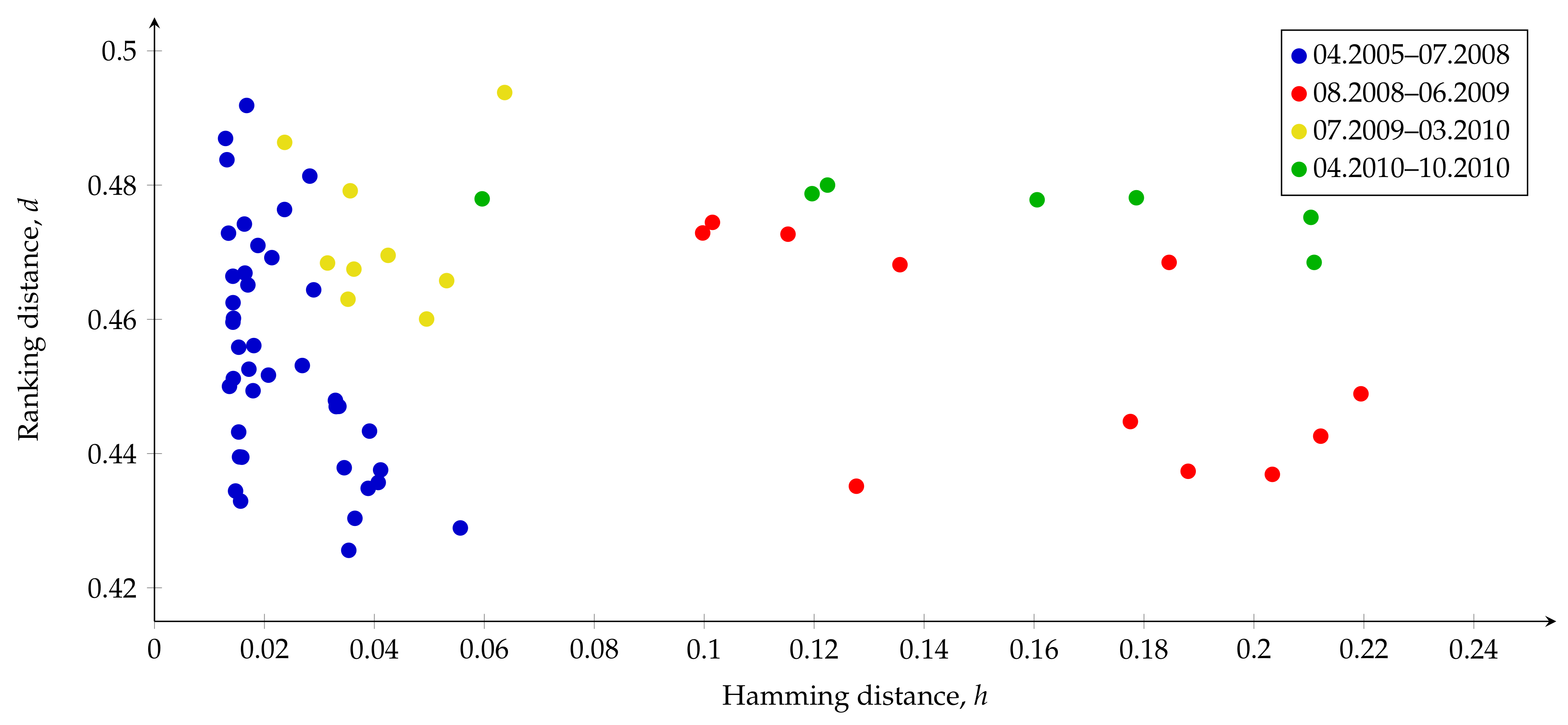
5.1. Similarity Analysis Using Measures h and d
5.2. QAP Correlation and Regression Analysis
- for related networks of co-mention,
- for time-related market graphs,
5.3. Multidimensional Scaling
- to visualize the dynamics of changes in the sequence of graphs;
- to find the number of components (factors) explaining the dynamics which is determined by adjacency matrices.
6. Conclusions
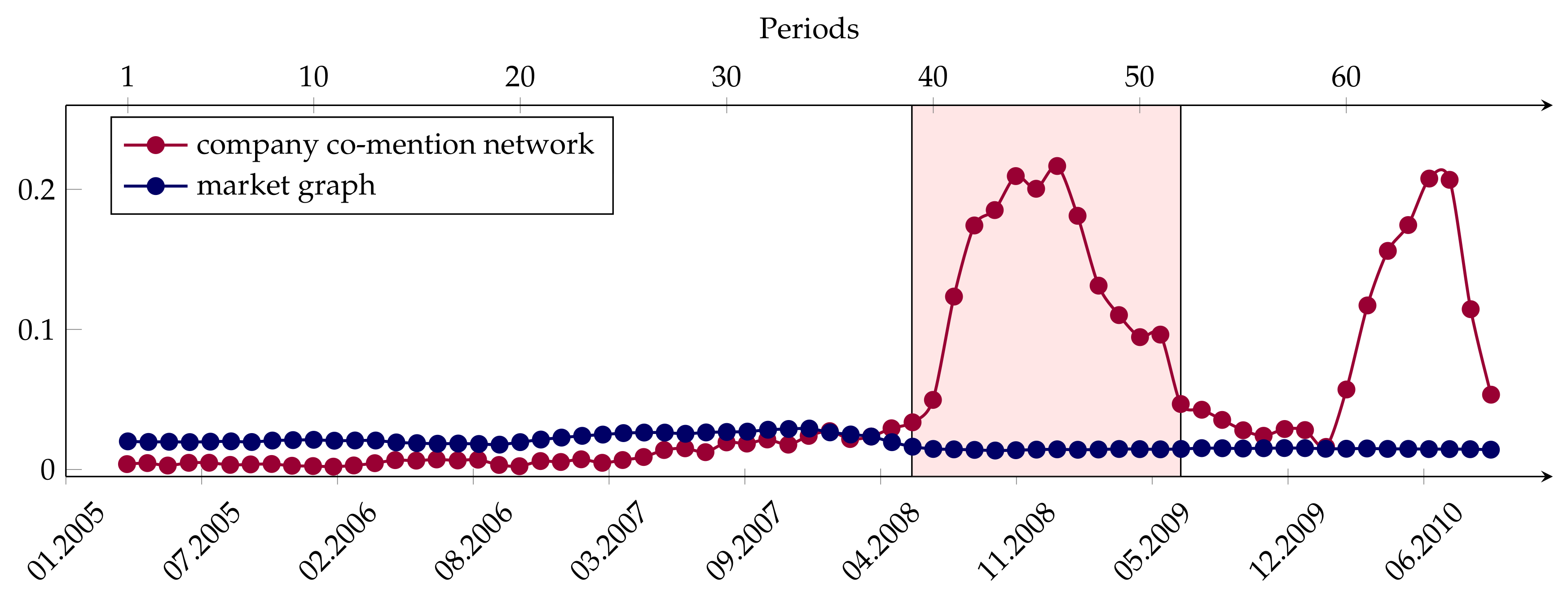
- We found that the market graph constructed based on correlations between financial asset returns was significantly less stable over time than the company co-mention network in the period 2005–2010. In fact, the value of the Hamming distance between two consecutive market graphs reached the value around 0.1 in some periods, i.e., about 10% of links were added or removed in the graph when the six-month sliding window was shifted one month ahead. At the same time, the value of the Hamming distance between any two consecutive company co-mention networks did not exceed 0.06. In addition, the values of the d metric for the market graph were twice or triple as great as for the co-mention network.
- A common and quite intuitive point of view is that the changes in the news flow intensity and structure may be the cause of the volatility in financial markets. On the other hand, sharply increased volatility can cause a sharp surge in the amount of news items published by news agencies. According to these ideas, the structure of the news flow and the level of volatility should be correlated. However, as our results show, the structure and intensity of the news flow is extremely stable and cannot be either the cause or the result of changes in the volatility of the financial market.
- According to empirical data, the structure of the co-mention network slightly changed approximately one year before the crisis began. However, these changes are minor and cannot explain the appearance of the global financial crisis that broke out a year after.
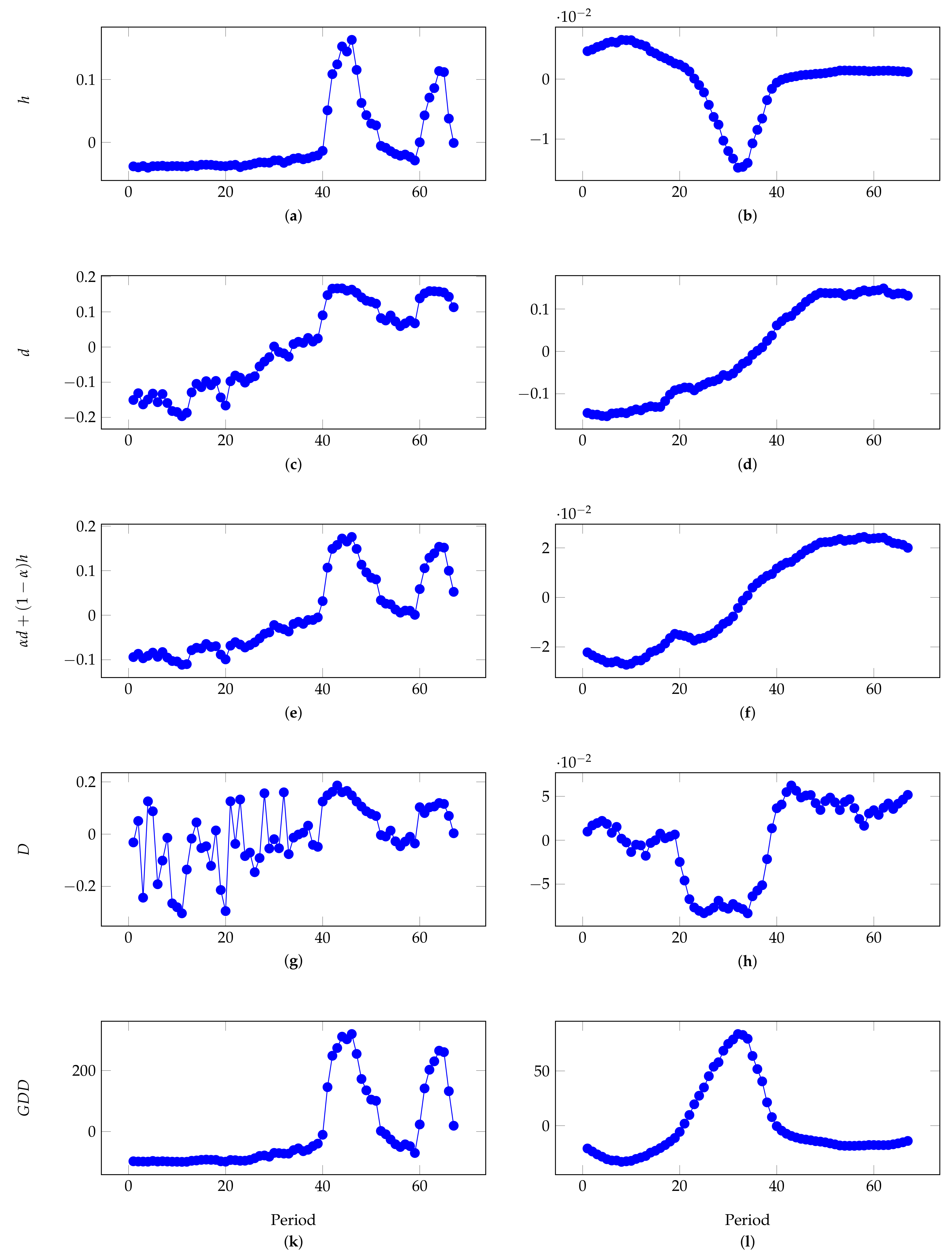
- Please note that changes of the market graph structure are either related to the increase in volatility caused by the fall in financial asset prices during the crisis (the first peak in Figure 2), or to the volatility associated with the subsequent increase in asset prices (the second hump in Figure 2). These changes of the market graph structure are also well reflected in the Figure 6a,c,e,g,k. Perhaps, one could make the market graph more stable in time applying the dynamic formation of the threshold .
- the development of methods for joint analysis of trends in the evolution of two simultaneously formed networks;
- the development of models and methods for the detection of local mutual causality in the evolution of company co-mention network and market graphs.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| the price of the asset i in day t | |
| the log return of asset i in day t defined by Equation (1) | |
| n | the number of assets |
| the Pearson correlation coefficient between random variables and defined in Section 2.1 | |
| , | any two different similarity measures |
| the sequence of the graphs representing the states of a complex system at time slots | |
| the matrix of pairwise distances between all pairs of graphs from the sequence using the measure | |
| the Hamming distance between networks and at two time slots and defined in Section 3.1 | |
| the adjacency matrix of graph G at time t | |
| the matrix representing information about relative ranking of nodes based on their centralities at time t | |
| the d-measure between and (the distance between the two rankings for the networks and ) defined by Equation (3) | |
| the D-measure (dissimilarity measure) between and defined by Equation (5) | |
| the graph diffusion distance between and described in Section 3.4 | |
| the linear combination of and defined by Equation (5) | |
| 67 market graphs corresponding to the 67 six-month periods | |
| 67 company co-mention networks corresponding to each of the 67 periods |
References
- Cheng, C.Y.; Chen, T.L.; Chen, Y.Y. An analysis of the structural complexity of supply chain networks. Appl. Math. Model. 2014, 38, 2328–2344. [Google Scholar] [CrossRef]
- Bellamy, M.; Basole, R. Network Analysis of Supply Chain Systems: A Systematic Review and Future Research. Syst. Eng. 2013, 16, 235–249. [Google Scholar] [CrossRef]
- Long, Q. Data-driven decision making for supply chain networks with agent-based computational experiment. Knowl.-Based Syst. 2018, 141, 55–66. [Google Scholar] [CrossRef]
- Long, Q. A framework for data-driven computational experiments of inter-organizational collaborations in supply chain networks. Inf. Sci. 2017, 399, 43–63. [Google Scholar] [CrossRef]
- Borgatti, S.P.; Li, X. On social network analysis in a supply chain context. J. Supply Chain. Manag. 2009, 45, 5–22. [Google Scholar] [CrossRef]
- Boss, M.; Elsinger, H.; Summer, M.; Thurner, S., IV. Network topology of the interbank market. Quant. Financ. 2004, 4, 677–684. [Google Scholar] [CrossRef]
- Affinito, M.; Pozzolo, A.F. The Interbank Network across the Global Financial Crisis: Evidence from Italy; Temi di discussione (Economic working papers) 1118, Bank of Italy, Economic Research and International Relations Area; Bank of Italy: Rome, Italy, 2017. [Google Scholar]
- Stefano, B.; Guido, C.; Marco, D.; Stefano, G. Leveraging the network: A stress-test framework based on DebtRank. Stat. Risk Model. 2016, 33, 117–138. [Google Scholar] [Green Version]
- Gofman, M. Efficiency and stability of a financial architecture with too-interconnected-to-fail institutions. J. Financ. Econ. 2017, 124, 113–146. [Google Scholar] [CrossRef]
- Bundi, N.; Khashanah, K. Complex Interbank Network Estimation: Sparsity-Clustering Threshold. In Complex Networks and Their Applications VII; Aiello, L.M., Cherifi, C., Cherifi, H., Lambiotte, R., Lió, P., Rocha, L.M., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 487–498. [Google Scholar]
- Gorgoni, S.; Amighini, A.; Smith, M. (Eds.) Networks of International Trade and Investment; Vernon Press: Wilmington, DE, USA, 2018. [Google Scholar]
- Hochberg, Y.V.; Lindsey, L.A.; Westerfield, M.M. Resource accumulation through economic ties: Evidence from venture capital. J. Financ. Econ. 2015, 118, 245–267. [Google Scholar] [CrossRef]
- Bygrave, W.D. The structure of the investment networks of venture capital firms. J. Bus. Ventur. 1988, 3, 137–157. [Google Scholar] [CrossRef]
- Xue, C.; Jiang, P.; Dang, X. The dynamics of network communities and venture capital performance: Evidence from China. Financ. Res. Lett. 2019, 28, 6–10. [Google Scholar] [CrossRef]
- Boginsky, V.; Butenko, S.; Pardalos, P.M. Innovations in Financial and Economic Networks; Edward Elgar Publishing Inc.: Northampton, UK, 2003; pp. 29–45, Chapter on Structural Properties of the Market Graph. [Google Scholar]
- Boginski, V.; Butenko, S.; Pardalos, P.M. Statistical analysis of financial networks. Comput. Stat. Data Anal. 2005, 48, 431–443. [Google Scholar] [CrossRef]
- Huang, W.Q.; Zhuang, X.T.; Yao, S. A network analysis of the Chinese stock market. Phys. Stat. Mech. Its Appl. 2009, 388, 2956–2964. [Google Scholar] [CrossRef]
- Tse, C.K.; Liu, J.; Lau, F.C.M. A network perspective of the stock market. J. Empir. Financ. 2010, 17, 659–667. [Google Scholar] [CrossRef]
- Boginski, V.; Butenko, S.; Pardalos, P.M. Network Models of Massive Datasets. Comput. Sci. Inf. Syst. 2004, 1, 75–89. [Google Scholar] [CrossRef]
- Onnela, J.P.; Kaski, K.; Kertész, J. Clustering and information in correlation based financial networks. Eur. Phys. J. B 2004, 38, 353–362. [Google Scholar] [CrossRef]
- Boginski, V.; Butenko, S.; Pardalos, P.M. Mining market data: A network approach. Comput. Oper. Res. 2006, 33, 3171–3184, Part Special Issue: Operations Research and Data Mining. [Google Scholar] [CrossRef]
- Emmert-Streib, F.; Dehmer, M. Identifying critical financial networks of the DJIA: Toward a network-based index. Complexity 2010, 16, 24–33. [Google Scholar] [CrossRef]
- Bautin, G.A.; Kalyagin, V.A.; Koldanov, A.P.; Koldanov, P.A.; Pardalos, P.M. Simple measure of similarity for the market graph construction. Comput. Manag. Sci. 2013, 10, 105–124. [Google Scholar] [CrossRef]
- Garas, A.; Argyrakis, P. Correlation study of the Athens Stock Exchange. Phys. A Stat. Mech. Its Appl. 2007, 380, 399–410. [Google Scholar] [CrossRef]
- Vizgunov, A.; Goldengorin, B.; Kalyagin, V.; Koldanov, A.; Koldanov, P.; Pardalos, P.M. Network approach for the Russian stock market. Comput. Manag. Sci. 2014, 11, 45–55. [Google Scholar] [CrossRef]
- Namaki, A.; Shirazi, A.H.; Raei, R.; Jafari, G.R. Network analysis of a financial market based on genuine correlation and threshold method. Phys. A Stat. Mech. Its Appl. 2011, 390, 3835–3841. [Google Scholar] [CrossRef]
- Bautin, G.A.; Kalyagin, V.A.; Koldanov, A.P. Comparative Analysis of Two Similarity Measures for the Market Graph Construction. In Models, Algorithms, and Technologies for Network Analysis; Goldengorin, B.I., Kalyagin, V.A., Pardalos, P.M., Eds.; Springer: New York, NY, USA, 2013; pp. 29–41. [Google Scholar]
- Shirokikh, O.; Pastukhov, G.; Boginski, V.; Butenko, S. Computational study of the US stock market evolution: A rank correlation-based network model. Comput. Manag. Sci. 2013, 10, 81–103. [Google Scholar] [CrossRef]
- Wang, G.J.; Xie, C.; Han, F.; Sun, B. Similarity measure and topology evolution of foreign exchange markets using dynamic time warping method: Evidence from minimal spanning tree. Phys. A Stat. Mech. Its Appl. 2012, 391, 4136–4146. [Google Scholar] [CrossRef]
- Kenett, D.Y.; Tumminello, M.; Madi, A.; Gur-Gershgoren, G.; Mantegna, R.N.; Ben-Jacob, E. Dominating Clasp of the Financial Sector Revealed by Partial Correlation Analysis of the Stock Market. PLoS ONE 2010, 5, e15032. [Google Scholar] [CrossRef] [PubMed]
- Kalyagin, V.A.; Koldanov, A.P.; Koldanov, P.A.; Pardalos, P.M. Optimal decision for the market graph identification problem in a sign similarity network. Ann. Oper. Res. 2018, 266, 313–327. [Google Scholar] [CrossRef]
- Faizliev, A.; Balash, V.; Vlasov, A.; Tryapkina, T.; Mironov, S.; Androsov, I.; Petrov, V. Analysis of the Dynamics of Market Graph Characteristics. In Proceedings of the Third Workshop on Computer Modelling in Decision Making (CMDM 2018), Saratov, Russia, 14–17 November 2018; Atlantis Press: Paris, France, 2019. [Google Scholar] [CrossRef] [Green Version]
- Mahdi, K.; Almajid, A.; Safar, M.; Riquelme, H.; Torabi, S. Social Network Analysis of Kuwait Publicly-Held Corporations. Procedia Comput. Sci. 2012, 10, 272–281. [Google Scholar] [CrossRef] [Green Version]
- Sankar, C.P.; Asokan, K.; Kumar, K.S. Exploratory social network analysis of affiliation networks of Indian listed companies. Soc. Netw. 2015, 43, 113–120. [Google Scholar] [CrossRef]
- Battiston, S.; Catanzaro, M. Statistical properties of corporate board and director networks. Eur. Phys. J. B 2004, 38, 345–352. [Google Scholar] [CrossRef]
- Vasques Filho, D.; O’Neale, D.R.J. Degree distributions of bipartite networks and their projections. Phys. Rev. E 2018, 98, 022307. [Google Scholar] [CrossRef] [Green Version]
- Bargigli, L.; Giannetti, R. The Italian corporate system in a network perspective (1952–1983). Phys. A Stat. Mech. Its Appl. 2018, 494, 367–379. [Google Scholar] [CrossRef]
- Sidorov, S.P.; Faizliev, A.R.; Balash, V.A.; Gudkov, A.A.; Chekmareva, A.Z.; Anikin, P.K. Company Co-mention Network Analysis. In Computational Aspects and Applications in Large-Scale Networks; Kalyagin, V.A., Pardalos, P.M., Prokopyev, O., Utkina, I., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 341–354. [Google Scholar] [CrossRef]
- Balash, V.; Chekmareva, A.; Faizliev, A.; Sidorov, S.; Mironov, S.; Volkov, D. Analysis of News Flow Dynamics Based on the Company Co-mention Network Characteristics. In Complex Networks and Their Applications VII; Aiello, L.M., Cherifi, C., Cherifi, H., Lambiotte, R., Lió, P., Rocha, L.M., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 521–533. [Google Scholar]
- Sidorov, S.P.; Faizliev, A.R.; Balash, V.A.; Gudkov, A.A.; Chekmareva, A.Z.; Levshunov, M.; Mironov, S.V. QAP Analysis of Company Co-mention Network. In Algorithms and Models for the Web Graph; Bonato, A., Prałat, P., Raigorodskii, A., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 83–98. [Google Scholar]
- Balash, V.A.; Faizliev, A.R.; Korotkovskaya, E.V.; Mironov, S.V.; Smolov, F.M.; Sidorov, S.P.; Volkov, D.A. The Evolution of Degree Distribution, Maximum Cliques and Maximum Independent Sets of Company Co-Mention Network over Time. WSEAS Trans. Syst. Control. 2019, 14, 97–103. [Google Scholar]
- Mitra, G.; Mitra, L. (Eds.) The Handbook of News Analytics in Finance; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Mitra, G.; Yu, X. (Eds.) Handbook of Sentiment Analysis in Finance; Albury Books: New York, NY, USA, 2016. [Google Scholar]
- Sidorov, S.; Faizliev, A.; Balash, V. Measuring long-range correlations in news flow intensity time series. Int. J. Mod. Phys. C 2017, 28, 1750103. [Google Scholar] [CrossRef]
- Donnat, C.; Holmes, S. Tracking network dynamics: A survey using graph distances. Ann. Appl. Stat. 2018, 12, 971–1012. [Google Scholar] [CrossRef]
- Aleskerov, F.; Shvydun, S. Stability and Similarity in Networks Based on Topology and Nodes Importance. In Complex Networks and Their Applications VII; Aiello, L.M., Cherifi, C., Cherifi, H., Lambiotte, R., Lió, P., Rocha, L.M., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 94–103. [Google Scholar]
- Schieber, T.A.; Carpi, L.; Díaz-Guilera, A.; Pardalos, P.M.; Masoller, C.; Ravetti, M.G. Quantification of network structural dissimilarities. Nat. Commun. 2017, 8, 13928. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hammond, D.K.; Gur, Y.; Johnson, C.R. Graph diffusion distance: A difference measure for weighted graphs based on the graph Laplacian exponential kernel. In Proceedings of the 2013 IEEE Global Conference on Signal and Information Processing, Austin, TX, USA, 3–5 December 2013; pp. 419–422. [Google Scholar] [CrossRef]
- Krackardt, D. QAP partialling as a test of spuriousness. Soc. Netw. 1987, 9, 171–186. [Google Scholar] [CrossRef]
- Hubert, L. Assignment Methods in Combinatorial Data Analysis; Dekker: New York, NY, USA, 1987. [Google Scholar]
- Dekker, D.; Krackhardt, D.; Snijders, T.A.B. Sensitivity of MRQAP Tests to Collinearity and Autocorrelation Conditions. Psychometrika 2007, 72, 563–581. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rossi, R.A.; Ahmed, N.K. Role Discovery in Networks. IEEE Trans. Knowl. Data Eng. 2015, 27, 1112–1131. [Google Scholar] [CrossRef]
- Bunke, H. Error correcting graph matching: on the influence of the underlying cost function. IEEE Trans. Pattern Anal. Mach. Intell. 1999, 21, 917–922. [Google Scholar] [CrossRef]
- Messmer, B.T.; Bunke, H. A new algorithm for error-tolerant subgraph isomorphism detection. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 493–504. [Google Scholar] [CrossRef] [Green Version]
- Bunke, H.; Dickinson, P.; Kraetzl, M.; Wallis, W. A Graphtheoretic Approach to Enterprise Network Dynamics; Birkhauser: Boston, MA, USA, 2007. [Google Scholar]
- Fernández, M.L.; Valiente, G. A graph distance metric combining maximum common subgraph and minimum common supergraph. Pattern Recognit. Lett. 2001, 22, 753–758. [Google Scholar] [CrossRef]
- Bunke, H.; Jiang, X.; Kandel, A. On the Minimum Common Supergraph of Two Graphs. Computing 2000, 65, 13–25. [Google Scholar] [CrossRef]
- Gardiner, E.J.; Raymond, J.W.; Willett, P. RASCAL: Calculation of Graph Similarity using Maximum Common Edge Subgraphs. Comput. J. 2002, 45, 631–644. [Google Scholar] [CrossRef]
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47–97. [Google Scholar] [CrossRef] [Green Version]
- Dill, S.; Kumar, R.; Mccurley, K.S.; Rajagopalan, S.; Sivakumar, D.; Tomkins, A. Self-similarity in the Web. ACM Trans. Internet Technol. 2002, 2, 205–223. [Google Scholar] [CrossRef]
- Borodin, A.; Roberts, G.O.; Rosenthal, J.S.; Tsaparas, P. Link Analysis Ranking: Algorithms, Theory, and Experiments. ACM Trans. Internet Technol. 2005, 5, 231–297. [Google Scholar] [CrossRef]
- Papadimitriou, P.; Dasdan, A.; Garcia-Molina, H. Web graph similarity for anomaly detection. J. Internet Serv. Appl. 2010, 1, 19–30. [Google Scholar] [CrossRef] [Green Version]
- Papadopoulos, A.; Manolopoulos, Y. Structure-Based Similarity Search with Graph Histograms. In Proceedings of the Tenth International Workshop on Database and Expert Systems Applications, DEXA 99, Florence, Italy, 3 September 1999. [Google Scholar]
- Kleinberg, J.M. Authoritative Sources in a Hyperlinked Environment. J. ACM 1999, 46, 604–632. [Google Scholar] [CrossRef]
- Blondel, V.D.; Gajardo, A.; Heymans, M.; Senellart, P.; Dooren, P.V. A Measure of Similarity Between Graph Vertices: Applications to Synonym Extraction and Web Searching. SIAM Rev. 2004, 46, 647–666. [Google Scholar] [CrossRef]
- Heymans, M.; Singh, A.K. Deriving phylogenetic trees from the similarity analysis of metabolic pathways. Bioinformatics 2003, 19, i138–i146. [Google Scholar] [CrossRef] [Green Version]
- Koutra, D.; Vogelstein, J.T.; Faloutsos, C. DeltaCon: A Principled Massive-Graph Similarity Function. In Proceedings of the 2013 SIAM International Conference on Data Mining. Society for Industrial and Applied Mathematics, Austin, TX, USA, 2–4 May 2013; pp. 162–170. [Google Scholar] [CrossRef]
- De Domenico, M.; Nicosia, V.; Arenas, A.; Latora, V. Structural reducibility of multilayer networks. Nat. Commun. 2015, 6, 6864. [Google Scholar] [CrossRef] [PubMed]
- Krackhardt, D. Predicting with networks: Nonparametric multiple regression analysis of dyadic data. Soc. Netw. 1988, 10, 359–381. [Google Scholar] [CrossRef]
- Rienties, B.; Héliot, Y.; Jindal-Snape, D. Understanding social learning relations of international students in a large classroom using social network analysis. High. Educ. 2013, 66, 489–504. [Google Scholar] [CrossRef] [Green Version]
- Barnett, G.A.; Park, H.W.; Jiang, K.; Tang, C.; Aguillo, I.F. A multi-level network analysis of web-citations among the world’s universities. Scientometrics 2014, 99, 5–26. [Google Scholar] [CrossRef]
- Cantner, U.; Graf, H. The network of innovators in Jena: An application of social network analysis. Res. Policy 2006, 35, 463–480. [Google Scholar] [CrossRef]
- Lee, W.J.; Lee, W.K.; Sohn, S.Y. Patent Network Analysis and Quadratic Assignment Procedures to Identify the Convergence of Robot Technologies. PLoS ONE 2016, 11, e0165091. [Google Scholar] [CrossRef] [PubMed]
- Mantel, N. The detection of disease clustering and a generalized regression approach. Cancer Res. 1967, 27, 209–220. [Google Scholar] [CrossRef] [PubMed]
- Kruskal, J.B. Multidimensional scaling by optimizing goodness of fit to a nonmetric hypothesis. Psychometrika 1964, 29, 1–27. [Google Scholar] [CrossRef]
- Borg, I.; Groenen, P.J.; Mair, P. Applied Multidimensional Scaling and Unfolding; Springer Briefs in Statistics; Springer International Publishing: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- GOWER, J.C. Some distance properties of latent root and vector methods used in multivariate analysis. Biometrika 1966, 53, 325–338. [Google Scholar] [CrossRef]
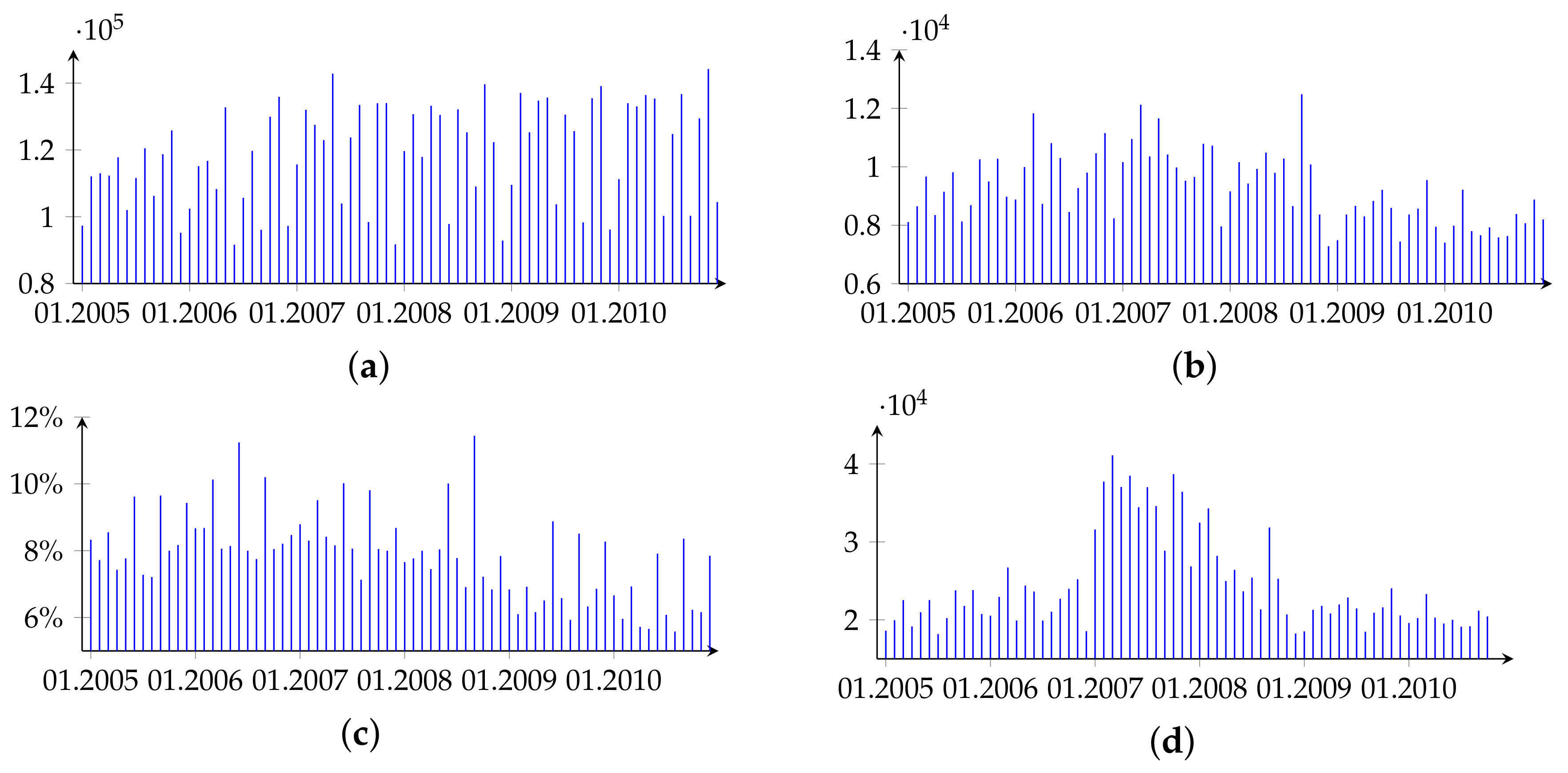
| Period | Start | End |
|---|---|---|
| 1 | 01.01.2005 | 30.06.2005 |
| 2 | 01.02.2005 | 31.07.2005 |
| 3 | 01.03.2005 | 31.08.2005 |
| … | … | … |
| … | … | … |
| 65 | 01.05.2010 | 31.10.2010 |
| 66 | 01.06.20010 | 30.11.2010 |
| 67 | 01.07.20010 | 31.12.2010 |
| K | Freq. | Percent | Cum. | Co-mentions | Co-mentions Percent. Cum. |
|---|---|---|---|---|---|
| 1 | 7,891,180 | 92.22 | 92.22 | 0 | 69.5 |
| 2 | 610,824 | 7.14 | 99.36 | 1,221,648 | 69.5 |
| 3 | 43,352 | 0.51 | 99.86 | 260,112 | 84.3 |
| 4 | 6887 | 0.08 | 99.94 | 82,644 | 89.0 |
| 5 | 1553 | 0.02 | 99.96 | 31,060 | 90.8 |
| 6 | 650 | 0.01 | 99.97 | 19,500 | 91.9 |
| 7 | 928 | 0.01 | 99.98 | 38,976 | 94.1 |
| 8 | 1611 | 0.02 | 100 | 90,216 | 99.2 |
| 9 | 126 | 0 | 100 | 9072 | 99.8 |
| 10 | 33 | 0 | 100 | 2970 | 99.9 |
| 11 | 11 | 0 | 100 | 1210 | 100.0 |
| 14 | 1 | 0 | 100 | 182 | 100.0 |
| Total | 8,557,156 | 100 | 1,757,590 | 100 |
| Year | Total Amount of News Items | News Items with Co-Mentions | The Share of News with Co-Mentions | Amount of Co-Mentions |
|---|---|---|---|---|
| 2005 | 1,332,680 | 109,560 | 8.22 | 252,344 |
| 2006 | 1,351,598 | 117,933 | 8.73 | 269,538 |
| 2007 | 1,460,248 | 124,299 | 8.51 | 422,912 |
| 2008 | 1,451,137 | 116,103 | 8 | 312,870 |
| 2009 | 1,471,312 | 101,339 | 6.89 | 254,352 |
| 2010 | 1,490,181 | 96,742 | 6.49 | 245,574 |
| Total | 8,557,156 | 665,976 | 7.78 | 1,757,590 |
| K | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | Total |
|---|---|---|---|---|---|---|---|
| 1 | 1,223,120 | 1,233,665 | 1,335,949 | 1,335,034 | 1,369,973 | 1,393,439 | 7,891,180 |
| 2 | 102,505 | 110,590 | 112,436 | 105,207 | 91,984 | 88,102 | 610,824 |
| 3 | 6395 | 6749 | 7408 | 8597 | 7655 | 6548 | 43,352 |
| 4 | 576 | 533 | 1384 | 1433 | 1335 | 1626 | 6887 |
| 5 | 65 | 45 | 449 | 309 | 300 | 385 | 1553 |
| 6 | 13 | 11 | 404 | 112 | 48 | 62 | 650 |
| 7 | 2 | 3 | 781 | 126 | 11 | 5 | 928 |
| 8 | 3 | 2 | 1314 | 276 | 3 | 13 | 1611 |
| 9 | 0 | 0 | 94 | 30 | 1 | 1 | 126 |
| 10 | 0 | 0 | 23 | 10 | 0 | 0 | 33 |
| 11 | 1 | 0 | 6 | 3 | 1 | 0 | 11 |
| 14 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| Total | 1,332,680 | 1,351,598 | 1,460,248 | 1,451,137 | 1,471,312 | 1,490,181 | 8,557,156 |
| Period | Correlation (Co-Mention) | Correlation (Market Graph) |
|---|---|---|
| 1–7 | 0.1663800 | 0.4318455 |
| 7–13 | 0.1577212 | 0.4616943 |
| 13–19 | 0.1782792 | 0.4442250 |
| 19–25 | 0.1536598 | 0.3278332 |
| 25–31 | 0.1512387 | 0.3656817 |
| 31–37 | 0.1410627 | 0.3898995 |
| 37–43 | 0.1688668 | 0.2300743 |
| 43–49 | 0.1985533 | 0.3901301 |
| 49–55 | 0.2044689 | 0.3643512 |
| 55–61 | 0.2031029 | 0.3365267 |
| 61–67 | 0.2148604 | 0.4209299 |
| Period | Const | ||
|---|---|---|---|
| 7 | 0.001910899 | 0.4188506 | 0.01213292 |
| 13 | 0.002533768 | 0.5131000 | 0.01116052 |
| 19 | 0.001461219 | 0.3769753 | 0.01076794 |
| 25 | 0.005083621 | 0.4708504 | 0.01105582 |
| 31 | 0.014121804 | 0.6001313 | 0.02234221 |
| 37 | 0.015031197 | 0.4376609 | 0.03331619 |
| 43 | 0.170657423 | 0.5866308 | 0.10848345 |
| 49 | 0.051671309 | 0.3141328 | 0.05271308 |
| 55 | 0.006632613 | 0.1917882 | 0.03442195 |
| 61 | 0.098391587 | 0.6550072 | 0.05076811 |
| 67 | 0.018766982 | 0.2941414 | 0.02956882 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faizliev, A.; Balash, V.; Petrov, V.; Grigoriev, A.; Melnichuk, D.; Sidorov, S. Stability Analysis of Company Co-Mention Network and Market Graph Over Time Using Graph Similarity Measures. J. Open Innov. Technol. Mark. Complex. 2019, 5, 55. https://doi.org/10.3390/joitmc5030055
Faizliev A, Balash V, Petrov V, Grigoriev A, Melnichuk D, Sidorov S. Stability Analysis of Company Co-Mention Network and Market Graph Over Time Using Graph Similarity Measures. Journal of Open Innovation: Technology, Market, and Complexity. 2019; 5(3):55. https://doi.org/10.3390/joitmc5030055
Chicago/Turabian StyleFaizliev, Alexey, Vladimir Balash, Vladimir Petrov, Alexey Grigoriev, Dmitriy Melnichuk, and Sergei Sidorov. 2019. "Stability Analysis of Company Co-Mention Network and Market Graph Over Time Using Graph Similarity Measures" Journal of Open Innovation: Technology, Market, and Complexity 5, no. 3: 55. https://doi.org/10.3390/joitmc5030055
APA StyleFaizliev, A., Balash, V., Petrov, V., Grigoriev, A., Melnichuk, D., & Sidorov, S. (2019). Stability Analysis of Company Co-Mention Network and Market Graph Over Time Using Graph Similarity Measures. Journal of Open Innovation: Technology, Market, and Complexity, 5(3), 55. https://doi.org/10.3390/joitmc5030055





