Traveling Wave Solutions for Time-Fractional mKdV-ZK Equation of Weakly Nonlinear Ion-Acoustic Waves in Magnetized Electron–Positron Plasma
Abstract
:1. Introduction
2. Preliminaries
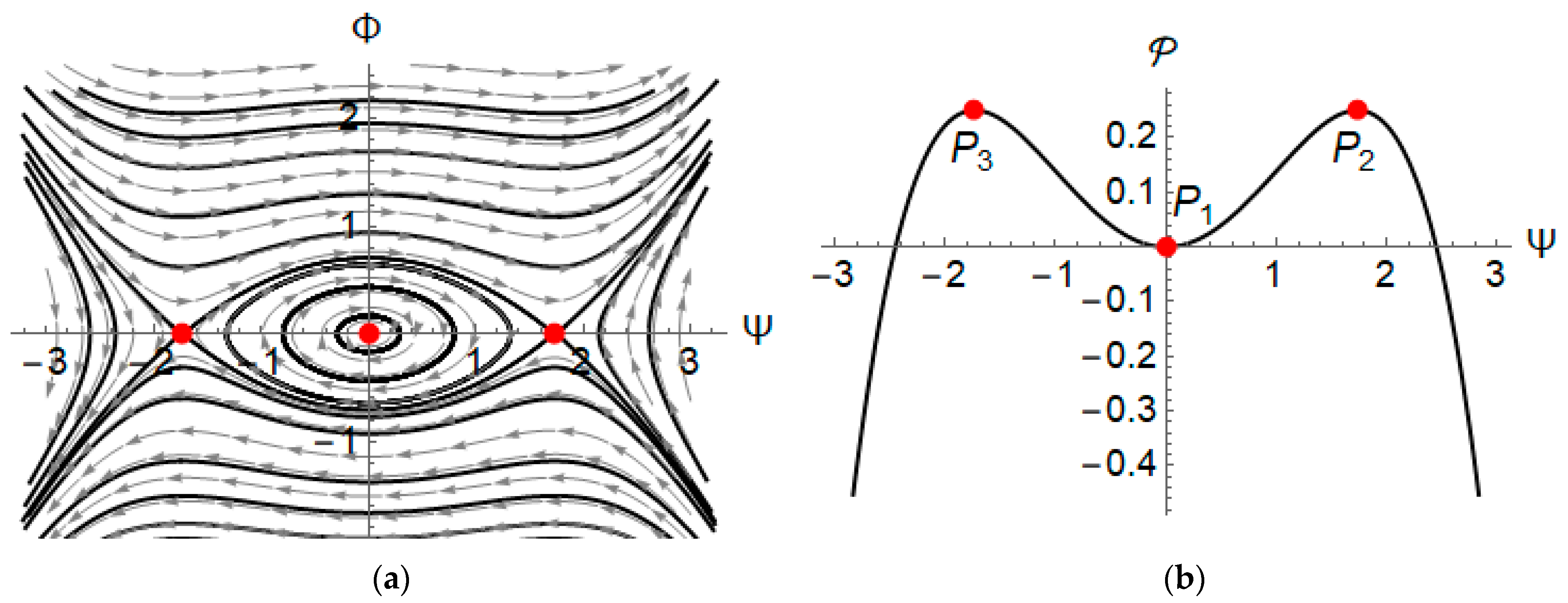
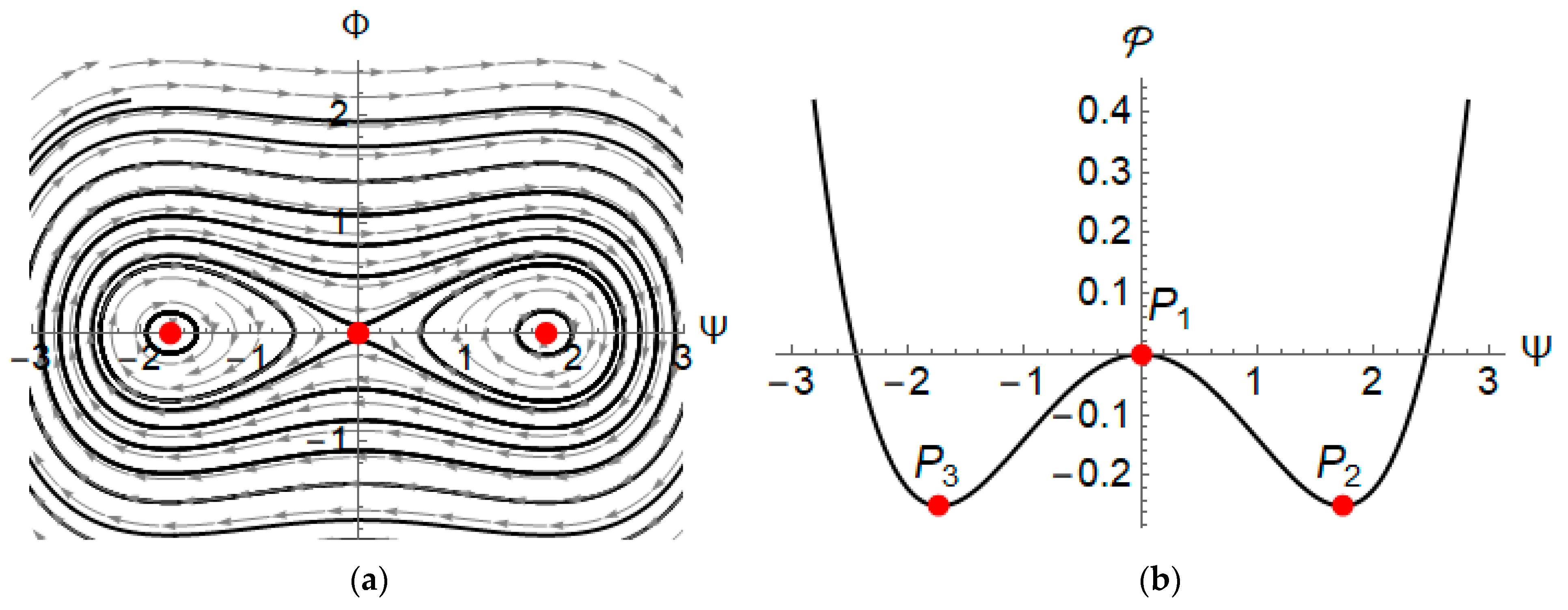
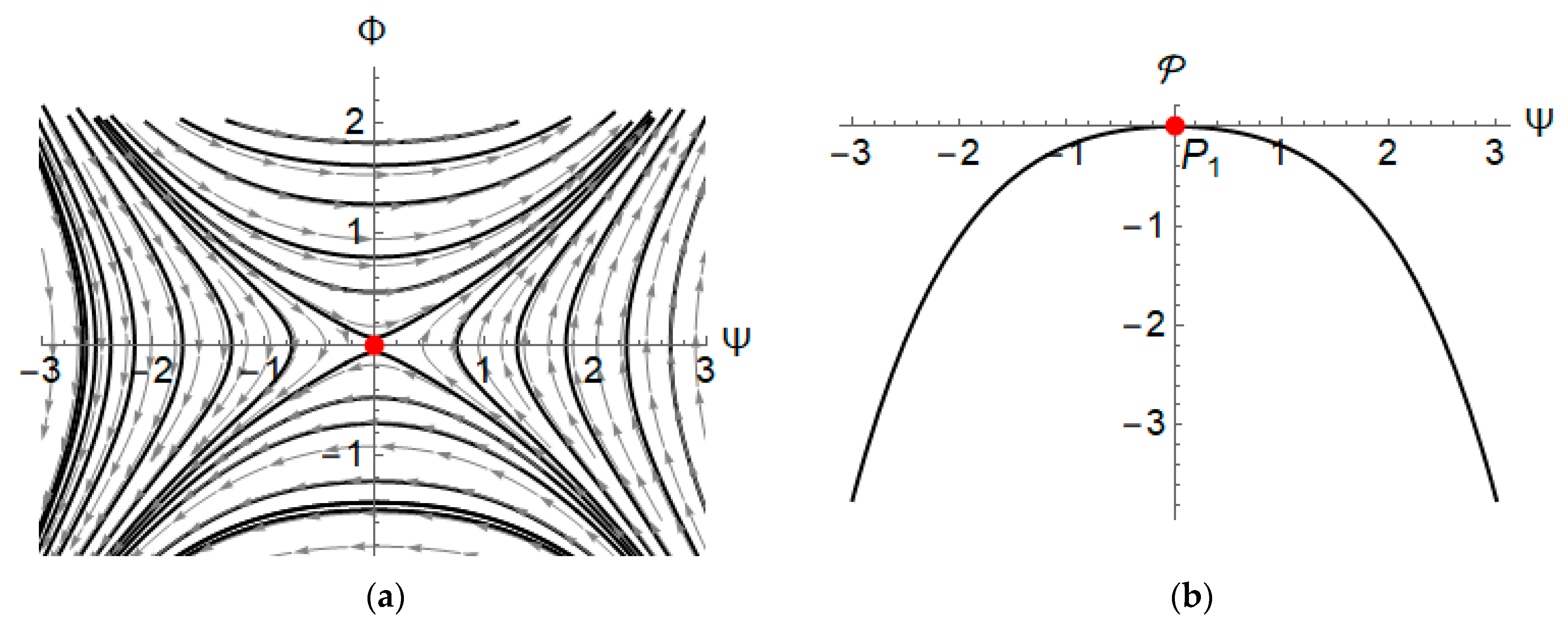
3. Existence of Traveling Wave Solutions
4. Traveling Wave Solutions
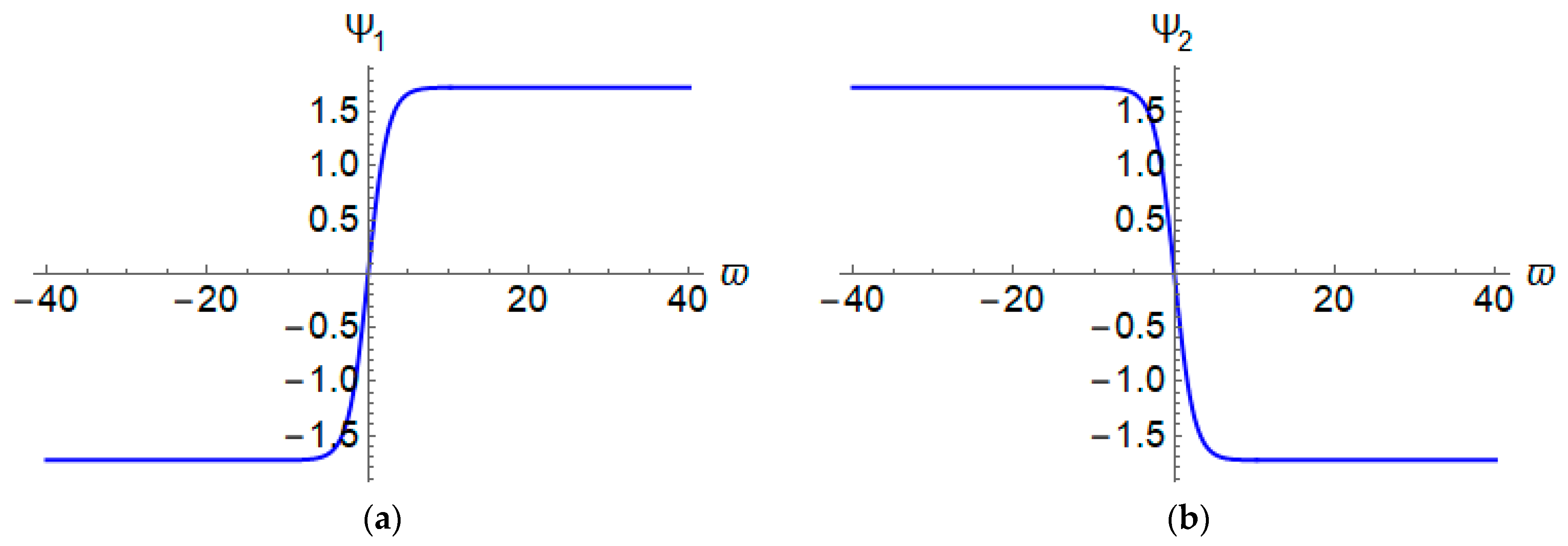
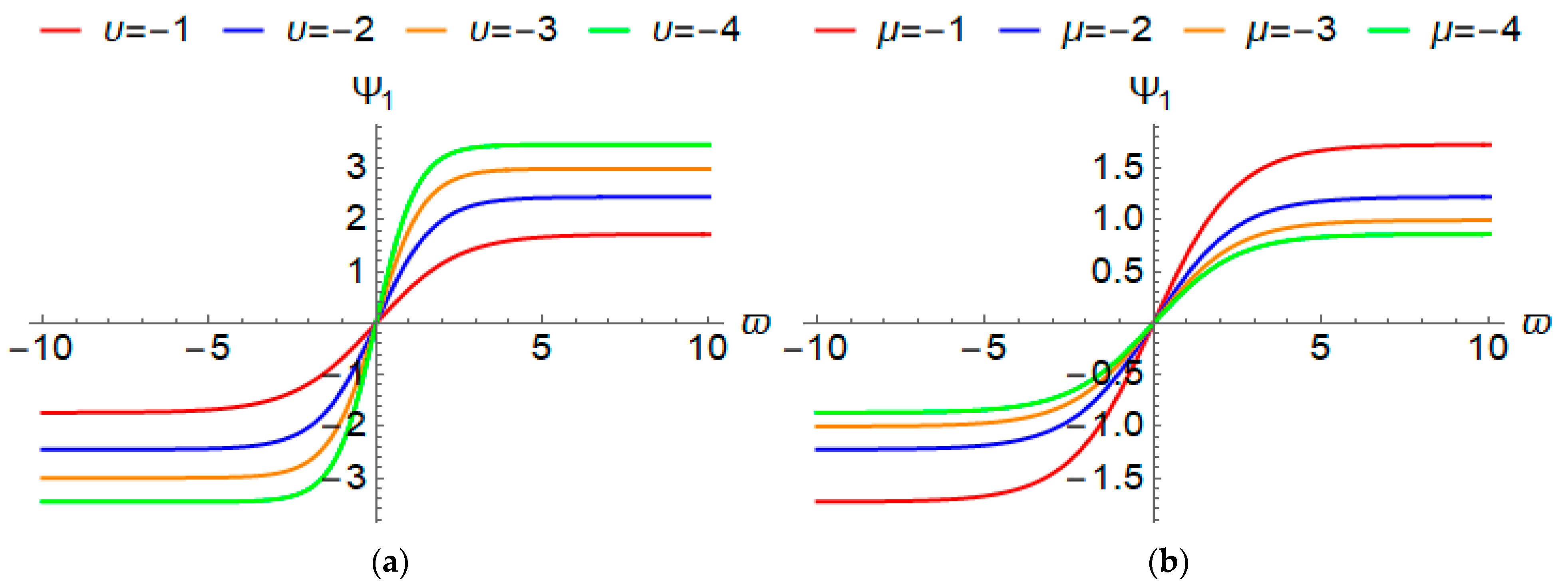
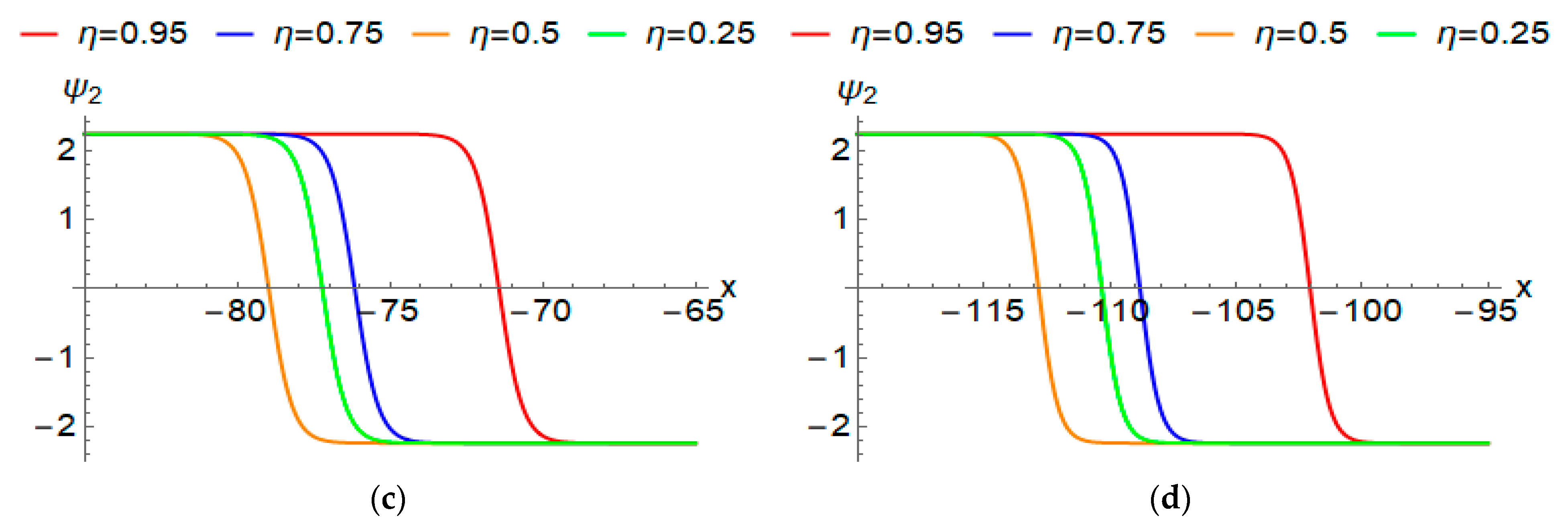
4.1. Kink Wave Solutions
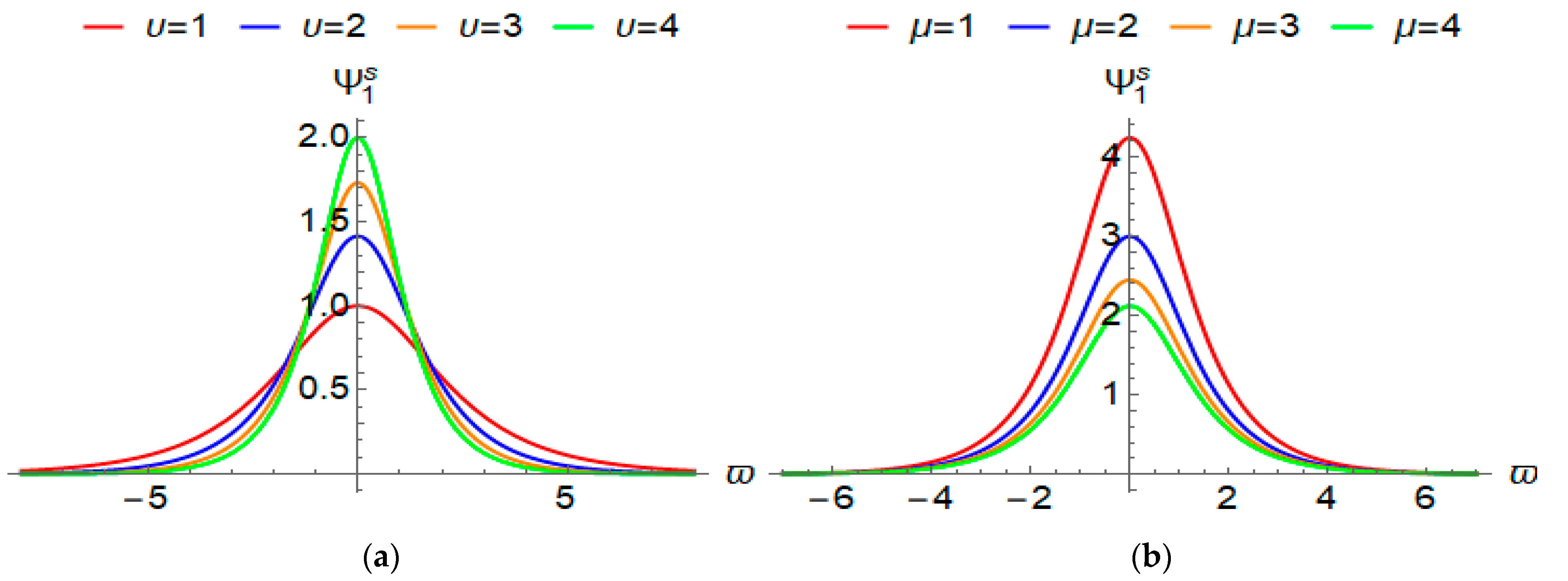
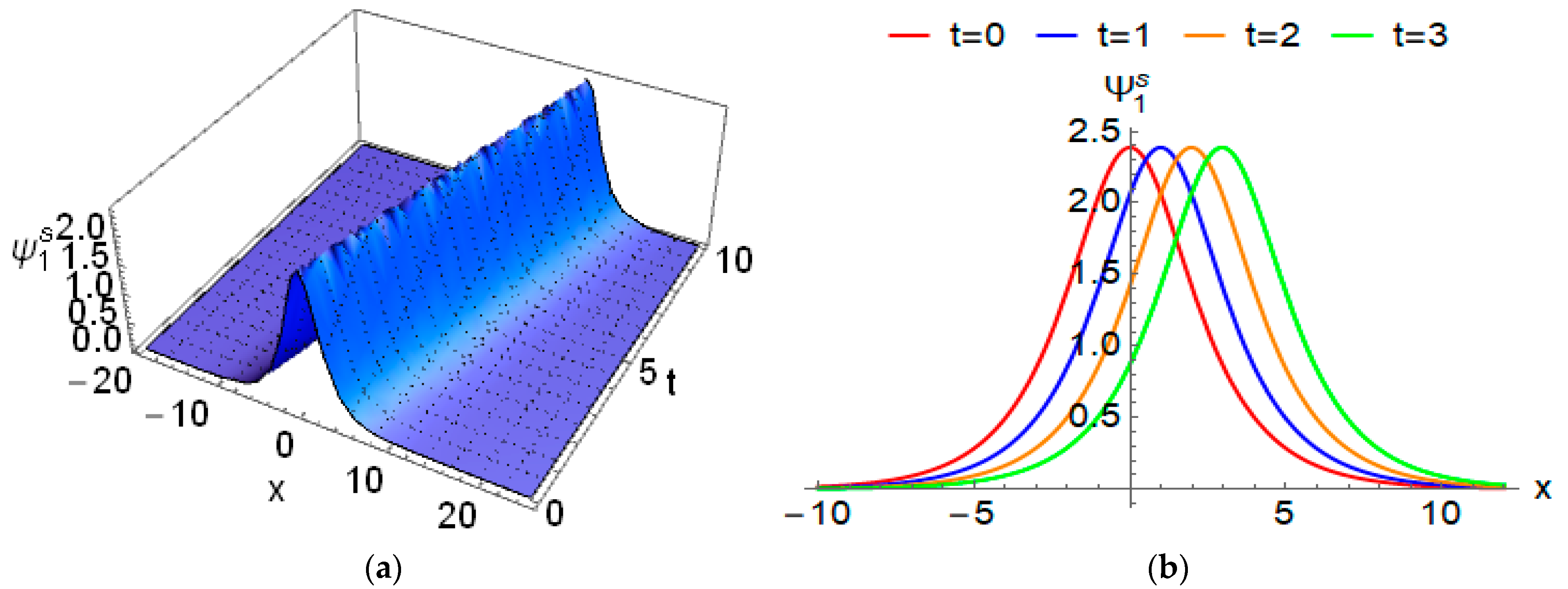
4.2. Solitary Wave Solutions
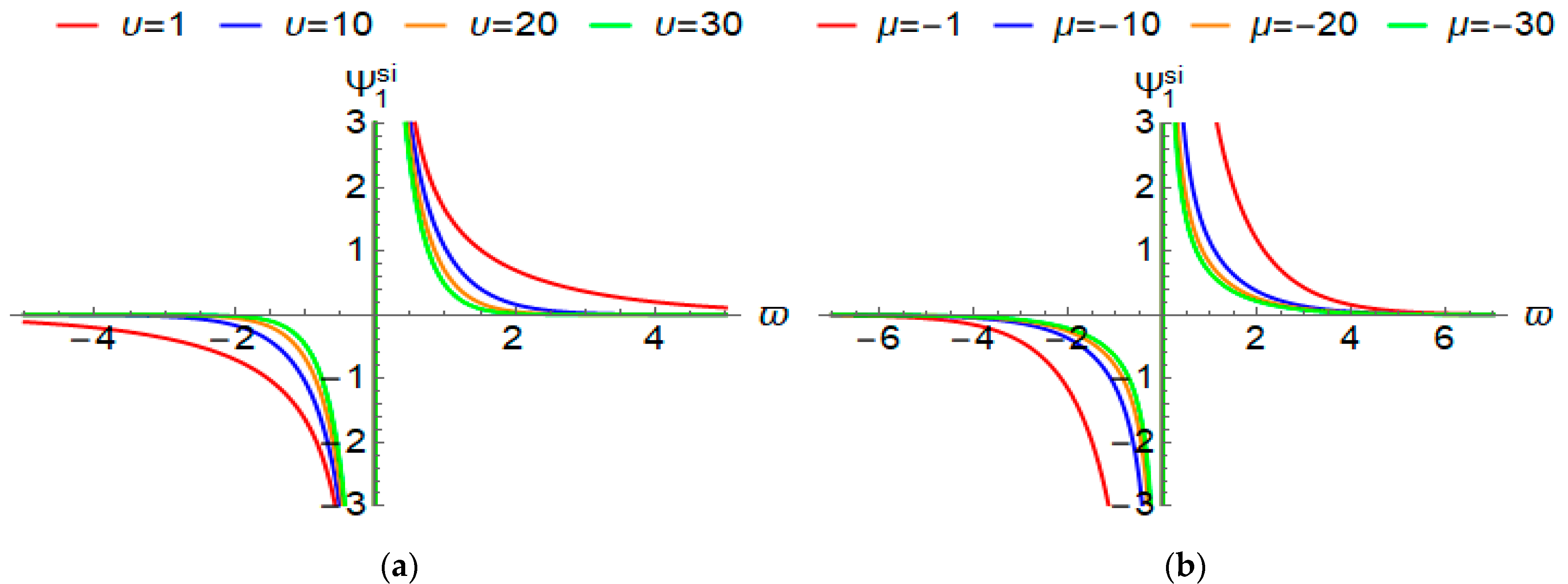
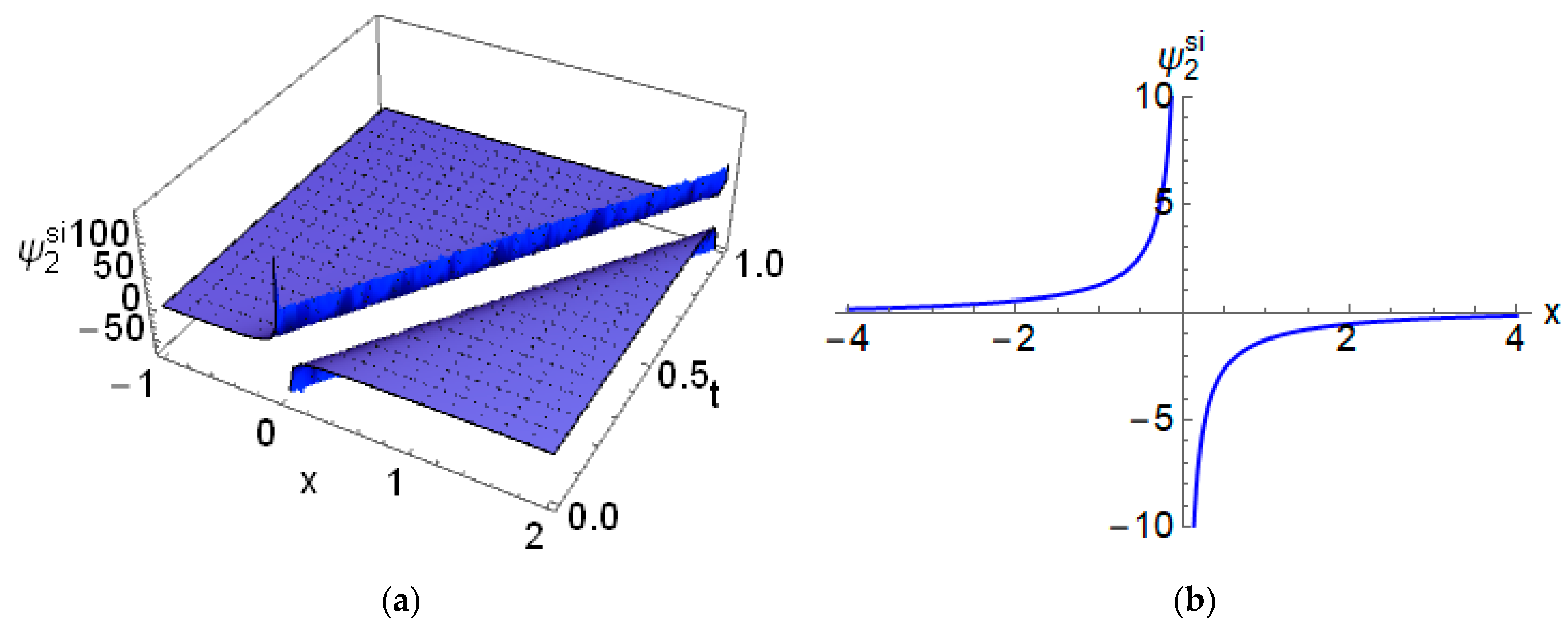
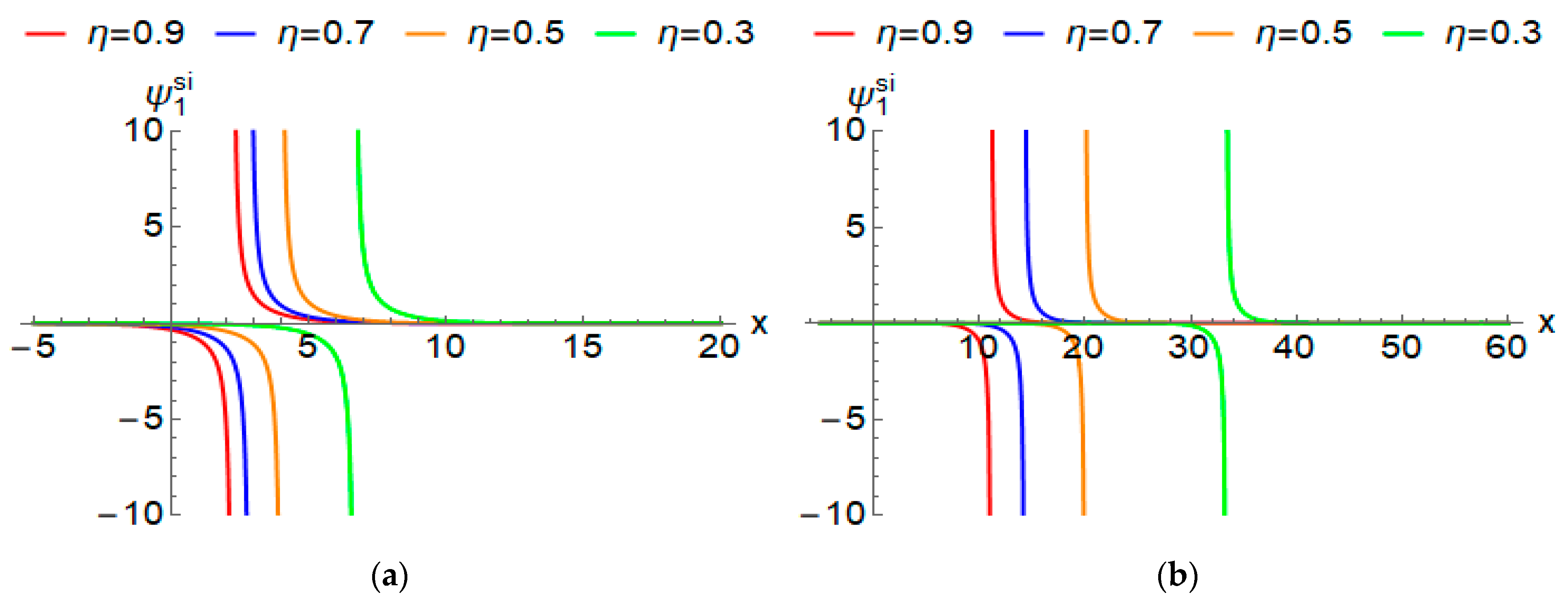
4.3. Singular Wave Solution
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rufai, O.R.; Bharuthram, R.; Singh, S.V.; Lakhina, G.S. Effect of excess superthermal hot electrons on finite amplitude ion-acoustic solitons and supersolitons in a magnetized auroral plasma. Phys. Plasmas 2015, 22, 102305. [Google Scholar] [CrossRef]
- Michel, F.C. Theory of pulsar magnetospheres. Rev. Mod. Phys. 1982, 54, 1. [Google Scholar] [CrossRef]
- Alinejad, H. Ion acoustic solitary waves in magnetized nonextensive electron-positron-ion plasma. Astrophys. Space Sci. 2013, 345, 85–90. [Google Scholar] [CrossRef]
- Ali, S.; Moslem, W.M.; Shukla, P.K.; Schlickeiser, R. Linear and nonlinear ion-acoustic waves in an unmagnetized electron-positron-ion quantum plasma. Phys. Plasmas 2007, 14, 082307. [Google Scholar] [CrossRef]
- Stenflo, L.; Shukla, P.K.; Yu, M.Y. Nonlinear propagation of electromagnetic waves in magnetized electron-positron plasmas. Astrophys. Space Sci. 1985, 117, 303–308. [Google Scholar] [CrossRef]
- Yinhua, C.; Yu, M.Y. Exact ion acoustic solitary waves in an impurity-containing magnetized plasma. Phys. Plasmas 1994, 1, 1868–1870. [Google Scholar] [CrossRef]
- Das, G.; Tagare, S.; Sarma, J. Quasipotential analysis for ion-acoustic solitary waves and double layers in plasmas. Planet. Space Sci. 1998, 46, 417–424. [Google Scholar] [CrossRef]
- Yadav, L.L.; Tiwari, R.S.; Maheshwari, K.P.; Sharma, S.R. Ion-acoustic nonlinear periodic waves in a two-electron-temperature plasma. Phys. Rev. E 1995, 52, 3045–3052. [Google Scholar] [CrossRef]
- Seadawy, A. Stability analysis for Zakharov-Kuznetsov equation of weakly nonlinear ion-acoustic waves in a plasma. Comput. Math. Appl. 2014, 67, 172–180. [Google Scholar] [CrossRef]
- Khater, A.H.; Callebaut, D.K.; Seadawy, A.R. Nonlinear Dispersive Instabilities in Kelvin–Helmholtz Magnetohydrodynamic Flows. Phys. Scr. 2003, 67, 340–349. [Google Scholar] [CrossRef]
- El-Labany, S.K.; Moslem, W.M.; El-Awady, E.I.; Shukla, P.K. Nonlinear dynamics associated with rotating magnetized electron–positron–ion plasmas. Phys. Lett. A 2010, 375, 159–164. [Google Scholar] [CrossRef]
- Verheest, F.; Mace, R.; Pillay, S.R.; Hellberg, M.A. Unified derivation of Korteweg-de Vries- Zakharov-Kuznetsov equations in multispecies plasmas. J. Phys. A Math. Gen. 2002, 35, 795–806. [Google Scholar] [CrossRef]
- Lazarus, I.J.; Bharuthram, R.; Hellberg, M.A. Modified Korteweg–de Vries–Zakharov-Kuznetsov solitons in symmetric two-temperature electron–positron plasmas. J. Plasma Phys. 2008, 74, 519–529. [Google Scholar] [CrossRef]
- Zhou, T.Y.; Tian, B.; Zhang, C.R.; Liu, S.H. Auto-Bäcklund transformations, bilinear forms, multiple-soliton, quasi-soliton and hybrid solutions of a (3+ 1)-dimensional modified Korteweg-de Vries-Zakharov-Kuznetsov equation in an electron-positron plasma. Eur. Phys. J. Plus 2022, 137, 912. [Google Scholar] [CrossRef]
- Rehman, H.; Seadawy, A.R.; Younis, M.; Rizvi, S.; Anwar, I.; Baber, M.; Althobaiti, A. Weakly nonlinear electron-acoustic waves in the fluid ions propagated via a (3+1)-dimensional generalized Korteweg–de-Vries–Zakharov-Kuznetsov equation in plasma physics. Results Phys. 2022, 33, 105069. [Google Scholar] [CrossRef]
- Younas, U.; Ren, J.; Baber, M.Z.; Yasin, M.W.; Shahzad, T. Ion-acoustic wave structures in the fluid ions modeled by higher dimensional generalized Korteweg-de Vries–Zakharov-Kuznetsov equation. J. Ocean Eng. Sci. 2022; in press. [Google Scholar] [CrossRef]
- Khater, M.M. Abundant stable and accurate solutions of the three-dimensional magnetized electron-positron plasma equations. J. Ocean Eng. Sci. 2022; in press. [Google Scholar] [CrossRef]
- Zureigat, H.; Al-Smadi, M.; Al-Khateeb, A.; Al-Omari, S.; Alhazmi, S.E. Fourth-Order Numerical Solutions for a Fuzzy Time-Fractional Convection–Diffusion Equation under Caputo Generalized Hukuhara Derivative. Fractal Fract. 2022, 7, 47. [Google Scholar] [CrossRef]
- Alabedalhadi, M.; Al-Smadi, M.; Al-Omari, S.; Karaca, Y.; Momani, S. New Bright and Kink Soliton Solutions for Fractional Complex Ginzburg–Landau Equation with Non-Local Nonlinearity Term. Fractal Fract. 2022, 6, 724. [Google Scholar] [CrossRef]
- Al-Smadi, M.; Abu Arqub, O.; Gaith, M. Numerical simulation of telegraph and Cattaneo fractional-type models using adaptive reproducing kernel framework. Math. Methods Appl. Sci. 2021, 44, 8472–8489. [Google Scholar] [CrossRef]
- Freihet, A.; Hasan, S.; Al-Smadi, M.; Gaith, M.; Momani, S. Construction of fractional power series solutions to fractional stiff system using residual functions algorithm. Adv. Differ. Equ. 2019, 2019, 95. [Google Scholar] [CrossRef] [Green Version]
- Freihet, A.; Hasan, S.; Alaroud, M.; Al-Smadi, M.; Ahmad, R.R.; Din, U.K.S. Toward computational algorithm for time-fractional Fokker–Planck models. Adv. Mech. Eng. 2019, 11, 1687814019881039. [Google Scholar] [CrossRef]
- Freihet, A.A.; Zuriqat, M. Analytical Solution of Fractional Burgers-Huxley Equations via Residual Power Series Method. Lobachevskii J. Math. 2019, 40, 174–182. [Google Scholar] [CrossRef]
- Alabedalhadi, M.; Al-Smadi, M.; Al-Omari, S.; Baleanu, D.; Momani, S. Structure of optical soliton solution for nonliear resonant space-time Schrödinger equation in conformable sense with full nonlinearity term. Phys. Scr. 2020, 95, 105215. [Google Scholar] [CrossRef]
- Shqair, M.; Alabedalhadi, M.; Al-Omari, S.; Al-Smadi, M. Abundant Exact Travelling Wave Solutions for a Fractional Massive Thirring Model Using Extended Jacobi Elliptic Function Method. Fractal Fract. 2022, 6, 252. [Google Scholar] [CrossRef]
- Alabedalhadi, M. Exact travelling wave solutions for nonlinear system of spatiotemporal fractional quantum mechanics equations. Alex. Eng. J. 2022, 61, 1033–1044. [Google Scholar] [CrossRef]
- Abdelhadi, M.; Alhazmi, S.E.; Al-Omari, S. On a Class of Partial Differential Equations and Their Solution via Local Fractional Integrals and Derivatives. Fractal Fract. 2022, 6, 210. [Google Scholar] [CrossRef]
- Alabedalhadi, M.; Al-Smadi, M.; Al-Omari, S.; Momani, S. New optical soliton solutions for coupled resonant Davey-Stewartson system with conformable operator. Opt. Quantum Electron. 2022, 54, 392. [Google Scholar] [CrossRef]
- Seadawy, A.R. Stability analysis solutions for nonlinear three-dimensional modified Korteweg–de Vries–Zakharov-Kuznetsov equation in a magnetized electron–positron plasma. Phys. A Stat. Mech. Its Appl. 2016, 455, 44–51. [Google Scholar] [CrossRef]
- Sahoo, S.; Ray, S.S. Improved fractional sub-equation method for (3+1) -dimensional generalized fractional KdV–Zakharov-Kuznetsov equations. Comput. Math. Appl. 2015, 70, 158–166. [Google Scholar] [CrossRef]
- Al-Ghafri, K.S.; Rezazadeh, H. Solitons and other solutions of (3+ 1)-dimensional space–time fractional modified KdV–Zakharov-Kuznetsov equation. Appl. Math. Nonlinear Sci. 2019, 4, 289–304. [Google Scholar] [CrossRef] [Green Version]
- Yel, G.; Sulaiman, T.A.; Baskonus, H.M. On the complex solutions to the (3+1)-dimensional conformable fractional modified KdV–Zakharov-Kuznetsov equation. Mod. Phys. Lett. B 2020, 34, 2050069. [Google Scholar] [CrossRef]
- Jin, Q.; Xia, T.; Wang, J. The Exact Solution of the Space-Time Fractional Modified Kdv-Zakharov-Kuznetsov Equation. J. Appl. Math. Phys. 2017, 5, 844–852. [Google Scholar] [CrossRef] [Green Version]
- Abdoon, M.A.; Hasan, F.L.; Taha, N.E. Computational Technique to Study Analytical Solutions to the Fractional Modified KDV-Zakharov-Kuznetsov Equation. Abstr. Appl. Anal. 2022, 2022, 2162356. [Google Scholar] [CrossRef]
- Sahoo, S.; Ray, S.S. Analysis of Lie symmetries with conservation laws for the (3+1) dimensional time-fractional mKdV-ZK equation in ion-acoustic waves. Nonlinear Dyn. 2017, 90, 1105–1113. [Google Scholar] [CrossRef]
- Alhejaili, W.; Salas, A.H.; El-Tantawy, S.A. Novel Approximations to the (Un)forced Pendulum–Cart System: Ansatz and KBM Methods. Mathematics 2022, 10, 2908. [Google Scholar] [CrossRef]
- Dong, S.-H. A New Approach to the Relativistic Schrödinger Equation with Central Potential: Ansatz Method. Int. J. Theor. Phys. 2001, 40, 559–567. [Google Scholar] [CrossRef]
- Sousa, J.V.D.C.; de Oliveira, E.C. On the local M-derivative. arXiv 2017, arXiv:1704.08186. [Google Scholar]
- Asjad, M.I.; Ullah, N.; Rehman, H.U.; Baleanu, D. Optical solitons for conformable space-time fractional nonlinear model. J. Math. Comput. Sci. 2022, 27, 28–41. [Google Scholar] [CrossRef]
- Asjad, M.I.; Ullah, N.; Rehman, H.U.; Gia, T.N. Novel soliton solutions to the Atangana–Baleanu fractional system of equations for the ISALWs. Open Phys. 2021, 19, 770–779. [Google Scholar] [CrossRef]
- Mohan Raja, M.; Vijayakumar, V. Optimal control results for Sobolev-type fractional mixed Volterra–Fredholm type integrodifferential equations of order 1< r < 2 with sectorial operators. Optim. Control Appl. Methods 2022, 43, 1314–1327. [Google Scholar]
- Raja, M.M.; Vijayakumar, V. Existence results for Caputo fractional mixed Volterra-Fredholm-type integrodifferential inclusions of order r∈(1, 2) with sectorial operators. Chaos Solitons Fractals 2022, 159, 112127. [Google Scholar] [CrossRef]
- Mohan Raja, M.; Shukla, A.; Nieto, J.J.; Vijayakumar, V.; Nisar, K.S. A note on the existence and controllability results for fractional integrodifferential inclusions of order r∈(1, 2] with impulses. Qual. Theory Dyn. Syst. 2022, 21, 1–41. [Google Scholar] [CrossRef]
- Ma, Y.K.; Raja, M.M.; Vijayakumar, V.; Shukla, A.; Albalawi, W.; Nisar, K.S. Existence and continuous dependence results for fractional evolution integrodifferential equations of order r∈(1, 2). Alex. Eng. J. 2022, 61, 9929–9939. [Google Scholar] [CrossRef]
- Ma, Y.-K.; Raja, M.M.; Nisar, K.S.; Shukla, A.; Vijayakumar, V. Results on controllability for Sobolev type fractional differential equations of order 1 < r < 2 with finite delay. AIMS Math. 2022, 7, 10215–10233. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Machado, J.T. What is a fractional derivative? J. Comput. Phys. 2015, 293, 4–13. [Google Scholar] [CrossRef]
- Katugampola, U.N. Correction to “What is a fractional derivative?” by Ortigueira and Machado [Journal of Computational Physics, volume 293, 15 July 2015, pages 4–13. Special issue on Fractional PDEs]. J. Comput. Phys. 2016, 321, 1255–1257. [Google Scholar] [CrossRef] [Green Version]
- Sousa, J.V.D.C.; De Oliveira, E.C. A New Truncated M-Fractional Derivative Type Unifying Some Fractional Derivative Types with Classical Properties. Int. J. Anal. Appl. 2018, 16, 83–96. [Google Scholar] [CrossRef] [Green Version]
- İlhan, E.; Kıymaz, İ.O. A generalization of truncated M-fractional derivative and applications to fractional differential equations. Appl. Math. Nonlinear Sci. 2020, 5, 171–188. [Google Scholar]
- Younis, M.; Rehman, H.U.; Iftikhar, M. Computational examples of a class of fractional order nonlinear evolution equations using modified extended direct algebraic method. J. Comput. Methods Sci. Eng. 2015, 15, 359–365. [Google Scholar] [CrossRef]
- Younis, M.; Rehman, H.U.; Iftikhar, M. Travelling wave solutions to some time–space nonlinear evolution equations. Appl. Math. Comput. 2014, 249, 81–88. [Google Scholar] [CrossRef]
- Rehman, H.U.; Inc, M.; Asjad, M.I.; Habib, A.; Munir, Q. New soliton solutions for the space-time fractional modified third order Korteweg–de Vries equation. J. Ocean Eng. Sci. 2022; in press. [Google Scholar] [CrossRef]
- Luo, D. Bifurcation Theory and Methods of Dynamical Systems; World Scientific: Singapore, 1997; Volume 15. [Google Scholar]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 42. [Google Scholar]
- Tamang, J.; Saha, A. Bifurcations of small-amplitude supernonlinear waves of the mKdV and modified Gardner equations in a three-component electron-ion plasma. Phys. Plasmas 2020, 27, 012105. [Google Scholar] [CrossRef]
- Dubinov, A.E.; Kolotkov, D.Y.; Sazonkin, M.A. Nonlinear theory of ion-sound waves in a dusty electron-positron-ion plasma. Tech. Phys. 2012, 57, 585–593. [Google Scholar] [CrossRef]
- Seadawy, A.R. Stability analysis for two-dimensional ion-acoustic waves in quantum plasmas. Phys. Plasmas 2014, 21, 052107. [Google Scholar] [CrossRef]
- Iqbal, Z.; Shah, H.; Qureshi, M.; Masood, W.; Fayyaz, A. Nonlinear Dynamical Analysis of Drift Ion Acoustic Shock Waves in Electron-Positron-Ion Plasma with Adiabatic Trapping. Results Phys. 2022, 41, 105948. [Google Scholar] [CrossRef]


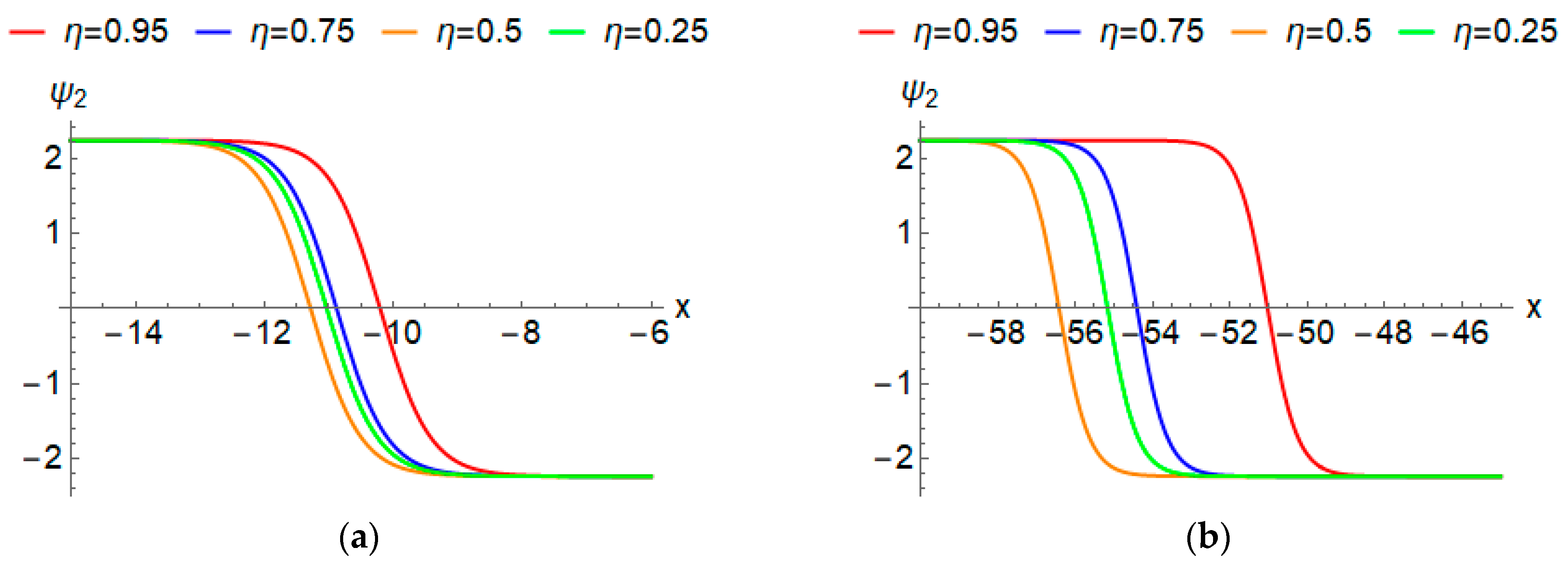
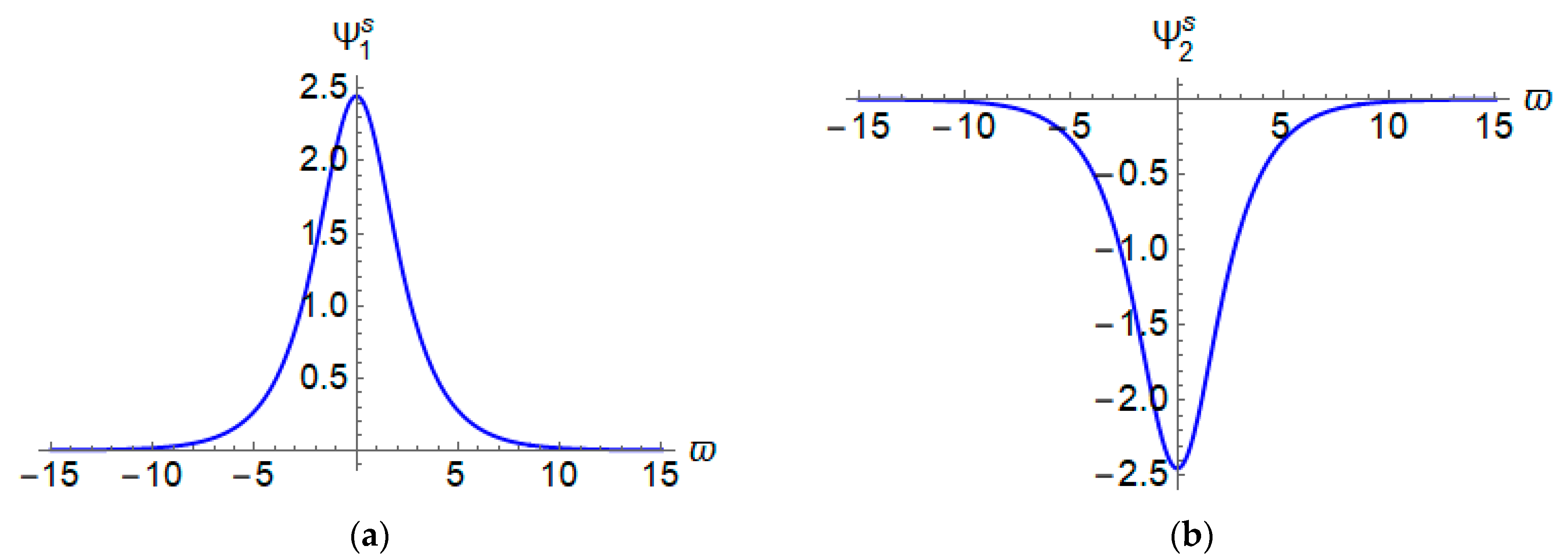


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alabedalhadi, M.; Al-Omari, S.; Al-Smadi, M.; Alhazmi, S. Traveling Wave Solutions for Time-Fractional mKdV-ZK Equation of Weakly Nonlinear Ion-Acoustic Waves in Magnetized Electron–Positron Plasma. Symmetry 2023, 15, 361. https://doi.org/10.3390/sym15020361
Alabedalhadi M, Al-Omari S, Al-Smadi M, Alhazmi S. Traveling Wave Solutions for Time-Fractional mKdV-ZK Equation of Weakly Nonlinear Ion-Acoustic Waves in Magnetized Electron–Positron Plasma. Symmetry. 2023; 15(2):361. https://doi.org/10.3390/sym15020361
Chicago/Turabian StyleAlabedalhadi, Mohammed, Shrideh Al-Omari, Mohammed Al-Smadi, and Sharifah Alhazmi. 2023. "Traveling Wave Solutions for Time-Fractional mKdV-ZK Equation of Weakly Nonlinear Ion-Acoustic Waves in Magnetized Electron–Positron Plasma" Symmetry 15, no. 2: 361. https://doi.org/10.3390/sym15020361
APA StyleAlabedalhadi, M., Al-Omari, S., Al-Smadi, M., & Alhazmi, S. (2023). Traveling Wave Solutions for Time-Fractional mKdV-ZK Equation of Weakly Nonlinear Ion-Acoustic Waves in Magnetized Electron–Positron Plasma. Symmetry, 15(2), 361. https://doi.org/10.3390/sym15020361








