Abstract
Nanofluids behave like non-Newtonian fluids in many cases and, therefore, studying their symmetrical behavior is of paramount importance in nanofluid heat transfer modeling. This article attempts to provide are flection on symmetry via thorough description of a variety of non-Newtonian models and further provides a comprehensive review of articles on non-Newtonian models that have applied symmetrical flow modeling and nanofluid heat transfer. This study reviews articles from recent years and provides a comprehensive analysis of them. Furthermore, a thorough statistical symmetrical analysis regarding the commonality of nanoparticles, base fluids and numerical solutions to equations is provided. This article also investigates the history of nanofluid use as a non-Newtonian fluid; that is, the base fluid is considered to be non-Newtonian fluid or the base fluid is Newtonian, such as water. However, the nanofluid in question is regarded as non-Newtonian in modeling. Results show that 25% of articles considered nanofluids with Newtonian base fluid as a non-Newtonian model. In this article, the following questions are answered for the first time: Which non-Newtonian model has been used to model nanofluids? What are the most common non-Newtonian base fluids? Which numerical method is most used to solve non-Newtonian equations?
1. Introduction
Most materials, ranging from industries to nature, are non-Newtonian and, for us, this is the main reason to investigate this critical subject. Fluids are divided into two types based on their behavior: Newtonian and non-Newtonian. To be more specific, it depends on the shear stress rate and the force or tension, as shown in Figure 1. When the slope of fluid versus the shear rate follows a linear rate, fluid is Newtonian but, on the other hand, if non-linear behavior occurs, it is called non-Newtonian fluid [1].
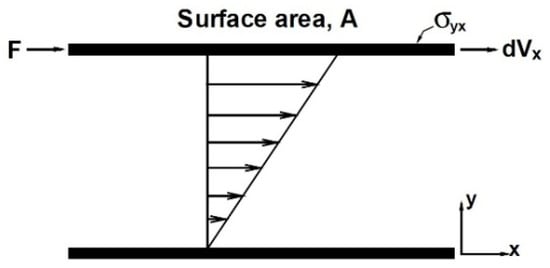
Figure 1.
Shear stress schematic diagram [2].
Non-Newtonian fluid is classified into two subdivided fluids: time-dependent and time-independent fluid [2]. For time-dependent fluid, there are two subdivisions: rheopectic and thixotropic. Figure 2 describes these types of fluids:
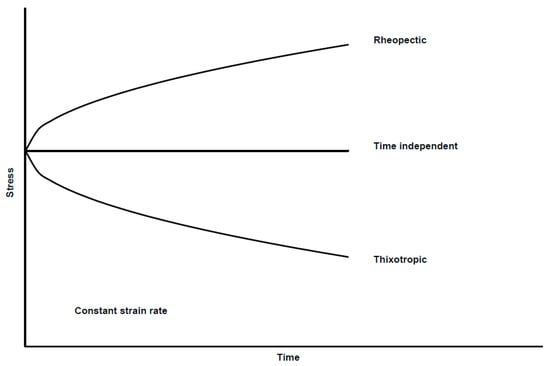
Figure 2.
Thixotropic and rheopectic fluid curves.
One promising application of nanotechnology in heat transfer is to increase the thermophysical properties of common fluids by adding nanoparticles. This suspension is called nanofluid. Some published papers about non-Newtonian fluids/nanofluids and their characteristics and applications can be seen in Refs [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31]. Nanofluids show higher conductivity than their base fluid, and the addition of nanoparticles increases the viscosity of the base fluid [4,12,27,29]. An increase in conductivity increases heat transfer and an increase in viscosity decreases it, especially in free convection [11,13]; the rheological behavior of nanofluid was first examined two decades ago [5]. To model the heat transfer of nanofluids with a Newtonian base fluid and with a low-volume fraction of nanoparticles, the nanofluid can be modeled as Newtonian, but in some cases, nanofluids with a Newtonian base fluid show the behavior of a non-Newtonian fluid [32,33,34,35,36,37,38,39,40,41]. It is known that heat transfer of nanofluids with non-Newtonian base fluids should be modeled in a non-Newtonian manner [42,43,44,45,46,47,48,49,50,51,52,53,54,55,56].
2. Non-Newtonian Nanofluid Heat Transfer
Cabaleiro et al. [57] researched rheological TiO2-ethylene glycol nanofluids at different temperatures ranging from 20 °C to 50 °C and they measured viscosity at different shear rates and showed that nanofluids have similar behavior with non-Newtonian Ostwald–de Waele models. The rheological behavior of polycarbonate containing 0.5 to 15 wt% was investigated by potschke et al. [58]. They reported that more than 2 wt% nanotubes show non-Newtonian behavior. Phuoc et al. [59] investigated the viscosity of multi-walled carbon nanotube nanofluids via experiments and found a 20% decrease in viscosity. Further, they reported, via increasing viscosity, that the fluid behaves as a non-Newtonian shear-thinning fluid. Aladag et al. [60] investigated temperature and shear rate on nanofluid nanotubes Al2O3-water and water-based CNT. They reported that CNT at a high shear rate is Newtonian, whereas Al2O3-water in the low-temperature range of the study shows non-Newtonian behavior. Tamjid and Guenther [61] investigated the rheology of silver nanofluids in diethylene glycol at 0.11–4.38 wt% and found that nanofluids behave as pseudoplastic. They compared the Herschel–Bulkley model and Bingham model by shear stress and shear rate curves. Moghadam et al. [62] investigated graphene–glycerol nanofluids at 0.0025–0.02 wt% and temperatures ranging from 20 to 60 °C. The results showed that nanofluid viscosity will decrease via increasing temperature, increasing by a mass fraction. They found that nanofluids act as non-Newtonian nanofluids. Some non-Newtonian models used for nanofluid behavior modeling can be seen in Table 1.

Table 1.
Models of non-Newtonian fluids with their applicability.
In the following, the flow and heat transfer of nanofluids modeled with non-Newtonian models mentioned in Table 1 are given:
Maleki et al. [70] considered CMC–water as a base flow and Al2O3,TiO2,CuO, and Cu as nanoparticles and by modeling non-Newtonian with power law and comparing the Newtonian model and non-Newtonian models by changing the power-law index which represents different types of non-Newtonian fluids, showing that by adding nanoparticles to the Newtonian model, there is no significant rise in heat transfer. Still, in non-Newtonian models, this is completely different. As shown in Figure 3, the Nusselt number increases via increasing the nanofluid volume fraction.
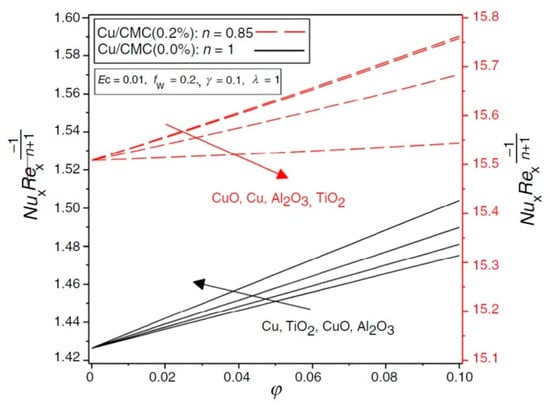
Figure 3.
Nanoparticle action on nanofluid heat transfer [70].
Ibrahim and Negera [71] investigated and compared upper-convected Maxwell and Williamson Nanofluid via the KBM method and found that melting and magnetic field parameter have more effect on the velocity boundary layer of Williamson nanofluid than upper-convected Maxwell nanofluid. The temperature distribution increases with an increase in the Eckert number. Upper-convected Maxwell fluids are less affected by the melting parameter when compared with Williamson fluids. Moreover, the velocity, temperature, and concentration distributions decrease for both fluids when the permeability parameter increases. This manner can be seen for Pr number (Figure 4). Furthermore, the temperature distribution increases with an increase in the Eckert number.
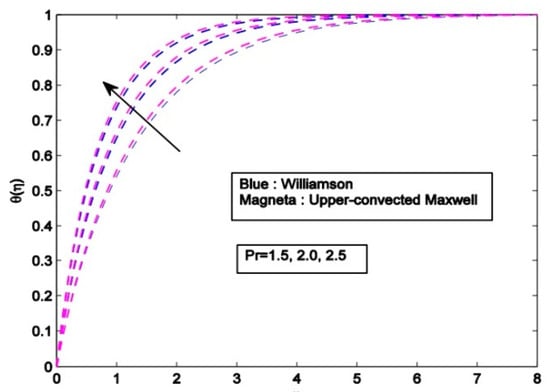
Figure 4.
Temperature curve via Pr number for both base fluids [71].
Abbasian Arani et al. [72] presented a cross model for Al2O3-Water through a lid-driven enclosure. They stated that with nanoparticles, the average Nusselt number is increasing in non-Newtonian nanofluid, but for Newtonian nanofluid, it is related to natural or forced convection flow and may decrease or increase via increasing the Re. The heat transfer rate increases for both Newtonian and non-Newtonian approaches (Figure 5).
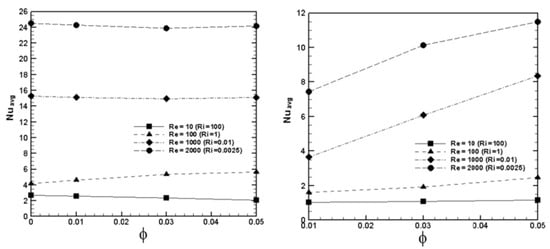
Figure 5.
Average Nu for different Re, Newtonian model for left and non-Newtonian for right [72].
Naseem et al. [73] focused on the gyrotactic microorganisms in the MHD biconvective flow of Powell Eyring nanofluid over a stretched surface. They compared Newtonian and Powell–Eyring fluid and found that the magnitude of velocity is greater in the case of Powell–Eyring fluid, and a comparison of temperature and velocity for Newtonian and non-Newtonian is shown in the Figure 6 as shown below:
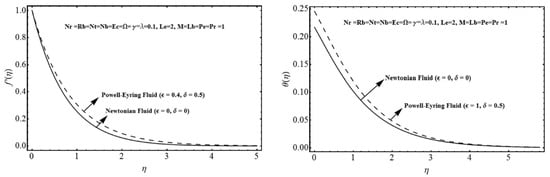
Figure 6.
Comparison of Newtonian and Powell–Eyring in velocity and temperature [73].
Kamran et al. [74] investigated the magneto hydrodynamics flow in Casson nanofluid combined with Joule heating and the KBM method was considered. They found that the Nusselt number declines and the Sherwood number rises by increasing the Eckert number. By increasing the Eckert number, the Nusselt number decreases and the Sherwood number increases. Hartman number has a direct effect on declining both Sherwood and Nu numbers. As shown in Figure 7, an increase in the Casson parameter decreases the fluid velocity, the opposite to temperature.
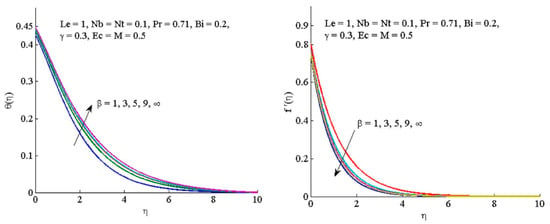
Figure 7.
Temperature and velocity profile with Casson parameter [74].
Sulochana and Ashwinkumar [75] investigated Carreau fluid for film flow in magnetic nanofluids and found that CoFe2O4–water nanofluid has a higher heat transfer rate compared to Fe3O4–water nanofluid, and when the Weissenberg number is increasing, the heat transfer will increase as well (Figure 8).
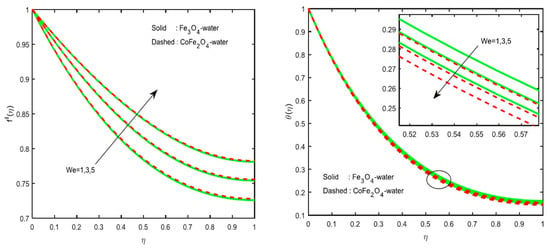
Figure 8.
Velocity and temperature graph with different We [75].
Eldabe and Abou-zeid [76] investigated MHD heat transfer intheBingham model through a non-Darcy porous medium using HPM. They found that velocity decreases by increasing thermophoresis, whereas it decreases (increases) the temperature; the velocity decreases when B increases. They also reported that the temperature distribution experiences an enhancement via increasing the Ecker number, while it decreases by increasing the Darcy number (Figure 9).
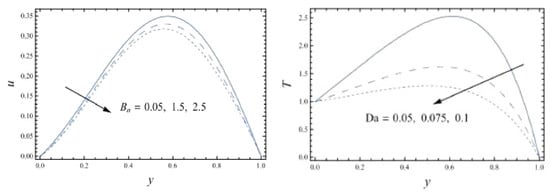
Figure 9.
Velocity graph with different Bingham parameters (left). Temperature distribution via Da number (right) [76].
Hayat et al. [77], using the Jeffrey model, found that the Hartman number on the temperature and concentration distributions is similar in quantity. Temperature and concentration distributions are increased by increasing Hartman number. They reported, as can be seen in Figure 10, thatan increment in Deborah number causes a decreasing manner for temperature and concentration distribution. Further, the Nu number reduces for larger Nt, but it remains constant for Nb.
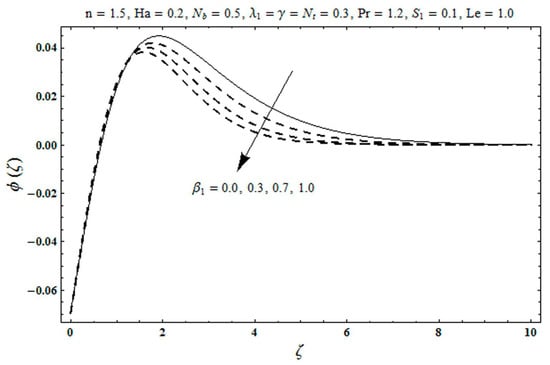
Figure 10.
Concentration for local Deborah number β [77].
Aziz and Shams [78] used water-based Cu and Al2O3 nanofluids on stretching sheet with entropy generation, heat source, and thermal conductivity plus thermal radiation. Via the Maxwell model and numerical simulation, they found that increasing values of the Maxwell parameter cause a decrease in heat transfer for both alumina–water and copper–water nanofluids. However, skin friction has the opposite behavior. Figure 11 shows the effects of nanofluid volume fraction on velocity and temperature.
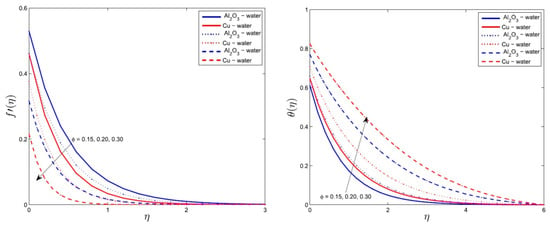
Figure 11.
Velocity and temperature with changing ϕ values [78].
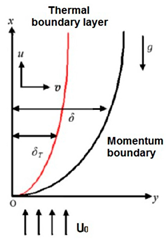
Hashemi and Shokouhmand [79] investigated the effects of Re and Ra on the heat transfer of Al2O3Propellant Dough nanofluid. They used the Herschel–Buckley model for the non-Newtonian model in the vertical plate shown in Figure 12 via a numerical method.
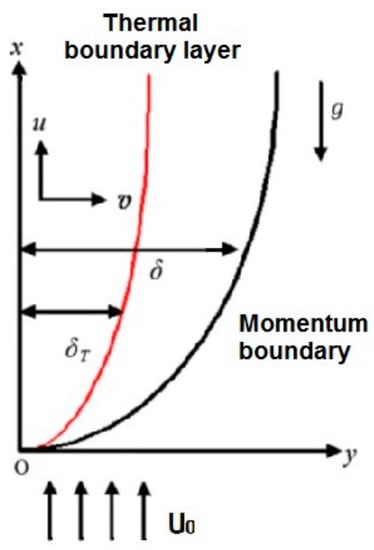
Figure 12.
Thermal boundary layer and momentum boundary [79].
Constant wall temperature boundary condition in heat exchangers was their view and goal in this investigation. In a paper by Hashemi and Shokouhmand, after introducing the rmophysical characteristics, they continue by presenting equations and the Herschel–Bulkley model; their most important results are presented below.
Figure 13 and Figure 14 show that by increasing the Reynolds number, the surface friction coefficient will decrease, and with our expectation, the Nu will increase. On the other hand, via increasing Ra, the Nu number will also increase. Elahi et al. [80] provided a series solution for MHD in the coaxial cylinder for non-Newtonian nanofluid considering slip condition. They chose constant and variable viscosity and nonlinear equations; they used the homotopic asymptotic method. They started with continuity and Navier–Stokes equations by considering incompressibility in the conservation of total mass, momentum, thermal energy, and nanoparticles. Figure 15 shows the thermophoresis effects on temperature and concentration distribution. They also studied the effects of nanoparticle Brownian motion on temperatures and velocity, as shown in Figure 16 and Figure 17, respectively.
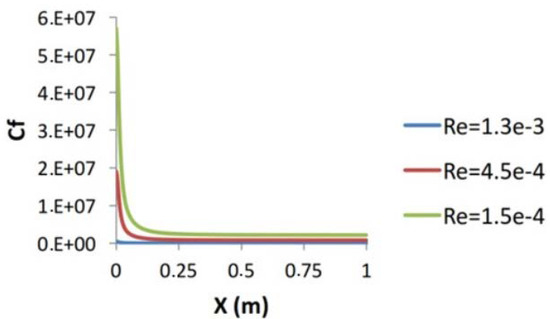
Figure 13.
Surface friction coefficient via different Reynolds number [79].
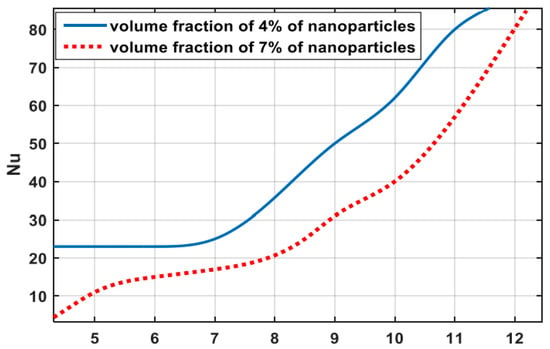
Figure 14.
Nusselt number profile along the vertical wall according to Rayleigh number [79].
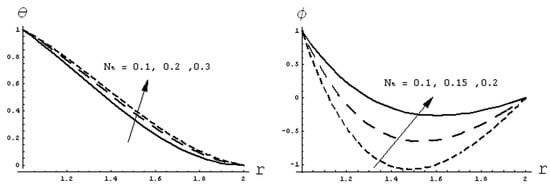
Figure 15.
Effect of Nt on temperature distribution and nanoparticle concentration when Nb = 0:1.
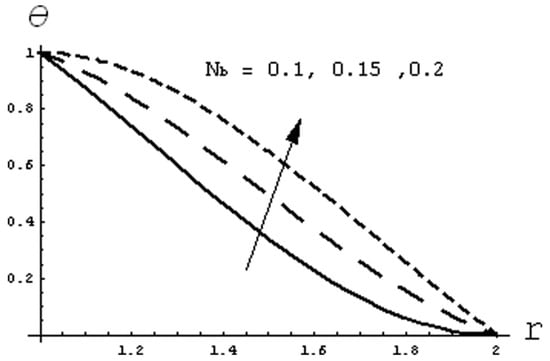
Figure 16.
Effect of Nb on temperature distribution when Nt = 0:1.
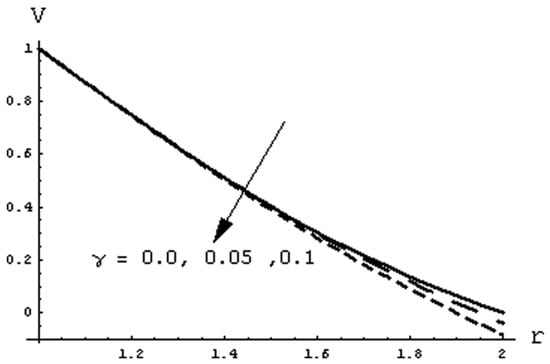
Figure 17.
Effect of g on velocity profile when Nb = 1, M = 0:5, and p = 0:25 for constant viscosity.
Table 2 is a review of non-Newtonian nanofluid articles that have been conducted until now and illustrates different aspects, comparing them in the table. In advance, the reference is in the first column, then detailed geometry, method, models, the remarkable parameters with their ranges, and finally, the non-Newtonian fluid and base fluid are shown and compared.

Table 2.
Geometry methodology and results of articles.
3. Statistics and Results
The following section exhibits a statistical report through the investigated articles [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102] with four questions:
3.1. Which Nanoparticles Were Used the Most?
The diagram shown here is about the most popular nanoparticles. As shown in Figure 18, the concentration ofAl2O3 was more than the others, and CuO and TiO2 are as follows. The chief reason to use Al2O3 is its efficiency in thermal conductivity and heat transfer compared to other nanoparticles.
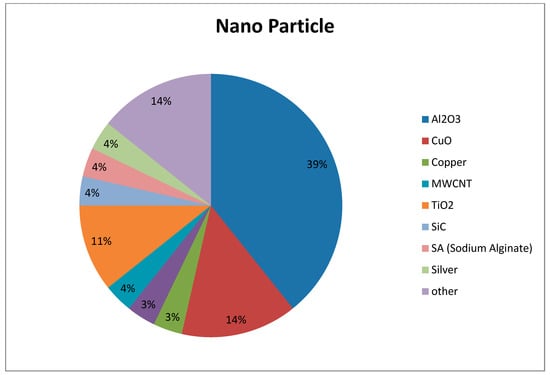
Figure 18.
Nanoparticle diagram.
3.2. Which BaseFluidswere Used the Most?
It is important to investigate the various base fluids through the articles, especially in non-Newtonian fluids. Using water and CMC (by specific volume fraction) was the most used base fluid, and approximately 50% of the articles use this mixture as a base non-Newtonian fluid.
It is also important to know what percentage of nanofluids that are considered non-Newtonian have a Newtonian base fluid such as water. Approximately 25% of the articles considered nanofluids in Newtonian base fluid as a non-Newtonian model as shown in Figure 18 and Figure 19.
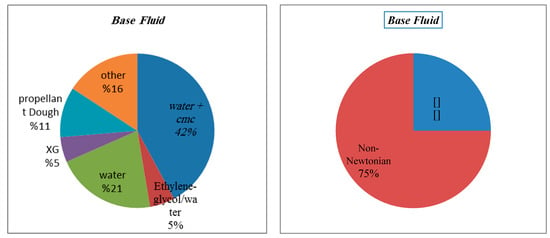
Figure 19.
Most popular base fluid (left); nanofluids with Newtonian base fluid (right).
3.3. Which Non-Newtonian Models Were Used the Most?
In Table 1, different models for non-Newtonian fluid are investigated and listed. The power law model was used in 65% of papers for modeling the non-Newtonian approach of nanofluid. After that, the Casson model was more important than others as shown in Figure 20.
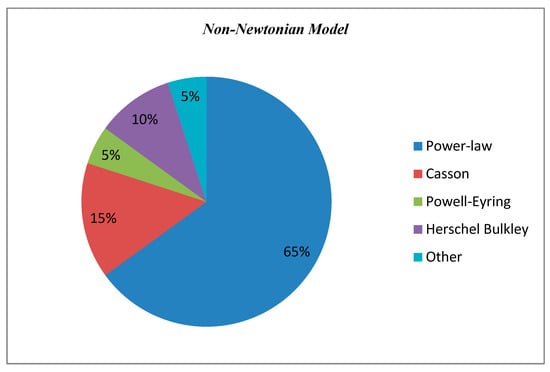
Figure 20.
Non-Newtonian model diagram.
3.4. Which Numerical/Analytical Methods Were Used the Most?
Despite the other issues, methodologies for solving equations were varied, and the numerical method was the most popular. In the diagram, the methods are shown among non-Newtonian nanofluid articles. The FVM is used more for numerical modeling of nanofluid heat transfer as shown in Figure 21.
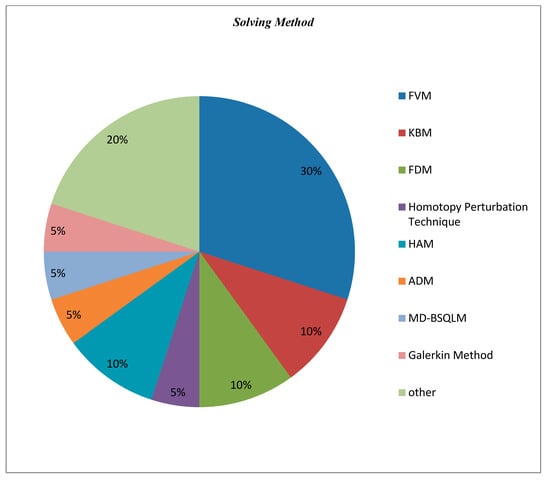
Figure 21.
Methodology for solving diagram.
4. Conclusions
This article provides a comprehensive analysis of non-Newtonian models, which have applied flow modeling and nanofluid heat transfer. This article discusses non-Newtonian nanofluids; also, a statistical analysis regarding the commonality of nanoparticles, base fluids, and methodology is presented in this article. The results demonstrate that:
- Al2O3was the most frequently used nanoparticle.
- 25% of nanofluids modeled as non-Newtonian have a Newtonian base fluid.
- The FVM numerical method is the most widely applied method.
- The water CMC base fluid is further investigated compared with other base fluids.
- The power-law model has been the most frequently applied non-Newtonian modeling of nanofluid heat transfer.
- In all non-Newtonian models, when nanofluid volume fraction increases, the forced convection heat transfer will be increased.
- Increasing non-Newtonian parameters, such as power-law index, Maxwell parameter, etc., leads to a decrease in heat transfer.
Author Contributions
All authors participated equally. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the Prince Sattam bin Abdulaziz University through the project number (2022/RV/14).
Data Availability Statement
Data available upon request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chhabra, R.; Richardson, J. Non-Newtonian Fluid. Behaviour 2008, 1–55. [Google Scholar] [CrossRef]
- Chhabra, R.P. Non-Newtonian Fluids: An Introduction. In Rheology of Complex Fluids; Springer: New York, NY, USA, 2010; pp. 3–34. [Google Scholar] [CrossRef]
- Chhabra, R.; Richardson, J. Non-Newtonian flow in the process industries: Fundamentals and engineering applications. In Non-Newtonian Flow Process Industries; Butterworth-Heinemann: Oxford, UK, 1999; pp. 73–161. [Google Scholar] [CrossRef]
- Yapici, K.; Osturk, O.; Uludag, Y. Dependency of nanofluid rheology on particle size and concentration of various metal oxide nanoparticles. Braz. J. Chem. Eng. 2018, 35, 575–586. [Google Scholar] [CrossRef]
- Pek, Y.S.; Wan, A.C.A.; Shekaran, A.; Zhuo, L.; Ying, J.Y. A thixotropic nanocomposite gel for three-dimensional cell culture. Nat. Nanotechnol. 2008, 3, 671–675. [Google Scholar] [CrossRef] [PubMed]
- Ghica, M.V.; Hîrjău, M.; Lupuleasa, D.; Dinu-Pîrvu, C.-E. Flow and Thixotropic Parameters for Rheological Characterization of Hydrogels. Molecules 2016, 21, 786. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Li, W.; Gong, X. Thixotropy of MR shear-thickening fluids. Smart Mater. Struct. 2010, 19, 125012. [Google Scholar] [CrossRef]
- Naderi, A.; Lindström, T. A comparative study of the rheological properties of three different nanofibrillated cellulose systems. Nord. Pulp Pap. Res. J. 2016, 31, 354–363. [Google Scholar] [CrossRef]
- Wang, G.; Nie, Q.; Zang, C.; Zhang, B.; Zhu, Q.; Luo, G.; Wang, S. Self-Assembled ThermoresponsiveNanogels Prepared by Reverse Micelle → Positive Micelle Method for Ophthalmic Delivery of Muscone, a Poorly Water-Soluble Drug. J. Pharm. Sci. 2016, 105, 2752–2759. [Google Scholar] [CrossRef]
- Das, M.R.; Paria, S. Rheological Behavior of Clay Water Slurry in the Presence of Cationic Surfactants and Electrolytes. Ph.D. Thesis, National Institute of Technology, Rourkela, India, 2013. [Google Scholar]
- Mahian, O.; Kolsi, L.; Amani, M.; Estellé, P.; Ahmadi, G.; Kleinstreuer, C.; Marshall, J.S.; Siavashi, M.; Taylor, R.A.; Niazmand, H.; et al. Recent advances in modeling and simulation of nanofluid flows-Part I: Fundamentals and theory. Phys. Rep. 2019, 790, 1–48. [Google Scholar] [CrossRef]
- Agi, A.; Junin, R.; Gbadamosi, A. Mechanism governing nanoparticle flow behaviour in porous media: Insight for enhanced oil recovery applications. Int. Nano Lett. 2018, 8, 49–77. [Google Scholar] [CrossRef]
- Okonkwo, E.C.; Wole-Osho, I.; Almanassra, I.W.; Abdullatif, Y.M.; Al-Ansari, T. An updated review of nanofluids in various heat transfer devices. J. Therm. Anal. Calorim. 2020, 145, 2817–2872. [Google Scholar] [CrossRef]
- Gbadeyan, J.; Titiloye, E.; Adeosun, A. Effect of variable thermal conductivity and viscosity on Casson nanofluid flow with convective heating and velocity slip. Heliyon 2020, 6, e03076. [Google Scholar] [CrossRef] [PubMed]
- Sivashanmugam, P. Application of Nanofluids in Heat Transfer. In An Overview of Heat Transfer; INTECH Publications: Reijka, Croatia, 2012. [Google Scholar] [CrossRef]
- Morrison, N.F.; Harlen, O.G. Inkjet printing of non-Newtonian fluids. Int. Conf. Digit. Print. Technol. 2011, 2011, 360–364. [Google Scholar]
- Travnicek, P.; Krcalova, E.; Vitez, T. Rheopectic behavior of rendered fat. Pol. J. Environ. Stud. 2013, 22, 1499–1504. [Google Scholar]
- Quanji, Z. Thixotropic Behavior of Cement-Based Materials: Effect of Clay and Cement Types; Iowa State University: Ames, IA, USA, 2010; p. 126. [Google Scholar]
- Bambang, N.; Ikhsan, M.; Tensiska; Sukri, N. Mahani Rheological Properties of Honey and its Application on Honey Flow Simulation through Vertical Tube. IOP Conf. Series: Earth Environ. Sci. 2019, 334, 012041. [Google Scholar] [CrossRef]
- Irgens, F. Rheology and Non-Newtonian Fluids; Springer International Publishing: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Barman, P.C.; Kairi, R.R.; Das, A.; Islam, R. An Overview of Non-Newtonian Fluid. Int. J. Appl. Sci. Eng. 2016, 4, 97. [Google Scholar] [CrossRef]
- Green, R.G. A Fundamental Study of the Flow of Dilatant Fluids. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 1966. [Google Scholar]
- Anon. Non-Newtonian Fluids: Introduction and Guide To Classification and Characteristics. Eng. Sci. Data Unit Data Items 1997, 1982, 97034. [Google Scholar]
- Worldwide, M.I. A Basic Introduction to Rheology. Whitepaper. 2016, pp. 1–19. Available online: https://cdn.technologynetworks.com/TN/Resources/PDF/WP160620BasicIntroRheology.pdf (accessed on 21 December 2022).
- Pinto, F.; Meo, M. Design and Manufacturing of a Novel Shear Thickening Fluid Composite (STFC) with Enhanced out-of-Plane Properties and Damage Suppression. Appl. Compos. Mater. 2017, 24, 643–660. [Google Scholar] [CrossRef]
- Hussain, S.; Shoeibi, S.; Armaghani, T. Impact of magnetic field and entropy generation of Casson fluid on double diffusive natural convection in staggered cavity. Int. Commun. Heat Mass Transf. 2021, 127, 105520. [Google Scholar] [CrossRef]
- Garg, J.; Poudel, B.; Chiesa, M.; Gordon, J.B.; Ma, J.J.; Wang, J.B.; Ren, Z.F.; Kang, Y.T.; Ohtani, H.; Nanda, J.; et al. Enhanced thermal conductivity and viscosity of copper nanoparticles in ethylene glycol nanofluid. J. Appl. Phys. 2008, 103, 074301. [Google Scholar] [CrossRef]
- Sahu, R.; Somashekhar, S.; Manivannan, P. Investigation on Copper Nanofluid Obtained through Micro Electrical Discharge Machining for Dispersion Stability and Thermal Conductivity. Procedia Eng. 2013, 64, 946–955. [Google Scholar] [CrossRef]
- Minea, A.A. A Review on Electrical Conductivity of Nanoparticle-Enhanced Fluids. Nanomaterials 2019, 9, 1592. [Google Scholar] [CrossRef] [PubMed]
- Seminara, G.; Lanzoni, S.; Pittaluga, M.; Solari, L.; Balmforth, N.; Provenzale, A. Geomorphological Fluid Mechanics. Lect. Notes Phys. 2001, 582, 319–338. [Google Scholar] [CrossRef]
- Aghakhani, S.; Pordanjani, A.H.; Karimipour, A.; Abdollahi, A.; Afrand, M. Numerical investigation of heat transfer in a power-law non-Newtonian fluid in a C-Shaped cavity with magnetic field effect using finite difference lattice Boltzmann method. Comput. Fluids 2018, 176, 51–67. [Google Scholar] [CrossRef]
- Rashidi, S.; Karimi, N.; Mahian, O.; Esfahani, J.A. A concise review on the role of nanoparticles upon the productivity of solar desalination systems. J. Therm. Anal. Calorim. 2019, 135, 1145–1159. [Google Scholar] [CrossRef]
- Wang, N.; Maleki, A.; AlhuyiNazari, M.; Tlili, I.; SafdariShadloo, M. Thermal Conductivity Modeling of Nanofluids Contain MgO Particles by Employing Different Approaches. Symmetry 2020, 12, 206. [Google Scholar] [CrossRef]
- Srinivasacharya, D.; Shafeeurrahaman, M. Mixed convection flow of nanofluid in a vertical channel with hall and ion-slip effects. Front. Heat Mass Transf. 2017, 8, 950–959. [Google Scholar] [CrossRef]
- Venkateswarlu, B.; Narayana, P.V.S. Cu-Al2O3/H2O hybrid nanofluid flow past a porous stretching sheet due to temperatue-dependent viscosity and viscous dissipation. Heat Transf. 2021, 50, 432–449. [Google Scholar] [CrossRef]
- Raju, A.; Ojjela, O. Effects of the induced magnetic field, thermophoresis, and Brownian motion on mixed convective Jeffrey nanofluid flow through a porous channel. Eng. Rep. 2019, 1, e12053. [Google Scholar] [CrossRef]
- Narayana, P.S.; Venkateswarlu, B.; Venkataramana, S. Thermal Radiation and Heat Source Effects on a MHD Nanofluid Past a Vertical Plate in a Rotating System with Porous Medium. Heat Transf. 2015, 44, 1–19. [Google Scholar] [CrossRef]
- Bubbico, R.; Celata, G.P.; D’Annibale, F.; Mazzarotta, B.; Menale, C. Comparison of the heat transfer efficiency of nanofluids. Chem. Eng. Trans. 2015, 43, 703–708. [Google Scholar] [CrossRef]
- Malvandi, A.; Hedayati, F.; Ganji, D.D. Fluid Flow and Heat Transfer of Nanofluids over a Flat Plate with Conjugate Heat Transfer. Chall. Nano Micro Scale Sci. Technol. 2014, 2, 108–117. [Google Scholar] [CrossRef]
- Narayana, P.V.S.; Tarakaramu, N.; Babu, D.H. Influence of chemical reaction on MHD couple stress nanoliquid flow over a bidirectional stretched sheet. Int. J. Ambient. Energy 2022, 43, 4928–4938. [Google Scholar] [CrossRef]
- Al Shdaifat, M.Y.; Zulkifli, R.; Sopian, K.; Salih, A.A. Thermal and Hydraulic Performance of CuO/Water Nanofluids: A Review. Micromachines 2020, 11, 416. [Google Scholar] [CrossRef]
- Saleem, S.; Rafiq, H.; Al-Qahtani, A.; El-Aziz, M.A.; Malik, M.Y.; Animasaun, I.L. Magneto Jeffrey Nanofluid Bioconvection over a Rotating Vertical Cone due to Gyrotactic Microorganism. Math. Probl. Eng. 2019, 2019, 1–11. [Google Scholar] [CrossRef]
- Shahzad, F.; Sagheer, M.; Hussain, S. Numerical simulation of magnetohydrodynamic Jeffrey nanofluid flow and heat transfer over a stretching sheet considering Joule heating and viscous dissipation. AIP Adv. 2018, 8, 065316. [Google Scholar] [CrossRef]
- Narayana, P.V.S.; Tarakaramu, N.; Sarojamma, G.; Animasaun, I.L. Numerical Simulation of Nonlinear Thermal Radiation on the 3D Flow of a Couple Stress Casson Nanofluid Due to a Stretching Sheet. J. Therm. Sci. Eng. Appl. 2021, 13, 021028. [Google Scholar] [CrossRef]
- Tarakaramu, N.; Narayana, P.S. Chemical Reaction Effects on Bio-Convection Nanofluid flow between two Parallel Plates in Rotating System with Variable Viscosity: A Numerical Study. J. Appl. Comput. Mech. 2019, 5, 791–803. [Google Scholar] [CrossRef]
- Naidu, K.K.; Babu, D.H.; Reddy, S.H.; Narayana, P.V.S. Radiation and Partial Slip Effects on Magnetohydrodynamic Jeffrey Nanofluid Containing Gyrotactic Microorganisms Over a Stretching Surface. J. Therm. Sci. Eng. Appl. 2021, 13, 031011. [Google Scholar] [CrossRef]
- Hussain, S.; Tayebi, T.; Armaghani, T.; Rashad, A.M.; Nabwey, H.A. Conjugate natural convection of non-Newtonian hybrid nanofluid in wavy-shaped enclosure. Appl. Math. Mech. 2022, 43, 447–466. [Google Scholar] [CrossRef]
- Hussain, S.; Pour, M.; Jamal, M.; Armaghani, T. MHD Mixed Convection and Entropy Analysis of Non-Newtonian Hybrid Nanofluid in a Novel Wavy Elbow-Shaped Cavity with a Quarter Circle Hot Block and a Rotating Cylinder. Exp. Tech. 2022, 1–20. [Google Scholar] [CrossRef]
- Gupta, S.; Gupta, S. MHD three dimensional flow of Oldroyd-B nanofluid over a bidirectional stretching sheet: DTM-Padé Solution. Nonlinear Eng. 2019, 8, 744–754. [Google Scholar] [CrossRef]
- Ibrahim, W.; Sisay, G.; Gamachu, D. Mixed convection flow of Oldroyd-B nano fluid with Cattaneo-Christov heat and mass flux model with third order slip. AIP Adv. 2019, 9, 125023. [Google Scholar] [CrossRef]
- Awad, F.G.; Ahamed, S.M.S.; Sibanda, P.; Khumalo, M. The Effect of Thermophoresis on Unsteady Oldroyd-B Nanofluid Flow over Stretching Surface. PLOS ONE 2015, 10, e0135914. [Google Scholar] [CrossRef] [PubMed]
- Sulaiman, M.; Ali, A.; Islam, S. Heat and Mass Transfer in Three-Dimensional Flow of an Oldroyd-B Nanofluid with Gyrotactic Micro-Organisms. Math. Probl. Eng. 2018, 2018, 1–15. [Google Scholar] [CrossRef]
- Rafique, K.; Anwar, M.I.; Misiran, M.; Khan, I.; Alharbi, S.O.; Thounthong, P.; Nisar, K.S. Numerical Solution of Casson Nanofluid Flow Over a Non-linear Inclined Surface with Soret and Dufour Effects by Keller-Box Method. Front. Phys. 2019, 7, 1–13. [Google Scholar] [CrossRef]
- Shah, Z.; Kumam, P.; Deebani, W. Radiative MHD Casson Nanofluid Flow with Activation energy and chemical reaction over past nonlinearly stretching surface through Entropy generation. Sci. Rep. 2020, 10, 4402. [Google Scholar] [CrossRef]
- Oyelakin, I.S.; Mondal, S.; Sibanda, P. Unsteady Casson nanofluid flow over a stretching sheet with thermal radiation, convective and slip boundary conditions. Alex. Eng. J. 2016, 55, 1025–1035. [Google Scholar] [CrossRef]
- Alzahrani, A.K.; Sivasankaran, S.; Bhuvaneswari, M. Numerical Simulation on Convection and Thermal Radiation of Casson Fluid in an Enclosure with Entropy Generation. Entropy 2020, 22, 229. [Google Scholar] [CrossRef]
- Cabaleiro, D.; Pastoriza-Gallego, M.J.; Gracia-Fernández, C.; Piñeiro, M.M.; Lugo, L. Rheological and volumetric properties of TiO2-ethylene glycol nanofluids. Nanoscale Res. Lett. 2013, 8, 286. [Google Scholar] [CrossRef]
- Pötschke, P.; Fornes, T.; Paul, D. Rheological behavior of multiwalled carbon nanotube/polycarbonate composites. Polymer 2002, 43, 3247–3255. [Google Scholar] [CrossRef]
- Phuoc, T.X.; Massoudi, M.; Chen, R.-H. Viscosity and thermal conductivity of nanofluids containing multi-walled carbon nanotubes stabilized by chitosan. Int. J. Therm. Sci. 2011, 50, 12–18. [Google Scholar] [CrossRef]
- Aladag, B.; Halelfadl, S.; Doner, N.; Maré, T.; Duret, S.; Estellé, P. Experimental investigations of the viscosity of nanofluids at low temperatures. Appl. Energy 2012, 97, 876–880. [Google Scholar] [CrossRef]
- Tamjid, E.; Guenther, B.H. Rheology and colloidal structure of silver nanoparticles dispersed in diethylene glycol. Powder Technol. 2010, 197, 49–53. [Google Scholar] [CrossRef]
- Moghaddam, M.B.; Goharshadi, E.K.; Entezari, M.H.; Nancarrow, P. Preparation, characterization, and rheological properties of graphene–glycerol nanofluids. Chem. Eng. J. 2013, 231, 365–372. [Google Scholar] [CrossRef]
- Aziz, T.; Mahomed, F.M. Applications of Group Theoretical Methods to Non-Newtonian Fluid Flow Models: Survey of Results. Math. Probl. Eng. 2017, 2017, 1–43. [Google Scholar] [CrossRef]
- Pawlek, R.A.; Tien, C. Laminar heat transfer to non-Newtonian fluids in the entrance region of a circular conduit. Can. J. Chem. Eng. 1964, 42, 222–227. [Google Scholar] [CrossRef]
- Malek, J. Introduction to non-Newtonian fluid mechanics. Von Karman Inst. Fluid Dyn. Non-Newton. Flows 2012, 57, 11–34. [Google Scholar]
- Yang, L.; Du, K. A comprehensive review on the natural, forced, and mixed convection of non-Newtonian fluids (nanofluids) inside different cavities. J. Therm. Anal. Calorim. 2020, 140, 2033–2054. [Google Scholar] [CrossRef]
- Sochi, T. Pore-Scale Modeling of Non-Newtonian Flow in Porous Media. arXiv 2010, arXiv:1011.076. [Google Scholar]
- Robertson, A.M. Lecture Notes on Non-Newtonian Fluids Part I: Inelastic Fluids. University of Pittsburgh Press: Pittsburgh, PA, USA, 2005. [Google Scholar]
- Sochi, T. Modeling the Flow of a Bautista-Manero Fluid in Porous Media. arXiv 2009, arXiv:0905.1960,. [Google Scholar] [CrossRef]
- Maleki, H.; Safaei, M.R.; Togun, H.; Dahari, M. Heat transfer and fluid flow of pseudo-plastic nanofluid over a moving permeable plate with viscous dissipation and heat absorption/generation. J. Therm. Anal. Calorim. 2019, 135, 1643–1654. [Google Scholar] [CrossRef]
- Ibrahim, W.; Negera, M. Melting and viscous dissipation effect on upper-convected Maxwell and Williamson nanofluid. Eng. Rep. 2020, 2, e12159. [Google Scholar] [CrossRef]
- Arani, A.A.A.; Sheikhzadeh, G.A.; Arani, A.G. Study of Fluid Flow and Heat Transfer of AL2O3-Water as a Non-Newtonian Nanofluid through Lid-Driven Enclosure. Chall. Nano Micro Scale Sci. Technol. 2014, 2, 118–131. [Google Scholar] [CrossRef]
- Naseem, F.; Shafiq, A.; Zhao, L.; Naseem, A. MHD biconvective flow of Powell Eyring nanofluid over stretched surface. AIP Adv. 2017, 7, 065013. [Google Scholar] [CrossRef]
- Kamran, A.; Hussain, S.; Sagheer, M.; Akmal, N. A numerical study of magnetohydrodynamics flow in Casson nanofluid combined with Joule heating and slip boundary conditions. Results Phys. 2017, 7, 3037–3048. [Google Scholar] [CrossRef]
- Sulochana, C.; Ashwinkumar, G. Carreau Model for Liquid Thin Film Flow of Dissipative Magnetic-Nanofluids over a Stretching Sheet. Int. J. Hybrid Inf. Technol. 2017, 10, 239–254. [Google Scholar] [CrossRef]
- Eldabe, N.; Abou-Zeid, M. Homotopy perturbation method for MHD pulsatile non-Newtonian nanofluid flow with heat transfer through a non-Darcy porous medium. J. Egypt. Math. Soc. 2017, 25, 375–381. [Google Scholar] [CrossRef]
- Hayat, T.; Aziz, A.; Muhammad, T.; Alsaedi, A. A revised model for Jeffrey nanofluid subject to convective condition and heat generation/absorption. PLOS ONE 2017, 12, e0172518. [Google Scholar] [CrossRef]
- Aziz, A.; Shams, M. Entropy generation in MHD Maxwell nanofluid flow with variable thermal conductivity, thermal radiation, slip conditions, and heat source. AIP Adv. 2020, 10, 015038. [Google Scholar] [CrossRef]
- Hashemi, S.; Shokouhmand, H. Study on the Vertical Wall Heat Transfer by Numerical Simulation of Non-Newtonion (Herschel-Bulkley Model) Nanofluid and Changes. J. Mater. Environ. Sci. 2018, 9, 1418–1430. [Google Scholar]
- Ellahi, R.; Aziz, S.; Zeeshan, A. Non-Newtonian nanofluid flow through a porous medium between two coaxial cylinders with heat transfer and variable viscosity. J. Porous Media 2013, 16, 205–216. [Google Scholar] [CrossRef]
- Pahlevaninejad, N.; Rahimi, M.; Gorzin, M. Thermal and hydrodynamic analysis of non-Newtonian nanofluid in wavy microchannel. J. Therm. Anal. Calorim. 2020, 143, 811–825. [Google Scholar] [CrossRef]
- Maghsoudi, P.; Shahriari, G.; Rasam, H.; Sadeghi, S. Flow and natural convection heat transfer characteristics of non-Newtonian nanofluid flow bounded by two infinite vertical flat plates in presence of magnetic field and thermal radiation using Galerkin method. J. Central South Univ. 2019, 26, 1294–1305. [Google Scholar] [CrossRef]
- Yang, L.; Du, K.; Zhang, Z. Heat transfer and flow optimization of a novel sinusoidal minitube filled with non-Newtonian SiC/EG-water nanofluids. Int. J. Mech. Sci. 2020, 168, 105310. [Google Scholar] [CrossRef]
- Singh, A.K.; Kishore, N. Laminar Mixed Convection of Non-Newtonian Nanofluids Flowing Vertically Upward Across a Confined Circular Cylinder. J. Therm. Sci. Eng. Appl. 2018, 10, 041012. [Google Scholar] [CrossRef]
- Rao, A.S.; Sainath, S.; Rajendra, P.; Ramu, G. Mathematical Modelling of Hydromagnetic Casson non-Newtonian Nanofluid Convection Slip Flow from an Isothermal Sphere. Nonlinear Eng. 2019, 8, 645–660. [Google Scholar] [CrossRef]
- Rajkotwala, A.; Banerjee, J. Influence of rheological behavior of nanofluid on heat transfer. WSEAS Trans. Heat Mass Transf. 2013, 8, 67–81. [Google Scholar]
- Mahdy, A.; Chamkha, A.J. Heat transfer and fluid flow of a non-Newtonian nanofluid over an unsteady contracting cylinder employing Buongiorno’s model. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 703–723. [Google Scholar] [CrossRef]
- Agbaje, T.; Mondal, S.; Motsa, S.; Sibanda, P. A numerical study of unsteady non-Newtonian Powell-Eyring nanofluid flow over a shrinking sheet with heat generation and thermal radiation. Alex. Eng. J. 2017, 56, 81–91. [Google Scholar] [CrossRef]
- Akinshilo, A.; Adingwupu, A.; Olofinkua, J. Further Evaluation of Squeezing Flow and Heat Transfer of non-Newtonian Fluid with Nanoparticles Conveyed through Vertical Parallel Plates. J. Mech. Eng. 2019, 3, 15–24. [Google Scholar] [CrossRef]
- Abdelsalam, S.I.; Bhatti, M.M. The study of non-Newtonian nanofluid with hall and ion slip effects on peristaltically induced motion in a non-uniform channel. RSC Adv. 2018, 8, 7904–7915. [Google Scholar] [CrossRef] [PubMed]
- Loenko, D.S.; Shenoy, A.; Sheremet, M.A. Natural Convection of Non-Newtonian Power-Law Fluid in a Square Cavity with a Heat-Generating Element. Energies 2019, 12, 2149. [Google Scholar] [CrossRef]
- Ling, Z.; He, Z.; Xu, T.; Fang, X.; Gao, X.; Zhang, Z. Experimental and Numerical Investigation on Non-Newtonian Nanofluids Flowing in Shell Side of Helical Baffled Heat Exchanger Combined with Elliptic Tubes. Appl. Sci. 2017, 7, 48. [Google Scholar] [CrossRef]
- Shamsi, M.R.; Akbari, O.A.; Marzban, A.; Toghraie, D.; Mashayekhi, R. Increasing heat transfer of non-Newtonian nanofluid in rectangular microchannel with triangular ribs. Phys. E: Low-dimensional Syst. Nanostructures 2017, 93, 167–178. [Google Scholar] [CrossRef]
- Hojjat, M. Modeling heat transfer of non-Newtonian nanofluids using hybrid ANN-Metaheuristic optimization algorithm. J. Part. Sci. Technol. 2017, 3, 233–241. [Google Scholar] [CrossRef]
- Jahanbakhshi, A.; Nadooshan, A.A. Numerical study of non-Newtonian fluid convection by power law model in a square enclosure with central heating source. Modares Mech. Eng. 2018, 17, 343–352. [Google Scholar]
- Zhang, Z.; Xie, Y.; Zhang, D.; Xie, G. Flow Characteristic and Heat Transfer for Non-Newtonian Nanofluid in Rectangular Microchannels with Teardrop Dimples/Protrusions. Open Phys. 2017, 15, 197–206. [Google Scholar] [CrossRef]
- Asl, M.S.; Toghraie, D.; Azimian, A.R. Numerical simulation of convective heat transfer in a turbulant non-Newtonian nanofluid flow through a horizontal circular tube. J. Model. Eng. 2018, 16, 113–120. (In Persian) [Google Scholar]
- Nabwey, H.A. A Hybrid Methodology to Extract Decision Rules of Heat and Mass Transfer of the Flow of a Non-Newtonian Nanofluid Towards a Vertical Stretching Surface. J. Nanofluids 2020, 9, 121–127. [Google Scholar] [CrossRef]
- Sajadifar, S.A.; Karimipour, A.; Toghraie, D. Fluid flow and heat transfer of non-Newtonian nanofluid in a microtube considering slip velocity and temperature jump boundary conditions. Eur. J. Mech.-B/Fluids 2017, 61, 25–32. [Google Scholar] [CrossRef]
- Akbari, O.A.; Toghraie, D.; Karimipour, A.; Marzban, A.; Ahmadi, G.R. The effect of velocity and dimension of solid nanoparticles on heat transfer in non-Newtonian nanofluid. Phys. E: Low-dimensional Syst. Nanostructures 2017, 86, 68–75. [Google Scholar] [CrossRef]
- Ternik, P.; Rudolf, R.; Žunič, Z. Heat-transfer characteristics of a non-newtonian Au nanofluid in a cubical enclosure with differentially heated side walls. Mater. Tehnol. 2015, 49, 87–93. [Google Scholar]
- Zhang, Y.; Zhang, M.; Bai, Y. Unsteady flow and heat transfer of power-law nanofluid thin film over a stretching sheet with variable magnetic field and power-law velocity slip effect. J. Taiwan Inst. Chem. Eng. 2017, 70, 104–110. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).