Improving the Performance of RLizard on Memory-Constraint IoT Devices with 8-Bit ATmega MCU

Abstract

We propose an improved RLizard implementation method that enables the RLizard key encapsulation mechanism (KEM) to run in a resource-constrained Internet of Things (IoT) environment with an 8-bit micro controller unit (MCU) and 8–16 KB of SRAM. Existing research has shown that the proposed method can function in a relatively high-end IoT environment, but there is a limitation when applying the existing implementation to our environment because of the insufficient SRAM space. We improve the implementation of the RLizard KEM by utilizing electrically erasable, programmable, read-only memory (EEPROM) and flash memory, which is possessed by all 8-bit ATmega MCUs. In addition, in order to prevent a decrease in execution time related to their use, we improve the multiplication process between polynomials utilizing the special property of the second multiplicand in each algorithm of the RLizard KEM. Thus, we reduce the required MCU clock cycle consumption. The results show that, compared to the existing code submitted to the National Institute of Standard and Technology (NIST) PQC standardization competition, the required MCU clock cycle is reduced by an average of 52%, and the memory used is reduced by approximately 77%. In this way, we verified that the RLizard KEM works well in our low-end IoT environments.

1. Introduction

In Internet of Things (IoT) environments, devices utilize cryptographic algorithms to communicate securely with each other. To do this, they are required to share a common key to perform encryption efficiently with neighboring nodes. Of the established cryptographic algorithms, the key encapsulation method (KEM) is a method that enables the generation of a shared key between devices that communicate with each other. It is suitable for IoT environments because key sharing is possible at low cost.

Owing to recent developments in the field of quantum computing, existing standard encryption algorithms, such as RSA, Diffie–Hellman, and Elliptic curve cryptography, are expected to be unavailable in the near future. This is because underlying problems associated with existing algorithms can be solved efficiently using quantum computing [1]. For this reason, we need a safe KEM based on hardness problems that are not easily breakable, even with quantum computers.

To find a new cryptographic algorithm that will be used after the advent of quantum computers, the National Institute of Standards and Technology (NIST) is in the process of standardizing post-quantum cryptography (PQC) algorithms. Unfortunately, even though 8-bit microcontroller-based devices with low-cost computing power and small memory size are widely used [2] in IoT environments, PQC standardization does not consider such a constrained environment. In addition, few studies have been conducted to determine the performance improvement of KEMs in such a low-cost environment.

We studied RLizard KEM, which is a Korean standard, from among various KEMs [3]. The security of RLizard relies on the ring learning with errors (RLWE) problem [4] and the ring learning with rounding (RLWR) [5] problem. In [6], they selected ARM Cortex-M3, which is used in high-end IoT environments, for the experiment, and showed that RLizard was more efficient than other PQC KEMs. Unfortunately, even if the method described in [6] is used, a large amount of memory was used in the algorithm, so it cannot be applied to limited environments where the available memory is 16 KB or less.

Therefore, in this study, we investigate an efficient implementation of RLizard in an environment where the memory size is limited and the clock frequency of the MCU is low. First, considering the poor performance of the MCU, we studied a method to improve the computational performance. We improved the original RLizard source code submitted by the NIST competition [7].

First, we used the following method to improve the computational performance. Specifically, we improved the efficiency of polynomial multiplication in the algorithm by utilizing the properties of the polynomials used in multiplication, which is common to all of the algorithms in the scheme.

The first method is to remove all of the multiplication operations between the coefficients of the terms used in the polynomial multiplication. Random polynomials multiplied by the other polynomial used in key generation, encryption, and decryption of RLizard KEMs have only −1, 0, and 1 as coefficients. Therefore, if the coefficient value of the term to be multiplied is 1 or −1, the result is the same as the input value of the other polynomial term to be multiplied or only the sign is changed, so that the multiplication operation can be omitted and the same result can be obtained. We provide an efficient tracking method to determine what coefficient value will be in the next multiplication between coefficients. We were able to replace all of the multiplication operations with either addition or subtraction operations.

The second improvement method is to reduce the number of iterations in the loops used to perform polynomial multiplications.

By utilizing the existing loop and given the fact that the body in the loops is small, we could eliminate approximately 25% of the iterations by adding only a few lines of code. Because the ring $Z\left[X\right]/\left(X^n+1\right)$ is used, when multiplication is performed, the resultant terms with degree of at least n should be reduced using the formula $X^n= -1$. Because of this, when performing multiplication operations, there are two inner loops in polynomial multiplication: the first one is to add the multiplication result to the suitable term of the output polynomial, and the other is to subtract the multiplication result obtained from the above reduction formula.

We appropriately changed the indices of the longer inner loop in order to transfer the burden of some coefficient multiplications to the smaller loop. By doing this, we were able to remove the size of the longer inner loop. This approach results in savings in tens of thousands of comparison operations, which is significant.

In addition, we aim to reduce SRAM usage in order to run RLizard KEM in a low-cost IoT environment; in this study, we focused on electrically erasable programmable read only memory (EEPROM). It was confirmed that all 8-bit ATmega boards have 4 KB of EEPROM. Therefore, we store the public key that occupies the largest space, and which is unchanged in all of the algorithms in KEM. We tried to store it in EEPROM and run it. In addition, because the read/write speed of EEPROM is much slower than that of SRAM, we attempted to minimize the burden of read operations of the public key. As a result, we ran our RLizard in an 8 KB SRAM environment, while minimizing the decrease in performance due to the use of EEPROM.

We compared the performance with the RLizard Code [7] submitted to the NIST PQC standard. Compared with the implementation submitted in the PQC standardization process, the MCU clock cycles used in the key generation, encryption, and decryption processes are reduced by 39%, 55%, and 17%, respectively. In addition, the memory (SRAM) used in the key generation, encryption, and decryption processes are decreased by 74%, 77%, and 78%, respectively. Further, compared with other KEM algorithms implemented in an 8-bit MCU environment, the proposed method is more efficient both in terms of the execution time and the required SRAM size.

The remainder of this paper is structured as follows. Section 2 explains the prior knowledge required to understand the paper, and Section 3 discusses the related studies. Section 4 introduces the methods proposed for improving the performance of RLizard. In Section 5, the experimental results are compared with those of other KEMs. Finally, the conclusion is presented in Section 6.

2. Preliminary

In this section, we explain the prior knowledge and notation used throughout this paper. We explain the notation in Section 2.1, and the RLizard KEM is introduced in Section 2.2.

2.1. Notation

The notations used throughout the rest of this paper are provided in

Table 1. Notation.

Notation	Description
${\mathbb{Z}}_q$	$\mathbb{Z} {{\displaystyle \cap }}^{ }\left(-\frac{q}{2},\frac{q}{2}\right]$
$D^n$	When $D$ is a finite set, $\left(n\ge 1\right) D^n$. means product of space of d
$n$	T dimension of LWE samples, a positive integer
${\mathsf{\Phi }}_{\mathrm{d}}\left(\mathrm{X}\right)$	For an integer d, let ${\mathsf{\Phi }}_{\mathrm{d}}\left(\mathrm{X}\right)$ be the d-th cyclotomic polynomial of degree n = $\mathsf{\Phi }\left(\mathrm{d}\right)$, where $\mathsf{\Phi }\left(·\right)$ is Euler’s totient function which denotes the number of coprime positive integers below the input. In out implementation it means $X^n+1$
$R, R_q$	Cyclotomic ring and its residue ring modulo an integer q: $R= \mathrm{Z}\left[\mathrm{X}\right]/\left({\mathsf{\Phi }}_{\mathrm{d}}\left(\mathrm{X}\right)\right)$ and $R_q={ \mathrm{Z}}_q\left[\mathrm{X}\right]/\left({\mathsf{\Phi }}_{\mathrm{d}}\left(\mathrm{X}\right)\right)$
${\mathcal{D}}_s$	A private key distribution over R
${\mathcal{D}}_r$	An ephemeral secet distribution over R
${\mathrm{DG}}_{\sigma }$	Discrete Gaussian distribution to sample, $\sigma$ as standard deviation
$H_r$	Hamming weight of coefficient vector $r$
$H_s$	Hamming weight of coefficient vector $s$
$t$	$R_t$ is the ring representing the plaintext space.$t$ is used to define the ring.
$p^{\prime },p$	The parameters used to define RLWR instances. They are used as parameters for RLizard.
$q$	The modulus of the ring
$d$	Bit-length of the shared key
$\mathrm{a}\stackrel{\$}{\leftarrow }D$	Sampling $a$ from Distribution $D$
[a, b], [a, b), (a, b], (a, b)	Indicates the range from a to b, a to b-1, a-1 to b, and a-1 to b-1, respectively. We deal with only integers.

.

2.2. RLizard

RLizard KEM is a ring version of Lizard KEM, which is a Korean standard for lattice-based post-quantum cryptography [8]. The security of RLizard is based on the hardness of the RLWE problem [6,7] and the RLWR problem [9], and it is realized by applying the Fujisaki–Okamoto transformation [10] to the RLizard encryption scheme.

RLizard [8] demonstrates the fast performance in encryption using the deterministic rounding operation in the process of sampling errors. In addition, the storage space required to use the public and secret keys required for the encryption and decryption processes is very compact to a few KBs. Because the size of the key is small, it is suitable for applications involving IoT endpoint devices whose memory (SRAM) is of the order of a few KB. RLizard KEM works with three algorithms and the setup step. The setup step, which is referred to as RLizard.KEM.Setup, focuses on setting up the parameters. The key generation algorithm, which is called RLizard.KEM.KeyGen, generates a key pair of an entity participating in the KEM protocol. The key encapsulation algorithm, which is referred to as RLizard.KEM.Encaps, generates a ciphertext that can be used to extract the shared key if the decapsulation is performed with the correct private key. The final decapsulation algorithm, which is referred to as RLizard.KEM.Decaps, decapsulates the ciphertext to extract the shared key.

Algorithms 1–4 present details of the four steps mentioned above.

Algorithm 1. RLizard.KEM.Setup.

Description: Set functions and variables used in the algorithms. Input:$\varnothing$ Output: params = ($n, t, p^{\prime }, p, q, d, {\mathcal{D}}_s, {\mathcal{D}}_r, \sigma$, G, H, H’)

Procedure 1: Choose positive integer $n, t, p^{\prime }, p$ such that $t\le p^{\prime }\le p\le q$. 2: Choose an integer $n$ as the power of 2. 3: Choose the value of $H_s$ and $H_r$ less than $n$. 4: Set the private key distribution ${\mathcal{D}}_s$, ephemeral secret distribution ${\mathcal{D}}_r$. 5. Choose $\sigma$ to create a Gaussian distribution. 6: Choose $d$ for use as the key length. 7: Set the hash functions that do the following calculation - G: $R_p\times$ $R_p\times$ ${\left\{0,1\right\}}^d\times$ $R_t \to$ ${\left\{0,1\right\}}^d$ - H: $R_t$ $\to$ $R_q$ - H′: $R_t$ $\to$ ${\left\{0,1\right\}}^d$

Algorithm 2. RLizard.KEM.KeyGen.

Description: Generate public key and secret key Input: params Output: Public key(pk) = $\left(\mathrm{a}, \mathrm{b}\right)$, Secret key(sk) = $\left(\mathrm{s}, \mathrm{k}\right)$

Procedure 1: Generate polynomial $\mathrm{a}\stackrel{\$}{\leftarrow }{R}_q$, the first element of pk, and polynomial $\mathrm{s}\stackrel{\$}{\leftarrow }{\mathrm{D}}_{\mathrm{s}}^{\mathrm{n}}$, the first element of sk. 2: Generate the second element of sk, $\mathrm{k}\in R_q$ through the random sampling. 3: Compute the second element of pk, $\mathrm{b}$: $\mathrm{b}\stackrel{\$}{\leftarrow }\mathrm{a}\times \mathrm{s}+\mathrm{e}\in R_q$ 4: Return pk = $\left(\mathrm{a}, \mathrm{b}\right)$ and sk = $\left(\mathrm{s}, \mathrm{k}\right)$.

Algorithm 3. RLizard.KEM.Encaps

Description: Generate cipher text and shared secret by using public key Input: params, pk Output: Cipher text(=c) = ($c_1, c_2, d$), Shared secret (=K) = G($c_1, c_2, d, \delta$)

Procedure 1: Generate $\delta$$\stackrel{\$}{\leftarrow }{R}_t.$ 2: Compute $r \stackrel{\$}{\leftarrow }H\left(\delta \right)$ and $d \stackrel{\$}{\leftarrow }H\prime \left(\delta \right)$. 3: Compute elements of c, $c_1, c_2$. - $c_1 \stackrel{\$}{\leftarrow }\left(\frac{p}{q}\right)\times a\times r \in R_p$ - $c_2\stackrel{\$}{\leftarrow }\left(\frac{p^{\prime }}{t}\right)\times \delta +\left(\frac{p^{\prime }}{q}\right)\times b\times r \in R{\prime }_{p }$ 4: Compute K = G$(c_1, c_2, d, \delta$). 5: Return K and c = $\left(c_1, c_2, d\right)$.

Algorithm 4. RLizard.KEM.Decaps.

Description: Generate a shared key by decrypting a cipher text. Input: params, sk, c Output: K

Procedure: 1: Compute ${\delta }^{\prime } \stackrel{\$}{\leftarrow }\left(\frac{t}{p}\right)\times (\left(\frac{p}{p^{\prime }}\right)\times c_2+s\times c_1\in R_t$. 2: Compute $r\prime \stackrel{\$}{\leftarrow }H\left(\delta \prime \right)$ and $d\prime \stackrel{\$}{\leftarrow }H\prime \left(\delta \prime \right)$. 3: Compute elements of c’, $a^{\prime }, b\prime$. - $a^{\prime }\stackrel{\$}{\leftarrow }\left(\frac{p}{q}\right)\times a\times r \in R_p$ - $b^{\prime }\stackrel{\$}{\leftarrow }\left(\frac{p^{\prime }}{t}\right)\times {\delta }^{\prime }+\left(\frac{p^{\prime }}{q}\right)\times b\times r\prime \in R{\prime }_p$ 4: Return K - If $c\ne c^{\prime }$, return K $=G\left(c_1, c_2, d, k\right)$. - Else if $c=c^{\prime }$, return K$=G\left(c_1, c_2, d, {\delta }^{\prime }\right)$.

3. Related Work

This section describes the related studies. We focus on research related to the implementation of PQC algorithms in the IoT environment.

In 2014, the authors in [11] implemented an authentication method in a very limited environment using the smart card as a target environment, and the NTRU algorithm and LP-LWE [12] algorithm in ARM7TDMI and AVR Atmega128. However, only the lattice-based authentication method is covered, and not KEM. In 2015, Zhe Liu et al. [13] presented a method that effectively implemented Regev’s RLWE-based encryption method using the ATxmega128A1 processor, which is an 8-bit CPU environment. In order to accelerate the reduction operation, the shift-add-multiply subtract-subtract (SAMS2) method and the byte-scanning technology are applied to minimize the execution time to increase the efficiency of the discrete Gaussian sampler based on the Knuth–Yao random walk algorithm [14]. However, it did not address memory optimization, and KEM was not covered. In 2017, Oscar et al. [15] presented a method for improving the performance of the NTRUEncryption algorithm in ARM Cortex-M0. To improve the speed of multiplication of polynomials, which consumes the most CPU cycles among operations, the product form [16] was applied to polynomial multiplication to show faster operation than conventional algorithms. However, an 8-bit MCU environment was not considered. Angshuman et al. [17] implemented both memory and speed-optimized versions of the SABER scheme in the ARM Cortex-M4 and Cortex-M0 environments. However, the 8-bit environment was not considered. James et al. [18] implemented the FrodoKEM algorithm in the ARM Cortex-M4 environment in 2018. By improving the performance through the design of field-programmable gate arrays (FPGAs) for fast calculation, the required clock cycle is improved to use only approximately 45% compared to the previously implemented FrodoKEM algorithm. However, for the same level of security, approximately 300 million cycles are required to run the algorithms, which is over 90 times that of Kyber [19]. In 2018, Saarinen et al. [20] implemented the Round5 algorithm targeting the embedded environment. However, they only targeted the Cortex-M4 environment, and the 8-bit environment was not considered. In 2019, Cheng et al. [21] implemented a hash function that was optimized in terms of the assembly language for NTRU Prime KEM, and it exhibited improved performance in an 8-bit AVR ATmega1284 environment. However, the maximum memory usage of the algorithm is 11,478 bytes, and the environment where the memory size is approximately 8 KB is not considered. In 2020, Shahriar et al. [22] implemented RLWE encryption algorithms in the microprocessor of the AVR ATxmega128A1 and ARM Cortex-M0 in a limited environment using the binary Ring-LWE algorithm. However, binary Ring-LWE requires many more bits compared to the Ring-LWE with ternary bits, and it is therefore not suitable for memory constraint devices.

Many studies have implemented and optimized KEM using grid-based encryption in an IoT environment. However, many studies have been conducted on the 32 bit-ARM Cortex-M series, and they have not considered more limited environments such as 8-bit microprocessors. However, the market for 8-bit IoT devices is also growing, and KEM’s performance improvement for these devices is also important [2]. Therefore, it is necessary to provide an efficient KEM by performing research on increasing speed and reducing memory usage in constrained environments.

4. Proposed Methods

This section shows how to reduce the number of required clock cycles and memory usage in the ATmega 8-bit environment. To support the 128-bit level of security, we assume that the following parameters in

Table 2. The parameters used in this work (for 128-bit security).

Parameter	Value	Parameter	Value	Parameter	Value
$n$	1024	log $p$	8	$H_s$	128
log $q$	10	$H_r$	128

are used in our implementation.

4.1. Representing A Sprase Polynomial with Coefficients −1,0, or, 1

We describe the data structure used for multiplication in the target implementation [7]. Because this is also used in the proposed method, its understanding is essential to understand the proposed method. Polynomial multiplication is used in the fourth step of the key generation algorithm (Algorithm 2) described in Section 2, the third step of the encapsulation algorithm (Algorithm 3), and the third step of the decapsulation algorithm (Algorithm 4).

In these polynomial multiplications, one polynomial ($s$ in Algorithm 2 and $r$ in Algorithms 3 and 4) has a special form. We explain this case using $r$.

Figure 1 shows $R_{idx}$, which is an array representing polynomial $r$. This array has the degrees of the terms whose coefficient values are 1 in front, in order from the largest to the smallest. Conversely, the degrees of the terms with −1 as a coefficient are stored in opposite directions starting from the last. When creating the polynomial $r$, the number of terms with 1 and −1 is fixed at $H_r$, so we can set the size of the array to it. In addition, the index of the array in which the term with the coefficient value of −1 starts is stored in a variable called neg_start.

In the key generation process, the $S_{idx}$ array is created for the polynomial $s$ in the same process, the size of the array is fixed to $H_s$, and a variable called neg_start is set with the same meaning as above.

4.2. Proposed Methods for Improving the Speed of RLizard

In this subsection, we propose two ways to reduce the required MCU clock cycles. Before discussing the details of the description, we explain the meaning of the symbols used in this and subsequent subsections.

$a$: An n-order polynomial, and coefficients are values that are sampled with a uniform distribution among the integers between $-\frac{q}{2}+1$ and $\frac{q}{2}$ (inclusive).

$c_1$: An array representing the polynomial to hold the result of $a\times r$. Depending on the algorithm used, it can finally be a ciphertext or information used to verify the ciphertexts in decapsulation.

The above two arrays have coefficients as values, and the index is the degree. Thus, their size is $n$.

$H_r$: this represents HR in our code.

The “original algorithm” in Figure 2 represents the implementation of [7], and the “improved algorithm” depicts the proposed implementation in the figure. Because the previous implementation did not use neg_start, it was not known whether 1 or −1 would be included in the branch variable. Therefore, the branch value was multiplied, as in the code of the existing implementation. We improved this and finally eliminated the multiplication by dividing the loop into two and replacing the branch value with a constant using neg_start so that the branch value can be known before the inner loop starts. Using the above method, the process of multiplication by $n\times H_r$ times has been eliminated. This has the effect of removing 131,072 multiplication operations from the above-described parameters. Moreover, because the multiplication operation generally requires three times as many cycles as the addition, the effect of removing them is very large.

Here, we describe the second method. As can be seen in lines 2 to 7 of the “Improved algorithm” in Figure 2, there are two inner loops: the first one executes the 4th–5th lines iterated with the index value in the range of [0,n-deg), and the second executes the 6th–7th lines iterated with the index value in the range of [n-deg,n].

Of the two inner loops, we reduce the number of iterations for which the number of iterations is longer by the number of iterations in the shorter loop. Then, we add the body of the longer loop in the shorter loop to compensate for the reduction in the number of iterations in the longer loop. Because the code size of the bodies in both loops is small, this works well without consuming a significant amount of memory.

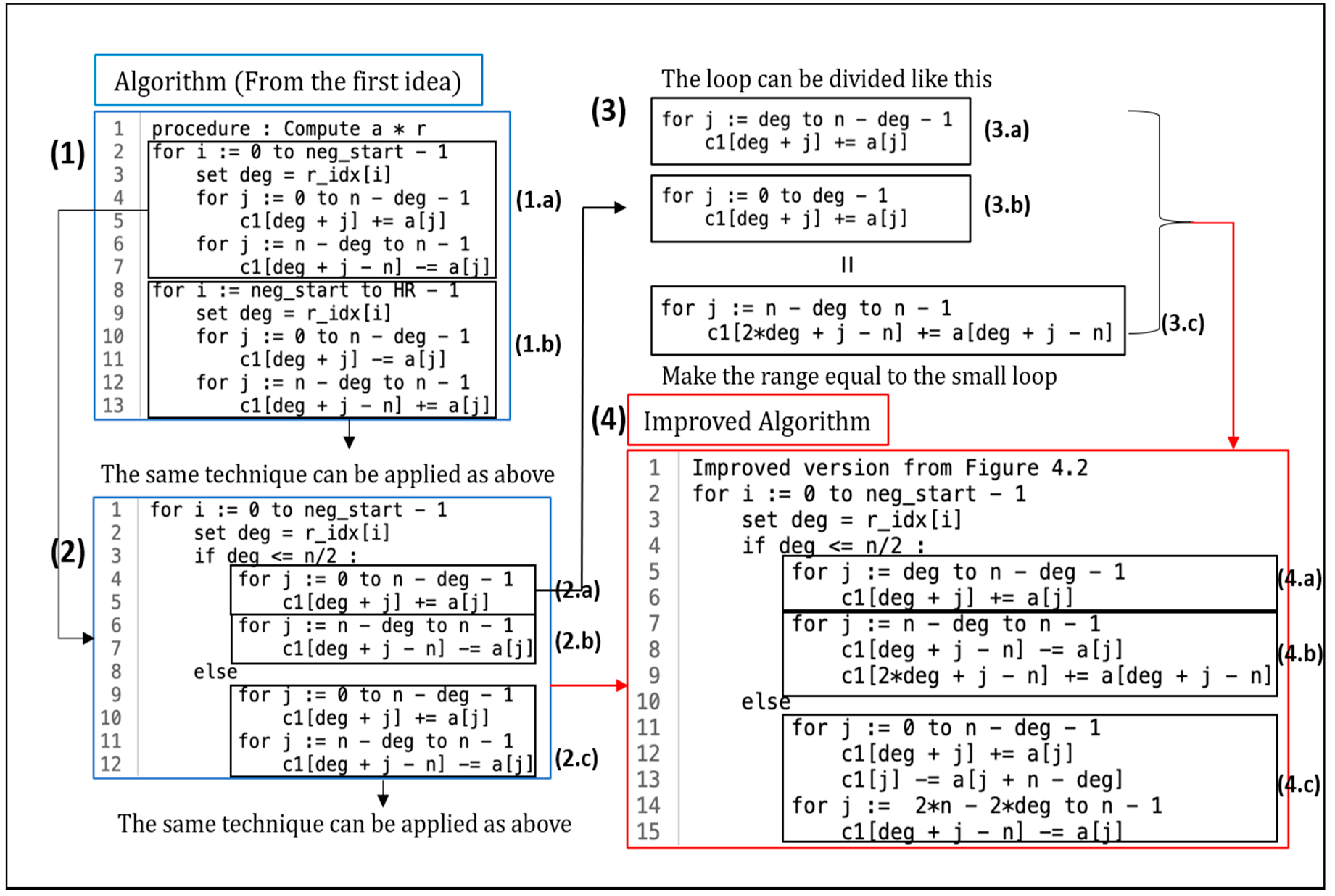
Figure 3 describes how the code changes from the form of the first proposed method that was applied to the form of the second proposed method that was applied, while preserving their functions.

First, part (1.a) in the figure was divided into parts (2.a) and (2.b), and part (2.c) in order to process differently depending on whether deg is less than or equal to n/2. It is important to consider whether deg is less than or equal to n/2. This is because of the two inner loops described in (1.a), the loop that has a large number of iterations depends on the deg value.

For convenience, we focus on parts (2.a) and (2.b) of the figure to explain only the cases where deg is greater than or equal to n/2. The loop in Figure (2.a) can be further divided into two loops, i.e., (3.a) and (3.b). We also transformed the loop (3.b) into (3.c), preserving its function by simply modifying the range of values of the iteration variable and adjusting the formula used as the indices of arrays c1 and a. Finally, (4.b) can be constructed by adding the body of (3.c) to the body of the existing (2.b) loop. In conclusion, it can be seen that (2.a) and (2.b) perform the same operation as (4.a) and (4.b), but the number of iterations of the loop decreased by deg.

Based on the above improvement, if deg is less than n/2, the inner loops (4.a) and (4.b) that are iterated n times in the original implementation are iterated by only n-deg times, and if deg is greater than n/2, it is iterated by deg times, as in (4.c). Because the deg value has an average value of n/2 and is selected from a uniform distribution in [0,n−1], the average number of executions of the entire loop is reduced to $\left(\frac{3n}{4}\right)\times H_r$, considering the outer loop. By reducing the number of iterations using the above method, we can speed up the multiplication of polynomials.

Algorithm 5 represents the description of the final version of the proposed implementation. All of the ideas for computational efficiency are applied to the pseudo code given in Algorithm 5. The r_idx array is explained in Section 4.1. Also, the variable neg_start is also explained in Section 4.1.

The algorithm consists of double loops. By applying the idea of (Figure 2), the multiplication process could be eliminated because the coefficient of polynomial $r$ was 1 in lines 2–15 and −1 in lines 16–29. Divide the loop based on the coefficient of r, then take out the order of polynomial $r$ from the line 3, 17 and save it in the deg. In addition, by applying the idea of (Figure 3), some of the computations to be done in the larger loop were modified to be done in the smaller loop. Thus, the multiplication operation of the polynomial is performed in inner loops lines 5–9, lines 11–15, lines 19–23, and lines 25–29. As a result, the result of multiplication of polynomials through double loops is stored in the c1 array.

4.3. SRAM Usage Improvement in 8-Bit ATmega Environment

The RLizard [7] implementation submitted to NIST uses up to 22 KB of memory. This is not a problem when running in a desktop environment. However, if we only have a few KB of SRAM, the code cannot be executed as is. Therefore, it is important to secure more SRAM space that can be used while running RLizard in order for it to run in a constrained environment where the SRAM size is about 8–16 KB.

Algorithm 5. The proposed implementation.

Description: Multiplication of two polynomials $a$, which is stored in the array a, and $r$, which is stored in the array r_idx. Please refer to Figure 1 to obtain the information about r_idx. Input: the arrays a and r_idx Output: the array c1 that contains the result of multiplication.

Procedure: 01: for i: = 0 to neg_start − 1       //Refer to Figure 1 for neg_start 02:  set deg = r_idx[i] 03:  if deg <= n/2: 04:    for j: = deg to n − deg − 1 05:       c1[deg + j] += a[j] 06:    for j: = n − deg to n − 1 07:       c1[deg + j − n] -= a[j] 08:       c1[2*deg + j − n] += a[deg + j − n] 09:  else 10:    for j: = 0 to n − deg − 1 11:       c1[deg + j] += a[j] 12:       c1[j] −= a[j + n − deg] 13:    for j: = 2*n − 2*deg to n −1 14:       c1[deg + j − n] −= a[j] 15: for i: = neg_start to HR − 1 16:  set deg = r_idx[i] 17:  if deg <= n/2: 18:    for j: = deg to n − deg − 1 19:       c1[deg + j] −= a[j] 20:    for j: = n − deg to n − 1 21:       c1[deg + j − n] += a[j] 22:       c1[2*deg + j − n] −= a[deg + j − n] 23:  else 24:    for j: = 0 to n − deg − 1 25:       c1[deg + j] −= a[j] 26:       c1[j] += a[j + n − deg] 27:    for j: = 2*n − 2*deg to n −1 28:       c1[deg + j − n] += a[j] 29:  return

The pk generated in the key generation process of RLizard KEM (Algorithm 2) is used to generate a ciphertext containing the shared key in the key encapsulation process of RLizard KEM (Algorithm 3). pk consists of two polynomials ($a,b$), and the coefficient of each has a length of 9 bits. Therefore, when $n$ = 1024, pk occupies slightly more than 2 KB of memory. This is a very large size considering the environment where the SRAM size is assumed to be in the range between 8–16 KB. Fortunately, we have found that all ATmega 8-bit environments have EEPROMs with sufficient size.

Table 3. 8-bit AVR products whose SRAM size is 8–16 KB.

8-bit Microcontroller	Product	Percentage of ATmega MCUs with 8–16 KB SRAM and 4 KB EEPROM
8-Bit AVR	ATmega1284, ATmega1284P, ATmega1280, ATmega1281, ATmega2560, ATmega2561, ATmega640, ATmega128, ATmega128A	100%

presents a list of the products mentioned [23].

We store pk in the EEPROM and use it. Because the value of pk does not change during the algorithm execution process, it is suitable for storing in EEPROM, where the update time is very slow. Using this, we are able to secure an additional SRAM of 2 KB or more.

In addition, 640 bytes of memory were saved by storing all constants used in the implementation of flash memory. Furthermore, by optimizing the bit length of the random seed used in Gaussian sampling employed in [4], it is possible to save a total of 2 KB of SRAM usage.

In conclusion, we reduced the size of the required SRAM to run the proposed method to 6576 bytes. Therefore, the RLizard can work well in the 8–16 KB SRAM environment that we aim to achieve.

5. Performance Evaluation

We analyzed the performance of the proposed implementation. We used ATmega2560 [24,25], which is an 8-bit CPU environment, as the implementation environment, to prove the suitability of RLizard in a more restrictive environment, unlike [6], where the performance was evaluated on 32-bit Cortex-M3. To obtain the required clock cycles correctly, we ran each algorithm 10,000 times, and then averaged their required clock cycles. In addition, the maximum usage of SRAM was also measured.

We compared our implementation with that submitted to the NIST PQC competition [7]. Unfortunately, because of its high SRAM usage, it did not work well in our environment. Therefore, the performance and SRAM usage of the existing implementation were measured in another environment of 32-bit Cortex-M0+. The details of the environment used for the performance analysis are shown in

Table 4. Environment for performance evaluation.

Arch.	SRAM	Flash Memory	EEPROM	Clock Speed
32-bit ARM Cortex-M0+	32 KB	256 KB	NONE	48 MHz
8-bit AVR ATmega2560	8 KB	256 KB	4 KB	16 MHz

.

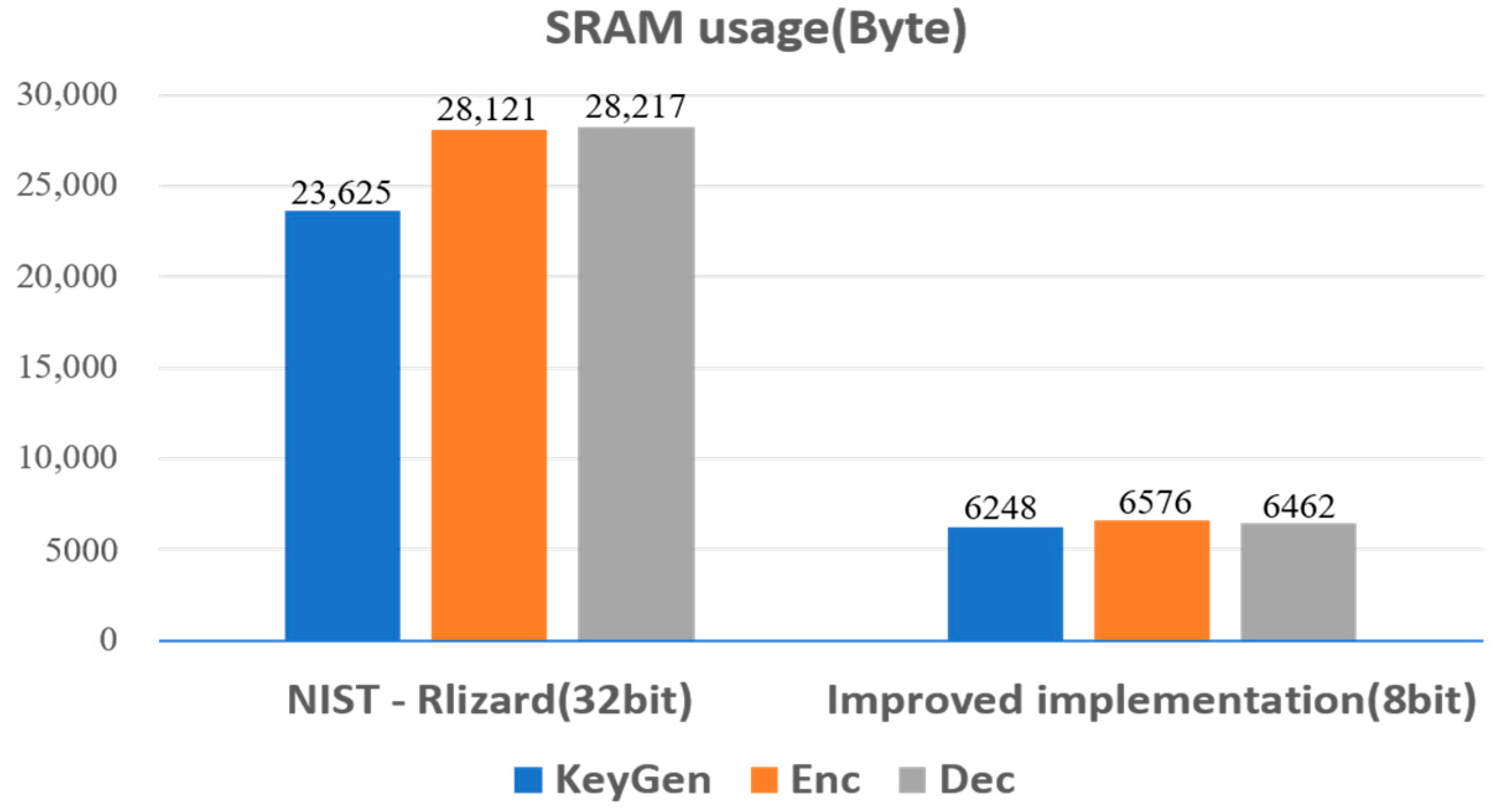
The performance analysis result is shown in the Figure 4, we can find that, compared to the implementation in [7], the proposed implementation requires 39%, 55%, and 17% fewer MCU clock cycles in key-generation, encapsulation, and decapsulation, respectively. As shown in Figure 5, the maximum SRAM usage is decreased in the proposed implementation to only 6248 bytes, 6576 bytes, and 6462 bytes in key-generation, encapsulation, and decapsulation, respectively. The required SRAM is small enough to be used in environments where the SRAM size is even 8 KB.

Table 5. Comparison with other implementations.

Work	Device Name	$\mathbf{Clock} \mathbf{Cycles} (\times 1000)$				SRAM Usage (Byte)
		Key Gen.	Enc.	Dec.	Total	Key Gen.	Enc.	Dec.
Our work	ATmega2560	1980	1978	6339	10,297	6248	6576	6462
[11] NTRU	ATmega64	76,444	2008	1390	79,842	13,721	13,721	13,721
[21] NTRU Prime	ATmega1284	-	8160	15,602	23,762	-	8694	11,478

shows the comparison with the implementation of other KEMs in an 8-bit MCU environment. As shown in the table, our implementation performs the best compared with those in [11,21] in terms of both the required clock cycles and the SRAM usage. In addition, the implementations in [11,21] cannot be used for our target environment whose SRAM size is 8–16 KB because the required SRAM is much greater than 8 KB.

The execution times of the improved algorithms are 118.0 ms (KeyGen), 117.8 ms (Enc.), and 377.8 ms (Dec.) on the same environment as Figure 4. Since they are less than a second, in terms of the computation time, it seems tolerable.

6. Conclusions

With the advent of the IoT era, there is a critical need to address security issues. In this study, we propose some methods with which IoT devices with a small amount of computational power and available SRAM can use KEM for data security. Focusing on the fact that 8-bit ATmega MCUs have an EEPROM of sufficient size, we proposed a method that allows the RLizard KEM to operate even in low-spec IoT devices with an SRAM size of 8–16 KB by maximizing the use of EEPROM and flash memory. In addition, the execution time of the RLizard algorithm has been improved to overcome the performance limitations of low-end IoT MCUs. Furthermore, by performing experiments, it was confirmed that the proposed method works efficiently in an environment with 8 KB SRAM. We hope that the results of this study can contribute to improving the security of low-cost IoT devices.