A Noniterative Radix-8 CORDIC Algorithm with Low Latency and High Efficiency
Abstract
:1. Introduction
2. Conventional CORDIC Rotator Algorithm
3. Noniterative Radix-8 CORDIC Algorithm
3.1. Narrow Input Angle θ Range
3.2. Explicit Formula of Convergence
- Observation (1): If , when , , which can be ignored.
- Observation (2): If or , when , , which can be ignored.
3.3. Scale Factor
3.4. Transformation of the Inputs and
- If , then .
- If , then .
- If , then .
- If , then .
- If , then .
- If , then .
4. Implementation and Analysis
4.1. Noniterative Implementation
- Compute via rounding .
- Compute via the constant values stored in registers and one subtractor in Equation (21).
- Compute by directly fetching bits from as in Equation (25).
- Compute A and B as in Equation (20) using at the third step, all of which are small integers. For example, is a 2-bit unsigned integer, and is a 5-bit signed integer, while is an unsigned integer no greater than 3-bit.
4.2. Resource Utilization and Performance Analysis
4.2.1. RU Comparison of Conventional CORDIC Algorithms
4.2.2. Performance Comparison of Newly Developed CORDIC Algorithms
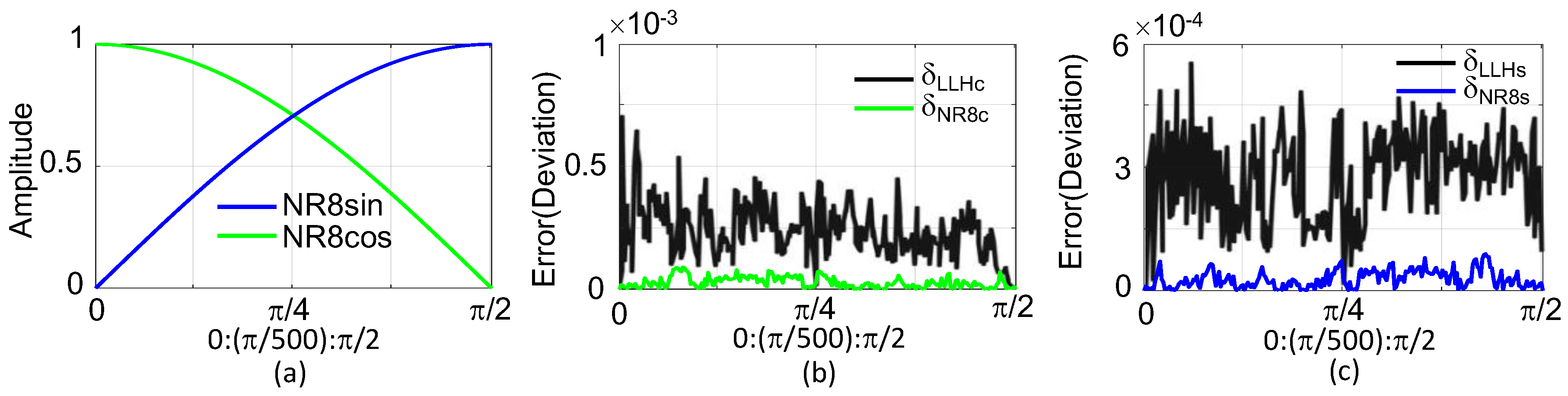
4.3. Error Analysis
4.3.1. Comparisons with Low-Latency Hybrid (LLH) CORDIC
| Algorithm 1. The descriptive codes of the NR-8 CORDIC. |
4.3.2. Comparison of Conventional CORDIC Algorithms
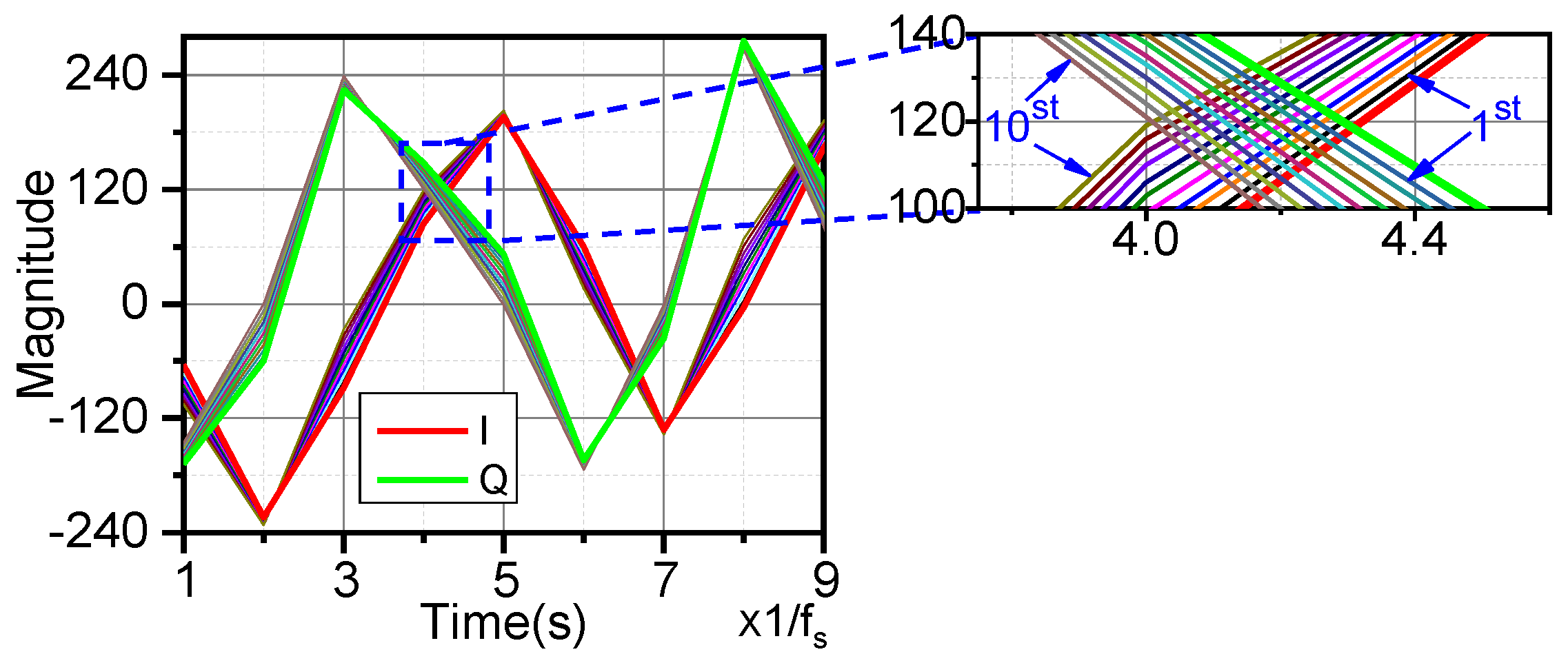
5. Application of the NR-8 CORDIC Algorithm to DBF
- , the phase angle of the nth delay beam or .
- , the phase difference between the nth delay beam and the original echo .
- = the desired steering angles.
- = the error of the phase shift.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fang, L.; Xie, Y.; Li, B.; Chen, H. Generation scheme of chirp scaling phase functions based on floating-point CORDIC processor. J. Eng. 2019, 2019, 7436–7439. [Google Scholar] [CrossRef]
- Vyas, P.; Vachhani, L. CORDIC-Based Azimuth Calculation and Obstacle Tracing via Optimal Sensor Placement on a Mobile Robot. IEEE/ASME Trans. Mechatron. 2016, 21, 2317–2329. [Google Scholar] [CrossRef]
- Wong, C.C.; Liu, C.C. FPGA realisation of inverse kinematics for biped robot based on CORDIC. Electron. Lett. 2013, 49, 332–334. [Google Scholar]
- Lee, H.; Oh, K.; Cho, M.; Jang, Y.; Kim, J. Efficient Low-Latency Implementation of CORDIC-Based Sorted QR Decomposition for Multi-Gbps MIMO Systems. IEEE Trans. Circuits Syst. II Express Brief 2018, 65, 1375–1379. [Google Scholar] [CrossRef]
- Jun, M.; Parhi, K.K.; Deprettere, E.F. Annihilation-Reordering Look-Ahead Pipelined CORDIC-Based RLS Adaptive Filters and Their Application to Adaptive Beamforming. IEEE Trans. Signal Process. 2000, 48, 2414–2431. [Google Scholar] [CrossRef]
- Nikolov, S.I.; Jensen, J.A.; Tomov, B.G. Fast parametric beamformer for synthetic aperture imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2008, 55, 1755–1767. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pilato, L.; Fanucci, L.; Saponara, S. Real-Time and High-Accuracy Arctangent Computation Using CORDIC and Fast Magnitude Estimation. Electronics 2017, 6, 22. [Google Scholar] [CrossRef] [Green Version]
- Lakshmi, B.; Dhar, A.S. CORDIC architectures: A survey. VLSI Des. 2010, 2010, 794891. [Google Scholar] [CrossRef]
- Ylostalo, J. Function approximation using polynomials. IEEE Signal Process. Mag. 2006, 23, 99–102. [Google Scholar] [CrossRef]
- Ercegovac, M.D.; Lang, T.; Muller, J.M.; Tisserand, A. Reciprocation, square root, inverse square root, and some elementary functions using small multipliers. IEEE Trans. Comput. 2000, 49, 628–637. [Google Scholar]
- Volder, J.E. The CORDIC Trigonometric Computing Technique. IEEE Trans. Electr. Comput. 1959, 8, 330–334. [Google Scholar] [CrossRef]
- Meher, P.K.; Valls, J.; Juang, T.B.; Sridharan, K.; Maharatna, K. 50 Years of CORDIC: Algorithms, Architectures, and Applications. IEEE Trans. Circuits Syst. I Regul. Pap. 2009, 56, 1893–1907. [Google Scholar] [CrossRef] [Green Version]
- Maharatna, K.; Banerjee, S.; Grass, E.; Krstic, M.; Troya, A. Modified virtually scaling-free adaptive CORDIC rotator algorithm and architecture. IEEE Trans. Circuits Syst. Video Technol. 2005, 15, 1463–1474. [Google Scholar]
- Antelo, E.; Villalba, J.; Bruguera, J.D.; Zapata, E.L. High performance rotation architectures based on the radix-4 CORDIC algorithm. IEEE Trans. Comput. 1997, 46, 855–870. [Google Scholar] [CrossRef] [Green Version]
- Rudagi, J.; Subbaraman, S. Comparative Analysis of Radix-2, Radix-4, Radix-8 CORDIC Processors. In Proceedings of the 2017 International Conference on Inventive Computing and Informatics (ICICI), Coimbatore, India, 23–24 November 2017; pp. 378–382. [Google Scholar]
- Shukla, R.; Ray, K. Low latency hybrid CORDIC algorithm. IEEE Trans. Comput. 2014, 63, 3066–3078. [Google Scholar] [CrossRef]
- Wu, C.S.; Wu, A.Y.; Lin, C.H. A High-Performance/Low-Latency Vector Rotational CORDIC Architecture Based on Extended Elementary Angle Set and Trellis-Based Searching Schemes. IEEE Trans. Circuits Syst. II Analog Digit. Signal Process. 2003, 50, 589–601. [Google Scholar]
- DSP48 Macro v3.0, Xilinx Inc., USA. 2015. Available online: https://www.xilinx.com/support/documentation/ip_documentation/xbip_dsp48_macro/v3_0/pg148-dsp48-macro.pdf (accessed on 12 August 2020).
- UltraScale Architecture Configurable Logic Block User Guide. Xilinx Inc., USA. 2017. Available online: https://www.xilinx.com/support/documentation/user_guides/ug574-ultrascale-clb.pdf (accessed on 12 August 2020).
- Fischman, M.A.; Le, C. Digital beamforming developments for the joint NASA/Air Force Space Based Radar. In Proceedings of the IGARSS 2004, 2004 IEEE International Geoscience and Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004; pp. 687–690. [Google Scholar]
- Lialios, D.I.; Ntetsikas, N.; Paschaloudis, K.D.; Zekios, C.L.; Georgakopoulos, S.V.; Kyriacou, G.A. Design of True Time Delay Millimeter Wave Beamformers for 5G Multibeam Phased Arrays. Electronics 2020, 9, 1331. [Google Scholar] [CrossRef]
- Cao, Y.X.; Xiao, W.A.; Jia, J. A Cordic-based Acceleration Method on FPGA for CNN Normalization layer. In Proceedings of the 2020 International Conference on High Performance Big Data and Intelligent Systems (HPBD&IS), Shenzhen, China, 23 May 2020. [Google Scholar]
- Parmar, Y.; Sridharan, K. A Resource-Efficient Multiplierless Systolic Array Architecture for Convolutions in Deep Networks. IEEE Trans. Circuits Syst. II Express Brief 2020, 67, 370–374. [Google Scholar] [CrossRef]








| Regions | |||
|---|---|---|---|
| Algorithms | CLB LUTs a (242,400)/UT (%) | FF (484,800)/UT (%) | DSPs (1920)/UT (%) | Clock b Latency | Power (Dynamic/Static) (W) |
|---|---|---|---|---|---|
| R-2 [11] | 1095/0.45 | 785/0.16 | 2/0.1 | 17 | 0.071/0.479 |
| R-4 [12] | 975/0.4 | 329/0.07 | 5/0.26 | 9 | 0.066/0.478 |
| R-8 [15] | 880/0.36 | 234/0.05 | 6/0.31 | 7 | 0.065/0.478 |
| NR-8 | 300/0.12 | 98/0.02 | 5/0.21 | 3 | 0.031/0.478 |
| Algorithms | Conventional CORDIC [12,13,15] | High-Performance R-4 [14] | Low-Latency Hybrid (LLH) [16] | High-Performance/Low-Latency [17] | Proposed NR-8 CORDIC | ||
|---|---|---|---|---|---|---|---|
| R-2 | R-4 | R-6 | |||||
| Iterations | m + 1 | (1/2)m | (3/8)m | m/2 | (3/8)m+1 | - | 0 |
| Complexity a | O(2m) | O(2m) | O((15/8)m) | O(m) | O(3m) | 16 Adders/28 Adders (m = 16) | |
| Timing (Critical path) b | Tadd/sub | Tadd/sub | Tadd/sub | Tadd/sub | 2Tadd/sub | 2Tadd/sub | 2Tadd/sub |
| Latency (m = 16) | 17 | 9 | 7 | 8 | 6 | 68TFA/26TFA c | 3 |
| Beams | (I,Q) | Beam_1 | Beam_2 | Beam_3 | Beam_4 | Beam_5 | Beam_6 | Beam_7 | Beam_8 | Beam_9 | Beam_10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (°) | −129.305 | −127.807 | −126.354 | −124.814 | −123.361 | −121.804 | −120.241 | −118.812 | −117.344 | −115.858 | −114.290 |
| (°) | 0 | 1.498 | 2.951 | 4.491 | 5.944 | 7.501 | 9.064 | 10.493 | 11.961 | 13.447 | 15.015 |
| (°) | 0 | 1.5 | 3.0 | 4.5 | 6.0 | 7.5 | 9.0 | 10.5 | 12.0 | 13.5 | 15.0 |
| (°) | 0 | −0.002 | −0.049 | −0.009 | −0.056 | 0.001 | 0.064 | −0.007 | −0.039 | −0.053 | 0.015 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, W.; Xu, F. A Noniterative Radix-8 CORDIC Algorithm with Low Latency and High Efficiency. Electronics 2020, 9, 1521. https://doi.org/10.3390/electronics9091521
Tang W, Xu F. A Noniterative Radix-8 CORDIC Algorithm with Low Latency and High Efficiency. Electronics. 2020; 9(9):1521. https://doi.org/10.3390/electronics9091521
Chicago/Turabian StyleTang, Wenming, and Feng Xu. 2020. "A Noniterative Radix-8 CORDIC Algorithm with Low Latency and High Efficiency" Electronics 9, no. 9: 1521. https://doi.org/10.3390/electronics9091521
APA StyleTang, W., & Xu, F. (2020). A Noniterative Radix-8 CORDIC Algorithm with Low Latency and High Efficiency. Electronics, 9(9), 1521. https://doi.org/10.3390/electronics9091521





